State-based Peridynamic Modeling for Dynamic Fracture ofPlane Stress

Ha Youn Doh

doi:10.7734/COSEIK.2015.28.3.301

Preview

Journal of the Computational Structural Engineering Institute of Korea. 2015. 301-307
https://doi.org/10.7734/COSEIK.2015.28.3.301

State-based Peridynamic Modeling for Dynamic Fracture ofPlane Stress

평면응력 문제의 상태 기반 페리다이나믹 동적파괴 해석 모델링

Ha Youn Doh

https://static.apub.kr/journalsite/sites/jcoseik/2015-028-03/09TK062015280306/images/coresp.png

Department of Naval Architecture and Ocean Engineering

• 본 논문에 대한 토의를 2015년 6월 30일까지 학회로 보내주시면 2015년 8월호에 토론결과를 게재하겠습니다.

^*Corresponding Author : ydha@kunsan.ac.kr

License:

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

결합 기반 페리다이나믹 모델을 통해 다양한 동적취성파괴 현상을 해석할 수 있었지만, 결합 기반 모델은 다양한 재료 구성 모델을 표현하는데 여러 한계를 보여왔다. 특히 결합 기반 모델은 각 결합들이 서로 독립적으로 작용하도록 가정하였기 때문에 3차원 모델에서 포아송비가 1/4로 고정되며 전단 변형이 표현되지 못하고 체적 변형만이 모사되는 문제점이 있다. 본 연구에서는 상태 기반 페리다이나믹 모델을 통한 동적취성파괴 해석을 제시한다. 상태 기반 모델은 일종의 일반화된 페리다이나믹 모델로서 일반적인 재료 구성모델로부터 직접 페리다이나믹 재료 모델을 구성한다. 또한 연결된 모든 결합의 변형을 통해 각 절점의 재료 응답이 결정되기 때문에 체적 및 전단 변형이 모두 표현된다. 본 논문에서는 선형 탄성체에 대해서 상태 기반 평면 응력 페리다이나믹 모델을 소개하고 상태 기반 모델에 적합한 손상 모델에 대해 논의한다. 페리다이나믹 비국부 영역을 축소시키는 δ-수렴성 연구를 통해 동적파괴 모델을 검증하고 상태 기반 모델이 동적 균열 전파를 모델링하는데 적합함을 확인하였다.

A bond-based peridynamic model has been shown to be capable of analyzing many of dynamic brittle fracture phenomena. However, there have been issued limitations on handling constitutive models of various materials. Especially, it assumes bonds act independently of each other, so that Poisson’s ratio for 3D model is fixed as 1/4 as well as taking only account the bond stretching results in a volume change not a shear change. In this paper a state-based peridynamic model of dynamic brittle fracture is presented. The state-based peridynamic model is a generalized peridynamic model that is able to directly use a constitutive model from the standard theory. It permits the response of a material at a point to depend collectively on the deformation of all bonds connected to the point. Thus, the volume and shear changes of the material can be reproduced by the state-based peridynamic theory. For a linearly elastic solid, a plane stress model is introduced and the damage model suitable for the state-based peridynamic model is discussed. Through a convergence study under decreasing the peridynamic nonlocal region(δ-convergence), the dynamic fracture model is verified. It is also shown that the state-based peridynamic model is reliable for modeling dynamic crack propagatoin.

키워드

상태 기반 페리다이나믹 모델, 동적파괴, 손상 모델, δ-수렴성

State-based peridynamic model, dynamic fracture, damage model, δ-convergence

MAIN

1. 서 론

결합 기반 페리다이나믹 모델(bond-based peridynamic model)은 유한한 범위 내에 흩어져 있는 절점들이 원거리 상관관계(long-range interaction)로 상호작용하는 연속체 기반 비국부(nonlocal) 해석 모델로써 기존 연속체 기반 모델들이 재료파괴를 해석하는 한계를 극복하기 위해 제안되었다(Silling, 2000). 유한요소 모델과 같은 국부(local) 해석 모델과 달리 페리다이나믹에서는 재료 및 거동의 불연속성을 해석하기 위해 운동방정식에서 응력 미분을 절점력들의 적분으로 대체한다. 절점 x와 시간 t에서 결합 기반 페리다이나믹 운동방정식은 다음과 같다.

ρ \overset{. .}{u} (x, t) = \int_{H_{x}}^{} f (u (x', t) - u (x, t),x' - x) d x' + b (x, t)

(1)

여기서, f는 범위 H_x에 속한 두 절점 x'과 x로 구성되는 페리다이나믹 결합(bond) 간의 상호작용력(pairwise force) 함수이며, u는 변위 벡터이다. b는 체적력, ρ는 밀도이다. 동적취성파괴 해석을 위한 결합 기반 페리다이나믹 모델에 주로 사용되는 미소탄성 재료(Silling, 2000)는 다음과 같이 상호작용력과 선형 미소탄성 포텐셜 ω의 관계로부터 다음과 같이 정의된다.

f (η,ξ) = \frac{\partial w (η,ξ)}{\partial η}

(2)

여기서, ε=x'-x, η=u'-u이다.

결합 기반 페리다이나믹 모델은 비교적 간단한 모델링으로 동적취성파괴 현상을 엄밀하게 모사할 수 있었다(Ha and Bobaru, 2010; Ha and Cho, 2011; Ha and Bobaru, 2011; Hu et al., 2011; Bobaru et al., 2012; Hu et al., 2012; Ha and Cho, 2012). 그러나 결합 기반 모델은 일반적으로 사용되는 구성 모델(constitutive model)을 사용하지 않고 비국부 영역 내에서 개별 결합들의 상호 작용을 가상의 스프링처럼 가정하여 모델링하기 때문에 간단한 형태의 탄성 모델 외에 다양한 재료 모델의 구현이 어렵다. 또한 개별 결합들이 서로 독립적으로 상호작용하기 때문에 포아송비가 1/4(3차원 모델 기준)로 한정되는 문제점이 있다. 보다 일반화되고 엄밀한 모델 구성 및 해석을 위해 상태 기반 페리다이나믹 모델(state-based peridynamic model)이 개발되었다(Silling et al., 2007). 상태 기반 모델에서는 연속체 기반 구성모델로부터 직접 페리다이나믹 모델을 구현하기 때문에 다양한 재료 거동 해석이 가능하다.

본 연구에서는 엄밀한 재료 구성 모델로부터 보다 정확한 동적파괴 해석을 하기 위해 상태 기반 페리다이나믹 모델을 사용한다. 평면 시편에 대한 동적취성파괴 거동 분석을 위해 선형 탄성체 모델의 평면응력 문제에 대한 상태 기반 페리다이나믹 모델(Le et al., 2014)을 구성한다. 또한 상태 기반 모델에 적합한 파괴 모델을 구성하고 균열패턴의 수렴성을 검증한다.

2. 상태 기반 페리다이나믹 모델

결합 기반 페리다이나믹 모델은 각 결합의 길이 변화만으로 구성되기 때문에 체적 변화는 표현이 가능하나 전단 방향의 변화는 표현되지 않는다. 반면 상태 기반 페리다이나믹 모델은 각 절점에 연결된 모든 결합의 변형 정보를 반영하여 해당 절점의 변형 및 재료 거동이 표현되기 때문에 체적 및 전단 변화를 포함하는 일반적인 재료 거동을 표현할 수 있다. 상태 개념 및 모델링에 대한 자세한 설명은 Silling 등(2007)에 있으므로 본 장에서는 상태 기반 모델을 간략히 소개하고 평면응력 모델은 다음 장에서 설명한다.

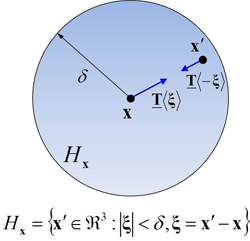
페리다이나믹 모델은 Fig. 1과 같이 유한한 길이 δ를 반경으로 하는 비국부 영역(H_x)으로 이산화된다. 유한요소와 같은 국부 모델에서는 각 요소 영역이 서로 겹치지 않도록 구성되는 반면, 페리다이나믹 모델에서는 비국부 영역들이 서로 교차하여 정보를 공유한다. 시간 t에서 절점 x에 대한 비국부 영역 내에 포함되는 모든 절점들의 상호작용력을 적분하여 페리다이나믹 운동방정식을 표현하면 다음과 같다.

https://static.apub.kr/journalsite/sites/jcoseik/2015-028-03/09TK062015280306/images/10.7734.28.3.301.F103.png

Figure 1

Force vector state in an ordinary, state-based peridynamic model and horizon

ρ \overset{. .}{u} (x, t) = \int_{H_{x}}^{} (\underline{T} [x, t] <ξ> - \underline{T} [x', t] < - ξ>) d V_{x'} + b (x, t)

(3)

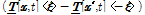는 절점 x'으로부터 x에 가해지는 힘 성분으로 단위는 힘/(체적)²이 된다. 여기서 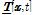는 힘 벡터 상태(force vector state)라고 하며, 절점 x와 연결되는 모든 절점에 작용한다. 결합 벡터 ε=x'-x에 대해 적용시킨 는 힘 벡터를 구성한다. 페리다이나믹 벡터 상태는 벡터를 변환한다는 점에서 이차텐서와 유사하지만 벡터 상태는 선형이거나 연속일 필요가 없다. Fig. 1과 같이 두 절점 결합의 방향에 평행하게 과 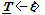이 작용하는 경우는 Ordinary 모델이라고 하며, 두 힘 벡터가 서로 평행하지 않는 경우를 Non-ordinary 모델이라고 한다. 이 때 두 힘 벡터의 크기는 서로 같지 않을 수 있다. 힘 벡터 상태와 대응하여 구성방정식을 구현하는 것은 변형 벡터 상태 가 된다. 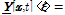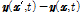변형된 절점 y와 y'로부터 로 정의된다. 참고로 위치 벡터 상태는 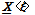=ξ이다. 힘 벡터 및 변형 벡터 상태를 변형기울기 텐서(deformation gradient tensor)로 구성되는 탄성체의 구성방정식에 대해 정식화하면 페리다이나믹 탄성체 모델을 구성할 수 있다. 페리다이나믹 상태 및 3차원 탄성체 정식화에 대한 자세한 설명은 Silling 등(2007)을 참조하기 바란다.

3. 평면응력 페리다이나믹 동적파괴 모델

이 장에서는 선형 탄성체의 평면응력 문제에 대한 상태 기반 페리다이나믹 모델을 구성하는 과정을 소개하고 상태 기반 모델에 대한 파괴 모델링 과정을 설명한다. 2차원 상태 기반 페리다이나믹 모델링에 대한 이론적 설명은 Le 등(2014)에 자세히 기술되어 있으므로 본 장에서는 이에 대해 간략히 소개하고 평면응력 수치 모델을 구현하는 과정 및 손상 모델에 대해 상세히 기술하기로 한다.

2차원 상태 기반 페리다이나믹 정식화는 3차원 정식화(Silling et al., 2007)과 유사하다. 다만 2차원 모델에서는 반경 δ의 비국부 영역(H_x)이 구가 아닌 둥근 디스크가 되며, 절점들은 1층의 디스크에 분포한다. 일반적인 연속체 모델에 대해 페리다이나믹 모델을 구성하기 위해서는 두 모델 간의 변형률-변위 관계를 동일하게 대응시켜야 한다. 결과적으로 두 모델 모두 동일한 변형에너지 밀도를 가지게 된다. 이를 통해 페리다이나믹 시스템은 동일한 하중 조건 하에서 일반적인 연속체 시스템과 같아지게 된다. 평면응력 선형탄성체에 대한 2차원 페리다이나믹 모델의 힘 벡터 상태를 유도하기 위해 먼저 평면 탄성 모델의 변형에너지 밀도 식 (4)와 페리다이나믹 변형에너지 밀도를 대응시킨다.

Ω = [\frac{k}{2} + μ {(\frac{(v + 1)}{3 (2 v - 1)})}^{2}] θ^{2} + μ \sum_{i, j = 1, 2} ε_{i j}^{d} ε_{i j}^{d}

(4)

여기서, θ는 체적팽창률(volume dilatation)을 의미하며 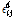는 편향변형률(deviatoric strain) 텐서를 의미한다. k와 μ는 각각 체적 및 전단 탄성계수이다. 이에 대응되는 페리다이나믹 변형에너지 밀도는 다음 식과 같다.

W (θ, \underline{e^{d}}) = \frac{k' θ^{2}}{2} + \frac{α}{2} (\underline{w} \underline{e^{d}}) \cdot \underline{e^{d}}

(5)

여기서, 페리다이나믹 상태에 대한 내적은 다음과 같이 정의된다.

\underline{A} \cdot \underline{B} = \int_{H_{x}}^{} \underline{A} <ξ> \cdot \underline{B} <ξ>d V_{ξ}

(6)

또한 페리다이나믹 모델에 대한 θ는 다음 식과 같다.

θ = \frac{2 (2 v - 1)}{(v - 1)} \frac{(\underline{w} \underline{x}) \cdot \underline{e}}{(\underline{w} \underline{x}) \cdot \underline{x}}

(7)

여기서, 는 결합의 변형 전 크기 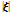를 나타내는 스칼라 상태이고, 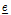는 결합의 길이 변화 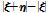를 나타내는 스칼라 상태이다. 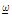는 비국부 영역 적분 시 사용되는 영향 함수(influence function)로서 일반적으로 비국부 영역 내에서 상수 1 혹은 삼각형 형태 등으로 정의된다. 이 함수의 형태가 해석 결과에 미치는 영향은 지속적으로 연구 중이다. 또한 편향 길이 변화 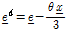이다. 두 변형에너지 밀도를 대응시켜 페리다이나믹 계수 k'과 α를 계산하면 다음과 같다.

α = \frac{8 μ}{(\underline{w} \underline{x}) \cdot \underline{x}}, k' = k + \frac{μ}{9} \frac{{(v + 1)}^{2}}{{(2 v - 1)}^{2}}

(8)

또한 탄성체의 힘 벡터 상태를 다음과 같이 구성할 수 있다.

\underline{T} = \underline{t} \frac{y' - y}{| y' - y |}

(9)

여기서, 힘 스칼라 상태는 다음과 같다.

\underline{t} = \frac{2 (2 v - 1)}{(v - 1)} (k' θ - \frac{α}{3} (\underline{w} \underline{e^{d}}) \cdot \underline{x}) \frac{\underline{w} \underline{x}}{(\underline{w} \underline{x}) \cdot \underline{x}} + α \underline{w} \underline{e^{d}}

(10)

이들을 구하는 상세한 과정은 Le 등(2014)에 기술되어 있다. 힘 벡터 상태를 식 (3)에 대입하면 평면응력 선형탄성체의 페리다이나믹 모델을 구성할 수 있다.

이상과 같이 정리된 상태 기반 페리다이나믹 모델을 수치적으로 구현한다. 먼저 이산화된 절점 x_i에서 비국부 영역 내의 다른 절점 x_p에 대한 여러 벡터 및 스칼라 상태를 구현하면 다음과 같다.

$\underline{X} < x_{p} - x_{i} > = x_{p} - x_{i}$

$\underline{Y} < x_{p} - x_{i} > = (x_{p} + u_{p}) - (x_{i} - + u_{i})$

$\underline{x} < x_{p} - x_{i} > = | x_{p} - u_{i} |$

$\underline{y} < x_{p} - x_{i} > = | {(x}_{p} + u_{p}) | - {(x}_{i} + u_{i})$

\underline{e} < x_{p} - x_{i} > = | {(x}_{p} + u_{p}) - {(x}_{i} + u_{i}) | - | x_{p} - x_{i} |

(11)

페리다이나믹 상태의 내적을 수치적으로 구현하기 위해 비국부 영역 내에 속하는 모든 이산화된 절점에 대해 표현하고 수치 적분을 하면 다음을 구할 수 있다.

m = (\underline{w} \underline{x}) \cdot \underline{x} \approx \sum_{p} \underline{w} < x_{p} - x_{i} > {| {(x}_{p} - x_{i}) |}^{2} V_{i p}

(12)

θ \approx \frac{2 (2 v - 1)}{m (v - 1)} \times \sum_{p} \underline{w} < x_{p} - x_{i} > | {(x}_{p} - x_{i}) | \underline{e} < x_{p} - x_{i} > V_{i p}

(13)

따라서 두 절점에 대한 편향 길이 변화는 다음과 같다.

\underline{e^{d}} < x_{p} - x_{i} > = \underline{e} < x_{p} - x_{i} > \frac{θ}{3} | x_{p} - x_{i} |

(14)

식 (11)~(14)를 사용하여 페리다이나믹 변형에너지 밀도를 수치적으로 구현하면 다음과 같다.

W \approx \frac{k' θ^{2}}{2} + \frac{α}{2} \sum_{p} \underline{w} < x_{p} - x_{i} > (\underline{e^{d}} < {x_{p} - x_{i} >)}^{2} V_{i p}

(15)

힘 벡터 상태는 다음과 같이 구현된다.

\underline{T} < x_{p} - x_{i} > = \underline{t} < x_{p} - x_{i} > \frac{(x_{p} + u_{p}) - (x_{i} + u_{i})}{| (x_{p} + u_{p}) - (x_{i} + u_{i}) |}

(16)

$\underline{t} < x_{p} - x_{i} > = k' θ \frac{2 (2 v - 1)}{m (v - 1)} \underline{w} < x_{p} - x_{i} > | x_{p} - x_{i} |$

$- (\frac{α}{3} \sum_{q} \underline{ω} < x_{q} - x_{i} > | x_{q} - x_{i} | \underline{e^{d}} < x_{q} - x_{i} > V_{i p})$

$\times \frac{2 (2 v - 1)}{m (v - 1)} \underline{ω} < x_{p} - x_{i} > | x_{p} - x_{i} |$

+ α \underline{ω} < x_{p} - x_{i} > \underline{e^{d}} < x_{p} - x_{i} >

(17)

최종적으로 상태 기반 페리다이나믹 모델의 운동방정식은 다음과 같다.

$ρ (x_{i}) \overset{. .}{u} (x_{i}, t)$

\approx \sum_{p} (\underline{T} < x_{p} - x_{i} > - \underline{T} < x_{i} - x_{p} >) V_{i p} + b (x_{i}, t)

(18)

본 연구에서는 공간 적분을 위해 중심점 수치적분(midpoint integration)을 사용하였으며, 수치적분의 정확도를 높이기 위해 다음과 같이 수정된 적분요소를 사용하였다.

\tilde{V_{i p}} = {\begin{matrix} V_{i p} & i f | x_{p} - x_{i} | \leq δ - \frac{γ_{p}}{2} \\ (\frac{1}{2} + \frac{δ - | x_{p} - x_{i} |}{γ_{p}}) V_{i p} & \begin{matrix} i f δ - \frac{γ_{p}}{2} \end{matrix} < \begin{matrix} | x_{p} - x_{i} | \end{matrix} \\ \begin{matrix} \begin{matrix} \leq \begin{matrix} \begin{matrix} δ + \frac{γ_{p}}{2} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \\ 0 & \begin{matrix} i f | x_{p} - x_{i} | \geq δ + \frac{γ_{p}}{2} \end{matrix} \end{matrix}

(19)

여기서, r_p는 x_p와 가장 인접해 있는 절점까지의 직선거리가 된다. 또한 동적 과도 응답 해석을 위해 Forward Euler 시간 적분을 사용하였다.

결합 기반 페리다이나믹 모델에서는 결합의 인장비(bond stretch) s가 허용 범위 s₀를 넘어서면 해당 결합을 끊고 한 번 끊어진 결합을 다시 복구되지 못하는 방식으로 손상 모델을 구성한다. 결합의 인장비와 파괴 모델에 대한 페리다이나믹 결합력은 다음 식들과 같다.

s = \frac{| ξ + η | - | ξ |}{| ξ |}

(20)

f (η,ξ) = \frac{ξ + η}{| ξ + η |} c s μ,μ = {\begin{matrix} 1, i f s < s_{0} \\ \begin{matrix} 0, i f s \geq s_{0} \end{matrix} \end{matrix}

(21)

여기서, c는 결합 기반 페리다이나믹 모델의 미소탄성재료 상수이다. 식 (21)에 의해 파괴된 결합은 더 이상 힘을 지지하지 못한다. 페리다이나믹 해석에서 파괴 단면(fracture surface)은 여러 결합들이 응집되어 연쇄적으로 끊어지면서 자연스럽게 발생하게 된다. 이때 결합 인장비의 허용 한계는 새로운 단위 파괴단면을 생성하는데 필요한 에너지해방율(energy release rate) G₀로부터 3차원의 경우 다음 식과 같이 유도된다.

https://static.apub.kr/journalsite/sites/jcoseik/2015-028-03/09TK062015280306/images/10.7734.28.3.301.F146.png

Figure 2

Schematic of fracture surface

s_{0} = \sqrt{\frac{10 G_{0}}{πc δ^{5}}}

(22)

G₀ 값은 재료파괴 시험을 통해 실험적으로 찾을 수 있다. 결합 기반 페리다이나믹 손상 모델에 대한 상세한 설명은 Silling (2000), Silling과 Askari(2005), Ha와 Bobaru(2010) 등을 참조하기 바란다.

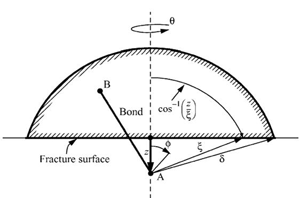
결합 기반 모델은 인접한 결합들이 스프링과 유사한 형태로 독립적으로 작동하기 때문에 결합의 인장비에 대해 간단히 손상 모델을 구성할 수 있었다. 그러나 상태 기반 모델에서는 인접한 절점들이 독립적으로 작용하지 않기 때문에 각 결합의 인장비를 기준으로 손상 모델을 구성할 수 없다. 본 연구에서는 힘 벡터 상태로부터 각 결합들에 대해 에너지 형태의 포텐셜을 구성할 수 있는 점에 착안하여 상태 기반 모델에 적합한 손상 모델을 구성하였다. Fig. 2와 같이 0 < z < δ인 점선을 따라 존재하는 모든 절점 A에 대해 파괴단면을 통과하여 연결되는 모든 점 B를 고려한다. 반경 δ인 비국부 영역을 고려하면 유효한 영역은 Fig. 2에서 빗금친 부분과 같이 3차원 구면의 일부분이 된다. 이 때 각 결합 A와 B가 수용할 수 있는 최대 변형에너지 포텐셜 ω₀를 가정하고 이를 빗금친 영역에 대해 적분하면 에너지해방율을 다음과 같이 계산할 수 있다.

G_{0} = 2 \int_{0}^{2 π} \int_{0}^{δ} \int_{z}^{δ} \int_{0}^{{c o s}^{- 1} (\frac{z}{ξ})} w_{0} ξ^{2} s i n ∅d ∅dξdzdθ

(23)

$= \frac{π w_{0} δ^{4}}{2}$

따라서 각 결합의 변형에너지 포텐셜 ω_ε이 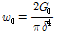보다 커지면 해당 결합을 끊어서 손상 모델을 구성할 수 있다. 이때 각 결합의 에너지 포텐셜은 다음과 같다.

w_{ξ} = \int_{0}^{η (t)} \underline{T} [x, t] < x' - x > - \underline{T} [x', t] <x - x' > \cdot d η

(24)

본 연구에서 사용하는 평면응력 모델에서는 Fig. 2의 유효영역이 θ 좌표가 없는 2차원 원형 디스크의 일부가 되므로 식 (23)을 조정하여 허용가능한 변형에너지 포텐셜을 다시 계산하면 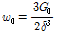이 된다. 또한 탄성재료는 변형에너지 밀도 W를 미분하면 에너지 포텐셜을 구성할 수 있기 때문에 식 (5,7)등으로부터 평면응력 탄성체 상태 기반 페리다이나믹 모델의 에너지 포텐셜은 다음과 같이 계산할 수 있다.

$w_{ξ} = \frac{d W}{d V_{ξ}} = k' θ \frac{2 (2 v - 1)}{m (v - 1)} \underline{ω} <ξ> | ξ | \underline{e} <ξ>$

+ \frac{α}{2} \int_{H}^{} \underline{ω} <ξ> {(\underline{e^{d}} <ξ>)}^{2} d V_{ξ}

(25)

4. 동적파괴 해석 모델 검증

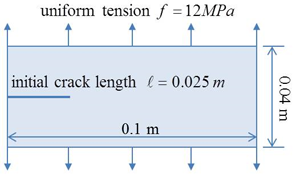
평면응력 문제의 수치예제를 통해 상태 기반 동적파괴 해석 모델을 검증한다. 해석 모델은 Fig. 3과 같이 가로, 세로가 각각 0.1m, 0.04m인 직사각형 평판이다. 평판의 좌측면 중앙에는 가로 방향으로 길이 0.025m의 초기 균열이 주어져 있다. 전산모델에서는 균열을 가로질러서 연결되는 페리다이나믹 결합이 없도록 초기 균열면을 구현하였다. 평면 시편의 상하면에 12MPa으로 일정한 인장력을 가한다. 이와 같은 조건의 모델은 처음에는 초기 균열방향으로 균열이 직진하다가 일정 조건이 되면 균열이 더 이상 직진하지 못하고 2개 이상으로 분기되어 전파되는 분기 균열이 발생하게 되는 것이 실험적(Ravi-Chandar and Knauss, 1984)으로 연구되었고 결합 기반 페리다이나믹 모델을 사용하여 전산 해석적으로도 확인되었다(Ha and Bobaru, 2010). 페리다이나믹 동적취성파괴 해석에 사용된 재료는 Soda-lime 유리로 기본 물성치 및 에너지해방율 등은 Table 1과 같이 균열실험(Döll, 1975)을 통해 측정된 값을 사용하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2015-028-03/09TK062015280306/images/10.7734.28.3.301.F154.png

Figure 3

Pre-notched glass plate model

https://static.apub.kr/journalsite/sites/jcoseik/2015-028-03/09TK062015280306/images/10.7734.28.3.301.F155.png

Figure 4

-convergence strategy

Table 1

Material properties of soda-lime glass


Density	2440kg/m³
Young’s modulus	72GPa
Poisson’s ratio	0.22
Energy release rate	135J/m²

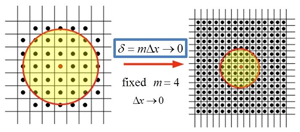
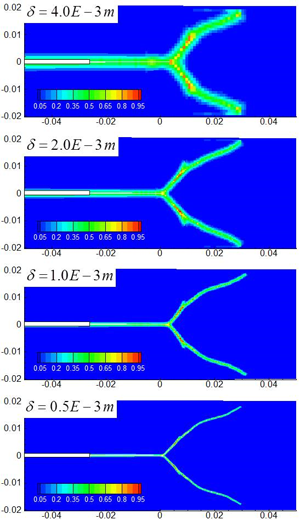
상태 기반 파괴 해석 모델을 검증하기 위해 비국부 영역을 줄여가면서 균열패턴의 수렴성을 검토하였다. 비국부 영역은 반경 δ인 원형 디스크로 설정하였고, 동일한 문제 조건에 대해 δ의 크기를 줄여가면서 균열패턴을 조사하였다. 균일 격자 구조를 사용하였고 비국부 영역인 원의 중심에서 가장자리 방향으로 4개 이내의 절점(m=4)이 포함되도록 δ의 크기를 정하여 이산화 레벨을 일정하게 유지(비국부 영역 당 최대 절점 수 49개)하였다. 따라서 Fig. 4와 같이 δ가 절반으로 줄어들면 해석 모델의 절점 간격(Δx)도 절반으로 줄여서 해석모델을 구성하였다. δ가 0.004m이고 총 절점 수가 4,326개인 모델에서부터 δ를 절반씩 줄여서 δ=0.002m (16,646개 절점), δ=0.001m(65,448개 절점), δ=0.0005m (258,566개 절점)의 4가지 해석모델에 대해서 수렴성을 검토하였다. 계산시간 간격은 가장 절점 간격이 작은 모델인 258,566개 절점으로 구성된 모델이 안정적으로 해석될 수 있도록 25ns으로 설정하였다(Ha et al., 2010). Fig. 5에서 2,400회 반복계산 후인 60μs에서 4개 모델에 대한 분기균열패턴을 비교하였다. 페리다이나믹 균열은 각 비국부 영역 내의 초기 결합의 수에 대한 끊어진 결합의 수의 비율을 손상지수로 사용하여 표현하였다. 즉, 손상지수가 0이면 초기 결합 대비 끊어진 결합이 없는 비손상 상태이고, 손상지수가 1이면 모든 결합이 끊어진 완전 손상 상태를 의미한다. 따라서 초기 균열면 주변에서 손상지수는 0.4~0.5가 된다. 비국부 영역의 크기가 줄어들면서 균열면의 폭은 줄어들지만 분기 균열이 발생하는 시점과 분기 각도, 균열전파 속도 등 전체적인 균열패턴은 4개 모델 모두 상당히 일치하는 것을 확인할 수 있었다. 이와 같은 δ-수렴성 조사는 비국부 모델을 사용하는 페리다이나믹 해석에 특징적인 것으로 해석 모델이 국부 모델의 특성을 잘 모사하면서 수렴해가는 것을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2015-028-03/09TK062015280306/images/10.7734.28.3.301.F157.png

Figure 5

Crack branching simulations with decreasing the nonlocal region

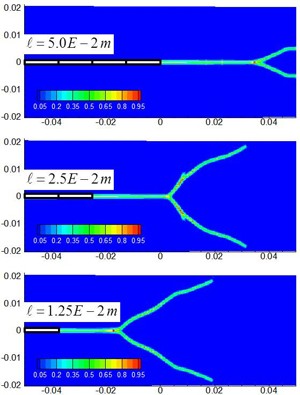
다음으로 동일한 하중 및 문제 조건에서 초기 균열면 길이에만 변화를 주면서 균열패턴을 비교하였다. 해석 모델은 수렴성 조사 모델에서 δ=0.001m(65,448개 절점)인 모델을 사용하였으며, 초기 균열면의 길이만 0.05m, 0.025m, 0.0125m로 변화시켜서 각각 동적파괴 해석을 수행하였다. Fig. 6에 동일 시점(60μs)에서 균열패턴을 비교하였다. 초기 균열면이 길수록 균열 전파가 쉽기 때문에 일직선으로 균열이 전파되는 경향을 볼 수 있었다. 이는 균열 분기가 일정 이상의 응력집중(stress intensity factor)에서 발생한다는 것을 잘 설명해 준다.

https://static.apub.kr/journalsite/sites/jcoseik/2015-028-03/09TK062015280306/images/10.7734.28.3.301.F158.png

Figure 6

Crack branching simulations with decreasing initial crack length

5. 결 론

본 연구에서는 상태 기반 페리다이나믹 모델을 사용하여 동적취성파괴 해석을 수행하였다. 평면 시편에 대한 분기균열 현상을 모사하기 위해 평면응력 선형 탄성체에 대해 상태 기반 페리다이나믹 모델을 유도하고 상태 기반 모델에 적합한 손상 모델을 적용하였다. 균열분기, 전파 문제에 대한 수렴성 검토 및 초기 균열면과 균열패턴의 상관관계를 분석하여 제시된 동적파괴 모델을 검증하였다. 본 연구는 다양한 재료에 대한 분기균열 현상 분석 및 엄밀한 손상 모델 개발 등의 확장된 연구를 위해 중요하다.

Acknowledgements

본 연구는 정부(미래창조과학부)의 재원으로 한국연구재단이 지원하는 일반 연구자 사업(No. 2012R1A1A1040019)의 지원을 받아 수행되었습니다.

References

F., Bobaru, Y.D., Ha and W., Hu, 2012. Damage Progression from Impact in Multilayered Glass Modeled with Peridynamics. Central European J. Eng., 2, pp.551-561.

10.2478/s13531-012-0020-6

W., Döll, 1975. Investigations of the Crack Branching Energy. Int. J. Fract., 11, pp.184-186.

10.1007/BF00034729

Y.D., Ha and F., Bobaru, 2010. Studies of Dynamic Crack Propagation and Crack Branching with Peridynamics. Int. J. Fract., 162, pp.229-244.

10.1007/978-90-481-9760-6_18

Y.D., Ha and F., Bobaru, 2011. Characteristics of Dynamic Brittle Fracture Captured with Peridynamics. Eng. Fract. Mech., 78, pp.1156-1168.

10.1016/j.engfracmech.2010.11.020

Y.D., Ha and S, Cho, 2011. Dynamic Brittle Fracture Captured with Peridynamics: Crack Branching Angle &Crack Propagation Speed. J. Comput. Struct. Eng. Inst. Korea, 24, pp.637-643.

Y.D., Ha and S, Cho, 2012. Nonlocal Peridynamic Models for Dynamic Brittle Fracture in Fiber-reinforced Composites: Study on Asymmetrically Loading State. J. Comput. Struct. Eng. Inst. Korea, 25, pp.279-292.

10.7734/COSEIK.2012.25.4.279

W., Hu, Y.D., Ha and F., Bobaru, 2011. Modeling Dynamic Fracture and Damage in Fiber-Reinforced Composites with Peridynamics. Int. J. Multiscale Comput. Eng., 9, pp.707-726.

10.1615/IntJMultCompEng.2011002651

W., Hu, Y.D., Ha and F., Bobaru, 2012. Peridynamic Model for Dynamic Fracture in Uidirectional Fiber-Reinforced Composites. Comput. Methods Appl. Mech. &Eng., 217, pp.247-261.

10.1016/j.cma.2012.01.016

Q.V., Le, W.K, Chan and J., Schwartz, 2014. A Two-Dimensional Ordinary, State-based Peridynamic Model for Linarly Elastic Solids. Int. J. Numer. Methods Eng., 98, pp.547-561.

10.1002/nme.4642

K., Ravi-Chandar and W.G., Knauss, 1984. An Experimental Investigation into Dynamic Fracture: IV. On the Interaction of Stress Waves with Propagating Cracks. Int. J. Fract., 26, pp.189-200.

10.1007/BF01140627

S.A., Silling, 2000. Reformulation of Elasticity Theory for Discontinuities and Long-Range Forces. J. Mech.& Phys. Solids, 48, pp.175-209.

10.1016/S0022-5096(99)00029-0

S.A., Silling and E., Askari, 2005. A Meshfree Method based on the Peridynamic Model of Solid Mechanics. Comput. &Struct, 83, pp.1526-1535.

10.1016/j.compstruc.2004.11.026

S.A., Silling, M., Epson, O., Weckner, J., Xu and E., Askari, 2007. Peridynamic States and Constitutive Modeling. J. Elast., 88, pp.151-184.

10.1007/s10659-007-9125-1

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

State-based Peridynamic Modeling for Dynamic Fracture ofPlane Stress

ABSTRACT

MAIN

Figure 1

Force vector state in an ordinary, state-based peridynamic model and horizon

Figure 2

Schematic of fracture surface

Figure 3

Pre-notched glass plate model

Figure 4

-convergence strategy

Table 1

Material properties of soda-lime glass

Figure 5

Crack branching simulations with decreasing the nonlocal region

Figure 6

Crack branching simulations with decreasing initial crack length

Acknowledgements

References