Proper Orthogonal Decomposition Based Intrusive Reduced Order Models to Accelerate Computational Speed of Dynamic Analyses of Structures Using Explicit Time Integration Methods

Young Kwang Hwang; Myungil Kim

doi:10.7734/COSEIK.2024.37.1.9

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 29 February 2024. 9-16
https://doi.org/10.7734/COSEIK.2024.37.1.9

Proper Orthogonal Decomposition Based Intrusive Reduced Order Models to Accelerate Computational Speed of Dynamic Analyses of Structures Using Explicit Time Integration Methods

외연적 시간적분법 활용 동적 구조해석 속도 향상을 위한 적합직교분해 기반 침습적 차수축소모델 적용 연구

Young Kwang Hwang¹^*

Myungil Kim²

황 영광¹^*

김 명일²

¹Senior Researcher, Intelligent Simulation Center, Korea Institute of Science and Technology Information, Daejeon, 34141, Korea

²Principal Researcher, Intelligent Simulation Center, Korea Institute of Science and Technology Information, Daejeon, 34141, Korea

¹한국과학기술정보연구원 지능형시뮬레이션센터 선임연구원

²한국과학기술정보연구원 지능형시뮬레이션센터 책임연구원

^{*Corresponding Author}

ABSTRACT

Using the proper orthogonal decomposition (POD) based intrusive reduced order model (ROM), the total degrees of freedom of the structural system can be significantly reduced and the critical time step satisfying the conditional stability increases in the explicit time integrations. In this study, therefore, the changes in the critical time step in the explicit time integrations are investigated using both the POD-ROM and Voronoi-cell lattice model (VCLM). The snapshot matrix is composed of the data from the structural response under the arbitrary dynamic loads such as seismic excitation, from which the POD-ROM is constructed and the predictive capability is validated. The simulated results show that the significant reduction in the computational time can be achieved using the POD-ROM with sufficiently ensuring the numerical accuracy in the seismic analyses. In addition, the validations show that the POD based intrusive ROM is compatible with the Voronoi-cell lattice based explicit dynamic analyses. In the future study, the research results will be utilized as an elemental technology for the developments of the real-time predictive models or monitoring system involving the high-fidelity simulations of structural dynamics.

Keywords

structural dynamics

seismic analysis

explicit time integration

proper orthogonal decomposition

reduced order model

Voronoi-cell lattice model

일반적으로 적합직교분해(proper orthogonal decomposition, POD) 기반의 침습적(intrusive) 차수축소모델(reduced order model, ROM)을 활용하면 구조 시스템의 전체 자유도를 크게 줄이고 외연적 시간 적분법에서 해의 안정성을 만족하는 임계 시간 간격을 증가시킬 수 있다. 따라서 본 연구에서는 POD-ROM을 활용하여 Voronoi-cell 격자 요소로 이산화된 구조 시스템의 축소와 이에 따른 외연적 시간 적분법의 임계 시간 간격 및 해석 정확도 변화를 살펴보았다. 또한 지진하중과 같은 불규칙한 하중 이력을 받는 구조물 응답 해석에 POD-ROM을 적용하였다. 해석 결과 ROM을 통해 해의 정확도를 충분히 확보하면서 연산 시간을 크게 단축할 수 있음을 확인하였다. 또한 POD-ROM과 VCLM의 연계 방안의 적절성을 확인하였다. 향후 해당 연구는 고정밀 대용량 동적 구조해석의 실용성을 높이고, 설계 변수에 따른 구조물 동적 거동의 실시간 예측을 위한 기반 연구로 활용될 수 있다.

키워드

구조동역학

지진해석

외연적 시간적분법

적합직교분해

차수축소모델

보로노이 셀 격자 모델

MAIN

1. 서 론
2. 본 론
2.1 Voronoi-Cell Lattice Model
2.2 외연적 시간적분법
2.3 차수축소모델(Reduced Order Model)
3. 해석 결과
4. 결 론

1. 서 론

최근 구조해석 및 설계 기술의 고도화와 병렬컴퓨팅 기술의 발전으로 건설, 기계, 재료, 항공, 우주, 기상 등 많은 분야에서 고정밀 대용량 시뮬레이션 기술이 활용되고 있다. 초고성능컴퓨팅 기술의 발전으로 공학 시뮬레이션에 소요되는 계산 시간이 크게 단축되었고 산업 및 연구 현장에서 그 활용도가 높아지고 있다. 따라서 종래 계산 시간이나 비용 측면에서 제한되었던 다물리(multi-physics), 다규모(multi-scale) 현상 시뮬레이션과 고충실도(high-fidelity) 모델 기반 3차원 동적해석 등의 연구가 활발히 수행되고 있다(Mira et al., 2023; Permann et al., 2020).

근래 디지털 트윈(digital twin) 기술(Fuller et al., 2020)에 대한 관심과 함께 실시간 수준의 고정밀 대용량 시뮬레이션 기술이 주목받고 있다. 해당 수준의 계산 속도 달성을 위해서는 초고성능컴퓨터와 같은 거대 계산자원 활용이 필요하며, 더불어 동일 계산 자원을 활용하면서도 빠르고 정확하게 해석을 수행할 수 있는 수치해석 방법 개발이 필요하다. 한편으로 대부분의 자연 및 공학 현상은 시간 이력에 따른 구조 및 유체의 물리적 변화를 수반하며, 이를 예측하기 위해 내연적(implicit) 또는 외연적(explicit) 시간적분 방법을 활용하여 초기 및 경계 조건 하에서 해석 대상의 거동을 계산한다(Chopra, 2011; Hughes, 2012). 특별히 외연적 시간적분법은 충돌, 폭발, 지진과 같은 충격 하중 상태에서 구조물의 대변형, 파괴와 같은 비선형 거동을 모의하는데 널리 사용된다. 외연적 시간적분법의 해는 조건적 안정성(conditional stability) 특징을 가지며 해당 조건을 만족하기 위해서는 임계 시간 간격(critical time step) 미만의 시간 간격을 유지해야 한다. 따라서 수치 해석 방법적인 측면에서 이러한 임계 시간 간격을 늘릴 수 있는 기술이 연구되어 왔다. 기본적으로 임계 시간 간격은 이산화된 구조 시스템의 최소 요소 크기에 따라 정해지기 때문에 구조 모델의 요소 크기 개선으로 해당 문제를 해결할 수 있다. 따라서 기하 형상의 복잡성이나 관심 대상 영역 등의 이유로 요소 망(mesh)이 조밀하게 형성된 영역을 개선하거나 단순화된 형태의 등가 모델 활용으로 요소 망의 크기와 관련된 임계 시간 간격을 늘릴 수 있다. 또한 연산 과정에서 질량 스케일링(mass scaling) 등을 활용하여 임계 시간 간격을 늘릴 수 있다(Cocchetti et al., 2013; Olovsson et al., 2005). 그 외에도 매시간 순간에서 최적의 시간 간격을 업데이트하여 이를 연산에 활용하는 변화 시간 간격(variable time step) 방법(Gomez-Gesteira et al., 2012; Holder et al., 2001)이 있다. 최근에는 기존 외연적 시간적분법에 머신러닝 및 딥러닝 등의 방법론을 결합한 해석 가속화 연구가 수행되고 있다(Meister et al., 2020; van der Sande et al., 2023).

이 외에도 적합직교분해(proper orthogonal decomposition, POD) 기반의 침습적(intrusive) 차수축소모델(reduced order model, ROM)을 활용하면 외연적 시간적분법의 임계 시간 간격을 크게 늘릴 수 있다고 알려져 있다(Krysl et al., 2001; Taylor et al., 2011). 따라서 본 연구에서는 구조 동역학 문제에서 해당 POD-ROM을 적용한 축소된 운동방정식과 그에 따른 외연적 시간적분법의 임계 시간 간격 변화를 살펴보고자 한다. 한편으로 POD 방법이 아닌 크리로프 부공간(Krylov subspace) 기반의 모델차수축소법을 활용할 수 있는데, 해당 방법은 POD 방법에 비하여 빠른 해의 수렴과 초기 구조 시스템 행렬만으로도 변환행렬 구축이 가능한 장점이 있다(Han and Kim, 2021). 이 외에도 집중질량모델(lumped-mass stick model)을 통한 등가 구조 모델 구축과 이를 활용한 구조물의 동적 응답 및 지진 해석 연구가 수행되고 있다(Kwag et al., 2022; Roh et al., 2012). 본 연구에서 다루는 POD-ROM은 투영행렬을 통해 초기 원형 모델을 나타내는 전체차수모델(full order model, FOM)로부터 ROM을 구축한다. 따라서 ROM을 통해 빠르게 축적된 해석 결과 데이터를 단순한 변환을 통해 FOM의 후처리 과정에 바로 활용할 수 있는 장점이 있다. 또한 POD 과정에서 특정 하중 이력 정보에 대한 구조물의 응답 데이터인 스냅샷 행렬(snapshot)을 활용하기 때문에 개발된 축소모델이 초기 구조물의 강성이나 질량 행렬 등의 정보와 더불어 외력 특성 정보를 모두 반영하는 특징이 있다.

본 연구에서는 향후 침습적 및 비침습적 ROM을 통한 비선형 구조 거동과 딥러닝 등의 데이터 기반 예측 기술과의 연계를 목적으로 POM 방법을 활용한 데이터 기반 ROM 구축 연구를 수행하였다. 또한 POD-ROM이 지진하중과 같이 불규칙한 하중이력을 받는 구조물 거동을 잘 모사할 수 있는지 살펴보았다. 구조해석을 위하여 지진, 충격 등의 동적 하중을 받는 구조물 거동 연구에 많이 활용되는 Voronoi-cell lattice model(VCLM)을 사용하였다(Choo et al., 2023; Hwang et al., 2016; 2022). VCLM은 일반적 구조해석 방법론에서 노드 별 3개의 병진 자유도를 고려하는 것을 포함하여 추가적으로 3개의 회전 자유도를 고려하기 때문에 구조 시스템 방정식의 축소에 따른 이점이 더 클 것으로 판단된다. 본문에서는 지진하중을 받는 외팔보 형태 구조물의 동적 거동을 대상으로 초기 구조 모델과 ROM의 모의 결과를 비교 분석하였고, 스냅샷 행렬에 대한 특이값 분해(singular value decomposition, SVD)로 얻는 적합 직교 모드 수에 따른 외연적 시간적분법의 임계 시간 간격 변화와 관련 해석 정확도를 살펴보았다.

2. 본 론

이 장에서는 본 연구에 사용한 수치해석 방법론에 대하여 설명하였다. 먼저 구조해석을 위한 VCLM 방법론과 외연적 시간적분법을 설명하고 POD-ROM을 통한 구조 시스템 축소 방법에 대해 살펴본다.

2.1 Voronoi-Cell Lattice Model

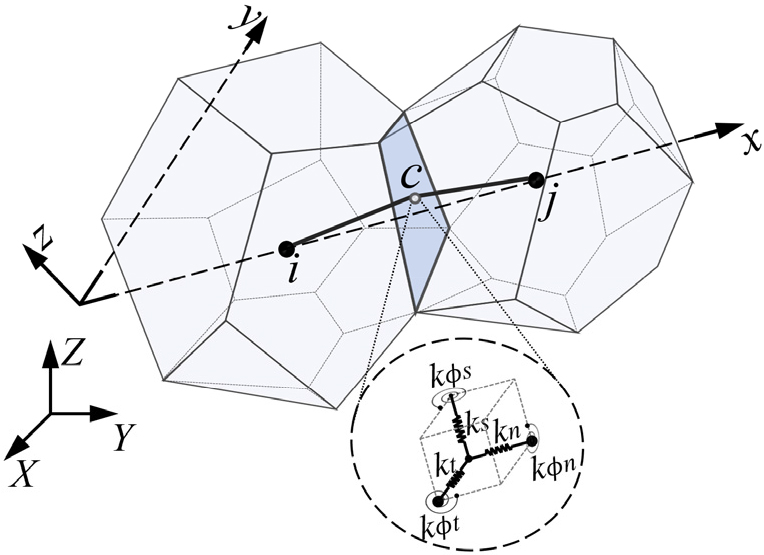
https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F1.jpg

Fig. 1.

3D Voronoi-cell lattice element i‐j with respect to the local (x-y-z) and global (X-Y-Z) coordinates

Fig. 1은 일반적인 비정형(irregular) 형태의 Voronoi-cell 격자 요소 $i - j$ 를 보여준다. 해당 요소에서 두 Voronoi 셀이 차지하는 영역은 노드 i와 j 각각에 할당된 부피 및 질량을 나타낸다. 각 노드와 두 셀의 공통면 상의 점 c 사이의 길이 $\bar{i c}$ 와 $\bar{j c}$ 는 강체 구속 조건으로 일정하게 유지된다. 따라서, 요소의 변형은 공통면의 중심점 c에 위치한 여섯 자유도의 스프링 셋(set)을 통해 나타나며 3방향의 병진 강성( $k_{n}, k_{s}, k_{t}$ ), 3방향의 회전 강성( $k_{ϕ n}, k_{ϕ s}, k_{ϕ t}$ )을 갖는다(Yip et al., 2006).

(1)

k_{s} = k_{t} = α k_{n} = α β \frac{E A_{e}}{h_{e}}, k_{ϕ n} = \frac{E J_{p}}{h_{e}}, k_{ϕ s} = \frac{E I_{22}}{h_{e}}, k_{ϕ t} = \frac{E I_{11}}{h_{e}}

여기서 E는 탄성계수, $A_{e}$ 는 공통면의 넓이, $h_{e}$ 는 요소 길이를 의미하며 𝛼와 𝛽는 포아송(Poisson) 효과를 고려하기 위한 계수이다. 또한 $J_{p}$ 는 공통면의 중심점 c에 대한 극 관성 모멘트, $I_{11}$ 와 $I_{22}$ 는 공통면의 각 주(principal) 방향 관성 모멘트를 의미한다. 식 (1)의 여섯 개의 스프링 계수를 대각 성분으로 갖는 강성행렬 $k_{s} (= d i a g [k_{n} k_{s} k_{t} k_{ϕ n} k_{ϕ s} k_{ϕ t}])$ 와 요소-스프링 변위 행렬 B, 좌표 변환 행렬 𝜞을 통해 다음과 같이 Voronoi-cell 격자 요소의 강성행렬을 구성할 수 있다(Yip et al., 2006).

(2)

K_{e} = Γ^{T} B^{T} k_{s} B Γ

이후 요소망의 연결정보를 바탕으로 시스템 강성행렬을 구성하고, 이를 통해 시스템 내력을 계산할 수 있다. 질량 행렬 구성 및 동적 구조해석 적용에 대한 상세 내용은 참고문헌(Choo et al., 2023; Hwang et al., 2016)을 통해 확인할 수 있다.

2.2 외연적 시간적분법

VCLM을 통해 이산화된 전체 구조 시스템에 대하여 n번째 시간 스텝에 대한 운동방정식은 다음과 같다.

(3)

M {\ddot{u}}_{n} + C {\dot{u}}_{n} + {Ku}_{n} = f_{n}^{e x t}

여기서 M, C, K는 각각 시스템 질량, 감쇠, 강성행렬을 나타내고, $\ddot{u}, \dot{u}, u$ 는 각각 가속도, 속도, 변위 벡터를 나타낸다. 또한 $f^{e x t}$ 는 구조 시스템의 외력 벡터를 나타낸다. 본 연구에서는 비감쇠(undamped) 거동을 고려하였다. 시간에 따른 구조 응답 계산을 위하여 다음과 같이 외연적 시간적분법의 일종인 중앙차분법(central difference method, CDM)의 시간적분자(time integrator)를 도입하였다(Hughes, 2012).

(4)

u_{n + 1} = u_{n} + ∆ t {\dot{u}}_{n} + \frac{∆ t^{2}}{2} u_{n}, {\dot{u}}_{n + 1} = {\dot{u}}_{n} + \frac{∆ t}{2} ({\ddot{u}}_{n} + {\ddot{u}}_{n + 1})

여기서 시간 간격 $∆ t$ 는 조건부 안정성(conditional stability) 조건을 만족해야 한다. 요소의 진동수 $ω_{e}^{h}$ 를 고려할 때 식 (4)의 $∆ t$ 범위는 다음과 같다.

(5)

∆ t \leq ∆ t_{c r} = \frac{Ω_{c r}}{ω^{h}}, ω^{h} \leq \max_{e} ω_{e}^{h}

여기서 $∆ t_{c r}$ 는 임계 시간 간격, $Ω_{c r}$ 는 임계 샘플링 진동수(critical sampling frequency)로 CDM의 경우 2와 같다(Hughes, 2012).

2.3 차수축소모델(Reduced Order Model)

해당 연구에서 사용하는 POD-ROM은 구조 상세 모델 또는 원형 참조 모델을 의미하는 FOM을 통해 획득한 시간 이력 데이터인 스냅샷 행렬 X₀의 특이값 분해(singular value decomposition, SVD) 결과를 활용한다(Lee, 2015; Taylor et al., 2011).

(6)

X_{0} = Φ \sum A^{T}, Φ \in ℝ^{m \times k}, \sum \in ℝ^{k \times k}, A \in ℝ^{k \times k}

여기서 $m$ 은 전체 시스템 자유도의 수, k는 적합 직교 모드의 수이다. 또한 $Φ (= [ϕ_{1} ϕ_{2} \dots ϕ_{k}])$ 는 좌특이 행렬이며 적합 직교 모드 또는 축소 기저 벡터 𝝓의 집합이고, A는 우특이 행렬이다. 특이값 행렬 $\sum (= diag [σ_{1} σ_{2} \dots σ_{k}])$ 는 각 모드의 기여도 또는 에너지를 나타내는 대각성분으로 구성된다. 일반적으로 k개의 축소 기저 벡터 중에서 에너지가 높은 순서로 r개의 벡터를 투영에 사용하며, 해당 투영 또는 변환 행렬 $\sum T (= [ϕ_{1} ϕ_{2} \dots ϕ_{r}])$ 를 통해 식 (3)의 운동방정식을 식 (7)과 같이 축소할 수 있다.

(7)

\hat{M} {\ddot{r}}_{n} + \hat{C} {\dot{r}}_{n} + \hat{K} r_{n} = {\hat{f}}_{n}^{e x t}

여기서 $\hat{M}, \hat{C}, \hat{K}$ 는 축소된 질량, 감쇠, 강성행렬이며 식 (8)과 같이 정의된다.

(8)

\hat{K} = T^{T} KT, \hat{M} = T^{T} MT, \hat{C} = T^{T} CT, \hat{M} \in ℝ^{r \times r}, \hat{C} \in ℝ^{r \times r}, \hat{K} \in ℝ^{r \times r}

또한 r과 $\hat{f}$ 는 각각 축소된 변위 벡터, 외력 벡터로서 다음과 같다.

(9)

r = T^{T} u, \hat{f} = T^{T} f, r \in ℝ^{r \times 1}, \hat{f} \in ℝ^{r \times 1}

일반적으로 축소 시스템의 자유도 r은 기존 시스템의 자유도 m에 비하여 매우 작은 값을 갖는다( $r < < m$ ). 따라서, 해당 행렬 연산에 소요되는 계산량을 크게 줄일 수 있다. 외연적 시간적분법의 경우 전체 시스템 강성행렬에 소요되는 역행렬 등의 계산이 소요되지 않아 해당 계산량 감소의 이점은 적다고 할 수 있지만, 축소된 시스템의 임계 시간 간격이 늘어나는 효과가 있어 연산 시간을 크게 단축할 수 있다. 또한 해석에 사용하는 VCLM 방법은 노드 별로 3개의 회전 자유도를 추가로 고려하기 때문에 해당 축소 효과는 더 크다고 할 수 있다.

일반적으로 POD-ROM 개발을 위해서는 먼저 FOM을 통해 설계 변수 변화에 따른 해석 결과 데이터를 축적하는 과정이 필요하다. 해당 데이터를 통해 개발된 ROM은 구조 최적 설계나 성능 예측을 신속하게 수행하는 도구로 활용될 수 있다. 한편으로 침습적 방식의 POD-ROM을 활용하면 축소된 지배 방정식을 직접 풀기 때문에 구축된 ROM을 통해 구조물의 시공간에 따른 원하는 정보를 출력 및 확인하는게 용이하다. 따라서 특정 하중을 받는 구조물의 건전성이나 시간에 따른 특정 영역의 응력 분포 등을 신속하게 확인하는 목적으로 활용할 수 있다. 본 논문에서는 외연적 시간적분법의 임계 시간 간격을 증가시킬 수 있는 방법으로써 침습적 POD-ROM의 활용을 검증하고 VCLM과의 연계 활용을 목적으로 간단한 구조물을 대상으로 연구를 수행하였다.

3. 해석 결과

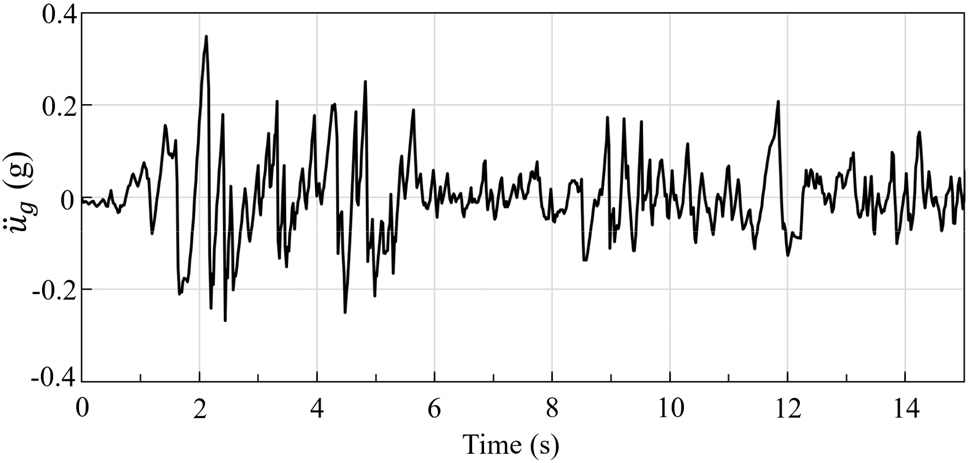
이 장에서는 지진하중을 받는 구조물을 대상으로 동적해석을 수행하고 해석 결과를 통해 축소 시스템의 임계 시간 간격 변화를 살펴보았다. 또한 POD 기반의 침습적 ROM과 VCLM의 연계를 통해 해당 수치해석 기술의 활용성을 검증하였다. 본 연구에 사용한 구조물은 Fig. 2에서 보는 바와 같다. 해당 구조물의 단면은 정사각 형태이며, 높이에 따라 단면적이 줄어드는 구조를 갖고 있다(Fig. 2(b)). 지진파 입력 조건 구현을 위해 구조물 바닥면의 자유도(Fig. 2(c))는 X-축 가진 방향을 제외한 방향을 모두 구속하였고, 시간에 따른 입력 가속도는 El Centro 지진파 데이터(Chopra, 2011)를 사용하였다(Fig. 3). Fig. 2(c)는 Voronoi-cell 격자 요소의 스프링 셋이 정의된 공통면(Fig. 1)을 기준으로 분할된 구조 모델을 보여준다. 구조물은 전체 시간 영역에서 탄성 거동을 나타냄을 가정하였고 전체적으로 균질한(homogeneous) 물성 분포를 가정하였다. 해당 물성치(𝜌 = 2400kg/m³, $E$ = 25.0GPa, $G$ = 12.5GPa)는 기존 참고문헌(Roh et al., 2012)의 값을 동일하게 활용하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F2.jpg

Fig. 2.

Geometric configurations of the structure: (a) side view, (b) top view, and (c) 3D view of the structural model

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F3.jpg

Fig. 3.

El Centro seismic data for ground acceleration

구조 모델의 이산화 수준은 해석 결과의 정확도와 소요 시간을 기준으로 결정하였다. 선행 연구(Hwang et al., 2022)에서 확인할 수 있는 바와 같이 해당 구조물의 횡방향 응답을 예측할 때 적은 수의 Voronoi-cell 격자 요소를 사용해도 높은 정확도의 결과를 얻을 수 있다. 본 연구에서는 ROM 적용에 따른 시스템 축소 효과와 해석 소요 시간 변화 분석을 위해서 보다 이산화된 형태의 구조 모델(205nodes, 688elements)을 사용하였고(Fig. 3(c)) 이를 FOM으로서 활용하였다.

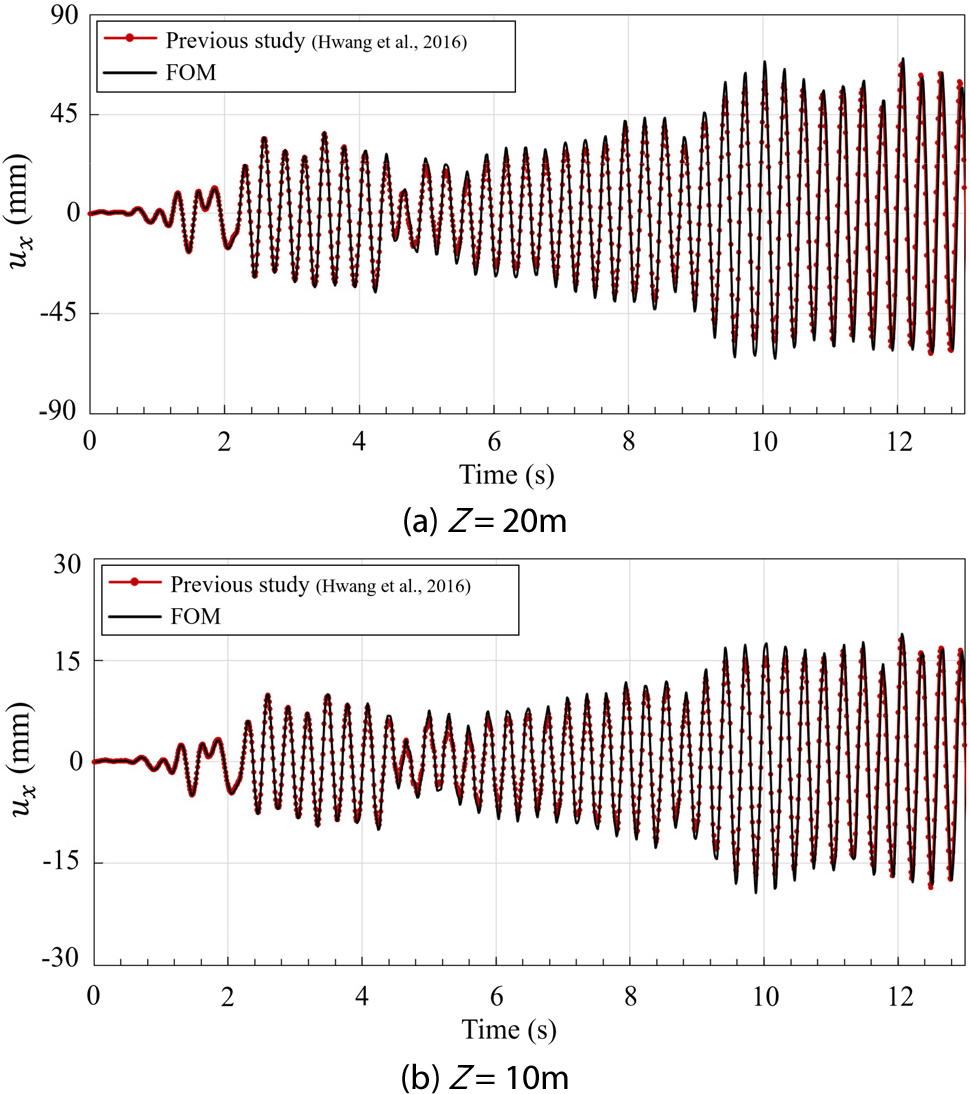
Fig. 4는 해석 결과로서 구조물의 정상층(z = 20m)과 중간층(z = 10m)에서의 횡방향 변위 응답을 보여준다. 해석 소요 시간을 감안하여 최대 변위 발생 이후 13.0s까지 해석을 수행하였다. 해석 결과의 비교 검증을 위하여 기존 연구에서 다룬 유한요소 해석 결과(Hwang et al., 2022)를 Fig. 4에 함께 도시하였다. 정상층과 중간층의 횡방향 변위 응답에 대한 평균 제곱근 오차(root mean square error, RMSE)는 각각 3.91mm와 1.28mm로 도출되었고, 비교 결과 VCLM을 통한 FOM의 해석 결과가 파의 주기나 진폭 측면에서 거의 동일한 수준임을 확인하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F4.jpg

Fig. 4.

Simulated results of the FOM for horizontal displacement histories at (a) Z = 20m and (b) 10m

이러한 FOM 해석 결과에 대한 기본 검증을 바탕으로 POD-ROM을 적용한 축소 시스템의 변위 응답과 임계 시간 간격 변화를 살펴보았다. 3차원에서 VCLM은 노드별로 병진 및 회전 자유도를 고려한 총 6개의 자유도를 갖는다. 따라서 해당 구조 시스템의 전체 자유도 m은 노드 수의 6배이며 POD에 사용하는 축소 기저 벡터의 수 r에 따라 구조 시스템의 축소 정도가 정해진다. 식 (6)의 X₀ 계산을 위하여 전체 자유도 m에 대한 FOM의 변위 응답을 시간 이력에 따라 0.02s 간격으로 추출하였다. 이후 시간에 따른 평균 성분을 제외한 최종 X₀를 계산하였다(Krysl et al., 2001; Taylor et al., 2011). 본 연구에서는 일련의 선행 해석을 통해 r 값에 따른 해석 결과의 정확도와 축소 정도를 살펴보았고, 최적의 r 값으로 15를 도출하였다. 이후 r 값이 줄어듦에 따라 해석 결과 정확도 및 임계시간 간격을 비교 분석하였다.

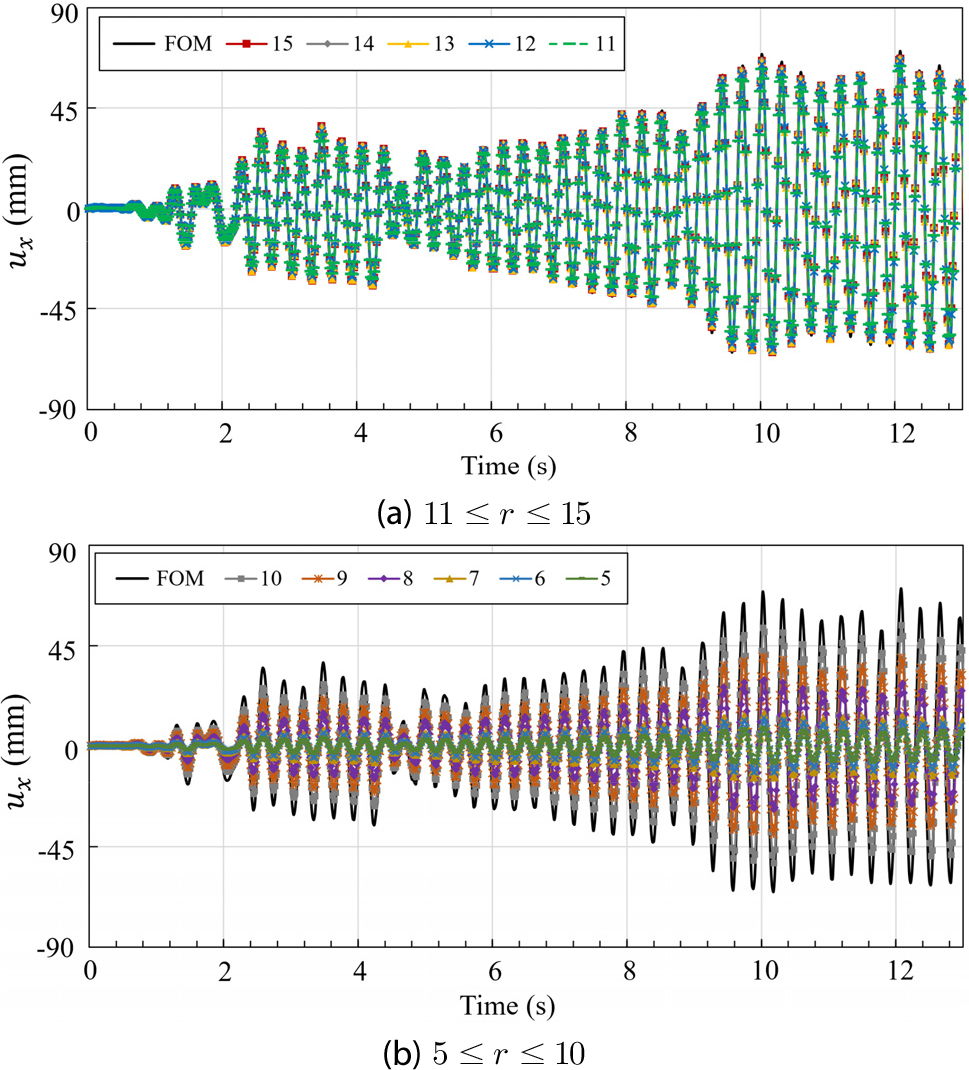
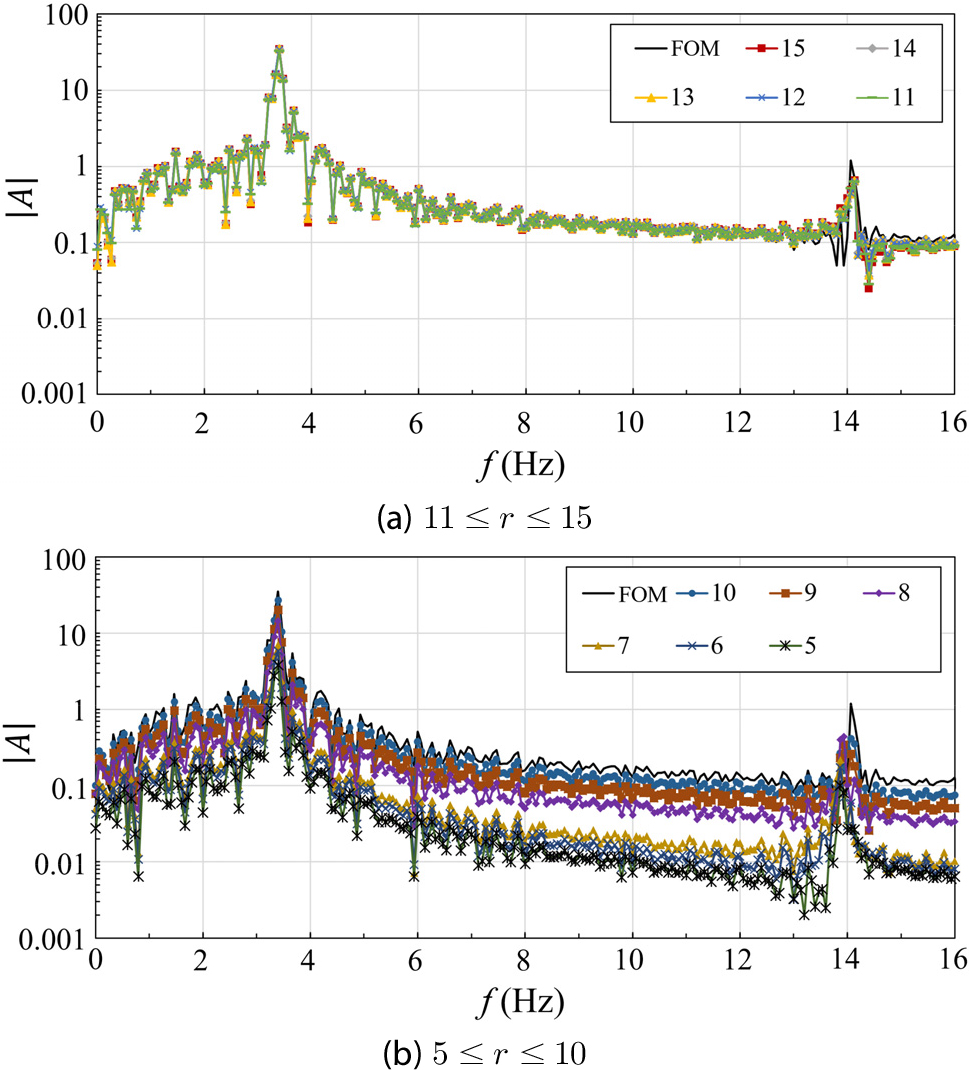
Fig. 5는 r 값에 따른 ROM의 횡방향 변위(z = 20m) 응답과 FOM의 결과를 함께 보여준다. 또한 해석 결과 비교의 용이성을 위해 Fig. 6에 12.0s과 12.5s 사이의 구간을 확대하여 나타내었다. 해당 결과를 통해 r 값이 줄어듦에 따라 변위 진폭이 줄어드는 것을 확인할 수 있는데, r 값이 15에서 11로 변할 때(Fig. 6(a))에 비하여 10 이하일 때(Fig. 6(b)) 변위 진폭이 상대적으로 크게 감소하는 것을 볼 수 있다. 한편 진동 주기는 Fig. 5에서 확인할 수 있는 바와 같이 전체적으로 유의미한 차이가 없지만 확대 구간(Fig. 6(b))을 통해 r 값의 감소에 따라 진동의 주기가 다소 길어지는 것을 관찰할 수 있다. 해당 내용은 고속 푸리에 변환(Brigham, 1988)을 통한 진동수 영역에서의 결과를 통해서도 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F5.jpg

Fig. 5.

Simulated results of the ROMs for the horizontal displacement histories at Z = 20m

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F6.jpg

Fig. 6.

Enlarged view for the horizontal displacements in the time range between 12.0 and 12.5s

Fig. 7은 진동수에 따른 변위 진폭 $| A |$ 에 대한 결과를 보여준다. 진동수 성분에 따른 진폭의 비교를 용이하게 하기 위하여 그래프의 세로 축은 로그 스케일로 나타내었다. 해당 구조물은 약 3.4Hz의 진동수에서 최대 진폭이 발생하고 약 3.0Hz와 4.0Hz 사이의 성분이 전체 구조 거동을 지배하는 것을 확인할 수 있다. Fig. 7(a)에서 확인할 수 있는 바와 같이 r 값이 11과 15 사이 범위의 경우 13.0Hz 이상의 상대적으로 높은 진동수 영역을 제외하고 ROM과 FOM의 결과와 거의 일치함을 확인하였다. 따라서 해당 축소 범위에서 ROM을 통해 구조물의 거동을 거의 정확하게 모사할 수 있음을 확인할 수 있다. 반면에 Fig. 7(b)에서 볼 수 있는 바와 같이 r 값이 10 이하로 줄어듦에 따라 모든 진동수 영역에서 FOM과 ROM의 결과 사이에 괴리가 발생하는 것을 확인할 수 있다. 특별히 r 값이 7 이하로 감소함에 따라 높은 진동수 영역에서 진폭이 0.01 이하인 구간이 점점 증가하는 것을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F7.jpg

Fig. 7.

Single-sided amplitude $| A |$ spectrum of the horizontal displacements at Z = 20m

해석 결과를 통해 ROM을 통한 축소 정도가 증가할수록 구조물의 전체 진동수 영역에서 진폭 크기가 감소하고 상대적으로 높은 진동수 영역에서 더 크게 진폭이 감소함을 확인하였다. 이는 식 (5)를 통해 유추할 수 있는 바와 같이 ROM 적용에 따라 외연적 시간적분법의 임계 시간 간격도 변할 수 있음을 의미한다. 일반적으로 ROM을 통한 축소 정도를 나타내는 적합 직교 모드의 수 r과 임계 시간 간격 $∆ t_{c r}$ 간의 엄밀한 수학적 관계식을 정의하기는 어렵다(Taylor et al., 2011). 또한 축소 대상이 되는 모델의 종류나 데이터 활용 방식 등에 따라 ROM의 결과가 어느 정도 달라질 수 있기 때문에 해석 결과 데이터를 기반으로 r에 따른 $∆ t_{c r}$ 의 변화 경향을 분석하였다.

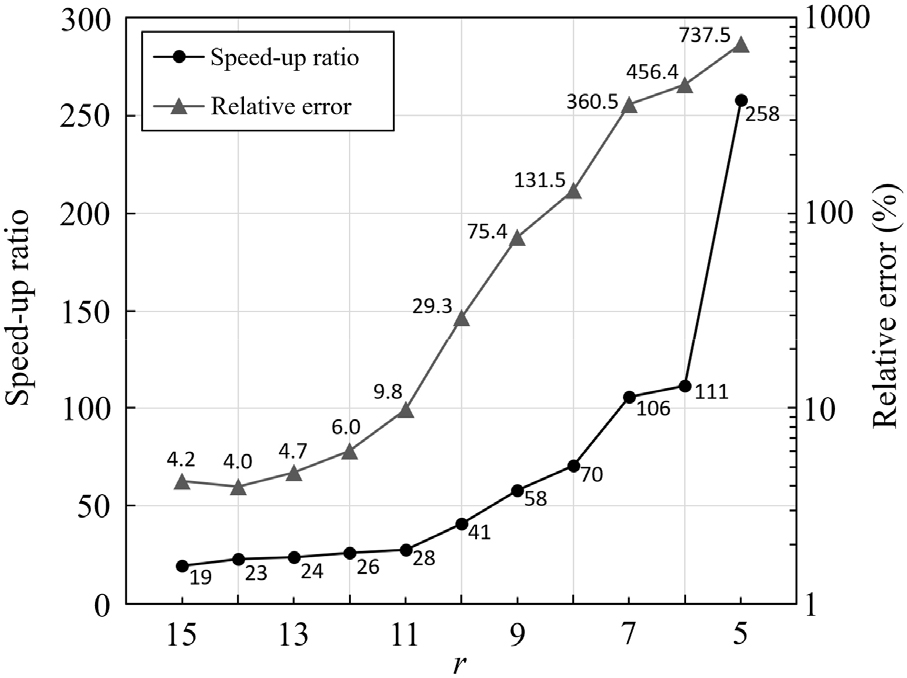
일련의 모의 과정을 통하여 특정 r 조건에서 해의 안정성을 해치지 않는 최대의 $∆ t$ 를 확인하였고 이를 $∆ t_{c r}$ 로 정의하였다. 이후 FOM의 $∆ t_{c r}$ 대비 r 값에 따른 ROM의 $∆ t_{c r}$ 의 비율인 속도 상승률(speed-up ratio)을 계산하였고 이를 Fig. 8에 그래프로 나타내었다. 그래프에서 가로 축은 r 값의 감소(축소 정도의 증가)에 따른 $∆ t_{c r}$ 의 증가 경향을 보기 위하여 역순으로 나타내었다. 가로축의 r 값이 15, 11, 8, 5인 경우 FOM 대비 ROM의 결과가 각각 19, 28, 70, 258배 빠른 결과를 도출할 수 있는 것을 확인할 수 있다. 또한 가로축의 r 값이 15에서 11 사이 구간의 경우 기울기가 대략 일정하게 유지되다가 11에서 8 사이의 구간에서는 더 가파른 기울기를 보이며, 이후 8보다 작은 값에서는 속도 상승률이 더욱 큰 폭으로 증가하는 것을 볼 수 있다. 그래프의 증가 경향은 전반적으로 지수함수적 증가 형태를 보이지만 일부 구간( $6 \leq r \leq 7$ )에서는 속도 상승률의 증가 수준이 줄어드는 구간도 확인할 수 있다. 이러한 세부적인 증가 정도 변화는 구조 모델의 종류나 이산화 정도, 해석 기법 종류에 따라 다를 것으로 판단된다. 더불어 축소 정도가 증가함에 따라 해석의 오차도 증가하는데, 이를 살펴보기 위하여 FOM과 ROM을 통해 도출한 해석 결과의 상대 오차 e를 계산하였다(Belytschko et al., 2013).

(10)

e (%) = \frac{{||u^{FOM} - u^{ROM}||}_{2}}{{||u^{FOM}||}_{2}} \times 100 (%)

여기서 $u$ 는 변위 벡터이며 정상층(z = 20)에서 시간 이력에 따른 횡방향 변위로 구성되고, ${||u||}_{2} (= \sqrt{u^{T} u})$ 는 $L_{2}$ norm 연산자를 의미한다. Fig. 8에서 확인할 수 있는 바와 같이 r 값이 감소함에 따라 상대 오차는 증가하는 경향을 보인다. 특별히 r이 15와 14일 때 오차가 각각 4.2%와 4.0%로 다소 감소하는데, 이는 식 (10)의 계산에 사용하는 데이터 분포에 따라 발생할 수 있는 차이로서 유의미한 차이로 보기는 어려우며 두 값(r = 15, 14) 모두 유사한 수준의 해석 정확도를 갖는 것으로 판단된다. 이후 r의 감소에 따라 오차가 꾸준히 증가하며, 특히 값이 11 때의 오차(9.8%)에서 10일 때의 오차(29.3%)가 크게 증가하는 것을 확인할 수 있다. 이는 앞서 Fig. 6과 Fig. 7의 해석 결과에서 확인할 수 있는 내용과 동일하다. 따라서 속도 상승률과 상대 오차 수준을 모두 감안할 때 해당 구조 모델의 경우 r 값을 11 이상의 범위에서 잡는 것이 타당함을 확인할 수 있었다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370102/images/Figure_jcoseik_37_01_02_F8.jpg

Fig. 8.

Speed-up ratio and relative error of the simulated results of ROMs

해석 결과를 바탕으로 POD-ROM의 적용을 통해 외연적 시간적분법의 임계 시간 간격을 증가시키고 전체 해석 시간을 크게 단축할 수 있음을 확인하였다. 이 외에도 POD-ROM을 동적 구조해석에서 적용함으로써 특정 시간 간격에 따라 매번 출력되는 구조 응답 데이터(변위, 속도 등)의 용량을 크게 줄일 수 있다. 축소 형태로 저장된 구조 응답 정보는 식 (9)의 역관계를 통해, 본래(FOM)의 자유도 수준으로 복원되어 이후의 후처리(post-processing) 과정에 사용될 수 있다. 따라서 POD-ROM을 통해 연산 과정에서 시간 응답 데이터의 입출력과 관련된 시간 및 비용을 크게 줄일 수 있다.

4. 결 론

본 연구에서는 POD-ROM을 통한 구조 시스템의 축소와 이에 따른 외연적 시간적분법의 임계 시간 간격 및 정확도 변화를 살펴보았다. 또한 VCLM을 통해 이산화된 운동방정식에 침습적 ROM을 적용하여 해당 수치해석 방법론의 정확성을 살펴보았다. 시간이력에 따른 불규칙한 구조 응답 데이터를 통해 구축한 POD-ROM의 우수성을 검증하기 위해서 지진하중을 받는 구조물의 거동 모의를 수행하였다. 이후 축소 정도에 따른 해석 결과의 정확성 및 속도 상승률을 비교 분석하였다. POD-ROM의 투영행렬을 구성하는 축소 기저 벡터의 수가 감소함에 따라 임계 시간 간격은 전반적으로 지수함수적으로 증가하는 것을 확인하였다. 이러한 증가 경향과 축소 정도에 따른 ROM의 오차와 비교하여 최적의 축소 기저 벡터의 수를 정할 수 있음을 확인하였다. 더불어 POD-ROM과 기존 VCLM을 통한 외연적 동적해석의 연계방안의 타당성을 확인하였고, 지진하중과 같은 불규칙한 패턴의 하중 상태에서도 POD-ROM이 잘 적용될 수 있음을 확인하였다.

비침습적 방식과 달리 침습적 ROM의 경우 직접 운동방정식을 계산하여 결과를 도출한다. 따라서 연구자나 설계자가 원하는 특정 위치나 시간에 따른 출력 값(응력, 변위 등)의 확인, 변경 등을 내부 해석 코드 수정을 통해 손쉽게 수행할 수 있다. 해당 연구 결과는 향후 설계 변수나 운영 조건에 따른 실시간 수준의 구조물 건전성 모니터링 등을 위한 요소 기술로서 활용될 수 있다. 특별히 본 연구에서 다룬 POD-ROM과 VCLM의 연계 방안을 확장하여 대변형 및 파괴 등을 수반하는 비선형 동적 거동 모의에 해당 축소 방법과 병렬컴퓨팅을 적용하는 연구를 수행할 예정이다.

Acknowledgements

본 연구는 한국과학기술정보연구원(KISTI)의 기본사업인 2023년 ‘산업 및 공공분야 문제 해결을 위한 초고성능컴퓨팅 활용 기술 개발(K-23-L02-C05-S01)’ 과제의 지원을 받아 수행되었습니다.

References

Belytschko, T., Liu, W.K., Moran, B., Elkhodary, K. (2013) Nonlinear Finite Elements for Continua and Structures, John Wiley & sons, p.823.

Brigham, E.O. (1988) The Fast Fourier Transform, Prentice-Hall, Inc., p.448.

Choo, B., Hwang, Y.K., Bolander, J.E., Lim, Y.M. (2023) Rigid-Body-Spring Network Model for Failure Simulation of Reinforced-Concrete Members Under Various Loading Rates, Int. J. Numer. & Anal. Methods Geomech., 47, pp.2213~2230. 10.1002/nag.3578

Chopra, A.K. (2011) Dynamics of Structures: Theory and Applications to Earthquake Engineering, Prentice Hall.

Cocchetti, G., Pagani, M., Perego, U. (2013) Selective Mass Scaling and Critical Time-Step Estimate for Explicit Dynamic Analyses with Solid-Shell Elements, Comput. & Struct., 127, pp.39~52. 10.1016/j.compstruc.2012.10.021

Fuller, A., Fan, Z., Day, C., Barlow, C. (2020) Digital Twin: Enabling Technologies, Challenges and Open Research, IEEE Access, 8, pp.108952~108971. 10.1109/ACCESS.2020.2998358

Gomez-Gesteira, M., Rogers, B.D., Crespo, A.J.C., Dalrymple, R.A., Narayanaswamy, M., Dominguez, J.M. (2012) SPHysics - Development of a Free-Surface Fluid Solver - Part 1: Theory and Formulations, Comput. & Geosci., 48, pp.289~299. 10.1016/j.cageo.2012.02.029

Han, J.S., Kim, S.H. (2021) Automation of Krylov Subspace Model Order Reduction for Transient Response Analysis with Multiple Loading, J. Comput. Struct. Eng. Inst. Korea, 34(2), pp.101~111. 10.7734/COSEIK.2021.34.2.101

Holder, T., Leimkuhler, B., Reich, S. (2001) Explicit Variable Step-Size and Time-Reversible Integration, Appl. Numer. Math., 39(3-4), pp.367~377. 10.1016/S0168-9274(01)00089-7

Hughes, T. (2012) The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Dover Publications, Mineola.

Hwang, Y.K., Bolander, J.E., Lim, Y.M. (2016) Simulation of Concrete Tensile Failure Under High Loading Rates Using Three-Dimensional Irregular Lattice Models, Mech. Mater., 101, pp.136~146. 10.1016/j.mechmat.2016.08.002

Hwang, Y.K., Lim, Y.M., Hong, J.-W. (2022) Simulation of Structural Vibrations Using Voronoi-Cell Lattice Models, J. Mech. Sci. & Technol., 36(2), pp.647~654. 10.1007/s12206-022-0112-z

Krysl, P., Lall, S., Marsden, J.E. (2001) Dimensional Model Reduction in Non-Linear Finite Element Dynamics of Solids and Structures, Int. J. Numer. Methods Eng., 51(4), pp.479~504. 10.1002/nme.167

Kwag, S., Eem, S., Jung, K., Jung, J., Choi, I.-K. (2022) A Study on the Effects of Nuclear Power Plant Structure-Component Interaction in Component Seismic Responses, J. Comput. Struct. Eng. Inst. Korea, 35(2), pp.83~91. 10.7734/COSEIK.2022.35.2.83

Lee, J. (2015) Proper Orthogonal Decomposition-Based Parametric Reduced Order Models for Structural Analysis and Design Optimization, Dissertation, Seoul National University.

Meister, F., Passerini, T., Mihalef, V., Tuysuzoglu, A., Maier, A., Mansi, T. (2020) Deep Learning Acceleration of Total Lagrangian Explicit Dynamics for Soft Tissue Mechanics, Comput. Methods Appl. Mech. & Eng., 358, p.112628. 10.1016/j.cma.2019.112628

Mira, D., Pérez-Sánchez E.J., Borrell, R., Houzeaux, G. (2023) HPC-Enabling Technologies for High-Fidelity Combustion Simulations, Proc. Combust. Inst., 39(4), pp.5091~5125. 10.1016/j.proci.2022.07.222

Olovsson, L., Simonsson, K., Unosson, M. (2005) Selective Mass Scaling for Explicit Finite Element Analyses, Int. J. Numer. Methods Eng., 63(10), pp.1436~1445. 10.1002/nme.1293

Permann, C.J., Gaston, D.R., Andrš, D., Carlsen, R.W., Kong, F., Lindsay, A.D., Miller, J.M., Peterson, J.W., Slaughter, A.E., Stogner, R.H., Martineau, R.C. (2020) MOOSE: Enabling Massively Parallel Multiphysics Simulation, SoftwareX, 11, p.100430. 10.1016/j.softx.2020.100430

Roh, H.-S., Youn, J.-M., Lee, H.-S., Lee, J.-S. (2012) Development of a New Lumped-Mass Stick Model using the Eigen-Properties of Structures, J. Earthq. Eng. Soc. Korea, 16(4), pp.19~26. 10.5000/EESK.2012.16.4.019

Taylor, Z.A., Crozier, S., Ourselin, S. (2011) A Reduced Order Explicit Dynamic Finite Element Algorithm for Surgical Simulation, IEEE Trans. Med. Imaging, 30(9), pp.1713~1721. 10.1109/TMI.2011.214372321511562

Van der Sande, K., Flyer, N., Fornberg, B. (2023) Accelerating Explicit Time-Stepping with Spatially Variable Time Steps Through Machine Learning, J. Sci. Comput., 96(1), pp.1~31. 10.1007/s10915-023-02260-z

Yip, M., Li, Z., Liao, B.-S., Bolander, J.E. (2006) Irregular Lattice Models of Fracture of Multiphase Particulate Materials, Int. J. Fract., 140, pp.113~124. 10.1007/s10704-006-7636-6

Journal of the Computational Structural Engineering Institute of KoreaISSN:1229-3059(Print) 2287-2302(Online)한국전산구조공학회

Preview

Proper Orthogonal Decomposition Based Intrusive Reduced Order Models to Accelerate Computational Speed of Dynamic Analyses of Structures Using Explicit Time Integration Methods

ABSTRACT

MAIN

Fig. 1.

3D Voronoi-cell lattice element i‐j with respect to the local (x-y-z) and global (X-Y-Z) coordinates

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Fig. 2.

Geometric configurations of the structure: (a) side view, (b) top view, and (c) 3D view of the structural model

Fig. 3.

El Centro seismic data for ground acceleration

Fig. 4.

Simulated results of the FOM for horizontal displacement histories at (a) Z = 20m and (b) 10m

Fig. 5.

Simulated results of the ROMs for the horizontal displacement histories at Z = 20m

Fig. 6.

Enlarged view for the horizontal displacements in the time range between 12.0 and 12.5s

Fig. 7.

Single-sided amplitude |A| spectrum of the horizontal displacements at Z = 20m

(10)

Fig. 8.

Speed-up ratio and relative error of the simulated results of ROMs

Acknowledgements

References

Single-sided amplitude $| A |$ spectrum of the horizontal displacements at Z = 20m