A Boundary-layer Stress Analysis of Laminated Composite Beams via a Computational Asymptotic Method and Papkovich-Fadle Eigenvector

Sin-Ho Kim; Jun-Sik Kim

doi:10.7734/COSEIK.2024.37.1.41

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 29 February 2024. 41-47
https://doi.org/10.7734/COSEIK.2024.37.1.41

A Boundary-layer Stress Analysis of Laminated Composite Beams via a Computational Asymptotic Method and Papkovich-Fadle Eigenvector

전산점근해석기법과 고유벡터를 이용한 복합재료 보의 경계층 응력 해석

Sin-Ho Kim¹

Jun-Sik Kim²^*

김 신호¹

김 준식²^*

¹Graduate Student, Department of Mechanical Engineering, Department of Aeronautics, Kumoh National Institute of Technology, Gumi, 39177, Korea

²Professor, Department of Mechanical System Engineering, Department of Aeronautics, Kumoh National Institute of Technology, Gumi, 39177, Korea

¹금오공과대학교 기계공학과 항공기계전자융합전공 박사과정

²금오공과대학교 기계시스템공학과 항공기계전자융합전공 교수

^{*Corresponding Author}

ABSTRACT

This paper utilizes computational asymptotic analysis to compute the boundary layer solution for composite beams and validates the findings through a comparison with ANSYS results. The boundary layer solution, presented as a sum of the interior solution and pure boundary layer effects, necessitates a mathematically rigorous formalization for both interior and boundary layer aspects. Computational asymptotic analysis emerges as a robust technique for addressing such problems. However, the challenge lies in connecting the boundary layer and interior solutions. In this study, we systematically separate the principles of virtual work and the principles of Saint-Venant to tackle internal and boundary layer issues. The boundary layer solution is articulated by calculating the Papkovich-Fadle eigenfunctions, representing them as linear combinations of real and imaginary vectors. To address warping functions in the interior solutions, we employed a least squares method. The computed solutions exhibit excellent agreement with 2D finite element analysis results, both quantitatively and qualitatively. This validates the effectiveness and accuracy of the proposed approach in capturing the behavior of composite beams.

Keywords

composite materials

boundary-layer stress

computational asymptotic analysis

papkovich-fadle eigenfunction

본 논문에서는 전산점근해석기법을 사용하여 복합재료 보에 대한 경계층 해를 계산하고, ANSYS 결과와 비교 검증하였다. 경계층 해는 내부해와 순수 경계층 효과의 합으로 표현되기 때문에, 내부 및 경계층에 대한 수학적으로 엄밀한 정식화를 요구한다. 전산점근해석기법은 수학적으로 매우 강력한 기법으로, 이러한 문제에 유용하다. 그러나 경계층과 내부 해들의 연결을 시키기 쉽지 않은데, 본 연구에서는 가상일의 원리를 통해 생브낭의 원리와 내부 및 경계층 문제를 체계적으로 분리하였다. 경계층 해는 팝코비치-패들 고유벡터를 계산하여, 실수부와 허수부 벡터들의 선형 조합으로 표현하고, 내부 해의 워핑 함수들을 보상할 수 있도록 최소오차 자승법을 적용하였다. 계산된 해들은 2차원 유한요소 해석 결과와 비교하여 정성적일 뿐만 아니라 정량적으로도 잘 일치하는 결과를 얻었다.

키워드

복합재료

경계층 응력

전산점근해석

팝코비치-패들 고유함수

MAIN

1. 서 론
2. 본 론
2.1 전산점근해석의 기초
2.2 내부해(Interior solution)
2.3 경계층해(Boundary-layer solution)
2.4 경계조건
2.5 점근적으로 정확한 경계조건
3. 수치 예제
3.1 등방성 보에서의 경계층 효과
3.2 횡등방성 보에서의 경계층 효과
3.3 복합재료 보에서의 경계층 효과
4. 결 론

1. 서 론

등방성 보에 관한 연구로부터 시작된 경계층 문제는 오랜 기간 응용 수학과 공학 분야에서 난제로 여겨져 왔다. 현대에는 컴퓨터의 발달로 구조 문제에서 경계층 문제는 어렵지 않게 해석할 수 있게 되었으나, 내부(interior)와 경계층(boundary-layer)를 이해하기 어렵다는 단점이 있다. 핵심은 경계층에 관한 엄밀해를 계산하기 어렵다는 것이다.

티모센코(Timoshenko and Goodier, 1970)의 외팔보 탄성해는 엄밀해가 아니며, 심지어는 정확한 내부해가 될 수 없다. Gregory와 Wan(1984)가 언급한 것처럼, 티모센코 탄성해에 사용한 경계조건은 수학적으로 엄밀하지 않기 때문이다. 따라서 경계조건 문제를 이해하기 위해서는 내부해와 경계층해를 구분할 필요가 있는데, 유한요소법을 포함한 일반적인 수치 해석적 방법론으로는 어려움이 있다. 경계층 해를 구하는 고전적인 방법으로는 Papkovich-Fadle 고유함수가 있다(Buchwald, 1964; Timoshenko and Goodier, 1970). 무한 외팔보에 대한 경계층 해는 Gregory와 Gladwell이 1982년에 계산하였으며, 후속 연구에서 경계조건을 얻는데 사용되었다. 이 방법론은 복합재료에 적용되었고(Buannic and Cartraud, 2001), 후에 복잡한 상반정리를 간략화한 평균 변위 경계조건이 개발되고 박판 보에 적용되었다(Kim et al., 2008). 평균 변위 경계조건을 개선한 응력 가중 변위 경계조건이 구속된 가상일의 원리로부터 유도되어 이방성 보의 해석에 사용되었다(Kim and Wang, 2011).

본 연구에서는 생브낭의 원리를 적용하여 고차의 섭동항을 계산하고(Jeong and Kim, 2016; Kim, 2012), 다중 축적법을 이용하여 내부해와 경계층해를 체계적으로 분리한다(Dauge and Gruais, 1998; Kim, 2022). 내부해의 경우에는 고전적인 점근해석기법을 적용하고, 경계층해는 Papkovich-Fadle 고유함수를 2차 고유치 문제로부터 계산한다. 얻어진 결과는 문헌에 보고된 결과 그리고 2차원 유한요소해석과 비교 검증한다. 등방성, 횡등방성 그리고 적층 복합재료 외팔보 문제의 경계층해를 고정단에서 계산하였다.

2. 본 론

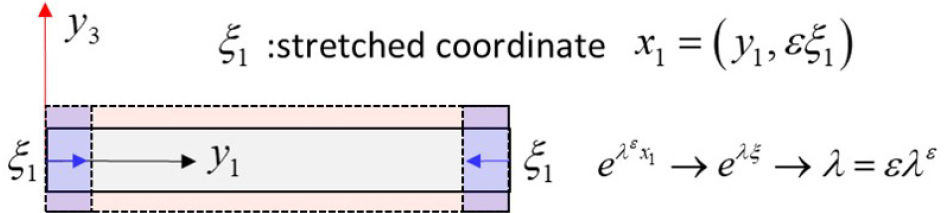
본 연구에서는 경계층 해와 내부 해를 동시에 계산하기 위하여, 다중 스케일 기법을 사용하였다(Fig. 1). 이를 적용하기 위한 방법론으로써 전산점근해석 기법 및 팝코비치-패들(Papkovich-Fadle) 고유함수를 도입하였다. 이 장에서는 이러한 방법론들을 소개하고, 다중 축적을 통해 내부해와 경계층해에 대한 정식화를 수행한다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370106/images/Figure_jcoseik_37_01_06_F1.jpg

Fig. 1.

Configuration and scale of composite beams for boundary-layers

2.1 전산점근해석의 기초

점근해석을 수행하기 위해서는 먼저 작은 매개변수(ε)의 항으로 적절한 축적(scale)이 선행되어야 한다. Fig. 1에서와 같이 축 방향으로는 빠른 축적과 느린 축적을 동시에 적용하고, 두께 방향으로는 빠른 축적만을 적용하였다. 이 축적을 적용한 2차원 변형률 벡터는 다음 식 (1), (2), (3)과 같이 쓸 수 있다.

(1)

γ^{ϵ} = \frac{1}{2} (\partial_{x_{j}} u_{i}^{ϵ} + \partial_{x_{i}} u_{j}^{ϵ}) = L_{1} \partial_{x_{1}} u^{ϵ} + L_{3} \partial_{x_{3}} u^{ϵ}

여기서

(2a)

γ^{ϵ} = {\{ε_{11}, ε_{33}, 2 ε_{13}\}}^{T}

(2b)

L_{1} = [\begin{matrix} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{matrix}], L_{3} = [\begin{matrix} 0 & 0 \\ 0 & 1 \\ 1 & 0 \end{matrix}], x_{1} = (y_{1}, ϵ ξ_{1}), x_{3} = ϵ y_{3},

미분에 다중 축적(multiple scale)을 적용하면 다음 식 (3)과 같고

(3)

\partial_{x_{1}} = \partial_{y_{1}} + \frac{1}{ϵ} \partial_{ξ_{1}} \equiv (∙)_{, 1} + \frac{1}{ϵ} (∙)_{, ξ_{1}}, \partial_{y_{3}} \equiv \frac{1}{ϵ} (∙)_{, 3}

이를 식 (1)에 적용하면 축적된 변형률 벡터를 얻는다.

(4)

γ^{ϵ} = L_{1} u_{, 1}^{ϵ} + \frac{1}{ϵ} (L_{3} u_{, 3}^{ϵ} + L_{1} u_{, ξ_{1}}^{ϵ})

섭동론에 따른 변위장의 점근전개는 아래와 같다.

(5)

u^{ϵ} (y_{i}, ξ_{1}; ϵ) = u^{(0)} (y_{1}) + ϵ u^{(1)} (y_{i}) + ϵ u^{(2)} (ξ_{1}, y_{i}) + \dots

여기서 0차 변위는 단순 강체운동을 1차 변위는 보의 기본 변위로써 0차 변형률을 0이 된다.

(6)

u^{(0)} = \{\begin{matrix} \begin{matrix} 0 \\ v_{3}^{(0)} \end{matrix} \end{matrix}\}, u^{(1)} = \{\begin{matrix} v_{1}^{(1)} - y_{3} v_{3, 1}^{(0)} \\ v_{3}^{(1)} \end{matrix}\} \equiv v^{(1)},

2차 변위부터는 이제 워핑(w)과 경계층(b) 효과를 고려하기 위해 아래와 같이 표현한다.

(7)

u^{(2)} (y_{i}, ξ_{1}) = v^{(2)} (y_{i}) + w^{(2)} (y_{i}) + b^{(2)} (ξ_{1}, y_{3}) .

식 (5)를 식 (4)에 대입하여 차수별로 정리하면 점근 전개된 변형률 벡터를 얻을 수 있으며, 구성방정식을 이용하여 점근 전개된 응력 벡터를 얻을 수 있다. 식 (7)을 식 (4)에 대입하면 변형률 벡터는 다음 식 (8), (9)와 같다.

(8)

γ^{ϵ} = γ_{I}^{ϵ} + γ_{B}^{ϵ} = ϵ (γ_{I}^{(1)} + γ_{B}^{(1)}) + ϵ^{2} (γ_{I}^{(2)} + γ_{B}^{(2)}) + \dots

여기서

(9a)

γ_{I}^{(k)} = Φ e^{(k)} + L_{1} w_{, 1}^{(k)} + L_{3} w_{, 3}^{(k + 1)}

(9b)

γ_{B}^{(k)} = L_{1} b_{, ξ_{1}}^{(k + 1)} + L_{3} b_{, 3}^{(k + 1)}

그리고 거시적 변형률 벡터 e는 아래 식 (10)과 같이 정의된다.

(10)

Φ = [\begin{matrix} 1 & - y_{3} \\ 0 & 0 \\ 0 & 0 \end{matrix}], e^{(k)} = \{\begin{matrix} v_{1, 1}^{(k)} \\ v_{3, 11}^{(k - 1)} \end{matrix}\}, k \geq 1 .

응력은 일반 이방성(general anisotropic, C) 재료에 대한 2차원 구성방정식을 사용하면 아래 식 (11)과 같이 쓸 수 있다.

(11)

σ_{I}^{(k)} = C γ_{I}^{(k)}, σ_{B}^{(k)} = C γ_{B}^{(k)}

이 응력 (11)과 변형률 (9)로 내부 가상일 밀도함수는 아래 식 (12)와 같이 점근 전개된 형태로 나타난다.

(12)

δ U = δ (γ^{ϵ})^{T} σ^{ϵ} = δ U^{(0)} + ϵ δ U^{(1)} + ϵ δ U^{(2)} + \dots

여기서 각 차수의 내부(internal) 가상일은 내부(interior)와 경계층(boundary-layer) 가상일로 구분할 수 있다. 0차 및 1차 에너지에서는 기본 변위장 식 (6)의 구성을 정당화하며, 첫 번째로 의미 있는 해는 2차 내부 가상일에서 얻을 수 있다.

(13)

δ U^{(2)} = δ {(γ_{I}^{(1)})}^{T} σ_{I}^{(1)} + \underline{δ {(γ_{I}^{(1)})}^{T} σ_{B}^{(1)} + δ {(γ_{B}^{(1)})}^{T} σ_{I}^{(1)}} + δ {(γ_{B}^{(1)})}^{T} σ_{B}^{(1)}

여기서 하첨자 ‘I’는 내부해를 ‘B’는 경계층해를 나타낸다. 이 식에서 밑줄 친 부분은 생브낭의 원리를 확인해 주는데, 경계층해와 내부해의 곱은 0이라는 것이다. 이는 내부해에 대한 정당성을 주며, 경계층해에 대한 구속조건 같은 역할을 한다.

2.2 내부해(Interior solution)

내부해는 식 (13)의 첫 번째 항을 풀면 얻을 수 있는데, 주요 변수인 워핑 함수와 거시적 보 방정식을 찾는 것이 목적이다. 워핑함수를 일반적인 재료와 형상에 대해 찾기 위해 1차원 유한요소 이산화를 수행하였다.

(14)

w^{(k)} (y_{i}) = S (y_{3}) {\bar{w}}^{(k)} (y_{1})

여기서 S는 전형적인 1차원 유한요소 보간함수이다. 식 (14)를 식 (13)의 첫 번째 대입하면

(15)

{(δ e^{(1)})}^{T} ⟨ Φ^{T} σ^{(1)} ⟩ + {(δ {\bar{w}}^{(2)})}^{T} ⟨ (L_{3} S_{, 3})^{T} σ^{(1)} ⟩

여기서 $< ∙ >$ 는 보의 두께 방향으로 적분을 의미한다. 식 (15)의 첫 번째 항은 거시적 보 방정식을 두 번째 항은 미시적 워핑 방정식을 나타내며, 먼저 미시적 방정식을 풀어 워핑함수를 찾는다. 이때 워핑함수는 보 단면의 강체운동에 직교한다는 구속조건을 걸어야 한다. 유한요소 해는 다음과 같이 벡터 형식으로 나타낼 수 있다.

(16)

{\bar{w}}^{(2)} = Γ_{e}^{(1)} e^{(1)}

식 (16)을 식 (11)에 대입하면 1차 응력을 계산할 수 있는데, 먼저 거시적 변형률 벡터 e를 찾아야 한다. 다만 경계조건을 정확하게 계산하기 위해서는 경계층 해를 먼저 계산해야 해서 다음절에서 자세히 다루고자 한다. 거시적 변형률 벡터를 찾고 나면 내부(interior) 응력은 다음 식 (17)과 같다.

(17)

σ_{I}^{(1)} = C (Φ + L_{3} S_{, 3} Γ_{e}^{(1)}) e^{(1)}

고차 내부해는 같은 방식으로 계산되며, 재귀 방정식 형태로 나타난다 (Buannic and Cartraud, 2001; Kim, 2022). 자세한 식은 제한된 지면 관계상 생략한다.

2.3 경계층해(Boundary-layer solution)

경계층해는 식 (13)의 마지막 항을 풀면 얻을 수 있다. 주요 변수로는 경계층 고유치와 고유벡터이며, 고유벡터의 해석해는 팝코비치-패들(Papkovich-Fadle) 고유함수로 알려져 있다(Buchwald, 1964). 이를 위해 경계층 변위 $b$ 를 1차원 유한요소법으로 이산화하였으며, 다음과 같은 형태로 가정할 수 있다.

(18)

b^{(2)} = \exp (λ ξ_{1}) S (y_{3}) {\bar{b}}_{v}^{(2)}

여기서 λ는 고유치이며, 마지막 항은 고유벡터이다. 식 (18)을 식 (13)에 대입하여 ξ₁에 대한 부분적분을 수행하고 정리하면 2차 고유치 문제(quadratic eigenvalue problem)로 나타나며 아래 식 (19), (20)과 같다.

(19)

[K_{33} + λ (K_{31} - K_{31}^{T}) - λ^{2} K_{11}] {\bar{b}}_{v}^{(2)} = 0

여기서

(20)

K_{33} = < (L_{3} S_{, 3})^{T} C (L_{3} S_{, 3}) >, K_{31} = < (L_{3} S_{, 3})^{T} C (L_{1} S) >, K_{11} = < (L_{1} S)^{T} C (L_{1} S) > .

식 (19)의 해는 고유치와 고유벡터로 이는 모든 차수에서 같은 함수를 가지므로, 한 번만 계산하면 된다. 이 고유벡터들에 기본 변위를 추가하여 급수로 경계층 변위를 표현한다. 이때 고유벡터들은 복소수이기 때문에 실수부와 허수부의 벡터를 독립적으로 취급한다.

(21)

{\bar{b}}^{(2)} = [\bar{Ψ}, B_{R}] {\bar{c}}_{R}^{(2)} + [\bar{Ψ}, B_{I}] {\bar{c}}_{I}^{(2)}, Ψ = S \bar{Ψ}

여기서,

(22)

Ψ = [\begin{matrix} 1 & 0 & y_{3} \\ 0 & 1 & 0 \end{matrix}], \begin{matrix} B_{R} = Re [{\bar{b}}_{v 1}, {\bar{b}}_{v 2}, \dots, {\bar{b}}_{vm}] \\ B_{I} = Im [{\bar{b}}_{v 1}, {\bar{b}}_{v 2}, \dots, {\bar{b}}_{vm}] \end{matrix}

식 (21)에서 미정 계수 벡터인 c는 경계조건으로부터 찾을 수 있으며, 이어지는 절에서 설명한다.

2.4 경계조건

여러 가지 경계조건 중에서도 변위 기술 경계조건이 어려운 문제 중의 하나이다. 본 연구에서는 대표적으로 고정단에서의 변위 경계조건의 문제에 대한 해를 제시하고자 한다. 0차 및 1차 변위는 통상적인 경계조건으로 기술되어 문제가 되지 않지만, 2차 변위부터는 워핑 변위로 인하여 변위 기술 경계에서 정확하게 만족하기 어렵다. 경계에서의 변위가 0이라는 조건은 최소 오차 자승법을 적용하여 아래와 같이 표현할 수 있다(Gregory and Gladwell, 1982).

(23)

\min_{c_{1}} < ∥ w^{(k)} + b^{(k)} ∥ > = 0, k \geq 2

이 식은 연립방정식을 구성하며 내부(interior) 워핑변위를 보상하는 경계층 변위를 계산할 수 있게 한다. 사용된 고유함수는 적게는 10개에서 많게는 200개까지가 필요하다. 이렇게 많은 함수가 필요한 이유는 경계에서 응력과 변위가 매우 급격하게 변하기 때문인데, 이러한 변화는 수치예제에서 그림으로 확인할 수 있다.

한편 자유단 경계조건은 응력이 기술된 조건으로 볼 수 있으며, 아래와 같이 쓸 수 있다.

(24)

\min_{c_{1}} < ∥ σ_{I}^{(k)} + σ_{B}^{(k)} ∥ > = 0, k \geq 1

식 (23)과 (24)는 경계층 해를 결정하며, 내부해를 직접적으로 결정하는 것은 아니다. 따라서 내부해에 대한 경계조건은 특별히 취급하여야 한다. 문헌에 따르면 멕스웰-베티(Maxwell-Betti) 정리를 이용하여 경계조건을 유도한다(Gregory and Wan, 1984).

(25)

(σ^{ϵ}, u_{I}^{ϵ}) - (σ_{I}^{ϵ}, u^{ϵ}) = 0 as ξ_{1} \to 0

이를 이용하면 고정단에서의 경계조건은 다음과 같다.

(26)

(σ^{ϵ}, u_{I}^{ϵ}) = 0, ∵ u^{ϵ} = 0 on S_{u}

식 (26)은 Kim과 Wang(2011)이 제안한 구속된 가상일의 원리에서의 변위 기술 경계조건과 같은 조건임을 알 수 있다. 라그랑지 승수법을 도입한 변위 경계조건은 아래와 같다.

(27)

{<(δ σ_{B}^{ϵ} + δ σ_{I}^{ϵ})^{T} u_{I}^{ϵ}>}_{S_{u}} = 0,

여기서 두 번째 항은 일반적인 보 이론에서의 변위 경계조건이며, 첫 번째 항은 경계층해가 내부에서 쇠하기 위한 조건으로 경계층이 내부에 영향을 주는 지를 나타내는 척도이다. 일반적인 등방성 구조물에서는 첫 번째 항의 영향은 미미하나, 이방성이 강한 구조물에서는 내부에 무시 못 할 영향을 준다.

2.5 점근적으로 정확한 경계조건

앞 절에서 언급한 것처럼, 경계조건은 차수별로 결정해야 하는데, 이를 점근적으로 정확한 조건이라 한다. 점근 전개된 내부 변위를 식 (27)에 대입하고 차수별로 정리하여 Table 1에 나타내었다. 표에서의 응력은 내부와 경계층 효과를 모두 포함하고 있다.

Table 1

Asymptotically correct boundary conditions

Energy Order	Boundary conditions at each order
0차 : ε²	$v_{1}^{(1)} = v_{3}^{(0)} = v_{3, 1}^{(0)} = 0$
1차 : ε³	$<δ σ_{11}^{(1)} u_{1}^{(2)} + δ σ_{13}^{(2)} {u_{3}}_{S_{u}}^{(1)}> = 0$
2차 : ε⁴	$<δ σ_{11}^{(1)} u_{1}^{(3)} + δ σ_{13}^{(2)} {u_{3}}_{S_{u}}^{(2)}> = 0$
3차 : ε⁵	$<δ σ_{11}^{(1)} u_{1}^{(4)} + δ σ_{13}^{(2)} {u_{3}}_{S_{u}}^{(3)}> = 0$

표에서 0차 경계조건은 고전적인 오일러-베르누이 보의 그것과 같으며, 1차 조건은 굽힘과 전단 연성이 있는 문제에서 0이 아닌 조건을 준다. 2차 경계조건은 전단변형에 대한 보정이며, 약한 경계층 효과를 포함한다. 3차 경계조건은 경계층 효과가 지배적인 조건이며, 여기서부터는 경계층 문제를 풀지 않는다면 큰 의미가 없다.

3. 수치 예제

먼저 이방성 보의 결과를 검증하고, 복합재료 보에 대한 경계층 응력의 영향을 시뮬레이션한다. 보의 길이 대 두께 비(S=L/h)는 10이며, 세 가지 재료에 대해 수치해석을 수행하였으며, 재질 상수들은 Table 2에 주어져 있다.

Table 2

Material properties

Type	Material properties
Isotropic	$E = 1 GPa, ν = 0.3$
Transversely Isotropic	$E = 1 GPa, ν = 0.3, G = 1 MPa$
Laminated Composite	$E_{L} = 172.4 GPa, E_{T} = 6.9 GPa, ν_{L T} = ν_{T T} = 0.3, G_{L T} = 3.45 GPa, G_{T T} = 1.38 GPa$

3.1 등방성 보에서의 경계층 효과

등방성 보에 대한 2차 고유치 문제(19)에서 첫 10개의 고유치를 Buchwald(1964) 그리고 Kim(2022)의 결과와 비교하여 Table 3에 나타내었다. 표에서 Buchwald의 결과는 Papkovich-Fadle 고유함수를 해석적으로 구한 것이기 때문에 엄밀해로 간주할 수 있으며, Kim의 결과는 워핑 함수에 기초하여 단순화된 식으로 계산된 것이다. 본 연구의 결과는 엄밀해와 수치적 오차로 생각될 정도의 차이를 보이지만, Kim의 결과는 1차 고유치만을 근사함을 알 수 있다. 이는 2차 고유함수부터는 두께 방향으로 고차 곡선의 형태를 가지기 때문이다.

Table 3

First six eigenvalues for the isotropic material

Mode		Eigenvalues
Mode		Symmetric	Anti-symmetric
1	Buchwald	-4.21239+2.25073i	-7.49768+2.76858i
	Kim	-4.58258+0.00000i	-7.00000+0.00000i
	Present	-4.21239+2.25073i	-7.49768+2.76868i
2	Buchwald	-10.7125+3.10319i	-13.9000+3.35221i
	Kim	-5.58570+0.00000i	-11.7488+0.00000i
	Present	-10.7125+3.10315i	-13.9000+3.35217i
3	Buchwald	-17.0734+3.55108i	-20.2385+3.71677i
	Kim	-7.74597+0.00000i	-12.4900+0.00000i
	Present	-17.0736+3.55089i	-20.2392+3.71618i

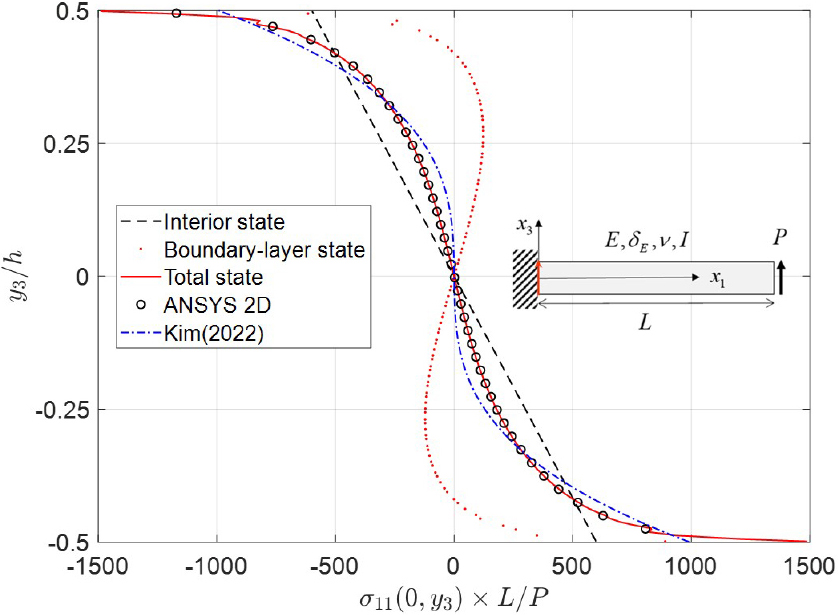
Table 3에서 보이는 고유치의 정확도는 외팔보의 끝단에 전단력(P)이 가해진 보의 고정단에서의 응력분포를 살펴봄으로써 알 수 있다. Fig. 2에는 고정단에서의 전단응력 분포를 현재의 방법론으로 계산한 결과를 ANSYS 2D 해석 결과 그리고 Kim(2022) 결과와 비교하여 도시하였다. 그림에서 보듯이 Kim의 결과는 간단한 해석으로 정성적인 분포는 묘사할 수 있으나, 정량적인 정확도가 떨어지며 본 논문에서 제시한 고유함수 방법은 2차원 유한요소해석의 결과와 잘 일치함을 알 수 있다. 다만 현재의 방법론은 ANSYS 해석과 거의 동등한 전산 자원을 요구한다는 단점이 있다. 그런데도 본 방법론이 가지는 의의는 내부해와 경계층해의 영향도를 구분할 수 있어 구조물에서 응력분포에 대한 이해도를 높일 수 있다는 점에 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370106/images/Figure_jcoseik_37_01_06_F2.jpg

Fig. 2.

The transverse shear stress through the thickness of a beam at the root for an isotropic cantilever loaded at the end

Table 3에서 보이는 고유치의 오차는 보의 변위에 있어서는 전혀 나타나지 않으며, 이를 쉐도우(shadow) 상태라 부르기도 한다(Dauge and Grais, 1998). 따라서 등방성 보의 경우 기준선에서의 보의 처짐은 모두 같은 결과를 보여준다. 이는 경계층 응력 상태가 고정단에서 멀어지면서 얼마나 빨리 쇠하는지를 보면 알 수 있는데, 이를 Fig. 3에 도시하였다. 그림에서 수직응력, 전단응력 그리고 횡방향 수직응력을 모두 볼 수 있으며, 두께의 0.3배 정도에서는 경계층 응력 상태는 거의 무시할 수 있는 수준이 된다. 이러한 빠른 쇠퇴는 경계층 해가 거시적 거동에 영향이 없다는 것을 뒷받침한다.

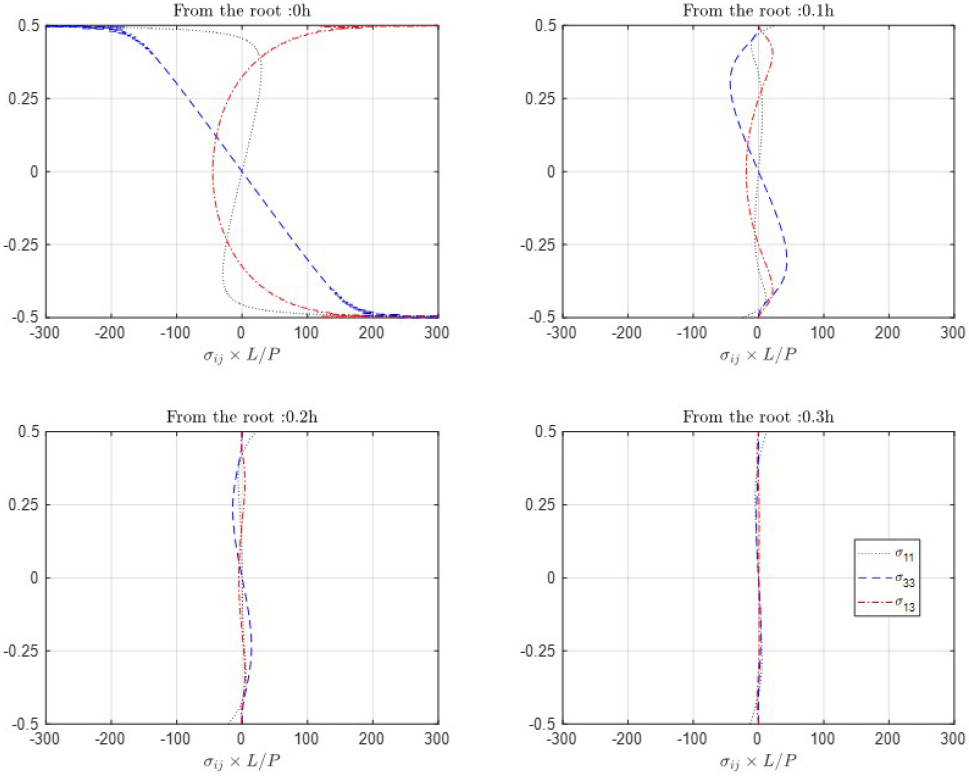
https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370106/images/Figure_jcoseik_37_01_06_F3.jpg

Fig. 3.

The decaying boundary-layer stress state at 0h, 0.1h, 0.2h, and 0.3h from the root for Fig. 2

3.2 횡등방성 보에서의 경계층 효과

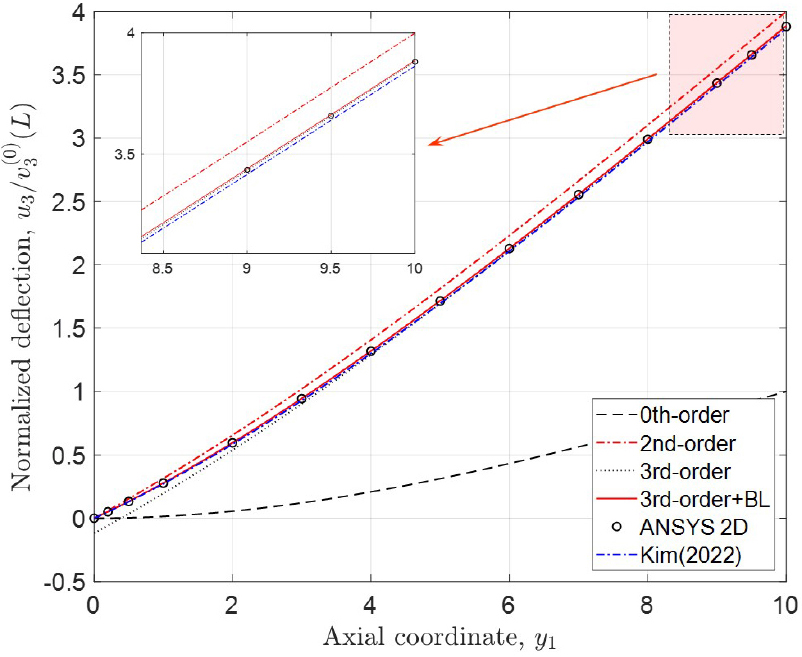
등방성 보에서의 경계층 효과는 거시적 거동에 매우 적은 영향을 미침을 앞 절에서 보았다. 경계층 효과의 극적인 효과를 확인하기 위하여 전단 계수(G)가 영계수(E)에 비해 매우 작은(Table 2) 전단변형에 취약한 외팔보를 고려하였다. 길이 방향으로의 처짐 곡선을 Fig. 4에 도시하였다. 그림에서는 0차, 2차, 3차, 그리고 3차+경계층 해를 ANSYS 및 Kim(2022) 결과와 비교하였다. 0차 해는 고전적인 오일러-베르누이 해와 같은 결과를 보여주며, 2차 해는 고정단에서의 기울기 보정을 3차 해는 처짐 보정을 받는다. 경계층 해를 고려한 본연구의 결과는 ANSYS와 일치함을 알 수 있다. 반면에 Kim의 결과는 적은 오차를 보이는데, 이는 앞서 설명한 것처럼 고유함수의 부정확성에 기인한다. 다만 거시적 거동의 정성적 예측에 있어서는 계산 노력 대비 매우 효율적인 방법이다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370106/images/Figure_jcoseik_37_01_06_F4.jpg

Fig. 4.

Normalized deflection along the axial coordinate for an transversely isotropic cantilever loaded at the end

등방성 보와는 매우 강한 경계층 상태가 고정단에서 발생하며 보의 내무 전 영역에 걸쳐 영향을 미친다. 고정단에서의 수직 응력분포를 Fig. 5에 도시하였다. 고정단 모서리에서 발생하는 특이 응력을 잘 모사하고 있으며, 2차원 유한요소해석보다 더 효율적이다. 2차원 유한요소법을 사용하여 특이 응력의 정밀한 계산을 위해서는 매우 세밀한 메시(mesh)가 필요하다. 한편 Kim의 결과는 정확도는 떨어지지만, 경계층 해의 정성적 분포를 잘 모사하는 것을 알 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370106/images/Figure_jcoseik_37_01_06_F5.jpg

Fig. 5.

The normal stress through the thickness of a beam at the root for an transversely isotropic cantilever loaded at the end

3.3 복합재료 보에서의 경계층 효과

마지막 예제로써 적층 복합재료 보의 경계층 해를 계산하였다. 직교 적층 배열은 [0/90/0]이며, 두께 좌표는 (-1/2,-1/6, 1/6, 1/2)이고, 재질 상수는 Table 2에 주어졌다. 먼저 경계층의 감쇠 정도를 확인하기 위해 2차 고유치 문제의 고유치와 고유벡터를 Table 4에 정리하였다. 표에는 첫 6개의 값을 도시하였으며, 첫 번째 감쇠비는 1.33으로 등방성의 4.2에 비해 느리게 쇠함을 알 수 있다. 이는 등방성에 비해 경계층의 범위가 보의 내부로 전파됨을 의미한다. 고유벡터의 분포는 적층 경계면을 기준으로 파장이 달라짐을 볼 수 있으며, 고차도 느리게 감소함을 알 수 있다.

Table 4

First six eigenvalues for [0/90/0] composite

Mode	Eigenvalues and Eigenvectors
Mode	Symmetric	Anti-symmetric
1	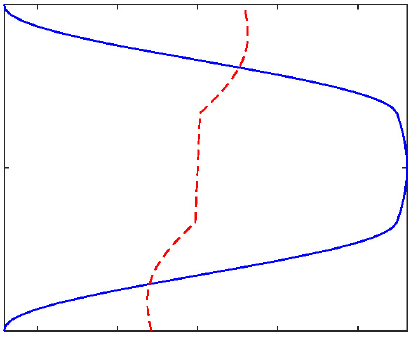-1.334086+0.00000i	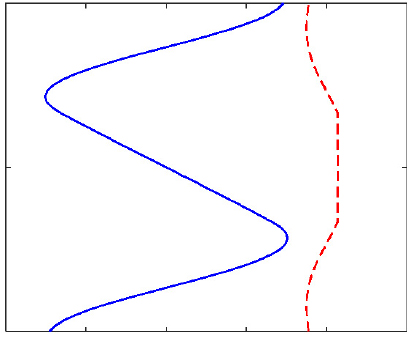-1.489395+0.00000i
2	-2.666105+0.00000i	-2.77577+0.00000i
3	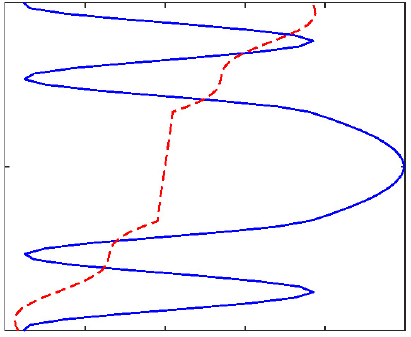-3.993444+0.00000i	-4.096993+0.00000i

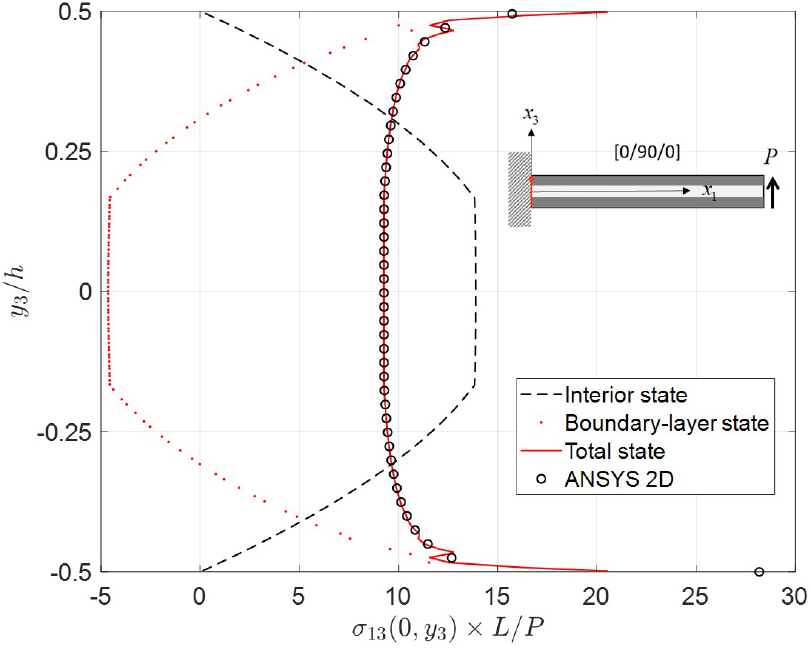
고정단에서의 전단 응력분포를 Fig. 6에 도시하였다. 등방성에서 보이는 경향성이 중간층에서 재질이 바뀜에 따라 보다 명확하게 보인다. 경계층 응력은 내부 응력과 크기가 같고 부호가 반대이며, 모서리에서는 응력이 무한대로 가는 경향성을 확인할 수 있다. 본 논문에서 제안한 팝코비치-패들 고유함수 방법을 통해 얻은 결과는 ANSYS 결과와 정성적일 뿐만 아니라 정량적으로도 잘 일치한다. 복합재료 구조물의 경계층 해석에 있어 2차원 유한요소해석을 대체할 수 있고, 해의 정확도 검증에 사용될 것으로 기대된다.

https://static.apub.kr/journalsite/sites/jcoseik/2024-037-01/N0040370106/images/Figure_jcoseik_37_01_06_F6.jpg

Fig. 6.

The transverse shear stress through the thickness of a beam at the root for a laminated composite [0/90/0] beam

4. 결 론

본 연구에서는 전산점근해석기법으로 내부해와 경계층해에 대한 정식화를 수행하였다. 경계층 해는 팝코비치-패들 고유함수 방법을 이용하여 계산하였으며, 멕스웰-베티 정리로부터 점근적으로 정확한 경계조건을 계산하였다. 이는 구속된 가상일의 원리에서 얻은 조건과 같으며, 3차 문제까지 계산하였다. 계산된 경계층과 경계조건은 등방성 및 적층 복합재료 보의 해석에 적용하였으며, 2차원 유한요소법의 결과와 잘 일치함을 알 수 있었다. Kim(2022)의 경계층 해에 대한 검증도 시도하였으며, 정성적으로 일치하지만, 정량적으로는 한계가 있음을 보였다. 본 연구에서 제시한 방법론은 경계층에 대한 기준으로서 역할을 할 것으로 기대된다.

Acknowledgements

이 연구는 금오공과대학교 학술연구비로 지원되었음(202103770001).

References

Buannic, P., Cartraud, P. (2001) Higher-order Effective Modeling of Periodic Heterogeneous Beams. II. Derivation of the Proper Boundary Conditions for the Interior Asymptotic Solution, Int. J. Solids & Struct., 38, pp.7163~7180. 10.1016/S0020-7683(00)00423-6

Buchwald, V. (1964) Eigenfunctions of Plane Elastostatics I. The Strip, Proc. Royal Soc. London. Ser. A, Math., Phys. Sci., 277, pp.385~400. 10.1098/rspa.1964.0029

Dauge, M., Gruais, I. (1998) Edge Layers in Thin Elastic Plates, Comput. Methodsn Appl. Mech. & Eng., 157, pp.335~347. 10.1016/S0045-7825(97)00244-2

Gregory, R.D., Gladwell, I. (1982) The Cantilever Beam under Tension, Bending or Flexure at Infinity, J. Elast., 12(3), pp.317~343. 10.1007/BF00042208

Gregory, R.D., Wan, F.Y. (1984) Decaying Sates of Plane Strain in a Semi-Infinite Strip and Boundary Conditions for Plate theory, J. Elast., 14, pp.27~64. 10.1007/BF00041081

Jeong, Y-M, Kim, J.-S. (2016) A Thermal Stress Analysis of Beams with Out-of-Plane Warping, J. Comput. Struct. Eng. Inst. Korea, 29(3), pp.229~235. 10.7734/COSEIK.2016.29.3.229

Kim, J.-S. (2012) Application of Saint-Venant's Principle to Anisotropic Beams, Trans. Korea Soc. Mech. Eng. A, 36(4), pp.451~455. 10.3795/KSME-A.2012.36.4.451

Kim, J.-S. (2022) Asymptotic Closed-form Solutions Including Boundary-Layers for Orthotropic Beams, Eur. J. Mech. A Solids, 94, p.104541. 10.1016/j.euromechsol.2022.104541

Kim, J.-S., Cho, M., Smith, E.C. (2008) An Asymptotic Analysis of Composite Beams with Kinematically Corrected End Effects, Int. J. Solids & Struct., 45, pp.1954~1977. 10.1016/j.ijsolstr.2007.11.005

Kim, J.-S., Wang, K.W. (2011) On the Asymptotic Boundary Conditions of an Anisotropic Beam Via Virtual Work Principle, Int. J. Solids & Struct., 48, pp.2422~2431. 10.1016/j.ijsolstr.2011.04.016

Timoshenko, S.P., Goodier, J.N. (1970) Theory of Elasticity, 3^rd Ed, McGraw-Hill, New York. 10.1115/1.3408648

Journal of the Computational Structural Engineering Institute of KoreaISSN:1229-3059(Print) 2287-2302(Online)한국전산구조공학회

Preview

A Boundary-layer Stress Analysis of Laminated Composite Beams via a Computational Asymptotic Method and Papkovich-Fadle Eigenvector

ABSTRACT

MAIN

Fig. 1.

Configuration and scale of composite beams for boundary-layers

(1)

(2a)

(2b)

(3)

(4)

(5)

(6)

(7)

(8)

(9a)

(9b)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

Table 1

Asymptotically correct boundary conditions

Table 2

Material properties

Table 3

First six eigenvalues for the isotropic material

Fig. 2.

The transverse shear stress through the thickness of a beam at the root for an isotropic cantilever loaded at the end

Fig. 3.

The decaying boundary-layer stress state at 0h, 0.1h, 0.2h, and 0.3h from the root for Fig. 2

Fig. 4.

Normalized deflection along the axial coordinate for an transversely isotropic cantilever loaded at the end

Fig. 5.

The normal stress through the thickness of a beam at the root for an transversely isotropic cantilever loaded at the end

Table 4

First six eigenvalues for [0/90/0] composite

Fig. 6.

The transverse shear stress through the thickness of a beam at the root for a laminated composite [0/90/0] beam

Acknowledgements

References