1. 서 론
2. 열전달 해석
2.1 콘크리트의 열특성
2.2 단면의 열전달 해석
2.3 3차원 기둥의 열전달 해석
3. 구조해석
3.1 콘크리트와 철근의 응력-변형률 관계
3.2 콘크리트 손상 소성 모델
3.3 구조해석 모델링
4. 순차 결합 열-응력 해석
4.1 해석 결과
5. 결 론
1. 서 론
건축 분야에서 가장 광범위하게 사용되고 있는 철근 콘크리트는 균질하지 않은 재료인 콘크리트와 철근이 함께 사용되기 때문에 상온에서의 거동도 매우 복잡하다. 철근 콘크리트 건축물에 화재가 발생하여 온도가 상승하게 되면, 상온보다 더 복잡한 형태의 거동을 보이기 때문에 이를 파악하는 것은 매우 어렵다.
국제 건축법 IBC(2021)에 의하면 현재는 지정된 방법으로 행한 내화시험을 기준으로 부재의 두께, 피복 등에 의하여 내화시간을 규정하고 있다. 하지만 실험에 의한 결과로 구조 부재의 내화성능을 평가하는 것은 실제 화재와는 다른 온도변화, 실험 부재 규모의 한계, 경계조건 등에 의해 부재의 내화성능을 과소 또는 과대평가할 가능성이 있으며, 따라서 내화성능 평가를 위한 보조 수단으로써 해석을 통한 연구가 필요하다.
철근 콘크리트 기둥의 내화성능을 평가하기 위해서 다양한 유한요소해석 프로그램을 통한 연구가 진행되고 있다. Alogla 와 Kodur(2018), Chinthapalli 등(2022)는 고온과 중심 축하중을 받는 기둥의 3차원 솔리드 요소를 사용한 유한요소해석을 수행하였으며, Gernay(2019)와 Tan과 Nguyen(2013)은 고온과 편심 축하중을 받는 세장한 기둥의 2차원 빔 요소를 사용한 유한요소해석을 수행하였다. 하지만 3차원 솔리드 요소를 사용한 고온과 편심 축하중을 받는 세장한 철근 콘크리트 기둥의 유한요소해석에 대해서는 쉽게 찾아보기 어렵다.
세장한 기둥에 편심 축하중이 가해지는 경우, 기하비선형에 의해 기둥 부재에 추가적인 모멘트가 발생하게 된다. 부재의 성능이 약화되는 고온의 경우에는 상온보다 더 큰 기하비선형 효과를 나타내게 된다. 단면의 온도 분포가 일정하지 않은 철근 콘크리트의 특성상 화재가 가해지면 부재의 온도 분포가 시간에 따라 계속해서 변화하기 때문에 온도에 따른 기하비선형 효과를 보다 정확하게 반영하기 위해서는 유한요소해석을 통해 부재의 내화성능을 평가하는 해석이 필요하다. 본 연구에서는 범용 유한요소해석 프로그램 Abaqus(2016)를 사용하여 고온과 편심 축하중을 받는 철근 콘크리트 기둥의 3차원 유한요소해석을 수행하였다. 해석은 Abaqus에서 제공하는 열전달 해석과 구조해석을 결합한 순차 결합 열-응력 해석을 사용하였으며, 단계별 해석 결과에 대해 비교・검증하였다.
2. 열전달 해석
순차 결합 열-응력 해석을 진행하기 위한 첫 번째 단계는 철근 콘크리트 기둥의 열전달 해석이다. 열전달 해석은 2차원 단면에 대한 해석을 먼저 진행하여 검증한 후, 3차원 요소로 확장하였다. 철근 콘크리트 단면에서 철근의 영향성은 철근이 위치한 부근에서만 빠르게 열이 전달되는 효과만 있을 뿐 전체적인 해석 결과에는 거의 영향을 미치지 않기 때문에 철근을 제외한 상태로 콘크리트 단면에 대한 열전달 해석을 수행하였다.
2.1 콘크리트의 열특성
철근 콘크리트 기둥에 열이 전달되는 메커니즘은 크게 세 가지로 구분할 수 있다. 화재가 발생하여 기둥 주변의 온도가 상승하게 되면, 대류와 복사로 인해 기둥 표면의 온도가 상승하게 되며, 기둥 자체에서는 전도를 통해 표면의 열이 기둥 내부로 열이 전달된다. 열전달 해석을 수행하기 위해서는 이와 같은 세 가지 열전달 메커니즘을 해석에 반영해야 한다.
먼저 대류는 표면 필름 조건(surface film condition)으로 화재가 가해지는 면 전체에 적용하며, 복사 역시 대류와 마찬가지로 화재가 가해지는 면 전체에 방사율(emissivity)로 적용하는데, 필름 계수(film coefficient)와 방사율은 Eurocode 2(CEN, 2004)에 따라 각각 25, 0.7을 사용하였다. 추가로 대류와 복사를 적용하는데 필요한 절대영도는 -273.15°C, 스테판-볼츠만 상수는 5.67×10-8 을 사용하였다.
전도는 재료 고유의 성질인 열전도율로 적용한다. 열전도율과 밀도, 비열은 온도에 따라 달라지는 재료 고유의 성질이며, 콘크리트 온도에 따른 열특성은 Eurocode 2에 따라 Table 1과 같이 적용하였다.
Table 1.
Thermal properties of concrete
2.2 단면의 열전달 해석
단면의 열전달 해석을 수행하기 위해서 먼저 초기 온도를 설정한 뒤, 표면에서 온도가 상승하는 현상을 모델링하기 위해 대류와 복사에 의한 온도변화를 하중의 형태로 적용하고, 온도가 변하지 않는 부분이나 온도가 고정되는 부분에 대해서 경계조건으로 설정해야 한다.
초기 온도는 상온을 20°C로 가정하여 전 단면에 적용하였으며, 온도의 변화는 Fig. 1과 같이 ISO(1975) 표준화재 곡선을 amplitude로 입력하여 화재가 가해지는 면에 대류와 복사로 각각 적용하였다. 단면의 열전달 해석에서는 온도변화가 발생하지 않아야 하는 부분이나, 특정 온도로 고정되는 부분이 존재하지 않기 때문에 별도의 경계조건은 설정하지 않았다.
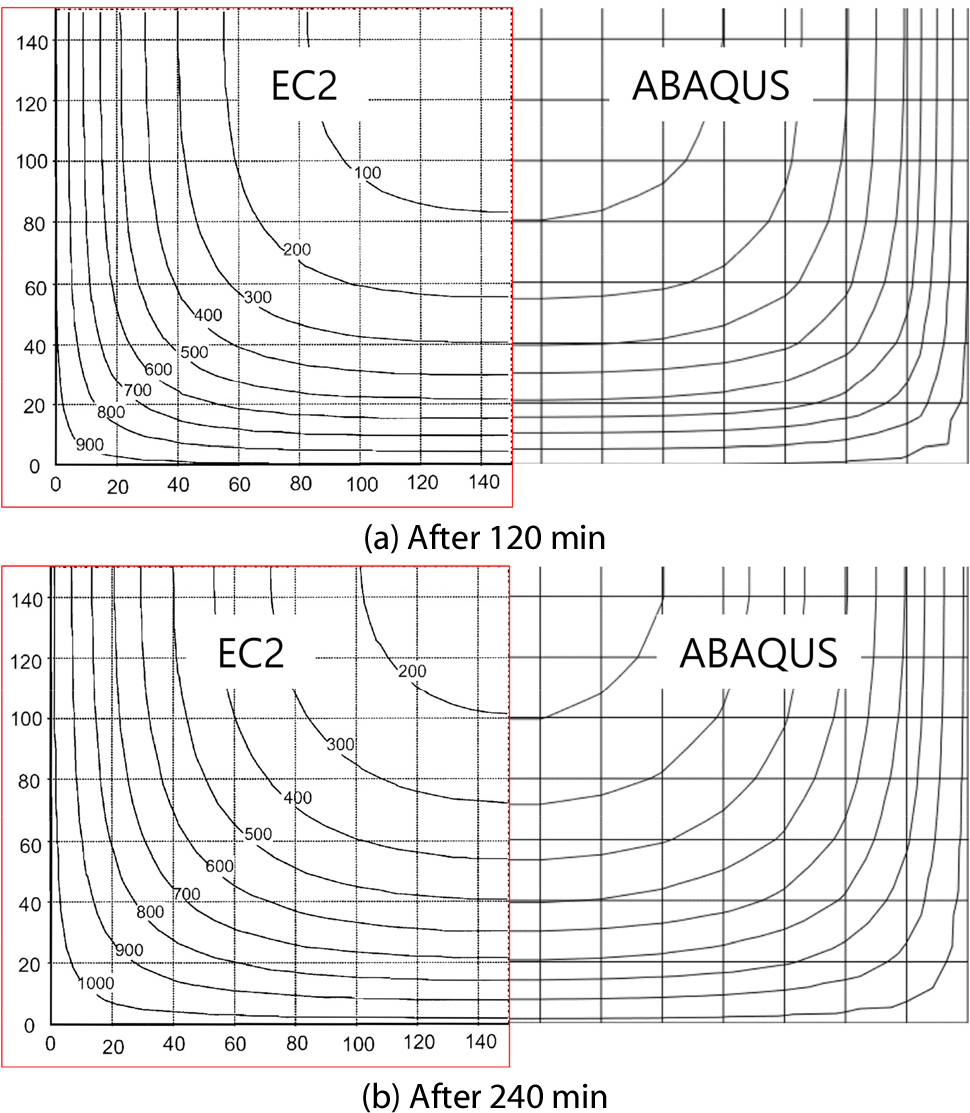
Abaqus를 통해 해석한 결과를 검증하기 위하여 Eurocode 2에 제시된 열전달 해석 결과 중 정사각형 단면의 해석 결과와 비교하여 검증하였으며, Fig. 2에 나타난 바와 같이 거의 동일한 결과를 얻었다.
2.3 3차원 기둥의 열전달 해석
2차원 열전달 해석을 비교・검증한 후 이를 3차원 요소로 확장하여 해석을 진행하였다. 3차원 해석을 진행할 때는 화재가 가해지는 각 면에 대해서 2차원 단면 해석과 같이 대류와 복사를 통해 표준화재 곡선에 의한 표면 온도 상승효과를 적용하였고, 실제로는 다른 부재와 연결되는 기둥의 상하부에 대해서는 별도의 경계조건을 적용하지 않아 열전달이 발생하지 않는 단열(heat insulation)효과가 적용되도록 하였다.
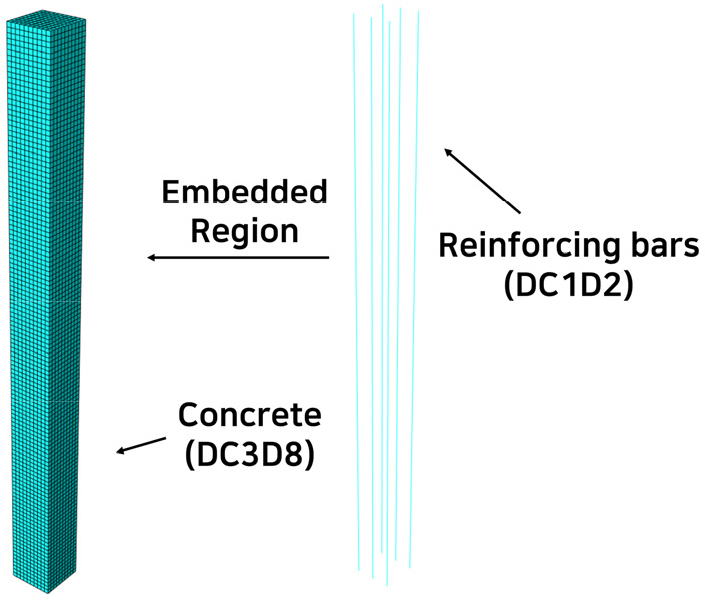
3차원으로 확장하여 열전달 해석을 진행할 때는 Fig. 3과 같이 단면 해석과는 다르게 철근을 함께 모델링하였다. 이는 열전달 해석 후, 절점의 온도 데이터를 이용하여 열-응력 해석을 진행하는 절차에서 철근이 위치한 절점의 온도 데이터를 함께 저장하여 시간이 지남에 따라 철근의 온도 역시 상승하고, 이에 따라 철근이 약화되는 것을 고려하기 위함이다. 철근은 절점이 2개인 트러스 요소로 모델링하기 때문에 열전달 해석에는 영향을 주지 않는다.
Abaqus에서 철근 콘크리트를 모델링하기 위해서는 철근과 콘크리트 사이에 제약조건(constraint)을 지정하여 두 재료 사이의 관계를 설정해야 한다. 제약조건으로는 콘크리트 내부에 존재하는 철근은 embedded region으로 콘크리트를 host region으로 하여 embedded region constraint를 적용하였다.
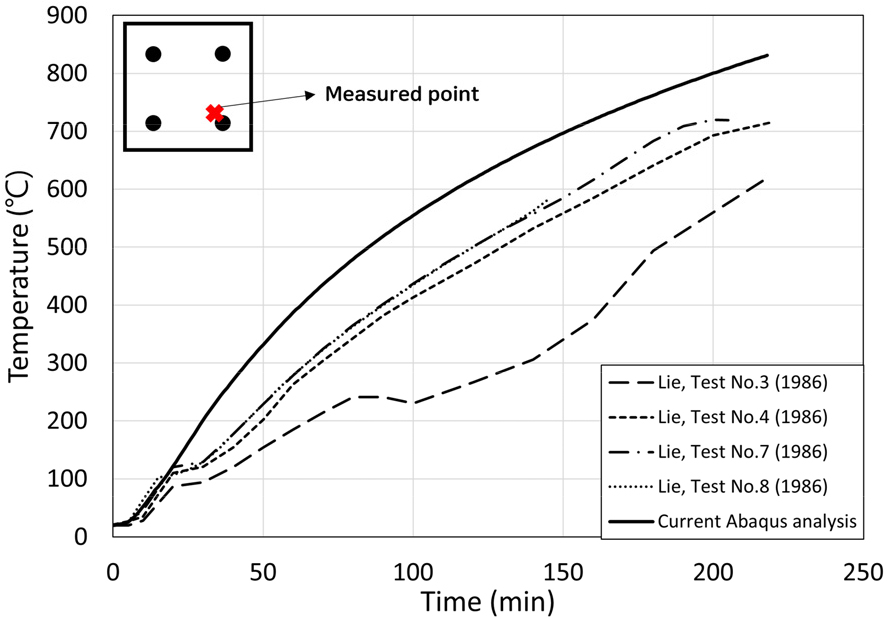
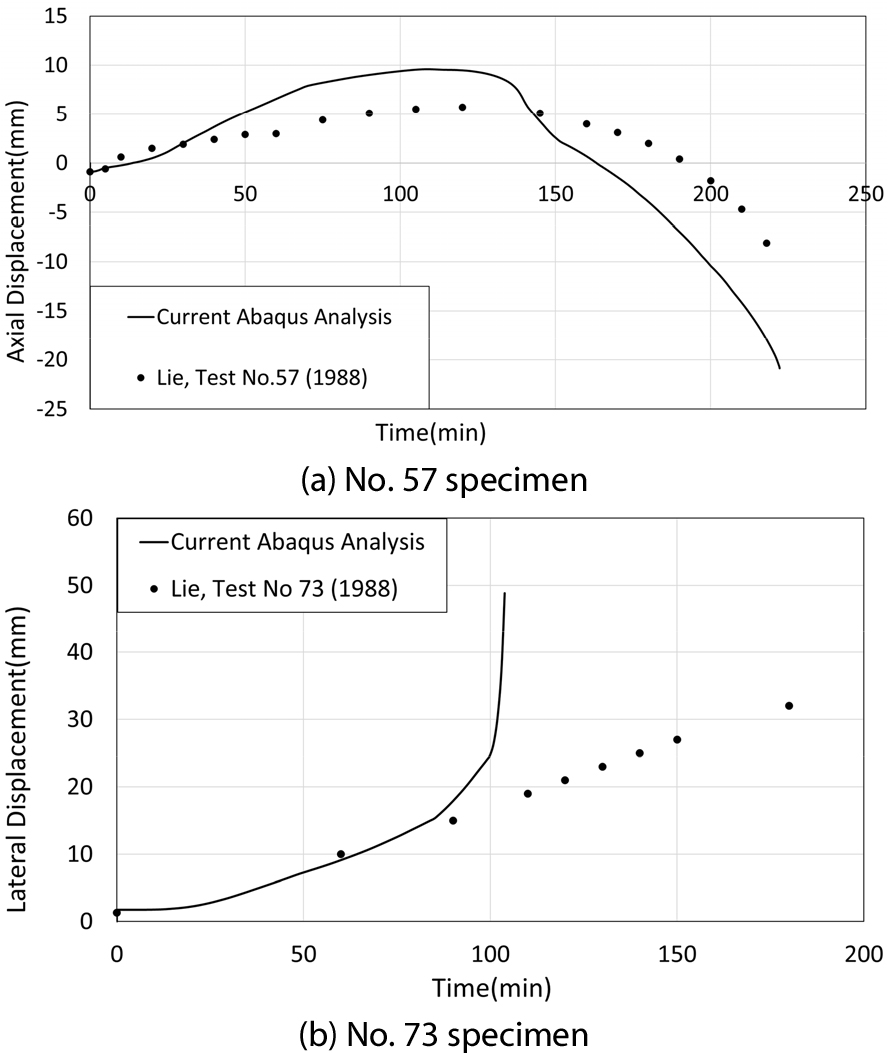
3차원 요소로 확장하여 해석을 수행한 결과에 대해 Lie와 Woollerton(1988)의 305mm×305mm 단면의 실험 결과와 비교하였으며, 비교한 결과는 Fig. 4와 같다. Fig. 4의 결과를 보면, 동일한 시험체임에도 실험에 의한 측정값에 오차가 큼을 알 수 있다.
3. 구조해석
3.1 콘크리트와 철근의 응력-변형률 관계
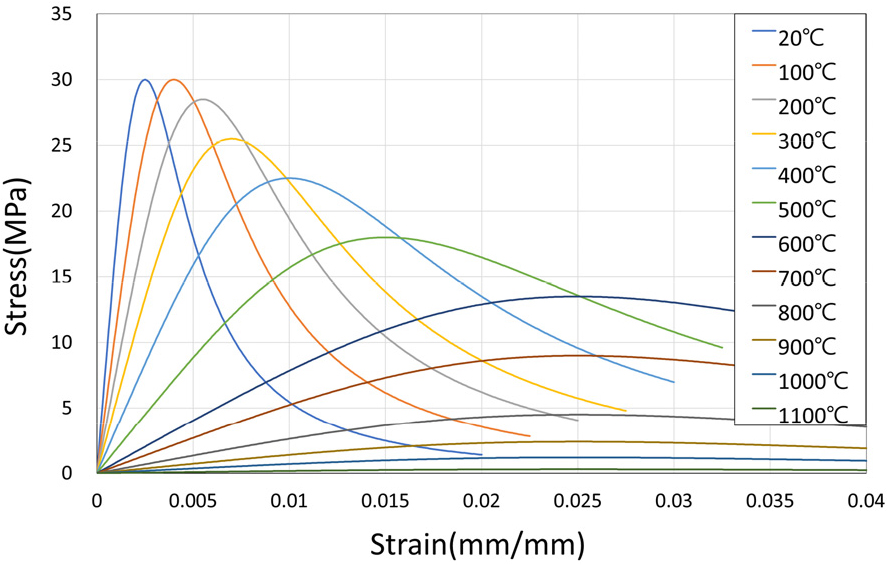
고온에서 콘크리트와 철근의 응력-변형률 관계는 상온과는 다른 거동을 보인다. 콘크리트의 경우 온도가 상승하면, 최대 응력은 감소하고, 최대 응력 상태의 변형률과 극한변형률은 증가하는 양상을 보인다.
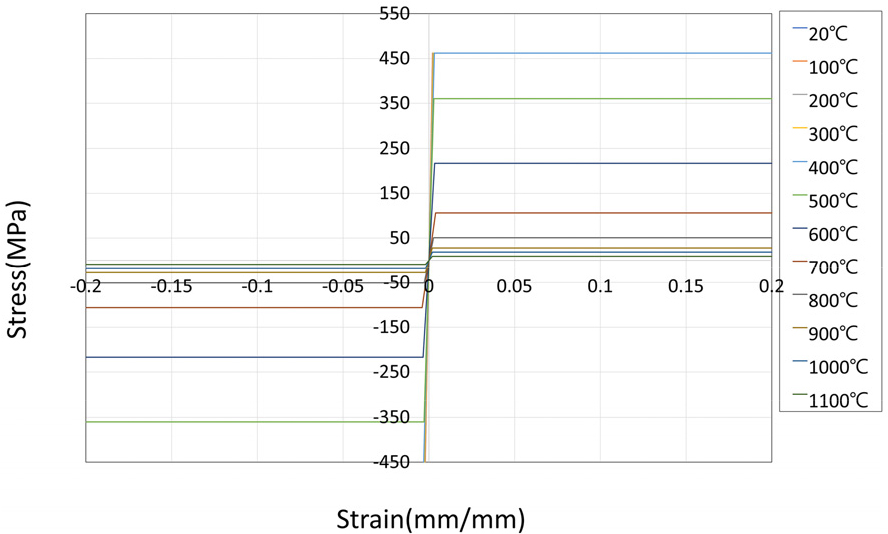
상온의 콘크리트의 압축 응력-변형률 관계에 대해서 식 (1)과 같이 Carreira와 Chu(1985) 모델을 사용하였고, 온도가 상승함에 따라 변하는 응력-변형률 관계에 대해서는 최대 강도 및 최대 강도에서의 변형률, 극한변형률을 Eurocode 2(2004)에서 제시하는 표 데이터를 사용하여 모델링하였으며, 온도에 따른 콘크리트의 압축 응력-변형률 관계는 Fig. 5와 같다.
여기서, 는 콘크리트의 압축강도, 은 최대 압축강도에서의 변형률이며, 𝛽는 Eurocode 2에 따라 3으로 적용하였다.
철근의 응력-변형률 관계에 대해서는 탄성-완전소성(Elastic- Perfectly Plastic) 모델을 사용하였으며, Eurocode 3(CEN, 2005)의 표 데이터를 통해 온도가 상승함에 따른 탄성계수 및 인장강도의 변화를 모델링하였다. 온도에 따른 철근의 응력-변형률 관계는 Fig. 6과 같다.
3.2 콘크리트 손상 소성 모델
3차원 철근 콘크리트 기둥을 해석하기 위해서 콘크리트의 재료 모델은 Abaqus에서 제공하는 삼축 응력 모델인 콘크리트 손상 소성(Concrete Damaged Plasticity, CDP) 모델을 사용하였다. CDP 모델은 5가지의 변수와 압축 영역의 응력-비탄성변형률(inelastic strain)의 관계 및 인장 증강 효과(tension stiffening effect)를 이용하여 삼축 응력 상태의 콘크리트를 모델링한다. 콘크리트 강도와 변형률에 따른 비탄성 변형률은 식 (2)와 같이 산정하였으며, 5가지 변수는 Table 2와 같이 Abaqus(2016)에서 제공하는 기본값을 사용하였다.
손상 계수(damage factor)는 하중이 제거된 상태에서 손상 회복의 정도를 제어하는 값으로, 반복하중이 가해지는 경우 해석에 큰 영향을 미치지만, 압축력을 가한 상태로 하중이 변하지 않는 해석에서는 큰 영향이 없으므로 압축 및 인장 영역 모두에서 기본값으로 설정된 0을 사용하였다.
Table 2.
Abaqus CDP model default parameters
| Parameters | Values |
| Dilation Angle | 30 |
| Eccentricity | 0.1 |
| fb0/fc0 | 1.16 |
| K | 0.6667 |
| Viscosity Parameter | 0 |
3.2.1 인장 증강 효과(tension stiffening effect)
세장하거나 편심 축하중이 작용하는 기둥의 경우, 휨에 의해 콘크리트에 인장 응력이 발생하며 균열이 생길 가능성이 크다. 이 경우 콘크리트 요소에 발생하는 인장 응력이 철근으로 전달되며 해석이 계속 진행되어야 하나, 인장 증강 효과가 제대로 적용되지 않은 경우, 콘크리트에 발생한 인장 응력이 철근으로 전달되지 못하고 해석이 중단되어 수렴하지 못하는 현상이 발생하게 된다. 따라서 인장 증강 효과를 과도하게 작게 보아 해석이 중단되는 현상을 방지하기 위하여 인장강도를 압축강도의 10%로 하여 Hillerborg 등(1976)과 같이 이선형(bilinear)으로 모델링한 뒤, 콘크리트의 최대인장변형률에 따른 수렴성을 확인하였다.
고온의 콘크리트의 인장강도는 Eurocode 2(CEN, 2004)에 따라 적용하였다. 온도에 따른 콘크리트의 압축 응력-변형률 관계를 보면 온도가 상승함에 따라 극한변형률은 증가하는 경향을 보인다. 콘크리트의 인장 영역 역시 비슷한 형태의 거동을 보일 것으로 예측되나, 콘크리트의 인장 응력은 해석에서 무시될 정도로 작으며, 고온의 콘크리트의 최대인장변형률을 측정하는 것이 매우 어렵기 때문에 관련 자료 역시 극히 드물다. 따라서 모든 온도에서 콘크리트의 최대인장변형률은 동일하게 고정하여 해석을 진행하였다.
해석 결과에 영향을 미치지 않으면서 수렴성을 확보하기 위한 최대인장변형률을 설정하기 위하여 Gernay(2019)에 제시된 실험 자료 중 Table 3과 같이 동일한 크기의 시험체에 편심 축하중이 30mm, 150mm 가해지는 두 경우에 대해 최대인장변형률을 0.001부터 0.005까지 변경하며 해석을 진행하였다.
Table 3.
Characteristics of test specimens
해석 결과, 편심이 작은 Fig. 7(a)의 경우, 최대인장변형률에 따른 수렴성 문제가 나타나지 않았고, 전체적인 거동 역시 비슷한 형태로 나타났다. 하지만 편심이 매우 큰 Fig. 7(b)의 경우, 0.003 이하의 최대인장변형률을 적용한 경우, 구조해석 단계에서 해석이 중단되었으며, 0.003 이상의 최대인장변형률을 적용한 경우, 해석에서 큰 차이가 나타나지 않았다. 인장 증강 효과에서 최대인장변형률을 너무 작게 할 경우, 수렴에 문제가 발생하고, 너무 크게 할 경우 실제와 다른 거동이 나타날 가능성이 있기 때문에, 본 연구에서는 수렴성과 해석 결과 모두 영향이 없도록 Fig. 8과 같이 콘크리트의 최대인장변형률을 0.003으로 적용하였다.
3.3 구조해석 모델링
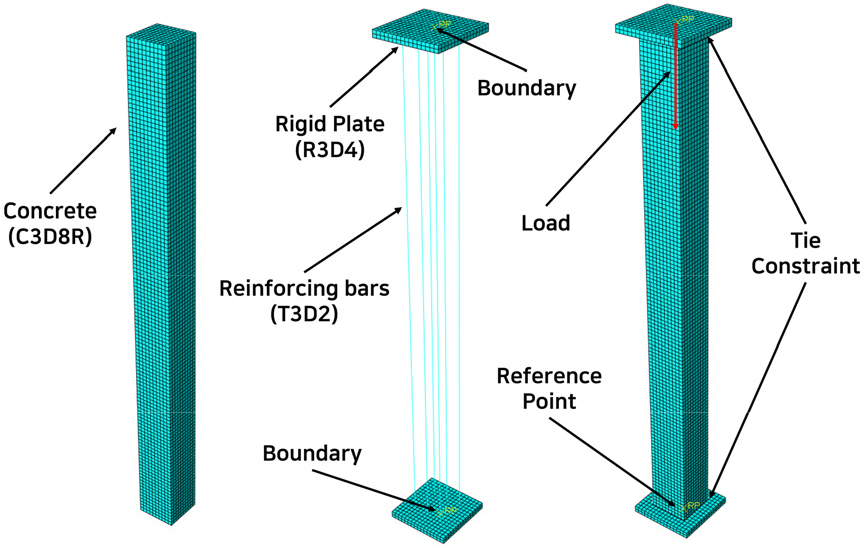
기둥에 축하중을 가하는 실험에서는 부재에 직접 국부적인 하중을 가하면 부재 일부분에 응력이 집중되는 현상이 발생하기 때문에 기둥 상하부에 플레이트를 설치하여 실험을 진행한다. 유한요소해석 역시 국부적인 하중을 부재에 직접 가하면 일부 요소에 응력이 집중되는 현상이 발생하기 때문에 해석을 진행할 때 Abaqus에서 제공하는 강체 플레이트(rigid plate)요소를 사용하였다.
플레이트와 콘크리트 사이의 접촉에 대해서는 기둥에 축력을 가하는 해석의 경우, 마찰 거동이 해석의 목적이 아닐 뿐만 아니라, 플레이트와 콘크리트를 일체화시키는 것이 해석 결과에 영향을 미치지 않기 때문에 tie constraint를 통해 콘크리트의 상하부 면을 각각의 플레이트와 일체화시키는 조건을 적용하였다.
실제 실험과 유사한 환경을 만들기 위해서 하중 작용점을 플레이트의 기준점으로 지정하고, 해당 기준점에 하중 및 경계조건을 설정하였다. 하중이 가해지는 상부 플레이트 기준점에는 길이 방향 변위 자유도를 구속하지 않고 하중을 가했으며, 기둥이 강체회전 하는 것을 막기 위해서 길이 방향 회전 자유도는 구속하였다. 하부 플레이트 기준점은 별도의 하중을 가하지 않은 상태로 길이 방향 변위 자유도를 구속하여 반력이 발생하도록 모델링하였다.
기하비선형해석에서 기둥의 초기 불완전성(initial imperfection)은 다양한 2차 효과를 설명하기 위해 도입되었으며, 빔 요소를 통해 초기 불완전성을 모델링하는 경우 기둥 중앙부의 변위가 L/1000이 되도록 단일 사인 곡선의 형태로 가정하기도 한다(Espinos, et al., 2010; Huang and Tan, 2003). 하지만 3차원 솔리드 요소를 이용하여 유한요소해석을 진행하는 경우, 단일 사인 곡선의 형태로 모델링하기가 어렵다. 따라서 본 연구에서는 중심 축하중이 작용하는 경우에만 초기 불완전성을 고려하기 위하여 해석 결과에는 큰 영향을 미치지 않도록 1mm의 편심을 둔 상태로 하중을 가하였다. 1mm의 편심을 가하였을 때, 세장하지 않은 기둥에서는 결과의 차이가 거의 나타나지 않았지만, 세장한 기둥에서는 2차 효과가 고려되어 해석의 결과가 달라지는 현상이 나타났다.
구조해석에서는 Fig. 9와 같이 응력 해석을 위한 모델링을 진행하였으며, 열전달 해석의 결과와 연결하여 해석을 수행하기 위해서 요소망은 열전달 해석과 동일하게 하였다.
4. 순차 결합 열-응력 해석
앞서 진행한 열전달 해석과 구조해석을 결합하여 순차 결합 열-응력 해석을 통해 고온과 축하중을 받는 철근 콘크리트 기둥의 유한요소해석을 수행하였다.
실제 기둥은 이미 축하중이 작용하고 있는 상태이며, 화재가 발생하면 축하중은 변하지 않은 상태에서 온도가 상승함에 따라 부재가 약화되어 결국 파괴에 이른다. 따라서 해석 역시 동일하게 하중을 먼저 가한 후, 온도가 상승하는 과정으로 진행하였다.
해석은 총 세 가지 step으로 나누어 진행하였다. initial step에서는 경계조건을 설정하고, 두 번째 step에서는 하중 조건을 지정하며, 마지막 step에서는 열전달 해석의 결과 얻어진 절점의 온도 데이터를 predefined field로 불러들여 적용하였다. 이때, 모든 step은 static-general step으로 진행하였다.
4.1 해석 결과
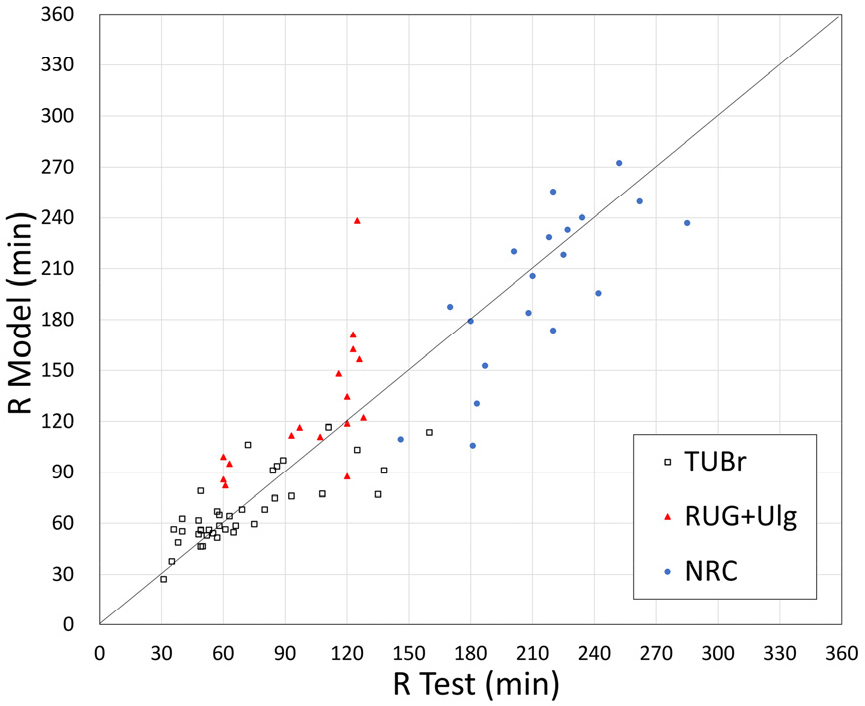
Gernay(2019)는 유한요소해석 프로그램 SAFIR를 이용하여 해석한 결과와 실제 실험의 데이터를 비교하여 제시하고 있다. Gernay(2019)의 경우, 3차원이 아닌 2차원 빔 요소를 사용하여 해석하였으며, TUBr(Technical University of Braunschweig in Germany), RUG(University of Ghent in Belgium), Ulg(University of Liege in Belgium), NRC(National Research Council Canada)의 4개 기관 74개의 실험 데이터에 대하여 해석과 실험 결과를 비교하였다. 비교는 내화시간을 기준으로 나타내었는데, 이는 내화시험의 경우 다양한 조건에 의해 실험 결과가 일정하지 않게 나타날 수 있으며, 실제로 Gernay(2019)에 제시된 실험 자료 중 동일한 조건의 시험체에 대해서 실험한 결과 약 60분의 내화시간 차이가 발생하는 등 실험 자체의 부정확성이 크기 때문에 많은 자료를 비교하여 경향성을 파악하기 위함이다.
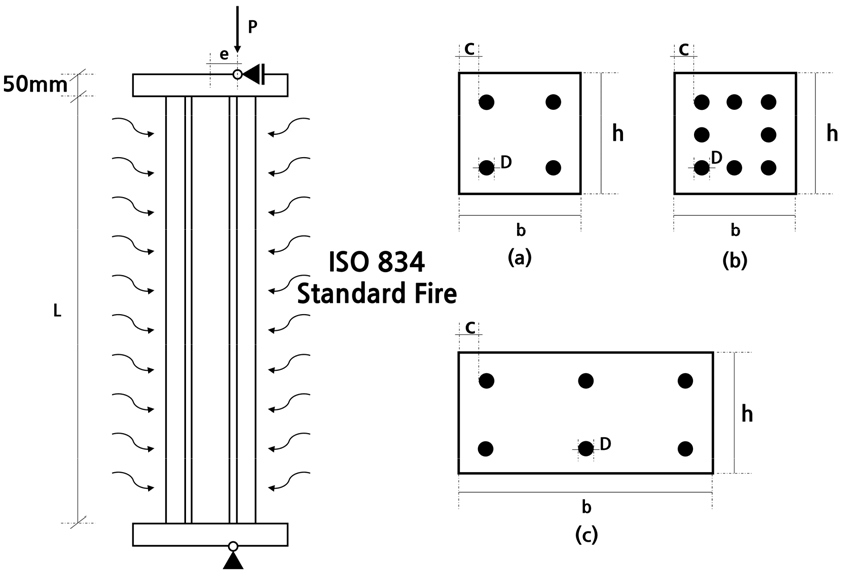
본 연구에서도 74개 시험체 모두에 대한 모델링을 진행하여 결과를 실험 및 Gernay(2019)의 해석과 내화시간을 기준으로 비교하였다. Abaqus 해석에 사용된 모델은 Fig. 10과 같으며, 단면은 Fig. 10의 (a), (b), (c)의 세 가지 종류로 이루어져 있다.
Fig. 11은 해석을 수행하여 실제 실험과 비교한 결과를 기관별로 나누어 나타낸 것이다. 내화시간에 대해서는 유한요소해석의 경우, 힘의 평형 조건을 맞추지 못하고 해석이 중단되는 시점으로 하였으며, 실험에서는 기둥이 더 이상 하중을 지지하지 못하고 파괴되는 시점으로 하였다. 해석 결과에 대해서는 해석으로 구한 내화시간을 실험에 의해 측정된 내화시간으로 나눈 값(해석/실험)으로 분석하였다.
TUBr의 실험은 대체적으로 세장하거나 편심이 매우 큰 경우에 해당하는 시험체로 구성되어 있어 상대적으로 내화시간이 짧게 측정되었으며, 해석 결과 1.04의 평균값을 나타내었다. RUG와 Ulg는 각각 상대적으로 세장하고 편심이 있는 경우와, 세장하지 않고 편심이 없는 경우에 대해 비교하고자 실험을 진행하였고, 두 기관 모두 1.27의 평균값을 나타내었다.
NRC는 대부분이 중심하중을 가하는 실험으로 상대적으로 내화시간이 길게 측정되었으며, 0.93의 평균값을 나타내었다.
Fig. 12는 네 기관 중 NRC 실험의 화재 노출 시간에 따른 변위가 제시된 Lie와 Woollerton(1988)의 동일 시험체에 각각 중심 축하중과 편심 축하중을 가한 경우의 시간-변위 관계에 대해 해석과 비교한 것이다. 비교적 자세하게 제시된 NRC의 실험은 총 19개의 시험체 중 2개의 시험체가 편심 축하중을 가하는 시험체이며, 해석 결과, 중심 축하중을 가하는 시험체에 비해 내화시간이 과소평가되고 있다.
4개 기관의 자료를 분석한 결과, 상대적으로 내화시간이 작은 시험체에서 비교적 정확한 결과를 얻을 수 있었고, NRC를 제외한 기관의 경우, 편심 축하중을 가하는 시험체에서 내화시간을 과대평가하는 경향이 나타났다. 이처럼 일정하지 않은 경향이 나타나는 이유는 수렴성이 온전히 확보되지 못하는 유한요소해석의 한계점과 기관에 따라 상이한 실험 조건 때문인 것으로 판단된다.
Fig. 13은 본 연구에서 구한 Abaqus의 솔리드 요소를 사용하여 해석한 결과와 Gernay(2019)의 빔 요소를 사용하여 해석한 결과를 비교한 것으로, Gernay(2019)에서는 전체적으로 0.95의 평균값을 얻었고, Abaqus를 통해 수행한 해석에서는 1.06의 평균값을 얻을 수 있었다.
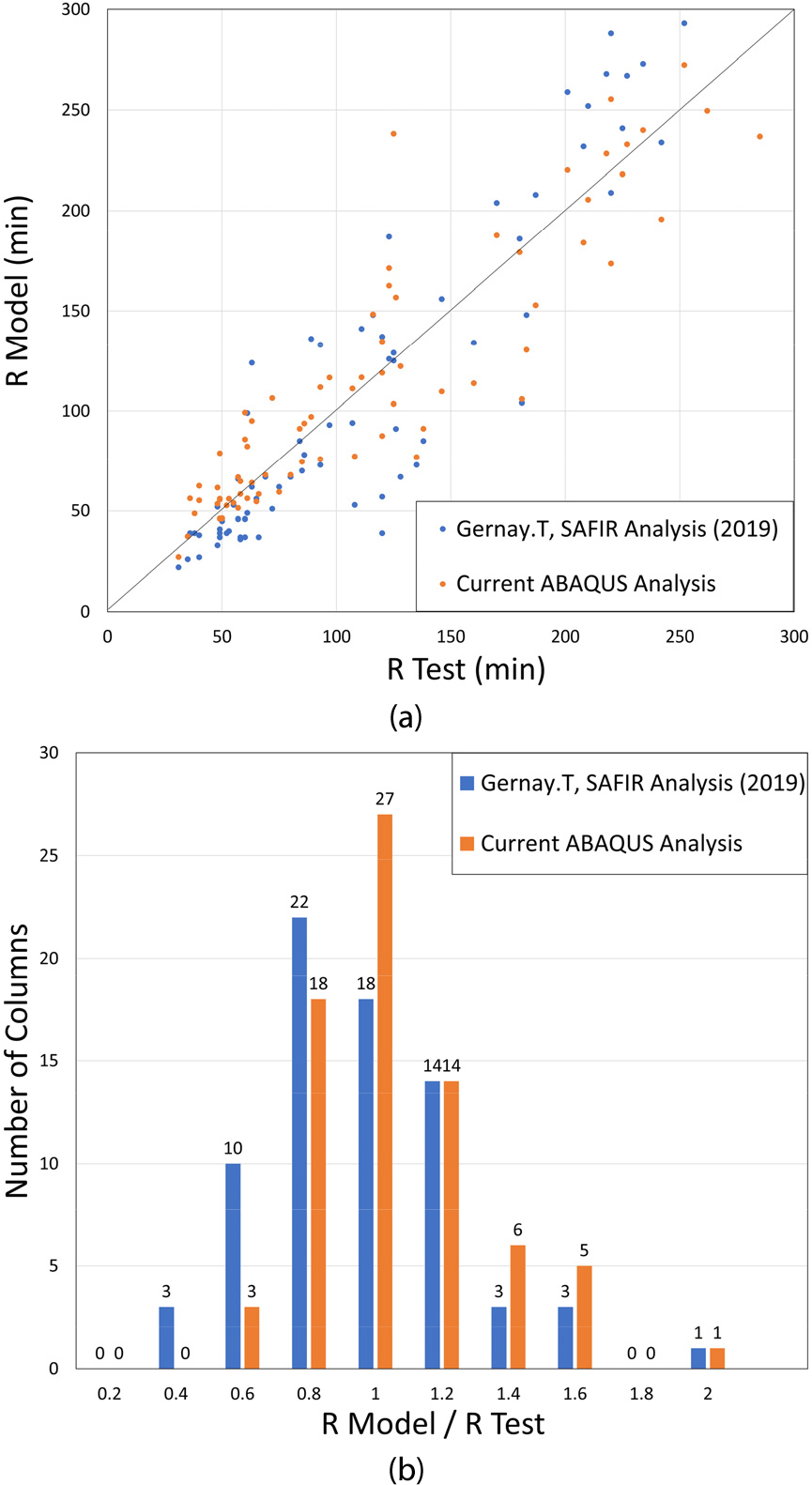
Fig. 13.
Comparison of Gernay(2019) analysis using beam elements and Abaqus analysis using solid elements
5. 결 론
본 연구에서는 범용 유한요소해석 프로그램 Abaqus에서 제공하는 순차 결합 열-응력 해석을 이용하여 고온과 편심 축하중을 받는 세장한 기둥에 대하여 3차원 솔리드 요소를 이용한 유한요소해석을 수행하고 실험 및 빔 요소를 이용하여 해석한 결과와 비교하였다.
기둥에 화재를 가하는 실험은 실제 화재의 상황을 정확하게 반영할 수 없을 뿐 아니라, 시험체의 불완전성이나 경계조건 등 실험의 조건에 따라 결과가 다르게 나타날 수 있다. 따라서 74개의 시험체에 대해서 해석을 수행한 결과를 경향성 및 평균값으로써 분석하였다.
해석의 과정에서 편심 축하중에 의해 기둥에 휨이 가해짐에 따라 콘크리트에 인장 응력이 발생했기 때문에 콘크리트의 인장 모델링이 수렴성에 영향을 주었다. 이를 해결하기 위해 콘크리트의 최대인장변형률을 0.003으로 고정하여 인장 증강 효과를 모델링함으로써 해석의 결과에는 영향을 미치지 않으면서 해석의 수렴성을 향상시킬 수 있었다.
모든 시험체에서 동일한 경향을 보이진 않았지만, 전체 시험체에서 평균적으로 6% 내외의 오차를 보였으며, 따라서 기존에 연구된 바가 거의 없는 3차원 솔리드 요소를 사용한 유한요소해석을 통해 고온과 편심 축하중을 받는 철근 콘크리트 기둥의 거동을 예측하고, 내화시간을 평가할 수 있게 되었다.
본 연구는 화재 시의 온도변화에 따른 구조부재의 거동을 정확하게 파악할 수 있는 해석 기술을 개발한 것으로 성능기반내화설계의 기반기술로 활용될 수 있다.