1. 서 론
2. 온라인 유한요소모델 업데이트
2.1 공분산유도 추계학적 부분공간식별
2.2 모델 업데이트를 위한 역고유치 신경망
3. 수치 예제
3.1 예제 구조물 및 하중 모델
3.2 예제 구조물의 운용중 모드 해석
3.3 유한요소모델 업데이트를 위한 역고유치함수 신경망 구성
3.4 온라인 모델 업데이트 시뮬레이션 1(Case S1)
3.5 온라인 모델 업데이트 시뮬레이션 2(Case S2)
4. 결 론
1. 서 론
교량과 같은 구조물의 공용 기간 중 유지 보수 및 성능 유지의 중요성이 증가함에 따라 해석적 방법을 이용한 성능 및 상태 평가 방법의 하나로서 계측 데이터를 이용한 유한요소모델 업데이트의 필요성이 증가하고 있다(Friswell and Mottershead, 2013). 특히, 화재, 충돌, 지진과 같이 구조물에 큰 변화가 발생할 경우에는 변화 전후에 대한 구조계의 모델을 확보하는 것이 필요한데, 이러한 이벤트는 언제 발생할지 예측할 수 없으므로 상시적으로 구조물의 변화를 추적할 수 있는 상시 업데이트가 필요하다. 최근 국내의 장대교량과 같은 주요 구조물에는 구조 건전도 모니터링(Structural Health Monitoring, SHM) 시스템이 갖추어져 있어 상시 데이터가 축적되고 있으나, 이들 자료를 활용한 구조물 유한요소모델은 상시로 업데이트 되고 있지 않은 실정이다. 이는 기존의 유한요소모델 업데이트 방법이 자료의 계측, 모델링, 업데이트 과정에 이르는 모든 절차에서 상당한 수준의 전문적 지식과 별도의 계산 및 시간이 요구되는 작업이기 때문이었다. 이 연구에서는 운용 중 별도의 오프라인 작업이나 사용자의 개입이 없이 자동화된 과정으로 계측과 거의 동시에 상시적으로 온라인 유한요소모델 업데이트를 수행할 수 있는 새로운 방법을 제안한다.
이 논문에서 제안하는 온라인 유한요소모델 업데이트는 구조물의 진동 응답으로부터 고유진동수 및 모드 형상 정보를 추출하고 이에 상응하는 유한요소모델의 파라미터를 구하는 동적 유한요소모델 업데이트 절차를 기반으로 한다. 즉, 계측신호로부터 모드 특성 값을 추정하는 구조 동특성 식별단계와 식별된 구조 동특성과 가장 유사한 유한요소모델 파라미터를 찾는 업데이트 단계의 두 단계로 구성된다. 온라인으로 결과를 얻기 위해 계측단계와 업데이트 단계 모두 자동화된 방법을 적용한다. 식별단계에서 운영중 모드 해석 방법인 자동화된 추계론적 부분공간 식별법(Stochastic Subspace Identification)을 적용하고, 역고유치 신경망을 이용한 업데이트 방법을 이용하여 목표 모드 정보에 대한 최적 유한요소모델 파라미터를 온라인으로 구한다. 이하 2장에 제시한 방법을 요약하고 3장에서 풍하중을 받는 20층 전단빌딩 모형에 대한 수치예제를 통해 적용성을 보인 후 4장 결론에서 제안한 방법의 의의와 한계 및 향후 필요한 연구 방향을 기술한다.
2. 온라인 유한요소모델 업데이트
이 장에서는 자동화된 온라인 유한요소모델 업데이트를 위해 이 연구에서 적용한 계측단계와 업데이트 단계의 방법론을 기술한다.
2.1 공분산유도 추계학적 부분공간식별
계측 단계의 자동화를 위해 이 연구에서는 센서 잡음에 비교적 견실한 특성을 보이고 온라인 식별 및 자동화 방법이 용이한 것으로 알려진 공분산유도 추계학적 부분공간식별법(Covariance-driven Stochastic Subspace Identification, Cov-SSI)을 적용하였다(Rainieri and Fabbrocino, 2014; Magalhaes et al., 2009). 이 방법은 입력하중에 대한 정보없이 출력 시간이력 신호만을 사용하여 구조계의 모드 특성을 식별하는 운용중 모드 해석(Operational Modal Analysis, OMA) 방법의 하나로서 널리 이용되고 있다. 구조물 진동의 출력 시간이력 신호에서 공분산 행렬을 구성하고 이를 통해 이산 상태공간 방정식의 시스템 행렬을 구하여 모드 정보를 추출하는 단계를 거친다. 알고리즘을 요약하면 다음과 같다.
출력 시간 이력 행렬 로부터 다음과 같은 공분산 행렬(covariance matrix) 를 구성한다.
여기서, 는 출력 신호 행렬 에서 번째 신호(열) 까지로 구성한 행렬이다.
식 (1)의 공분산 행렬을 이용하여 다음과 같은 블록 Toeplitz 행렬 를 구성한다.
모드 특성 값은 다음과 같이 얻어지는 시스템 행렬과 출력행렬로부터 결정할 수 있다.
여기서, 은 식 (2)의 블록 Toeplitz 행렬의 특이값 분해 에서 구한 값으로, 각각 특이치 값이 0인 행과 열을 제거하고 남은 개의 특이 벡터와 특이치 행렬이다. 시스템의 고유진동수, 감쇠는 시스템 행렬 의 고유치 분해 를 통해 결정한다. 모드 벡터 행렬은 로 결정된다.
이 절차에서는 구하고자 하는 시스템의 차수 을 사용자가 미리 결정해야 한다. 그러나 실제 구조물의 차수는 미리 알 수 없으므로 자동화된 알고리듬에서는 차수를 낮은 차수부터 높은 차수로 증가시켜 가며 모드 정보를 추출하는 과정을 거친다. 이 때 충분히 높은 진동수의 모드를 추출하기 위해서 큰 값이 필요하지만 높은 차수를 이용하여 시스템 식별 작업을 진행할 경우 물리적 모드와는 다른 수치적으로만 존재하는 허위 모드(nonphysical spurious mode)가 검출되므로 이를 구분하기 위한 알고리즘이 필요하나, 자동화 알고리즘에서는 이 과정을 위해 여러 가지 모드 식별 기준과 클러스터링 기법을 이용하여 안정화된 모드를 추출한다. 이 연구에서는 Cheynet(2020)등이 제안한 자동화 알고리즘을 적용하였다. 이 알고리즘에서는 인접한 고유진동수와 모드벡터를 응집형 계층적 클러스터링(agglomerative hierarchical clustering) 기법을 사용하여 자동적으로 구분하였다.
2.2 모델 업데이트를 위한 역고유치 신경망
일반적으로 동적 유한요소모델 업데이트는 유한요소모델의 고유진동수 및 고유벡터와, 2.1에서 제시한 방법 등으로 구한 계측 자료에 기반한 구조물 고유진동수 및 고유벡터 사이의 오차를 최소화하는 모델 파라미터 벡터 를 구하는 최적화 문제로 정식화 할 수 있다. 이러한 정식화 과정은 직관적이고 명료하고 매우 다양한 최적화 방법을 이용하여 풀 수 있기 때문에 가장 널리 사용된다. 그러나 이러한 최적화 방법은 운용 중 온라인 업데이트에는 적합하지 않은 면이 있는데, 최적화 알고리즘 파리미터의 선정, 목적함수 계산에 소요되는 시간, 반복계산에 따라 수렴하기 까지 걸리는 시간 등이 그것이다. 이러한 제약을 극복하기 위한 방법으로 역고유치함수 모사 신경망을 사용한 새로운 모델업데이트 방법이 제안되었다(Gong and Park, 2019). 이 방법에서는 계측에 의한 목표 고유값 가 주어질 때, 이에 상응하는 최적 유한요소모델 파라미터 벡터 를 다음과 같은 역 고유치 함수를 통해 직접 구하는 형태로 모델 업데이트 문제를 정식화 한다.
식 (5)에 나타낸 바와 같은 고유 값에 대응하는 구조물 유한요소 모델의 파라미터를 결정하는 역 고유치 함수 를 구하기 위한 다층 신경망을 이용한 방법은 다음과 같이 나타낼 수 있다.
여기서, 는 신경망 입력 데이터 벡터이고 는 신경망의 번째 층을 나타내는 함수이다. 즉 다층 신경망은 입력 층에서 시작하여 각 층에 연쇄적으로 전달되는 벡터 데이터를 최종적으로 출력하는 연결된 벡터 입출력 함수로 볼 수 있다. 이러한 다층 신경망에서는 입력층 , 출력층 사이의 은닉층 수와, 이를 구성하는 노드의 개수, 활성화 함수 등을 결정하는 것이 신경망 설계 문제가 된다. 입력 데이터 벡터 와 이에 대한 최적 파라미터 의 관계를 구성하는 신경망 모델이 학습되면 계측 자료에 의해서 입력으로 주어지는 임의의 목표 교유치 값에 대한 최적의 유한요소모델 파라미터 벡터를 반복 계산등의 작업이 없이 거의 즉시로 계산할 수 있다. 다음 3장의 수치 예제를 통해 적용 방법을 제시하였다.
3. 수치 예제
이 장에서는 수치 예제를 통해 제시한 온라인 유한요소 업데이트 방법의 적용성을 보인다. 대상 구조물은 풍하중을 받는 20층 빌딩으로 하였고, 가속도 응답을 계측하여 모드 식별 및 업데이트를 수행하는 예제를 보인다. 예제에서는 다음 두 가지 경우에 대하여 온라인 업데이트를 수행하는 것을 모사하였다. 첫 번째 모사(S1)에서는 일반적인 모델 업데이트 상황에 대한 시뮬레이션을 수행한다. 즉, 실제 구조물의 강성 및 질량이 설계 시에 가정한 공칭 값과는 다른 값을 가지게 될 때 계측 응답을 사용하여 자동으로 업데이트 파라미터를 찾는다. 두 번째 모사(S2)에서는 계측 중에 구조 파라미터에 변동이 있을 경우에 대한 시뮬레이션을 수행한다. 구조물의 강성이나 질량이 원 상태에서 변화가 있을 경우에 계측 응답을 사용한 온라인 업데이트로 이를 적절히 추정할 수 있는지에 대하여 살펴본다.
3.1 예제 구조물 및 하중 모델
예제 구조물인 풍하중을 받는 20층 전단 빌딩 모델을 Fig. 1에 나타내었다. 설계 시에 가정한 공칭 값 및 두 가지 시뮬레이션 S1, S2에서 가정한 구조물의 실제 강성 및 질량 값을 Table 1에 나타내었다. 이 연구에서 고려하는 빌딩 구조물 모델의 파라미터는 총 5개로서 각 파라미터는 Fig. 1에 나타낸 것과 같이 20개층의 횡 강성을 5개 구역으로 나누어 그룹화 한 것으로 하였다.
Table 1.
Structural properties of the 20-story building structure for nominal design, simulation S1 and S2
| Nom. | S1 | S2 | ||
| (ton) | 665.14 | |||
| (ton) | 630.38 | |||
| (ton) | 571.87 | |||
| (kN/m) | 3930 | 3494 | 3599 to 3239 | |
| (kN/m) | 3930 | 4463 | 4644 | |
| (kN/m) | 3930 | 4156 | 4364 | |
| (kN/m) | 2590 | 3073 | 3049 | |
| (kN/m) | 2590 | 2737 | 2570 | |
구조물의 유한요소 모델은 평면 전단 빌딩 모델로서 다음과 같은 운동 방정식으로부터 응답을 구한다.
식 (7)에서 는 각 층 변위 벡터, 질량행렬 은 Table 1의 각 층 질량을 대각성분으로 하는 대각행렬이고, 강성행렬 은 전단 빌딩 모델로부터,
이며 감쇠 행렬 는 두 개의 저차 모드 감쇠비를 특정하여 나머지 고차 모드 감쇠까지 생성할 수 있는 Rayleigh 감쇠로부터 정하였으며, 1차 및 2차 두 저차 모드의 감쇠비를 0.02로 하여 감쇠행렬을 생성하였다.
구조물 진동 응답을 도출하기 위한 풍하중 시간이력은 각 층에 작용하는 것으로 하였다. 풍하중 모형은 백색잡음으로 가정한 변동 풍속으로부터 생성하였다. 빌딩 모델의 i번째 층에 작용하는 풍하중 시간이력 는 다음과 같이 나타낼 수 있다.
여기서, 는 공기밀도, 는 i번째 층의 수풍 면적, 는 빌딩 단면 형상에 따른 풍압계수, 는 i번째 층 높이 에서의 풍속 프로파일 계수, 는 변동풍속이다. 풍속 프로파일 계수는 다음과 같이 정하였다.
식 (10)에서 는 높이에 따른 풍속 프로파일 곡선을 결정하는 프로파일 지수이다. 시간에 따른 변동 풍속 는 ambient vibration을 가정하여 백색잡음으로 모델링 하였다. 이는 일반적으로 진동수별 특성이 다른 특정 스펙트럼 형상을 갖는 강풍에 의한 풍하중보다는 평상시의 진동 상태에서의 계측을 가정한 것으로, 진동 신호에서 하중 특성을 제외하고자 하는 의도이다. 이 풍하중 모형에 사용된 각 계수 값을 Table 2에 나타내었다.
Table 2.
Parameters of wind load model
| Air density | 1.25 |
| Height of each floor | 3.5 |
| Width of each floor | 40 |
| Windward area of each floor | 140 |
| Wind pressure coefficient | 1.2 |
| Wind profile exponent | 0.16 |
3.2 예제 구조물의 운용중 모드 해석
2장에서 제시한 자동화된 Cov-SSI 방법을 적용하여 예제 구조물의 모드 정보를 식별하기 위해 다음과 같은 절차를 거쳤다. 먼저 구조물에 설치되는 센서는 모드 형상을 고려하여 4,8,13,16,20층의 수평 가속도 응답만을 계측하는 것으로 가정하였다. 일반적으로 센서의 개수가 많을수록 계측할 수 있는 모드의 수도 증가하나, 상시 운용하는 계측 시스템은 목적에 따라 제한된 개수의 센서를 설치하게 되므로 이 예제에서는 5개 층만의 가속도 응답을 사용하는 것으로 가정하였다.
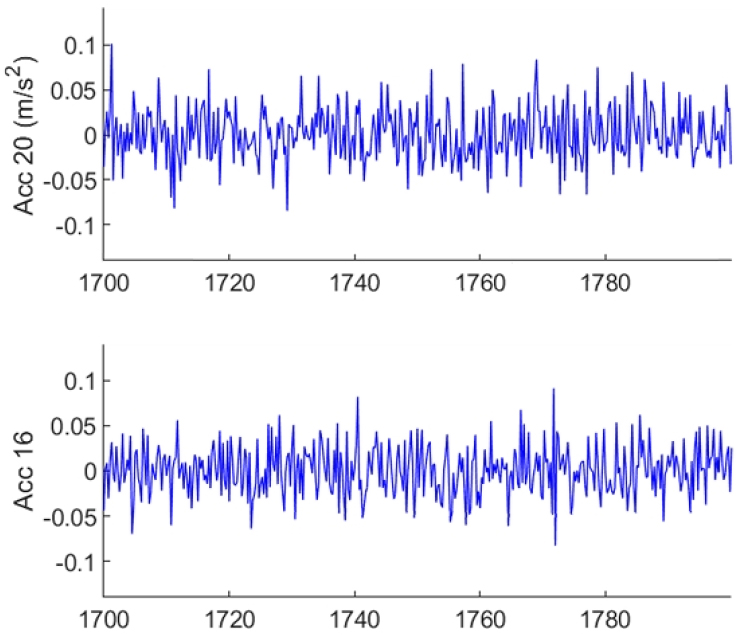
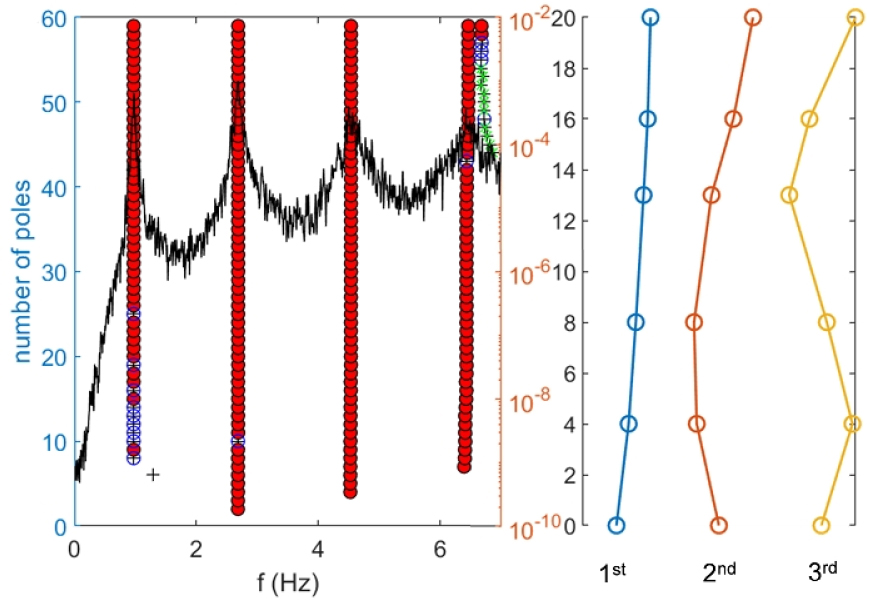
자동화된 Cov-SSI 방법을 적용하기 위해 결정해야 하는 주요 파라미터로는 샘플링 레이트(sampling rate) 와 시간 지연(time lag) , 측정 윈도우 시간 가 있다. 샘플링 레이트 는 계측하고자 하는 최고차 진동수가 Nyquist 진동수 보다 크지 않도록 결정해야 하고, 시간 지연 는 시간 지연 샘플 개수 와 센서 출력 개수 의 곱이 식별하고자 하는 상태공간방정식 시스템 행렬의 차수 보다 크도록 결정해야 한다. 측정 윈도우 시간은 상관계수 행렬이 충분히 안정된 값을 얻을 수 있도록 길어야 한다. 이 예제에서는 100Hz로 하고 안정적인 모드 진동수를 추출 할 수 있는 값을 시행착오법에 의해 결정하였다. 가속도 응답 시간이력을 사용하여 1,800초 동안 60초 간격으로 식별하였다. 안정된 식별 값을 보이는 파라미터로서 =2.4초, 600초를, 시스템 폴(pole) 수는 최소 2개 최대 60개를 사용하였다. Fig. 2에 16층과 20층의 가속도 시간이력 예를, Fig. 3에 stabilization diagram과 식별된 모드의 예를 나타내었다.
3.3 유한요소모델 업데이트를 위한 역고유치함수 신경망 구성
3.2절의 결과를 바탕으로 하여 이 예제를 위한 역고유치 함수 신경망을 구성한다. 5개 층의 가속도 응답으로부터 자동화된 Cov-SSI 방법을 적용하여 3개 저차 모드에 대한 고유진동수 및 고유벡터를 식별한 결과를 이용한다. 신경망의 입력층 은 로 구성된 에 대한 총 18개 노드로 하였다. 출력층은 업데이트 할 유한요소 모델의 횡강성 파라미터 5개 를 고려한 최적 유한요소모델 파라미터 벡터 의 5개 노드로 구성하였다. 이 연구에서서는 은닉층 개수는 1개부터 4개까지 변화시키고, 각 층의 노드 개수는 50개~300개 까지 변화시켜 가며 최적 구조를 탐색하였다.
모델 업데이트를 위한 역고유치 함수 학습을 위해 유한요소모델 파라미터 벡터 와 이에 대한 고유진동수 및 모드 행렬 데이터 쌍을 구축한다. 이 연구에서는 Table 1의 공칭값으로부터 20%의 변동폭을 갖는 정규화 파라미터 벡터 를 추출하고, 각 파라미터를 적용한 유한요소모델의 질량 및 강성행렬로부터 고유치해석을 통해 고유진동수 벡터와 모드 행렬을 생성하였다. 모델 파라미터 벡터 는 구간 내 조합 분포가 고르게 되도록 LHS(Latin Hypercube Sampling)방법을 사용하였으며 총 20,000 쌍의 입출력 데이터 집합을 생성하여 신경망을 학습 시켰다.
이 연구에서 최종적으로 선택한 신경망은 층당 200, 400, 200개의 노드를 가진 은닉층 수 3개의 구조로서, 은닉층의 활성화 함수(activation function)는 tangent sigmoid 함수를 사용하였다. 학습 성능 지표인 목표 값과 신경망 출력 값 사이의 평균제곱오차(MSE) 값은 이하까지 줄일 수 있었으며 학습 소요시간은 2.4GHz intel CPU를 사용한 PC환경에서 약 12 시간 정도였다. 신경망 학습은 MATLAB의 Deep Learning Toolbox를 사용하여 프로그래밍 하였다.
3.4 온라인 모델 업데이트 시뮬레이션 1(Case S1)
이 절에서는 3.1절에서 제시한 20층 빌딩 구조물의 가속도 응답 계측 값으로부터 3.2~3절에 제시한 방법을 이용하여 유한요소 모델을 자동으로 업데이트 하는 시뮬레이션 예를 보인다. 일반적으로 실제 구조물은 설계시에 가정한 공칭 값과는 다른 강성 및 질량 값을 가지게 된다. 이 시뮬레이션에서는 임의로 가정한 질량 및 강성 값을 실제 구조물의 값으로 하여 제시한 온라인 업데이트 방법으로 가정한 참 값을 추정할 수 있는지 확인한다.
풍하중을 받는 예제 구조물의 4,8,13,16,20층의 가속도 응답을 1,800초 동안 계측하면서 동시에 온라인 업데이트 절차가 진행되도록 시뮬레이션을 수행하였다. 계측한 가속도 시간 이력 데이터를 3.2에서 설계한 Cov-SSI 방법의 입력으로 하여 고유 진동수 및 모드 형상 데이터를 추출하고, 이를 바로 3.3에서 학습된 역고유치 신경망에 입력 하고 업데이트 파라미터를 출력하여 시간별로 저장하였다. 데이터의 획득부터 업데이트 파라미터 출력까지 모든 과정은 사용자의 개입 없이 온라인으로 이루어졌다.
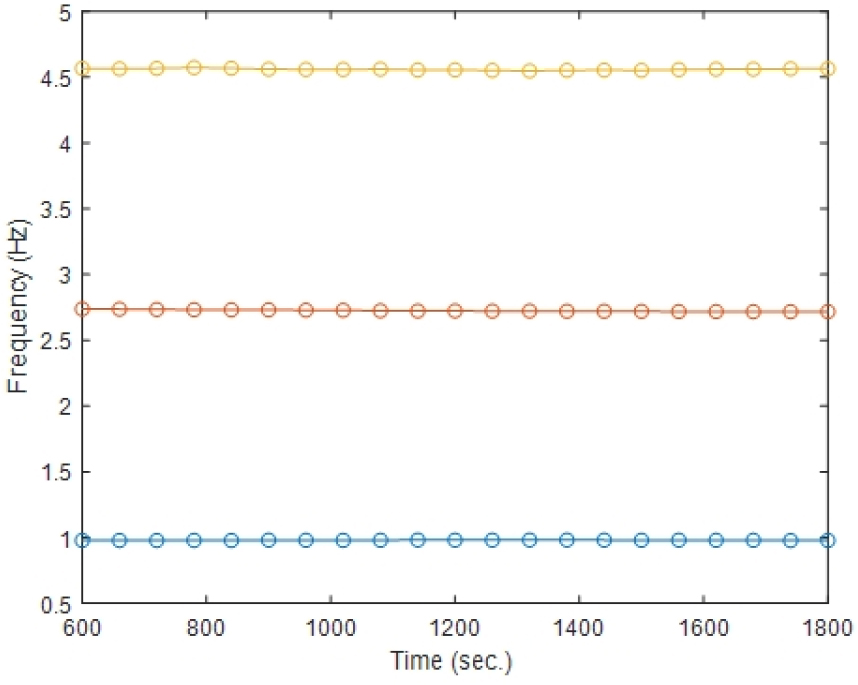
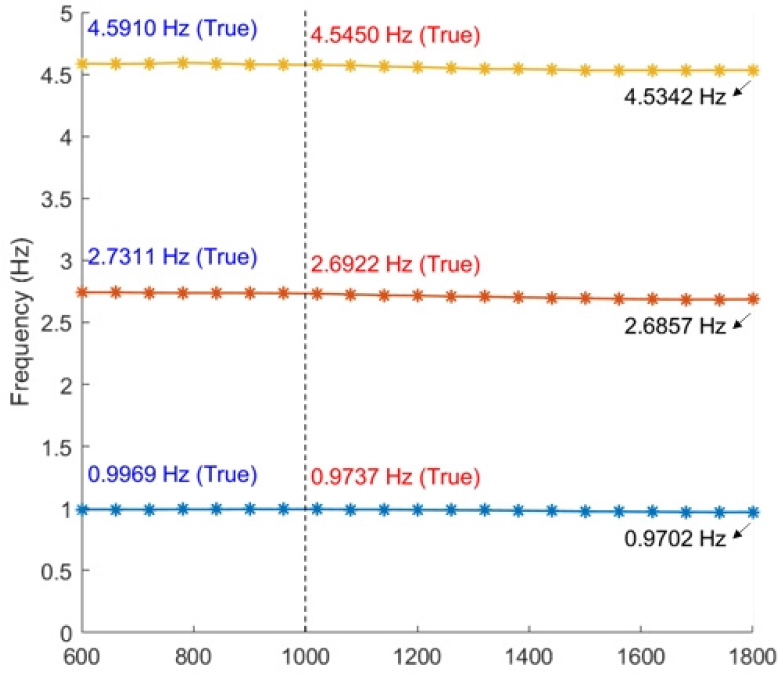
시뮬레이션 결과 추출한 고유진동수 시간이력을 Fig. 4에, 모델 파라미터 ~ 의 업데이트 시간이력을 Fig. 5에 나타내었다. 식별 및 업데이트는 60초 간격으로 진행하였으며, 식별 순간 시간으로부터 이전 600초 동안의 가속도 응답 시간 이력을 이용하였다.
시뮬레이션 결과 제시한 방법은 60초 간격으로 3개의 고유진동수 및 모드 벡터를 안정적으로 추출하였고 그에 대한 구조 파라미터를 업데이트 할 수 있었다. 총 21개의 시점에서 식별한 고유진동수와 시뮬레이션에서 사용한 참 값과의 비교 결과 고유진동수는 최소 0.0154% 최대 0.570%, 전체 평균 0.236% 의 오차를 보여 성공적으로 모드 식별이 이루어진 것으로 파악되었다. 각 모드별 고유진동수 참 값 및 오차를 Table 3에 나타내었다.
Table 3.
True and identified mode frequencies(case S1)
| 1st mode | 2nd mode | 3rd mode | |
| True freq.(Hz) | 0.9812 | 2.7251 | 4.5732 |
| Max. error(%) | 0.418 | 0.445 | 0.570 |
| Min. error(%) | 0.0197 | 0.0390 | 0.0154 |
| Ave. error(%) | 0.185 | 0.217 | 0.306 |
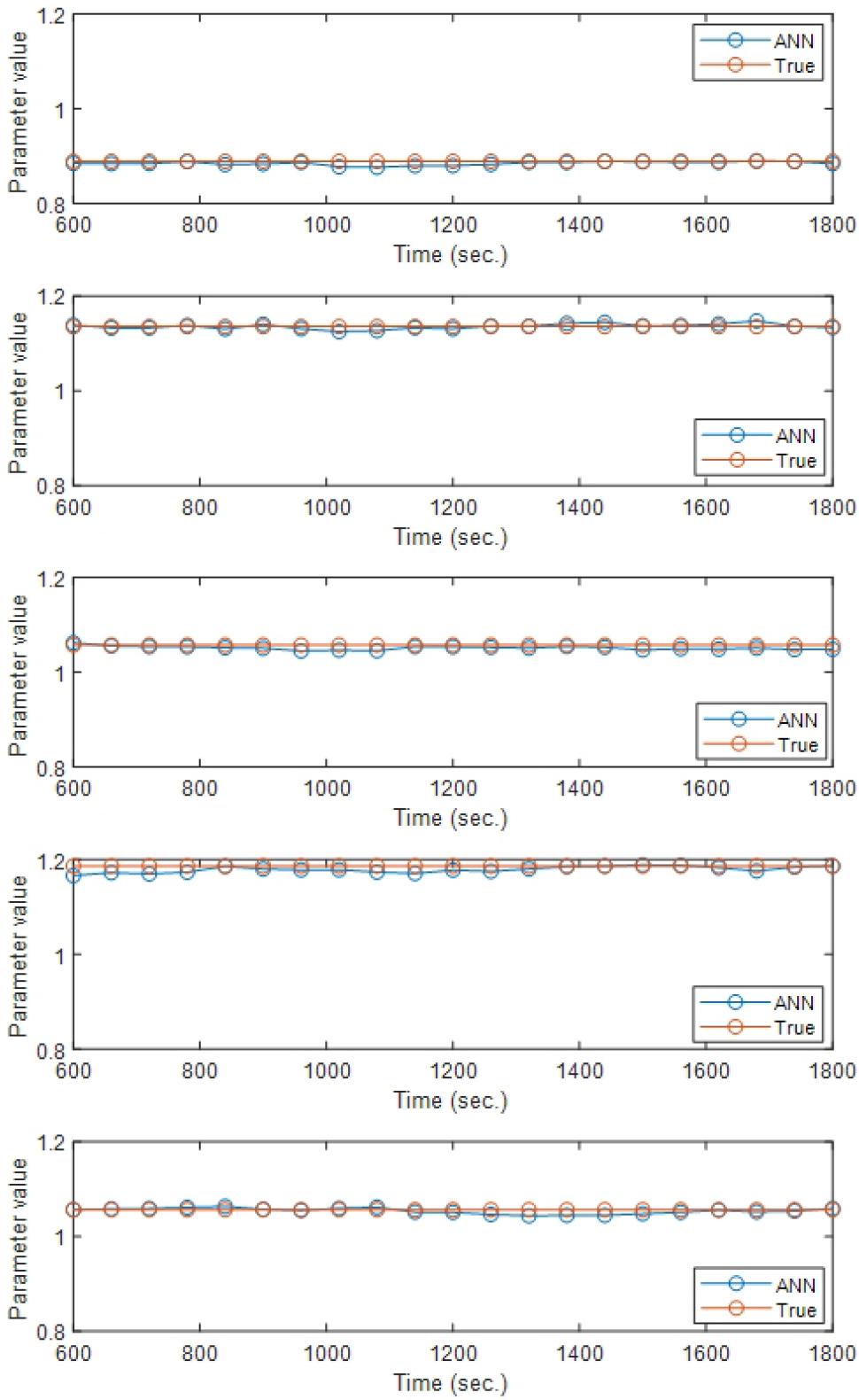
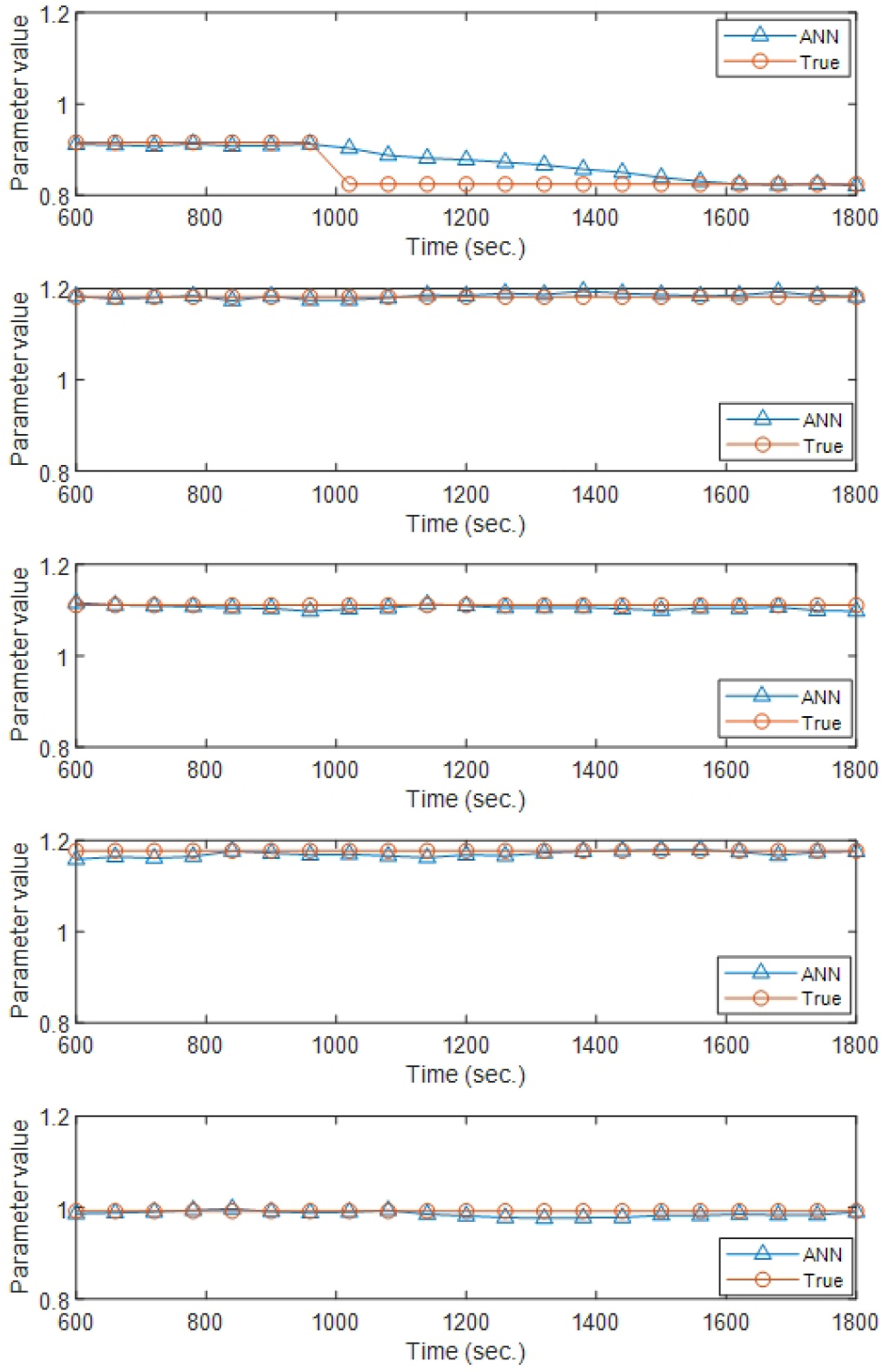
식별된 모드 특성 값을 이용한 유한요소모델 파라미터의 실시간 업데이트 결과를 Fig. 5에 나타내었다. 60초 간격으로 식별된 모드 특성 값을 학습한 신경망에 입력하여 총 21개 시점에서 모델 파라미터를 추출하였다. 시뮬레이션에서 설정한 참 값과의 비교 결과를 Table 4에 나타내었다. 파라미터는 최소 0.0005% 최대 1.717%, 평균 0.538%의 오차를 나타내어 제시한 방법을 통해 매우 정확하게 시간별로 파라미터를 업데이트 할 수 있음을 확인하였다.
Table 4.
True and identified FE model parameters(case S1)
| True | 0.8889 | 1.1357 | 1.0574 | 1.1866 | 1.0569 |
| Max. error(%) | 1.418 | 1.054 | 1.186 | 1.717 | 1.228 |
| Min. error(%) | 0.0118 | 0.0661 | 0.179 | 0.0005 | 0.0039 |
| Ave. error(%) | 0.592 | 0.400 | 0.632 | 0.665 | 0.493 |
3.5 온라인 모델 업데이트 시뮬레이션 2(Case S2)
이 절에서 보이는 시뮬레이션 예제는 구조물의 변화가 있을 경우에 이를 식별할 수 있는지 확인하기 위한 것이다. Case S1과 마찬가지로 구조물의 질량 및 강성을 임의로 가정하고 계측 및 업데이트를 시작하되, 계측 중간에 구조물의 강성이 변화하는 경우를 가정하였다. 실제 구조물에서 강성은 일반 사용 상태에서 온도 변화에 따라 변하고, 장기간에 걸친 구조물의 열화 등에 따라 변화한다. 또 다른 경우로는 강진, 충돌, 피로 파괴 등으로 인해 구조물 일부에 갑작스런 변화가 발생하는 경우이다. 이 시뮬레이션에서는 후자의 경우로서 특정 이벤트에 의해 구조물의 일부분 강성이 비교적 크게 변하는 경우를 상정하였다.
시뮬레이션 시나리오는 Table 1의 S2 구조물에 대하여 총 1,800초의 계측 시간 중 100초에서 대상 구조물 1층부터 4층의 강성이 10% 감소하도록 하고 이후 변동된 강성을 유지하도록 하였다. 실제 상황에서는 이러한 불연속적인 급격한 변화는 충돌 등 극단적인 상황을 제외하고 발생하기 어렵지만 제시한 방법의 성능을 검토하기 위한 예제로서 이러한 시나리오를 대상으로 하였다.
시뮬레이션 결과 고유진동수 시간이력을 Fig. 6에, 모델 파라미터의 업데이트 시간이력을 Fig. 7에 나타내었다. 식별 및 업데이트는 60초 간격으로 진행하였으며, 식별 순간 시간으로부터 이전 600초 동안의 가속도 응답 시간 이력을 이용하였다.
시뮬레이션 결과 제시한 방법은 성공적으로 구조 강성 파라미터의 변화를 검출할 수 있었다. 강성 저하 이벤트가 발생한 1,000초 시점에서 Cov-SSI 알고리즘의 측정 윈도우 시간 인 600초가 완전히 지나기 전인 1,600초 까지는 변동 전후의 시스템 신호가 공존하는 시간으로서, 측정 윈도우 시간 내에서 시스템의 변화가 없다고 가정하는 Cov-SSI 방법에서는 정확한 값을 추출할 수 없으므로 이에 상응하는 천이(transient) 구간의 고유진동수 값과 이에 따른 구조 파라미터가 추출되는 것을 확인할 수 있다. 강성 변화 이후 시스템 특성 값이 고정된 1,600초 이후 구간에서는 변화된 고유진동수, 모드벡터 및 구조파라미터의 업데이트가 안정적으로 이루어졌다. 강성 변화 후 최종 참 값과의 비교결과 고유진동수는 최소 0.238%, 최대 0.361%, 평균 0.280% 의 오차를 보였으며 강성 파라미터는 최소 0.0493%, 최대 1.156%, 평균 0.385%의 오차를 나타내어 제시한 방법을 통해 매우 정확하게 구조 강성 파라미터의 변동을 업데이트할 수 있음을 확인하였다.
4. 결 론
공용중인 구조물의 유한요소 모델을 계측값을 이용하여 온라인으로 업데이트 할 수 있는 방법을 제안하였다. 제안한 방법에서는 자동화된 운용중 모드 해석(Operational Modal Analysis)방법의 하나인 Cov-SSI알고리즘을 통해 구조물의 진동 계측 시간이력으로부터 고유진동수 및 모드 형상을 식별하고, 이를 다시 구조물 유한요소모델 업데이트를 위한 역 고유치 신경망에 입력하여 최종적으로 업데이트된 유한요소 모델의 파라미터를 추정한다. 풍하중을 받는 20층 전단 빌딩 구조 모형에 대한 수치예제를 통해 제시한 방법은 운용중 사용자의 개입 없이 자동으로 온라인에서 연속적인 유한요소모델 업데이트를 할 수 있음을 확인하였다. 자동화된 Cov-SSI 방법은 적절한 설계 과정을 거친 후 안정적으로 중요 모드를 식별할 수 있었으며, 역고유치 신경망은 매우 높은 정확도로 해당 모드 정보에 대한 모델 파라미터를 추정할 수 있었다. 계측 도중 구조물의 정보가 변화하는 시나리오에 대한 예제에서 급격한 변화 이벤트의 경우 구조물의 변화가 일어나는 시점과 변화 후 변동된 구조 모델 파라미터 값을 성공적으로 추정할 수 있음을 확인하였다.
제시한 온라인 업데이트 방법에서 추가적으로 주목할 만한 것은 계측부터 업데이트까지 소요되는 계산 시간이다. 이 시뮬레이션의 계산 수행 부분은 구조물의 응답 계측 부분을 제외한 나머지 부분은 실제와 동일한 상황이라 할 수 있으므로, 계측 이후 업데이트에 소요된 시간을 확인하여 보았다. 시뮬레이션에 사용된 총 업데이트는 60초 간격으로 총 21회가 이루어 졌으며, 각 업데이트시 소요된 시간은 Cov-SSI 과정에서 약 2초, 신경망을 통한 파라미터 업데이트 과정에서 1초 미만이 소요되었다. 이는 제시한 방법이 실시간에 거의 가깝게 모델 업데이트를 할 수 있음을 의미한다.
제안한 방법은 계측 시스템과 유한요소모델이 주어질 경우에 이를 이용하여 업데이트하는 방법이며, 본질적인 계측 오차와 모델링 오차를 고려하지 못하는 한계가 있다. 제안한 방법의 적용성을 높이기 위해서 향후 연구에서 좀 더 개선이 필요한 부분으로는 CoV-SSI 적용시의 설계 파라미터 선정을 위한 체계적인 방법의 개발, 시스템 차수의 변화에 따른 모델 업데이트가 가능한 유연 또는 강인한 신경망 모델의 개발을 생각할 수 있다. 적용 예로서 시뮬레이션이 아닌 실험 모형 또는 실구조물의 계측을 활용하는 것도 필요한 부분이다.