Modified K&amp;C Model for Numerical Analysis of Steel-Fiber-Reinforced Concrete Structure

Gang-Kyu Park; Minjoo Lee

doi:10.7734/COSEIK.2021.34.2.85

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 April 2021. 85-91
https://doi.org/10.7734/COSEIK.2021.34.2.85

Modified K&C Model for Numerical Analysis of Steel-Fiber-Reinforced Concrete Structure

강섬유 보강 콘크리트 구조물의 해석을 위한 K&C모델의 보정

Gang-Kyu Park¹^*

Minjoo Lee²

박 강규¹^*

이 민주²

¹Postdoctoral Research Fellow, Structural Engineering Research Division, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

²Graduate Student, Department of Civil and Environmental Engineering, Korea Advanced Institute of Science and Technology, Daejeon, 34141, Korea

¹한국건설기술연구원 인프라안전연구본부 박사후연구원

²한국과학기술원 건설 및 환경공학과 박사과정

^{*Corresponding Author}

ABSTRACT

This paper introduces a modified Karagozian & Case concrete model (K&C model) for the numerical analysis of a steel-fiber-reinforced concrete (SFRC) structure subjected to projectile impact. The original K&C model was calibrated to consider the effects of steel fibers accurately by modifying the strength surfaces and input parameters. Single element tests were then conducted and compared with uniaxial and triaxial compressive data to verify the modified model. With the application of a dynamic increase factor, the finite element model of the SFRC structure subjected to projectile impact was constructed. Thereafter, the applicability of the modified material model was examined by comparisons with the experimental results.

Keywords

K&C model

steel-fiber-reinforced concrete

finite element model

dynamic analysis

본 연구에서는 섬유보강콘크리트(SFRC) 구조물의 수치해석을 위한 K&C모델의 보정기법을 소개하였다. SFRC 1축 및 3축 압축강도 실험결과를 기반으로 보정을 수행하였으며, 단일요소 해석결과를 실험결과와 비교함으로써 보정 기법의 검증을 수행하였다. 또한, 변형률 속도의 영향을 반형하기 위해 동적증가계수(DIF)를 고려하여 SFRC 구조물의 발사체 관통해석을 수행함으로써 보정기법의 적용 가능성을 확인하였다.

키워드

K&C모델

강섬유보강 콘크리트

유한요소해석

동적 해석

MAIN

1. 서 론
2. 본 론
2.1 기존 K&C모델
2.2 K&C 모델의 보정
2.3 수치해석
3. 결 론

1. 서 론

콘크리트 구조물에 폭발 및 충격과 같이 짧은 시간에 큰 하중이 작용할 경우, 배면파괴 및 파편 등으로 인해 심각한 인명 및 재산 피해가 발생할 수 있다. 이러한 현상을 방지하고 폭발 및 충격에 대한 구조물의 저항성을 높이기 위해 강섬유를 추가한 강섬유 보강 콘크리트(steel fiber reinforced concrete, SFRC)의 개발이 활발하게 이루어지고 있다(Bencardino et al., 2008; Ou et al., 2012; Yoo et al., 2015; Gholampour and Ozbakkaloglu, 2018; Abbass et al., 2018). 강섬유의 추가되면 콘크리트의 강도, 연성, 에너지 흡수 등 성능이 향상되며, 강섬유의 가교역할(bridging effect)로 균열의 급속한 증가를 억제할 수 있어 구조적 성능이 개선되는 효과가 있다. 이와 같은 섬유보강 콘크리트의 개선된 성능을 해석적으로 반영할 수 있는 연구가 진행 중이다.

상용 프로그램 중 하나인 LS-DYNA에서는 콘크리트 구조물의 폭발 및 충격해석을 수행하기 위한 여러 가지 재료모델이 존재한다. Wu 등(2012)은 LS-DYNA에서 가장 많이 사용되는 재료모델 중 Karagozian & Case(K&C) 모델, Winfrith 모델, 그리고 CSC모델의 간략한 이론적 배경과 목적에 맞는 재료모델을 선택할 수 있도록 각 모델의 장단점을 설명하였다. 그 중 K&C모델은 콘크리트의 구속효과(confinement effect)와 연성 거동(softening behavior)을 잘 묘사할 수 있어 정적, 폭발, 그리고 충격 해석 수행 시 적절하게 사용될 수 있다고 하였다(Wu et al., 2012). 실제로 K&C모델을 이용한 콘크리트 구조물의 폭발 및 충격해석 연구가 많이 이루어지고 있다(Tu and Lu, 2009; Hong et al., 2017; Wu et al., 2019).

K&C 모델은 49개의 입력 변수들이 존재하지만, 압축응력값만 입력하더라도 1나머지 변수들은 자동으로 제공된다. 따라서, 자세한 콘크리트 물성에 대한 정보없이 압축강도만으로도 K&C모델을 이용하여 해석을 수행할 수 있다. 하지만 K&C모델에서 자동으로 제공하는 변수들은 일반 콘크리트를 기반으로 얻어진 것이기 때문에 강섬유로 보강된 콘크리트 구조물 해석 시에는 바로 적용하기 힘들다. 따라서 이전 많은 연구에서는 K&C모델에서 손상발전변수(damage evolution parameter) $b_{1}$ 와 $b_{2}$ 또는 손상 함수(damage function) $η (λ)$ 를 수정함으로써 강섬유의 영향을 반영할 수 있도록 하였다(Mao et al., 2014; Hong et al., 2017; Kong et al., 2017; Lin and Gravina, 2017; Yang et al., 2018). 아직까지는 SFRC 응력-변형률 관계에 대한 실험결과가 충분하지 않고 편차 또한 크기 때문에 보강 섬유의 형태 및 함유량에 따른 응력-변형률 관계의 경향성을 정량화하기에는 어려움이 따른다.

본 연구에서는 기존 K&C모델의 강도 곡선(strength surfaces)와 $η (λ)$ 관계를 보정하여 SFRC의 강섬유 영향을 해석에 반영하는 방법을 제안하였다. 우선, 기존 SFRC의 1축 및 3축 압축강도 데이터를 기반으로 기존 K&C의 강도 곡선(strength surfaces)을 수정하였다. 그리고 데미지 함수 $η (λ)$ 를 수정하여 강섬유 함유량에 따른 응력-변형률 관계의 변화를 반영할 수 있도록 하였다. 단일요소해석을 수행하여 이전 실험 연구를 통해 얻은 SFRC 응력-변형률 관계와 보정기법을 통해 얻은 해석결과를 비교하였다. 마지막으로, 변형률 속도의 영향을 반영하기 위해 동적 증가 계수(dynamic increase factor, DIF)를 도입하여 SFRC 구조물의 발사체 관통해석을 수행하였으며, 이를 통해 본 연구에서 제안한 보정기법의 적용 가능성을 검증하였다.

2. 본 론

2.1 기존 K&C모델

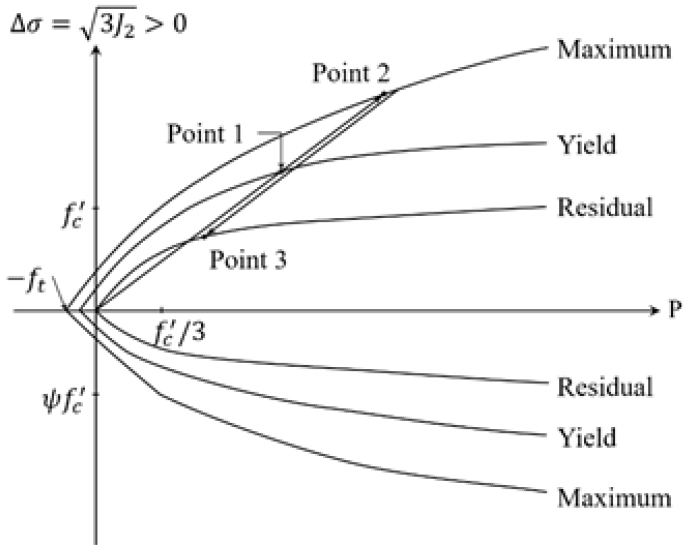
K&C모델은 3개의 독립적인 강도 곡선으로 표현되며, Fig. 1과 같이 압력( $P$ )과 응력차( $∆ σ$ )의 관계로 나타낼 수 있다. 기존 K&C에서 각 강도 곡선을 구성하기 위한 식은 다음과 같다(Malvar et al., 1997).

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F1.jpg

Fig. 1

Three strength surfaces

- 최대 강도 곡선(Maximum strength surface)

(1)

∆ σ = \{\begin{matrix} a_{0} + \frac{p}{a_{1} + a_{2} p}, for p \geq \frac{f_{c}}{3} \\ \frac{3}{2 ψ} (p + f_{t}) \begin{matrix} , f o r \{0 \leq p \leq \frac{f_{c}}{3}\} or \\ \{λ \leq λ_{m} and - T \leq p \leq \leq \frac{f_{c}}{3}\} \end{matrix} \\ 3 (\frac{p}{η} + f_{t}), f o r p \leq 0 and λ > λ_{m} \end{matrix}

- 항복 강도 곡선(Yield strength surface)

(2)

∆ σ_{y} = \{\begin{matrix} a_{0 y} + \frac{p}{a_{1 y} + a_{2 y} p}, for P \geq \frac{f_{y c}}{3} \\ 1.35 f_{t} + 3 p (1 - \frac{1.35 f_{t}}{f_{y c}}), for \{0 \leq p \leq \frac{f_{y c}}{3}\} \\ 1.35 (p + f_{t}), for p \leq 0 \end{matrix}

- 잔존 강도 곡선(Residual strength surface)

(3)

∆ σ_{y} = \frac{p}{a_{1 f} + a_{2 f} p}

각각의 강도 곡선은 편차응력(deviatoric stress) $∆ σ$ 의 2차 불변량 $J_{2}$ (second invariant)을 기반으로 결정되며 $∆ σ = \sqrt{3 J_{2}} =$ $\sqrt{3 / 2 (S_{1}^{2} + S_{2}^{2} + S_{3}^{2})}$ 으로 표현된다. 각각의 변수 $a_{i}$ , $a_{i y}$ , $a_{i f}$ 은 기존 K&C에서 자동으로 생성한다. 또한, $f_{c}$ 는 압축강도, $f_{t}$ 는 인장강도, $f_{y c} = 0.45 f_{c}$ , $p$ 는 정수압이며, $ψ$ 는 인장측 자오선(tensile meridian)과 압축측 자오선(compressive meridian)의 비를 의미한다. 더 자세한 내용은 이전 연구에서 확인할 수 있다(Malvar et al., 1997; Crawford et al., 2012).

항복 강도 곡선에 도달 후 현재 강도 곡선(current strength surface)는 최대 강도 곡선과 항복 강도 곡선 사이의 선형보간법을 통해 얻어진다. 이와 마찬가지로, 최대 강도 곡선에 도달 후 강도 곡선은 최대 강도 곡선과 잔존 강도 곡선 사이의 선형보간법을 통해 얻을 수 있다. 이를 다음 식과 같이 나타낼 수 있다(Malvar et al., 1997).

(4)

∆ σ = \sqrt{3 J_{2}} = \{\begin{cases} r' [η (∆ σ_{m} - ∆ σ_{y}) + ∆ σ_{y}], for s t r a i n h a r d e n i n g \\ r' [η (∆ σ_{m} - ∆ σ_{r}) + ∆ σ_{r}], for s t r a i n s o f t e n i n g \end{cases}

여기서, $r'$ 은 현재 강도 곡선과 압축측 자오선의 비를 말하며, $η$ 는 현재 강도 곡선의 상대적인 위치를 의미하며 손상 변수인 $λ$ 의 함수로 표현된다(Malvar et al., 1997; Crawford et al., 2012).

(5)

λ = \{\begin{cases} \int_{0}^{\bar{ε^{p}}} \frac{d \bar{ε^{p}}}{r_{f} (1 + p / r_{f} f_{t})^{b_{1}}}, for p \geq 0 \\ \int_{0}^{\bar{ε^{p}}} \frac{d \bar{ε^{p}}}{r_{f} (1 + p / r_{f} f_{t})^{b 2}}, for p < 0 \end{cases}

여기서, 유효소성변형률증분(effective plastic strain increment)은 $d \bar{ε^{p}} = \sqrt{(2 / 3) d ε_{i j}^{p} d ε_{i j}^{p}}$ 로 표현되며, 손상진화변수(damage evolution parameters) $b_{1}$ 과 $b_{2}$ 은 각각 압축측과 인장측 응력-변형률 관계의 연성부분을 담당한다. $r_{f}$ 는 변형률속도의 영향을 고려하기 위한 동적강도증가계수(dynamic increase factor, DIF)이다.

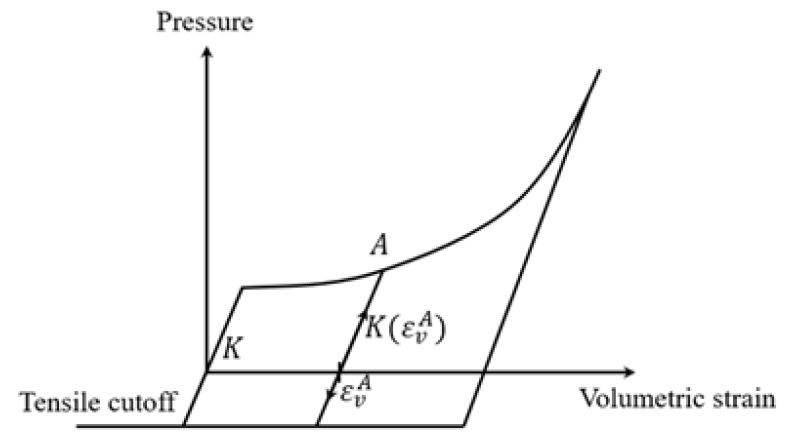
또한, 콘크리트 재료 거동을 묘사하기 위해서는 상태 방정식(equation of state, EOS)이 정의되어야 한다. LS-DYNA상에서 K&C모델은 EOS_TABULATED_ COMPACTION 카드를 이용해 상태 방정식을 정의할 수 있으며, 이는 현재 압력과 체적 변형률(volumetric strain)의 관계로 나타낼 수 있으며, 해당 관계를 Fig. 2에 나타내었다(Crawford et al., 2012).

(6)

p = K ε_{v}^{e}

여기서, $K$ 는 체적계수, $ε_{v}^{e} = \ln (1 + \frac{∆ V}{V_{0}}) - ε_{v}^{p}$ 은 탄성 체적 변형률, $∆ V$ 은 체적의 변화량, $V_{0}$ 는 초기 체적, $ε_{v}^{p}$ 는 소성 체적 변형률을 의미한다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F2.jpg

Fig. 2

Pressure–volumetric strain curve for EOS

2.2 K&C 모델의 보정

2.2.1 강도 곡선 보정

기존 K&C모델에서는 일반 강도 콘크리트 45.4MPa의 1축 및 3축 압축 실험 데이터를 기반으로 각 강도 곡선을 정의하였으며, 이와 관련된 식은 다음과 같이 표현된다(Crawford et al., 2012).

(7)

a_{0} = 0.2956 f_{c} a_{1} = 0.4463 a_{2} = 0.0808 / f_{c} a_{0 y} = 0.2232 f_{c} a_{1 y} = 0.625 a_{2 y} = 0.2575 / f_{c} a_{0 f} = 0.0 a_{1 f} = 0.4417 a_{2 f} = 0.1183 / f_{c}

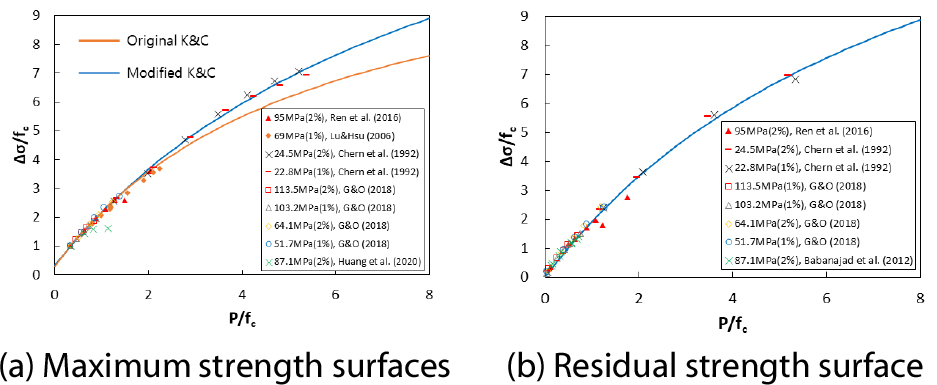
강섬유 보강 콘크리트의 경우 재료의 물성이 달라지기 때문에 위와 같은 강도 곡선 변수들은 SFRC 해석에 직접 적용하기에는 어려움이 따른다. 본 연구에서는 SFRC 시편의 1축 및 3축 압축 실험결과(Chen et al., 1992; Farnam et al., 2010; Ren et al., 2016; Gholampour and Ozbakkaloglu, 2018)를 바탕으로 각 강도 곡선을 보정했다. Origin 프로그램을 이용한 비선형 회귀분석을 통해 SFRC의 강도 곡선을 보정하였으며, 이를 통해 얻은 강도 곡선과 변수 $a_{i}$ , $a_{i y}$ , $a_{i f}$ 는 각각 Fig. 3과 식 (8)에 나타내었다.

(8)

a_{0} = 0.3434 f_{c} a_{1} = 0.4907 a_{2} = 0.0555 / f_{c} a_{0 y} = 0.2861 f_{c} a_{1 y} = 0.7905 a_{2 y} = 0.1452 / f_{c} a_{0 f} = 0.0 a_{1 f} = 0.4669 a_{2 f} = 0.0542 / f_{c}

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F3.jpg

Fig. 3

Modified strength surfaces of the K&C

기존 K&C에서 자동으로 제공되는 상태 방정식(EOS)은 일반 콘크리트를 대상으로 구성되어 있으며, volumetric scaling method를 통해 압축강도 변화에 따른 압력과 체적탄성계수가 결정된다(Crawford et al., 2012). 일반 콘크리트에 관해 결정된 상태 방정식은 SFRC에 대해 수정이 필요하지만 SFRC의 압축강도에 따른 상태 방정식을 얻기 위한 실험데이터가 상당히 제한적이다. 따라서, 본 연구에서는 이전 연구와 마찬가지로(Yang et al., 2018; Lin, 2018), 기존 K&C에서 자동으로 제공하는 상태 방정식에서 압력-체적 변형률 곡선의 첫 번째 변곡점은 식 (9)을 기반으로 SFRC 탄성계수가 반영된 체적탄성계수(elastic bulk modulus)를 수정하여 해석에 적용하였다.

(9)

K = \frac{d p}{d ε_{v}} = \frac{E_{c}}{3 (1 - 2 ν)}

2.2.2 $η$ 와 $λ$ 의 관계의 보정

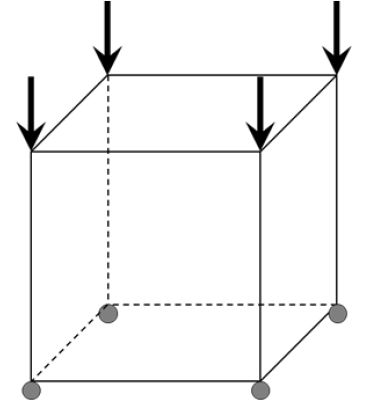
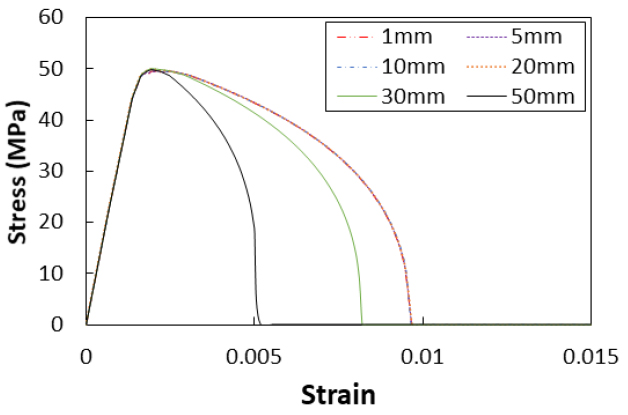
사용되는 요소 크기에 따라서 해석상의 응력-변형률 관계는 달라진다. 따라서, 요소 크기에 따른 해석결과의 수렴성을 확인하기 위한 단일요소해석(single element analysis)를 수행하였으며, 이를 Fig. 4에 나타내었다. 상부 4개의 절점에 변위재하 방식으로 변형률 속도(strain rate)가 0.0001/s로 유지되도록 설정하였다. 또한, 경계조건은 변위재하 방향으로만 고정하여 단일요소해석을 수행하였다. Fig. 5에 K&C모델을 이용하여 요소 크기에 따른 응력-변형률 관계를 나타내었다. 그림에서 확인할 수 있듯이 20mm 이하의 요소를 사용할 경우 거의 동일한 해석결과를 보여주는 것으로 나타난다. 폭발 및 충격해석 시 일반적으로 상당히 작은 요소를 사용하는 것으로 알려져 있으며, 본 연구에서 제안하는 보정방법을 적용해 일관성 있는 응력-변형률 관계를 얻기 위해 20mm 요소를 대상으로 단일요소해석을 수행하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F4.jpg

Fig. 4

Single element model

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F5.jpg

Fig. 5

Stress-strain relationship of a single element according to element sizes

기존 K&C모델에서 기본적으로 제공하는 $η$ 과 $λ$ 의 관계가 존재하며, 이 관계는 해석을 통해 얻은 응력-변형률 곡선 형태에 직접적인 영향을 미친다. 기본적으로 제공되는 관계를 사용하는 것이 편리할 수 있지만, 강섬유로 보강된 SFRC 관계를 정확하게 반영할 수 없다. 따라서, 강섬유 함유에 따른 응력-변형률 곡선의 변화를 반영하기 위해 $η$ 과 $λ$ 의 관계의 보정이 필요하다. $η$ 과 $λ$ 의 관계를 정의하기 위해서는 각각 13개, 총 26개의 변수값이 필요하다. 이 관계를 효율적으로 정의하기 위해서 이전 연구(Hong et al., 2017)에서 사용한 식을 채택하였으며, 그 식은 다음과 같다.

(10)

η (λ) = \{\begin{cases} α \frac{λ}{λ_{m}} + (3 - 2 α) {(\frac{λ}{λ_{m}})}^{2} + (α - 2) {(\frac{λ}{λ_{m}})}^{3}, λ < λ_{m} \\ \frac{λ / λ_{m}}{α_{c} (λ / λ_{m} - 1)^{α_{d}} + λ / λ_{m}}, λ \geq λ_{m} \end{cases}

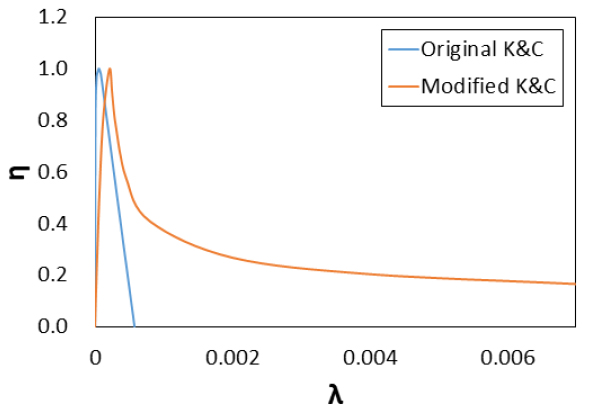
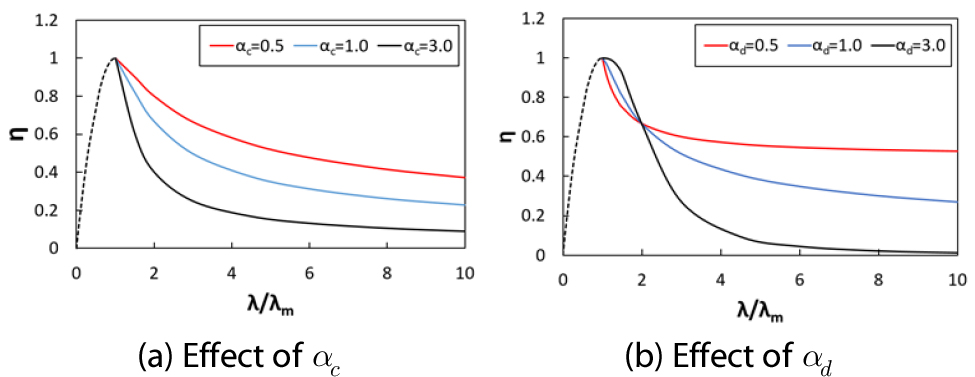
여기서, $α$ 는 변형률 경화 단계에 영향을 미치는 변수이며, $α_{c}$ 와 $α_{d}$ 는 변형률 연화 단계에 영향을 미치는 변수이다. 변수 $λ_{m}$ 은 $η = 1$ 일 때의 변수를 의미하며, 이는 압축강도에 해당하는 변형률 값에 영향을 미친다. 이전 연구(Libre et al., 2011; Afroughsabet et al., 2016)에 따르면 강섬유의 보강은 변형률 경화 단계에는 큰 영향을 미치지 않는다고 보고되었다. 따라서 본 연구에서는 변형률 경화 단계에 사용되는 $α$ 를 2로 고정하여 사용하였다. 그에 반해, SFRC의 변형률 연화 부분은 강섬유의 함유량 등에 따라 변하기 때문에 변수 $α_{c}$ 와 $α_{d}$ 는 조건에 따라 값을 조정해야 한다. 대표적인 예로 $λ_{m} = 0.00021$ , $α_{c} = 1.3$ , $α_{d} = 1.4$ 를 식 (10)에 대입해서 얻은 $η$ 와 $λ$ 의 관계와 기존 K&C에서 제공하는 $η$ 와 $λ$ 의 관계를 Fig. 6에 나타내었으며, 기존 K&C모델에서 제공한 $η$ 와 $λ$ 관계와 차이를 확인할 수 있다. 또한, Fig. 7에 $α_{c}$ 와 $α_{d}$ 값이 $η$ 와 $λ$ 의 관계에 미치는 영향을 나타내었다. 세 변수 $λ_{m}$ , $α_{c}$ 와 $α_{d}$ 를 이용하여 SFRC의 압축강도에 해당하는 변형률과 변형률 연화영역을 보다 정확하게 묘사할 수 있도록 하였다. Fig. 7에 $α_{c}$ 와 $α_{d}$ 값에 따른 $η$ 와 $λ$ 의 관계의 변화를 나타내었다. 두 개의 변수를 이용하여 변형률 연화영역을 보다 정확하게 묘사할 수 있도록 하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F6.jpg

Fig. 6

Comparison of the $η - λ$ relations

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F7.jpg

Fig. 7

Effect of $α_{c}$ and $α_{d}$ on the relation of $η - λ$

2.2.3 단일요소해석

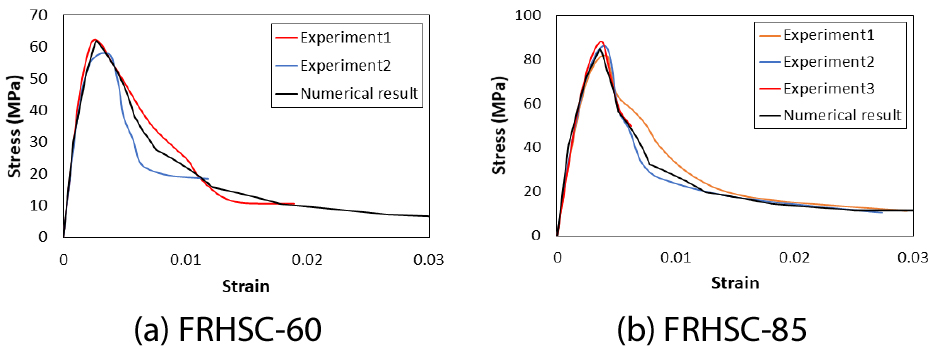
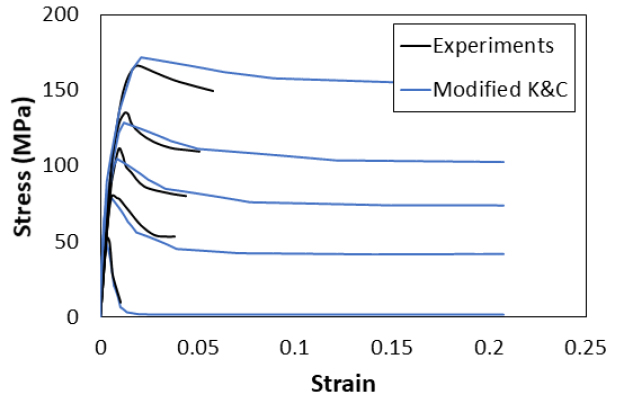
앞서 언급한 보정방법을 이용하여 단일요소해석을 수행하였으며, 이를 통해 얻어진 해석결과를 1축 및 3축 압축 실험결과와 비교하였다. 검증을 위해서 다음 2.3 수치해석 파트에서 사용될 Wang 등(2016) 실험논문에 제시한 SFRC 1축 압축 응력-변형률 관계(FRHSC-60과 FRHSC-85)를 채택하였다. 실험을 통해 얻은 압축 응력-변형률 관계를 해석에 반영하기 위해 $α_{c}$ 와 $α_{d}$ 는 각각 1.3과 1.4를 사용하였다. 각각의 해석결과를 위해 사용된 $η$ 와 $λ$ 의 관계는 Table 1에 나타내었으며, 이를 통해서 얻은 해석결과는 실험결과와 같이 Fig. 8에 나타내었다. 그림에서 확인할 수 있듯이 해석 결과는 실험결과와 유사한 결과를 보인다.

Table 1.

Input parameter in the $η$ and $λ$ relation

FRHSC-60		FRHSC-85
$η$	$λ$	$η$	$λ$
0	0	0	0
0.000025	0.3056	0.00003	0.2653
0.00005	0.5556	0.00007	0.5556
0.0001	0.8889	0.00012	0.8163
0.00015	1.0000	0.00021	1.0000
0.0002	0.8268	0.00025	0.9032
0.0003	0.6061	0.0003	0.7825
0.00045	0.4665	0.00045	0.5776
0.0009	0.3266	0.0008	0.4083
0.002	0.2334	0.002	0.2673
0.004	0.1791	0.004	0.2033
0.007	0.1456	0.007	0.1649
1.00E+10	0.0000	1.00E+10	0.0000

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F8.jpg

Fig. 8

Single element results for SFRC

추가적으로 구속압을 받는 SFRC 3축 압축 응력-변형률의 해석적 검증을 위해 본 연구에서는 Gholampour와 Ozbakkaloglu (2018)가 실험한 C50-1시편을 사용하였다. 이 실험 논문에서는 51.7MPa의 C50-1시편에 5MPa, 10MPa, 15MPa, 그리고 25MPa의 구속압을 가하여 각 구속압에 따른 SFRC 시편의 응력-변형률을 측정하였다. 해당 실험 결과와 함께 K&C모델을 보정하여 얻은 3축 압축 응력-변형률 관계를 Fig. 9에 나타내었다. 그림에서 볼 수 있듯이 앞서 설명한 절차와 같이 SFRC 해석을 위해 보정한 K&C모델의 해석결과는 실험결과를 잘 묘사할 수 있는 것으로 확인된다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F9.jpg

Fig. 9

Stress-strain relatinoship with different confining pressures

2.3 수치해석

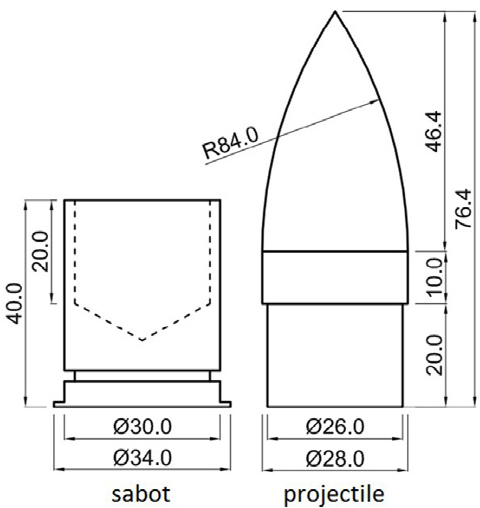
앞서 설명한 보정방법을 이용하여 SFRC 구조물의 거동 예측을 검증하기 위해 Wang 등(2016)이 실험한 SFRC 구조물 발사체 관통실험을 사용하였다. 실험 시편의 크기는 600mm × 600mm × 400mm이며, 발사체 상세는 Fig. 10에 나타내었다. 실험에서는 발사체 속도에 따른 SFRC 강도별 관통깊이를 측정하였다. 더 자세한 정보는 Wang 등(2016)에서 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F10.jpg

Fig. 10

Details of the projectile(Wang et al., 2016)

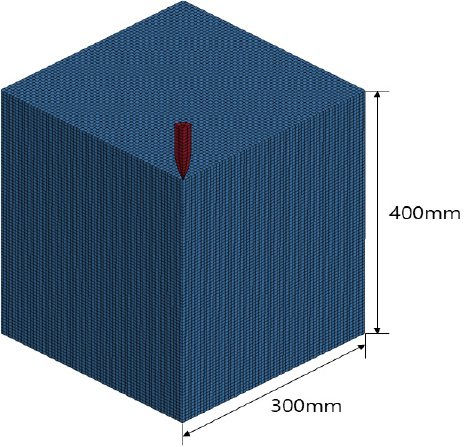
본 연구에서는 위의 실험결과 중 특정 발사체 속도에 따른 강도별 관통깊이를 측정한 실험결과를 사용하였다. 본 해석에 사용된 시편의 정보는 Table 2에 나타내었다. 발사체는 시편의 중앙 표면에 수직 방향으로 가해지도록 설계되어 해당 실험을 1/4 크기로 유산요소 모델링하였으며, 이를 Fig. 11에 나타내었다. 해석에 사용된 발사체는 Wang 등(2016)과 같이 강체로 모델링하였고 두 해석에 사용된 응력-변형률 관계는 Fig. 8과 같이 강섬유의 영향을 반영하여 해석에 적용하였다. 인장측의 경우 해당 실험에서 제공하지 않아 압축강도와 인장강도 사이의 경험식을 통해 인장강도를 계산하였다. 본 연구에서는 여러 경험식들 중에(Abbass et al., 2018; Perumal, 2015) 수치해석에서 사용하는 시편의 압축강도와 유사한 고강도 SFRC 실험데이터를 기반으로 인장강도를 보수적으로 예측하는 Abbass 식을 적용하였다( $f_{t} = 0.508 {(f_{c})}^{0.499}$ ). 또한, 변형률 속도의 영향을 고려하기 위해 동적증가계수(DIF)로는 압축측에 Wang 등(2011) 그리고 인장측에 Park 등(2017)이 제안한 식을 해석에 적용하였다.

Table 2.

Information on the penetration tests

	$f_{c}$ (MPa)	steel fiber volume	Velocity (m/s)	Penetration depth (mm)
FRHSC-60	60.5	0.5%	401	79
FRHSC-85	85.4	0.5%	392	77

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F11.jpg

Fig. 11

Finite element model for SFRC

수치해석에서는 ‘CONTACT_ERODING_SURFACE_TO _ SURFACE“ 키워드를 사용하여 발사체와 SFRC 구조물의 접촉부를 묘사하였다. 또한, 구조물의 관통해석을 수행하기 위해서는 ’Erosion’ 기준을 설정해야 한다. 이 설정을 통해 요소의 특정 변수가 특정값에 도달하게 되면, 그 요소는 즉시 제거된다. 이 제거된 요소는 다시 복구되지 않고 더 이상의 저항력을 제공하지 않게 된다. 이러한 현상을 묘사하기 위해서 이전 연구들은 다양한 erosion 기준들은 사용해 오고 있다(Teng et al., 2008; Wang et al., 2009; Wang et al., 2010; Li and Zhang, 2011; Ren et al., 2016; Lai et al., 2018). 하지만, 이 기준은 아직까지 명확한 기준 없이 연구자의 경험에 의존에서 결정되기 때문에 발표된 논문들에 따라 사용된 기준들이 다르다. 본 연구에서는 최대 주 변형률(maximum principal strain)을 erosion 기준으로 설정하였으며 0.2를 해석에 적용하였다.

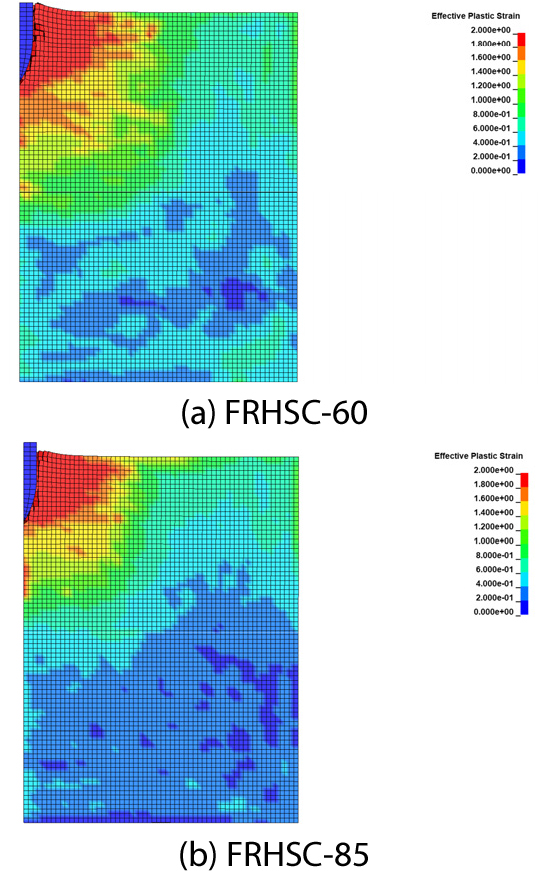
발사체 관통해석 결과는 Fig. 12에 나타내었다. 관통 깊이는 FRHSC-60의 경우 79.8mm, 그리고 FRHSC-85의 경우 74mm로 나타났다. 강도의 증가로 인해서 관통 깊이가 줄어드는 것을 확인할 수 있으며, 두 해석 결과는 실험 결과와 유사한 관통 깊이를 보이는 것으로 판단된다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340203/images/Figure_jcoseik_34_02_03_F12.jpg

Fig. 12

Side view of the numerical results

3. 결 론

본 연구에서는 기존 K&C모델을 기반으로 강섬유 보강 콘크리트의 영향을 반영하기 위한 보정기법을 설명하였다. 우선 SFRC 1축 및 3축 압축강도 실험결과를 기반으로 강도 곡선을 수정하였으며, 강섬유 함유량에 따라 변형률 연화 영역의 변화를 반영하기 위해 $η (λ)$ 에 식을 도입하였다. 검증을 위해 1축 및 3축 압축에 대한 단일요소해석을 수행하였다. 동적증가계수를 도입하여 변형률 속도의 영향을 고려하였으며, 강섬유의 영향을 반영하기 위해 K&C모델을 보정 후 발사체 관통해석을 수행하였다. 해석결과는 실험결과와 유사한 것으로 확인되었으며, 본 연구에서 제안한 보정기법은 해석을 SFRC 콘크리트 구조물 동적 해석에 효과적으로 사용될 수 있음을 확인하였다.

Acknowledgements

이 논문은 2019년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. NRF-2019R1 A6A3A03034028).

References

Abbass, W., Khan, M.I., Mourad, S. (2018) Evaluation of Mechanical Properties of Steel Fiber Reinforced Concrete with Different Strengths of Concrete, Constr. & Build. Mater., 168, pp.556~569. 10.1016/j.conbuildmat.2018.02.164

Afroughsabet, V., Biolzi, O., Ozbakkaloglu, T. (2016) High- Performance Fiber-Reinforced Concrete: A Review, J. Mater. Sci., 51, pp.6517~6551. 10.1007/s10853-016-9917-4

Bencardino, F., Lizzuti, L., Spadea, G., Swamy, R.N. (2008) Stress-Strain Behavior of Steel Fiber-Reinforced Concrete in Compression, J. Mater. Civ. Eng., 20, pp.255~263. 10.1061/(ASCE)0899-1561(2008)20:3(255)

Chen, J.C., Yang, H.J., Chen, H.W. (1992) Behavior of Steel Fiber Reinforced Concrete in Multiaxial Loading, ACI Mater. J., 89, pp.32~40. 10.14359/1242

Crawford, J., Wu, Y., Choi, H., Magallanes, J., Lan, S. (2012) Use and Validation of the ReleaseIII K&C Concrete Material Model in Ls-Dyna, Karagozian & Case.

Farnam, Y., Moosavi, M., Shekarchi, M., Babanajad, S.K., Bagherzadeh, A. (2010) Behavior of Slurry Infiltrated Fiber Concrete (SIFCON) under Triaxial Compression, Cement & Concr. Res., 40, pp.1571~1581. 10.1016/j.cemconres.2010.06.009

Gholampour, A., Ozbakkaloglu, T. (2018) Fiber-Reinforced Concrete Containing Ultra High-Strength Micro Steel Fibers under Active Confinement, Constr. & Build. Mater., 187, pp.299~306. 10.1016/j.conbuildmat.2018.07.042

Hong, J., Fang, Q., Chen, L., Kong, X. (2017) Numerical Predictions of Concrete Slabs under Contact Explosion by Modified K&C Material Model, Constr. & Build. Mater., 155, 1013~1024. 10.1016/j.conbuildmat.2017.08.060

Kong, X., Fang, Q., Li, Q.M., Wu, H., Crawford, J.E. (2017) Modified K&C Model for Ccratering and Scabbing of Concrete Slabs under Projectile Impact, Int. J. Impact Eng., 108, pp.217~228. 10.1016/j.ijimpeng.2017.02.016

Lai, J., Yang, H., Wang, H., Zheng, X., Wang, Q. (2018) Properties and Modeling of Ultra-High-Performance Concrete Subjected to Multiple Bullet Impacts, J. Mater. Civ. Eng., 30, pp.1~11. 10.1061/(ASCE)MT.1943-5533.0002462

Li, J., Zhang, Y.X. (2011) Evolution and Calibrration of a Numerical Model for Modelling of Hybrid-Fibre ECC Panels under High-Velocity Impact, Compos. Struct., 93, pp.2714~2722. 10.1016/j.compstruct.2011.05.033

Libre, N.A., Shekarchi, M., Mahoutian, M., Soroushian, P. (2011) Mechanical Properties of Hybrid Fiber Reinforced Lightweight Aggregate Concrete Made with Natural Pumice, Constr. & Build. Mater., 25, pp.2458~2464. 10.1016/j.conbuildmat.2010.11.058

Lin, X. (2018) Numerical Simulation of Blast Responses of Ultra- High Performance Fibre Reinforced Concrete Panels with Wtrain-Rate Effect, Constr. & Build. Mater., 176, pp.371~382. 10.1016/j.conbuildmat.2018.05.066

Lin, X., Gravina, R.J. (2017) An Effective Numerical Model for Reinforced Concrete Beams Strengthened with High Performance Fibre Reinforced Cementitious Composites, Mater. & Struct., 50, pp.1~13. 10.1617/s11527-017-1085-8

Malvar, L.J., Crawford, J.E., Wesevich, J.W., Simons, D. (1997) A Plasticity Concrete Material Model For Dyna3D, Int. J. Impact Eng., 19, pp.847~873. 10.1016/S0734-743X(97)00023-7

Mao, L., Barnett, S., Begg, D., Schleyer, G., Wight, G. (2014) Numerical Simulation of Ultra High Performance Fibre Reinforced Concrete Panel Subjected to Blast Loading, Int. J. Impact Eng., 64, pp.91~100. 10.1016/j.ijimpeng.2013.10.003

Ou, Y.C., Tsai, M.S., Liu, K.Y., Chang, K.C. (2012) Compressive Behavior of Steel-Fiber-Reinforced Concrete with a High Reinforcing Index, J. Mater. Civ. Eng., 24, pp.207~215. 10.1061/(ASCE)MT.1943-5533.0000372

Park, J.K., Kim, S.W., Kim, D.J. (2017) Matrix-Strength-Dependent Strain-Rate Sensitivity of Strain-Hardening Fiber-Reinforced Cementitious Composites under Tensile Impact, Compos. Struct., 162, pp.313~324. 10.1016/j.compstruct.2016.12.022

Perumal, R. (2015) Correlation of Compressive Strength and Other Engineering Properties of High-Performance Steel Fiber- Reinforced Concrete, J. Mater. Civ. Eng., 27(1), pp.1~8. 10.1061/(ASCE)MT.1943-5533.0001050

Ren, G.M., Wu, H., Fang, Q., Liu, J.Z., Gong, Z.M. (2016) Triaxial Compressive behavior of UHPCC and Applications in the Projectile Impact Snalyses, Constr. & Build. Mater., 113, pp.1~14. 10.1016/j.conbuildmat.2016.02.227

Teng, T.L., Chu, Y.A., Chang, F.A., Shen, B.C., Cheng, D.S. (2008) Development and Validation of Numerical Model of Steel Fiber Reinforced Concrete for High-Velocity Impact, Comput.l Mater. Sci., 42, pp.90~99. 10.1016/j.commatsci.2007.06.013

Tu, Z., Lu, Y. (2009) Evaluation of Typical Concrete Material Models used in Hydrocodes for High Dynamic Response Simulations, Int. J. Impact Eng., 36, pp.132-146. 10.1016/j.ijimpeng.2007.12.010

Wang, S., Le, H.T.N., Pho, L.H., Feng, H., Zhang, M.H. (2016) Resistance of High-Performance Fiber-Reinforced Cement Composites Against High-Velocity Projectile Impact, International Int. J. Impact Eng., 95, pp.89~104. 10.1016/j.ijimpeng.2016.04.013

Wang, Z.L., Konietzky, H., Huang, R.Y. (2009) Elastic-Plastic- Hydrodynamic Analysis of Crater Blasting in Steel Fiber Reinforced Concrete, Theor. & Appl. Fract. Mech., 52, pp.111~116. 10.1016/j.tafmec.2009.08.005

Wang, Z.L., Wu, J., Wang, J.G. (2010) Experimental and Numerical Analysis on Effect of Fibre Aspect Ratio on Mechanical Properties of SFRC, Constr. & Build. Mater., 24, pp.559~565. 10.1016/j.conbuildmat.2009.09.009

Wang, S., Zhang, M.H., Quek, S.T. (2011) Effect of High Strain Rate Loading on Compressive Behaviour of Fibre-Reinforced High-Strength Concrete, Mag. Concr. Res., 63, pp.813~827. 10.1680/macr.2011.63.11.813

Wu, H., Ren, G.M., Fang, Q., Liu, J.Z. (2019) Response of Ultra-High Performance Cementitious Composites Filled Steel Tube (UHPCC-FST) Subjected to Low-Velocity Impact, Thin-Walled Struct., 144, p.106341. 10.1016/j.tws.2019.106341

Wu, Y., Crawford, J.E., Magallanes, J.M. (2012) Performance of LS-DYNA Concrete Constitutive Models, 12th International LS-DYNA User Conference, pp.1~14.

Yang, L., Lin, X., Gravina, R.J. (2018) Evaluation of Dynamic Increase Factor Models for Steel Fibre Reinforced Concrete, Constr. and Build. Mater., 190, pp.632~644. 10.1016/j.conbuildmat.2018.09.085

Yoo, D.Y., Yoon, Y.S., Banthia, N. (2015) Flexural Response of Steel-Fiber-Reinforced Concrete Beams: Effects of Strength, Fiber Content, and Strain-Rate, Cement & Concr. Compos., 64, pp.84~92. 10.1016/j.cemconcomp.2015.10.001

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집