1. 서 론
2. 폭발 하중을 받는 구조물의 폭발 해석법
2.1 충격파 폭발 하중의 이상화
2.2 SDOF 시스템의 메커니즘과 해석 방법
2.3 MDOF 모델링과 해석 방법
3. SDOF 해석 수정계수 개발
3.1 SDOF 해석의 최대응답 오차율 비교
3.2 수정계수 도출 방안
3.3 수정계수 적용
4. 결 론
1. 서 론
재난 또는 테러에 의한 폭발 피해가 상당한 비율로 증가했으며 이는 폭발과 같은 극한 하중 조건에 노출되기 쉬운 구조물의 내폭 설계 기술 개발이 필요함을 보여준다(Haitham, 2016). ASCE(2021)는 폭발을 포함한 사고들의 위험을 줄이기 위한 일반적인 설계 방법론을 제시한다. PDC-TR 06-08(2008)과 UFC 3-340-02(2008)은 변위 기반의 내폭 성능 평가 방식을 사용하고 있다.
폭발 하중은 지속시간이 짧고 하중의 크기가 큰 동적 하중 특성으로 인해 구조시스템 단위로 해석하는 것이 아닌 부재별 구조해석을 수행한다(Dusenberry, 2010). 폭발 하중을 받는 부재 해석방법은 단자유도(SDOF, single degree of freedom) 시스템 해석과 다자유도(MDOF, multi degree of freedom) 시스템 해석 등이 있다. Haitham(2016)에 의하면 SDOF 해석은 짧은 시간에 동적 거동의 근사치를 얻기 위해 사용되며 실무에서 널리 쓰이는 방법이다. MDOF 유한요소 해석(FEA, finite element analysis)은 SDOF 해석보다 해석 시간은 길지만 정밀 해석이 필요한 경우 사용된다.
Astarlioglu 등(2013)은 폭발 하중을 받는 부재의 실험 결과, MDOF FEA 해석 결과와 축력 효과를 고려한 SDOF 해석 결과를 비교했으며 최대 변위의 차이가 10% 미만으로 MDOF FEA와 SDOF 해석 결과가 실제 거동과 유사함을 보였다. SDOF는 실제 거동을 유사하게 표현할 수 있지만 정확하게는 표현하지 못한다. 이에 따라 Geng 등(2021)은 탄성 및 소성영역에서의 SDOF 시스템의 미분 방정식을 결합하여 연성비에 따른 새로운 동적증가계수 유도식을 도출하였다. Rong과 Li(2008)은 폭발 하중 조건에서 개선된 강성 식을 제안하여 반복 계산을 통해 SDOF 해석의 정확도를 높이는 방안을 제시하였다.
SDOF 시스템 해석 시 사용하는 변환계수는 탄성 거동을 가정한 값과 소성 거동을 가정한 값으로 나누어져 있다. 구조물이 탄성 거동을 할 경우 탄성 하중-질량 변환계수(load-mass transformation factor)를 사용하여 구조물의 거동을 모사할 수 있다. 반면 구조물이 소성 거동을 할 경우 탄성 거동 후 소성 거동을 하기 때문에 변환계수 선택에 문제가 있으며 이 과정에서 SDOF 해석의 오차가 발생하게 된다(Rong and Li, 2008).
현재 내폭 설계 지침서(ASCE, 2010)에서는 탄성 영역과 소성 영역 모두 고려할 수 있는 방안으로 하중-질량 변환 계수를 탄성 영역에서의 하중-질량 변환계수와 소성 영역에서의 하중-질량 변환계수의 평균 값을 사용하고 있다. 하지만, 하중-질량 변환계수는 탄성-소성 구간에서 연속적으로 값이 변하기 때문에 여전히 상당한 오차가 발생한다.
따라서 본 연구에서는 연속적인 하중-질량 변환 계수를 반영한 SDOF 해석의 단일 수정계수를 개발한다. MDOF 해석은 탄성-소성 영역에서 구조물의 거동을 모사할 수 있기 때문에 연속적인 하중-질량 변환계수 변화를 내재적으로 반영한다. 수정계수는 다양한 매개변수에서 MDOF 해석과 SDOF 해석의 비율로 도출한다. 본 연구 결과는 폭발 하중을 받는 부재의 SDOF 해석 정확도를 높이는 간단한 방법으로 실무에서 쉽게 활용될 수 있다.
2. 폭발 하중을 받는 구조물의 폭발 해석법
2.1 충격파 폭발 하중의 이상화
ASCE(2010)는 충격파 폭발 하중의 실제 폭발 곡선 Fig. 1(a)와 실제 폭발을 이상화 시킨 곡선 Fig. 1(b)을 제시하였다. 음압(Pso-)은 일반적으로 양압(Pso)에 비해 압력이 매우 작기 때문에 음압 구간(tn)을 무시하고 곡선을 삼각형 형태로 유도한다(Nassr et al., 2013).
2.2 SDOF 시스템의 메커니즘과 해석 방법
SDOF 해석 방법은 폭발 해석에 널리 사용되는 방법이다(Yokoyama, 2015). SDOF 시스템의 동적 평형은 식 (1)과 같이 운동방정식으로 표현된다.
여기서, 은 부재의 질량, 은 부재의 가속도, 는 부재의 강성, 는 부재의 변위, 은 부재의 극한 저항력, 는 시간에 따른 폭발 하중을 의미한다.
일반적으로 동적 평형 방정식에서 감쇠를 고려하지 않은 이유는 폭발 하중의 지속시간이 건물의 고유주기보다 짧고, 첫 번째 주기에서 최대 변위가 도출되는 것이 보수적인 결과를 초래하기 때문에 SDOF 해석에서 감쇠를 고려하지 않았다(Cui et al., 2021 ; Liu et al., 2018).
SDOF 시스템의 거동은 이선형 저항력-변위 함수로 나타낼 수 있다. 등가 SDOF 시스템의 근사치를 얻기 위한 절차는 적용된 하중에서 실제 부재의 변형된 형상과 SDOF 근사치 사이의 변형 에너지 등가성을 기반으로 한다. SDOF 시스템의 응답 지점은 부재의 최대 응답 지점을 사용한다. 균일한 단면을 가진 구조물의 SDOF 시스템의 동적 평형 방정식인 식 (1)은 식 (2)와 같이 등가 SDOF 시스템으로 이상화 시킬 수 있다(Biggs, 1964).
여기서, 는 근사형태의 형상 함수, 은 질량변환계수, 은 하중변환계수 또는 강성변환계수이다.
SDOF 시스템의 운동 방정식 식 (1)를 단일 변수 하중-질량 변환계수를 사용하여 식 (3)과 같이 나타낼 수 있다. 등분포 하중을 받는 일방향 구조부재에 대한 변환계수는 Table 1과 같다.
여기서, 는 하중-질량 변환계수, 이다.
Table 1
Transformation Factors for uniformly loaded members with various boundary conditions
SDOF 해석은 Table 1에 제시된 변환계수, 강성, 저항력을 사용했으며, 수치해석 절차는 Chopra(2014)에 제시된 뉴마크 평균가속도법(Newmark average acceleration method)을 사용하였다.
2.3 MDOF 모델링과 해석 방법
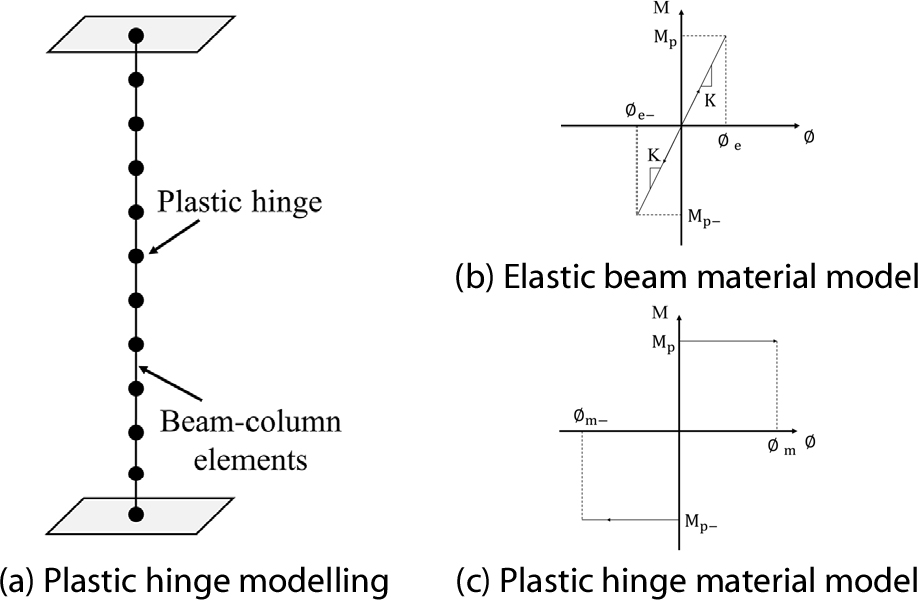
SDOF 해석의 오차를 평가하기 위한 MDOF 해석은 OpenSees (McKenna, 1997) 프로그램을 사용하였다. 유한요소 모델은 Fig. 2(a)와 같이 다자유도 보 요소로 나누고 보 요소 양 끝단에 집중 소성힌지(Lumped plastic hinge)를 적용하였다. 보 요소는 20개로 나누었으며, 각 노드는 3개의 자유도를 가진다. 보 요소의 재료 모델은 Fig. 2(b)와 같이 선형 모델을 사용하였다. 소성힌지 재료 모델은 Fig. 2(c)와 같이 초기 탄성 구간에서는 해석에 관여하지 않고, 소성모멘트에 도달하면 모멘트가 일정하도록 모델링 되었다. 비선형 동적 해석에 사용된 수치 해석 방법은 뉴마크 평균가속도법과 뉴턴-랩슨법(Newton-Raphson method)을 사용하였다.
MDOF 해석과 SDOF 해석의 최대 응답 오차를 분석하기 위해 동일한 물성치를 적용하였다. 폭발 하중을 받는 부재의 MDOF 해석 결과 1차 모드, 첫 번째 주기에서 모두 최대 응답이 도출되었다. 두 해석의 초기 거동을 검증하기 위해서 Fig. 3의 단면을 가지는 구조 부재에 대해서 항복 변위와 고유주기를 비교하였다.
4개의 경계조건에 대해서 항복 변위와 고유 주기를 비교한 결과는 Table 2에 나와 있다. 두 해석 결과 모두 동일한 강성과 극한 저항력을 사용했기 때문에 항복 변위는 4개의 경계조건 모두에서 동일하다. MDOF 해석에서 사용된 고유치 해석 방법은 저차 모드의 고유치 해석에 효과적인 Lanczos법을 사용하였고, SDOF 해석에서는 식 (4)을 이용하여 고유주기를 도출하였다. 1차 모드의 고유주기는 수치적 오류로 인해 0.5% 미만의 오차가 발생한 것을 제외하고는 두 해석 간에 차이가 없었다.
여기서, 은 부재의 고유 주기, 은 탄성 영역에서의 하중-질량 변환계수이다.
Table 2
Comparison of yield displacement and natural period between MDOF and SDOF with various boundary conditions
3. SDOF 해석 수정계수 개발
이 장에서는 SDOF 해석의 최대 변위 오차율을 분석한다. SDOF 해석의 정확도를 높이기 위해 매개변수 연구를 통해 소성 영역에 따른 단일 수정계수 식을 제시한다. 마지막으로 수정계수를 적용하여 SDOF 해석 오차 감소량을 확인하고, 수정계수의 효율성을 확인한다.
3.1 SDOF 해석의 최대응답 오차율 비교
SDOF 시스템 해석은 탄성 하중-질량 변환계수, 소성 하중-질량 변환계수, 탄성과 소성 하중-질량 변환계수의 평균 값, 세 가지 값을 사용하였다. SDOF 해석의 오차는 구조물의 소성 정도와 경계조건에 따라서 값이 변한다. 구조물의 소성 정도는 연성비를 통해 판단한다. 따라서 SDOF 해석의 오차 분석 방법은 연성비와 경계조건에 따른 MODF 해석 결과와 최대 변위 오차율을 분석한다. 연성비의 변화는 동일한 하중 지속시간에 대하여 폭발 하중의 크기를 증가시켜 도출하였다.
SDOF 해석, MDOF 해석은 Fig. 3의 부재와 4개의 경계 조건에 대해서 진행하였다. 재료의 물성치는 콘크리트 압축강도 27MPa, 철근 항복강도 400MPa, 극한 저항력 309.5kN이다. 폭발 하중은 Fig. 1(b)와 같이 이상화된 충격파 형태의 하중을 사용했으며 폭발의 지속시간(td)은 고유 주기와 하중 지속시간 비(td/Tn) 값 0.3을 기준으로 산정하였다. 폭발 하중은 연성비에 따른 연속적인 최대 변위 데이터를 얻기 위해 1kPa에서 300 kPa까지 10kPa 등간격으로 증가시켰다.
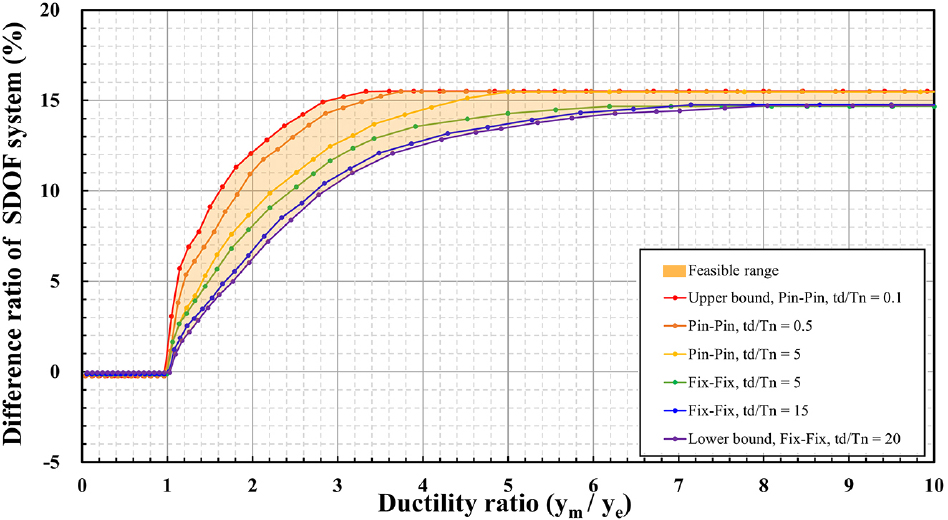
Fig. 4는 4개의 경계조건에서 연성비에 따른 SDOF 해석 오차율을 나타낸다. 그래프의 x축은 탄성 하중-질량 변환계수를 사용했을 때 SDOF의 연성비를 나타내고, y축은 MDOF 해석의 최대 변위에 대한 SDOF 해석의 최대 변위 오차율을 나타낸다.
연성비가 1.0 미만인 구간에서, 탄성 하중-질량 변환계수를 사용한 경우 4개의 경계조건에서 모두 오차율이 0이다. 연성비가 증가할수록 탄성 하중-질량 계수의 경우 오차율이 증가하고 반대로 소성 하중-질량 계수는 오차율이 감소한다. 특정 연성비에 도달하면 초기 탄성 거동보다 소성 거동이 지배하므로 소성 하중-질량 계수의 오차율이 0으로 수렴한다. 소성 거동이 지배하는 연성비는 경계조건과 단면에 따라서 바뀌게 되고, 일반적으로 4.0~6.0이다. 최대 오차율과 최소 오차율은 식 (5)으로 구할 수 있다.
여기서, DiffMax는 SDOF 해석의 최대 오차율, DiffMin는 SDOF 해석의 최소 오차율, 은 소성 영역에서의 하중-질량 변환계수이다.
식 (5a), (5b)는 SDOF 해석의 최대 변위 오차율이 탄성 하중-질량 계수와 소성 하중-질량 계수의 비에 따라서 결정되는 것을 보여준다. 경계조건에 따른 SDOF 해석의 최대, 최소 오차율은 Table 3과 같다.
Table 3
Maximum, minimum difference ratio of equivalent SDOF system
| Boundary condition | DiffMax (%) | DiffMin (%) |
| Pin-Pin | 15.5 | -18.3 |
| Fix-Pin | 15.0 | -17.6 |
| Fix-Fix | 14.7 | -17.3 |
| Cantilever | 1.5 | -1.5 |
평균 하중-질량 변환계수는 탄성, 소성 하중-질량 변환계수의 평균 값을 사용한 것으로 탄성 하중-질량 변환계수와 소성 하중-질량 변환계수의 중간 정도의 오차율이 도출된다. 평균 하중-질량 변환계수 오차율은 캔틸레버에서 1% 미만의 오차율이 발생하여 해석의 정확도가 높지만, 나머지 3개의 경계조건에 대해서는 여전히 7%~9%의 오차율이 발생한다. 따라서 본 연구에서는 캔틸레버를 제외한 세 개의 경계조건을 고려하는 단일 수정계수를 도출한다.
3.2 수정계수 도출 방안
SDOF 해석의 단일 수정계수를 개발하기 위해 매개변수 연구를 진행하였다. 첫 번째 매개변수는 경계 조건이다. 두 번째 매개변수는 고유주기(Tn)와 폭발 하중의 지속시간(td)이다. NORSOK(2013)는 고유주기와 하중 지속시간 비(td/Tn)에 따라 하중을 분류하였고, UFC3-340-02(2008)는 고유 주기와 하중 지속시간 비(td/Tn), 구조물의 저항력과 폭발하중 비에 따라 SDOF 시스템의 응답차트를 제공한다. UFC3-340-02(2008) 응답차트의 고유주기와 하중 지속시간 비(td/Tn) 범위인 0.1~20과 폭발하중과 구조물의 저항력 비 범위인 0.1~2.0으로 매개변수 연구를 진행하였다.
고유주기와 하중 지속시간의 비(td/Tn)와 경계조건에 따른 SDOF 해석 오차를 분석하기 위해 Table 4의 물성치를 가지는 부재들을 사용하였다. Fig. 5은 양단 핀 지지, 양단 고정 지지 조건에서 고유주기와 하중 지속시간의 비(td/Tn) 값이 0.1, 0.5, 15, 20인 부재의 SDOF 해석의 오차율을 보여준다.
Table 4
Properties of MDOF system and SDOF system
| td/Tn | Natural periods, Tn (ms) | Bending resistance, R (kN) |
| 0.1 | 50.17 | 125 |
| 0.5 | 42.54 | 680 |
| 1 | 27.97 | 229 |
| 5 | 16.35 | 972 |
| 10 | 6.78 | 1100 |
| 15 | 37.78 | 765 |
| 20 | 11.25 | 6750 |
매개변수 연구 결과 동적 하중은 소성 거동 지배 연성비가 작고 정적 하중과 유사할수록 소성 거동 지배 연성비가 연속적으로 커진다. Table 3에 제시된 것처럼 경계조건에 따라 SDOF 해석의 최대 오차율이 달라진다. 따라서 두 특징으로 인해 SDOF 해석의 최대 변위 오차 경계가 형성된다.
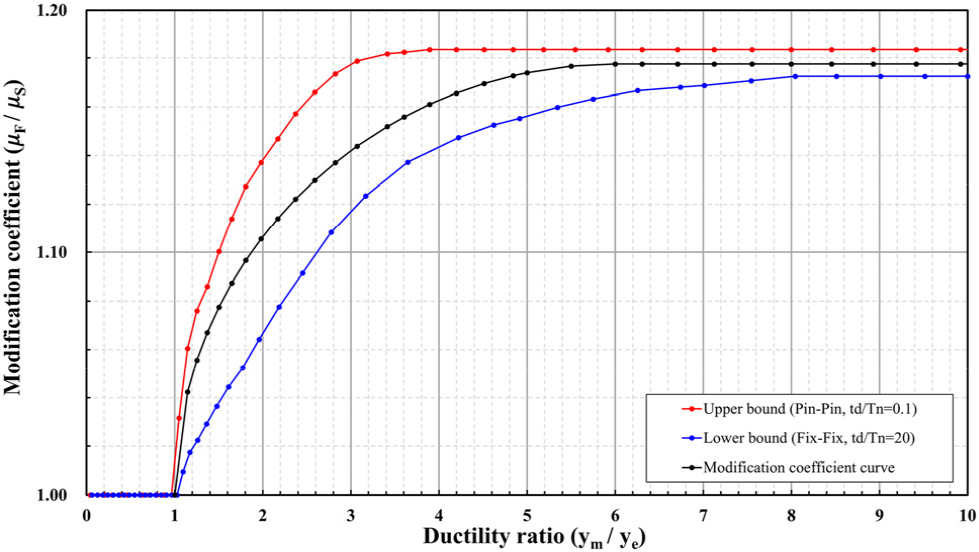
탄성 하중-질량 변환계수를 기준으로 SDOF 해석의 수정계수를 산정한다. 수정계수를 도출하는 방안으로 상한, 하한 매개변수 경계를 설정하였다. 상한 매개변수 경계는 양단 핀 지지, 고유주기와 하중 지속시간의 비(td/Tn) 0.1, 하한 매개변수 경계는 양단 고정 지지, 고유주기와 하중 지속시간의 비(td/Tn) 20으로 설정하였다.
Fig. 6은 상한, 하한 매개변수 경계와 수정계수 곡선을 보여준다. 그래프의 x축은 탄성 하중-질량 변환계수를 사용한 SDOF의 연성비, y축은 수정계수 값으로 MDOF 해석의 최대 응답과 SDOF 해석의 최대 응답의 비를 나타낸다.
수정계수 곡선은 탄성 영역, 탄성-소성 영역, 소성 영역으로 나뉜다. 탄성 영역과 소성 영역은 SDOF 해석의 최대 응답 오차율이 일정하기 때문에 수정계수 곡선이 상수값이 된다. 탄성-소성 영역에서는 타원 방정식을 사용하여 도출하였다. 장축은 연성비 1.0부터 상한, 하한 매개변수 경계의 소성 지배 연성비 평균값까지의 거리이다. 단축은 상한, 하한 매개변수 경계의 최대 수정계수 평균값이다. 제안된 수정계수 식은 식 (6)이다.
여기서,은 수정계수, 𝜇는 SDOF 해석의 연성비이다.
3.3 수정계수 적용
수정계수를 적용하기 위해서는 우선 탄성 거동을 가정한 탄성 하중-질량 변환계수를 이용하여 SDOF 해석을 수행해야 한다. 다음 과정은 도출된 SDOF 해석의 최대 변위를 이용하여 연성비를 구한다. 마지막으로 식 (6)의 수정계수 식을 이용하여 수정계수를 결정하고, 기존 최대 변위에 수정계수를 곱하여 수정된 최대 변위를 도출한다.
수정계수의 효과를 확인하기 위해 Table 5의 단면을 사용하였다. 재료의 물성치는 콘크리트 압축강도 27MPa, 철 항복강도 400MPa이다. 폭발 하중은 Fig. 1(b)의 이상화된 충격파 폭발 하중을 사용하였고, 각 부재의 고유주기, 극한 저항력은 Table 6에 제시되어 있다.
Table 5
Cross section of numerical examples
Table 6
Dynamic properties of numerical examples
| Type | td/Tn |
Natural periods, Tn (ms) |
Bending resistance, R (kN) |
| Case 1 | 0.3 | 7.25 | 6328 |
| Case 2 | 1.1 | 17.04 | 638 |
| Case 3 | 3.5 | 5.49 | 2778 |
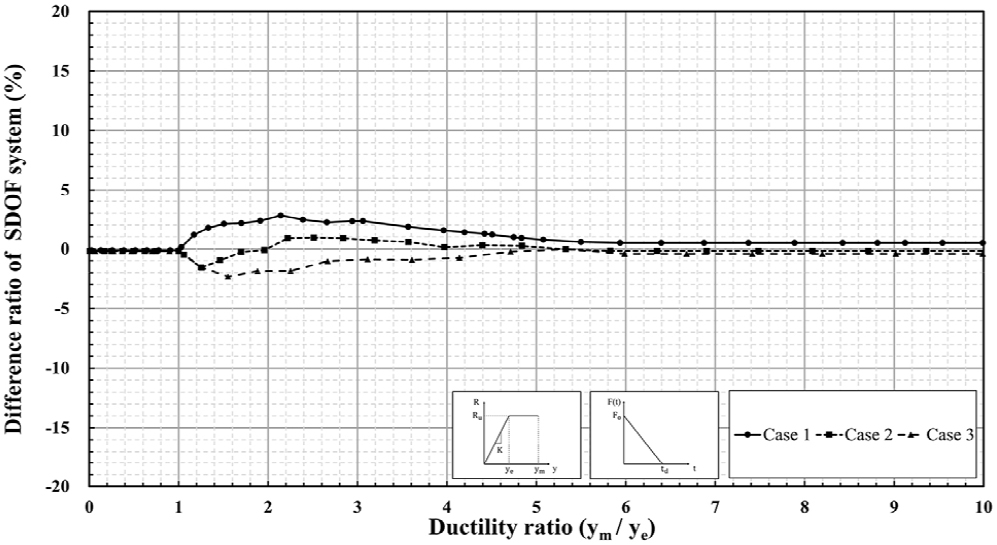
Fig. 7은 수정계수를 적용하기 전 탄성 하중-질량 변환계수를 사용한 SDOF 해석의 최대 변위 오차율을 보여준다. Fig. 8은 수정계수 식 (6)을 적용한 SDOF 해석의 최대 변위 오차율을 나타낸다. Fig. 7와 Fig. 8의 그래프 축은 모두 Fig. 4의 그래프 축과 동일하다. 수정계수를 적용하기 전과 후의 SDOF 해석의 최대 오차율 비교 결과는 Table 7에 제시되어 있다. 수정계수를 적용하여, 기존의 SDOF 해석에서 최대 변위의 최대 오차율이 15%에서 2%~3% 수준으로 줄어들었다. 이는 해석의 효율성이 크게 향상되었음을 보여준다.
4. 결 론
본 연구에서는 SDOF 폭발 해석과 보 요소와 소성 힌지 모델을 사용한 MDOF 해석을 수행하였다. 두 해석 결과를 비교하여 SDOF 해석의 오차율을 분석하였다. 또한, SDOF 해석의 오차율에 영향을 주는 변수들을 선정하여 매개변수 연구를 진행하였다. 매개변수 연구를 토대로 소성 범위를 고려한 SDOF 해석 수정계수를 개발하였다.
탄성 하중-질량 변환계수, 소성 하중-질량 변환계수, 탄성과 소성 하중-질량 변환계수의 평균 값들을 사용했을 때 오차율을 분석하였다. 그 결과 탄성 하중-질량 변환계수와 소성 하중-질량 변환계수의 차이만큼 오차율이 달라지는 것을 확인하였고, -18%~15% 정도의 오차가 발생하였다.
본 연구의 주요 매개변수는 경계조건과 고유 주기와 하중 지속시간의 비(td/Tn)이다. 경계조건에 따라서 최대, 최소 오차율이 변하며, 고유주기와 하중 지속시간의 비(td/Tn)가 클수록 더 큰 연성비에서 소성 거동이 지배한다는 것을 확인하였다.
SDOF 해석 수정계수는 상한, 하한 매개변수 경계를 설정하여 도출하였다. 상한 매개변수 경계는 양단 핀 지지, 고유 주기와 하중 지속시간의 비(td/Tn) 0.1, 하한 매개변수 경계는 양단 고정 지지, 고유 주기와 하중 지속시간의 비(td/Tn) 20으로 설정하였다. 수정계수 곡선은 상한 매개변수 경계와 하한 매개변수 경계의 평균 값을 가지는 타원의 방정식을 이용하여 도출하였다. SDOF 해석 수정계수를 서로 다른 단면과 경계조건을 가지는 3개의 예제에 적용하였다. 적용한 결과 최대 오차율이 80%~90% 감소하는 효과적인 해석법이라는 것을 확인하였다.
본 연구의 결과는 폭발 하중을 받는 부재에 SDOF 해석 수정계수를 도입하여 정확도를 향상시킬 수 있으므로 폭발 해석에 널리 사용될 수 있다.