1. 서 론

재료와 화약의 발달로 개인 화기는 끊임없이 개량되어 왔으며 이와 더불어 위협을 줄이거나 막기 위한 고효율 방탄재료에 대한 연구개발과 연구도 끝없이 진행되어 왔다. 방탄재료에 대한 지속적인 발전을 효과적으로 견인하기 위해 여러 기관이 만들어졌으며 표준이 제시되어 왔다. NIJ(National Institute of Justice)와 STANAG(Standardization Agreement)같은 표준화 기관과 표준이 핵심적인 역할을 하고 있다(Armor, 2008; Coufal et al., 2022). 이런 표준이 제공하는 믿을 수 있는 테스트 방법과 성능 기준을 통해 방호성능에 대한 목표를 명확히 할 수 있으며 방호장비의 성능을 체계적으로 평가하는 정량 평가 도구를 제공받게 된다. 또한 방호 성능에 대한 호환성지표를 제공하기 때문에 원하는 방호성능 공동 개발이 가능하다.

고에너지 화기의 위협에 대응하기 위해서 강철과 합금강 등 금속 소재를 활용하여 방탄성능을 극대화하려는 연구가 지속적으로 진행되어 왔다. 금속 방탄재는 우수한 강도와 내구성을 제공하나 높은 면밀도로 인하여 무겁고 이로 인하여 기동성과 편의성에 제한이 생기게 된다. 최근에는 방탄 설계가 단순히 방호 성능을 넘어서 목적에 따라 사용자의 움직임과 편의성을 고려한 경량화 및 유연성도 중요하게 다루어지고 있다. 특히, 섬유 강화 복합재는 낮은 면밀도에도 불구하고 우수한 방탄 성능을 발휘하며 섬유의 구조적 특성 충격 에너지를 효과적으로 분산시킨다. 더불어 다양한 재료를 적층하여 방탄 성능을 최적화하려는 하이브리드 장갑 모델이 주목받고 있고 연구 또한 활발히 되고 있다(Kim et al., 2023).

섬유 복합재와 같은 경량 소재에 관심에도 불구하고 높은 면밀도를 가진 금속 방탄재는 군용차량의 외장 장갑재와 차세대 방탄장비 등에 사용되며 여전히 중요한 역할을 하고 있으며, 무게가 중요한 개인 방호구에는 제한적으로 사용되고 있다. 금속 방탄재는 극한의 온도 변화나 열적 충격에 대한 우수한 내구성으로 일관된 방호 성능을 유지하는 장점을 가지고 있다. 현대에는 금속 방탄재는 섬유복합재 등과 결합된 하이브리드 구조로 사용되어 더욱 향상된 방탄 성능을 실현하고 있으며 금속 방탄재의 역할은 더욱 확장되고 있다(Flores-Johnson et al., 2011; Garcia-Avila et al., 2015).

개발 초기 체계적인 방호구조물 설계 전에는 금속재료의 기계적 특성과 방탄 성능 간의 상관관계에 대한 포괄적인 지식이 없었기에 금속 장갑재의 방탄 성능은 일반적으로 면밀도의 역수로 특정되어지고는 했다. Srivathsa와 Ramakrishnan(1997)은 강도 및 탄성 계수와 같은 기계적 특성 측면에서 금속 장갑 재료에 대한 방탄 성능 지수를 추론하였다. 하지만 탄환과 표적 사이의 고속 충돌 중 발생하는 재료의 복잡한 비선형 변형과 열적-기계적 상호작용 등 다양한 물리적 현상이 상호 작용하기에 방탄성능을 결정하는 주요 물성을 평가하는 것은 여전히 어려운 문제이다.

본 연구에서는 분산분석(ANOVA, Analysis of Variance)을 이용해 방호 성능을 결정짓는 기계적 물성치를 통계적으로 평가하는 연구를 수행한다. 분산분석은 다양한 독립변수들이 종속변수에 미치는 영향을 평가하고 각 요인들의 상대적 중요성과 상호작용을 정량적으로 분석하는데 유용한 도구이다. 이전 연구들에서도 방탄 성능을 분석하는데 분산분석 활용되었다. 분산분석을 이용하여 섬유직물과 고분자 수지의 합침 비율에 따른 방탄성능의 차이를 평가하는데 사용되었으며(de Oliveira Braga et al., 2017), 복합 패널의 적층 방법 및 적층 순서에 따른 방탄 성능을 확인하기도 하였다(Doddamani and Kulkarni, 2012; Naveen et al., 2019).

기존 연구에서는 다양한 연구 방법을 통해 방탄 성능을 결정짓는 금속재료의 물성치를 평가하는 연구가 수행되었지만 분산분석을 통해 기계적 물성치의 상호관계를 확인한 연구는 아직 진행되지 않았음을 확인하였다. 따라서 본 논문에서는 분산분석을 통해 방호 성능을 결정짓는 핵심 기계적 물성치에 대한 평가를 수행하였다. 방탕 성능 확인을 위해 비관통 조건과 관통 조건을 각각 고려하여 각기 다른 조건에서 물성치를 평가하였으며, 충돌 해석을 위한 유한요소해석은 LS-Dyna를 이용하여 수행되었다.

2. 탄환 고속 충돌 유한요소해석

2.1 고속 충돌 해석을 위한 유한요소 모델 구축

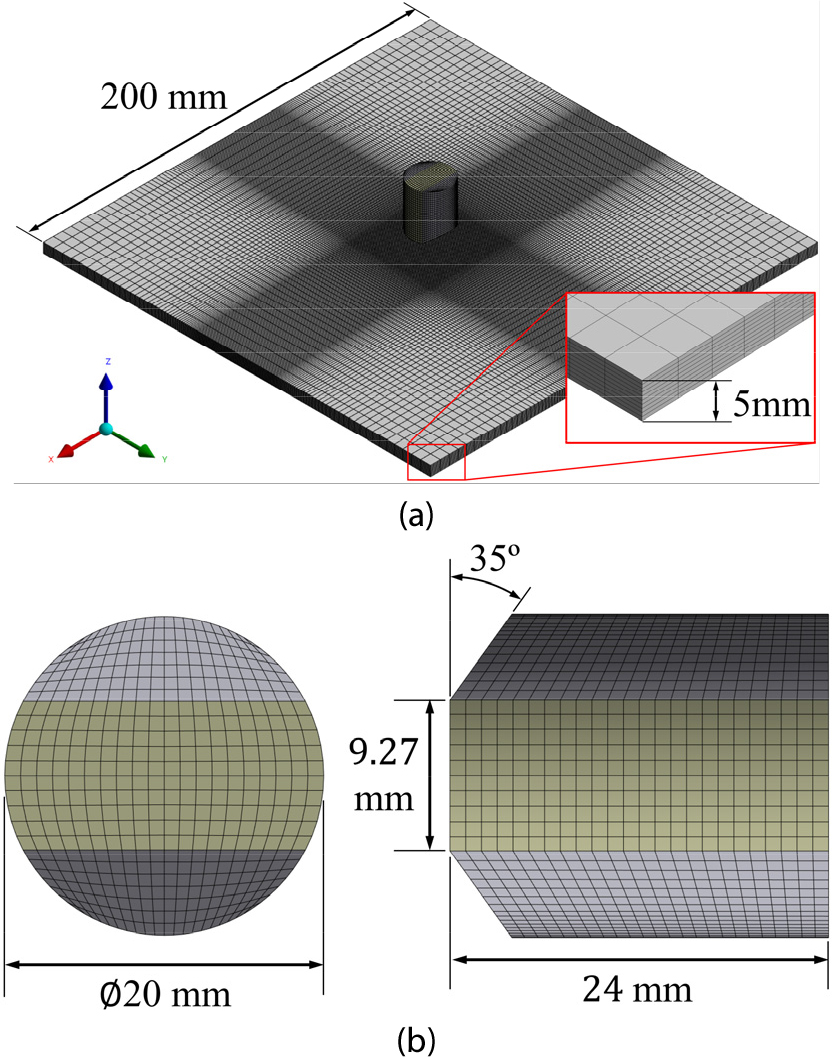
금속 방탄판의 방호성능에 영향을 주는 물성치에 대한 분산분석을 수행할 때, 통계적 유의성을 확보하기 위한 실험 설계의 타당성과 방호성능의 변동성의 원인을 정량적으로 계산할 수 있는 시뮬레이션 실험 모델이 필요하다. 물리적으로 탄두 형상에 따라 방호 성능 및 한계가 영향을 받기 때문에 금속 방탄판의 방호성능을 정확히 평가하기 위해서 먼저 정확한 탄두 시뮬레이션 모델이 필요하다. 본 연구에서는 이를 위해서 파편모의탄(FSP, fragment simulating projectile)을 이용하였다. 파편모의탄은 NATO 회원국의 STANAG 표준화 협정에서 제의되어 탄두에 따른 일관된 위협 평가와 비교를 위해 사용하기 적합하다고 알려져 있다.

기본 물성이 될 대표적인 금속 방탄재로는 Armox 500T steel을 이용하였다. Armox 500T은 6mm의 두께로 NIJ Level 3(7.62 × 51mm NATO 탄환이 847m/s 속도로 충돌) 위협에 대응 가능한 금속 방탄재이다(Ranaweera et al., 2023). 200mm × 200mm, t = 5mm인 Armox500T 금속판을 표적으로 설정하였으며 발사체로는 53.8g의 20mm FSP를 사용하여 비관통과 관통 조건에 따라 속도를 다르게 설정하였다. 비관통 조건에서는 STANAG 4569 Level 2 기준인 630m/s 속도를 관통 상황에서는 STANAG 4569 Level 4 기준인 960m/s의 속도를 모사하여 시뮬레이션을 수행하였다. Ls-Dyna를 이용하여 Fig. 1에서 볼 수 있듯이 파편모의탄이 Armox500T 플레이트를 충돌하는 시뮬레이션 모델을 구축하였다. 해석의 정확성을 높이기 위하여 파편모의탄이 충돌하는 부분에 조밀한 유한요소격자를 사용하였다.

Fig. 1.

A schematic of the finite element model of the 200mm × 200mm × 6t metal plate and 20mm FSP used in impact simulation

2.2 시뮬레이션 구축

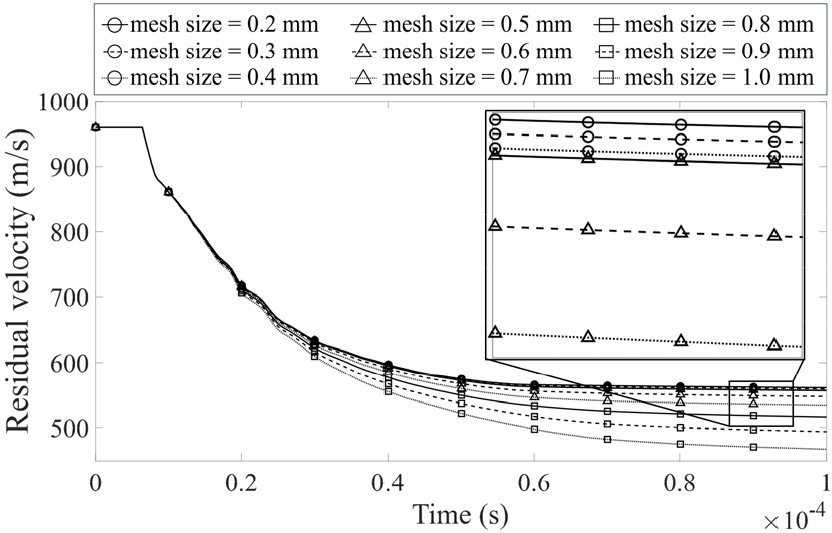
분산분석을 위한 신뢰성 높은 반응표면 모델을 만들기 위해서는 많은 해석 데이터가 필요하다. 따라서 해석 시간이 짧으면서도 안정적인 시뮬레이션 모델을 구축하는 것이 중요하다. 고속충돌과 같은 동적해석은 해석 중 매 사이클마다 가장 작은 요소의 특성길이(Characteristic length)에 의해 시간 단계가 결정되어진다. 계산 시간과 비용을 줄이기 위해 탄환과 표적의 충돌지점의 특성길이 수준이 유사하게 요소를 구성하여 해석의 효율성을 높였다. Fig. 2에서 볼 수 있듯이 관통 조건을 기준으로 표적 중심부의 격자 크기의 유효성을 검증하였다. Modified Johnson-Cook 재료모델을 적용한 고속 충돌 모델에서 격자 크기의 수렴성을 강조한 연구(Børvik et al., 2004)와 마찬가지로 본 연구에서 또한 격자의 크기가 0.5mm에서부터 0.2mm로 가까워질수록 잔류 속도가 수렴하는 것을 확인하였다. 많은 데이터를 확보해야 하는 본 연구의 특성상 정확도와 해석 시간의 효율성을 고려하여 0.5mm의 격자 크기를 선택하였고 이는 분산분석을 수행하기 위한 신뢰성 높은 격자 크기로 판단하였다. 또한 탄환과 표적의 충돌지점 요소들의 종횡비(Aspect Ratio)가 1.45 이하가 될 수 있도록 정육면체에 가까운 격자를 구성하였다. 이는 충돌 시 발생하는 국부적인 변형을 정확하게 구현 가능하게 한다고 알려져 있다(Zukas and Scheffler, 2000). 3차원 요소(3D Hex solid)요소에서 발생하는 hourglass 수치적 불안정성을 해결하기 위해 Belytschko-Bindeman 방법을 적용하였고 과한 에너지 흡수가 발생하지 않도록 0.1의 계수를 적용하였다. 고속 충돌과정에서 발생하는 큰 변형과 탄환과 표적 사이의 동적인 접촉 조건으로는 LS-Dyna의 *CONTACT_AUTOMATIC_SINGLE_SURFACE를 이용하였다. 비관통과 관통 조건 시뮬레이션에서 모두 내부에너지(Internal energy), 운동에너지(Kinetic energy), 모래시계에너지(Hourglass energy) 그리고 접촉에너지(Contact energy)의 불균형 없는 수치적으로 안정적이며 신뢰성 높은 시뮬레이션 모델을 구축하였다.

Fig. 2.

Projectile residual velocity results from mesh refinement study on Armox 500T target impacted by 20mm FSP at 960m/s

2.3 재료 모델 정의

금속 재료의 고속 충돌과정에서의 변형을 정확히 구현하기 위해서는 적절한 재료 모델을 선택하는 것이 중요하다. 탄환과 표적에 LS-Dyna의 식 (1)과 같이 MAT_107: Modified Johnson-Cook(MJC) 모델을 사용함으로써 재료의 변형률과 열적 연화를 고려하여 고속 충돌 재료의 변형을 구현하였다(Hallquist, 2007). 기존 Johnson-Cook 모델에 비해 변형률 속도의 로그 항에 선형계수를 지수함수의 형태로 수정된 형태로서 경화와 재료의 온도 민감도를 정확히 모델링할 수 있다.

위의 식에서 𝜎은 유효응력, A는 항복 강도, B는 변형률 경화 계수, εp는 등가 소성 변형률, n은 변형률 경화지수, C는 변형률 민감도 계수, ε0는 기준 변형률 속도, Tr은 기준 온도, Tm은 용융 온도, m은 열 연화지수이다. 위의 식을 이용하여 충돌과정에서 발생하는 변형 경화효과(Straining Hardening) 및 변형률 속도(Strain Rate) 그리고 온도변화를 모두 고려하여 금속재료의 응력 변화를 정확하게 모델링할 수 있도록 한다.

본 연구에서는 금속재료의 연성 파괴를 예측하기 위해 식(2)의 Cockroft-Latham(CL) 파괴 기준을 적용하였다. 재료의 σ1은 최대 주응력이며, W은 단위 부피당 소성 변형률 값이다. 임계 소성 변형률 Wcr 도달 시 요소는 침식(Erosion)된다. CL 파괴 기준은 재료의 손상 누적을 기반으로 하여 임계 값에 도달 시 파괴가 발생한다고 가정하게 된다. 이는 Johnson-Cook 파손 모델에 비해 재료의 파손을 간단하게 결정하도록 하는 이점이 있다. Table 1에 본 연구에서 사용한 발사체 20mm FSP와 금속 방탄재 Armox 500T에 사용된 MJC모델의 물성치를 정리하였다.

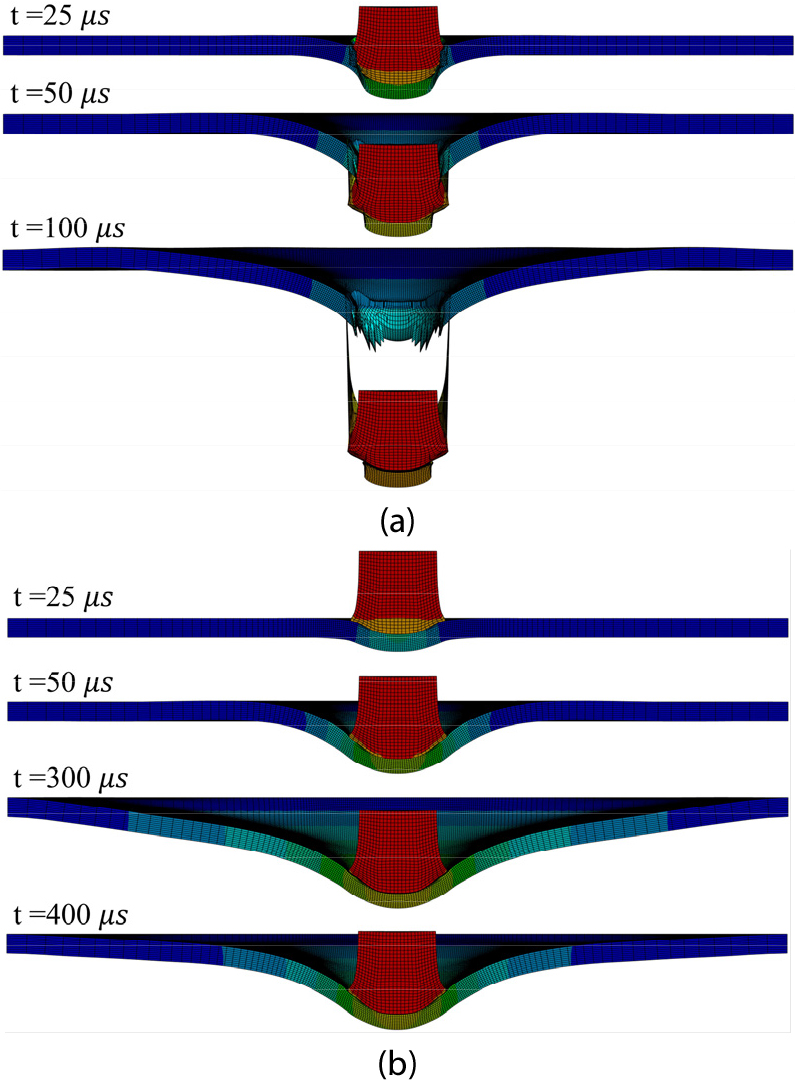
Fig. 3의 (a)와 (b)는 각각 참조 물성치를 바탕으로 비관통 조건과 관통 조건에서 금속 방탄재에 충돌하는 20mm FSP 시뮬레이션 결과를 보여준다. 비관통 조건에서는 시뮬레이션 종료시간을 400µs로 설정하였으며, 관통 조건에서는 100µs로 설정하여 충돌과정을 분석하였다. 비관통 조건에서는 탄환의 충돌 직후 탄환의 운동에너지가 방탄재에 전달되어 소성 변형을 일으키며 이와 동시에 재료의 강도가 증가하는 경화 과정이 진행된다. 탄환의 운동에너지 소실 시 방탄재는 최대 후면 변형에 도달하며 이후 방탄재의 복원력에 의해 탄환은 튕겨져 나가게 된다. 반면에 관통 조건에서는 방탄재가 탄환의 에너지를 충분히 흡수하지 못해 누적된 소성 변형으로 인해 균일이 발생하고 확대되면서 관통이 일어난다.

Fig. 3.

Cross-section views of Armox 500T post-impact: (a) simulated at 630m/s under non-penetration conditions for 400µs, (b) simulated at 960m/s under penetration conditions for 100µs.

3. 실험계획법

3.1 인자(독립변수) 및 반응(종속변수) 선택

본 연구에서는 분산분석을 수행하기 위한 핵심 물성으로 금속의 기본적인 기계적 특성인 밀도와 탄성계수를 선택하였으며, 더불어 변형 중 발생하는 경화 거동의 기계적 성질을 결정하는 MJC 모델의 파라미터인 항복강도, 경화계수, 경화지수를 포함한 총 5가지의 기계적 물성을 선택하였다. MJC 모델에서 방탄성능을 결정짓는 대표 물성들은 기계적 물성 외에도 열적 물성 또한 방탄성능에 있어서 중요한 지표가 된다. 허나 본 연구에서는 기계적 물성에만 초점을 맞춰 각 핵심 인자들이 방탄 성능에 미치는 영향을 확인하고자 한다. 선택된 인자 외의 Armox 500T의 기본 물성들은 모두 고정하였다.

실제 방호 평가 시험방법에서는 방탄재의 성능을 평가하기 위해 두가지 방법이 주로 사용된다. 방탄재 후면에 점토를 배치하여 변형정도를 측정하여 방탄성능을 평가하는 P-BFS 시험과(Armor, 2008), 방탄재가 완전 관통 또는 부분 관통이 될 확률이 50%인 방호 임계속도를 측정하는 V50 시험이다(MIL- STD, 1997). 본 연구에서는 이를 고려하며 비관통 조건과 관통 조건에서 핵심이 되는 주요 물성이 다를 것이라 판단하였고, 시뮬레이션 결과를 바탕으로 관통조건과 비관통 조건을 구분하여 금속 방탄재의 주요 물성에 대한 분산분석을 수행하였다. 비관통 조건일 경우에는 금속방탄재의 최대 후면 변형 값을 통해 방탄재료의 후면 보호능력을 평가하였고, 관통조건에서는 시뮬레이션 종료 시 탄환의 최종 잔류 속도를 확인하여 금속 방탄재의 탄환 에너지 흡수능력을 확인하였다.

3.2 반응표면모델

본 연구에서는 비관통과 관통 조건에서 중심합성계획법(CCD: Central Composite Design)을 적용하였다. CCD는 비교적 적은 수의 실험점으로도 인자의 주효과와 교호작용 효과를 확인할 수 있으며, 특히 금속 재료의 충돌과 같은 비선형성이 큰 문제에서 인자의 비선형 효과를 평가하기에 적절하다. CCD는 2차 모형을 통해 변수 간의 비선형적 반응과 상호작용을 모델링할 수 있으며(Khuri and Mukhopadhyay, 2010), 이는 충돌로 인해 발생하는 복잡한 물리적 현상을 분석하는 데 적합하다. 충돌 시 발생하는 금속 재료의 변형과 파손 과정에서 발생하는 비선형성을 포착할 수 있어 관통 문제에서 유의미한 분석을 제공한다. 각 조건마다 2⁵(꼭지점) + 2 × 5(축점) + 1(중심점)으로서, 총 43개의 실험점을 설계하였다. Table 2에 제시된 바와 같이, Armox 500T의 기본 물성을 중심점으로 지정하고, 인자들의 상/하한 범위를 설정하여 실험점을 배치하였다. 이 실험점들은 충돌 시 발생하는 비선형적 응답을 다각도로 탐색하기 위한 적절한 범위를 제공한다. 각 인자들의 상호작용 및 영향을 분석하기 위해 다음 식을 기반으로 반응표면모델(RSM: Response Surface Model)을 생성하였다.

비관통과 관통 조건 모두 반응 변수 Y와 독립변수 X의 관계를 완전2차 표면모델(Full quadratic model)로 나타내었으며, CCD에 의한 인자들의 주효과, 비선형 효과, 교호작용 효과를 모두 확인하였다. 실험요인 배치 및 분산분석은 통계 소프트웨어인 Minitab의 평가판을 이용하여 수행하였으며, 각 실험점에서 유한요소해석을 통해 얻은 결과 값을 토대로 분산분석을 수행하였다.

4. 분산분석(Analysis of Variance)

4.1 반응표면모델 신뢰성검증

Table 3는 비관통과 관통 상황에서 분산분석에 사용된 회귀 모형의 적합도 결과를 보여준다. 이 표에서 R-Square 값이 모두 90% 이상으로 각 분산분석 모델에 사용된 회귀 모형의 신뢰성을 검증하고 각 인자들의 유효성을 정량적으로 확인할 수 있다. 모델의 오차는 표준오차(standard error)로 나타내었으며. R-Squared 값은 회귀 모형이 종속변수의 총 변동에서 설명하는 비율을 나타낸다, 또한 수정된 R-Squared은 독립변수의 추가에 따른 모델의 과적합을 고려하고, 예측된 R-Square은 새로운 데이터에 대한 예측력을 평가하는데 사용된다. 비관통 RSM의 경우 99% 이상의 매우 높은 신뢰성을 확인할 수 있으며, 관통 RSM도 92% 이상의 높은 신뢰성 모델임을 확인할 수 있다.

Table 4와 Table 5는 비관통과 관통 해석 조건에서 앞서 설정한 5개 인자들에 대한 분산분석 결과를 보여준다. 전체자유도(DF)는 통계적 모델이 데이터의 변동성을 설명하기 위한 정보의 수를 의미한다. 분산분석 결과 전체모델에서 주효과(Linear), 비선형성(Quadratic), 교호작용(Interaction)의 효과를 모두 평가하였다. 조정된 제곱항(Adjusted Sum of Squares)은 특정 독립변수가 종속변수의 변동을 얼마나 잘 설명하는지를 나타낸다. F-value가 클수록 독립변수가 종속변수에 통계적으로 유의미한 영향을 끼친다는 것을 검정하는 통계량을 의미한다. P-value는 독립변수가 종속변수에 영향 없음이라는 귀무가설이 참일 때 F-value가 나타낼 가능성을 나타내며, 이는 P-value 값이 낮을수록 F-value가 우연에 의한 것이 아닌 독립변수의 유의성을 보조하는 증거가 된다.

4.1.1 비관통 조건

탄환의 충돌 후 방호 한계 내에서 관통되지 않는 조건에서 금속 방탄재의 기계적 물성 인자들이 방탄재의 후면 변형량에 미치는 영향을 평가하기 위해 분산분석을 수행하였다. Table 4는 금속방탄재의 최대 후면 변형량을 반응변수로 한 분산분석 결과를 나타내었다.

분산분석 결과 모든 주효과 인자들은 높은 F-value로서 후면 변형량에 미치는 영향력이 있음을 확인하였고, P-value가 0의 값을 가져 후면 변형량에 통계적 유의성 확인하였다. 다만 비선형성과 교호작용은 각각 F-value가 40.33과 60.63으로서 주효과에 비해서는 영향이 크지 않음을 확인하였다. 이는 각 인자들이 후면 변형량에 대해 주효과로서 큰 영향을 미친다는 것을 의미한다.

특히 금속 방탄재의 항복강도(Yield Stress)의 F-value가 19776.53으로 가장 높아 방탄재의 후면 변형량에 매우 강한 영향을 미치고 있음을 확인할 수 있으며, 다른 인자들 모두 통계적으로 유의미한 영향을 미치는 것을 확인할 수 있다. 금속 방탄재료의 높은 항복강도는 충격 시 더 많은 에너지를 흡수하고 분산시켜 후면 변형량을 최소화할 수 있음을 의미한다. 그 다음으로 경화계수와 경화지수가 주효과로서 높은 영향을 보임을 확인하였다. 이를 통해 경화 특성이 높을수록 소성 변형 이후 충격흡수 능력을 향상시켜 후면 변형량을 감소에 효과 있음을 알 수 있다.

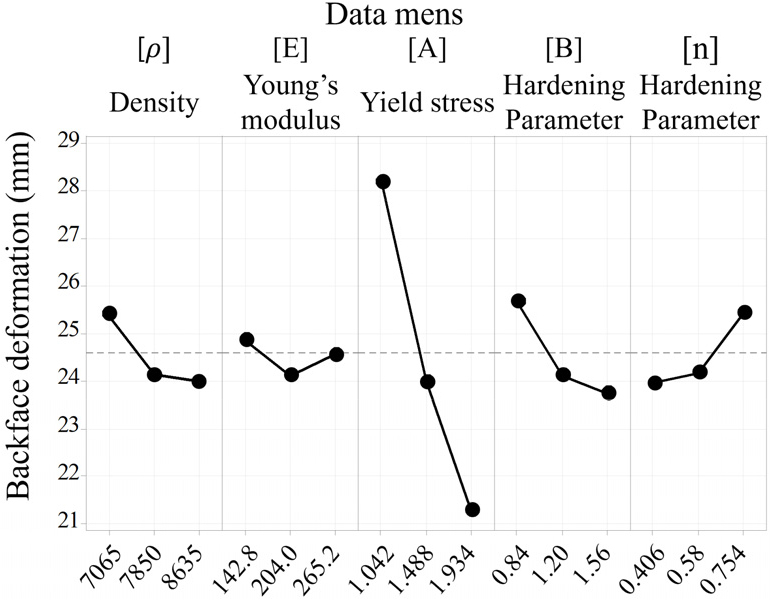
Fig. 4는 금속 방탄재가 비관통 조건에서 후면 변형량에 영향을 미치는 기계적 물성치들의 주효과도이다. 후면 변형량 감소에는 항복 강도의 증가가 가장 큰 영향을 끼치는 것을 확인할 수 있고, 그 다음으로 경화계수와 밀도가 비슷한 수준의 비례 영향을 갖는 것을 알 수 있다. 반면 경화지수가 증가할수록 후면 변형량이 증가하는 경향을 보였다. 이는 경화지수가 커질수록 응력이 소성 변형률에 대해 지수함수적으로 증가하기 때문에 재료의 초기 변형단계에서 빠르게 경화되면서 국부적 변형이 더 많이 발생하여 후면 변형이 증가할 수 있음을 의미한다. 이는 일반적인 재료의 소성변형 특성과 일치한다.

Fig. 4.

Main effects plot for backface deformation of the plate under non-penetration simulation

탄성계수는 주효과도에서 비선형적인 패턴을 보이지만 탄성계수의 F-value는 37.45로 다른 인자들에 비해 후면 변형량에 미치는 영향이 매우 작아 실질적인 의미가 없는 것으로 판단된다. Table 4와 Fig. 5에서도 확인할 수 있듯이 탄성계수와 관련된 비선형 효과와 교호작용 효과 모두 미약한 것으로 나타났다. 이는 탄성계수가 재료의 초기 탄성 응답을 주로 결정하나, 재료가 소성변형 단계로 빠르게 전이되는 고속 충돌 상황에서는 재료의 소성 특성이 더 중요한 역할을 하는 것을 의미한다.

Fig. 5.

Interaction plot between design variables under non-penetration simulation.

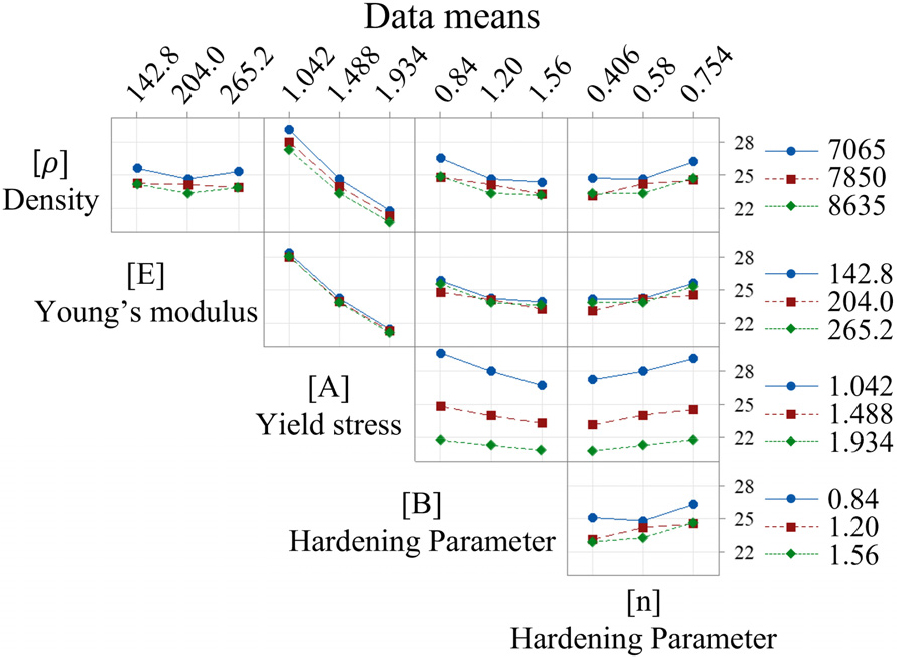
Fig. 5는 금속 방탄재의 후면 변형량에 영향을 미치는 물성치를 인자로 한 교호작용도이다. Table 4에서 볼 수 있듯이 대부분의 인자들 간 교호작용은 F-value가 낮아 후면 변형량에 대한 영향력이 없으며, P-value 또한 0.05 이상으로 통계적으로 유의미하지 않음을 확인하였다. 유일하게 항복강도와 경화계수 B의 교호작용에 관한 F-value가 409.88로 비교적 약한 교호작용이 존재함을 확인할 수 있다. 마찬가지로 교호작용도에서도 항복강도와 경화지수 사이의 약한 교호작용이 존재함을 확인할 수 있다. 특히 항복강도가 낮을 때는 경화 계수의 변화에 따라 후면 변형량이 크게 변하는 경향을 보인다. 이러한 결과는 방탄재료의 성능을 최적화하기 위해서는 항복강도와 경화계수의 조합을 고려한 설계가 필요함을 의미한다.

4.1.2 관통 조건

금속 방탄재의 방호 한계 속도를 초과하여 관통이 발생한 조건에서 방탄재료의 기계적 인자들이 탄환의 잔류속도 감소효과에 미치는 영향을 평가하기 위해 분산분석을 수행하였다. Table 5는 탄환의 잔류속도를 반응 변수로 한 분산분석 결과를 요약하였다. 분산분석 결과 교호작용 항의 F-value은 낮은 값을 가지며 잔류속도 감소에 영향력이 작으며, P-value가 0.05보다 커 통계적으로 유의하지 않음을 확인하였다. 따라서 본 연구에서는 관통 조건에서는 교호작용 그래프를 논문에 포함하지 않았다. 대신 유의미한 영향을 가진 주효과를 중심으로 분석하였다. 모든 주효과 인자들이 P-value가 0.05 이하로 통계적으로 유의미함을 확인했으나 밀도를 제외한 인자들은 탄환의 잔류 속도를 감소시키는 효과가 작은 것으로 확인된다.

밀도의 주효과에 대한 F-value가 977.67로 다른 인자 대비 압도적으로 높다. 이는 방호 한계를 초과하는 상황에서 탄환의 에너지를 흡수하여 잔류속도를 효과적으로 감소시키기 위해서는 밀도의 영향이 가장 중요함을 알 수 있다. 또한 항복강도와 경화계수의 교호작용에 대한 F-value가 42.23으로 밀도를 제외한 인자들의 주효과에 준하는 수준으로 높은 것을 확인할 수 있다. 이 두 관계는 비선형과 교호작용 효과에서 유일하게 P-value가 0.05 이하의 0값으로써 통계적 유의함 또한 확인 가능하다.

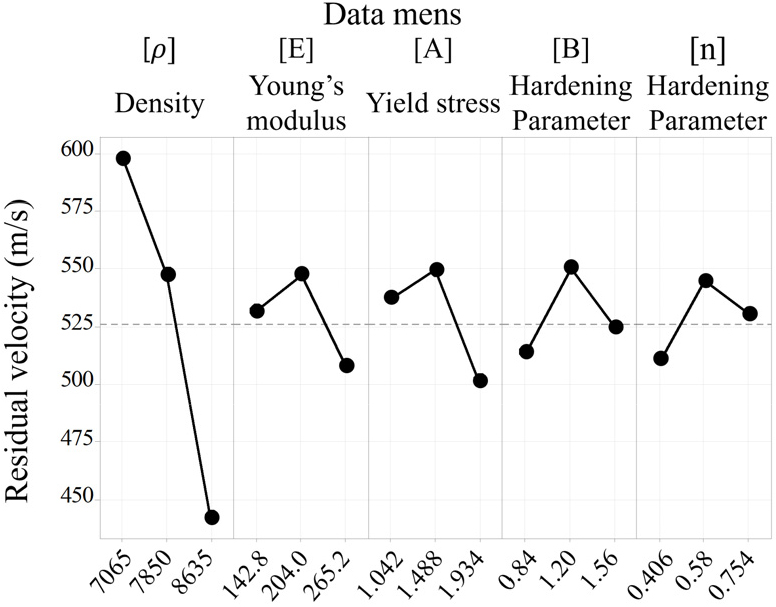
Fig. 6는 금속 방탄재의 충돌 조건에서 탄환 잔류속도 감소에 영향을 미치는 물성치들의 주효과도이다. 밀도가 증가할수록 잔여속도의 감소 기울기가 급격하게 감소하는 것을 확인할 수 있다. 이는 밀도가 증가함에 따라 방호한계에 가까워질수록 잔류 속도 감소 효과가 극대화됨을 의미한다.

Fig. 6.

Main effects plot for residual velocity of the projectile under penetration simulation

5. 결 론

본 연구에서는 분산분석을 이용하여 금속 방탄재의 기계적 물성 인자들이 방탄성능에 미치는 영향을 통계적으로 확인함으로써 물성평가의 복잡성을 단순화하였다. 방탄성능의 핵심이 되는 인자를 비관통 조건과 관통 조건을 s구분하여 분석하고자 LS-Dyna를 이용하여 각각의 유한요소 모델을 만들었다. 파편모의탄과 Armox 500T 금속 방탄재의 고속 충돌 과정에서의 발생하는 변형을 정확히 구현하기 위해 Modified Johnson-Cook 재료 모델이 적용하였다. 분산분석을 통해 밀도, 탄성계수, 항복강도, 경화계수 그리고 경화 지수 총 5가지의 인자들이 방탄성능에 미치는 영향을 통계적으로 해석하고 분석하였다.

비관통 조건에서는 항복강도가 가장 큰 영향을 미치며 그 다음으로 경화 관련 물성 인자들이 중요한 역할을 하는 것을 확인하였다. 또한 항복강도와 경화 물성 인자들 사이의 교호작용이 유의미함을 확인하였다. 관통 조건에서는 타 인자 대비 밀도의 영향이 지배적이며 방호한계에 가까워질수록 밀도의 영향이 비선형적으로 증대됨을 확인하였다. 추가 연구를 통해 더 큰 표본과 다양한 조건에서 금속 방탄재료의 핵심 인자들을 고려하여 주효과 및 교호작용을 분석할 필요가 있다고 판단된다.

본 연구 결과를 통해 향후 금속재료가 사용된 방탄재료의 성능을 최적화하는데 있어 지침을 제공할 것이며 향후 방탄재 설계 및 개발에 있어 유용한 참고자료가 될 것으로 기대한다.