1. 서 론

신기후체제 이후, 유엔기후변화협약을 통해 각국은 탄소중립 목표를 설정하였으며, 국내 건설분야에서는 2030년까지 탄소 배출량을 18.1% 감축하는 것을 목표로 하였다(Lee, 2022). 이에 따라 건설산업에서 탄소감축을 위하여 LCA(Lifecycle Assessment)를 이용한 내재 탄소배출량(Embodied Carbon Emission) 산정 및 적용성의 관심이 증대되고 있다.

재사용(Reuse) 구조는 보와 기둥과 같은 주요 구조체를 볼트 체결과 같은 메커니즘으로 조립 및 해체하여, 주요 구조체를 재사용하거나 교체함으로써 장수명화를 이루는 구조 시스템이다(Fujita and Iwata, 2008). 특히 강구조물에서 표준화된 부재를 사용한 재사용 구조시스템은 부재 절감, 비용 효율성, 신속한 시공으로 LCA단계인 자재단계(A1-A3), 시공단계(A4-A5), 보수 및 교체단계(B3-B5), 폐기단계(C1-C4), 재생단계(D)에서 지속가능한 탄소배출량을 줄이는 것이 가능하다(Hermwille, 2016).

건축의 내재 탄소배출량에 영향을 미치는 장수명화는 지진을 경험할 확률이 증가함에 따라 내진성능 확보가 필요하다. 모멘트 저항 골조(MRF, Moment Resisting Frame)는 지진력 저항시스템으로서 적절한 강성과 충분한 소성변형능력을 갖추어 횡 하중에 저항성이 우수하여 지진 위험 지역에서 주로 사용된다(Lisperguier et al., 2023).

표준화된 구조와 단면 효율성으로 역학적인 이점을 갖는 박스형 강관기둥과 H형강 보의 다양한 모멘트 접합이 개발되어 왔다(Sherman, 1996). 실무에서 H형강 보에서 각관 기둥으로의 하중 전달에는 외다이어프램, 내다이어프램, 관통형 다이어프램을 많이 사용하지만, 제작 과정에서 각관의 폐쇄된 단면의 특성으로 절단과 용접이 어려워 품질과 시공성에 영향을 미친다. 또한, 현장에서 시공 시, 보이음에서 소요되는 이음판 및 볼트가 많아 시공성 및 안전성의 어려움이 있다(Shin et al., 2004).

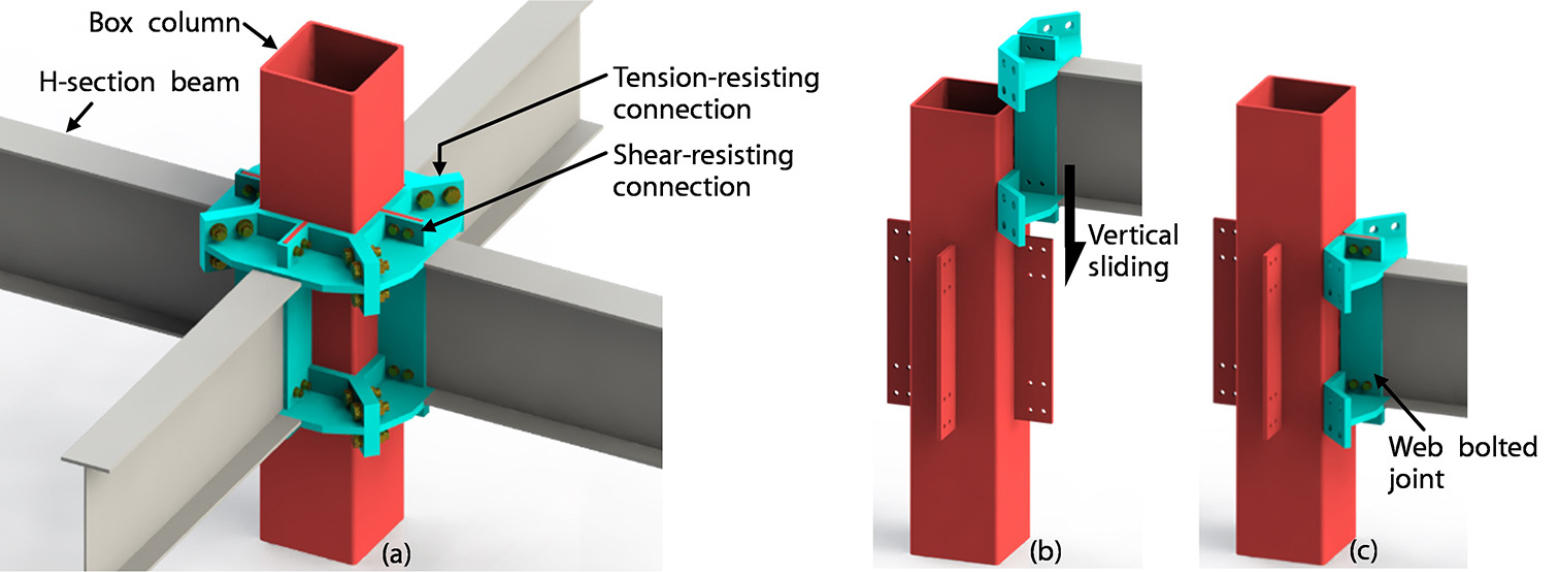
이러한 배경에서 건축물의 탄소감축을 위한 조립 해체가 용이한 각관 기둥과 H형강보의 접합시스템(Carbon Neutrality Dismantle Connection, CNDC)이 제안되었다. 이 시스템은 현장에서의 추가적인 용접없이 볼트 체결만으로 급속 시공 및 해체가 가능하다. 또한 사다리꼴형 접합부(TZcon, Trapezoidal Connection)을 포함한 각 부재는 표준화가 가능하여 운반 효율성 및 품질면에서 모듈러 시스템의 이점을 취한다.

이 시스템은 TZcon 모듈과 전단 탭(Shear Tab)이 부착된 각관 기둥과 H형강 보로 구성되며, 응력전달에서 휨 모멘트는 TZcon 모듈의 모서리부 인장 볼트가, 전단력은 전단 탭과 체결된 전단 볼트가 초기 응력을 전달한다(Fig. 1a). 시공 시, 공장에서 TZcon과 H형강 보에 용접되어 사전 제작되어 현장으로 운송하여 수직 슬라이딩 방식으로 기둥의 전단 탭과 TZcon 수직 플레이트와 전단 볼트 체결한다(Fig. 1b-c). 이후 같은 방식으로 체결한 후, 맞닿는 모서리 플레이트끼리 인장 볼트를 체결한다.

Fig. 1.

The concept of CNDC

제안된 TZcon접합부를 가진 CNDC시스템의 내진성능을 검증하기 위해 실대형 실험(Full-scale Experiment)을 진행하였다. 실험 결과 CNDC 시험체는 비교시험체(전형적인 외다이어프램)에 비해 대비 강성과 연성(회전성능)에서 약 20% 높은 우수한 성능을 보였지만, 이력곡선에서 핀칭현상(Pinching Phenomenon)으로 야기된 에너지 소산량은 상대적으로 저하된 값을 얻었다.

이에 본 연구에서는 이전에 실험한(Choi et al.., 2024) 탄소 감축을 위한 해체가 용이한 접합부의 실험적 한계를 유한요소해석(FEA, Finite Element Analysis)을 통하여 입증하고자 해석적 연구를 수행하였다. 실험조건과 유사한 환경을 지닌 신뢰성 있는 해석모델(FE-Model) 구축과 함께 실험과 해석의 비교를 통하여 접합부의 거동 및 한계의 원인을 논의하였다. 내용은 다음과 같다:

2장에서는 시험체의 3차원 유한요소해석을 수행한다. 제안된 접합부의 거동을 이해하기 위해 해석에 사용된 재료 물성 보정(Material Property Calibration), 경화 규칙(Hardening Rule), 그리고 두 가지 모델링 방식(Tied, Bolt-Slip Modeling)을 제시한다.

3장에서는 실험 결과와 3차원 유한요소해석 결과를 비교한다. 제안된 접합부의 거동에 대해 전체적(Global) 및 국부적(Local) 측면에서 실험과 해석의 유사점과 차이점을 논의한다.

2. 3차원 유한요소해석(3D-FEA)

2.1 시험체의 3차원 모델링(3D Modeling)

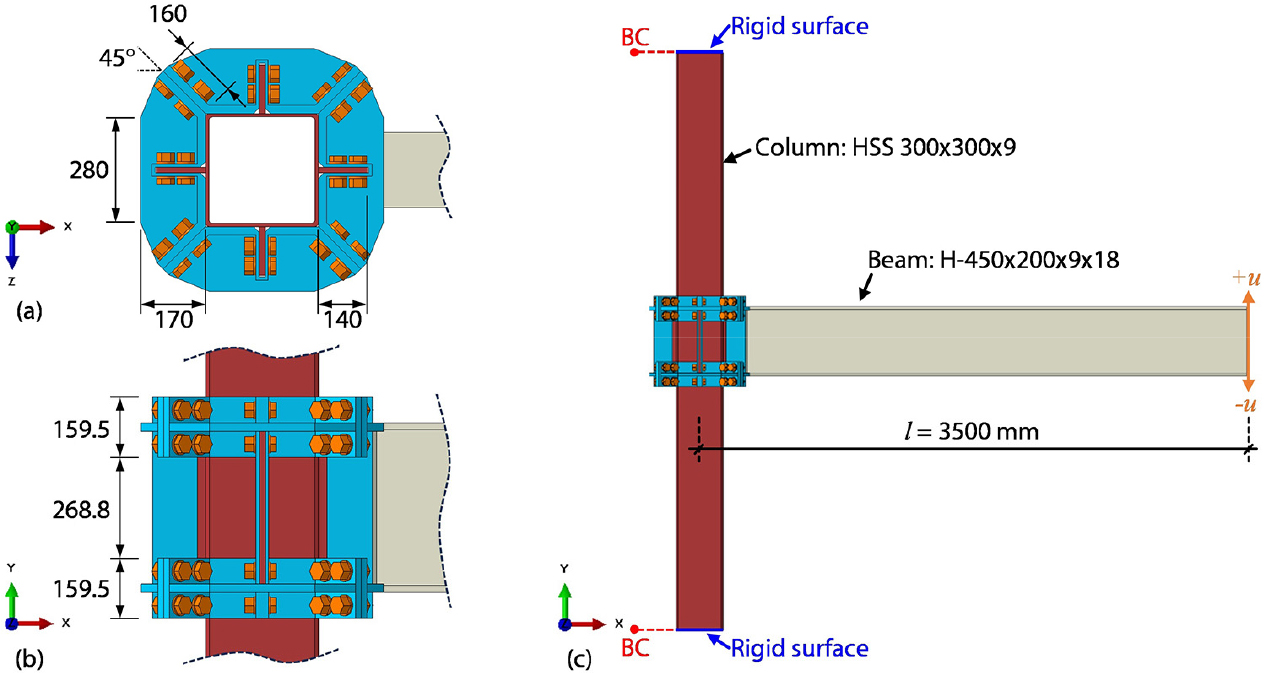
Fig. 2a는 인천 포스코 글로벌 R&D 센터(POSCO Global Research & Development Center)에서 수행된 탄소 감축을 위한 해체가 용이한 접합부 시험체의 셋업을 보여준다. 기둥의 상단과 하단은 시험 프레임(반력벽)에 힌지 상태로 구속되었다. 보 단부에는 액추에이터(Actuator)를 사용하여 수직 방향으로 주기적 하중을 가했으며(Fig. 2b), 이 하중은 SAC Joint Venture의 접합부 내진 성능 평가 기준에 따른 층간변위각(SDR, Story Drift Ratio)을 변위 제어 방식으로 변환하여 적용하였다(FEMA, 2000). 층간변위각은 보 단부의 변위(u)를 보 길이 l(=3500mm)로 나누어 계산된다. 또한 보 플랜지의 횡 좌굴을 방지하기 위해 지지대를 배치하여 횡 변위 발생을 방지하였다.

Fig. 2.

(a) Experimental setup of the full-scale rapid-disassembly carbon-minimized dismantle connection, and (b) test loading protocol

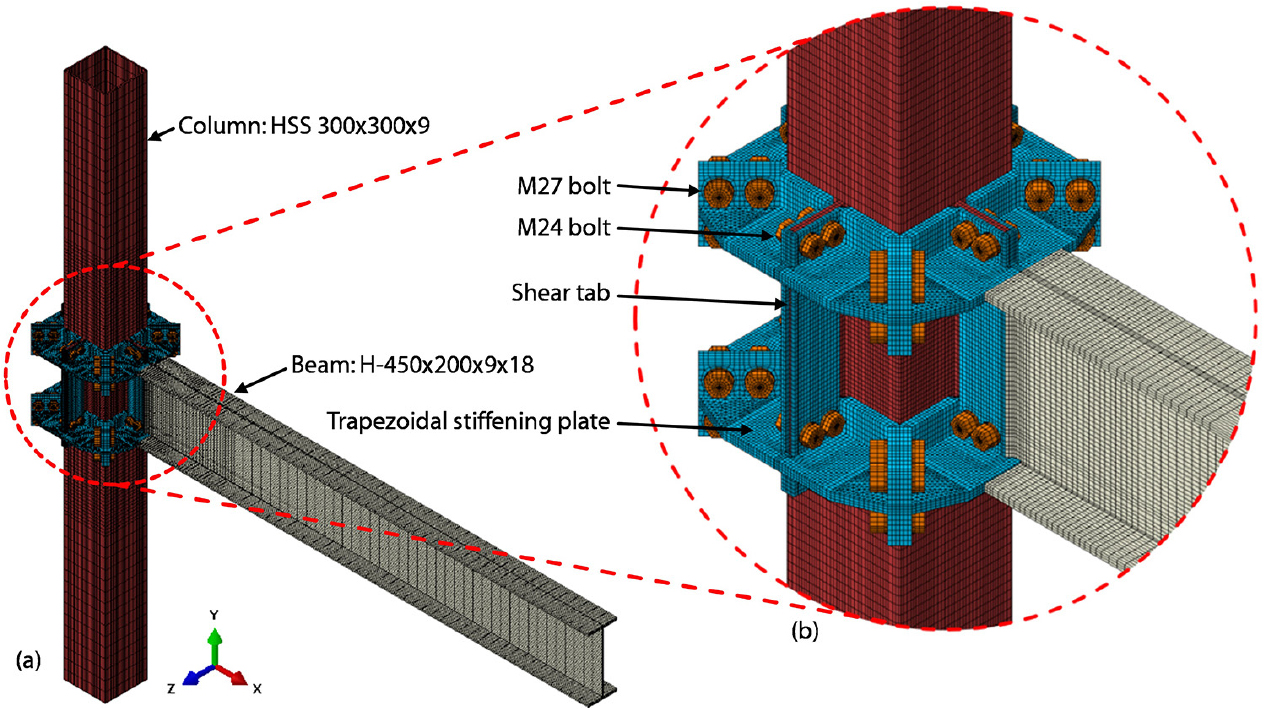
Fig. 3과 4에서 보이듯이 전체 시험체는 ABAQUS(2022)를 사용하여 3차원 유한요소해석을 위해 모델링 되었다. Fig. 3에서 기둥의 상단과 하단은 강체 면(Rigid surface)로 간주될 수 있으며, 경계 조건을 나타내는 점 BC에 구속된다. 실제 힌지 구속 지지대를 모사하기 위해 점 BC의 모든 방향 병진 자유도(DOF)와 X 및 Y 회전자유도가 구속되었다. 따라서 오직 점 BC의 Z 회전 자유도만이 구속되지 않았다. 한편, 변위 제어 사이클 하중은 하중 프로토콜(Fig. 2b)을 따라 보 끝단에서 수직, 즉 Y 방향 변위를 제어하여 적용된다. 또한, 수렴 안정성을 위해 시험 에서와 같이 구속되지 않은 보의 측면 이동을 모사하기 위해 보 끝단의 Z 방향 변위 자유도를 구속하였다.

Fig. 3.

Specification of Model: (a), (b) Detail of TZcon, and (c) Test specimens with indicated boundary conditions and application of cyclic loading

Fig. 4.

Meshed 3D model: (a) entire column-beam assembly, and (b) close-up of the joint.

기둥-보 어셈블리에서 FE-Model은 응력 집중에 따라 정밀한 해석결과 및 해석의 간소화를 위해서 접합부 부근은 조밀하게 기둥과 보 끝 부분은 조밀하지 않게 Solid Brick 요소망(Mesh)으로 분할하였다(Fig. 4a). 볼트의 본체(Shank), 머리(Head), 너트(Nut), 그리고 와샤(Washer)와의 접촉면(Contact)이 모두 모델링되었다(Fig. 4b). 볼트의 프리텐션(Pre-tensioning), 마찰력(Friction), 그리고 수직 항력(Normal force)은 3D-FE 해석에 고려하였다.

또한, 볼트 구멍의 직경은 건축강구조 표준접합 상세지침에 따라, M24 볼트의 경우 27mm 직경 구멍, M27 볼트의 경우 30mm 직경 구멍으로 모델링하였고, 볼트와 플레이트의 슬립 및 슬라이딩 성분을 포함하여 해석을 진행하였다.

2.2 3차원 유한요소해석을 위한 재료물성 정의

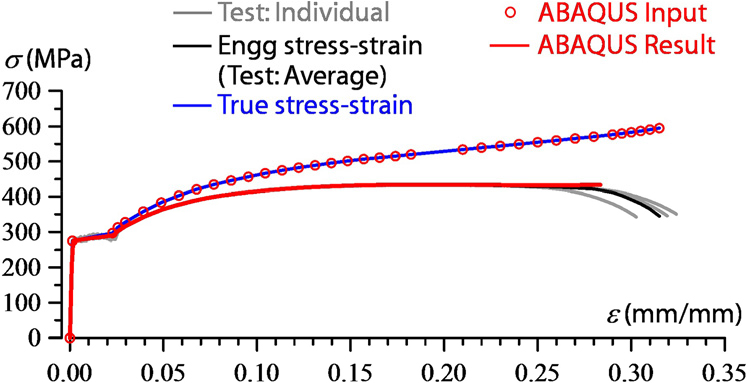
실대형 시험(Fig. 2a)을 수행하기 전에, 기둥(HSS-300 × 300 × 9) 및 보(H-450 × 200 × 9 × 18)에 사용된 강재의 재료 특성을 결정하기 위해 재료 인장시험(Coupon Test)이 수행되었다. Fig. 5에는 각각의 두께별로 강재 인장 시험(회색 곡선)과 평균값(흑색 곡선)의 응력-변형률 곡선(Stress-Strain curve)이 나와 있다. 기둥 및 보 강재의 항복응력 σ_y는 275MPa이다. 시험에서 얻은 응력-변형률 값은 공칭응력(Engineering Stress) 값이며, ABAQUS에서는 강재 물성을 정의하는 데 사용하지 않는다. 대신, 진응력(True Stress) 값과 진변형률(True Strain) 값이 해석을 위한 재료 물성 입력 값으로 사용된다. 진응력 σ_true와 진변형 ε_true는 아래의 식과 같이 결정된다.

여기서, σ_engg와 ε_engg은 각각 공칭응력(Engineering Stress)과 공칭변형(Engineering Strain)를 의미한다. Fig. 5와 같이 플롯된 진응력-진변형률 곡선(청색 곡선) 공칭응력-공칭변형률 곡선(흑색 곡선)보다 높은 값을 나타낸다. 3D-FE 해석을 위해 탄성 및 소성 영역 데이터(적색 점)를 재료 물성의 입력 값으로 사용하였으며, 이후 해석상에서 인장시험(Tension Coupon Test) 결과(적색 곡선)는 해석상에서 강재의 물성이 정확하게 보정(Calibration)되었음을 나타낸다. 볼트의 항복 응력은 850MPa이다.

Fig. 5.

Stress-strain curve: Material calibration of steel for analysis

2.3 강재의 소성 경화

강재가 Fig. 5와 같이 경사진 소성 경화(Plastic hardening)를 갖고 주기적인 하중을 받을 때 ABAQUS에서 경화 모델(Hardening rules)을 적절히 설정해야 한다(Hartloper et al.., 2021). 2.2절에서 언급된 바와 같이 3D-FE Model(Fig. 4)의 해석수행에 사용된 강재 인장시험은 보정된 결과를 가져 온 것이며, 바우싱거 효과(Bauschinger effect)를 모사하기 위해 ABAQUS에서 Half.-Cycle Data(Back stress=2)를 고려한 복합 경화 모델(Combined Hardening)을 사용하였다. 또한 해석의 간소화를 위해 초기 해석에서 모든 접촉면은 서로 구속되어 있는 Tied 조건을 가정하였다. 즉, 슬립(Slipping)과 분리(Separation) 성분이 포함되지 않으며 볼트의 프리텐션도 제외하였다.

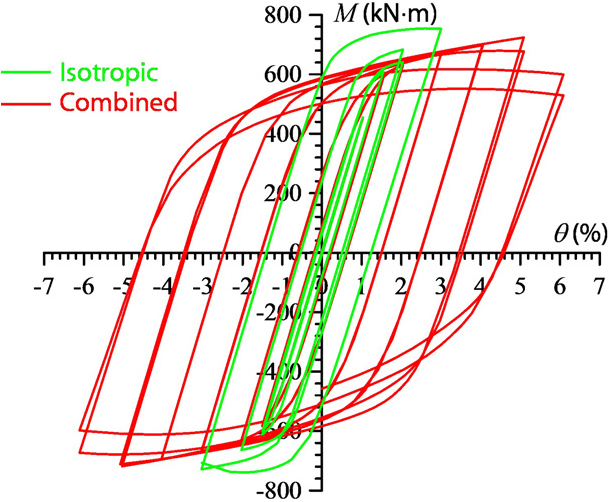
이후, Fig. 6은 등방성(Isotropic) 경화모델과 복합(Combined, Isotropic + Kinematic)경화모델의 모멘트-회전각 이력 곡선을 비교한 것이다. 등방성 경화모델을 사용한 해석에서는 “소성 경화(Plastic Hardening)” 단계 동안 이력 곡선이 계속 확장됨을 볼 수 있다. 반면, 복합 경화모델을 사용한 해석은 주기적 하중 시험에서 볼 수 있는 시험과 유사한 이력 곡선을 보여준다(적색). 따라서 이후 해석에서는 복합 경화 모델(Combined Hardening)을 사용하였다.

Fig. 6.

Moment-rotation curve obtained from analysis using isotropic hardening vs. combined hardening

2.4 Tied Model과 Bolt-slip Model

2.3장의 강재 물성을 복합 경화 모델로 적용한 “Tied Model”은 접촉 면의 슬립과 분리의 성분은 없기 때문에 볼트 접합에 있어 가장 바람직하거나 이상적인 이력 거동을 보여준다. 하지만 이 모델은 실제 볼트 접합 같이 접촉면에 슬립과 분리성분이 포함되어 있지 않다. 따라서 실제 볼트 접합을 잘 모사하기 위하여 모든 접촉면의 분리하여 복합 경화 모델을 적용한 “Bolt-slip Model”으로 해석을 수행하였다.

Fig. 4와 동일한 3D-FE 모델을 사용하여 Bolt-Slip Model의 접촉조건을 적용하였다. 약 0.7의 볼트 항복 응력(F_pretension » 0.7σ_y of bolt)에 해당하는 프리 텐션 볼트를 설정하였고, 모든 접촉 면은 “Hard Contact”으로 설정하였으며, 볼트 와샤와 강재 플레이트 사이의 마찰계수(μ, friction coefficient)는 0.1, 강재 플레이트와 강재 플레이트 사이의 마찰계수는 0.3으로 설정하여 Bolt-slip Model 해석을 수행하였다.

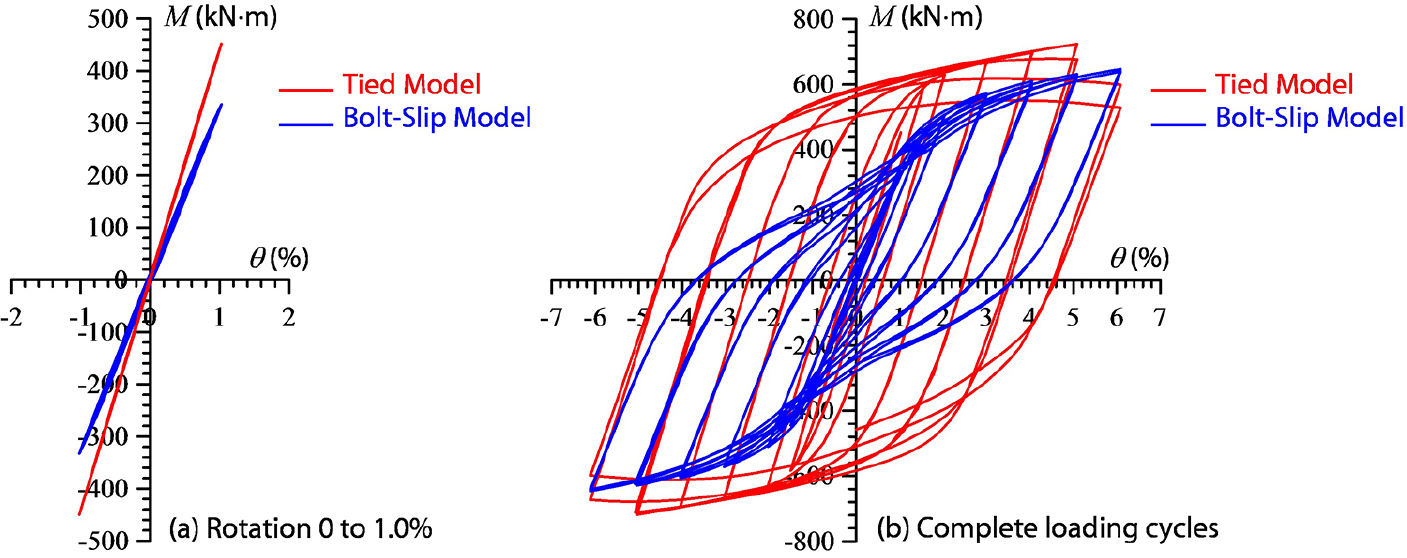
Fig. 7은 Tied Model과 Bolt-slip Model에서 얻은 모멘트-회전 곡선을 비교한 결과를 보여준다. 두 모델의 초기 강성은 동일하지만, Bolt-slip Model은 접촉 면에서의 작은 슬립으로 인해 낮은 회전 하중에서 즉시 비선형성을 나타낸다(Fig. 7a). 이는 회전 하중(θ = 0 to 1.0%)에 대해 Tied Model보다 강성이 더 낮게 나타나는 것을 분명히 보여준다.

Fig. 7.

Moment-rotation curves obtained from tied model vs. bolt-slip model

피크 진폭이 증가하는 주기적 하중이 계속되면, 두 모델은 소성 변형을 겪으며 Fig. 7b에 나타난 이력 거동을 보이게 된다. 두 모델 모두 이력곡선에서의 면적을 지녀 에너지 소산 능력을 가지고 있지만, Tied Model은 안정적인 이력 곡선을 가지고 있으며, Bolt-slip Model은 핀칭 현상을 보인다. 결과적으로 Bolt-slip Model은 Tied Model의 에너지 소산 능력의 약 0.54만큼에 그친다. 이러한 핀칭 현상은 (1) 볼트와샤와 플레이트 표면 사이의 슬라이딩, (2) 강판과 강판 사이의 접촉면에서의 슬라이딩 및 분리, 그리고 (3) 볼트의 소성 변형, (4) 기둥 표면에서의 현저한 부풀림(Bulging)과 딤플링(Dimpling) 등의 국부적 결함에서 비롯될 수 있다.

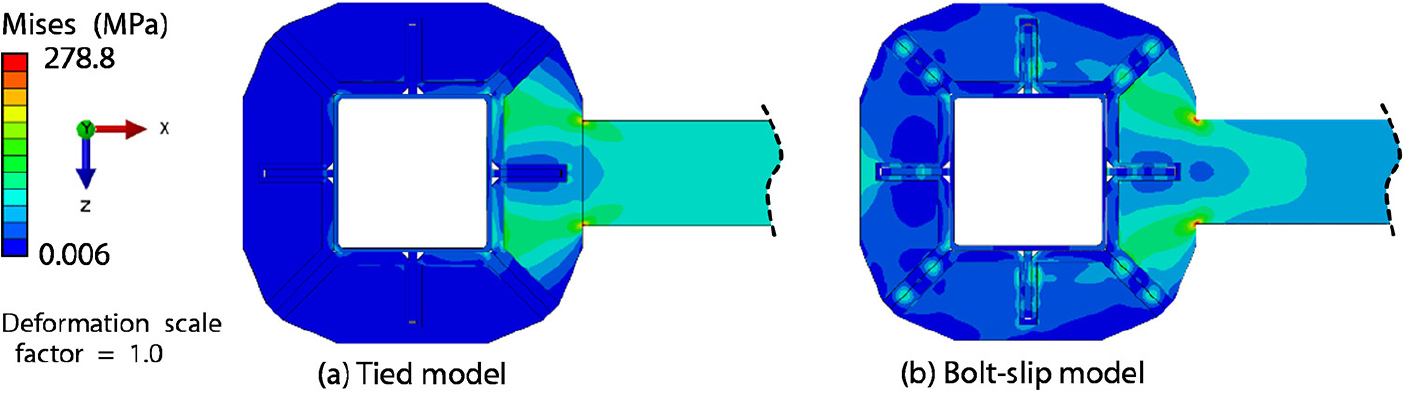
Tied Model은 보와 기둥의 접합부에서 이상적인 강 접합(Rigid Joint)을 나타낸다. Fig. 8a에서 확인할 수 있듯이, 보에 부착된 TZcon 모듈만이 기둥으로 보의 응력을 전달하는 역할을 한다. 보의 응력은 기둥 면으로 직접 전달되며, 인접한 TZcon 모듈로의 하중 전달은 거의 없이 값이 0에 가까웠다. 반면 Bolt-slip Model은 Tied Model보다 접합 거동이 더 복잡한 모습을 보인다. Fig. 8b에서 볼 수 있듯이, 모든 네 개의 TZcon 모듈은 낮은 진폭의 주기적 하중(θ = -0.375%)에서도 보에서 기둥으로의 응력 전달하는데 작용한다. 이는 높은 진폭의 하중에서, TZcon 모듈을 체결하는 M27 볼트의 축 인장력이 보 응력의 인장 성분을 전달할 때 상당히 증가할 수 있음을 나타낸다.

Fig. 8.

Mises stress indicating the stress flow at the TZcon modules in (a) tied model and (b) bolt-slip model at θ = -0.375%

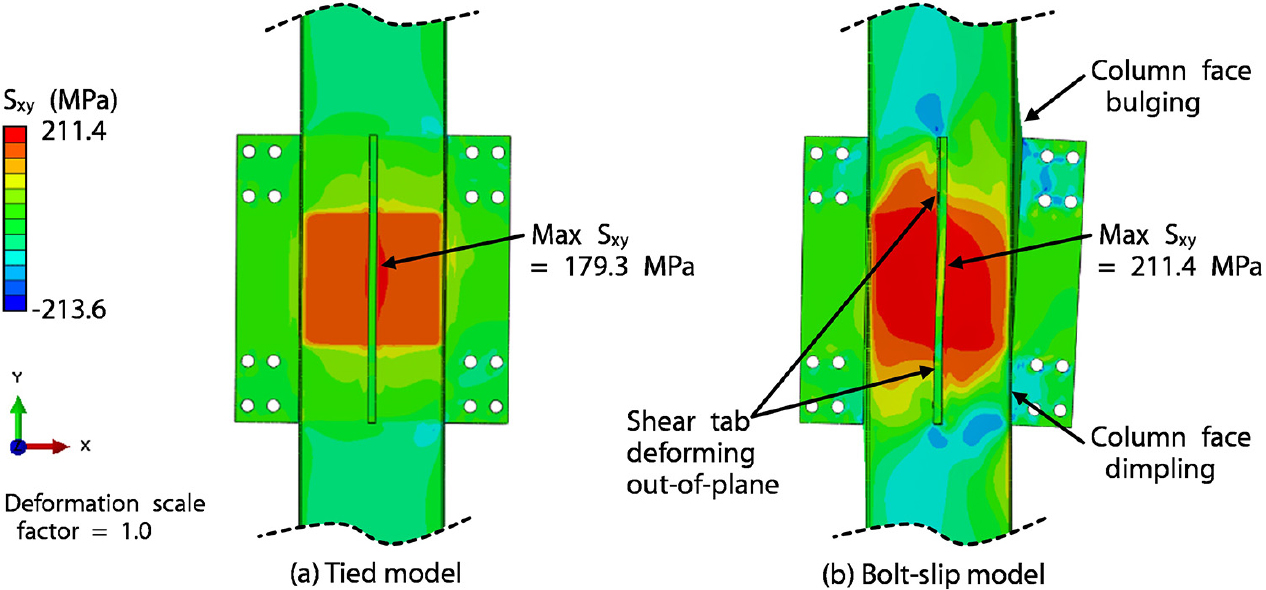
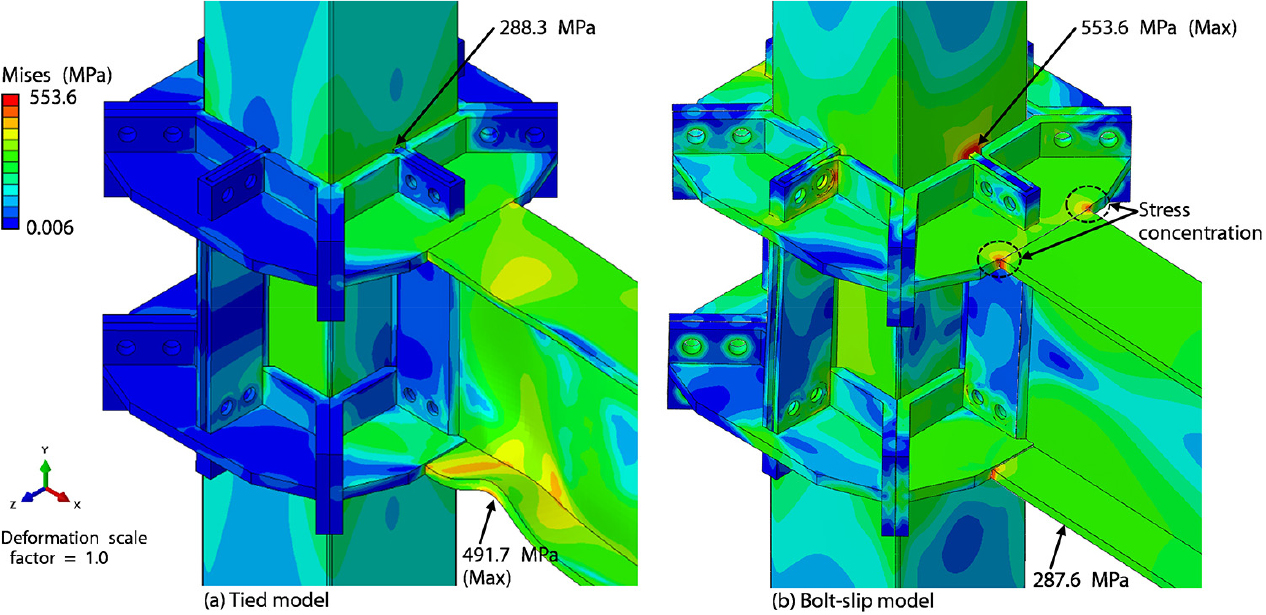
또한, Fig. 9는 표면 접촉 조건에 따라 기둥이 어떻게 거동하는지 보여준다. Tied Model(Fig. 9a)의 경우, 기둥의 전단 패널 존(Shear Panel Zone)은 직사각형 형상을 보이며 강한 접합의 전형적인 특성을 보여준다. θ = -6.0%일 때, 최대 S_xy 값은 179.3MPa로 나타났다. 한편 Bolt-slip Model(Fig. 9b)의 경우, 전단 탭의 상단과 하단에 있는 수직 항력으로 인해 불규칙한 형상의 패널 영역을 형성했다. 이러한 수직 항력은 TZcon 모듈에서 발생하며 전단 탭의 면외(Out of Plane) 변형을 유발했다. θ = -6.0%일 때 최대 S_xy 값은 211.4MPa로, 이는 Tied Model의 1.18배에 해당한다.

Fig. 9.

Shear stress Sxy at the column obtained from (a) tied model versus (b) bolt-slip model at θ = -6.0%

또한 Bolt-slip Model(Fig. 9b)에서 플레이트의 슬립과 분리는 보에 연결된 전단 탭에 전단력(Shear Force) 뿐만 아니라 모멘트(Moment)를 전달하도록 유도한다. 이는 주로 모멘트의 인장 거동에서 발생하고 해석상의 거동에서 기둥 면의 Bulging과 Dimpling을 통해 확인할 수 있다. 전단 탭의 상단(또는 하단) 부분이 기둥 면에서 순간적으로 당겨지며, 전단 탭은 회전하여 하단(또는 상단) 부분이 기둥 면 쪽으로 밀려나게 된다. 하지만 이러한 국부적인 변형과 전단 탭이 받는 모멘트 효과는 각관 기둥의 두께를 증가시켜 완화할 수 있다.

표면 접촉 조건이 다르기 때문에 기둥-보 어셈블리의 항복 위치도 다르게 나타난다. Tied Model(Fig. 10a)의 경우, 보에서 소성 힌지(Plastic Hinge)가 발생하며 최대 Mises Stress는 491.7MPa를 보였다. 반면, Bolt-slip Model(Fig. 10b)의 경우, 소성 힌지가 발생한 동일한 위치에서 최대 Mises stress는 287.6MPa로, 이는 Tied Model의 0.58배에 해당하며, 항복 응력보다 약 4.6% 높지만 보 에서의 소성 힌지는 발생하지 않았다. Bolt-slip Model의 최대 Mises stress는 전단 탭이 부착된 기둥 표면에서 발견되며, 값은 553.5MPa로 Tied Model의 거의 2배에 해당하는 값이다.

Fig. 10.

Mises stress distribution at the column-beam joint for θ = -6.0% loading.

위에서 수치적으로 입증된 바와 같이 탄소 감축을 위한 해체가 용이한 접합부(CNDC)의 이상적인 거동을 위해서는 모든 접촉면의 슬립과 분리를 허용하지 않는 것이 중요하다(Tied Model). 그러나 실제현장에서는 볼트 체결로 인해 접촉면이 슬립과 분리가 되는 경향이 있으며, 이는 기둥 표면의 Bulging 및 Dimpling과 같은 국부적인 파손을 발생시킬 수 있다(Bolt-slip Model). 따라서 Bolt-slip Model의 실험에 대한 추가적인 통찰과 이해를 제공할 수 있음을 시사한다.

3. 실험과 수치해석의 비교

3.1 전체적 거동

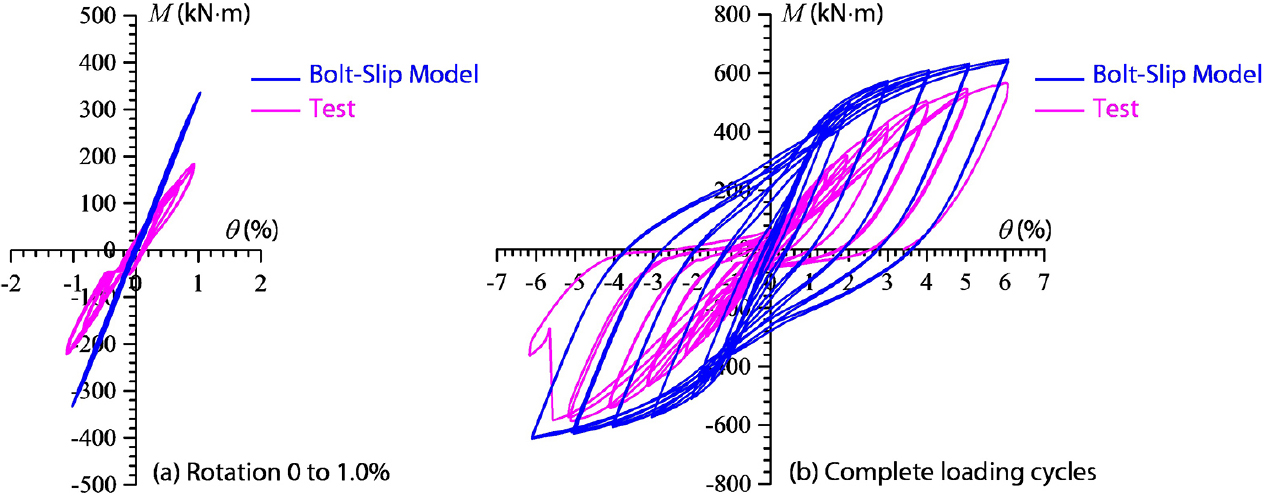
모멘트-회전 이력곡선을 비교하여 실험과 해석(Bolt-slip Model)의 전체적인 거동을 비교한 결과, Fig. 11에서 볼 수 있듯이, 3D-FE 해석과 유사한 핀칭 이력을 가진다. 그러나 해석과 달리 실험에서의 M-θ 곡선은 Force가 0에 접근할 때 기울기가 거의 수평이 되며 이력곡선의 안으로 파고드는 과도한 핀칭 이력을 가지며, 이에 따라 실험에서의 에너지 소산량은 해석의 비해 불과 약 0.46배의 상대적으로 낮은 값을 나타낸다.

Fig. 11.

Moment-rotation curves obtained from analysis vs. test

2.4절에서 언급된 바와 같이, 핀칭 현상은 주로 볼트의 사전 장력과 마찰력에 의해 제어되는 접촉면의 미끄럼 및 분리로 인해 발생할 수 있다. 그러나 볼트 항복 응력의 약 0.7 대신 0.3에 해당하는 낮은 볼트 프리텐션과 마찰계수 0.3 대신 0.1의 값을 사용한 Bolt-Slip Model 분석결과, M-θ 곡선 또한 실험에서 얻은 결과와 일치하지 않았다. 또한, Fig. 11a의 M-θ 곡선을 면밀히 비교해보면, 초기 낮은 회전하중(즉, 하중 적용 직후)에서 시스템의 강성은 약10% 정도의 미미한 차이를 보인다. 실험과 Bolt-Slip Model 모두 하중이 진행됨에 따라 비선형적으로 동작하지만, Bolt-Slip Model이 낮은 진폭의 하중(θ= 0 to 1.0%, 시스템이 여전히 탄성단계)에서 보다 더 많은 비선형성을 나타낸다.

낮은 하중에서 항복이 발생할 가능성은 낮아, 실험에서 관찰되는 두드러진 심각한 비선형성은 실제 거동에 영향을 미칠 수 있는 마찰요인 뿐만 아니라 또 다른 요인에서 비롯됨을 알 수 있다. 마찰력은 이상적으로 적용된 Bolt-Slip 보다 낮았으며, 시뮬레이션된 Bolt-Slip Model에 포함되지 않은 상대적으로 심한 슬립 성분이 나타났다. 실험에서 관찰된 이러한 심각한 비선형성은 이상적인 접촉면의 간극(gap)과 감소를 유발하는 제조상의 불완전성(Imperfection)에서 기인한 것이다.

3D-FE 모델에서는 모든 접촉면의 간극거리가 0이라고 가정하였다. 그러나 실험에서는 TZcon 모듈의 제작 및 체결에서의 오류로 인해 육안으로 관찰 가능한 약 5-10mm의 간극이 존재하였다(Fig. 12b). 이로 인해 Fig. 11b에 표시된 바와 같이, 특히 힘의 방향이 변하는 시점(인장에서 압축력, 또는 그 반대)에서 시험체 볼트접합 체결 성능이 악화된다. 이 시점에서는 압축을 받는 TZcon 수평 플레이트와 인장을 받는 모서리 볼트가 틈으로 인해 힘을 제대로 전달하지 못한다. 그러나 하중이 증가함에 따라 조인트 연결은 다시 강성을 회복하는 것처럼 보인다. 이는 압축 측의 간극이 닫히며, 쉽게 말해서 분리된 면이 다시 접촉하게 되기 때문이다. 이로 인해 접촉면 간의 힘이 전달되고, 인장 측의 볼트도 다시 힘을 전달하게 된다.

Fig. 12.

Local failure of joint: view from (a) the top of beam flange, and (b) bottom showing flange-web connection

3.2 국부적 파단

실험과 Bolt-slip model의 모멘트-회전 이력곡선(Fig. 11)은 서로 일치하지 않았지만, 시험에서 시각적으로 관찰된 국부적 파단은 해석 결과와 일치한다. Fig. 12에서 보여 지듯이, 시험에서 보 플랜지 상단와 TZcon 모듈 사이에서 균열이 발생하였다. 이 균열은 보 플랜지와 TZcon 수평 플레이트의 90°의 맞댐 부(용접 부)에서 시작되어 전단 탭 부근으로 진행되어 파단이 발생하였다.

4. 결 론

본 연구에서는 이전에 시험한 탄소감축을 위한 해체가 용이한 급속 분해 접합부의 3차원 유한요소(3D-FE)해석을 수행하였다. 모멘트 접합으로서 기둥-보 접합에서 이상적인 강 접합을 조사하기 위해 “Tied Model”(슬립 및 분리 성분을 고려하지 않은 모델)을 사용하였으며, 실험의 거동특성을 조사하기 위해 “Bolt-slip Model”(슬립 및 분리 성분을 고려한 모델)을 사용하여 볼트의 프리 텐션을 포함한 해석을 수행하였다. 다음과 같은 결론을 도출하였다.

1) 3D-FE 모델의 접촉조건에서 슬립 및 분리 성분을 고려하지 않았을 때, 본 연구의 접합 시스템은 이상적인 모멘트 접합으로서 강 접합의 거동을 보이며 보에서 소성 힌지가 발생하였다.

2) 그러나 슬립 및 분리 성분이 포함된 경우, 접합 시스템은 모멘트 작용으로 인해 전단 탭을 통해 응력을 보에서 기둥으로 전달하며, 이로 인해 전단 탭 기둥 부착면에서 높은 응력 집중이 발생함을 발견하였다.

3) Bolt-slip Model은 손상모델은 고려하지 않았지만, 실험결과 특히 국부적인 파괴 거동과 일치하였다.

4) 제조상의 불완전한 오류로 인해 TZcon의 모서리 플레이트의 간극이 발생하여 실험값은 전체적인 이력양상에서 Bolt-slip Model에 비해 전반적으로 다른 거동을 보였다.

5) 실험에서 핀칭 현상이 낮은 하중에서도 비선형성(연화)이 나타나는 것을 발견하였고, 이는 제조 과정에서 발생한 TZcon 모듈의 간극으로 발생한 것임을 밝혀내었다.