State-Space Equation Model for Motion Analysis of Floating Structures Using System-Identification Methods

Jun-Sik Seong; Wonsuk Park

doi:10.7734/COSEIK.2024.37.2.85

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 April 2024. 85-93
https://doi.org/10.7734/COSEIK.2024.37.2.85

State-Space Equation Model for Motion Analysis of Floating Structures Using System-Identification Methods

부유식 구조체 운동 해석을 위한 시스템 식별 방법을 이용한 상태공간방정식 모델

Jun-Sik Seong¹

Wonsuk Park²^*

성 준식¹

박 원석²^*

¹Graduate Student, Department of Civil Engineering, Mokpo National University, Muan, 58554, Korea

²Associate Professor, Department of Civil Engineering, Mokpo National University, Muan, 58554, Korea

¹국립목포대학교 토목공학과 석사과정

²국립목포대학교 토목공학과 부교수

^{*Corresponding Author}

ABSTRACT

In this paper, we propose a method for establishing a state-space equation model for the motion analysis of floating structures subjected to wave loads, by applying system-identification techniques. Traditionally, the motion of floating structures has been analyzed in the time domain by integrating the Cummins equation over time, which utilizes a convolution integral term to account for the effects of the retardation function. State-space equation models have been studied as a way to efficiently solve floating-motion equations in the time domain. The proposed approach outlines a procedure to derive the target transfer function for the load-displacement input/output relationship in the frequency domain and subsequently determine the state-space equation that closely approximates it. To obtain the state-space equation, the method employs the N4SID system-identification method and an optimization approach that treats the coefficients of the numerator and denominator polynomials as design variables. To illustrate the effectiveness of the proposed method, we applied it to the analysis of a single–degree-of-freedom model and the motion of a six–degree-of-freedom barge. Our findings demonstrate that the presented state-space equation model aligns well with the existing analysis results in both the frequency and time domains. Notably, the method ensures computational accuracy in the time-domain analysis while significantly reducing the calculation time.

Keywords

floating structures

motion analysis

state-space equation

system-identification methods

이 논문에서는 파랑 하중을 받는 부유식 구조체의 운동 해석에 있어서 시스템 식별 방법을 이용한 상태공간방정식 모델을 수립하고 해석하는 방법을 제안하였다. 상태공간방정식 모델의 수립 방법으로는 주파수영역에서 하중-변위 입출력 관계에 대한 목표 전달함수를 구하고 이에 가장 근접하는 상태공간방정식을 구하는 절차를 제시하였다. 전통적으로 부유식 구조체 운동의 시간영역 해석은 지연함수의 합성곱적분을 포함하는 Cummins 방정식을 시간적분하여 이루어진다. 상태공간방정식 모델은 이러한 시간영역해석을 효과적으로 수행하기 위한 방법의 하나로서 연구되어 왔다. 제안하는 방법에서는 시스템 식별방법인 N4SID 와 전달함수의 분모 및 분자 다항식의 계수를 설계변수로 하는 최적화방법을 사용하여 목표 전달함수에 상응하는 상태공간방정식을 구한다. 제안하는 방법의 적용성을 보이는 예제로서 단자유도 수치모델 및 6자유도 바지의 운동을 해석하였다. 제시하는 상태공간방정식 모델은 주파수영역 및 시간영역에서 모두 기존의 해석결과와 잘 일치하고 시간영역해석에서는 계산의 정확도를 확보하면서 계산 시간을 크게 줄일 수 있음을 확인하였다.

키워드

부유식 구조체

운동 해석

상태공간방정식

시스템 식별 방법

MAIN

1. 서 론
2. 부유체 운동방정식의 상태공간방정식 표현
2.1 부유체의 선형 운동방정식
2.2 상태공간방정식 모델링 절차
3. 부유체 운동의 상태공간방정식 모델링 예제
3.1 단자유도 부유체 운동방정식
3.2 바지(barge)의 RAO
3.3 계류된 바지선의 시간이력응답 해석
4. 결 론

1. 서 론

해상이나 수상에 구조물을 설치하는데 있어서 기초구조물을 사용하지 않는 부유식 구조물은 심해의 원유나 가스 시추를 위한 전통적인 해양 플랫폼(offshore platform)에 적용되며, 해상 풍력, 해상 태양광 발전을 위한 구조로도 개발이 이루어지고 있다(Cho et al., 2016; Goupee et al., 2014; Kim et al, 2021; 2022). 또한 부유식 해상 교량에 대한 제안과 연구도 지속적으로 이루어지고 있으며(Moan and Eidem, 2020), 부유식 공항(Kashiwagi, 2004), 항만, 에너지시설, 해상 도시 등 본격적인 인프라 시설을 부유식 방법으로 해상에 설치하려는 시도가 계속되고 있다.

이와 같은 부유식 구조의 설계에서는 주기하중 특성을 갖는 파랑하중에 대하여 응답을 평가하는 것이 중요하고, 동유체력 계수(hydrodynamic coefficient)인 부가질량과 방사감쇠 등 이 주파수 의존적 특성을 가지므로 주파수영역해석이 기본이 된다. 시간영역해석은 계류력, 풍력, 조류력, 점성항력, 파랑표류력 등의 영향을 받는 계류된 부유체의 운동해석에서 비선형 힘을 고려하기 위해 주로 사용된다(Wang et al., 2020). 부유식 교량, 해상 도시와 같은 부유식 인프라 구조체의 경우에는 부유체에 직접 작용하는 하중뿐만 아니라 상부 구조물에 작용하는 교통하중, 풍하중 등에 대한 고려도 필요하며 선박에 대한 충돌하중 등 비주기적 특성을 갖는 시계열 하중에 대한 해석이 필요하다. 또한 대형 부유식 구조체를 모듈 형식으로 제작할 경우에는 모듈들을 연결장치를 통해 연성 또는 강성으로 연결하게 되는데 이때 연결장치의 피로해석 등에도 시간영역해석이 사용된다. 부유체의 변형을 고려하는 해석에서도 재료 비선형 등이 포함되는 경우 시간이력 해석이 필요하다(Yoon and Lee, 2017). 또한 최근에는 디지털 트윈 등 실시간으로 구조물 응답을 모니터링하고 해석할 때 시긴영역해석이 적용되고 있다.

일반적으로 부유체의 시간영역운동 해석은 변위 및 변위의 미분으로 표현되는 속도와 가속도항 이외에 합성곱 적분(convolution integral)항으로 표현되는 감쇠가 포함된 Cummins 방정식을 수치적으로 시간적분하여 해석하는 방법이 가장 널리 사용된다(Cummins, 1962). 이를 위해서는 각 시간 스텝에서 지연함수를 포함한 합성곱 적분항을 계산해야 한다. 즉, 각 시간 스텝에서 다음 스텝의 응답을 구하는데 필요한 계산 시간에 적분항의 계산이 포함되어야 하는데, 이러한 지연함수의 계산은 전체 해석 시간의 증가 및 비효율성, 오차의 누적 등의 문제가 있을 수 있음이 지적되었다(Fossen, 2002; Lu et al., 2019). 따라서 이러한 전통적인 방법이외에 지연함수 계산의 효율성을 높여 전체 운동방정식의 시간 적분을 효율적으로 하기 위한 방법이 개발되어 왔다.

이러한 방법 중의 하나로 상태공간방정식(state-space equation)을 이용한 계산 방법이 개발되어 왔다(Lu et al., 2020; Taghipour et al., 2008). 상태공간방정식은 임의 차수의 미분방정식을 상태벡터(state vector)에 대한 일차의 벡터-행렬 미분방정식으로 표현한다. 시간 적분을 단순한 차분형으로 나타낼 수 있고 컴퓨터의 행렬-벡터 연산의 계산 효율성이 높아 효과적인 시간이력해석에 용이한 방법이다. 하중과 센서 등 입력과 출력관계를 표현하는데 매우 편리하고, 시스템 행렬에 관한 여러 가지 수학적 성질들이 잘 알려져 있어 제어시스템 설계, 시스템 식별 등의 응용분야에서 주로 사용되고 있다.

부유체 운동의 해석에 있어서 상태공간방정식을 이용한 연구도 꾸준히 이루어지고 있다(Jordán and Beltrán-Aguedo, 2004; Lu et al., 2022; Schmiechen, 1973). 부유체 운동 방정식을 상태공간에서 표현하기 위한 방법은 크게 주파수영역 방법과 시간영역을 이용하는 방법이 있다(Duarte et al., 2013). 주파수영역 방법은 주로 전달함수(transfer function) 또는 주파수응답함수(frequency-response function)을 사용하여 상태공간 시스템 및 입출력 행렬을 찾아내는 방법이다. 시간영역 방법에서는 임펄스응답함수(impulse response function)을 사용한다. 선형 시스템에서 전달함수와 임펄스응답함수는 라플라스변환을 통해 변환되는 동치의 관계이므로 이론적으로 두 방법은 동일하지만 구현하는 수치적 방법과 원 데이터의 충실도 등에 따라 결과적으로 구한 상태공간방정식의 정확도와 안정성이 달라질 수 있다.

가장 널리 알려진 Cummins 방정식을 상태공간방정식을 이용하여 해석하는 방법은 지연함수를 포함하는 합성곱 적분항을 대체하여 나타내는 방법에 따라 크게 세 가지로 구분할 수 있다(Taghipour et al., 2008). 첫 번째 방법은 주파수 의존적인 부가 질량과 지연함수가 포함된 적분항을 등가의 부가 질량 및 선형 감쇠로 치환한 후 이를 상태공간 방정식으로 푸는 방법이다. 두 번째 방법은 지연함수가 포함된 적분항이 어떤 동적 특성을 갖는 선형시스템의 응답과 같음을 이용하여 이 적분항의 값을 출력으로 하는 상태공간 방정식을 구축하여 운동 방정식과 연계하는 방법이다. 세 번째 방법은 부유체의 하중-운동(force to motion) 관계, 즉 입출력 관계 전체를 상태공간 방정식으로 모델링하는 방법이다. 이 방법에서는 부가 질량과 방사 감쇠의 주파수 의존성과 지연함수를 포함한 적분항의 동력학적 특성이 하나의 동적시스템으로 모델링되며 시스템의 출력이 부유체의 변위 및 속도 벡터가 되도록 하여 해석을 수행하게 된다.

이 연구에서는 주파수영역의 전달함수를 사용하고 부유체의 하중-운동 관계를 상태공간 방정식으로 표현하는 방법을 제시한다. 제시하는 방법은 크게 목표 전달함수를 구하고, 목표 전달함수에 상응하는 상태공간방정식을 얻는 절차로 구성된다. 목표 전달함수에 상응하는 상태공간방정식을 구하는 방법으로서는 시스템 식별방법인 N4SID(numerical algorithms for subspace state space system identification)와 전달함수의 분모 및 분자 다항식의 계수를 설계변수로 하는 최적화방법을 사용하였다. 제시하는 방법은 주파수영역의 동유체력 계수(hydrodynamic coefficient)인 부가질량과 방사감쇠를 구하기 위해 상용 소프트웨어인 Ansys AQWA(Ansys Ins., 2023)를 사용하고, 이를 이용해 목표전달함수 구성 및 상태공간방정식 추출을 위해 MATLAB을 사용하였다(The Mathwork Inc., 2022). 제시하는 상태공간방정식 모델링 절차를 2장에 기술하였다. 3장에는 제시하는 방법의 적용성을 보이는 해석 예제로서, 단자유도 부유체 방정식과 6자유도 바지(barge) 부유체의 운동해석 결과를 제시하고 4장에 결론을 제시하였다.

2. 부유체 운동방정식의 상태공간방정식 표현

2.1 부유체의 선형 운동방정식

이 연구에서는 선형 이론에 바탕을 둔 부유체의 운동방정식을 고려한다. 일반적으로 부유체의 운동을 시간영역에서 해석하는데 있어서는 두 가지의 접근법을 생각할 수 있다. 첫 번째는 직접 시간영역에서 운동방정식을 정식화하는 방법이고 두 번째는 주파수 영역에서 선형 운동방정식을 정식화 하고 이를 푸리에 변환(Fourier transform)을 통하여 시간영역으로 바꾸는 방법이다. 후자의 방법은 주파수-시간 영역 하이브리드 모델로 통칭되며 Cummins 방정식으로 널리 알려져 있다(Cummins, 1962). 부유체의 거동은 선형 방정식으로 유도되었으나 이 선형 모델에 여러 가지 비선형 효과를 편리하게 추가시켜 해석할 수 있으므로 부유체의 시간이력 해석에 현재 가장 널리 사용되는 모델이다.

일반적으로 전진 속도가 0(zero forward speed)인 부유체의 운동에 대하여 Cummins 식은 다음 식 (1)과 같은 부유체 운동의 주파수 영역 운동방정식을 푸리에 변환하여 식 (2)와 같이 시간영역에서 나타낸 식이다.

(1)

- ω^{2} [M + A (ω)] X (ω) + i ω B (ω) X (ω) + K X (ω) = F (ω)

(2)

[M + A^{\infty}] x ¨ (t) + \int_{0}^{t_{m}} R (t - τ) x ˙ (τ) d τ + K x (t) = f (t)

여기서, $X (ω), x (t)$ 는 주파수 𝜔와 시간 $t$ 에서 부유체 자유도 변위, $M$ 은 부유체의 질량, $A (ω), A^{\infty}$ 는 부가질량 및 부가질량의 고주파 극값, $B (ω)$ 는 부유체 방사 감쇠(radiation damping), $K$ 는 유체에 의한 복원력을 나타내는 정유체력(hydrostatic force)으로 부터 구한 복원력 상수(강성) 행렬, $F (ω), f (t)$ 는 각각 주파수 영역 및 시간 영역에서 외부 하중이다.

식 (2)에서 합성곱 적분항 함수 $R (∙)$ 은 다음 식 (3)과 같이 표현되는 기억함수(memory function) 또는 지연함수(retardation function)로서 시간 영역에서 방사 감쇠 효과를 나타내며, $t_{m}$ 은 지연함수 값이 0에 가까운 한계 시간이다.

(3)

R (t) = \frac{2}{π} \int_{0}^{\infty} B (ω) \cos (ω t) d ω

일반적으로 부유체의 운동방정식 해석은 식 (1)의 주파수 영역 해석, 식 (2)의 시간 영역 해석으로 이루어 질 수 있다.

2.2 상태공간방정식 모델링 절차

상태공간방정식은 잘 알려진 바와 같이 임의 차수의 선형 미분방정식으로 표현되는 동적 시스템을 다음 식 (4)와 같은 시간영역에서 행렬-벡터 일차 미분방정식인 상태방정식과 식 (5)와 같은 대수방정식인 출력방정식으로 표현한 것이다(Chen, 1984).

(4)

\dot{x} (t) = A_{s} x (t) + B_{s} u (t)

(5)

y (t) = C_{s} x (t) + D_{s} u (t)

여기서, $x (t) \in R^{n \times 1}$ 는 상태벡터, $u (t) \in R^{p \times 1}$ 는 외력(제어력)벡터, $y (t) \in R^{q \times 1}$ 는 출력벡터이며, $A_{s} \in R^{n \times n}$ 는 시스템 행렬, $B_{s} \in R^{n \times p}$ 는 입력행렬, $C_{s} \in R^{q \times n}$ 는 출력행렬, $D_{s} \in R^{q \times p}$ 는 앞먹임(feedthrough)행렬이다.

이 연구에서 제안하는 방법은 주파수 영역에서 부유체 운동 시스템의 전달 함수(transfer function)를 먼저 구하고 그 전달함수에 상응하는 시간영역의 상태공간방정식을 찾아내는 방법이다. 일반적으로 식 (1)로부터 주파수 영역에서 부유체의 운동방정식은 다음 식 (6)과 같이 쓸 수 있다.

(6)

Z (i ω) X (i ω) = F (i ω)

여기서, $Z (i ω)$ 는 임피던스함수(impedance function)이고 다음과 같이 정의된다.

(7)

Z (i ω) = K - ω^{2} [M + A (ω)] + i ω B (ω)

이 시스템의 전달함수를 $H (i ω)$ 라 하면 $X (i ω) = H (i ω) F (i ω)$ 이므로 다음 관계가 성립한다.

(8)

H (i ω) = Z^{- 1} (i ω)

여기서, 6 자유도를 갖는 부유체의 운동에 대하여 $H (i ω)$ 는 각 주파수 𝜔에 대한 6 × 6 행렬로 구해진다.

일반적으로 식 (4), (5)의 시간영역 상태공간방정식은 주파수 영역에서 다음 식 (9)와 같은 전달함수로 표현된다.

(9)

H_{s} (i ω) = C_{s} [i ω I - A_{s}]^{- 1} B_{s} + D_{s}

이 연구에서 제안하는 방법은 식 (8)의 전달함수와 식 (9)의 전달함수 차이가 최소가 되도록 하는 상태공간방정식 행렬 $A_{s}, B_{s}, C_{s}, D_{s}$ 를 구하는 것이다. 주어진 전달함수 행렬 $H (i ω)$ 에 상응하는 상태공간방정식 행렬 $A_{s}, B_{s}, C_{s}, D_{s}$ 를 구하는 것은 선형 시스템 및 시스템 식별 분야에서 매우 잘 알려진 문제로서 여러 알고리즘이 존재한다. 이 연구에서는 크게 두 가지 방법을 사용하여 상태공간방정식을 구하였다. 첫 번째 방법은 잘 알려진 상태공간 시스템 식별 방법인 N4SID(numerical algorithms for subspace state space system identification) 알고리즘을 사용하고(Van Overschee and De Moor, 1994), 두 번째로는 유리 다항식으로 표현된 전달함수의 계수를 오차 최소화 과정을 통해 결정하고 이를 상태공간방정식으로 변환하는 방법이다.

부공간 상태공간 시스템 식별 방법인 N4SID는 입출력 데이터로 생성한 Hankel 행렬 또는 Toeplitz 행렬 등을 특이치 분해하여 이를 상태공간 행렬로 변환하는 방법이다. 주로 입출력 시계열 데이터를 이용하여 상태공간방정식을 추출하는데 많이 사용되지만 주파수 영역 응답함수로도 동일한 알고리즘을 적용할 수 있다(McKelvey et al., 1996). 이 연구에서는 MATLAB System Identification Toolbox의 n4sid() 함수를 사용하였다.

전달함수 변환 방법에서는 전달함수행렬의 각 항을 분자 다항식과 분모 다항식으로 표현하고 각 다항식의 계수를 주어진 전달함수 데이터와 오차가 최소화되도록 결정한다. 이 연구에서는 MATLAB의 tfest() 함수를 사용하였으며 이 함수에서는 비선형 최소 자승법에 기반한 최적화 방법이 사용된다. 이 연구에서 제시하는 부유체 운동에 대한 상태공간방정식 모델링 절차는 다음과 같다.

[Step1] 주어진 부유체에 대하여 질량행렬 $M$ , 정유체력 강성행렬 $K$ 를 구하고 주파수 영역 해석을 수행하여 부가질량 $A (ω)$ , 감쇠 $B (ω)$ 를 구한다.

[Step2] 주요 주파수대역에 대하여 식 (7)의 임피던스함수 행렬 $Z (i ω)$ 을 구하고 식 (8)을 이용하여 목표 전달함수 행렬 $H (i ω) = Z^{- 1} (i ω)$ 를 구한다.

[Step3] 목표 전달함수 행렬 $H (i ω)$ 에 대하여 N4SID 또는 전달함수 변환 알고리즘을 적용하여 임의 차수의 상태공간방정식 행렬 $A_{s}, B_{s}, C_{s}, D_{s}$ 를 구한다.

[Step4] 구한 상태공간방정식 $A_{s}, B_{s}, C_{s}, D_{s}$ 로부터 식 (9)에 의한 전달함수 행렬 $H_{s} (i ω)$ 를 구하고 이를 목표 전달함수 행렬 $H (i ω)$ 와 비교한다.

[Step5] 목표 오차 이내가 되는 최소 차수의 상태공간방정식 행렬 $A_{s}, B_{s}, C_{s}, D_{s}$ 를 구할 때까지 Step 3, 4를 반복한다.

전달함수 변환 알고리즘이나 N4SID 방법에서는 상태공간 방정식의 차수를 늘려가며 각 차수에서의 Hankel 특이값(Hanke singular values)를 조사할 수 있고, 이 특이값이 큰 순서대로 상태 변수를 정렬하면 일정 값 이하의 상태 변수는 시스템에 큰 영향을 미치지 않는 값으로 판단할 수 있어 적정한 차수를 선택할 수 있다.

3. 부유체 운동의 상태공간방정식 모델링 예제

3.1 단자유도 부유체 운동방정식

해석 예제로서 식 (2)로 주어지는 단자유도 부유체 운동방정식을 생각한다(Liu et al., 2017; Lu et al., 2022; Taghipour et al., 2008). 이 예제에서 $M = 1, K = 8$ 이고, 부가질량 $A (ω)$ 와 방사감쇠 $B (ω)$ 는 각각 다음과 같은 식으로 주어진다.

(10)

A (ω) = 0.5 + \frac{(μ^{2} + ν^{2} - ω^{2}) (ν + 1)}{(μ^{2} + ν^{2} - ω^{2})^{2} + 4 μ^{2} ω^{2}}

(11)

B (ω) = \frac{2 μ (ν + 1) ω^{2}}{(μ^{2} + ν^{2} - ω^{2})^{2} + 4 μ^{2} ω^{2}}

여기서, 𝜇=0.2, 𝜈=2이고, 식 (10)로부터 $A^{\infty} = 0.5$ 임을 알 수 있다. 식 (10), (11)로 주어진 값을 사용하면 수치적 방법이 아닌 해석해로서 식 (2)의 입력 $f (t)$ , 출력 $x (t)$ 인 목표 전달함수 $H (i ω)$ 를 다음 식 (12)와 같이 구할 수 있다 .

(12)

H (s) = \frac{s^{2} + 0.4 s + 4.04}{1.5 s^{4} + 0.6 s^{3} + 17.06 s^{2} + 3.2 s + 32.32}

여기서, $s = i ω$ 이다.

식 (12)의 목표 전달함수에 대하여 N4SID 알고리즘을 적용하여 상태공간방정식 행렬을 구한 결과는 다음 식 (13), (14), (15), (16)과 같다.

(13)

A_{s} = [\begin{array}{cccc} - 0.2002 & - 3.029 & - 0.6178 & 0.4362 \\ 2.723 & - 0.1092 & - 0.8995 & 0.1053 \\ 0.1376 & 0.6200 & - 0.0547 & 1.655 \\ - 0.2617 & 0.03672 & - 1.402 & - 0.0359 \end{array}]

(14)

B_{s} = [\begin{matrix} - 0.1265 \\ 0.2126 \\ - 0.08759 \\ - 0.08485 \end{matrix}]

(15)

C_{s} = [- 0.747 - 0.4911 - 0.4674 0.366]

(16)

D_{s} = 0

이 행렬을 사용하여 식 (9)의 전달함수를 구하고 이를 식 (12)의 전달함수와 비교한 결과를 Fig. 1에 나타내었다. 그림에서 실선은 목표 전달함수이고 원형표식은 상태공간방정식으로 구한 전달함수이다. 보인 바와 같이 제안하는 방법에 의한 상태공간방정식의 전달함수는 목표 전달함수와 매우 잘 일치하고 있음을 확인할 수 있다. 일반적으로 상수 계수를 갖는 n자유도 운동방정식은 2 $n$ × 1의 상태벡터를 가진 상태공간방정식으로 표현 가능하다. 이는 운동방정식이 시간에 대한 2차 미분을 최고차항으로 가지기 때문이다. 그러나 식 (2)와 같이 주파수 의존성이 있는 동적 계수를 포함하는 경우에는 이를 표현하기 위한 동적 시스템이 상태공간방정식에 포함되어야 하며 결과적으로는 유리함수로 표현되는 전달함수의 최고차항 차수가 상태벡터의 크기를 결정한다. 이 예제의 경우에는 단자유도 시스템이 최종적으로 4 × 1의 상태벡터로 표현되었으며 이는 식 (10), 식 (11)과 같은 주파수 의존성 계수로 인해 4차의 전달함수 식 (12)를 표현하는 상태공간방정식을 구한 것으로 이해할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F1.jpg

Fig. 1.

Transfer function plots of the SDOF system

3.2 바지(barge)의 RAO

해석 예제로서 Fig. 2와 같은 바지선을 고려한다(Pinkster, 1979). 해석에 사용한 바지선의 제원은 Table 1에 나타내었다. 부유체인 바지는 강체로 모델링하며 병진 방향 3개 자유도와 각 축에 대한 회전 자유도 3개의 총 6개 자유도를 갖는다. 이 절에서는 단위 파고 파랑(wave)에 대한 바지선 각 자유도 변위 응답 진폭인 RAO(response amplitude operator)을 구한다. 파고 $η_{0}$ , 주파수 𝜔인 파랑에 의해 부유체에 작용하는 하중은 부유체의 형상 및 입사파의 방향에 따라 달라진다. 일반적으로 선형 포텐셜 이론을 적용하는 경우 이 힘은 입사파에 의한 힘(Froud-Krylov force) $F^{I} (ω)$ 와 산란파에 의한 힘(diffraction force) $F^{D} (ω)$ 의 합 $F^{I + D} (ω) = F^{I} (ω) + F^{D} (ω)$ 으로 나타낼 수 있다. 일반적으로 j번째 자유도의 $R A O_{j}$ 는 주파수 영역에서 다음과 같이 구할 수 있다.

(17)

R A O_{j} = \frac{X_{j} (ω)}{η_{0}} = \sum_{k = 1}^{6} H_{j k} (ω) F_{k}^{I + D} (ω), j = 1, \dots, 6

여기서, $F_{k}^{I + D} (ω)$ 는 k번째 자유도 하중이다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F2.jpg

Fig. 2.

A view of the barge model

Table 1.

Characteristic values of the barge

Size (m)	150 × 50 × 10
Point mass (ton)	75,593.75
I_xx (ton-m²)	30,237,500
I_yy (ton-m²)	114,973,966.368
I_zz (ton-m²)	114,973,966.368

이 예제에서는 상용 해석 소프트웨어인 Ansys AQWA에서 구한 RAO값과 제시한 방법으로 구한 상태공간방정식을 이용해 구한 RAO값을 비교한다.

2.2절의 절차에 따라 먼저 Ansys AQWA를 이용해 제시한 예제의 부가질량 행렬, 감쇠 행렬, 강성 행렬, 질량 행렬을 구한다. 각 행렬은 모두 6 × 6 행렬로 구성된다. 부가질량 행렬과 감쇠 행렬의 일부 원소인 $A_{11} (ω)$ 와 $B_{11} (ω)$ 를 Fig. 3에 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F3.jpg

Fig. 3.

Added mass A₁₁ (𝜔) (upper figure) and radiation damping B₁₁ (𝜔) (lower figure)

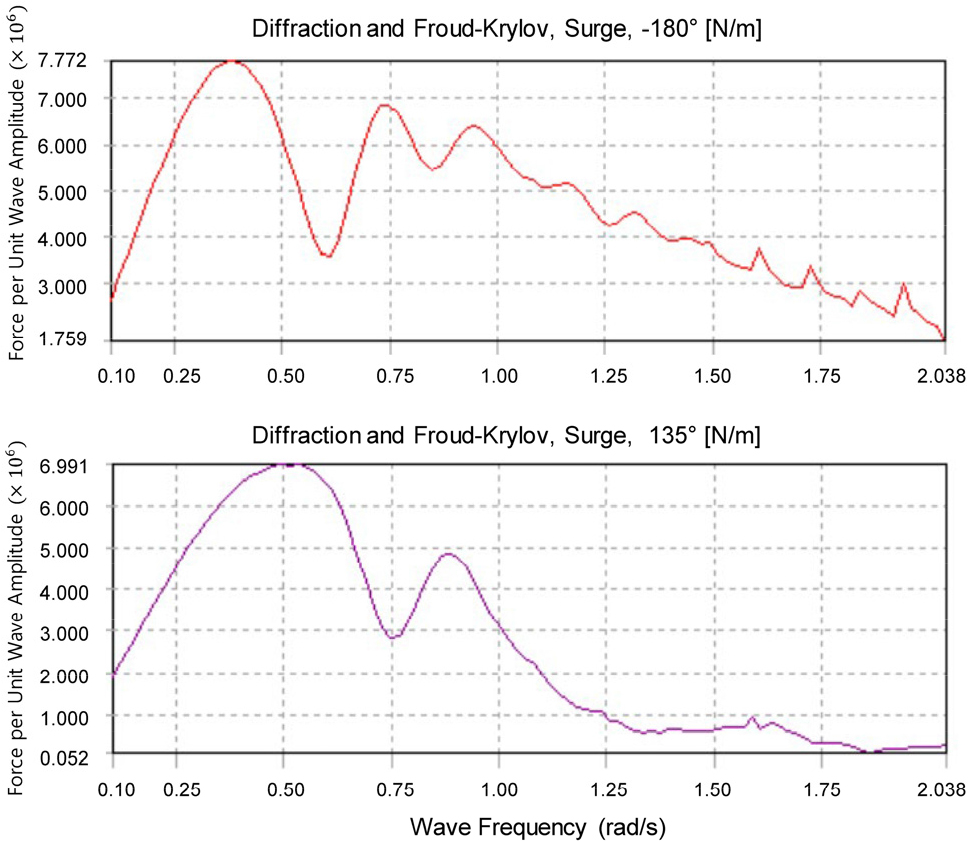
다음으로 식 (8)을 이용하여 목표 전달함수 행렬을 구하고 전달함수 변환 알고리즘을 적용하여 상태공간방정식 행렬을 구하였다. 이 상태공간방정식 행렬로 구한 식 (9)의 전달함수와 목표 전달함수 행렬을 비교한 결과 오차가 작은 최소 크기의 상태공간방정식으로 36 × 36의 시스템 행렬 A_s를 선택하였다. 입사파향에 따라 각 자유도의 RAO를 계산하기 위한 단위 진폭 파에 대한 주파수별 하중 $F_{k}^{I + D} (ω)$ 는 Ansys AQWA를 사용하여 구하였다. Fig. 4에 서지(surge) 방향의 주파수별 파랑 하중 $F_{1}^{I + D} (ω)$ 를 파향 -180도와 135도에 대해 구한 결과를 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F4.jpg

Fig. 4.

Froud-Krylov force and diffraction force $F_{1}^{I + D} (ω)$ with respect to wave frequencies; -180 degree wave direction (upper figure) and 135 degree wave direction (lower figure)

상태공간방정식을 이용해 구한 전달함수행렬과 Ansys AQWA에서 구한 단위 진폭 파랑 하중 $F_{k}^{I + D} (ω)$ 을 이용해 식 (17)에 의해 각 자유도의 RAO를 구하고 이를 Ansys AQWA의 해석 결과와 비교하였다(Fig. 5). 예제 바지선에 대하여 제시한 방법에 의한 상태공간방정식 모델은 Ansys AQWA의 RAO 해석 결과와 전반적으로 잘 일치함을 확인하였다. Fig. 5에 나타낸 0에서 2.5rad/s까지 100개의 주파수에 대한 RMS 오차는 히브(heave) 자유도는 0.042m, 피치(pitch) 자유도는 7.57 × 10^-4rad로 계산되었으며, 제시한 방법과 Ansys AQWA로 구한 RAO가 잘 일치하고 있음을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F5.jpg

Fig. 5.

Motion RAOs calculated by the state-space model and Ansys AQWA; heave RAO (upper figure) and pitch RAO (lower figure)

3.3 계류된 바지선의 시간이력응답 해석

해석 예제로서 Fig. 6와 같이 계류된 바지선을 고려한다. 바지선의 제원은 Table 1과 같으며 계류 효과는 프리스트레싱된 4개의 선형 탄성봉을 수평으로 배치하여 나타내었다. 이 계류 모형은 해저 지반에 계류되는 실제 계류선을 모사한 것은 아니며 수평방향 운동에 대한 강성을 효과적으로 도입하기 위해 고안된 것이다. 시간이력해석은 Orcaflex를 이용하였으며(Orcina, 2023) 계류 모형은 직선 요소인 link 요소를 사용하여 모델링하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F6.jpg

Fig. 6.

A view of the barge model with 4 mooring links

계류선 링크의 변형전 길이는 282.84m이며, 축방향 변형에 대한 강성은 3057.58kN/m, 초기도입 인장력은 8.2936kN으로 하였다.

이 예제의 상태공간방정식 행렬 $A_{s}, B_{s}, C_{s}, D_{s}$ 는 3.2에서 구한 것과 같다. 계류선이 추가되면 6방향 변위에 대하여 탄성 계류력 $f_{m} (t) = - K_{a} y (t)$ 이 외력으로 작용하게 된다. 여기서 $K_{a} \in R^{6 \times 6}$ 는 계류선에 의한 강성행렬이다. 상태공간방정식에서 외력은 $B_{s} f_{m} (t) = - K_{a} C_{s} x (t)$ 로 식 (4)에 더해지므로 다음과 같이 전체 시스템에 대한 상태공간방정식이 구성된다.

(18)

\dot{x} (t) = (A_{s} - B_{s} K_{a} C_{s}) x (t) + B_{s} u (t)

(19)

y (t) = C_{s} x (t)

여기서, 식 (19)의 출력방정식은 3.2에서 구한 $D_{s}$ 가 0행렬임을 고려한 것이다.

계류 장치 도입에 의한 효과를 시간영역에서 살펴보기 위해 외력이 없는 초기조건에 의한 자유 감쇠(free decay) 운동을 해석하였다. Orcaflex를 이용한 해석 결과와 식 (18), (19)의 상태공간방정식 모델의 시간이력 해석결과를 비교하였다(Fig. 7). 비교 결과 제시한 상태공간 방정식 모델의 응답은 Orcaflex의 해석 결과와 잘 일치하였다. Fig. 7에 나타낸 50초까지 시간응답에 대한 RMS 오차는 서지(surge) 변위 0.032m, 히브(heave) 변위 0.190m로 계산되었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F7.jpg

Fig. 7.

Motion time history calculated by the state-space model and Orcaflex; surge (upper figure) and heave (lower figure) displacement

파랑 하중에 의한 변위 응답의 시간이력해석을 위해 1m 단위 진폭 파에 의한 계류된 바지선의 응답 해석을 수행하였다. Fig. 8에 𝜔 = 0.1rad/s 주파수의 파랑 하중에 의한 서지 변위 응답을 나타내었다. 서지 변위 응답은 천이 구간을 지나 약 1000초 이후 정상 상태 구간에 이르는데 이 정상 상태 구간에서의 진폭이 계류된 바지선의 RAO값이 된다. 제시한 상태공간방정식 시간이력으로 구한 RAO값을 Orcaflex로 해석한 시간이력 응답과 비교한 결과 두 해석 결과가 잘 일치하는 것으로 확인되었다(Table 2).

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370202/images/Figure_jcoseik_37_02_02_F8.jpg

Fig. 8.

Surge motion time history for wave force (𝜔 = 0.1rad/s) by the state-space model

Table 2.

Surge RAO obtained from state-space equations and time-history analysis in Orcaflex

Wave frequency 𝜔 (rad/s)	Surge RAO (m)		Relative Error (%)
Wave frequency 𝜔 (rad/s)	State-space model	Orcaflex	Relative Error (%)
0.1	0.5059	0.5068	-0.18
0.198	1.9097	1.9364	-1.38
0.394	1.2782	1.2835	-0.42
0.491	0.5969	0.5729	4.19

4. 결 론

이 논문에서는 파랑 하중을 받는 부유식 구조체의 운동 해석에 있어서 시스템 식별 방법을 이용한 상태공간방정식 모델을 수립하고 해석하는 방법을 제안하였다.

상태공간방정식 모델의 수립 방법으로는 주파수영역에서 하중-변위 입출력 관계에 대한 목표 전달함수를 구하고 시스템 식별 방법인 N4SID와 전달함수 매개변수 최적화 방법을 통해 목표 전달함수에 가장 근접하는 상태공간방정식을 구하는 절차를 제시하였다. 단자유도 수치모델 및 6자유도 바지에 대한 해석 예제를 통해 제시한 방법의 적용성을 보였다. 해석 결과 제시하는 상태공간방정식 모델은 주파수영역 및 시간영역에서 모두 기존의 해석결과와 잘 일치하는 것을 확인할 수 있었다.

제시하는 상태공간방정식 모델에서는 주파수의존성이 있는 부가질량과 방사감쇠가 동적시스템으로 작용하고, 이는 운동방정식의 자유도와 연계되어 결과적으로 상태벡터의 크기가 커지게 된다. 이 연구의 예제에서는 1자유도 운동방적식에 대하여 4개, 6자유도 바지선에 대하여 36개의 상태벡터 성분으로 모델링되었다. 일반적으로 상수인 질량, 감쇠, 강성을 갖는 6자유도 운동방정식은 6개의 변위와 6개의 속도를 포함하는 12개의 성분을 갖는 상태벡터를 사용하여 상태공간방정식을 구축할 수 있음을 고려할 때 제시한 방법에서는 24개의 추가적인 상태벡터가 부가질량 및 방사감쇠의 동적시스템 표현에 사용된 것을 알 수 있다. 그러나 추가적인 상태벡터성분을 포함하여도 전체 상태벡터, 시스템행렬의 크기가 절대적으로 크지 않으므로 계산효율성에 영향을 끼치지는 않는다. 예를 들어 계류된 바지선 예제의 경우 3600초의 동적응답해석에 걸리는 계산시간을 동일한 컴퓨터 시스템에서 살펴보면, Orcaflex를 사용하는 경우 약 9.7초의 계산시간이 소요된 데 반하여 MATLAB에서 상태공간방정식을 이용해 해석하는 경우에는 약 0.25초의 시간이 소요되어 제시하는 방법의 계산시간 효율성이 매우 높음을 확인하였다.

상태공간방정식 모델은 입출력관계에 기반한 모델이므로 부유식 구조체가 다른 시스템과 연계되는 경우에 해석이 용이하다. 3.3절에 나타낸 바와 같이 연결되는 계류 시스템의 강성이 쉽게 고려될 수 있으며, 이는 감쇠의 경우에도 동일하다. 이 연구에서는 고려되지 않았지만 향후 연구에서는 현수선 케이블과 같이 장력과 변위관계가 비선형성인 계류시스템을 상태공간방정식 모델과 연결하여 해석하는 연구에도 효과적으로 활용할 수 있을 것으로 기대된다. 또한 시간이력해석시에 상대적으로 짧은 해석 시간이 소요되므로 많은 해석 횟수가 요구되는 시뮬레이션기반 신뢰성 평가나 설계에 활용하는 향후 연구를 기대할 수 있다.

Acknowledgements

이 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호 RS-2023-00250727 다목적 해상 부유식 인프라 건설기술 개발).

References

ANSYS, Inc. (2023) Ansys, Release 18.1.

Chen, C.T. (1984) Linear System Theory and Design, Saunders College Publishing.

Cho, J.-R., Jeon, S.-H., Jeong, W.-B. (2016) Numerical Analysis of Dynamic Response of Floating Offshore Wind Turbine to the Underwater Explosion using the PML Non-Reflecting Technique, J. Comput. Struct. Eng. Inst. Korea, 29(6), pp.521~527.

10.7734/COSEIK.2016.29.6.521

Cummins, W.E. (1962) The Impulse Response Function and Ship Motions, Schiffstechnik, 9 (1661), pp.101~109.

Duarte, T., Sarmento, A., Alves, M., Jonkman, J. (2013) State-Space Realization of the Wave-Radiation Force within FAST (No.NREL/CP-5000-58099), National Renewable Energy Lab.(NREL), Golden, CO (United States).

10.1115/OMAE2013-10375

Fossen, T.I. (2002) Marine Control Systems-Guidance, Navigation, and Control of Ships, Rigs and Underwater Vehicles, Marine Cybernetics, Trondheim, Norway, Org. Number NO 985 195 005 MVA, www.marinecybernetics.com, ISBN: 82 92356 00 2.

Goupee, A.J., Koo, B.J., Kimball, R.W., Lambrakos, K.F., Dagher, H.J. (2014) Experimental Comparison of Three Floating Wind Turbine Concepts, J. Offshore Mech. & Arct. Eng., 136(2), p.020906.

10.1115/1.4025804

Jordán, M.A., Beltrán-Aguedo, R. (2004) Optimal Identification of Potential-Radiation Hydrodynamics for Moored Floating Structures - a New General approach in State Space, Ocean Eng., 31(14-15), pp.1859~1914.

10.1016/j.oceaneng.2004.01.007

Kashiwagi, M. (2004) Transient Responses of a VLFS during Landing and Take-off of an Airplane, J. Marine Sci. & Technol., 9, pp.14~23.

10.1007/s00773-003-0168-0

Kim, H.S., Park, B., Lee, K. (2022) Parametric Study on Effect of Floating Breakwater for Offshore Photovoltaic System in Waves, J. Comput. Struct. Eng. Inst. Korea, 35(2), pp.109~117.

10.7734/COSEIK.2022.35.2.109

Kim, H.S., Park, B., Sung, H.G., Lee, K. (2021) LMU Design Optimization for the Float-over Installation of Floating Offshore Platforms, J. Comput. Struct. Eng. Inst. Korea, 34(1), pp.43~50.

10.7734/COSEIK.2021.34.1.43

Liu, F., Chen, J., Qin, H. (2017) Frequency Response Estimation of Floating Structures by Representation of Retardation Functions with Complex Exponentials, Mar. Struct., 54, pp.144~166.

10.1016/j.marstruc.2017.04.001

Lu, H., Chang, S., Chen, C., Fan, T., Chen, J. (2022) Replacement of Force-to-Motion Relationship with State-Space Model for Dynamic Response Analysis of Floating Offshore Structures, Appl. Ocean Res., 119, p.102977.

10.1016/j.apor.2021.102977

Lu, H., Fan, T., Zhou, L., Chen, C., Yu, G., Li, X., Hou, F. (2020) A Rapid Response Calculation Method for Symmetrical Floating Structures based on State-Space Model Solving in Hybrid Time-Laplace Domain, Ocean Eng., 203, p.107227.

10.1016/j.oceaneng.2020.107227

Lu, H., Tian, Z., Zhou, L., Liu, F. (2019) An Improved Time-Domain Response Estimation Method for Floating Structures based on Rapid Solution of a State-Space Model, Ocean Eng., 173, pp.628~642.

10.1016/j.oceaneng.2018.12.073

McKelvey, T., Akçay, H., Ljung, L. (1996) Subspace-based Multivariable System Identification from Frequency Response Data, IEEE Trans. Autom. Control, 41(7), pp.960~979.

10.1109/9.508900

Moan, T., Eidem, M.E. (2020) Floating Bridges and Submerged Tunnels in Norway - The History and Future Outlook, Proc. World Conf. Float. Solut., Springer Singapore, pp.81~111.

10.1007/978-981-13-8743-2_5

Orcina (2023) OrcaFlex (Version 11.0), Orcina Ltd.

Pinkster, J.A. (1979) Mean and Low Frequency Wave Drifting Forces on Floating Structures, Ocean Eng., 6(6), pp.593~615.

10.1016/0029-8018(79)90010-6

Schmiechen, M. (1973) On State Space Models and Their Application to Hydromechanic Systems, University of Tokyo, Department of Naval Architecture, Hongo, Bunkyo-Ku, NAUT Report 5002.

Taghipour, R., Perez, T., Moan, T. (2008) Hybrid Frequency-Time Domain Models for Dynamic Response Analysis of Marine Structures, Ocean Eng., 35(7), pp.685~705.

10.1016/j.oceaneng.2007.11.002

The MathWorks Inc. (2022) MATLAB version: 9.13.0 (R2022b), Natick, Massachusetts: The MathWorks Inc.

Van Overschee, P., De Moor, B. (1994) N4SID: Subspace Algorithms for the Identification of Combined Deterministic-Stochastic Systems, Autom., 30(1), pp.75~93.

10.1016/0005-1098(94)90230-5

Wang, K., Er, G.K., Zhu, Z. (2020) 3D Nonlinear Dynamic Analysis of Cable-Moored Offshore Structures, Ocean Eng., 213, p.107759.

10.1016/j.oceaneng.2020.107759

Yoon, J.S., Lee, P.S. (2017) Towards Hydro-Elastoplastic Analysis of Floating Plate Structures, J. Fluids & Struct., 71, pp.164~182.

10.1016/j.jfluidstructs.2017.03.008

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

State-Space Equation Model for Motion Analysis of Floating Structures Using System-Identification Methods

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

Fig. 1.

Transfer function plots of the SDOF system

(17)

Fig. 2.

A view of the barge model

Table 1.

Characteristic values of the barge

Fig. 3.

Added mass A11 (𝜔) (upper figure) and radiation damping B11 (𝜔) (lower figure)

Fig. 4.

Froud-Krylov force and diffraction force F1I+D(ω) with respect to wave frequencies; -180 degree wave direction (upper figure) and 135 degree wave direction (lower figure)

Fig. 5.

Motion RAOs calculated by the state-space model and Ansys AQWA; heave RAO (upper figure) and pitch RAO (lower figure)

Fig. 6.

A view of the barge model with 4 mooring links

(18)

(19)

Fig. 7.

Motion time history calculated by the state-space model and Orcaflex; surge (upper figure) and heave (lower figure) displacement

Fig. 8.

Surge motion time history for wave force (𝜔 = 0.1rad/s) by the state-space model

Table 2.

Surge RAO obtained from state-space equations and time-history analysis in Orcaflex

Acknowledgements

References

Added mass A₁₁ (𝜔) (upper figure) and radiation damping B₁₁ (𝜔) (lower figure)

Froud-Krylov force and diffraction force $F_{1}^{I + D} (ω)$ with respect to wave frequencies; -180 degree wave direction (upper figure) and 135 degree wave direction (lower figure)