1. 서 론
2. 코어부 적용 해석 기법
2.1 유한요소 모델 작성
2.2 재료모델
2.3 경계조건 및 하중조건
3. 해석 결과
3.1 1차 해석 결과
3.2 2차 해석 결과
4. 결 론
1. 서 론
원자력발전소 구조물에 항공기 충돌이 발생하는 경우, 항공기 전체의 충격에 의한 전반거동과 항공기 엔진 속 회전축(Shaft)에 의한 국부손상이 함께 발생하는 것이 일반적이다. 국부손상은 항공기 엔진 속 회전축(Shaft)과 같은 강성 충돌체에 의한 구조물의 국부적인 손상을 의미하며 다음과 같은 세 가지 단계로 진행된다. 1) 미사일의 타겟 관입. 2) 타겟의 전면 박리 및 후면 박리, 3) 관입이 진행됨에 따른 미사일의 타겟 완전관통. 여기서 후면박리란 미사일과 타겟의 충돌 반대면에서 타겟의 일부가 떨어져 파편화 되는 것을 의미하며, 이를 배면파쇄(Scabbing)라고도 한다(NEI07-13, 2011).
배면파쇄가 발생하면 원전 벽체 내부의 시스템 및 사용자의 피해를 초래할 수 있기 때문에 배면파쇄의 발생 유무 및 범위를 파악하는 것은 중요하다. 설계 시 배면파쇄가 발생하지 않는 원전 벽체의 두께는 일반적으로 실험을 통해 예측된 산정식을 사용하여 결정한다. 하지만 대부분의 국부손상 산정식은 콘크리트의 강도, 벽체 두께, 발사체의 충돌속도 및 직경 등의 영향만을 고려하여 평가하고, 철근 및 강재라이너의 영향은 포함되어 있지 않다. 따라서 많은 연구자들이 수치 해석적 방법으로 충격하중을 받는 콘크리트 구조물의 파괴거동을 파악하기 위한 선행 연구를 진행하였으며, 이를 통하여 변형률속도가 적용되는 충돌해석에는 상황에 따른 변수(요소 파괴기준, 콘크리트 재료모델, 요소의 크기 등)에 의해서 해석 결과가 민감하게 변화하는 것이 확인되었다(Choi et al., 2011; Kong et al., 2016; Kwak et al., 2014; Liu et al., 2023; Yun et al., 2013). 또한, 라그랑지안 요소(Lagrangian Element)를 사용한 충돌해석에서 발생하는 요소의 과도한 왜곡으로 인한 Negative Volume 문제를 해결하기 위해 SPH(Smoothed Particle hydrodynamics) 방식을 사용한 충돌 해석 연구가 진행되었다(Kala and Hušek, 2016; Lee et al., 2021; Terranova et al., 2018). SPH 방식은 요소 왜곡 현상을 효과적으로 극복할 수 있지만 과도한 계산 비용이 발생하며, 배면파쇄 영역을 정량적으로 파악하기에는 적절하지 않은 것으로 판단되었다.
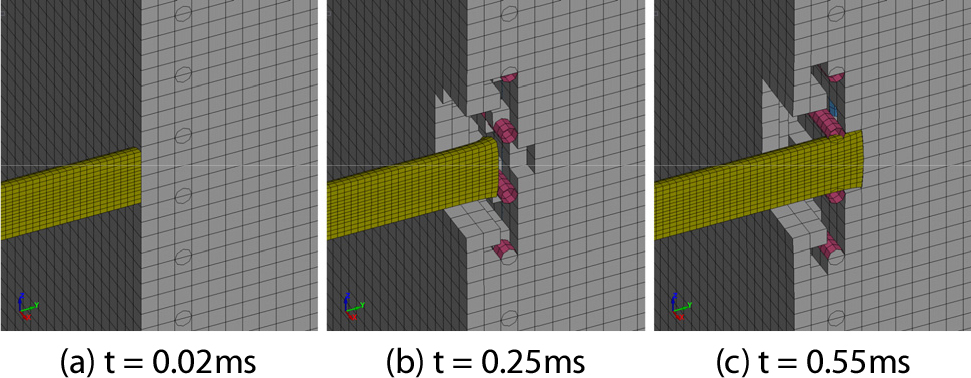
따라서 본 연구에서는 라그랑지안 요소를 사용함과 동시에 Negative Volume 문제를 해결하기 위하여 3차원 범용 유한요소해석 프로그램인 LS-DYNA의 erosion 기능을 사용하여 해석을 진행하였다. erosion은 재료모델이 적용된 요소의 파괴 또는 손상이 발생하였을 경우 해당 요소를 자동으로 삭제하는 기능이다. 이는 충격을 받아 파괴된 부분의 요소를 삭제하여 Negative Volume으로 인한 해석적 문제를 방지하며, 구조물의 손상 정도를 시각화하는 데 유용하다. LS-DYNA의 erosion 기능은 *MAT_ADD_EROSION을 통해 사용자가 설정한 파괴기준 임계치를 기준으로 작동하며, 이는 재료의 특성을 고려한 파괴 거동을 가능케 한다. 그러나 *MAT_ADD_EROSION을 적용하여 파괴 시 최대 주변형률(MXEPS), 파괴 시 최소 주변형률(MNEPS), 파괴 시 전단변형률(EPSSH)을 변수로 충격하중을 받는 철근 콘크리트 벽체의 파괴 거동에 대한 매개변수 연구를 진행해 본 결과, 초기 충돌이 발생하는 매우 짧은 시간 동안 주요 타격부 주위의 압축력을 받는 요소가 대량으로 삭제되었다(Fig. 1(b)). Fig. 1에 충돌 직후 짧은 시간 동안(0.02ms~0.55ms)의 파괴 형상을 나타내었으며, 발사체가 Fig. 1(a) 이후 Fig. 1(c)의 위치에 도달할 때까지 요소와의 접촉이 발생하지 않음을 확인할 수 있다. 이 문제는 짧은 시간 동안 큰 변형을 동반하는 유한요소 해석에서 주로 발생한다. erosion이 적용된 유한요소 해석에서는 1 Timestep 동안 파괴기준을 충족한 모든 요소가 삭제된다. 따라서 Timestep의 크기가 삭제되는 요소의 양에 영향을 미치며, 해석상 과도하게 많은 요소의 삭제는 현실의 파쇄과정과 다르게 연속적인 충돌을 발생하기 어렵게 만든다. 또한 실제 실험에서는 충격으로 인해 파쇄된 콘크리트의 파편이 격자 형태의 철근망 내부에 잔류하게 되어 발사체의 운동에 대한 추가 저항을 유발한다(Yu et al., 2020). 하지만 erosion 기능을 사용한 수치해석에서는 철근망에 의해 내부에 포집되어야 할 콘크리트 파편들이 파괴기준에 도달하여 삭제되었고, 이로 인하여 발사체의 운동에 연속적으로 저항할 수 없는 문제가 발생하였다. 따라서 발사체의 잔류속도가 실제 실험보다 높게 나타났고, 발사체의 운동에너지를 벽체 전체로 충분히 전달할 수 없어 실제 실험에서의 배면파쇄 영역보다 작은 배면파쇄 영역이 나타났다.
이를 해결하기 위해 충돌 위치와 근접한 중심부 콘크리트 영역에 요소 삭제 기능을 적용하지 않는 모델링 기법을 제안한다. 이 기법은 발사체와 벽체의 충돌 위치를 중심으로 일정 영역의 콘크리트를 따로 구분하고, 이 부분을 제외한 콘크리트 요소에만 요소 삭제 기능을 적용하여 수치해석을 진행하는 모델링 기법이다. 해당 모델링 기법은 인장과 전단 변형에 의해 강성을 잃어버린 요소가 삭제되지 않고 각각의 자리에 남아 있음으로써 발사체에 의한 지속적인 압축력에 저항할 수 있다. 해당 기법의 검증을 위하여 요소 삭제가 발생하지 않는 영역(이하 코어부)의 범위와 해당 범위를 제외한 나머지 콘크리트 부분에 적용되는 요소 삭제 기준인 인장 변형률 값을 변수로 해석을 진행하였고, 발사체의 잔류속도와 벽체의 배면파쇄 영역을 실험 결과와 비교하였다.
2. 코어부 적용 해석 기법
본 연구는 발사체가 벽체에 충돌하는 주요 타격부 및 관통부의 요소가 삭제됨에 따라 해당 위치에서 파괴 이후의 압축 저항 능력을 상실하여 실제와 같은 충돌에너지의 전달을 모사하지 못하는 문제를 해결하고자 하였다. 제안한 코어부의 적절성을 확인하기 위해 1차 해석과 2차 해석으로 나누어 해석하였다. 1차 해석에서는 제안된 기법을 RC 벽체 충돌실험결과와 비교하여 배면파쇄를 더 잘 모사할 수 있는 코어부의 범위와 코어부를 제외한 부분의 요소 삭제 기준값을 결정하였다. 2차 해석에서는 1차 해석에서 결정된 변수의 값을 다른 실험 케이스에 적용하여 해당 수치가 배면파쇄를 적절히 모사할 수 있는지 검증하였다.
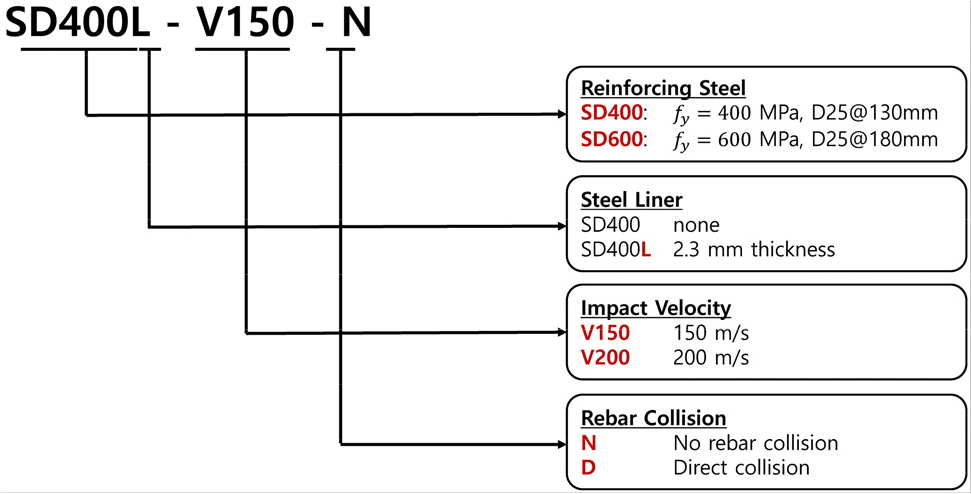
본 연구는 2023년도에 수행된 원전 벽체에 대한 중속 충돌실험(Ye, 2023)의 실험체를 수치해석의 대상으로 삼았다. 해당 실험에서는 철근의 간격, 강재라이너의 적용 여부, 충돌속도 및 충돌조건의 4가지 변수에 대하여 총 10 케이스의 실험을 수행하였으며, 본 연구에서는 그 중 5 케이스를 선택하여 수치해석을 수행하였다. 선택한 실험 케이스와 실험 결과 및 분류기준을 Table 1과 Table 2 및 Fig. 2에 나타내었다.
Table 1.
Test plan (Ye, 2023)
Table 2.
Test results (Ye, 2023)
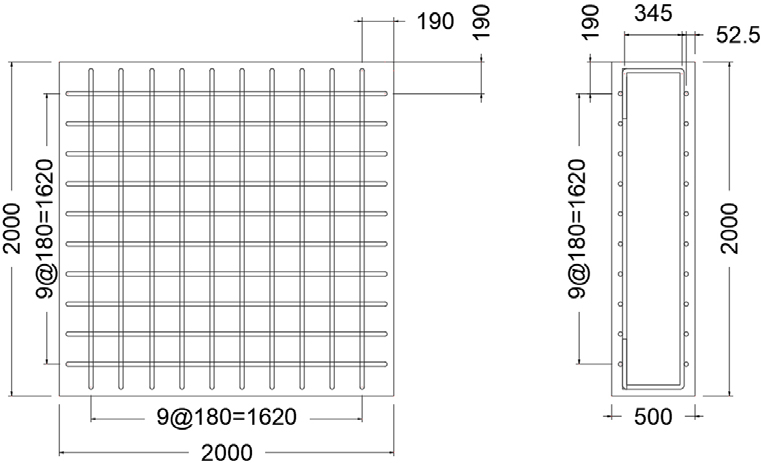
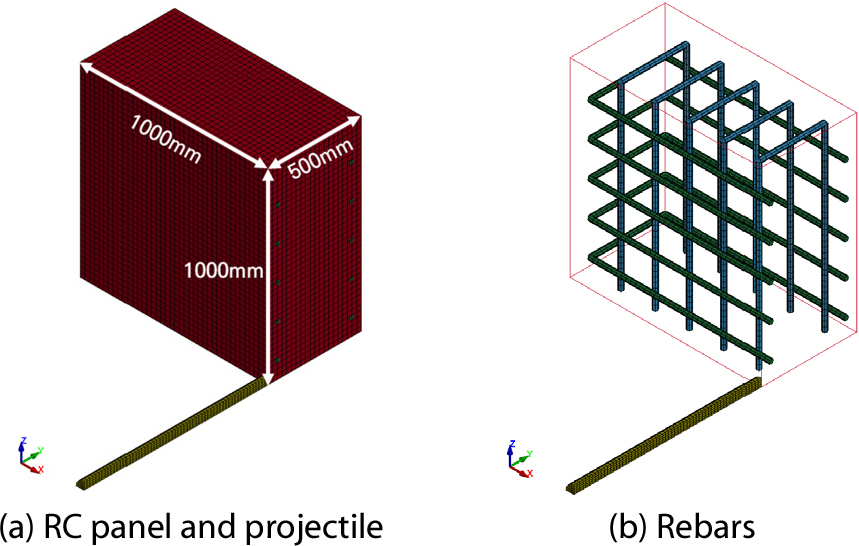
1차 해석의 대상으로는 강재라이너가 부착되지 않고 잔류속도와 배면파쇄 영역이 모두 측정되어 비교에 용이한 SD600-V200-N 케이스의 실험체를 선택하였다. 2차 해석에는 배면파쇄 영역이 나타난 모든 케이스(SD400_V200_N, SD600_V150_N, SD600_V200_N, SD400_V200_D, SD600_V200_D)에 대한 해석을 수행하였다. 1차 해석에 사용된 실험체(SD600_V200_N)의 발사체 및 벽체의 형상 및 치수는 Fig. 3, Fig. 4와 같다.
2.1 유한요소 모델 작성
1차 해석은 코어부의 범위(3N, 4N)와 코어부를 제외한 콘크리트에 적용된 요소 삭제 기준인 최대 인장변형률(MXEPS) 값을 기준으로 구분하였으며, 코어부를 적용하지 않은 모델(이하 Initial 모델)도 함께 해석하여 비교하였다. 요소 삭제 기준은 *MAT_ADD_EROSION을 적용한 사전 연구에서 배면파쇄에 가장 큰 영향을 미치는 것으로 확인된 최대 인장변형률을 중심으로 설정하였다. 이를 Table 3에 48개의 케이스로 나타내었다. 본 해석의 경우 매우 짧은 시간 동안 발생하는 충돌에 대한 해석이므로 자중을 고려하지 않았다. 또한 발사체가 철근 콘크리트 벽체의 정중앙을 타격한다는 가정하에 대칭 조건을 부여하여 1/4 모델로 제작하였다.
Table 3.
Cases of 1st analysis
콘크리트 및 발사체는 8절점 solid 요소를 사용하였고 1/4 모델로 제작된 콘크리트 벽체의 너비와 높이는 Fig. 5(a)와 같다. 콘크리트 벽체의 요소 크기는 한 변이 25mm인 정육면체로 구성되었으며, 발사체가 관통하는 방향으로 20개의 요소층으로 이루어졌다. 1/4 모델로 제작된 발사체는 직경 85mm, 길이 980mm의 원기둥을 4 분할하여 모델링 되었다. 발사체를 구성하는 solid 요소 하나의 크기는 한 변당 약 7mm~16mm 수준의 육면체로 구성되었다. 요소의 크기가 해석의 결과에 미치는 영향을 고려하여 콘크리트 벽체와 발사체에 사용된 요소의 크기를 변수로 파라미터 스터디를 수행하였으며, 그 결과를 바탕으로 요소의 크기를 결정하였다.
철근은 2절점 beam 요소로 수직 철근과 수평 철근 모두 D25 철근이 사용되었으며, beam 요소의 크기는 22.5mm로 모델링 하였다. 콘크리트 벽체와 철근의 결합은 Yang 등(2021)의 연구에서도 적용된 바 있는 *CONSTRAINED_BEAM_IN_SOLID(이하 CBIS)를 사용하여 모사하였다.
2차 해석의 경우 1/4 모델과 Full 모델로 나누어 진행되었으며, Full 모델에 철근의 결속을 추가한 Spotweld 모델도 추가로 진행하였다. 이를 Table 4에 나타내었다. 2차 해석의 콘크리트 모델은 1차 해석의 모델과 동일한 요소 크기로 작성되었으며, Full 모델은 너비와 높이가 2,000mm, 두께는 500mm인 콘크리트 벽체로 작성되었다. 발사체 또한 1차 해석과 동일한 모델로 작성되었으며 Full 모델로 작성된 해석 케이스의 경우, 분할하지 않은 원기둥 형태로 작성하였다. 철근은 2절점 beam 요소로 SD400, SD600 각각의 철근 간격을 고려하여 요소 하나당 21.5~22.5mm의 길이로 모델링 되었다. 콘크리트와 철근은 1차 해석과 동일하게 CBIS를 사용하여 결합하였다. 2차 해석의 경우 철근의 결속을 고려한 케이스를 추가하여 수평 철근과 수직 철근의 결속이 콘크리트의 파쇄에 미치는 영향을 확인하였다. Table 4에 Spotweld로 분류된 케이스는 *CONSTRAINED_SPOTWELD를 사용하여 철근의 결속을 모사한 해석 모델을 의미하며 철근 결속의 파단은 고려하지 않았다.
Table 4.
Cases of 2nd analysis
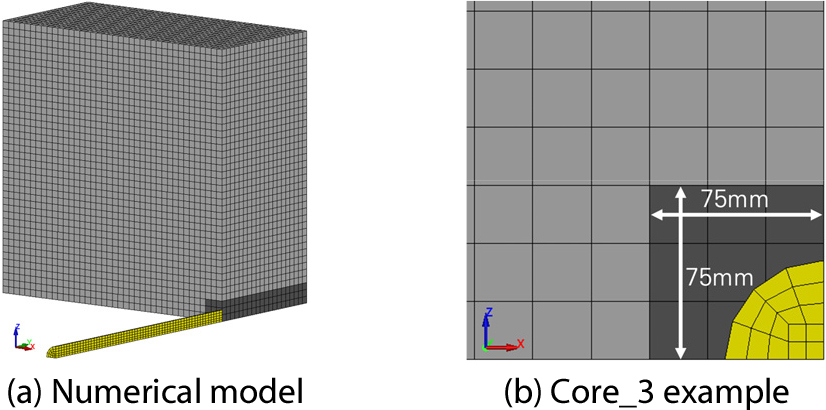
요소 삭제 기능이 적용되지 않는 코어부에는 *CONTROL_TIMESTEP의 Negative Volume 발생 시 요소를 삭제시키는 기능만을 사용하여 해석의 진행을 위한 최소한의 요소 삭제만을 허용하였다. 발사체와 벽체가 충돌하는 점을 기준으로 발사체의 진행 방향에 수직인 두 방향(X축 및 Z축 방향)으로 N(N= 1,2,3 ...)개의 요소, 발사체의 진행 방향(Y축 방향)으로 전 두께에 해당하는 직육면체 영역을 Core_N (N= 1,2,3 ...)라고 정의한다. 예를 들어 Fig. 6의 Core_3은 발사체와 벽체가 충돌하는 지점(대칭 조건의 중심)을 기준으로 X와 Z축 방향으로 각각 75mm(= 25mm × 3)만큼, Y축 방향(관통 방향)으로 500mm만큼의 범위에 있는 모든 요소로 이루어진 직육면체 영역에 요소 삭제 기능을 적용하지 않은 모델이다.
2.2 재료모델
2.2.1 콘크리트
콘크리트의 비선형 재료거동은 LS-DYNA의 Winfrith 모델, CSCM(Continuous Surface Cap Model) 모델 Concrete Damage Rel.3 모델 등을 사용하여 모사할 수 있다. 본 연구에서는 Chung 등(2015)의 연구결과를 참고하여 관통, 관입 및 배면파쇄 영역을 효과적으로 모사할 수 있는 콘크리트의 재료모델로 *MAT_CSCM_CONCRETE를 사용하였다(Murray, 2007). 이 모델은 콘크리트의 비선형적 거동과 변형률속도 효과를 고려할 수 있어 충돌 및 폭발 해석을 수행하는 많은 연구자들이 사용한다. 본 해석에서 사용된 콘크리트의 압축강도는 Ye(2023)의 일축 압축강도 시험 결과를 기반으로 49.8MPa을 입력하였다.
2.2.2 철근 및 발사체
철근과 발사체의 재료모델은 모두 *MAT_PLASTIC_KINEMATIC을 사용하였으며, 철근은 SD400과 SD600의 두 가지 종류가 사용되었다. 수직 철근과 수평 철근 모두 지름은 25mm이다. 철근과 발사체의 재료실험에서 구해진 응력-변형률 곡선을 통해 탄성계수와 ETAN 값을 도출하였으며 BI-LINER 형태로 입력하였다. 철근과 발사체의 변형률속도 효과를 고려하기 위해서 Cowper-Symonds 모델을 사용하였다. Cowper-Symonds 모델에서 사용되는 재료상수 C와p는 식 (1)과 식 (2)를 통해 계산하여 입력하였다(Lee and Kim, 2007).
Table 5에 각 재료모델에서 사용한 입력값을 나타내었다.
Table 5.
Material properties
| Material properties | Rebar | Projectile | |
| SD400 | SD600 | ||
| Modulus of Elasticity (GPa) | 197.0 | 196.0 | 186.6 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 |
| Yield Stress (MPa) | 433.0 | 648.0 | 451.0 |
| Elongation | 0.20 | 0.14 | - |
2.3 경계조건 및 하중조건
1/4 모델의 콘크리트 벽체, 발사체 및 철근 절단면에는 각각 대칭조건을 부여하였고, 1/4 모델과 전체 모델의 콘크리트 벽체 끝단에는 지점조건을 주어 모든 자유도를 구속하였다. 발사체와 벽체의 접촉조건은 *CONTACT_ERODING_SURFACE_TO_SURFACE(이하 ESTS)을 사용하였고, 발사체와 철근의 접촉조건은 *CONTACT_AUTOMATIC_NODE_TO_SURFACE(이하 NSTS)를 사용하였다.
발사체의 초기 속력을 적용하기 위해서 *INITIAL_VELOCITY_GENERATION 명령어를 사용하였으며, 실험 조건에 따라 150m/s 와 200m/s의 두 가지 속력으로 적용하였다. 본 해석의 경우 높은 속도의 충돌이 발생하는 해석이므로, 급격한 요소의 변형이 발생할 수 있어 외연적 동적해석 기법(Explicit dynamic analysis)을 사용하여 해석을 진행하였다.
3. 해석 결과
3.1 1차 해석 결과
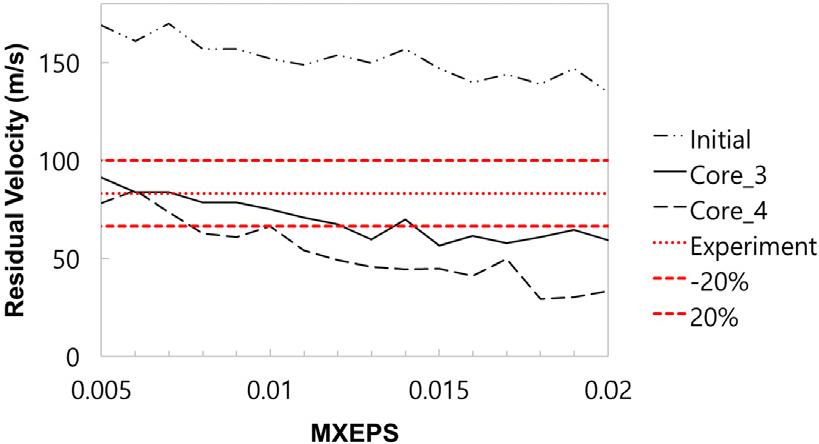
Fig. 7는 SD600-V200-N 모델에 인장변형률 파괴기준을 0.005부터 0.02까지 변화시켜가며 발사체의 잔류속도를 비교한 결과이다. 코어부를 적용하지 않은 Initial 모델은 잔류속도의 감소 폭이 매우 작아 실험결과의 약 2배 수준으로 높은 잔류속도를 나타내었다. Core_3 모델은 MXEPS 0.050~0.130 구간에서 실험 잔류속도에 대한 오차범위 ±20% 이내의 결과가 나타났으며, Core_4 모델은 MXEPS 0.070 이하인 구간에서 실험 잔류속도에 대한 오차범위 ±20% 이내의 결과가 나타났다. Initial 모델과 Core 모델의 잔류속도 차이를 통해 제안된 기법이 발사체의 운동을 실제와 근접하게 감속시킬 수 있음을 확인하였으며, 코어부 영역의 크기에 따라 감속의 정도가 다르게 나타남을 확인하였다.
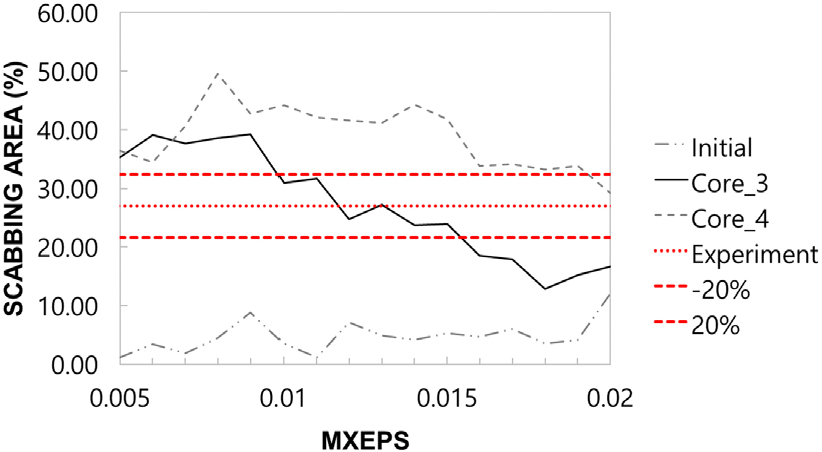
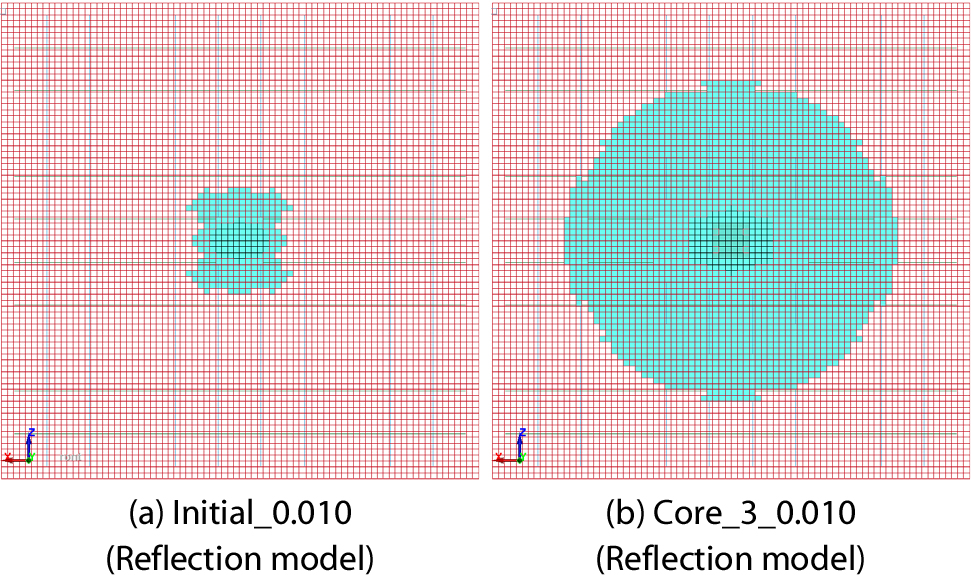
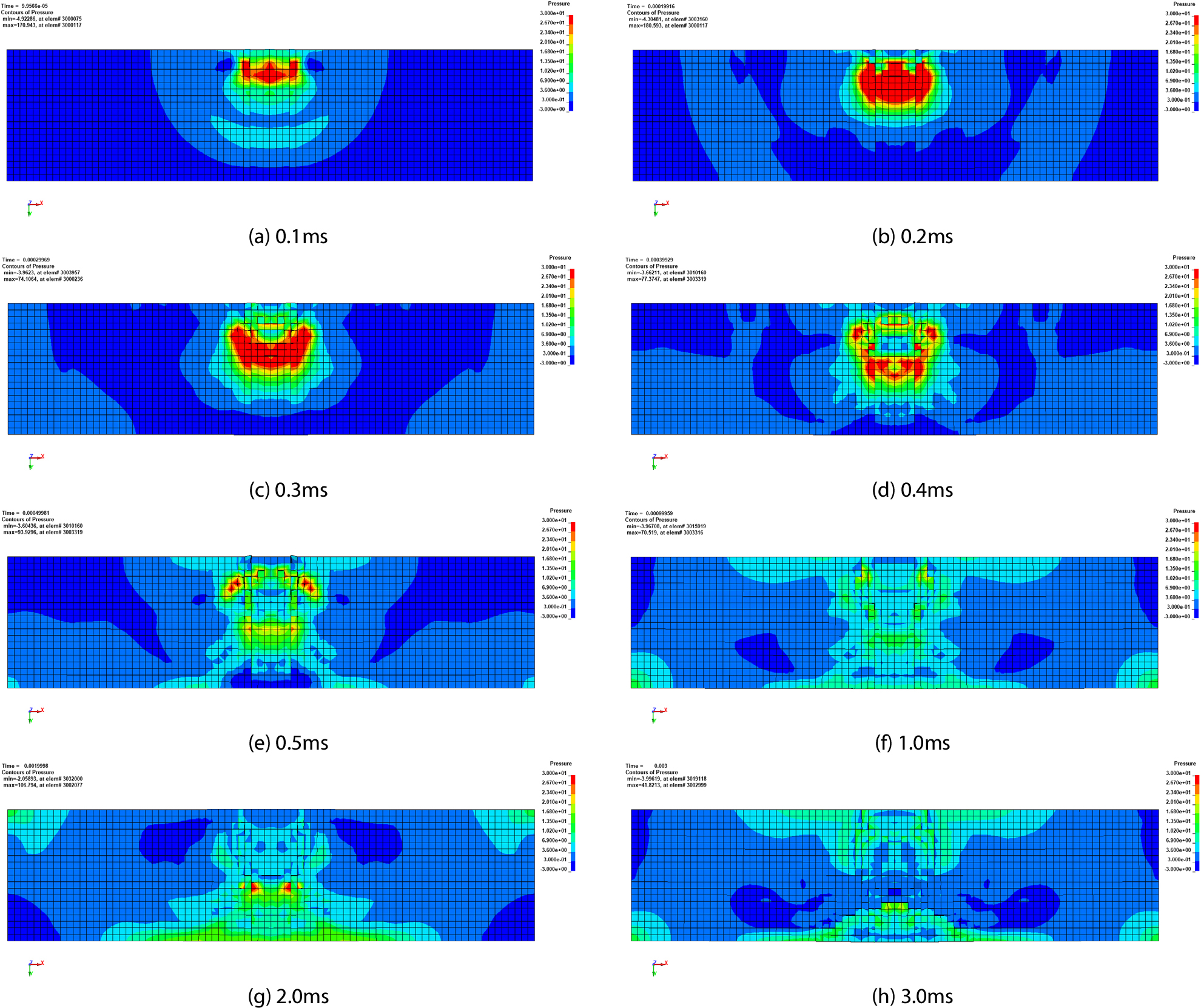
Fig. 8은 인장변형률 파괴기준을 변화시켜가며 RC 벽체의 배면파쇄 영역을 비교한 결과이다. 배면파쇄 영역은 후면 철근이 노출된 콘크리트 부분의 면적으로 측정하였다. 측정된 배면파쇄 영역의 예시를 Fig. 9(b)에 나타내었다. Core_3 모델은 MXEPS 값이 0.011 이하인 구간에서 측정된 배면파쇄 영역 이상의 결과를 나타내었으며, Core_4 모델은 모든 구간에서 측정된 배면파쇄 영역 이상의 결과가 나타났다. Initial 모델은 모든 구간에서 측정된 배면파쇄 영역에 미치지 못하였다. 실험에서 측정된 배면파쇄 영역과 잔류속도에 근접한 결과를 도출한 Core_3_0.010 모델의 배면파쇄 면적과 요소 내 압력 전파 양상을 Fig. 10(b) 및 Fig. 11에 나타내었다. Fig. 11에 나타난 바와 같이 충격에 의해 발생된 응력파가 시편 내에서 전파되는 현상이 적절히 모사되었으며, 이로 인해 Fig. 10(b)와 같이 넓은 범위에서 배면파쇄가 발생하였다. 동일한 MXEPS 값으로 수행된 Initial_0.010 모델은 Fig. 10(a)에 나타낸 바와 같이 관통부 주변의 작은 영역에서만 배면파쇄가 발생하였다.
이러한 결과는 코어부의 요소가 삭제되지 않고 발사체의 충돌에너지를 연속적으로 전달해 주는 것이 실제 RC 벽체의 파괴 거동 모사에 효과적임을 의미한다. 따라서 코어부 사용 기법이 중속 충돌에 대한 철근 콘크리트의 파괴 거동을 효과적으로 모사하는 데 중요한 역할을 한다고 판단하였으며, 코어부가 다른 충돌 조건(철근 간격, 충돌 속도, 철근 충돌 여부)에서도 적용 가능한지 검토하기 위하여 Core_3과 MXEPS 0.010을 기준값으로 2차 해석을 진행하였다.
3.2 2차 해석 결과
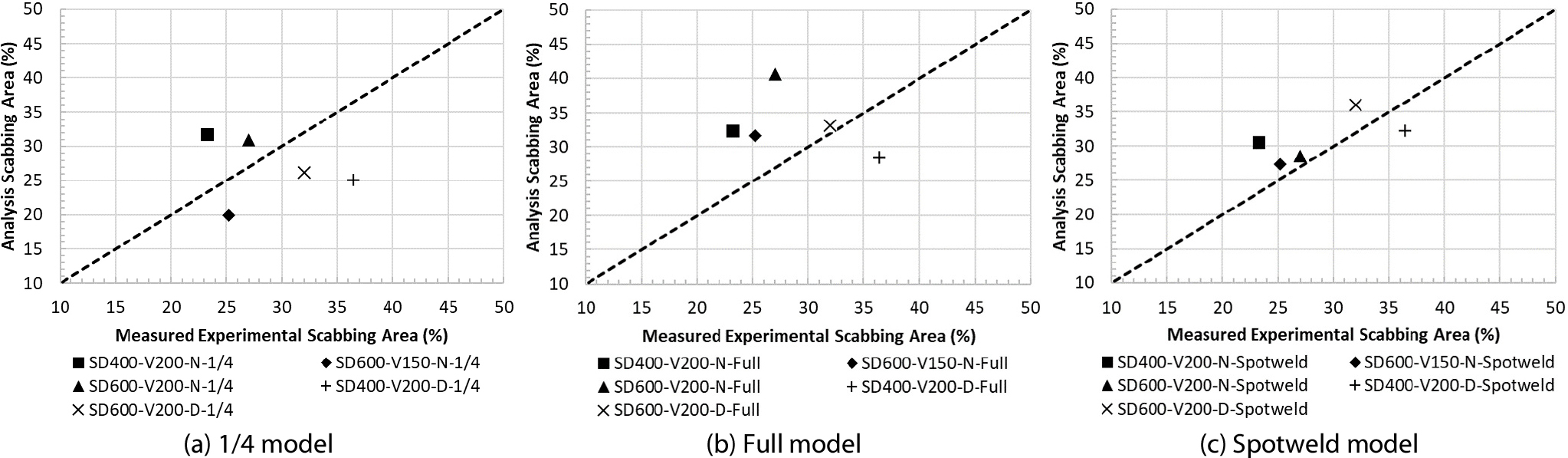
2차 해석의 결과를 Table 6, 실험 배면파쇄 영역과 해석 배면파쇄 영역에 대한 산점도를 Fig. 12에 나타내었으며, 식 (3)을 통해 평균 절대 비율 오차(Mean Absolute Percentage Error)를 구하였다.
Table 6.
Experimental result of core test
1/4 모델의 해석 결과, 1차 해석의 대상인 SD600-V200-N-1/4을 제외한 4개의 케이스(SD400-V200-N-1/4, SD600-V150-N-1/4, SD400-V200-D-1/4, SD600-V200-D-1/4)에서 모두 20% 이상의 높은 오차율이 나타났으며, 1/4 모델 총 5 케이스에 대한 평균 오차율은 24.13%로 나타났다. 특히 철근과 직접 충돌하는 경우인 SD400-V200-D-1/4과 SD600-V200-D-1/4 케이스에서는 실험 배면파쇄 영역보다 각각 11.36%, 5.75% 작은 배면파쇄 영역이 해석에서 나타났다. 발사체가 철근과 직접 충돌하는 경우에는 대칭조건을 적용한 1/4 모델이 실험 결과를 적절히 모사하지 못할 수 있다고 판단되어 대칭조건을 사용하지 않은 Full 모델의 해석을 추가로 진행하였다.
Full 모델의 해석 결과, 평균 오차율은 28.01%로 나타났으며, SD400-V200-D-Full을 제외한 모든 케이스에서 실험 결과를 초과하는 배면파쇄 영역이 해석에서 나타났다. 또한 배면파쇄 영역은 모든 케이스에서 1/4 모델보다 증가하였다. 1/4 모델보다 Full 모델에서 배면파쇄 영역이 더 크게 나타난 것은 대칭 조건을 적용하면 배면파쇄 영역이 더 작게 평가됨을 의미한다. 실제 실험에서는 발사체가 직진 방향뿐만 아니라 6 자유도 방향으로도 운동하며 관입 및 관통이 진행된다. 하지만 대칭 조건을 사용할 경우 발사체의 x축 및 z축 방향 운동이 구속되어 직진 방향으로의 충돌 에너지가 과대 평가되는 결과가 나타난 것으로 판단된다.
수직 철근과 수평 철근의 결속을 모사한 Spotweld 모델의 해석 결과, 평균 오차율은 13.93%로 1/4 모델과 Full 모델의 평균 오차율 24.13%, 28.01% 보다 현저히 낮은 값을 보였다. 발사체가 철근과 직접 충돌하지 않는 SD400-V200-N-Spotweld, SD600-V150-N-Spotweld, SD600-V200-N-Spotweld 케이스에서는 Full모델보다 1.80%, 4.28%, 12.01% 작은 배면파쇄 영역이 나타났으며, 발사체가 철근과 직접 충돌하는 SD400-V200-D-Spotweld와 SD600-V200-D-Spotweld 케이스에서는 Full 모델보다 각각 3.78%, 2.94% 더 큰 배면파쇄 영역이 나타났다. 이러한 결과는 철근의 결속 조건을 해석 모델에 반영하는 것이 발사체와 철근 사이의 직접 충돌 여부에 따라 배면파쇄 영역에 다르게 영향을 미침을 의미한다. 또한 전반적으로 실험 결과에 대한 오차율이 감소하므로 철근의 결속 조건을 반영하는 것이 철근 콘크리트 벽체의 충격 저항 성능을 모사하는 데 효과적임을 의미한다.
4. 결 론
본 연구에서는 중속 충돌이 발생하는 철근 콘크리트 벽체의 배면파쇄를 모사하는 과정에서 요소 삭제 기능이 연속적인 하중을 전달하는 과정에 영향을 미치고, 배면파쇄 영역이 과소평가되는 문제를 발생시킨다고 파악하였다. 이러한 문제를 해결하기 위해 충돌 위치와 근접한 중심부 콘크리트 영역에 요소 삭제 기능을 적용하지 않는 모델링 기법을 제안하였다. 본 기법을 적용한 해석의 결과, 연속적인 하중의 전달이 철근 콘크리트 벽체의 파괴 거동을 모사하는 데 중요한 요인임을 확인하였다. 본 연구를 통하여 얻은 결론은 다음과 같다.
1) 1차 해석 결과, 코어부를 적용하지 않은 Initial 모델은 잔류속도가 실험 결과보다 약 2배 높았으나, Core_3 모델과 Core_4 모델은 각각 MXEPS 0.050~0.130 구간과 0.070 이하 구간에서 실험 잔류속도에 대한 오차범위 ±20% 이내의 해석 결과를 얻을 수 있었다. 이는 해당 기법이 발사체의 운동을 실제와 근접하게 감속시킬 수 있음을 의미한다. 또한 Core_3 모델과 Core_4 모델은 측정된 배면파쇄 영역보다 큰 결과를 나타냈고, Initial 모델은 배면파쇄 영역을 지나치게 과소평가하는 것으로 나타났다. 이는 코어부를 적용함으로써 발사체의 충돌에너지를 연속적으로 전달해 실제 RC 벽체의 파괴 거동을 효과적으로 모사할 수 있음을 의미한다. 다른 충돌 조건에서도 적용 가능한지를 검토하기 위해 Core_3과 MXEPS 0.010을 기준으로 2차 해석을 진행하였다.
2) 2차 해석 결과, 제안된 기준을 통해 해석한 1/4 모델의 평균 오차율은 24.13%로 나타났으며, 철근과 직접 충돌하는 케이스는 측정된 실험 결과보다 작은 배면파쇄 영역이 나타났다. 해당 결과를 통해 대칭 조건이 RC 벽체의 충돌 저항 성능에 영향을 미칠 수 있다고 판단하였으며, Full 모델의 해석을 진행하였다. Full 모델의 평균 오차율은 28.01%이며, 모든 케이스에서 1/4 모델보다 증가한 배면파쇄 영역이 나타났다. 이러한 결과를 통해 대칭 조건을 사용하였을 때 배면파쇄 영역이 더 작게 평가됨을 확인하였다.
3) 철근의 결속을 모사한 Spotweld 모델의 해석결과, 평균 오차율은 13.93%로 1/4 모델과 Full 모델과 비교하였을 때 현저히 낮은 값을 나타냈다. Full 모델과 비교하였을 때, 철근과 발사체가 접촉하는 케이스에서는 배면파쇄 영역이 증가하였고, 접촉하지 않는 케이스에서는 배면파쇄 영역이 감소하였다. 이는 철근의 결속을 모사하는 것이 발사체와 철근 간의 접촉 여부에 따라 배면파쇄 면적에 다른 영향을 미침을 의미하며, 전반적인 오차율이 감소하는 것으로 보아 철근의 결속을 모사하는 것이 RC 벽체의 파괴 거동을 모사하는 데 효과적인 것으로 나타났다.