Effect of Pulse-like Ground Motions with Various Pulse Indicators on the Seismic Fragility of Bridges

Sina Kong; Yeeun Kim; Sinith Kung; Jiho Moon; Jong-Keol Song

doi:10.7734/COSEIK.2024.37.5.327

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 October 2024. 327-335
https://doi.org/10.7734/COSEIK.2024.37.5.327

Effect of Pulse-like Ground Motions with Various Pulse Indicators on the Seismic Fragility of Bridges

교량의 지진취약도에 대한 다양한 펄스지표를 가지는 펄스형 지진의 영향

Sina Kong¹

Yeeun Kim²

Sinith Kung²

Jiho Moon³

Jong-Keol Song⁴^*

꽁 씨나¹

김 예은²

꽁 씨닛²

문 지호³

송 종걸⁴^*

¹Graduate Student, Department of Civil Engineering, Kangwon National University, 24341, Korea

²Graduate Student, Department of Civil Engineering, Kangwon National University, 24341, Korea

³Assistant Professor, Department of Civil Engineering, Kangwon National University, 24341, Korea

⁴Professor, Department of Civil Engineering, Kangwon National University, 24341, Korea

¹강원대학교 건축･토목･환경공학부 박사과정

²강원대학교 건축･토목･환경공학부 석사과정

³강원대학교 건축･토목･환경공학부 부교수

⁴강원대학교 건축･토목･환경공학부 교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Pulse-like ground motions cause significant damage to structures. The presence and intensity of velocity pulses in seismic acceleration records can be evaluated by calculating the pulse indicator (PI). The PI values for the same earthquake differ by approximately 20 depending on the change in the incidence angle. In this study, PIs were evaluated according to changes in the incidence direction of seismic waves, and the seismic response and seismic fragility of bridge structures were evaluated using a pair of 40 seismic waves according to five PI percentiles (0, 25, 50, 75, and 100). The results show that as the PI of ground motion increases, the acceleration response spectrum also tends to increase proportionally. It was observed that the seismic response of the bridge increased with the PI of the seismic wave, which increased the seismic fragility. For seismic acceleration records with the maximum PI, the seismic fragility of piers tended to increase by approximately 25-27% on average compared to the case of seismic acceleration records with the minimum PI.

Keywords

velocity pulse

pulse indicator

incidence direction

bridge

seismic fragility++

펄스형 지진은 구조물에 손상을 크게 유발한다. 펄스지표의 계산에 의해 지진 가속도 기록에 대한 속도펄스의 존재 유무와 그 세기의 평가가 가능하다. 입사각의 변화에 따른 펄스지표 값이 동일 지진에 대하여 대략 20 정도 차이가 난다. 지진파의 입사각의 변화에 따른 펄스지표를 평가하고, 5가지 펄스지표 백분위수(0, 25, 50, 75, 100 백분위수)에 따른 한 쌍의 40개 지진파를 사용하여 교량구조물의 지진응답과 지진취약도 평가를 수행하였다. 펄스지표가 큰 지진파일수록 가속도응답스펙트럼 또한 이에 비례하여 증가하는 경향을 나타냄을 알 수 있다. 지진파의 펄스지표(PI)가 증가할수록 교량의 지진응답을 증가시켜 지진취약도를 증가시키는 경향을 나타냄을 알 수 있다. 최대 펄스지표의 지진파의 경우가 최소 펄스지표의 지진파의 경우에 비하여 교각의 지진취약도를 대략 평균적으로 25~27% 정도 증가시키는 경향이 있다.

키워드

속도펄스

펄스지표

입사 방향성

교량

지진취약도

MAIN

1. 서 론
2. 지진파의 입사방향성을 고려한 교량의 지진해석
2.1 교량의 구조해석 모델링
2.2 입력 지진
2.3 입사방향에 따른 펄스지표(PI)의 분석
3. 지진파의 펄스지표에 따른 교량의 지진취약도 영향
3.1 지진취약도 해석기법
3.2 펄스지표에 따른 교각의 지진취약도 평가
4. 결 론

1. 서 론

근단층 펄스형 지반운동은 진앙이 약 10km 이내인 지역에서 관측되는 지반운동으로 장주기의 속도펄스 성분을 가진다. 펄스형 지반운동은 단층의 파열 진행 방향과 전단파의 진행 방향이 일치할 때 발생하며 두 파가 유사한 속도를 가질 경우 서로 간섭하여 큰 펄스 형태의 속도파를 생성한다. 펄스형 지반운동은 강진 지역에서 주로 관측되며 구조물에 큰 손상을 유발하는 특성을 가진다. 교량해석에서 펄스형 지진은 큰 지진응답을 유발하는 특성이 있으며, 지진파가 펄스형인지 비펄스형인지를 분류하기 위해서는 펄스지표(Pulse Indicator, PI)를 사용하여 평가할 수 있다.

많은 연구자들은 펄스형 지반운동에 대하여 속도펄스 유무의 판정을 위한 다양한 웨이블릿(wavelet)을 이용한 방법들을 제시하였다. Mavroeidis와 Papageorgiou(2003)는 근단층 지반운동에 대한 수학적 모델을 제안하여 펄스 형태의 지반운동을 정성적 및 정량적으로 표현하는 웨이블릿 모델을 개발하였다. 이 모델은 물리적 의미가 명확한 입력 매개변수를 가지고 있으며 다양한 실제 지진파 기록을 기반으로 개발되었다. Shahi와 Baker(2014)는 강한 속도펄스를 가진 지반 운동에 대한 효율적이고 정량적인 분류 방법을 제시하였다. 웨이블릿을 이용하여 임의의 입사방향에 대한 지진파의 펄스를 식별할 수 있는 알고리즘을 제안하였다. Kardoutsou 등(2017)은 지반 운동을 펄스 형태와 비펄스 형태로 분류하기 위한 새로운 펄스 지표(PI)를 제안하였다. 이 펄스지표는 주요 펄스와 기존 지반운동기록의 상호 상관관계를 나타내는 교차 상관계수로 나타낸다. PI가 0.65보다 크면 펄스형 지반운동으로, PI가 0.55보다 작으면 비펄스형 지반운동으로 분류한다.

교량의 지진취약도를 평가하는 과정에서 지진파의 입사 방향성을 고려하여 지진해석을 수행하는 것은 입사방향성에 따라서 지반운동의 특성이 변하기 때문에 중요하다. 지진해석은 구조 및 지반 시스템의 지진 성능을 시뮬레이션하기 위해 개발된 오픈소스 프레임워크인 OpenSEES 프로그램을 활용하였다(Mazzoni et al., 2007). 지진 입사 방향을 고려한 교량의 지진해석은 X방향(교축방향)과 Y방향(교축직각방향)에 한쌍의 수평방향의 지진파를 동시에 가진하여 교각에 대한 지진응답을 분석하였다. 이러한 교량의 구성요소에 대한 지진응답 평가로부터 내진성능(capacity)과 지진요구도(demand)를 평가할 수 있으며 이를 통해서 교량에 대한 확률론적 지진취약도를 평가하였다.

2. 지진파의 입사방향성을 고려한 교량의 지진해석

2.1 교량의 구조해석 모델링

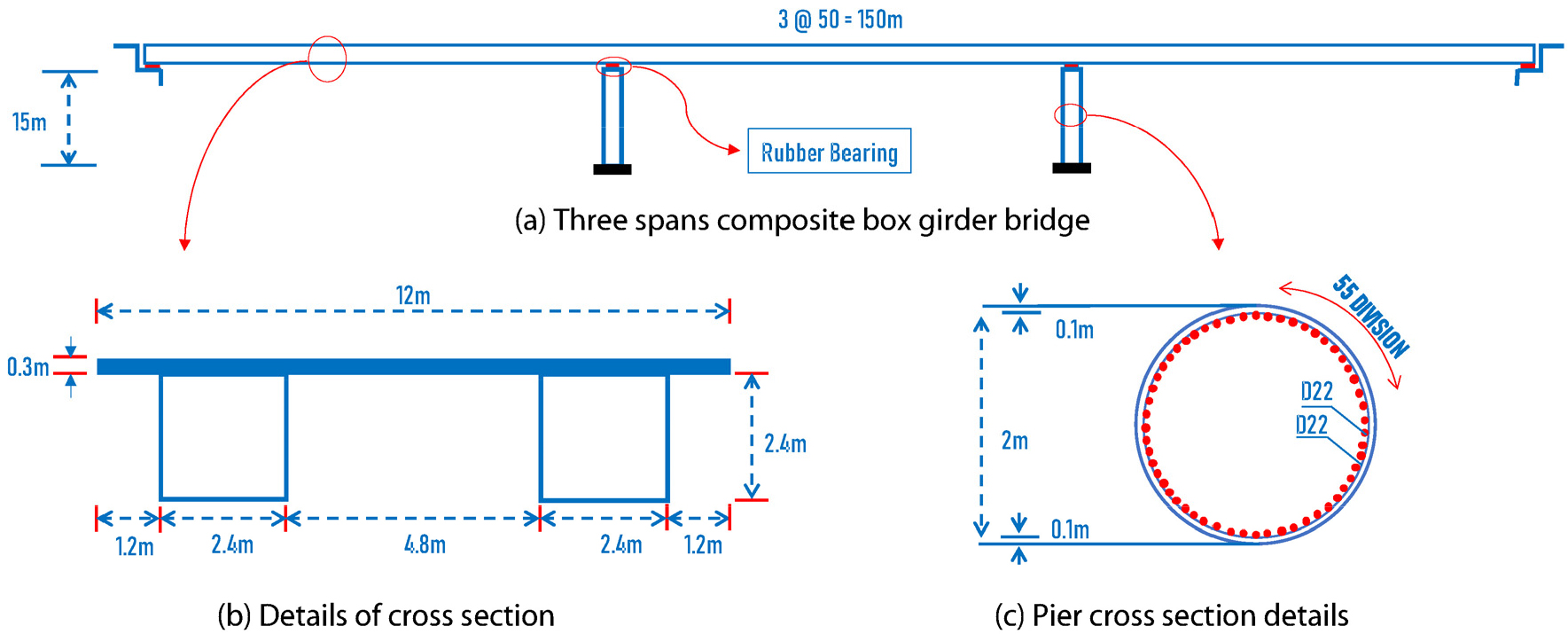
지진파의 입사방향성에 따른 지진응답 평가를 위해 3경간 강상자형 합성거더교를 사용하였다. 예제 교량에 대한 자세한 모델링과 제원은 Fig. 1에 나타내었다. 교각의 높이와 경간장은 각각 15m과 50m이다. 교각의 형상비는 7.5(형상비 = 교각의 높이/교각의 단면폭)이며 형상비가 크므로 휨거동에 의한 손상이 지배적이다. 상부 구조물에 대한 거더의 높이와 교폭은 각각 2.4m과 12m이며 콘크리트 바닥 슬래브의 두께는 0.3m이다. 강상자형의 오른쪽 벽과 왼쪽 벽의 두께는 0.01m이며 하부 두께는 0.012m이다. 두 개의 동일한 형상을 가진 강상자형이 콘크리트 바닥 슬래브에 일체로 연결되어 있는 거더 형태이다. 교각은 지름 2m인 원형 단면을 가지며 피복 콘크리트 두께는 0.1m이다. 교각에 배치된 주철근의 수는 55개의 D22 철근(직경: 22mm)으로 한 줄로 배근되었다. 심부구속 콘크리트와 주철근을 구속하기 위한 띠철근은 교각의 횡방향으로 0.15m 간격으로 배근되었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F1.jpg

Fig. 1.

Specifications of steel composite box girder bridge

2.2 입력 지진

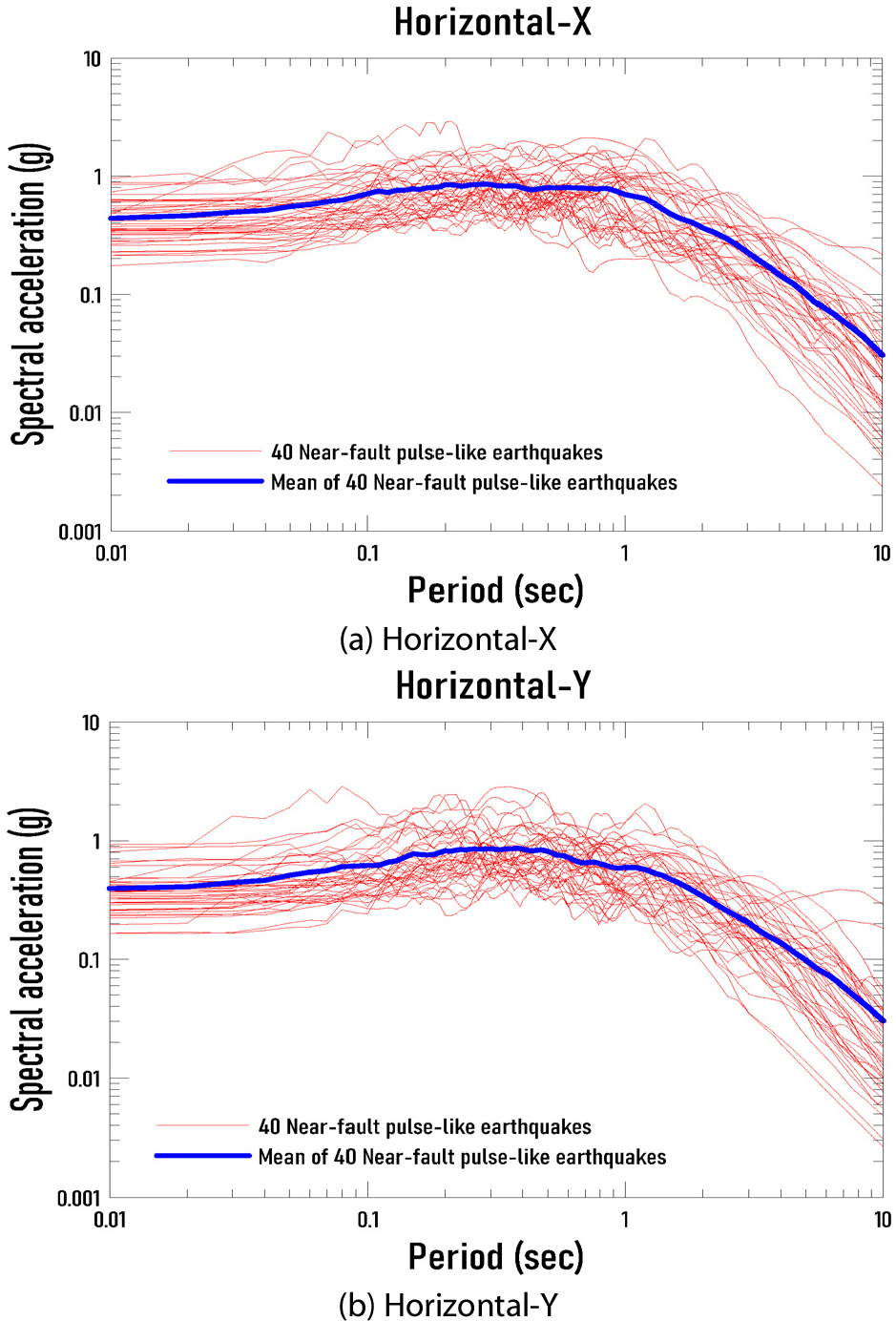
입력 지진으로는 PEER(Pacific Earthquake Engineering Research Center)에서 구축한 NGA-West2 지반운동 데이터베이스에서 계측위치가 진앙으로부터 10km 이내에 위치한 근거리 펄스형 지진(Near-Fault Pulse-like, NFP)을 40개 세트(1세트는 직교하는 수평방향 한쌍의 지진) 선정하여 사용하였다. Kong 등(2024)이 사용한 지진과 동일하며 상세한 지진데이터 정보는 이 논문을 참조하기 바란다. NFP에 대한 가속도 응답 스펙트럼은 로그 스케일을 적용하여 Fig. 2에 직교하는 두 수평방향에 대하여 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F2.jpg

Fig. 2.

Response spectra for 40 near fault pulse-like ground motions

2.3 입사방향에 따른 펄스지표(PI)의 분석

지진파가 가진 속도펄스(velocity pulse) 여부를 평가하는 펄스지표(PI)는 지진 파형이 얼마나 펄스 형태에 가까운지를 정량적으로 평가가능하게 한다. 지진 기록은 지진 계측 센서가 설치된 위치와 방향에 따라 지진가속도가 기록되고 지진 계측기는 세 방향으로 직교하는 지진가속도를 측정하는데, 수직 방향은 항상 일정하지만 수평의 두 방향은 계측기의 설치 방향에 따라 지진가속도의 측정 응답이 다르게 기록될 수 있다.

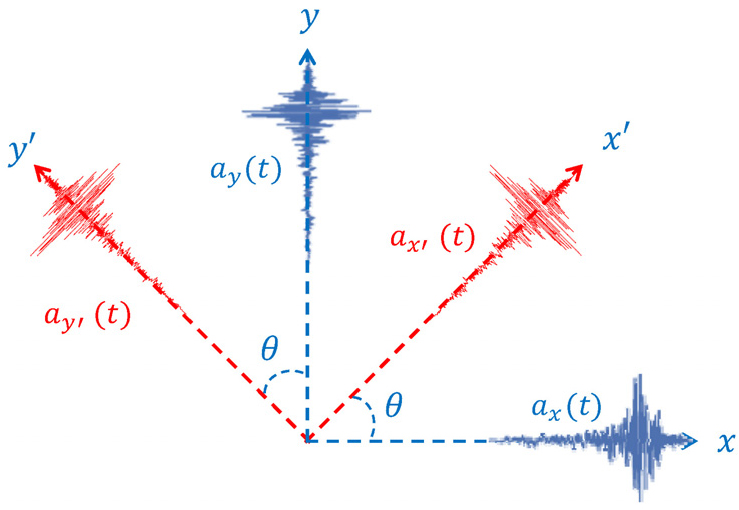
계측기의 설치방향의 변화를 지진파의 회전각(𝜃)의 변화로 본다면 회전각에 따른 두 개의 직교하는 지진가속도의 크기( $a_{x'} (t, θ), a_{y'} (t, θ)$ )를 구하는 방법은 식 (1)과 식 (2)와 같다.

(1)

a_{x'} (t, θ) = a_{x} (t) \cos (θ) + a_{y} (t) \sin (θ)

(2)

a_{x'} (t, θ) = - a_{x} (t) \sin (θ) + a_{y} (t) \cos (θ)

여기서, $a_{x} (t)$ 과 $a_{y} (t)$ 는 계측된 지반가속도에 대한 직교하는 한쌍의 두 수평성분을 의미한다. $t$ 는 시간이며, 𝜃는 지진파의 회전 방향성의 변화를 회전각으로 나타낸 것이다. $a_{x'} (t, θ)$ 로 구한 지진가속도 기록은 교량의 교축방향으로 가진하였고 $a_{y'} (t, θ)$ 로 구한 지진가속도 기록은 교축직각방향으로 가진하는 두 방향 동시가진하는 해석을 수행하였다. 이러한 지반가속도의 회전방향각에 따른 지진파의 구하는 개념을 Fig. 3에 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F3.jpg

Fig. 3.

Concept of directionality based on rotation angle

1쌍의 계측된 지반운동에 대하여 X방향 수평성분을 기준으로 지진파의 입사각을 고려하여 식 (1)과 식 (2)를 적용하여 0도에서 90도까지 1도씩 회전각을 증가시키며 직교하는 두 수평방향 성분의 총 91개의 입력지진세트를 생성하였다. 91개의 회전각을 달리하는 각각의 지진파 세트를 4차 Daubechies 웨이블릿 변환을 사용하여 속도 펄스와 잔여지반운동(residual ground motion)의 속도를 평가하고 Shahi와 Baker(2014)가 제시하는 펄스지표(PI) 평가 방법을 적용하여 PI를 평가하였다. 지진파의 시간 이력은 시간에 따라 지반운동의 진폭과 진동수가 모두 변하는 비정상 신호이다. 이러한 지반운동의 비정상적 특성으로 인해 지진파의 시간 영역에 대한 펄스와 같은 특징을 분석하는 과정은 복잡하다. 펄스(Pulse)는 짧은 시간 간격에서 높은 에너지를 가지며 에너지가 특정 진동수 영역에 집중되기 때문에 시간과 진동수 특성을 통해서 해석할 수 있다. 4차 Daubechies의 웨이블릿 변환에 대한 크기조정과 변환된 모-웨이블릿(mother wavelet) 함수의 합을 정의하여 식 (3)과 같이 나타낼 수 있다(Daubechies, 1988).

(3)

Φ_{s, l} (t) = \frac{1}{\sqrt{s}} ϕ (\frac{t - l}{s})

여기서, $ϕ (∙)$ 과 $Φ (∙)$ 는 시간( $t$ )에 대한 모-웨이블릿(mother wavelet)과 변환된 웨이블릿을 의미한다. 이러한 웨이블릿은 스케일 매개변수( $s$ )를 변경하여 진동수 영역에서 변환되고 (스케일 매개변수( $s$ ) : 모-웨이블릿을 늘이고 축소하는 역할) 시간 영역에서는 위치 매개변수( $l$ )가 변경되어 변환된다(위치 매개변수( $l$ ) : 시간 축에서 웨이블릿 모양을 변환시키는 역할).

웨이블릿 변환은 푸리에 변환과 유사하다. 푸리에 변환(fourier transform)은 진동수가 시간에 따라 일정한 사인파(sine wave)와 코사인파(cosine wave)의 합으로 신호를 분해한다. 반면에 웨이블릿 변환은 신호를 시간 영역과 진동수 영역에서 분해하여 해석이 가능한 특징이 있다. 이로 인해 웨이블릿은 신호의 진동수 특성이 시간에 따라 변하는 지진 운동과 같은 비정상 신호를 나타내는데 적합하다. 지진파의 신호에 대한 연속 웨이블릿 변환 계수 $(c)$ 는 식 (4)를 사용하여 다음과 같이 구할 수 있다.

(4)

c (s, l, θ) = \frac{1}{\sqrt{s}} \int_{- \infty}^{\infty} ⌊ f (t, θ) ⌋ ϕ (\frac{t - l}{s}) d t

여기서, $s$ 와 $l$ 는 스케일 매개변수와 위치 매개변수이며 𝜃는 회전각이다. 그리고 $f (t, θ)$ 는 시간함수와 회전각에 대한 지진파이며, $t$ 는 지진파의 시간 간격을 의미한다.

웨이블릿 계수 해석을 통해서 기존 지반운동에 대한 속도 펄스와 잔여 지반운동의 속도를 평가할 수 있으며, 이러한 기존 지반운동과 잔여 지반운동에 대하여 에너지 비율( $E n e r g y_{r a t i o} = E n e r g y_{r e s i d u a l} / E n e r g y_{o r i g i n a l}$ )과 PGV 비율( $P G V_{r a t i o} = P G V_{r e s i d u a l} / P G V_{o r i g i n a l}$ )를 구할 수 있다. 이러한 관계로부터 Shahi와 Baker (2014)가 제시하는 PI 방법을 다음과 같은 식 (5), (6)으로 나타낼 수 있다.

(5)

P C = 0.63 \times (P G V_{r a t i o}) + 0.777 \times (E n e r g y_{r a t i o})

(6)

P I = 9.384 (0.76 - P C - 0.061 \times P G V) \times (P C + 6.914 \times 10^{- 4} \times P G V - 1.072) - 6.179

여기서, PC와 PI는 주성분 해석(principal component analysis)과 펄스지표(pulse indicator)를 의미한다. 여기서, PI가 0보다 크면 펄스형, 0보다 작으면 비펄스형으로 분류한다.

입사 방향성에 따른 입사각의 변화 0°~90°에 범주 내에서 1°씩 증가시킨 91개의 입사각에 대한 지진파 한쌍을 식 (1)과 식 (2)를 적용하여 생성하고, 지진파에 대한 펄스지표(PI)의 값을 식 (6)을 이용하여 평가하여 구한 후에 펄스지표의 크기 순으로 백분위수를 구한 후에 백분위수 0, 25, 50, 75, 100에 해당하는 5가지 지진파 세트를 선택하여 지진해석에 적용하였다. 선택된 지진파의 명칭으로 ID-X-XP(No.)를 사용하였다. 여기서 ID는 입사 방향성(Incidence Directional)을 의미하며 지진파는 두 직교성분이 한 쌍인데 X는 교축방향으로의 입사되는 지진을, Y는 교축직각방향으로의 입사되는 지진을 의미한다. XP(No.)는 X방향 지진파에 대한 펄스지표(PI)의 값을 백분위수(Percentile)로 나타낸 것이다. 한쌍의 지진파이므로 Y방향 지진파를 기준으로 백분위수를 정하였다면 YP(No.)로 나타낸다. 지진응답을 비교하는데 편의상 P00, P25, P50, P75, P100의 다섯 가지 백분위수에 대응하는 지진파 한쌍씩을 사용하였다. 따라서 “ID-X-XP00”는 X방향의 지진파 91개 중에서 입사각의 변화에 따른 펄스지표(PI) 값이 가장 작은 지진파를 나타낸다. “ID-X-XP100”는 X방향의 지진파 91개 중에서 입사각의 변화에 따른 펄스지표(PI) 값이 가장 큰 지진파를 의미한다. ID-X-XP25는 25번째 백분위수, ID-X-XP50는 중앙값, ID-X-XP75는 75번째 백분위수에 해당하는 지진파를 의미한다.

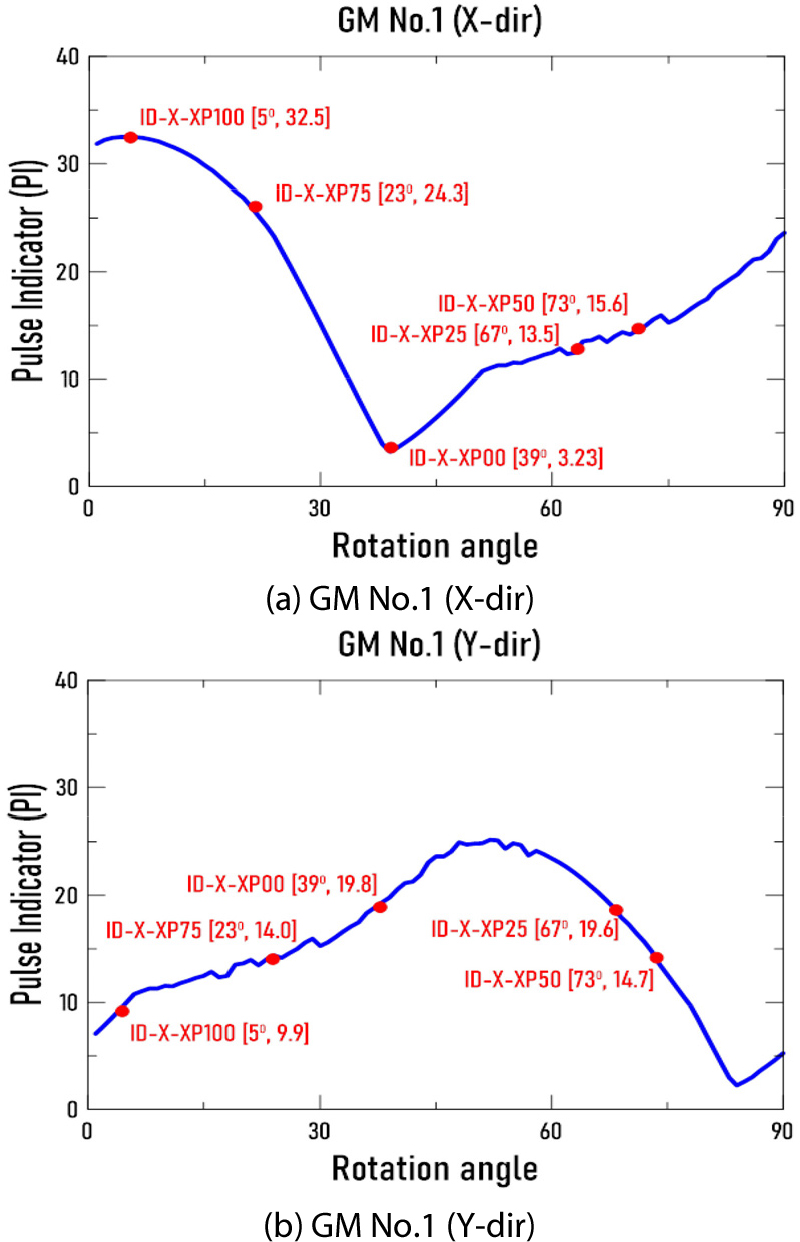
입사각(𝜃)의 변화에 따른 지진파의 특성의 변화를 분석하기 위하여 입사각에 대한 PI의 백분위수를 평가하였다. 대표적인 예로 GM No.1 지진의 경우에 0°에서 90°까지의 회전각에 따라 X방향(교축방향) 지진을 펄스 지표(PI)를 구하여 Fig. 4(a)에 나타내었다. Fig. 4(a)에 나타낸 펄스지표(PI)의 값이 ID-X-XP00는 입사각 39°에서 3.23, ID-X-XP25는 입사각 67°에서 13.5, ID-X-XP50는 입사각 73°에서 15.6, ID-X-XP75는 입사각 23°에서 24.3, ID-X-XP100는 입사각 5°에서 32.5로 나타난다. 지반운동은 직교하는 두 수평성분으로 이루어졌기 때문에 ID-X-XP00에 대응하는 직교방향 지진성분은 ID-Y-XP00로 표기한다. ID-Y-XP00에서 Y의 의미는 직교하는 지진을 의미하지만 지진의 백분위수는 X방향의 지진에 의해 결정된 것을 의미한다. Fig. 4(b)에 나타낸 바와 같이 교축직각방향(Y방향)에 대한 펄스지표(PI)의 값이 ID-Y-XP00는 19.8, ID-Y-XP25는 19.6, ID-Y-XP50는 14.7, ID-Y-XP75는 14.0, ID-Y-XP100는 9.9 등으로 나타난다. ID-X-XP00와 ID-Y-XP00는 동일한 입사각의 직교하는 한쌍의 지진파를 나타낸다. Fig. 4를 통하여 교축방향에서 ID-X-XP100가 펄스지표(PI)가 최대가 되는 지진이지만, 이 지진파와 한쌍으로서 직교하는 성분인 ID-Y-XP100는 반대로 펄스지표(PI)가 최소 값에 근접한 작은 값을 나타내는 경향이 있음을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F4.jpg

Fig. 4.

The PI of GM No.1 in the direction of longitudinal and transverse according by rotated angle

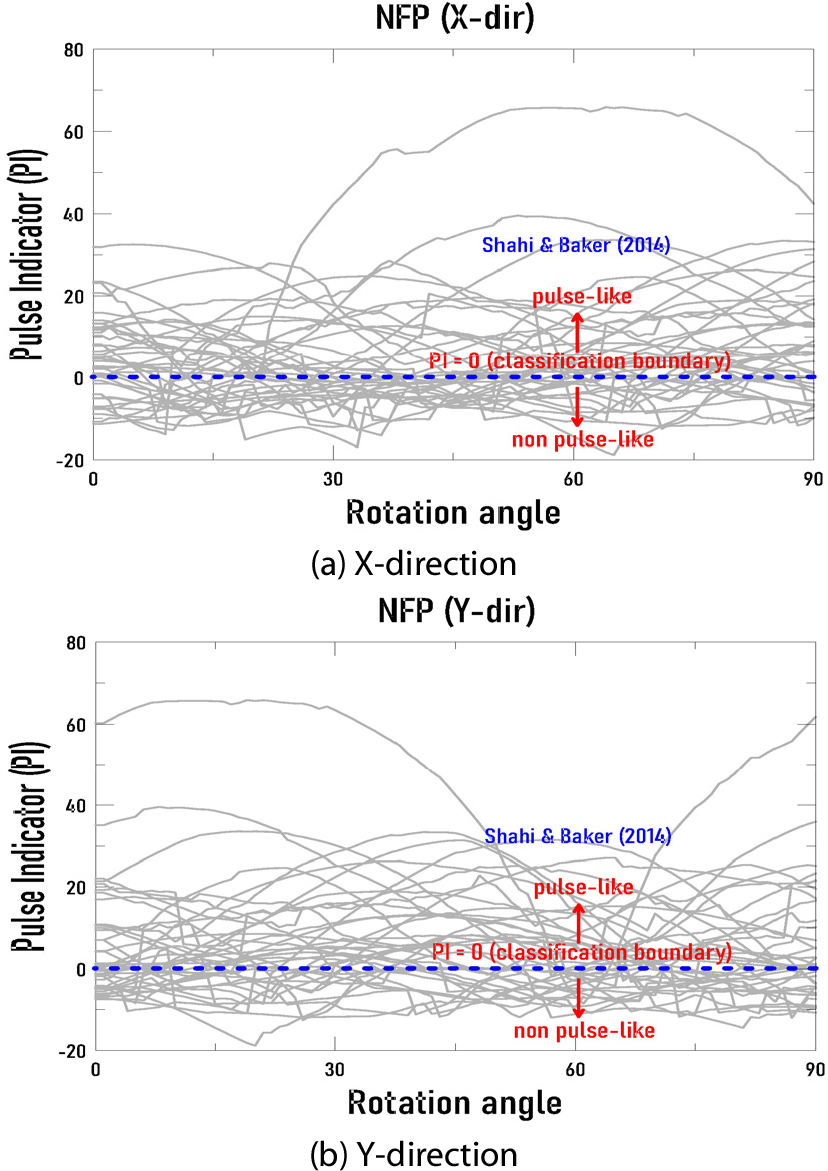
40개 지진들에 대하여 개별 지진당 0°~90°까지 회전각의 변화에 따른 91개 수평방향 지진파 세트를 추출하여 식 (6)을 사용하여 펄스지표(PI)를 평가하여 Fig. 5에 나타내었다. 펄스지표(PI)가 0보다 크면 펄스형 지진으로 분류하고 0보다 작으면 비펄스형 지진으로 분류된다. Fig. 5에 나타낸 바와 같이 지진파의 펄스지표(PI) 값이 회전각에 따라 음수와 양수로 점진적으로 변동하는 경향이 나타나며, 이는 동일한 지반운동의 지진파의 경우에도 회전각에 따라서 지반운동이 펄스를 가진 경우와 아닌 경우로 변할 수 있음을 의미한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F5.jpg

Fig. 5.

The PI of all ground motion in the direction of X and Y-direction according by rotated angle

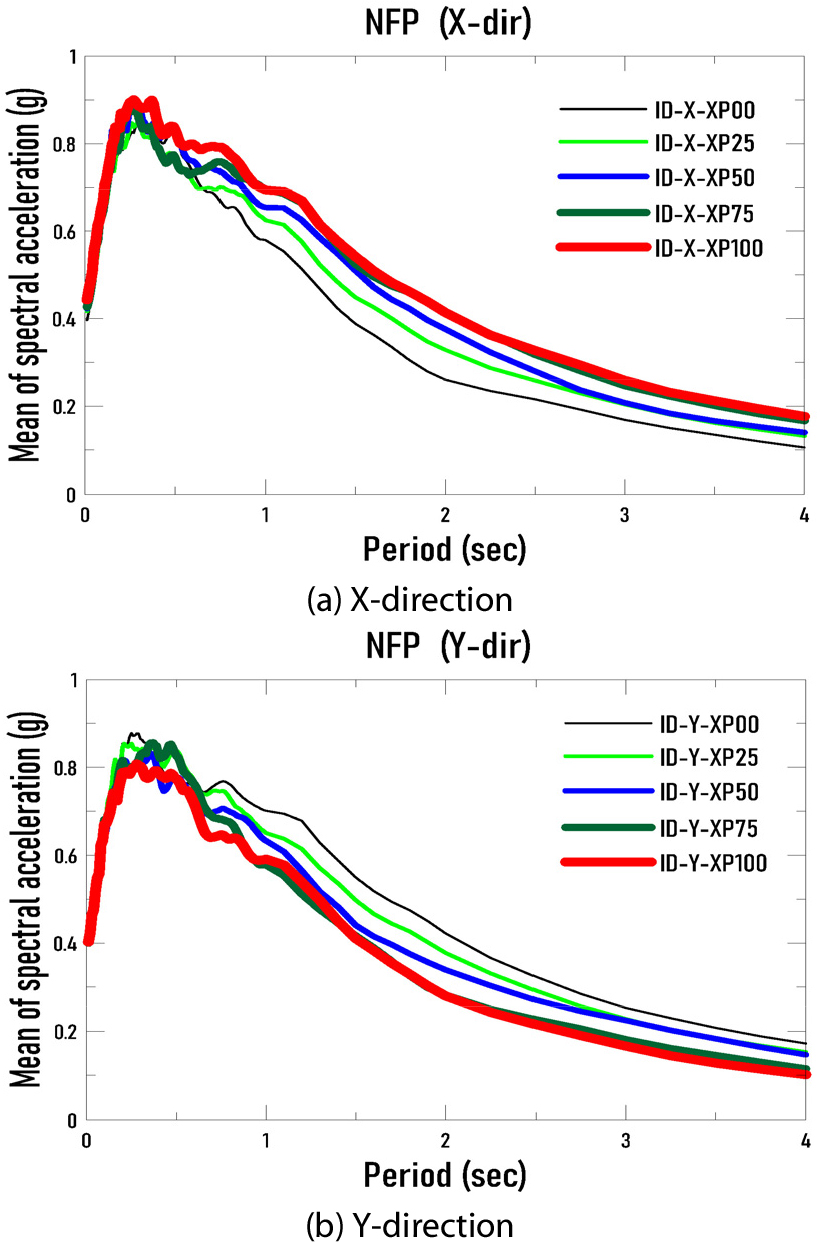
펄스 지표(PI)를 기반으로 한 쌍의 지진파는 입사각 변화에 따른 5가지 백분위수에 해당하는 5쌍의 지진파로 구한 후에 가속도응답스펙트럼 평가하여 Fig. 6에 나타내었다. Fig. 6(a)의 가속도 응답스펙트럼에서 ID-X-XP100은 40개 지진파의 X방향 성분의 지진중에서 입사각에 변화에 따른 PI 백분율이 가장 큰 경우에 대한 가속도응답스펙트럼의 평균을 나타낸 것이며, Fig. 6(b)에 나타낸 ID-Y-XP100은 ID-X-XP100에 대응하는 40개의 직교하는 지진파에 대한 가속도응답스펙트럼의 평균을 나타낸다. ID-X-XP100의 가속도응답스펙트럼이 전반적으로 가장 큰 값을 가지며 이와 직교하는 지진파의 경우인 ID-Y-XP100의 가속도응답스펙트럼은 전반적으로 가장 작은 값을 나타낸다. 즉, 직교하는 두 수평 방향의 지진파는 입사각의 변화에 따라 한 쌍의 지진파 중 임의의 방향의 지진파에 대한 응답 스펙트럼(또는 지진의 세기)이 증가하면 이에 직교하는 다른 방향의 지진파의 가속도 응답스펙트럼은 감소하는 경향을 보이다. 지진파의 입사각에 따른 변환 중에서 펄스지표가 클수록 가속도응답스펙트럼 또한 이에 비례하여 증가하는 경향을 나타냄을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F6.jpg

Fig. 6.

Comparison of mean acceleration response spectra according to five percentiles of pulse indicator for 40 NFP ground motions

5개의 백분위수에 대응하는 40개 지진파 세트에 대한 평균 펄스 지표(PI)를 Table 1에 나타내었다. 백분위수가 증가할수록 X방향(교축방향) 평균 펄스지표 값이 증가하지만 Y방향 (교축직각방향)에서는 반대로 감소하는 경향을 나타낸다. 즉, 한쌍의 수평방향 지진파에서 임의의 회전각에 대한 지진파의 변환에서 어느 한 방향의 지진파가 펄스지표가 증가하는 경향을 나타낸다면 이에 직교하는 방향의 지진파는 펄스지표가 감소하는 경향을 나타내는 것을 의미한다.

Table 1.

Mean pulse indicator (PI) according to five percentiles of pulse indicator for 40 NFP ground motions

Incident Direction	Mean Pulse Indicator (PI)
Incident Direction	X-Dir	Y-Dir
XP00	-7.90	13.01
XP25	2.01	10.68
XP50	5.70	6.10
XP75	12.08	0.16
X100	16.21	-2.49

3. 지진파의 펄스지표에 따른 교량의 지진취약도 영향

3.1 지진취약도 해석기법

지진취약도 해석은 구조물에 발생할 수 있는 잠재적인 손상 정도를 정량화하는 방법이다. 이 방법은 교량에 대한 지진파와 해석 모델 변수의 내재적 불확실성을 고려하여 손상될 확률을 계산한다. 지진취약도 함수는 다음 식 (7)과 같이 나타낼 수 있다.

(7)

P_{f} = P [D e m a n d > C a p a c i t y | I M]

여기서, $P_{f}$ 는 교량의 지진응답이 한계상태를 초과하여 손상될 확률이다. $D e m a n d$ 과 $C a p a c i t y$ 는 각각 지진요구도와 내진성능이다. IM는 지진하중의 크기를 의미하며 주기 1초에 대응하는 가속도 응답스펙트럼( $S_{a - T 1}$ )을 사용하였다. 하지만 실제로 예제교량의 고유주기는 1초 이상 나타내었으며 기존 연구자들은 응답스펙트럼 1초를 사용하여 많이 해석하였다. 지진취약도 해석을 위한 지진응답은 Cornell(2002)이 제시한 다음 식 (8)과 같은 확률론적 지진요구도 모델을 사용하여 평가하였다.

(8)

\ln (D e m a n d_{m e d i a n}) = \ln (a) + b \ln (I M)

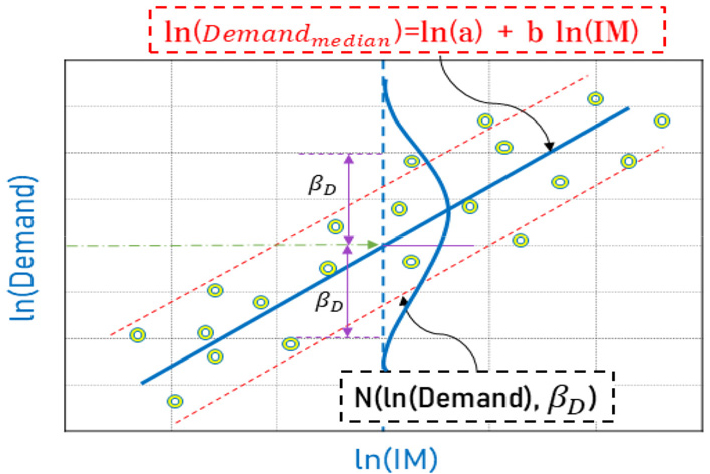
여기서, $D e m a n d_{m e d i a n}$ 는 교량부재에 대한 지진요구도의 중앙값을 의미한다. $a$ 와 $b$ 는 지진응답에 대한 선형회귀곡선의 변수이고 교량부재의 지진요구도는 대수정규분포(Shinozuka et al., 2000)를 가지는 것으로 가정한다. Cornell(2002)의 확률론적 지진요구도 모델은 Fig. 7에 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F7.jpg

Fig. 7.

Probabilistic seismic demand model (PSDM) in the lognormal space

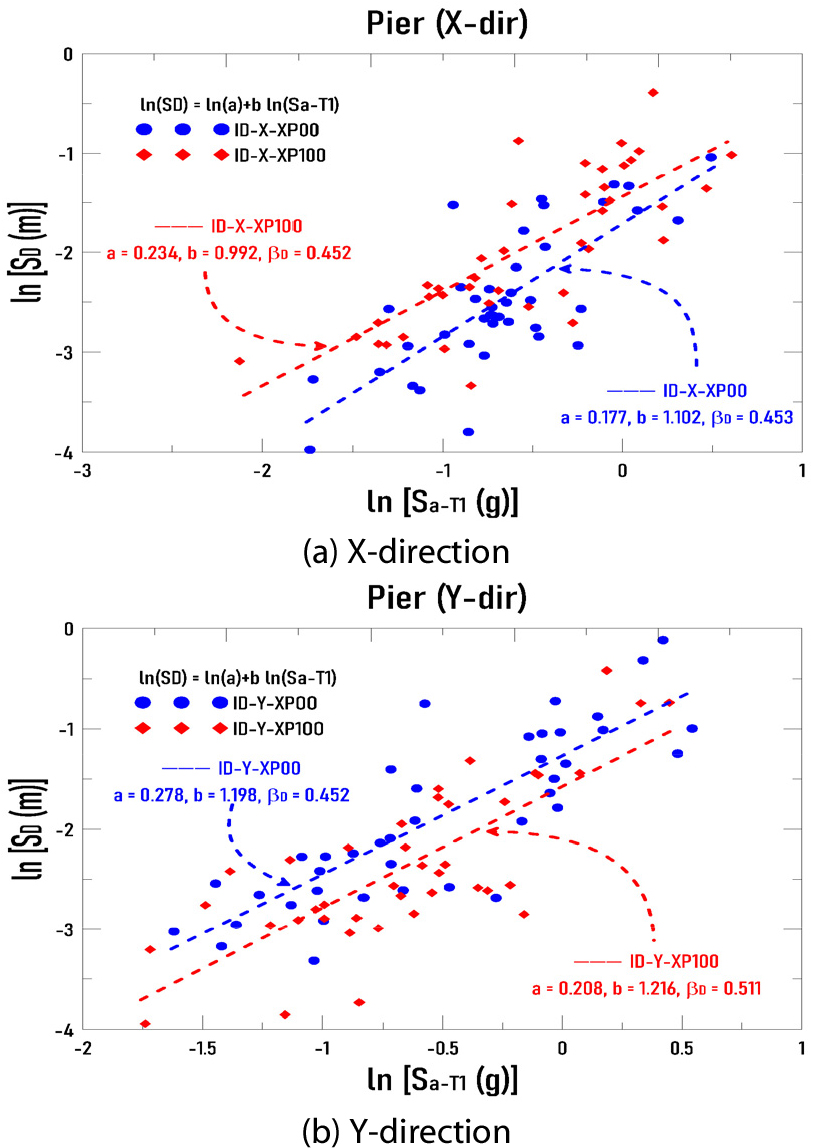
지진해석에 대한 지진응답으로 교각에 대한 확률론적 지진요구도 모델의 비교는 5쌍 지진파 중에 입사 방향에 따라 X방향에서의 백분위수가 최소(XP00)와 최대(XP100) 두 가지 경우로 구분하여 Fig. 8에 각각 나타내었다. a와 b(기울기)는 식 (9)에 나타낸 바와 같이 지진응답의 선형회귀곡선의 변수이며 $β_{D}$ 는 지진요구도의 대수표준편차를 의미한다. Fig. 8에 나타난 교각에 대한 지진요구도는 경향이 유사하며 X 방향의 지진요구도는 ID-X-XP100가 ID-X-XP00보다 크게 나타나며 Y방향 지진파의 지진요구도는 ID-Y-XP00가 ID-Y-XP100보다 크게 나타남을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F8.jpg

Fig. 8.

Comparison of PSDM for pier subjected to 40 ground motions with different pulse indicator

지진취약도 함수는 일반적으로 다섯 가지 손상 상태(Damage State, DS)를 고려하여 다음과 같이 정의된다. 손상 없음(DS0), 미소손상(DS1), 중간손상(DS2), 심각손상(DS3), 그리고 완전붕괴(DS4)이다. 교량의 내진성능과 지진요구도는 대수 정규 분포를 따른다면 $j$ 번째 손상상태에 대한 지진취약도 함수는 다음 식과 같이 표현될 수 있다.

(9)

F_{j} (I M_{i}; c_{j}, ζ_{j}) = Φ \{\frac{\ln (I M_{i}) - \ln (c_{j})}{ζ_{j}}\}

여기서, $c_{j}$ 는 지진취약도를 나타내는 대수정규분포함수의 중앙값을 의미하고 $ζ_{j}$ 는 대수표준편차(logarithmic standard deviation)를 의미하며, 각각 식 (10)과 식 (11)과 같이 나타낼 수 있다.

(10)

c_{j} = \exp \{\frac{\ln (S_{C j}) - \ln (a)}{b}\}

(11)

ζ_{j} = \frac{\sqrt{β_{D}^{2} + β_{C j}^{2} + β_{M}^{2}}}{b}

여기서, $S_{C j}$ 는 $j$ 번째 손상상태에 대한 교량이 보유한 내진성능의 중앙값이고, $β_{C j}$ 는 내진성능에 대한 대수표준편차이다. $β_{D}$ 는 대수정규분포를 가지는 지진요구도에 대한 대수표준편차이다. Dutta(1999)가 제시하는 연구결과에 의하며 해석방법의 불확실성을 나타내는 $β_{M}$ 은 0.2로 가정하고 $β_{C j}$ 는 0.25로 가정하였다.

3.2 펄스지표에 따른 교각의 지진취약도 평가

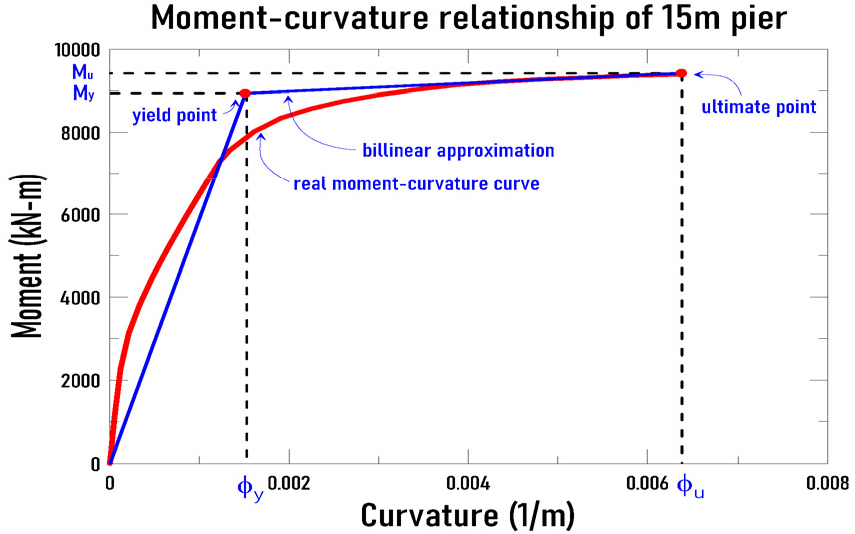
교각의 손상상태의 평가에 필요한 변위연성도를 평가하기 위하여 비탄성 정적해석을 수행하여 교각의 모멘트-곡률관계를 구하고 이를 billinear로 이상화하여 항복변위( $d_{y}$ )와 극한변위( $d_{u}$ )를 구할 수 있으며 모멘트-곡률 관계를 billinear로 이상화한 그림은 Fig. 9에 나타내었다. 교각의 항복변위( $d_{y}$ )와 극한변위( $d_{u}$ )의 평가에 의해서 Moschonas 등(2009)가 제시하는 교각의 손상상태( $D S_{j}$ )에 대응하는 성능값( $S_{C j}$ )은 Table 2와 같이 정의하였다. 그리고 변위연성도는 ( $μ_{c}$ )는 식 (12)과 같이 나타낼 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F9.jpg

Fig. 9.

Bilinear approximation for moment-curvature relationship of pier

Table 2.

Definition of damage states for pier

Damage state		Threshhold values of $S_{C j}$ ( $d$ = seismic displacement demand)
DS₀	None	$d \leq 0.7 ∙ d_{y}$
DS₁	Minor / slight	$d > 0.7 ∙ d_{y}$
DS₂	Moderate	$d > min \{\begin{cases} 1.5 \cdot d_{y} or \\ d_{y} + (\frac{1}{3}) \cdot (d_{u} - d_{y}) \end{cases}$
DS₃	Major / extensive	$d > min \{\begin{cases} 3.0 \cdot d_{y} or \\ d_{y} + (\frac{2}{3}) \cdot (d_{u} - d_{y}) \end{cases}$
DS₄	Failure / collapse	$d > d_{u}$

(12)

μ_{c} = \frac{d_{u}}{d_{y}}

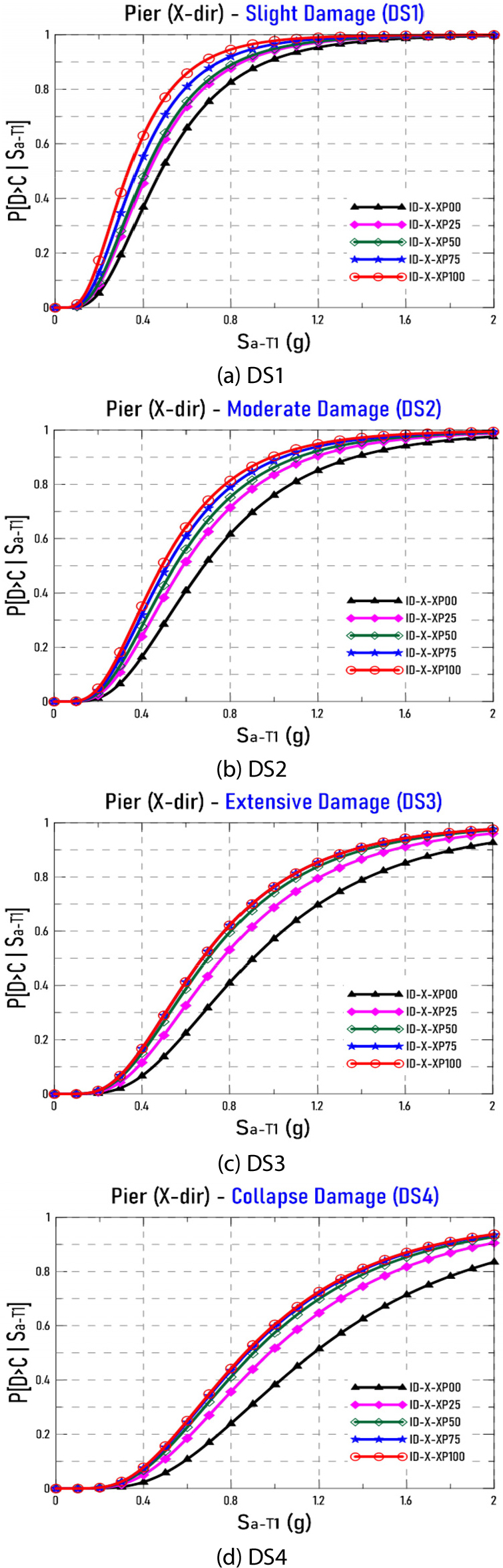
교각에 대하여 X방향에 대한 5가지 방향성의 지진취약도를 미소손상(DS1), 중간손상(DS2), 심각손상(DS3), 완전붕괴(DS4) 등의 4가지 손상상태의 지진취약도를 비교하여 Fig. 10에 나타내었다. Fig. 10에 나타낸 바와 같이 5가지 방향성의 지진취약도 비교에서 백분위수가 가장 큰 지진파가 다른 백분위수의 지진파보다 지진취약도가 크게 나타나고 있음을 알수 있다. X방향과 Y방향에 대한 5가지 펄스지표에 대한 중앙값( $c_{j}$ )과 대수표준편차( $ζ_{j}$ )를 Table 3와 Table 4에 각각 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-05/N0040370505/images/Figure_jcoseik_37_05_05_F10.jpg

Fig. 10.

Seismic fragility curves of pier according to incidence direction percentile

Table 3.

Median value ( $c_{j}$ ) and log-normal standard deviation( $ζ_{j}$ ) for fragility curve of pier in X-direction

Incidence direction percentile	$c_{j}$ (g)				$ζ_{j}$
Incidence direction percentile	DS1	DS2	DS3	DS4	All damage states
ID-X-XP00	0.48	0.68	0.91	1.18	0.54
ID-X-XP25	0.43	0.59	0.77	0.98
ID-X-XP50	0.41	0.55	0.71	0.91
ID-X-XP75	0.37	0.52	0.68	0.88
ID-X-XP100	0.33	0.49	0.68	0.87

Table 4.

Median value ( $c_{j}$ ) and log-normal standard deviation( $ζ_{j}$ ) for fragility curve of pier in Y-direction

Incidence direction percentile	$c_{j}$ (g)				$ζ_{j}$
Incidence direction percentile	DS1	DS2	DS3	DS4	All damage states
ID-Y-XP00	0.34	0.48	0.63	0.80	0.59
ID-Y-XP25	0.34	0.49	0.68	0.91
ID-Y-XP50	0.35	0.53	0.78	1.07
ID-Y-XP75	0.41	0.59	0.81	1.08
ID-Y-XP100	0.46	0.63	0.82	1.08

X방향에 대한 Table 3의 결과로부터 펄스지표 백분위수가 큰 지진파일수록 모든 손상상태에 대한 지진취약도의 중앙값이 작아지는 경향을 나타내고 있음을 알 수 있다. 4가지 손상상태에 대한 지진취약도의 중앙값에서 ID-X-XP100가 ID-X-XP75보다 약 3%, ID-X-XP50보다 약 8%, ID-X-XP25보다 약 14%, ID-X-XP00보다 27% 정도 작게 나타난다. 이는 다시 말하면 ID-X-XP100가 ID-X-XP75보다 약 3%, ID-X-XP50보다 약 8%, ID-X-XP25보다 약 14%, ID-X-XP00보다 27%정도 교각의 손상확률이 증가함을 의미한다. 그리고 X방향에 대한 모든 손상상태의 평균 대수표준편차는 손상상태별 취약도곡선의 비정상적인 역전현상을 방지하고자 평균적인 값을 취하여 0.54로 나타내었다. Y방향에 대한 지진취약도의 중앙값은 Table 4에 나타난 바와 같이 ID-Y-XP00가 다른 백분위수의 지진파보다 지진취약도가 증가하는 경향이 나타내었다. 그 중에서 ID-Y-XP00가 ID-Y-XP100보다 약 25% 정도 작아짐을 나타내었다. 이는 ID-Y-XP00가 ID-Y-XP100보다 약 25% 정도 교각의 손상확률이 증가함을 의미한다. 따라서 X방향 백분위수가 큰 지진파로 갈수록 교각의 지진취약도가 증가하는 경향이 나타나지만 Y방향에서는 지진취약도가 작아짐을 나타내고 있으며, 이는 X방향과 Y방향의 지진파는 한 쌍으로서 한 방향의 지진파의 크기가 증가하거나 감소하면 이와 쌍을 이루는 직교하는 방향의 지진파는 반대로 감소하거나 증가하거나 하는 경향을 나타내기 때문이다. 이러한 현상은 펄스형 지진파 뿐만 아니라 대부분의 지진파의 일반적인 특성으로 볼 수 있다. 지진파가 내포한 지진에너지가 입사방향성에 따라서 변하지 않고 일정할 것이므로 수평방향 중 한 방향의 세기가 증가하면 직교하는 다른 방향은 세기가 감소하는 특성을 나타낸다. 이러한 특성은 임의의 요소의 응력에서 두 직교방향의 주응력의 특성과 유사한 것이다. 즉, 미소의 응력요소가 임의 방향으로 회전함에 따라서 한 방향이 최대응력 방향이 된다면 이에 직교하는 방향에서는 최소 응력이 작용하는 것과 유사한 특성이라고 할 수 있다.

4. 결 론

다양한 입사각을 고려하여 수평방향 한쌍의 지진파에 대한 펄스지표(PI)를 평가하였다. 펄스지표의 크기를 기준으로 5가지 백분위수에 해당하는 입사각이 다른 수평방향의 1쌍 지진파를 각각 선택하였고 이 수평방향의 한쌍의 지진을 동시에 가진하여 교량부재 중 교각의 지진취약도를 평가하여 다음과 같은 결론을 얻었다.

1) 지진파는 입사방향각인 회전각의 변화에 따라서 지진파의 세기 등과 같은 특성이 변한다. 입사방향각에 따라서 지진파의 펄스지표도 최대와 최소의 차이가 약 20정도 날 정도로 변화함을 확인하였다. 수평방향의 한쌍의 지진파에서 한 방향의 펄스지표(PI)가 증가하면 이에 직교하는 방향의 펄스지표는 감소하는 경향을 나타낸다.

2) 펄스지표(PI)가 클수록 지진파에 속도펄스의 특성이 강하게 나타나는 것을 의미하며, 5가지 펄스지표 백분위수에 대한 수평방향 한쌍의 지진파를 선정하여 지진응답을 평가하였다. X방향에서 펄스지표 백분위수가 큰 지진파로 갈수록 가속도응답스펙트럼이 증가하는 경향을 나타내고, Y방향에서는 감소하는 경향을 나타낸다. 이는 수평방향 한쌍의 지진파가 한 방향의 지진응답이 증가하면 직교하는 다른 방향의 지진응답은 감소함을 의미한다. 직교하는 두 수평방향의 이러한 특성은 펄스형 지진파 뿐만 아니라 대부분의 지진파에 나타나는 특성이다.

3) 교축방향(X방향)에 대한 교각의 지진취약도는 ID-X-XP100가 ID-X-XP75보다 약 3%, ID-X-XP50보다 약 8%, ID-X-XP25보다 약 14%, ID-X-XP00보다 약 27% 정도 손상확률이 증가함을 나타내었다. 그러나 Y방향에서는 X방향과 반대로 ID-Y-XP00가 다른 펄스지표 백분위수 보다 교각의 손상확률이 증가함을 나타내었다. 이는 지진파의 펄스지표(PI)가 증가할수록 교각의 지진응답을 증가시켜 지진취약도를 증가시키는 경향을 나타냄을 의미한다. 입사방향성에 따른 펄스지표가 최대 및 최소인 경우에 동일한 지진파에 대하여 교각의 손상정도가 대략 평균적으로 25~27% 정도 차이가 날 수 있음을 의미한다.

Acknowledgements

이 논문은 2021년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(No. 2021R1I1A3047237)으로 이에 감사드립니다.

References

Cornell, C.A., Jalayer, F., Hamburger, R.O., Foutch, D.A. (2002) Probabilistic Basis for 2000 SAC Federal Emergency Management Agency Steel Moment Frame Guidelines, J. Struct. Eng., 128(4), pp.526~533.

10.1061/(ASCE)0733-9445(2002)128:4(526)

Daubechies, I. (1988) Orthonormal bases of Compactly Supported Wavelets, Commun. Pure & Appl. Math., 41(7), pp.909~996.

10.1002/cpa.3160410705

Dutta, A. (1999) On Energy-based Seismic Analysis and Design of Highway Bridges, State University of New York at Buffalo.

Kardoutsou, V., Taflampas, I., Psycharis, I.N. (2017) A New Pulse Indicator for the Classification of Ground Motions, Bull. Seismol. Soc. Am., 107(3), pp.1356~1364.

10.1785/0120160301

Kong, S., Kim, Y., Kung, S., Moon, J., Song, J.K. (2024) Influence of Incidence Direction of Seismic Wave on the Probabilistic Seismic Fragility Assessment of Bridges, J. Comput. Struct. Eng. Inst. Korea, 37(3), pp.151~162.

10.7734/COSEIK.2024.37.3.151

Mavroeidis, G.P., Papageorgiou, A.S. (2003) A Mathematical Representation of Near-Fault Ground Motions, Bull. Seismol. Soc. Am., 93(3), pp.1099~1131.

10.1785/0120020100

Mazzoni, S., McKenna. F., Scott, M.H., Fenves. G.L. (2007) OpenSees: Open System of Earthquake Engineering Simulation, Pacific Earthquake Engineering Center.

Moschonas, I.F., Kappos, A.J., Panetsos, P. Papadopoulos, V., Makarios, T., Thanopoulos, P. (2009) Seismic Fragility Curves for Greek Bridges: Methodology and Case studies, Bull Earthq. Eng., 7, pp.439~468.

10.1007/s10518-008-9077-2

Shahi, S.K., Baker, J.W. (2014) An Efficient Algorithm to Identify Strong-Velocity Pulses in Multicomponent Ground Motions, Bull. Seismol. Soc. Am., 104(5), pp.2456~2466.

10.1785/0120130191

Shinozuka, M., Feng, M.Q, Lee, J., Naganuma, T. (2000) Statistical Analysis of Fragility Curves, J. Eng. Mech., 126(12), pp.1224~1231.

10.1061/(ASCE)0733-9399(2000)126:12(1224)

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Effect of Pulse-like Ground Motions with Various Pulse Indicators on the Seismic Fragility of Bridges

ABSTRACT

MAIN

Fig. 1.

Specifications of steel composite box girder bridge

Fig. 2.

Response spectra for 40 near fault pulse-like ground motions

(1)

(2)

Fig. 3.

Concept of directionality based on rotation angle

(3)

(4)

(5)

(6)

Fig. 4.

The PI of GM No.1 in the direction of longitudinal and transverse according by rotated angle

Fig. 5.

The PI of all ground motion in the direction of X and Y-direction according by rotated angle

Fig. 6.

Comparison of mean acceleration response spectra according to five percentiles of pulse indicator for 40 NFP ground motions

Table 1.

Mean pulse indicator (PI) according to five percentiles of pulse indicator for 40 NFP ground motions

(7)

(8)

Fig. 7.

Probabilistic seismic demand model (PSDM) in the lognormal space

Fig. 8.

Comparison of PSDM for pier subjected to 40 ground motions with different pulse indicator

(9)

(10)

(11)

Fig. 9.

Bilinear approximation for moment-curvature relationship of pier

Table 2.

Definition of damage states for pier

(12)

Fig. 10.

Seismic fragility curves of pier according to incidence direction percentile

Table 3.

Median value (cj) and log-normal standard deviation(ζj) for fragility curve of pier in X-direction

Table 4.

Median value (cj) and log-normal standard deviation(ζj) for fragility curve of pier in Y-direction

Acknowledgements

References

Median value ( $c_{j}$ ) and log-normal standard deviation( $ζ_{j}$ ) for fragility curve of pier in X-direction

Median value ( $c_{j}$ ) and log-normal standard deviation( $ζ_{j}$ ) for fragility curve of pier in Y-direction