SPH-Based Wave Tank Simulations

Sangmin Lee; Mujong Kim; Kwonhwan Ko; Jung-Wuk Hong

doi:10.7734/COSEIK.2021.34.1.59

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 28 February 2021. 59-69
https://doi.org/10.7734/COSEIK.2021.34.1.59

SPH-Based Wave Tank Simulations

SPH 기법 기반의 파동수조 시뮬레이션

Sangmin Lee¹

Mujong Kim¹

Kwonhwan Ko¹

Jung-Wuk Hong²^†

이 상민¹

김 무종¹

고 권환¹

홍 정욱²^†

¹Graduate Student, Department of Civil and Environmental Engineering, Korea Advanced Institute of Science and Technology, Daejeon, 34141, Korea

²Professor, Department of Civil and Environmental Engineering, Korea Advanced Institute of Science and Technology, Daejeon, 34141, Korea

¹한국과학기술원 건설 및 환경공학과 박사과정

²한국과학기술원 건설 및 환경공학과 교수

^*j.hong@kaist.ac.kr

ABSTRACT

Recently, large-scale offshore and coastal structures have been constructed owing to the increasing interest in eco-friendly energy development. To achieve this, precise simulations of waves are necessary to ensure the safe operations of marine structures. Several experiments are required in the field to understand the offshore wave; however, in terms of scale, it is difficult to control variables, and the cost is significant. In this study, numerical waves under various wave conditions are produced using a piston-type wavemaker, and the produced wave profiles are verified by comparing with the results from a numerical wave tank (NWT) modeled using the smoothed particle hydrodynamics (SPH) method and theoretical equations. To minimize the effect by the reflected wave, a mass-weighted damping zone is set at the right end of the NWT, and therefore, stable and uniform waves are simulated. The waves are generated using the linear and Stokes wave theories, and it is observed that the numerical wave profiles calculated by the Stokes wave theory yield high accuracy. When the relative depth is smaller than two, the results show good agreement irrespective of the wave steepness. However, when the relative depth and wave steepness are larger than 2 and 0.04, respectively, the errors are negligible if the measurement position is close to the excitation plate. However, the error is 10% or larger if the measurement position is away from the excitation location. Applicable target wave ranges are confirmed through various case studies.

Keywords

smoothed particle hydrodynamics (SPH)

numerical wave tank (NWT)

wave steepness

stokes wave

최근 친환경 에너지 개발에 대한 관심의 증가로 해상 및 연안 지역에서 대규모 해양구조물들이 건설되고 있다. 해양구조물은 항상 파랑 하중에 노출되어 있으므로 구조적인 안전성을 확보하기 위해서는 파랑에 대한 정확한 이해와 분석이 필수적이다. 실해역에서 수행되는 실험은 해양파를 이해하기 위한 가장 정확한 방법이지만, 변수의 통제가 어렵고 비용과 규모 측면에서 실험이 제한되는 경우가 많다. 본 연구에서는 수치파동수조를 이용하여 다양한 조건의 파를 생성하고 및 이론식과 비교를 통해 파랑 생성 능력을 검증하였다. 입자 기반 수치해석법인 SPH(Smoothed Particle Hydrodynamics) 기법을 이용하여 3차원 수조 및 피스톤 조파기를 모델링하였으며, 반사파에 대한 영향을 최소화하기 위해 수로 끝단에 질량 가중 감쇠 영역을 설정하여 안정적인 파고 및 유속 계산이 수행될 수 있게 하였다. 목표 파랑 조건에서,상대 수심이 2 이하를 만족하는 경우 파형경사에 관계없이 파고와 유속을 계산한 결과가 이론값과 높은 정확도를 보였다. 그러나 상대수심과 파형경사의 목표값이 증가하고, 측정 위치가 멀어짐에 따라서 최대 10% 이상의 오차가 발생하였다. 수치해석을 이용하여 정확한 계산이 가능한 파랑 범위를 무차원 변수를 이용하여 제안하였으며, 차후 수치해석을 이용한 수치파동수조 검증기준과 유체-구조물 상호작용 해석분야 연구에 효과적으로 활용될 수 있다.

키워드

SPH(Smoothed Particle Hydrodynamics)

수치파동수조

파형경사

스토크파

MAIN

1. 서 론
2. 이 론
2.1 이론적 배경
2.2 지배방정식과 상태방정식
2.3 조파기 이론
3. 수치파동수조
4. 결과 및 분석
4.1 수치파동수조 검증
4.2 다양한 파 조건을 이용한 수치파 생성 능력 분석
5. 결 론

1. 서 론

최근 신재생·친환경 에너지 개발 분야에 관심이 집중되고 있으며, 해양에서 에너지를 획득하기 위한 대규모 풍력, 조류, 파력 발전단지 등의 해상구조물을 건설 및 조성하기 위한 다양한 계획이 추진 중이다(Kim et al., 2017). 또한, 새롭게 건설된 구조물로 인해 변형된 연안 지형 및 파랑을 방재하기 위해 수중 잠제와 방파제 등의 다양한 연안 구조물이 건설되고 있다. 해양구조물에는 바람 및 지형에 의해 생성된 쇄파 및 저기압으로 인해 발생하는 장주기의 너울성 파랑 등이 작용하며, 태풍과 같이 단기간에 고강도의 하중을 주는 외력 또한 존재한다. 다양한 외력에 대한 해양구조물의 구조적인 안정성을 검토하기 위해서 실해역 기반의 실험적 검증이 요구되나, 여러 변수에 대한 통제가 쉽지 않다는 단점이 있다. 이에 대한 대안으로써, 수조를 이용하여 파랑을 생성하고 파력을 측정하는 실내 실험이 다수 수행되었다(Morison et al., 1950; Schäffer, 1996; Wienke and Oumeraci, 2005; Lee et al., 2020b).

파랑을 생성하기 위해서 사용하는 실험용 조파기의 종류는 다양하지만, 대표적으로 피스톤 조파기와 플랩 조파기가 많이 사용된다(Dean and Dalrymple, 1991). Haveloc(1929)과 Dean과 Dalrymple(1991)은 선형파 이론을 이용하여 피스톤과 플랩 조파기의 해석해를 상대수심의 함수로 제안하였으며, Ursell 등(1960)은 피스톤 조파기에서 발생한 선형 파의 정확도를 확인하고, 파형경사(wave steepness)에 따른 이론값과 실험값의 오차를 분석하였다. Goda(1967)는 실험 수로에서 생성된 선형파와 같이 작은 진폭의 파는 단일파가 아닌 두 개 이상의 파로 분리됨을 밝히고, 2차 이상의 파를 섭동법(Perturbation theory)을 이용하여 파형경사와 상대수심으로 표현하였다. Madsen(1971)은 선형파를 발생시키는 조파기를 이용하여 추가 비선형항을 고려한 2차 조파기 이론을 유도하였으며, Schäffer(1996)는 피스톤과 플랩조파기에 대한 2차 해를 유도하고 실험 검증에 활용하였다. Le Méhauté(2013)은 쇄파 현상을 분석하기 위해 여러 파 이론을 정리하여 수심에 따른 쇄파 발생 기준을 세웠다. Krvavica 등(2018)과 Lee 등(2020a)은 각각 플랩 및 피스톤 조파기를 이용하여 파형경사에 의한 쇄파 발생 지점을 추정하는 무차원 경험식을 제안하였다.

최근에는 큰 규모를 갖는 문제에 적용할 수 있고 유체와 구조물의 상호작용과 같은 복잡한 문제를 해결하기에 용이한 수치파동수조(Numerical Wave Tank, NWT)를 이용한 연구들이 다수 수행되고 있다. 이 중 Smoothed Particle Hydrodynamics(SPH) 기법은 입자에 기반한 수치해석 기법으로 Lucy(1977), Gingold and Monaghan(1977)에 의해 개발되었으며 주로 천문학 분야의 물리현상을 이해하기 위한 분야에 적용되었다. Monaghan (1994)은 댐 붕괴, 파 전파와 같은 유체 표면의 흐름 문제로 SPH 기법의 적용 범위를 확장하였다. Crespo 등(2007)은 고정된 벽 입자와 지배방정식을 공유하는 동적 경계 입자 기법을 사용하였으며 댐 붕괴 등의 모의에서 반발력과 투수 문제를 해결하였다. Dalrymple과 Rogers(2006)는 권파(plunging breaker), 댐 붕괴 등 다양한 문제에 SPH 기법을 적용하였다. Didier과 Neves(2012)는 SPH 기법을 이용하여 선형파를 생성하였고, 반사파를 감소시키기 위해 능동 반사파 흡수 시스템을 적용하였다. Altomare 등(2017)은 피스톤 조파기를 사용하여 선형, 2차 비선형 스토크파를 생성하였다. 능동·수동 반사파 흡수 영역을 수치파동수조에 적용하였고, 벽에 작용하는 파력을 계산하고 실험 결과와 비교함으로써 SPH 기법 기반의 수치모델의 계산 능력을 검증하였다. 최근에는 CFD(Computational fluid dynamics)를 이용하여 수치 파랑을 생성하는 연구도 활발히 진행중이다. Finnegan과 Goggins(2012)은 상용 CFD 프로그램인 ANSYS CFX를 이용하여 피스톤 조파기로 규칙파를 발생시키고 계산된 파고를 이론값과 비교하였다. CFD 모델의 최적화를 위해 격자 크기, 파의 반사와 흡수가 되는 지점의 바닥 경사, 계산시간 간격의 영향 또한 분석하였다. Prasad 등(2017)은 피스톤 조파기를 사용하여 CFD에 기반한 수치해석을 진행하였다. 계산된 파고와 조파기의 성능이 검증되었고, 실험결과와 잘 일치함을 보여주었다.

2. 이 론

2.1 이론적 배경

임의의 지점 x에서 특정한 물리량을 찾기 위해서 델타 함수로부터 계산 범위( $Ω$ ) 주위에 분포된 입자들의 물리량을 근사시킨다(Lee and Hong, 2020a).

(1)

\tilde{f} (x) = \int_{Ω}^{} f (x') δ (x - x') d x'

여기서, $f (x)$ 는 $x'$ 위치의 특정한 물리량을 의미하며, $δ (x - x')$ 는 디락 델타 함수, $x$ 는 임의의 위치 벡터, $x$ 은 $x$ 주위의 공간이다. 델타 함수를 완화 거리(smoothing length) $h$ 를 사용한 커널(kernel) 함수 $W (x_{i} - x_{j}, h)$ 를 이용하여 대체하고, 합의 형태로 표현하면 SPH 기본식은 다음과 같이 나타낼 수 있다.

(2)

f (x_{i}) = \sum_{j = 1}^{N} \frac{m_{j}}{ρ_{j}} f (x_{j}) W (x_{i} - x_{j}, h)

식 (2)에서 $N$ 은 완화 거리 이내에 있는 점의 숫자이고, $m_{j}$ , $ρ_{j}$ 는 $j$ 번째 입자의 질량과 밀도이다. 커널 함수로는 cubic B-spline이 사용되었고, 식은 아래와 같이 정의된다(Hallquist, 2006; 2007).

(3)

W (ξ_{i j}, h) = C \times \{\begin{matrix} 1 - \frac{3}{2} ξ_{i j}^{2} + \frac{3}{4} ξ_{i j}^{3} for ξ_{i j} \leq 1 \\ \frac{1}{4} (2 - ξ_{i j})^{3} for 1 < ξ_{i j} \leq 2 \\ 0, for 2 < ξ_{i j} \end{matrix}

여기서, $C$ 는 차원에 따라 결정되는 값으로 차원에 따라 각각 2차원에서 $C = 10 / (7 π h^{2})$ , 3차원에서 $C = 1 / (π h^{3})$ 이고, $ξ_{i j} =$ $∥ x_{i} - x_{j} ∥ / h$ 이다. SPH 기법에 대한 보다 자세한 이론적 설명은 Lee와 Hong(2020a; 2020b)에서 확인할 수 있다.

2.2 지배방정식과 상태방정식

일반적인 유체의 거동을 해석하기 위한 지배방정식은 다음과 같은 연속 방정식과 운동량 방정식이 있다.

(4)

\frac{D ρ}{D t} + ρ \frac{\partial v^{β}}{\partial x^{β}} = 0

(5)

- \frac{D v^{α}}{D t} + \frac{1}{ρ} \frac{\partial σ^{α β}}{\partial x^{β}} + F^{α} = 0

여기서, $ρ$ 는 밀도, $α, β = \{x, y, z\}$ , $x^{β}$ 는 좌표계, $v^{α}, v^{β}$ 는 좌표계 방향 속도, $σ^{α β}$ 는 전응력, $F^{α}$ 는 외력을 나타낸다. 식 (2)를 이용하여 SPH 기법 형태로 변환하면, 식 (4), (5)은 다음과 같이 표현된다.

(6)

\frac{D ρ_{i}}{D t} = \sum_{j = 1}^{N} m_{j} (v_{i}^{β} - v_{j}^{β}) \frac{\partial W_{i j}}{\partial x_{i}^{β}}

(7)

\frac{D v_{i}^{α}}{D t} = \sum_{j = 1}^{N} m_{j} (\frac{σ_{i}^{α β}}{ρ_{i}^{2}} + \frac{σ_{j}^{α β}}{ρ_{j}^{2}}) \frac{\partial W_{i j}}{\partial x_{i}^{β}} + F_{i}^{α}

여기서, $ρ_{i}$ 는 $i$ 번째 입자의 밀도를 나타낸다. 전응력 $σ^{α β}$ 는 압력과 전단응력으로 표현되고, 물과 같은 뉴턴 유체는 전단응력이 전단변형율에 비례하여 다음과 같이 표현된다.

(8)

σ^{α β} = - P δ^{α β} + τ^{α β}

(9)

τ^{α β} = μ ϵ^{α β}

여기서, $δ^{α β}$ 는 Kronecker delta, $τ^{α β}$ 는 점성에 의한 전단응력, $μ$ 는 점성계수, $ε$ 는 전단변형율을 나타낸다. 유체의 압력( $P$ )은 상태방정식(equation of state)을 통해 계산되는데, 유체의 압력과 물질의 특성에 따라 값이 정해진다. 다양한 상태방정식 중 Tait 상태방정식이 SPH 기법에서 주로 사용된다(Altomare et al., 2017).

(10)

P = \frac{c_{o}^{2} ρ_{o}}{γ} [{(\frac{ρ}{ρ_{o}})}^{γ} - 1]

여기서, $γ = 7$ , $ρ_{o}$ 는 기준밀도, $c_{o}$ 는 기준밀도에서의 음속을 나타낸다.

2.3 조파기 이론

조파기 이론은 비압축성, 비회전성 유체에 대해서 전파해 가는 2차원 파도를 대상으로 한다. 이러한 유체의 속도포텐셜은 2차원 라플라스 방정식을 만족한다(Dean and Dalrymple, 1991).

(11)

\nabla^{2 ϕ} = 0

수평한 해저면에서 유동이 없는 조건의 바닥 경계조건은 다음과 같이 표현된다.

(12)

- \frac{\partial ϕ}{\partial z} = 0

여기서, $z = η (x, t)$ 를 만족하며, 자유수면에서는 운동학적 자유수면 경계조건과 동적 자유수면 경계조건이 있는데 다음과 같이 각각 표현된다.

(13)

- \frac{\partial ϕ}{\partial z} = \frac{\partial η}{\partial t} - \frac{\partial ϕ}{\partial x} \frac{\partial η}{\partial x}

(14)

\frac{1}{2} [{(\frac{\partial ϕ}{\partial x})}^{2} + {(\frac{\partial ϕ}{\partial z})}^{2}] - \frac{\partial ϕ}{\partial t} + g η = C (t)

여기서, $ϕ$ 는 속도포텐셜, $η$ 는 수평평면( $z = 0$ )에 대한 자유수면의 변위이다. 위의 식을 이용하여 구한 속도포텐셜은 다음과 같다.

(15)

ϕ = - \frac{H g \cosh k (h + z)}{2 σ \cosh k h} \sin (k x - σ t)

여기서, $H$ 는 파고, $g$ 는 중력가속도, $k$ 는 파수, $h$ 는 수심, $σ$ 는 각 주파수를 나타낸다. 이 식은 조파기에서 만들어진 전진파를 나타내고 있고, 추가적으로 파가 진행하면서 사라지는 정재파를 추가하면 다음과 같이 표현된다.

(16)

ϕ = A_{p} \cosh k_{p} (h + z) \sin (k_{p} x - σ t) + \sum_{n = 1}^{\infty} C_{n} e^{- k_{s} (n) x} \cos [k_{s} (n) (h + z)] \cos σ t

조파기의 접촉경계면의 조건을 이용하여 파의 진폭( $A_{p}$ )을 구하면 다음과 같다.

(17)

A_{p} = \frac{- \int_{- h}^{0} \frac{S (z)}{2} σ \cosh k_{p} (h + z) d z}{k_{p} \int_{- h}^{0} \cosh^{2} k_{p} (h + z) d z}

이 속도포텐셜을 이용하여 자유수면 변위와 수평·수직방향 유속을 구하면

(18)

η (x, t) = \frac{H}{2} \cos (k x - σ t)

(19)

u = - \frac{\partial ϕ}{\partial x} = \frac{H}{2} σ \frac{\cosh k (h + z)}{\sinh k h} \cos (k x - σ t)

(20)

w = - \frac{\partial ϕ}{\partial x} = \frac{H}{2} σ \frac{\cosh k (h + z)}{\sinh k h} \sin (k x - σ t)

식 (17)을 식 (18)에 대입하면, 파고에 대한 조파거리의 비를 다음과 같이 표현할 수 있다.

(21)

\frac{H}{S} = \frac{2 (\cosh 2 k h - 1)}{\sinh 2 k h + 2 k h}

여기서, $S$ 는 조파기의 스트로크(stroke)를 의미한다. 수심, 파고, 파수 값이 정해지면 아래와 같이 피스톤 형태의 조파기의 수평방향 함수를 정할 수 있다.

(22)

x_{p i s t o n} = \frac{S}{2} \sin (σ t)

2차 섭동법을 이용하여 정리하면 다음과 같이 속도포텐셜과 수면변위를 구할 수 있다.

(23)

ϕ = - \frac{H g}{2 σ} \frac{\cosh k (h + z)}{\cosh k h} \sin (k x - σ t) - \frac{3}{32} H^{2} σ \frac{\cosh 2 k (h + z)}{\sinh^{4} k h} \sin 2 (k x - σ t)

(24)

η = \frac{H}{2} \cos (k x - σ t) + \frac{H^{2} k}{16} \frac{\cosh k h}{\sinh^{3} k h} (2 + \cosh 2 k h) \cos 2 (k x - σ t)

이때, 추가항으로 인해 최대·최소값은 감소하고 위상 차이로 인해 파가 진행하면서 변형된다. 속도포텐셜을 이용하여 수평·수직방향 유속을 구하면 다음과 같다.

(25)

u = \frac{H}{2} \frac{g k}{σ} \frac{\cosh k (h + z)}{\cosh k h} \cos (k x - σ t) + \frac{3}{16} \frac{H^{2} σ k \cosh 2 k (h + z)}{\sinh^{4} k h} \cos 2 (k x - σ t)

(26)

w = \frac{H}{2} \frac{g k}{σ} \frac{\sinh k (h + z)}{\cosh k h} \sin (k x - σ t) + \frac{3}{16} \frac{H^{2} σ k \sinh 2 k (h + z)}{\sinh^{4} k h} \sin 2 (k x - σ t)

최종적으로 피스톤 형태의 조파기를 이용하여 스토크파를 발생하기 위한 피스톤의 변위는 다음과 같이 표현된다(Madsen, 1971; Altomare et al., 2017).

(27)

x_{p i s t o n} = \frac{S}{2} \sin (σ t) + [\frac{H^{2}}{32 h} \frac{3 \cosh k h}{\sinh^{3} k h} - \frac{2 S}{H}] \sin (2 σ t)

2차 이상의 고차 해양파에 대한 이론은 Dean과 Dalrymple (1991)에서 참조하길 바란다.

3. 수치파동수조

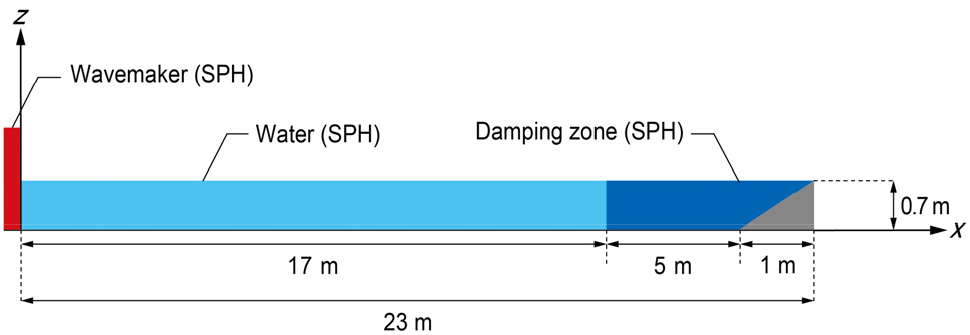
Schäffer(1996)는 길이 20m, 넓이 0.6m, 깊이 1.0m의 수조에서 수심을 0.7m로 고정하고 선형파 및 스토크파 이론을 이용하여 파를 생성하였으며, 파고의 시계열 자료를 조파기로부터 1m, 4m, 4.4m 8.7m 떨어진 지점에서 측정하였다. 본 연구에서는 입자를 이용한 수치해석법인 SPH 기법을 이용하여 Schäffer (1996)의 실험 수조와 유사한 크기의 수치파동수조를 모델링 하였다. 실험과 유사하게, 피스톤 조파기를 좌측 끝단에 배치하였으며, 17m 길이의 물과 5m 길이의 감쇠 영역이 설치되었다. 수치파동수조를 구성하는 물, 조파기, 감쇠 영역은 모든 방향으로 2cm 간격의 SPH 입자로 이루어져 있으며, 사용된 전체 입자 수는 약 1,200,000개이다. 모델에 사용된 수조는 Fig. 1에 나타내었다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F1.jpg

Fig. 1.

Schematics of the numerical wave tank

피스톤 조파기는 길이 0.16m, 폭 0.6m, 높이 1.6m로, 수평 방향을 제외한 모든 자유도는 고정되었다. 또한, 중력가속도에 의한 유체 입자의 재배열 후에 파랑을 생성하기 위해서 조파기에 해석 시작 후 약 1초 동안의 안정화 시간을 부여하였다(Lee and Hong, 2020a). 식 (22) 및 (27)이 조파기를 구성하는 입자에 적용되어 수평 방향으로 움직이며, 밀려난 물은 선형파 및 스토크파의 형태로 파랑이 생성된다. 조파기를 구성하는 입자에는 유체 입자와 같은 지배방정식 및 상태방정식(2.1~2.2절)이 사용되며, 별도의 접촉 알고리즘 없이 유체와 조파기의 상호작용을 효과적으로 모사할 수 있다(Lee and Hong, 2020b). 반사파에 의한 파고 교란을 최소화하기 위해서 질량 가중 감쇠영역을 수조 우측 끝단에 설치하였으며, 유체 입자와 동일한 재료적 성질을 가지고 지배방정식이 계산된다. Lee와 Hong(2020b)은 감쇠 영역의 형태와 크기에 따른 최적의 감쇠 계수를 제안하였으며, 본 연구에서 다룬 모든 수치해석 모델의 감쇠 계수는 1이 사용되었다. 해석에 사용된 상세한 파라미터는 Table 1에 나타냈다.

Table 1.

Material properties of SPH particles and numerical parameters(Lee and Hong, 2020b)

Density( $k g / m^{3}$ )	1000
Dynamic viscosity( $P a ∙ s$ )	0.001
Speed of sound of water( $m / s$ )	1478
Numerical speed of sound $C_{0}$	32.4

입자를 이용하여 유체의 침투를 방지하는 경계 기법을 적용하여 수조벽을 구성하였으며, 경계 주변의 유체 입자와 벽 입자는 접선 방향 속도 성분이 반대 부호를 가지므로 노슬립 경계조건을 만족한다(Lee and Hong, 2020b). SPH 기법을 이용한 보다 상세한 수치해석 방법에 관해서는 Lee 등(2020a)에서 참조할 수 있다. 본 연구에서는 Schäffer(1996)가 수행한 실험 결과와 수치해석 결과를 비교하여 수치파동수조의 파랑 생성 능력을 검증하였으며(4.1절), 4.2절에서는 목표 파고를 3종류로 나누고 파형경사(wave steepness) 및 상대 수심(relative depth)에 따른 파랑 생성 정확도를 비교하였다.

4. 결과 및 분석

4.1 수치파동수조 검증

4.1절에서는 3절에서 제안한 수치파동수조를 이용하여 선형파 및 스토크파를 생성하였으며, Schäffer(1996)의 실험결과와 비교를 통해서 생성된 수치파랑의 정확도를 검증하였다. 목표 파 조건은 Table 2에 나타내었으며, 선형파 및 스토크파 스트로크 식은 2.3절에서 확인할 수 있다.

Table 2.

Parameters of linear and Stokes wave in the experiment(Schäffer, 1996)

Wave height H(m)	0.14
Wave period T(s)	3
Water depth d(m)	0.7
Relative depth kd	0.591
Wavelength L(m)	7.446
Wave steepness H/L	0.019

피스톤 조파기의 스트로크에 의해서 수조 내부의 유체가 밀리면서 파랑이 생성되기 시작하며, 파랑을 구성하는 SPH 입자는 타원형 형태로 운동을 한다. 따라서, 초기( $t = 0$ )에 측정 지점에 위치한 유체 입자의 변위-시간 이력을 특정 지점에서의 파고로 결정할 수 없다. 정확한 파고의 시계열을 계산하기 위해서, 모든 유체 입자들의 수직 및 수평 방향 좌표와 변위, 속도의 시계열을 계산하였다. 수평 방향(x 방향) 좌표를 이용하여 측정 지점을 지나는 입자들을 분류하고, 수직 방향 좌표(z 방향)를 이용하여 수면의 입자들만 선별한다. 이 때, 측정 지점을 지나는 모든 유체 입자들중에서 수면( $z = 0$ )을 기준으로 절대값이 가장 큰 입자들의 좌표값 차이가 파고를 나타낸다고 판단하였으며, 동일한 입자의 수평방향 및 연직방향 속도 시계열을 유속으로 판단하였다. 이와 같은 방법으로 모든 해석에서 파고, 연직 및 수평 유속을 계산하였다.

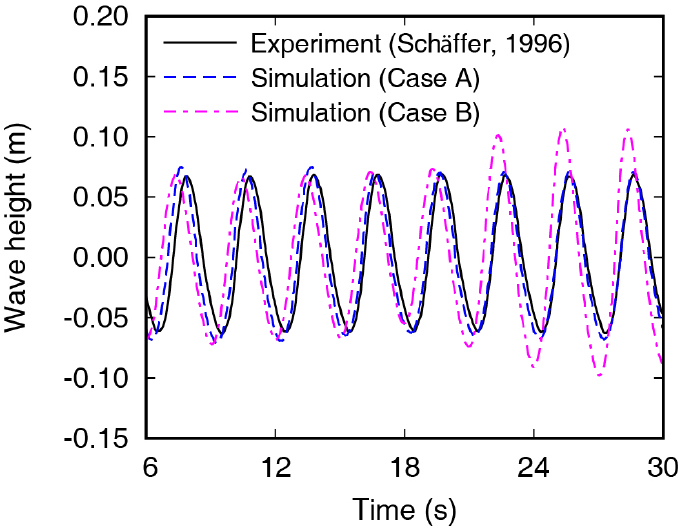
Fig. 2에는 조파기로부터 1m 떨어진 지점에서 측정된 실험 결과와 감쇠영역이 적용된 모델(Case A) 및 감쇠영역이 적용되지 않은 수치파동수조(Case B)의 파고 시계열을 나타냈다. 실험결과와 비교할 때, Case B를 이용하여 계산한 파고의 경우 20초 이후 반사파의 영향으로 인하여 파고가 약 0.2m까지 43% 증가하는 양상을 보였으나 Case A의 파고는 실험결과와 유사하게 0.143m로 계산되었다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F2.jpg

Fig. 2.

Comparison of experimental and numerical wave heights

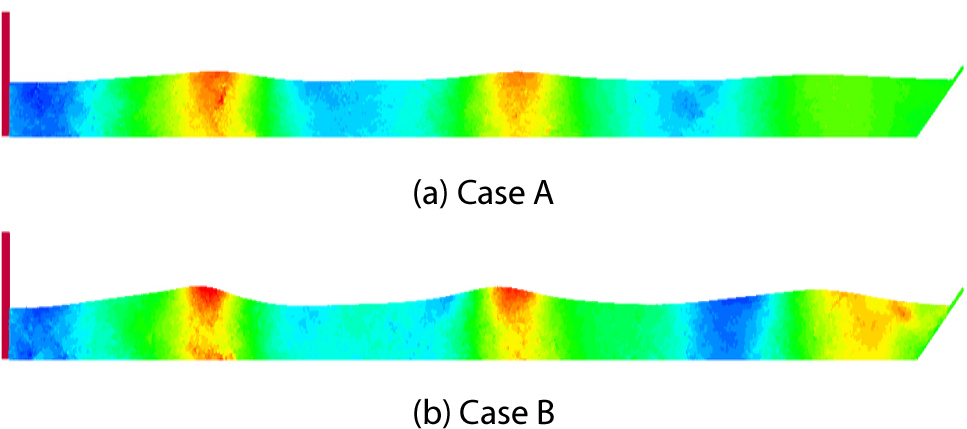
Fig. 3에는 Case A와 Case B 모델의 수평유속 분포를 나타냈다. Case A의 경우 파정에서 최대 수평유속이, 파저에서 최소 수평유속이 측정되었으며, 감쇠영역의 역할로 수조의 전 구역에서 균일한 유속 분포를 보였다. 반면, Case B의 경우에는 수조의 우측 끝단에서 반사파로 인해 유속 분포가 균일하지 않게 계산되었으며, 파고 또한 간섭으로 과도해지는 양상을 보였다. 수치파동수조의 감쇠영역은 반사파를 효과적으로 제거할 수 있으며, 장시간 동안 균일한 파의 생성에 사용할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F3.jpg

Fig. 3.

Lateral view of horizontal particle velocities by use of (a) the NWT without a damping zone and (b) with a damping zone

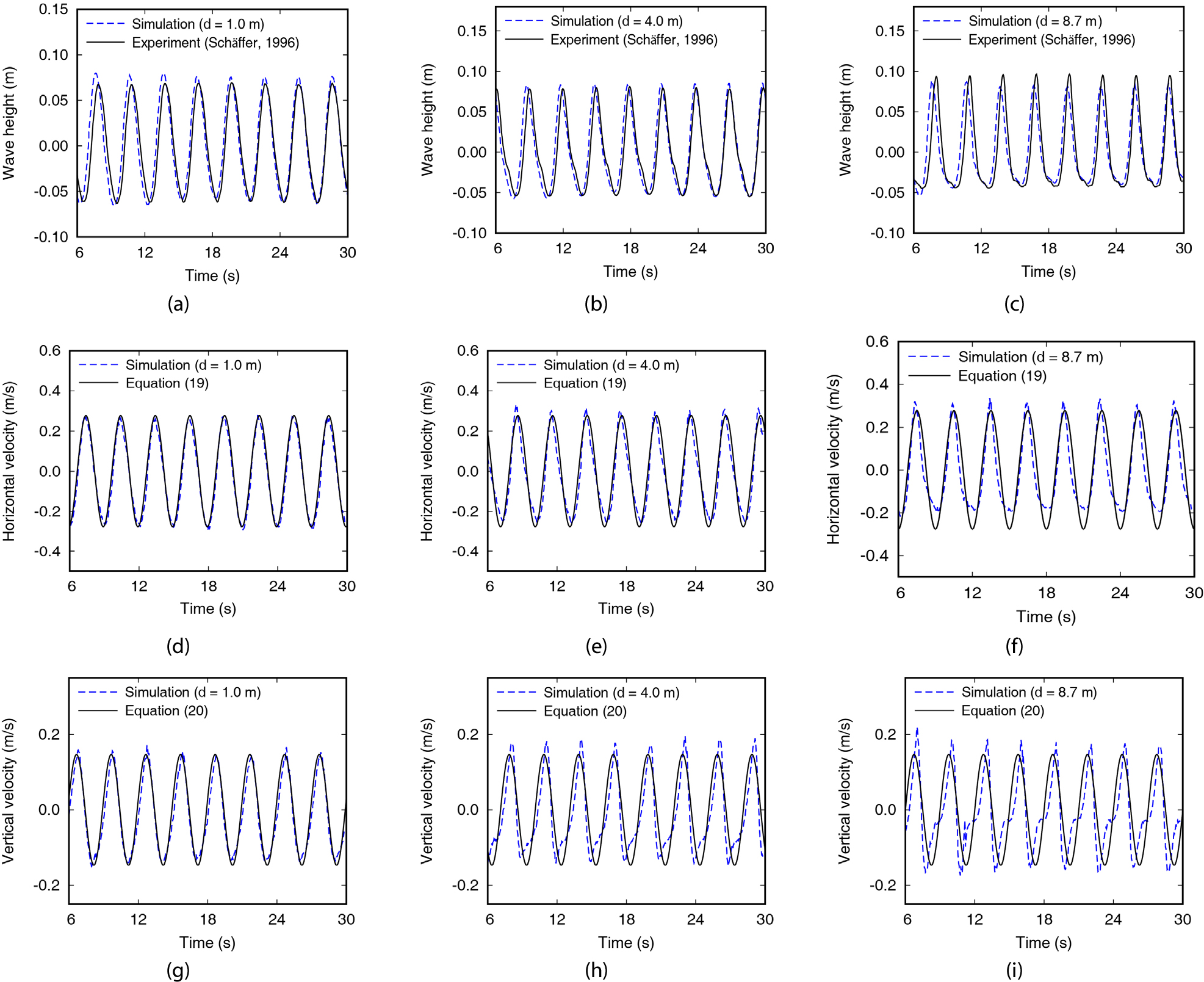
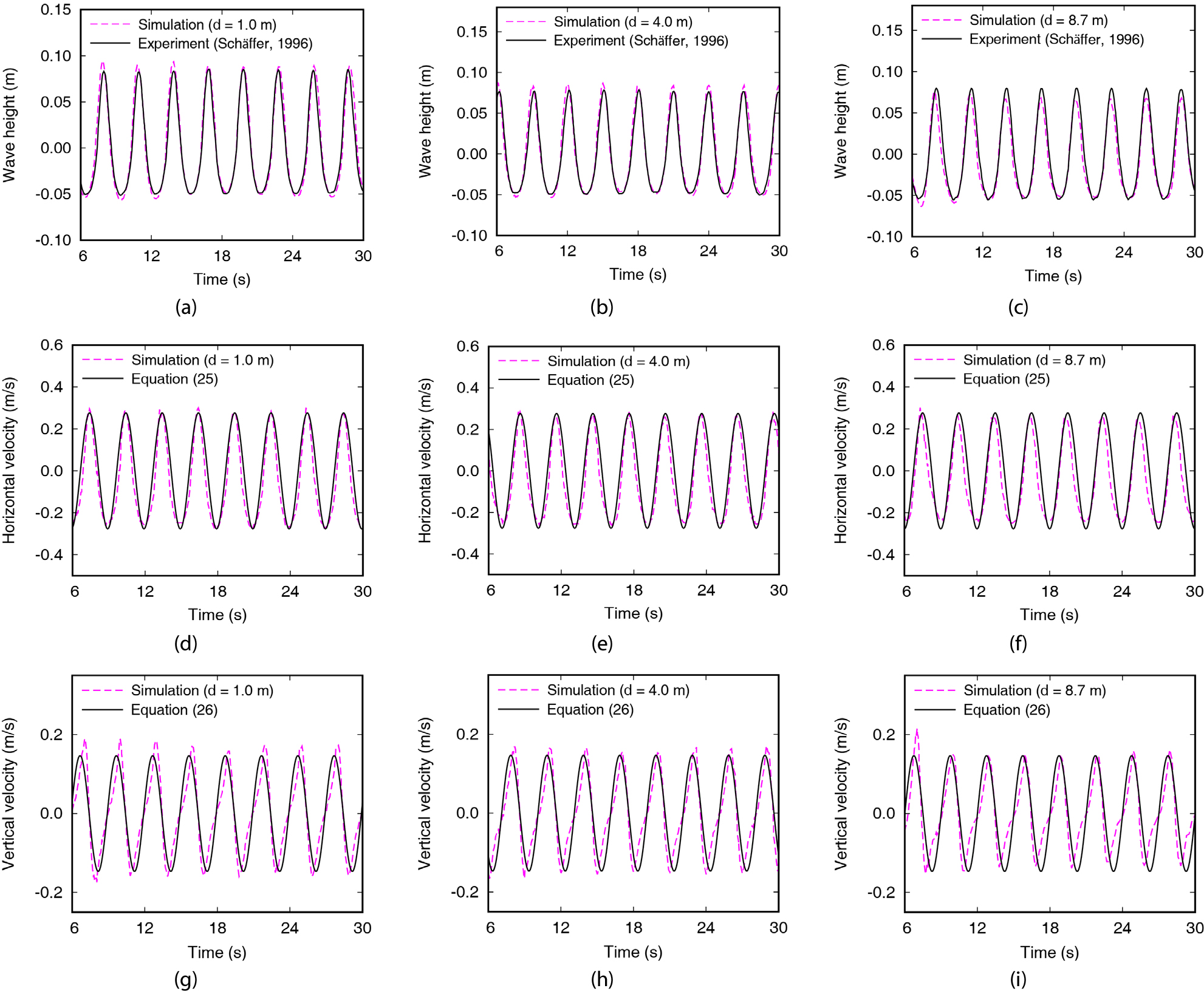
측정지점에 따른 해석 정확도를 비교하기 위해서 조파판으로부터 1, 4, 8.7m 떨어진 지점에서 측정된 파고와 수치해석 파고의 시계열을 비교하였으며, 같은 위치에서의 연직 및 수평 유속을 선형파 이론식과 비교하였다. Figs. 4(a), (b)를 보면, 조파판에서 각각 1m, 4m 떨어진 지점에서 계산된 수치해석 파고는 실험에서 관측된 결과보다 약간 과도하거나 유사하게 계산되었으며, 8.7m 떨어진 지점에서 계산한 파고(Fig. 4(c))의 경우 이론값보다 약간 과소하게 계산되었다. 이론식과 비교할 때, 수평유속과 연직유속 모두 조파판에서 멀어질수록 오차가 증가하는 경향을 보였으며, 연직유속은 파저에서 비선형적인 형상으로 계산되었다(Figs. 4(h) and (i)).

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F4.jpg

Fig. 4.

Comparison of the wave heights, horizontal and vertical velocities of linear waves in experiments and simulations

Fig. 5에는 선형파와 동일한 파랑 조건(Table 2)을 이용하여 스토크파 이론을 이용하여 수행한 해석 결과를 나타내었다. 파고의 경우, 조파판으로부터 가장 멀리서 측정한 Fig. 5(c)에서 약간 과소하게 측정되었으나, 선형파 이론을 적용한 Fig. 4(c)의 결과보다 더 실험결과와 유사하게 계산되었다. 수평유속의 경우 측정위치에 관계없이 이론식과 높은 일치도로 계산되었으며, 연직유속 또한 선형파 결과보다 정확하게 계산되었다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F5.jpg

Fig. 5.

Comparison of the wave heights, horizontal and vertical velocities of Stokes waves in experiments and simulations

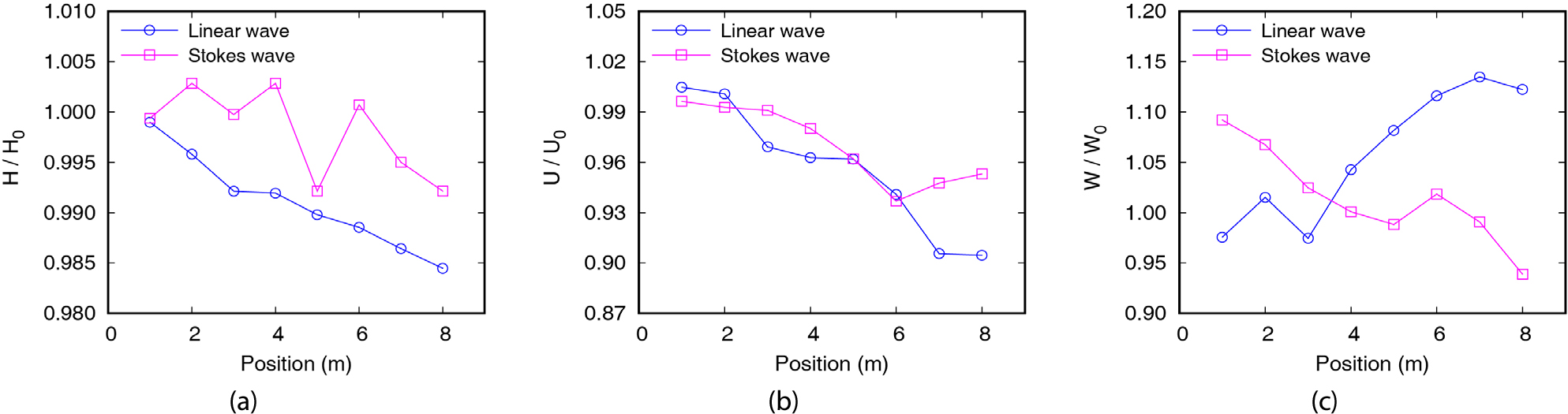
조파판으로부터 측정지점까지 거리 변화에 따른 파고 및 유속 생성 정확도를 분석하기 위해서 Fig. 6에 무차원화된 변수를 이용하여 해석 결과를 나타냈다. $H_{0}$ 는 목표 파고인 0.14m이고, $U_{0}$ 와 $W_{0}$ 는 선형파 및 스토크파 이론식으로부터 계산한 수평 및 연직 속도 함수 최댓값이다. $H$ , $U$ , $W$ 는 각각 수치파동수조에서 조파판으로부터 1m 간격으로 계산한 파고, 수평 및 연직 유속이다. $H_{0} / H$ , $U_{0} / U$ , $W_{0} / W$ 는 파랑성분의 정확도를 판단할 수 있는 무차원 변수이며, 1에 가까울수록 목표 파고 및 유속과 해석결과의 일치도가 높음을 의미한다. Fig. 6을 보면 $H_{0} / H$ 과 $U_{0} / U$ 의 경우 조파판으로부터 측정지점이 멀어질수록 감소하는 양상을 보였으며, 선형파 이론을 이용한 $W_{0} / W$ 는 1보다 커지는 경향을 보였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F6.jpg

Fig. 6.

Comparison of the wave heights, horizontal and vertical velocities along the measurement positions

Table 2에서 언급하였듯이, 목표파의 파장은 7.446m이고, 파형경사는 0.019이다. Ursell 등(1960)의 선행 연구에서 파형경사 0.03보다 작은 경우, 실험에서 측정한 파고는 이론식보다 약 3-4% 작게 측정되었으며, Lee와 Hong(2020b)도 또한 파형경사가 0.045보다 작을 때, 실험 및 수치해석을 이용하여 4% 이내의 오차로 파랑을 생성하였다.

Table 3에는 무차원 변수들의 값과 오차를 나타냈다. 선형파 이론을 이용한 수치파고의 최대 오차는 1.55%이고, 스토크파 이론을 적용한 모델의 수치파고 최대 오차는 0.79%이다. 수평 및 연직유속의 경우 선형파 이론을 적용한 모델의 평균오차는 각각 4.52%, 7.03%로 계산되었으며, 스토크파 이론을 적용할 때 약 3.6% 이내의 오차로 계산되었다. 파고의 최대 오차는 모두 조파판에서 8m 떨어진 지점에서 발생하였다. 수치파고의 오차는 선행연구들이 제안한 오차범위에 포함되며, Ursell 등(1960)이 제안한 작은 파형경사(small wave steepness)의 범위에 포함되는 목표파 조건의 경우 파장보다 긴 거리에서도 안정적인 규칙파를 생성할 수 있다.

Table 3.

Errors in numerical wave profiles in accordance with the measurement positions

	1	2	3	4	5
$H / H_{0}$ (Linear)	0.999	0.996	0.992	0.992	0.990
$H$ Error(%)	0.10	0.42	0.79	0.81	1.02
$U / U_{0}$ (Linear)	1.005	1.001	0.969	0.963	0.962
$U$ Error(%)	0.48	0.08	3.08	3.72	3.82
$W / W_{0}$ (Linear)	0.976	1.015	0.975	1.043	1.082
$W$ Error(%)	2.44	1.52	2.55	4.27	8.18
$H / H_{0}$ (Stokes)	0.999	1.003	1.000	1.003	0.992
$H$ Error(%)	0.06	0.29	0.03	0.29	0.79
$U / U_{0}$ (Stokes)	0.996	0.993	0.991	0.980	0.962
$U$ Error(%)	0.36	0.72	0.90	1.99	3.79
$W / W_{0}$ (Stokes)	1.092	1.067	1.025	1.001	0.988
$W$ Error(%)	9.22	6.74	2.47	0.09	1.18
	6	7	8	Average
$H / H_{0}$ (Linear)	0.989	0.986	0.984	0.990
$H$ Error(%)	1.15	1.36	1.55	0.90
$U / U_{0}$ (Linear)	0.941	0.906	0.905	0.956
$U$ Error(%)	5.92	9.45	9.54	4.52
$W / W_{0}$ (Linear)	1.116	1.134	1.122	1.058
$W$ Error(%)	11.62	13.47	12.24	7.03
$H / H_{0}$ (Stokes)	1.001	0.995	0.992	0.998
$H$ Error(%)	0.07	0.50	0.79	0.35
$U / U_{0}$ (Stokes)	0.937	0.948	0.953	0.970
$U$ Error(%)	6.32	5.23	4.69	3.00
$W / W_{0}$ (Stokes)	1.018	0.991	0.939	1.015
$W$ Error(%)	1.84	0.92	6.12	3.57

4.2 다양한 파 조건을 이용한 수치파 생성 능력 분석

4.1절에서 다룬 목표파의 파형경사는 0.019로, 수치파동수조의 파랑 생성 능력을 검증하기 위해서는 다양한 파형경사를 갖는 파를 생성하고 분석할 필요가 있다. Table 4와 같이, 수조의 수심은 고정하고 상대수심이 0.5 간격이 되도록 목표 주기를 조절하였으며, 목표 파고를 0.03m( $H_{1}$ ), 0.05m( $H_{2}$ ), 0.10m( $H_{3}$ )로 변화를 주어 파형경사를 조절하였다.

Table 4.

Parameters of waves in numerical simulations

Case No.	1	2	3	4
Wave period $T$ ( $s$ )	3.500	1.900	1.440	1.200
Relative depth $k h$	0.5	1.0	1.5	2.0
Wave steepness $H_{1} / L$	0.003	0.007	0.010	0.014
Wave steepness $H_{2} / L$	0.006	0.012	0.017	0.023
Wave steepness $H_{3} / L$	0.011	0.023	0.034	0.046
Case No.	5	6	7	8
Wave period $T$ ( $s$ )	1.065	0.970	0.895	0.840
Relative depth $k h$	2.5	3.0	3.5	4.0
Wave steepness $H_{1} / L$	0.017	0.021	0.024	0.027
Wave steepness $H_{2} / L$	0.029	0.034	0.040	0.045
Wave steepness $H_{3} / L$	0.057	0.068	0.080	0.091

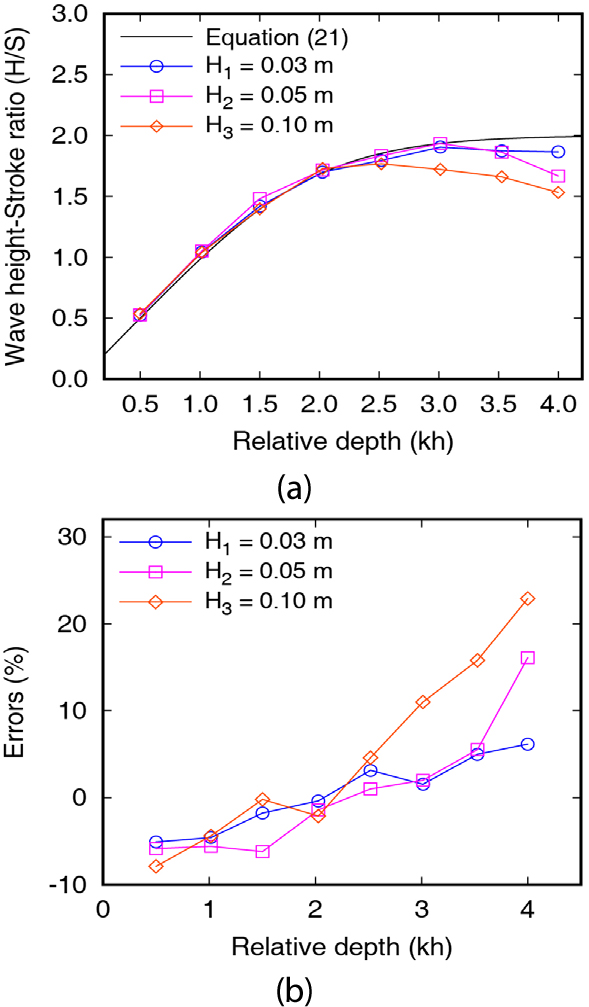
Fig. 7(a)는 이론 및 수치해석을 이용하여 구한 파고-스트로크 비를, Fig. 7(b)에는 상대수심에 대한 오차를 나타냈다. Fig. 7(a)의 파고-스트로크 비를 보면, 상대수심이 2 이하인 파를 생성하는 경우, 목표 파고에 관계없이 이론식과 유사한 파고를 생성할 수 있다. 그러나 $H_{2}$ 사례들의 경우 상대수심이 3을 초과할 때 수치 파고-스트로크 비가 이론식보다 과소하게 계산되었으며, $H_{3}$ 의 경우 상대수심이 2를 초과할 때 이론값보다 작은 파고가 생성되었다. 파고-스트로크 비가 이론값보다 현저하게 작아지는 상대수심은 Fig. 7(b)에서 파고 오차가 10%를 초과하는 시점임을 알 수 있다. 따라서 파고-스트로크비 이론식보다 수치해석 결과가 과소하게 계산되는 시점은 상대수심 뿐만 아니라 목표 파고의 영향 또한 받기 때문에 파고-파장비(파형경사)에 따른 오차범위 확인이 필요하다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F7.jpg

Fig. 7.

Comparison of the wave height to stroke ratio obtained using linear wavemaker theory and via numerical simulation

Fig. 7(b)와 Table 4를 보면, 목표파고가 $H_{1}$ 인 사례들은 모든 주기에서 0.03 이하의 작은 파형경사 범위에 포함되며, 모든 파랑을 6% 이내의 오차로 생성할 수 있다. $H_{2}$ 와 $H_{3}$ 의 경우에는 파형경사가 각각 0.045( $H_{2}$ -Case 8), 0.068( $H_{3}$ -Case 6)일 때 오차가 10%를 초과한다. 하지만 $H_{3}$ -Case 4의 파형경사는 0.046으로 $H_{2}$ -Case 8과 유사한 파형경사를 갖지만, 상대수심은 2 이하이며, 오차는 아주 작다. 따라서 정확하게 생성 가능한 파랑 조건의 범위는 상대수심과 파형경사를 모두 고려하여 결정되어야 한다. 제안한 수치파동수조의 경우에는 목표파고가 수심의 1/7 이하일 때, 상대수심 2 이내의 파는 6% 이내의 오차로 생성할 수 있다. 그러나 상대수심이 2 이상이고, 파형경사 또한 0.04 이상인 경우에는 최대 10% 이상의 오차가 발생할 수 있다.

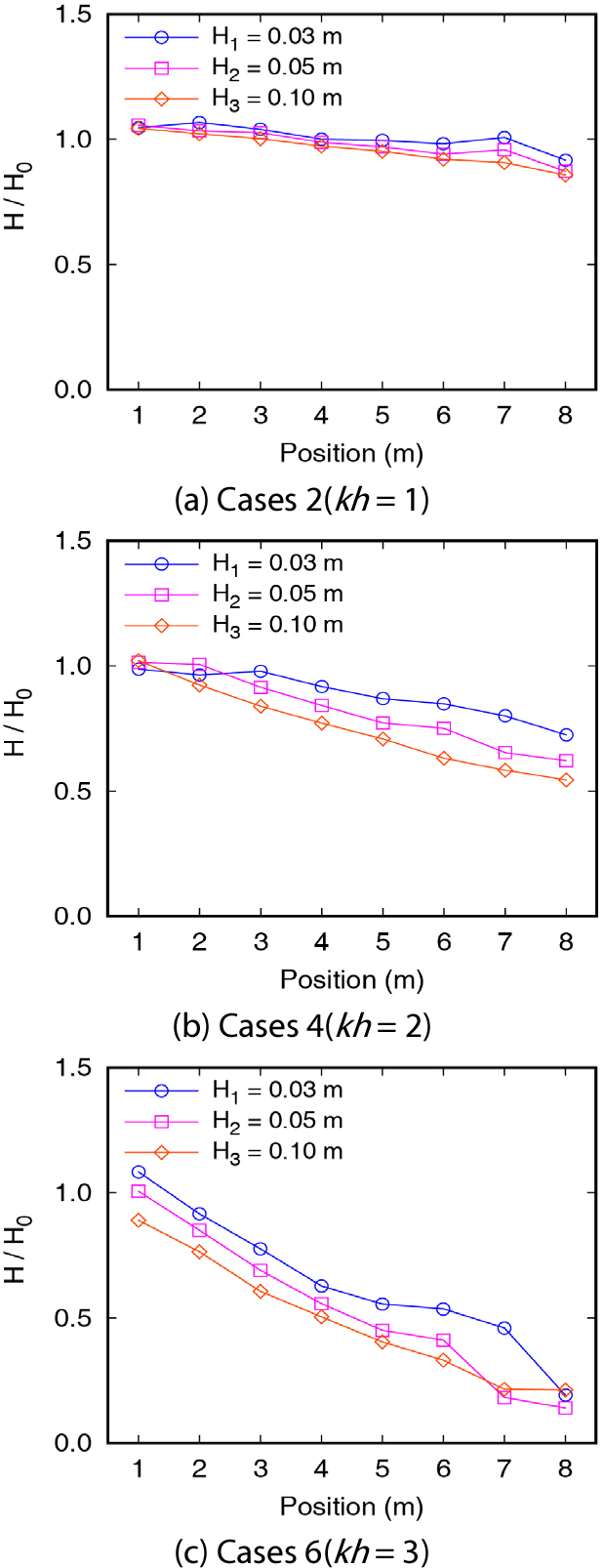
다음으로 측정위치에 따른 파고 오차를 확인하기 위해서, 상대수심이 각각 1, 2, 3인 사례들의 $H / H_{0}$ 를 Fig. 8에 나타냈다. 상대수심이 증가할수록 조파기로부터의 측정위치가 멀어질수록 $H / H_{0}$ 가 감소하는 경향을 보였다. 상대수심이 1일 때, 수치 파고는 측정위치와 목표파고 값에 관계없이 8.37% 이내의 오차로 계산되었으나, 상대수심이 3인 경우에는 측정위치에 따른 오차가 가파르게 증가하였다. 따라서, 본 연구에서 제안한 수치파동수조는 주기가 짧고(상대수심이 크고), 파형경사가 큰 파를 생성하고 조파판으로부터 먼 관측위치에서 파고를 얻고자 할 때는 주의가 필요하다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-01/N0040340108/images/Figure_jcoseik_34_01_08_F8.jpg

Fig. 8.

Comparison of the wave heights along the measurement position

5. 결 론

본 연구에서는 입자기반 수치해석법인 SPH(Smoothed Particle Hydrodynamics) 기법을 이용하여 수치파동수조를 모델링하였으며, 선형파 및 스토크파 이론을 적용하여 파랑을 생성하고 실험 결과와 비교를 통하여 검증하였다. 또한, 조파 능력을 검증하기 위해서 다양한 범위를 갖는 파랑을 생성하고 파고-스트로크 비 이론식과 비교하여 안정적으로 조파가 가능한 파형경사 범위 및 상대수심을 제안하였다. 실제 해양문제에 효과적인 적용을 위해서 감쇠 영역의 효과와 조파기로부터의 측정 위치에 따른 정확도 또한 분석되었다.

제안한 수치파동수조를 검증하기 위해서 선형파 및 스토크파 이론을 적용하여 파랑을 생성하고, 약 30초간의 파고, 연직 및 수평 유속의 시계열을 Schäffer(1996)의 실험결과 및 이론식과 비교를 통하여 검증하였다. 감쇠영역이 없는 모델의 경우 반사파의 영향으로 인하여 계산된 파고가 목표파고 대비 43% 증가하였으나, 감쇠 영역이 적용된 모델의 경우 실험결과와 유사하게 파고가 생성되었다. 조파판으로부터 측정지점이 멀어짐에 따라서 수치 파고와 유속 모두 감소하는 경향을 보였으나, 목표 파장보다 더 먼 지점에서도 1% 이내의 오차로 계산되었다. 또한, 유사한 조건의 파랑을 생성할 때, 스토크파 이론이 적용된 모델의 파고 및 유속 결과가 선형파를 이용한 결과보다 더 좋은 일치도를 보였다.

파의 생성 능력을 검증하기 위해서 목표 파고 및 주기에 변화를 주며 해석이 수행되었다. 목표 파고가 수심의 1/7 이하일 때, 상대수심이 2 이하인 경우, 목표 파고에 관계없이 6% 이내의 오차범위에서 파랑을 생성할 수 있다. 또한 파형경사가 0.03 이하인 경우 파고의 측정위치가 목표파장보다 긴 곳에서도 정확한 수치파를 생성할 수 있다. 그러나 상대수심과 파형경사가 각각 2, 0.04 이상인 경우, 최대 10% 이상의 오차가 발생할 수 있다. 또한 조파판으로부터 측정 위치가 멀어짐에 따라서 파고의 정확도는 감소하는 경향을 보였으며, 주기가 짧고 파형경사가 큰 파를 만들 때는 목표 파장 이내 거리에서 정확도가 확보된다.

제안한 수치파동수조는 적절한 감쇠 계수가 적용될 때, 반사파를 효과적으로 제거할 수 있으며, 다양한 파형경사와 상대수심을 갖는 파랑을 파장 범위에 포함되는 측정점에서는 정확하게 생성할 수 있음을 보였다. 본 연구에서 제안한 수치파동수조를 이용하여 유체-구조물 상호작용 해석 문제로 확장할 수 있으며, 다양한 주기와 파고를 갖는 여러 해양문제 해석에 적용할 수 있다. 또한, 감쇠 영역을 이용하여 해석 규모를 줄여 효율적인 해석이 가능할 것으로 기대된다.

Acknowledgements

이 논문은 국토교통부의 스마트시티 혁신인재육성사업으로 지원되었습니다. 또한 본 연구는 과학기술정보통신부의 재원으로 한국연구재단의 지원(No. 2017R1A5A1014883)을 받아 수행되었습니다. 이에 감사드립니다.

References

Altomare, C., Domínguez, J.M., Crespo, A.J.C., González-Cao, J., Suzuki, T., Gómez-Gesteira, M., Troch, P. (2017) Long- Crested Wave Generation and Absorption for SPH-based DualSPHysics Model, Coast. Eng., 127, pp.37~54. 10.1016/j.coastaleng.2017.06.004

Crespo, A.J.C., Gómez-Gesteira, M., Dalrymple, R.A. (2007) Boundary Conditions Generated by Dynamic Particles in SPH Methods, Comput. Mater. & Contin., 5(3), pp.173~184.

Dalrymple, R.A., Rogers, B.D. (2006) Numerical Modeling of Water Waves with the SPH Method, Coast. Eng., 53(2-3), pp.141~147. 10.1016/j.coastaleng.2005.10.004

Dean, R.G., Dalrymple, R.A. (1991) Water Wave Mechanics for ENgineers and Scientists, Advanced Series on Ocean Engineering, 2, World Scientific Publishing Company, Singapore, pp.170~186. 10.1142/1232

Didier, E., Neves, M.G. (2012) A Semi-infinite Numerical Wave Flume Using Smoothed Particle Hydrodynamics, Int.J. Offshore & Polar Eng., 22(03), pp.193~199.

Finnegan, W., Goggins, J. (2012) Numerical Simulation of Linear Water Waves and Wave-structure Interaction, Ocean Eng., 43, pp.23~31. 10.1016/j.oceaneng.2012.01.002

Goda, Y. (1967) Travelling Secondary Wave Crests in Wave Channels, Port and Harbour Research Institute, Ministry of Transport, Japan, 13, pp.32~38.

Gingold, R.A., Monaghan, J.J. (1977) Smoothed Particle Hydrodynamics: Theory and Application to Non-spherical Stars, Mon. Not. R. Astron. Soc., 181(3), pp.375~389. 10.1093/mnras/181.3.375

Havelock, T.H. (1929) LIX. Forced Surface-Waves on Water, The Lond. Edinb. & Dublin Philos. Mag. & J. Sci., 8(51), pp.569~576. 10.1080/14786441008564913

Hallquist, J.O. (2006) LS-DYNA Theory Manual.

Hallquist, J.O. (2007) Ls-dyna Keyword User's Manual. Livermore Software Technology Corporation.

Kim, T.Y., Jang, S.J., Kim, C.K. (2017) Application of InVEST Offshore Wind Model for Evaluation of Offshore Wind Energy Resources in Jeju Island, J. Korean Assoc. Geogr. Inf. Stud., 20(2), pp.47~59.

Krvavica, N., Ružić, I., Ožanić, N. (2018) New Approach to Flap-type Wavemaker Equation with Wave Breaking Limit, Coast. Eng., 60(1), pp.69~78. 10.1080/21664250.2018.1436242

Le Méhauté, B. (2013) An Introduction to Hydrodynamics and Water Waves, Springer Science and Business Media, Berlin, Heidelberg, p.205.

Lee, S., Hong, J.W. (2020a) Parametric Studies on Smoothed Particle Hydrodynamic Simulations for Accurate Estimation of Open Surface Flow Force, Int. J. Naval Arch. & Ocean Eng., 12, pp.85~101. 10.1016/j.ijnaoe.2019.07.003

Lee, S., Hong, J.W. (2020b) A Semi-Infinite Numerical Wave Tank Using Discrete Particle Simulations, J. Mar. Sci. & Eng., 8(3), pp.159~162. 10.3390/jmse8030159

Lee, S., Ko, K., Hong, J.W. (2020a) Comparative Study on the Breaking Waves by a Piston-type Wavemaker in Experiments and SPH Simulations, Coast. Eng., 62(2), pp.267~284. 10.1080/21664250.2020.1747141

Lee, K., Ha, Y.J., Kim, K.H., Hong, S.Y. (2020b) Evaluation of Structural Response of Cylinderical Structures Based on 2D Wave-Tank Test Due to Wave Impact, J. Comput. Struct. Eng. Inst. Korea, 33(5), pp.287~296. 10.7734/COSEIK.2020.33.5.287

Lucy, L.B. (1977) A Numerical Approach to the Testing of the Fission Hypothesis, The Astron. J., 82(12), pp.1013~1024. 10.1086/112164

Madsen, O.S. (1971) On the Generation of Long Waves, J. Geophys. Res., 76(36), pp.8672~8683. 10.1029/JC076i036p08672

Monaghan, J.J. (1994) Simulating Free Surface Flows with SPH, J. Comput. Phys., 110(2), pp.399~406. 10.1006/jcph.1994.1034

Morison, J.R., Johnson, J.W., Schaaf, S.A. (1950) The Force Exerted by Surface Waves on Piles, J. Pet. Technol., 2(05), pp.149~154. 10.2118/950149-G

Prasad, D.D., Ahmed, M.R., Lee, Y.H., Sharma, R.N. (2017) Validation of a Piston Type Wave-maker Using Numerical Wave Tank, Ocean Eng., 131, pp.57~67. 10.1016/j.oceaneng.2016.12.031

Schäffer, H.A. (1996) Second-order Wavemaker Theory for Irregular Waves, Ocean Eng., 23(1), pp.47~88. 10.1016/0029-8018(95)00013-B

Ursell, F., Dean, R.G., Yu, Y.S. (1960) Forced Small-amplitude Water Waves: a Comparison of Theory and Experiment, J. Fluid Mech., 7(1), pp.33~52. 10.1017/S0022112060000037

Wienke, J., Oumeraci, H. (2005) Breaking Wave Impact Force on a Vertical and Inclined Slender Pile-theoretical and Large-scale Model Investigations, Coast. Eng., 52(5), pp.435~462. 10.1016/j.coastaleng.2004.12.008

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

SPH-Based Wave Tank Simulations

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

Fig. 1.

Schematics of the numerical wave tank

Table 1.

Material properties of SPH particles and numerical parameters(Lee and Hong, 2020b)

Table 2.

Parameters of linear and Stokes wave in the experiment(Schäffer, 1996)

Fig. 2.

Comparison of experimental and numerical wave heights

Fig. 3.

Lateral view of horizontal particle velocities by use of (a) the NWT without a damping zone and (b) with a damping zone

Fig. 4.

Comparison of the wave heights, horizontal and vertical velocities of linear waves in experiments and simulations

Fig. 5.

Comparison of the wave heights, horizontal and vertical velocities of Stokes waves in experiments and simulations

Fig. 6.

Comparison of the wave heights, horizontal and vertical velocities along the measurement positions

Table 3.

Errors in numerical wave profiles in accordance with the measurement positions

Table 4.

Parameters of waves in numerical simulations

Fig. 7.

Comparison of the wave height to stroke ratio obtained using linear wavemaker theory and via numerical simulation

Fig. 8.

Comparison of the wave heights along the measurement position

Acknowledgements

References