1. 서 론
2. 무조인트 교량
3. 수치해석 모델
3.1 구조모델
3.2 지반모델
4. 수치해석
4.1 대상 교량
4.2 해석 범위
4.3 해석 위치
4.4 분석 방법
5. 해석결과
5.1 A 교 모델
5.2 B 교 모델
5.3 C 교 모델
5.4 D 교 모델
6. 결 론
1. 서 론
최근 국내에서는 차량의 대형화와 교통량의 증가로 인해 교량에서 신축이음장치(expansion joint)의 파손이 빈번하게 발생되고 있다. 신축이음장치는 온도 변화에 따른 교량의 신축량을 흡수하기 위해 설치되었으나 파손으로 인해 교량에 막대한 피해를 입히고 있다. 신축이음장치의 파손으로 인해 소음 발생, 주행감 저하 등을 일으키고 파손된 틈으로 오염물질들이 유입되어 교량 받침 등과 같은 교량 주요 부재의 내구성을 저하시킨다. 이와 같은 문제점들을 해결하기 위해 신축이음장치를 설치하지 않고 상부구조와 교대를 일체화하는 무조인트 교량(Jointless bridge) 공법이 1930년대 이후 미국, 캐나다를 중심으로 개발되어 적용되고 있다(KECRI, 2018b).
국내에서 무조인트 교량은 1999년 A교가 최초 시공되었고 2009년 B교 시공 이후 본격적으로 도입되었다. 하지만 국내의 무조인트 교량은 해외의 경우에 비해 공용기간이 짧고, 시공 및 설계 사례 또한 부족한 상황이므로 무조인트 교량의 구조적 거동에 대한 신뢰도가 부족하다. 그러므로 무조인트 교량의 신뢰도 입증 및 확대 적용을 위해 무조인트 교량의 구조적 거동에 대한 지속적인 추적과 분석을 통한 연구가 활발하게 진행되어야 한다.
무조인트 교량의 구조적 거동은 현장 계측 데이터와 수치해석 결과의 비교를 통해 분석할 수 있다(Noh et al., 2021). 선행 연구(Noh et al., 2021)에서는 무조인트 교량의 거동을 분석하기 위한 수치해석 모델을 제시하였고 민감도 해석을 통해 수치해석 모델을 평가한 바 있다. 무조인트 교량의 수치해석 모델은 solid 요소 기반 모델과 변위 형상이 가장 유사하고 실용적인 shell 요소 기반 모델이 가장 적합한 것으로 제안되었다. 따라서 본 연구에서는 선행연구(Noh et al., 2021)에서 제안된 shell 요소 기반 모델과 solid 요소 기반 모델의 교대 벽체 상단, 중앙, 하단에서의 거동을 비교・분석하고자 한다.
무조인트 교량의 다양한 시공 및 설계 조건을 반영하기 위해 지반조건, 온도하중, 사각을 변수로 하여 해석하였다. 수치해석은 상용 유한요소 프로그램인 MIDAS Civil(MIDAS IT, 2020)과 ABAQUS(SIMULIA, 2020)를 사용하였다. 수치해석 모델간 거동 비교는 변위 형상 그래프와 상대오차 분석을 통한 정량적 평가에 의해 비교・분석하였다. 상대오차는 solid 요소 기반인 모델을 기준으로 하여 평균값을 산정하였다.
2. 무조인트 교량
무조인트 교량이란 기존 교량 형식에서 신축이음장치를 제거하고 교량의 상부구조와 단부 벽체를 일체화하는 교량을 의미한다. 현재 고속도로에 주로 사용되는 무조인트 교량은 신설구간에 주로 적용되는 완전일체식 교대 교량과 반일체식 교대 교량, 그리고 공용중에 적용할 수 있는 흉벽일체식(무조인트화) 교대 교량으로 분류된다. 완전일체식 교대 교량은 상부구조가 단부 벽체 및 기초부에 완전일체화되고 교량 받침이 없는 형식이다. 반일체식 교대 교량은 상부구조를 단부 벽체로 일체화시키고 온도 신축에 의한 상부구조의 수평 이동이 가능하도록 단부 벽체 하부와 교대벽체 상면에 교량받침을 두어 상부와 하부 구조물이 분리 시공된 단경간 또는 장경간 연속교이다(KECRI, 2019b). 흉벽일체식 교대 교량은 기존 조인트 교량의 신축이음장치를 제거한 후 상부구조와 교대 흉벽을 현장타설 철근 콘크리트로 일체화하여 무조인트 교량 형식으로 변경하는 공법이다(KECRI, 2019a). 이와 같은 무조인트 교량은 2018년 개정된 설계지침에 의해 사각은 교축 직각 방향을 기준으로 최대 30°까지 허용되었다. 또한 연장한계가 완전일체식 교대 교량의 경우 콘크리트교 180m, 강교 150m 이하, 반일체식 교대 교량의 경우 콘크리트교 500m, 강교 400m 이하로 대폭 늘어났다(KECRI, 2018a).
3. 수치해석 모델
3.1 구조모델
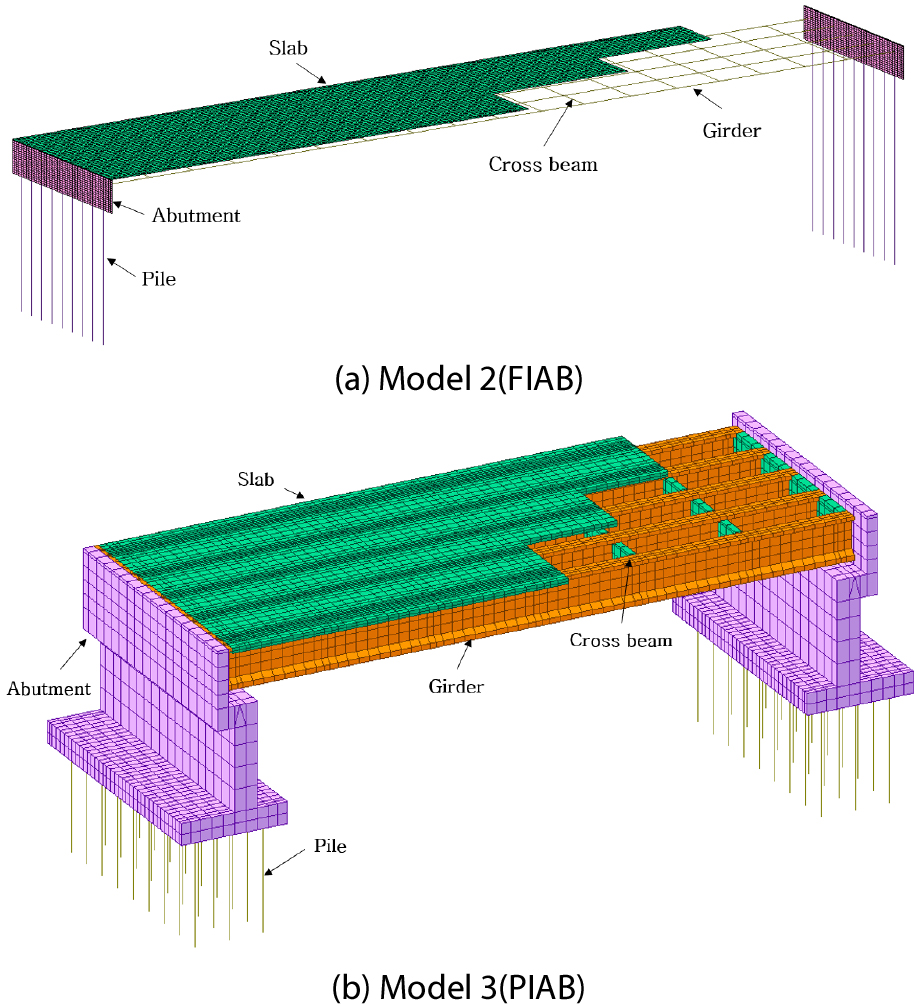
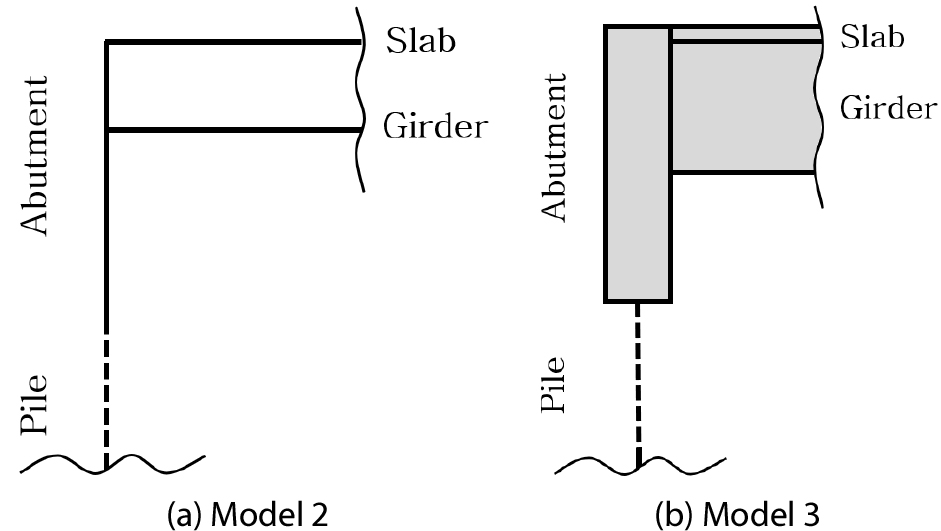
구조모델은 교량의 주요 부재인 바닥판, 거더, 교대 벽체 등을 유한요소를 사용하여 교량의 기하형상을 구현한 모델이다. 본 연구에서 사용된 구조모델은 Table 1과 같이 선행연구(Noh et al., 2021)에서 제시된 구조모델 중 모델 2(M2)와 모델 3(M3)을 사용하였다. 모델 2는 shell 요소 기반 구조모델이며 거더와 가로보, 말뚝의 경우는 모델링의 편의성을 고려하여 beam 요소를 적용하였다. 모델 3은 solid 요소 기반으로 한 구조모델이며 말뚝의 경우 beam 요소가 적용되었다. 단, 강박스 거더교의 경우 거더와 가로보는 shell 요소를 적용하였다. 여기서 각각의 구조모델의 요소망(mesh)은 정확한 비교・분석을 위해 모두 동일하게 적용하였다. 이와 같은 구조모델은 완전일체식 교대 교량(FIAB)의 모델 2와 흉벽일체식 교대 교량(PIAB)의 모델 3을 예시로 하여 Fig. 1에 나타냈다.
Table 1.
Classification of Structural models(Noh et al., 2021)
|
Structural Model | Slab | Girder | Cross beam | Abutment | Pile |
| M 2 | shell | beam | beam | shell | beam |
| M 3 | solid |
solid(PSC-I girder) shell(steel box girder) | solid | beam | |
3.2 지반모델
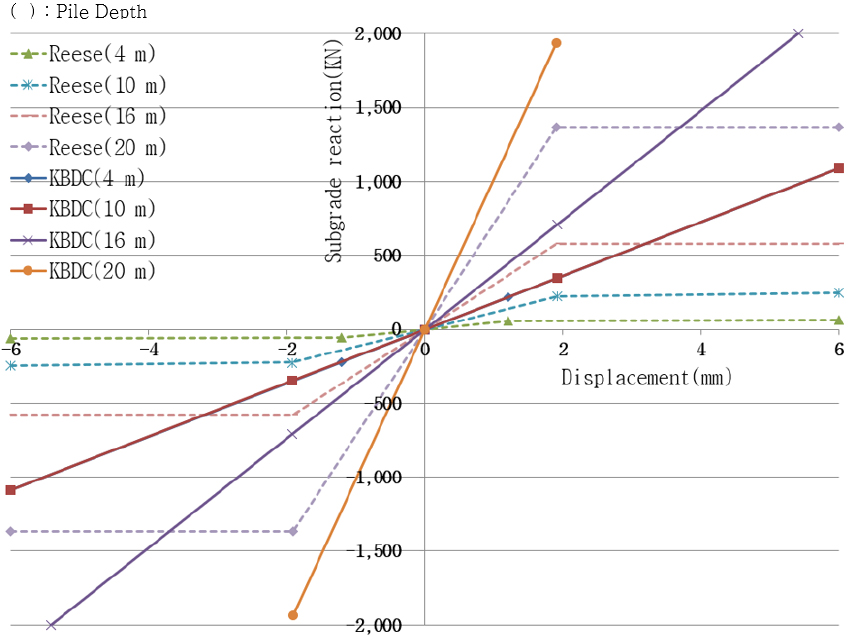
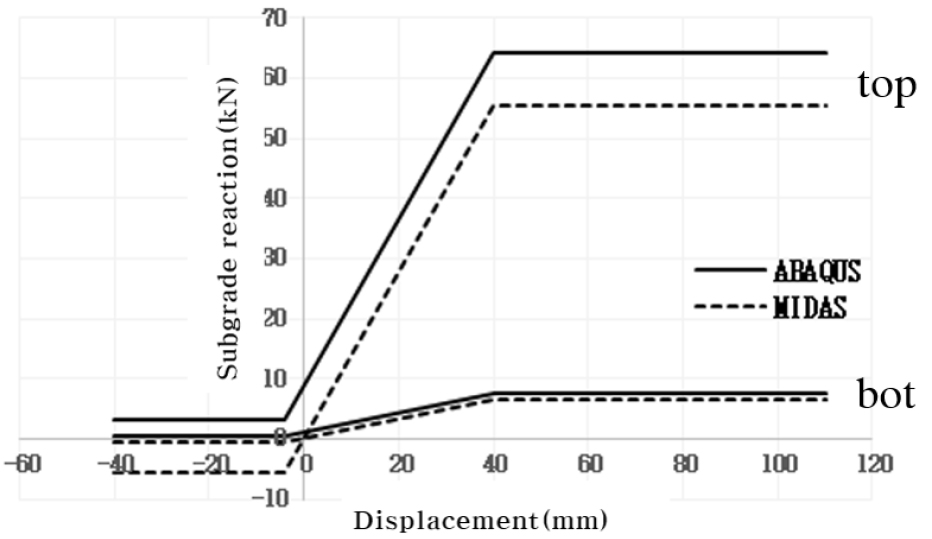
지반모델에서는 토압 또는 지반과 구조물간의 상호작용에 의한 변위와 지반반력의 거동을 구현한다(Noh et al., 2021). 본 연구에서 사용된 지반모델은 선행연구에서 사용된 조건을 적용하였다. 이는 국내・외 연구문헌에서 가장 많이 사용된 것으로 선형과 비선형 스프링 모델을 의미한다. Table 2에서 Case 1의 KBDC는 선형 스프링 모델이고 Case 2의 NCHRP 및 Reese 모델은 비선형 스프링 모델이다(KECRI, 2016). Fig. 2는 지반-교대에 대한 스프링 모델이며 수평변위와 지반반력의 관계를 KBDC의 선형 스프링 모델과 NCHRP의 비선형 스프링 모델로 나타낸 그림이다. KBDC 조건은 실선, NCHRP 조건은 점선으로 나타냈다. Fig. 3은 지반-말뚝에 대한 스프링 모델이며 수평변위와 지반반력의 관계를 KBDC의 선형 스프링 모델과 Reese의 비선형 스프링 모델로 나타낸 그림이다. KBDC 조건의 경우는 실선, Reese의 경우는 점선으로 표현하였다.
Table 2.
soil model for sensitivity analysis(Noh et al., 2021)
| Categorize | Soil model | |
| Case 1 | Case 2 | |
| Soil-Abutment | KBDC | NCHRP |
| Soil-Pile | KBDC | Reese |
4. 수치해석
4.1 대상 교량
수치해석 대상 교량의 교량 형식과 구조적 기하 조건을 Table 3에 나타냈다. 대상 교량은 Noh(2021)의 선행연구에서 선정된 무조인트 교량의 형식별 대표 교량을 사용하였다. 반일체식 교대 교량(SIAB:Semi-Integral Abutment Bridge)은 steel box 거더 형식인 A 교와 PSC-I형 거더 형식인 B 교를 대상으로 하였다. 완전일체식 교대 교량(FIAB: Full-Integral Abutment Bridge)과 흉벽일체식 교대 교량(PIAB: Parapet wall-Integral Abutment Bridge)은 PSC-I형 거더 형식인 C 교와 D 교를 대상으로 하였다. 수치해석은 대상 교량의 자체를 분석한 것이 아니고 대상 교량의 기초 데이터를 기반으로 해석 변수의 변화에 따른 교량 형식별 거동을 분석한 것이다.
Table 3.
Sensitivity analysis target bridge(Kim et al., 2021)
4.2 해석 범위
구조모델은 Table 1의 모델 2(M2), 3(M3)을 사용하였고, 지반모델은 Table 2의 Case 1, 2를 적용하였다. 사각 0°는 직교를 분석하기 위함이고 15°는 일반적으로 설계에서 직교로 취급하는 한계를 고려한 값이다. 그리고 30°는 무조인트 교량의 설계지침(KECRI, 2018a)에서 허용하는 최대 사각을 적용한 값이다. 온도 하중은 설계 표준 온도인 10°C를 기준으로 도로교설계기준(MOLIT, 2016)의 강합성교와 콘크리트교의 설계 시 최저, 최대 온도를 고려하여 -30°C와 +30°C를 적용하였다. 이와 같은 해석 범위는 Table 4에 나타냈다.
Table 4.
Sensitivity analysis range(Noh et al., 2021)
| Bridges | Form | Structural model | Soil model | Skew(°) | Temp.(°C) |
| A | SIAB |
M2 M3 |
Case 1 Case 2 |
0 15 30 |
+30 -30 |
| B | SIAB | ||||
| C | FIAB | ||||
| D | PIAB |
4.3 해석 위치
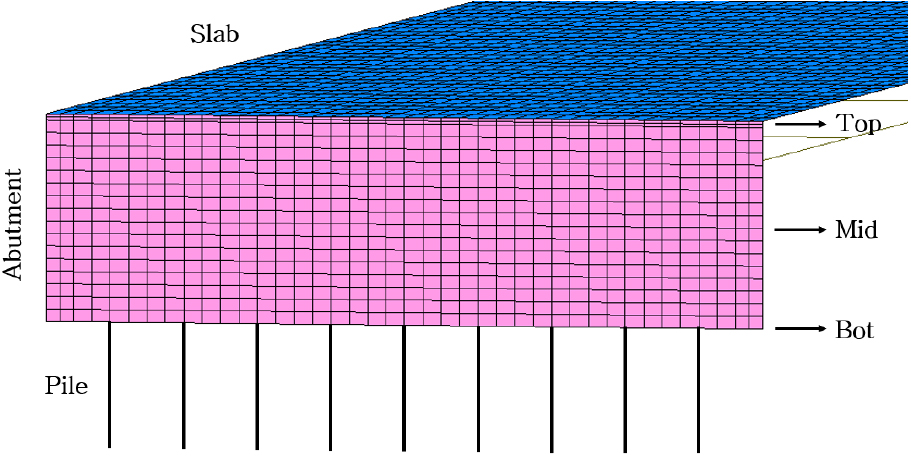
벽체 깊이별 변위 거동 변화 형상을 분석하기 위해 Fig. 4와 같이 교대 벽체 상단, 중앙, 하단을 해석 위치로 선정하였다. Fig. 4는 완전일체식 교대 교량인 C 교의 벽체 형상이며 해석 위치를 나타내기 위한 예시이다.
4.4 분석 방법
구조 및 지반모델, 해석 프로그램에 따른 벽체 변위 거동의 변화를 Table 5와 같이 평균 상대오차를 사용하여 분석하였다. 모델간 비교의 경우 모델 3을 기준으로 하였고 해석 프로그램간 비교의 경우 ABAQUS를 기준으로 하였다.
5. 해석결과
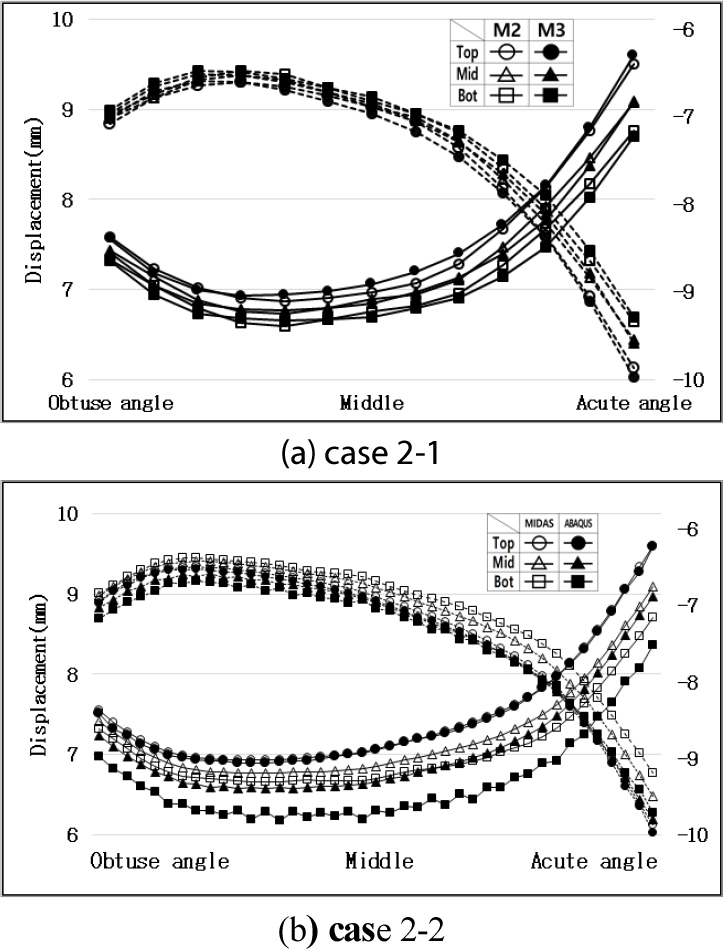
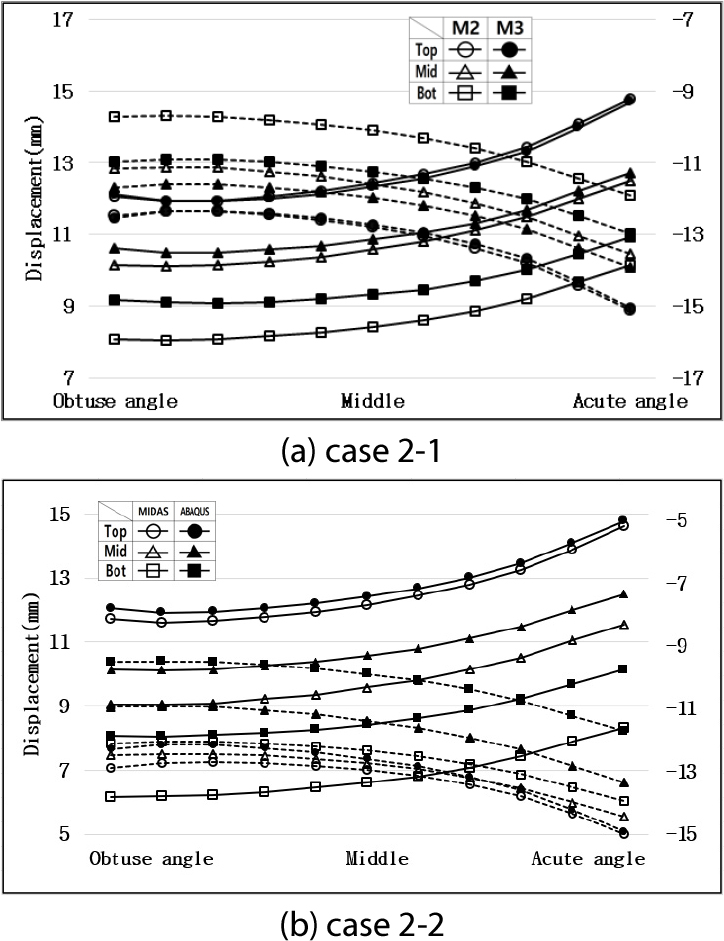
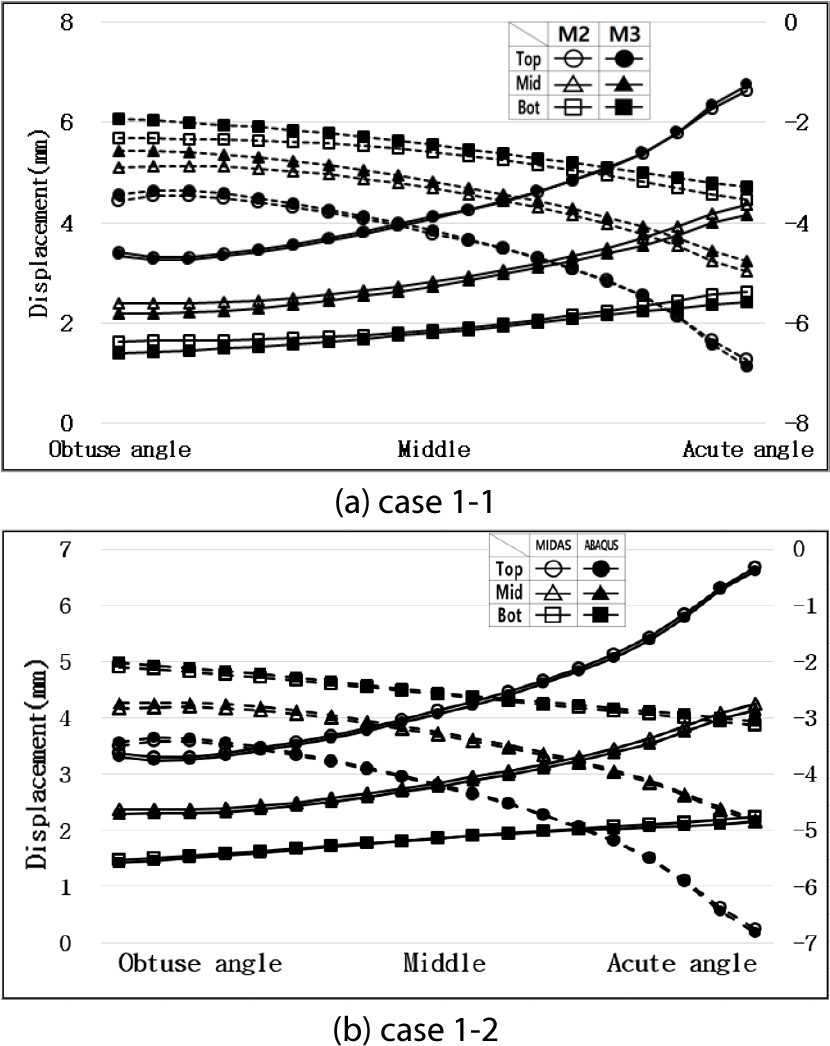
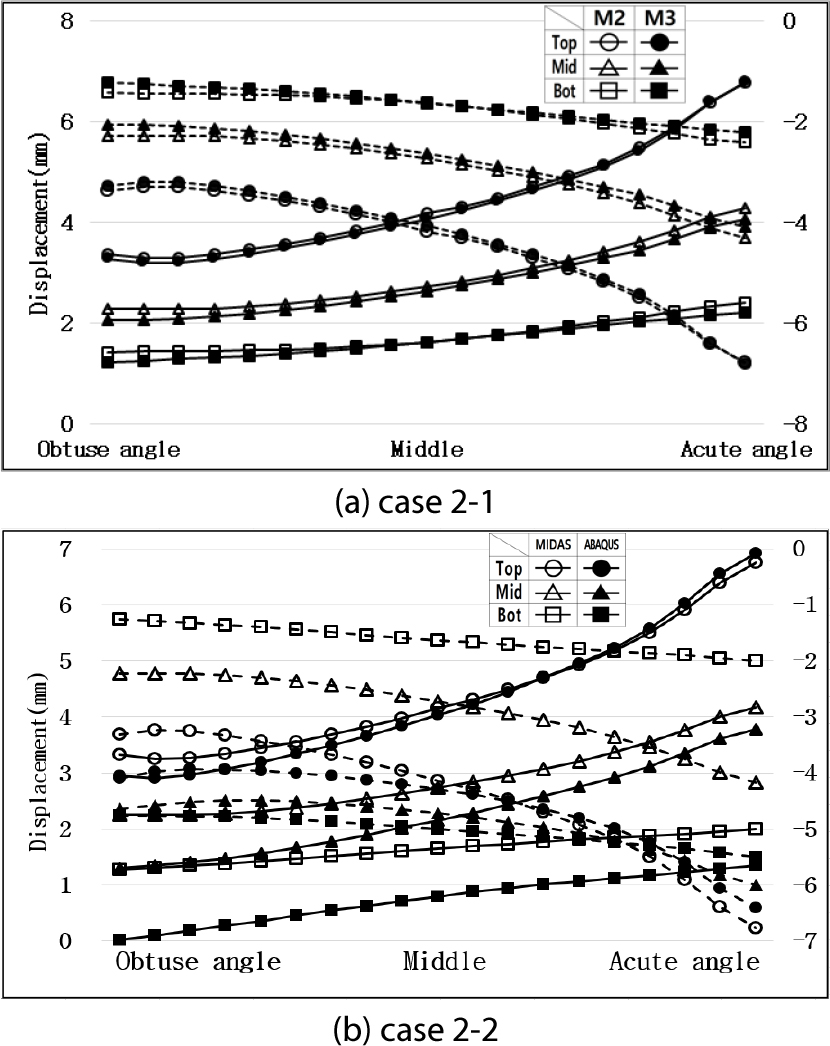
사각 0°, 15°, 30°의 경우의 벽체 깊이에 따른 벽체 변위 거동의 변화와 상대오차는 유사하였다. 그중 상대오차가 가장 큰 30°의 경우를 기준으로 하여 지반조건에 따라 구조모델, 해석 프로그램간 비교를 하였다. Figs. 5, 6, 8, 9, 10, 11, 13, 14에서 교대 벽체 상단, 중앙, 하단은 각각 원형, 삼각형, 사각형으로 나타냈다. (a)의 경우 내부가 비어있는 것은 모델 2, 채워져있는 것은 모델 3의 변위를 의미한다. (b)의 경우 내부가 비어있는 것은 MIDAS, 채워져 있는 것은 ABAQUS의 변위를 의미한다. 실선 그래프는 +30°C의 경우를 의미하고 좌측의 변위값으로 읽는다. 점선 그래프는 -30°C의 경우를 의미하고 우측의 변위값으로 읽는다.
5.1 A 교 모델
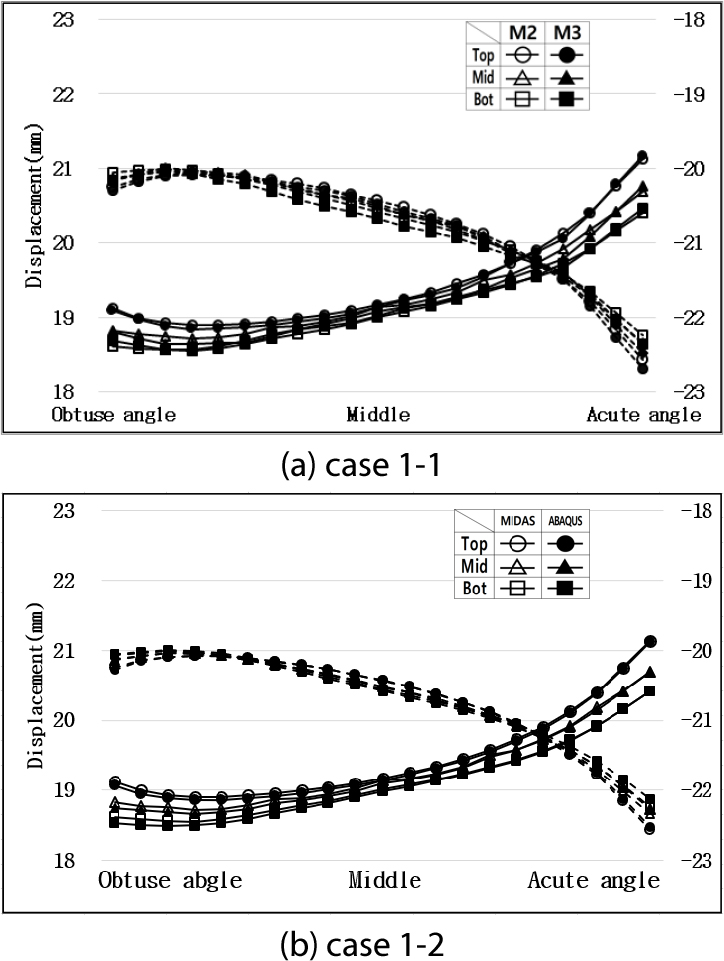
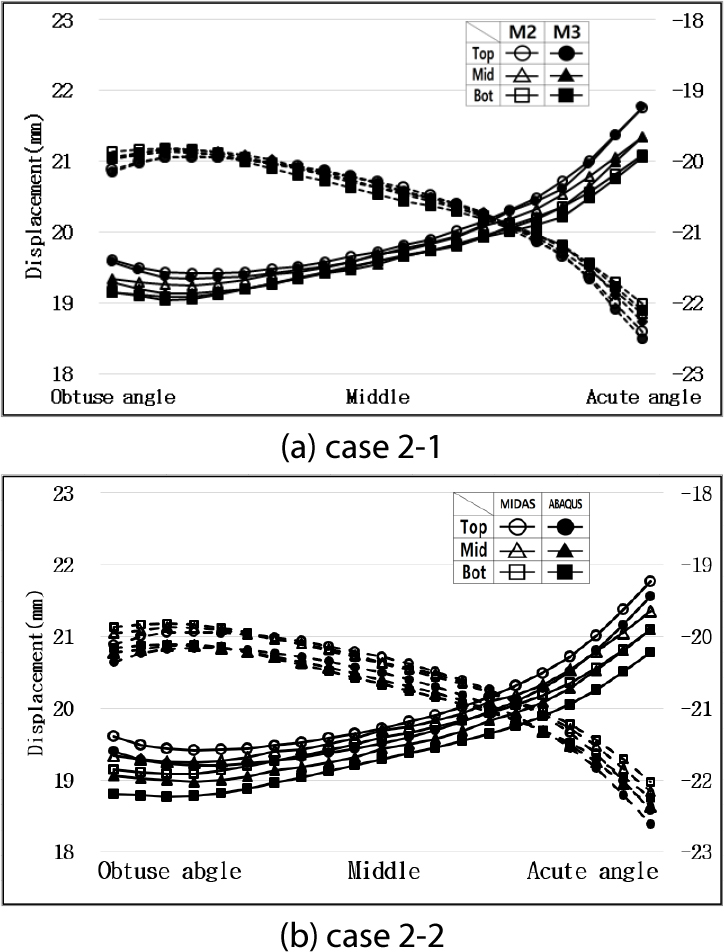
Fig. 5는 선형 스프링 지반조건인 Case 1, Fig. 6은 비선형 지반조건인 Case 2이며 구조모델간, 해석 프로그램간 벽체 변위 형상을 나타냈다. Table 6에서는 이에 대한 평균 상대오차를 산정하였다.
Table 6.
Average relative errors of A bridge(unit:%)
| Case | 1-1 | 1-2 | 2-1 | 2-2 | ||||
| Temp.(°C) | +30 | -30 | +30 | -30 | +30 | -30 | +30 | -30 |
| Top | 0.7 | 0.9 | 0.2 | 0.2 | 0.8 | 0.8 | 0.4 | 0.6 |
| Mid | 0.7 | 0.7 | 0.2 | 0.3 | 0.7 | 0.7 | 2.5 | 2.9 |
| Bot | 1.1 | 0.8 | 0.6 | 0.6 | 1.0 | 0.9 | 6.0 | 4.9 |
선형 스프링 지반 조건인 Case 1의 경우 +30°C(실선)일 때 벽체 깊이가 깊어질수록 지반반력의 영향으로 인해 변위값은 감소하였다. 반면 -30°C(점선)일 때는 지반반력이 작용하지 않으므로 벽체 깊이에 따른 변위 변화가 미소하였다. 비선형 스프링 지반 조건인 Case 2의 경우는 +30°C, -30°C 모두 지반반력이 작용하므로 벽체 깊이가 깊어짐에 따라 변위값이 감소하였다.
Fig. 5와 Table 6에서 보는 바와 같이 Case 1의 경우에는 모델 2와 모델 3의 거동 형상은 상대오차 1.1% 이내로 유사하였고 해석 프로그램간 오차도 0.6% 이내로 미소하였다. 반면, Fig. 6과 Table 6에서 보는 바와 같이 Case 2의 경우는 모델 2와 모델 3의 거동 형상은 상대오차 1.0% 이내로 유사하였으나 해석 프로그램간 상대오차는 벽체 깊이가 깊어질수록 증가하여 6.0%까지 차이가 발생하였다.
이와 같이 비선형 지반 조건에서 선형 지반 조건보다 상대오차가 크게 발생하였다. 이는 Fig. 7과 같이 해석 프로그램에 따른 지반모델의 적용 방법 차이로 인한 것으로 판단된다. ABAQUS의 경우 입력한 지반모델과 적용된 지반모델은 동일하였고 MIDAS의 경우 지반모델 그래프가 원점을 지나도록 수직 이동시켜 적용되었다. 따라서 +30°C의 경우에는 ABAQUS가 MIDAS보다 지반반력이 크게 반영되어 변위값이 더 작게 나타났다. -30°C의 경우에는 MIDAS의 지반반력이 음수값을 가지므로 교량이 수축하는 반대 방향으로 지반반력이 작용한다. 따라서 변위값은 ABAQUS가 MIDAS보다 더 크게 나타났다. 또한 벽체 깊이가 깊어질수록 지반반력의 크기가 증가하여 해석 프로그램간 오차는 점점 증가하였다.
5.2 B 교 모델
Fig. 8은 Case 1, Fig. 9는 Case 2의 구조모델간, 해석 프로그램간 벽체 변위 형상을 나타냈다. Table 7에서는 이에 대한 평균 상대오차를 산정하였다.
Table 7.
Average relative errors of B bridge(unit: %)
| Case | 1-1 | 1-2 | 2-1 | 2-2 | ||||
| Temp.(°C) | +30 | -30 | +30 | -30 | +30 | -30 | +30 | -30 |
| Top | 0.2 | 0.2 | 0.2 | 0.1 | 0.3 | 0.1 | 1.0 | 1.0 |
| Mid | 0.4 | 0.2 | 0.2 | 0.1 | 0.5 | 0.2 | 1.3 | 1.2 |
| Bot | 0.2 | 0.4 | 0.2 | 0.2 | 0.2 | 0.3 | 1.6 | 1.3 |
Case 1의 경우 +30°C일 때 벽체 깊이가 깊어질수록 지반반력의 영향으로 변위값은 감소하였다. 반면 -30°C일 때는 지반반력이 작용하지 않으므로 벽체 깊이에 따른 변위 변화가 미소하였다. Case 2의 경우는 +30°C, -30°C 모두 지반반력이 작용하므로 벽체 깊이가 깊어질수록 변위값이 감소하였다.
Table 7에서 보는 바와 같이 Case 1의 경우에는 모델 2와 모델 3의 거동 형상은 상대오차 0.4% 이내로 유사하였고 해석 프로그램간 오차도 0.2% 이내로 미소하였다. 반면, Case 2의 경우는 모델 2와 모델 3의 거동 형상은 상대오차 0.5% 이내로 유사하였으나 해석 프로그램 간 상대오차는 벽체 깊이가 깊어질수록 증가하여 1.6%까지 차이가 발생하였다. 이는 해석 프로그램 간 비선형 스프링의 적용 방식에 차이가 있기 때문이다.
5.3 C 교 모델
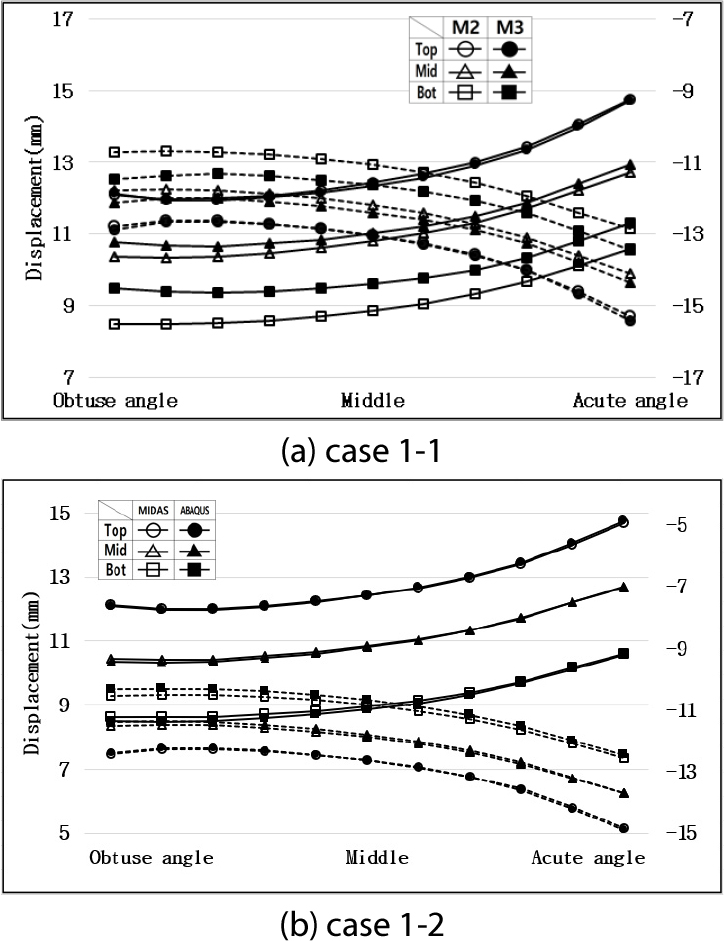
Fig. 10은 Case 1, Fig. 11은 Case 2의 구조모델간, 해석 프로그램간 벽체 변위 형상을 나타냈다. Table 8에서는 이에 대한 평균 상대오차를 산정하였다.
Table 8.
Average relative errors of C bridge(unit: %)
| Case | 1-1 | 1-2 | 2-1 | 2-2 | ||||
| Temp.(°C) | +30 | -30 | +30 | -30 | +30 | -30 | +30 | -30 |
| Top | 0.5 | 0.2 | 0.2 | 0.3 | 0.6 | 0.6 | 2.1 | 2.7 |
| Mid | 2.3 | 1.7 | 0.4 | 0.6 | 2.7 | 3.4 | 10.3 | 10.3 |
| Bot | 7.9 | 4.9 | 1.0 | 1.4 | 9.6 | 10.0 | 26.9 | 19.1 |
Case 1의 경우 +30°C일 때 벽체 깊이가 깊어질수록 지반반력의 영향과 말뚝의 저항력으로 인하여 변위값은 점점 감소하였다. -30°C일 때 지반반력은 작용하지 않으나 말뚝의 저항력으로 인하여 벽체 깊이가 깊어짐에 따라 변위값은 감소하였다. 단, +30°C의 경우 지반반력이 작용하므로 -30°C보다 변위 감소폭이 더 크게 나타났다. Case 2의 경우는 +30°C, -30°C 모두 지반반력이 작용하므로 벽체 깊이가 깊어질수록 변위값이 감소하였다.
Figs. 10(a), 11(a)에서 보는 바와 같이 벽체 깊이가 깊어질수록 모델 2와 모델 3의 변위 형상은 점점 차이가 발생하였다. Table 8과 같이 벽체 깊이가 깊어질수록 상대오차가 증가하여 최대 10.0%까지 발생하였다. 이는 완전일체식 교대 교량인 C 교의 구조모델에 적용된 요소 차이에 의한 것으로 판단된다. C 교의 구조모델은 Fig. 12와 같다. 모델 2의 거더는 beam 요소, 모델 3의 거더는 solid 요소가 적용되었다. 여기서 모델 3의 거더는 온도 하중에 의한 교축 및 교축 직각 방향 신축과 교대 벽체의 구속력으로 인하여 벽체 깊이 방향으로의 곡률이 발생하게 된다. 그러나 모델 2의 거더는 beam 요소이므로 교축 방향으로의 신축만 발생하기 때문에 벽체 깊이 방향으로의 곡률이 발생하지 않는다. 따라서 벽체 깊이가 깊어질수록 모델 2는 모델 3보다 변위가 감소하였고 이에 따라 상대오차는 증가하였다.
Table 8에서 보는 바와 같이 Case 1의 경우에는 해석 프로그램에 따른 상대오차는 미소하였고 Case 2에서는 해석 프로그램에 따른 상대오차가 26.9%까지 발생하였다. 이는 비선형 스프링 적용의 차이로 인한 것으로 판단된다.
5.4 D 교 모델
Fig. 13은 Case 1, Fig. 14는 Case 2의 구조모델간, 해석 프로그램간 벽체 변위 형상을 나타냈다. Table 9에서는 이에 대한 평균 상대오차를 산정하였다.
Table 9.
Average relative errors of D bridge(unit: %)
| Case | 1-1 | 1-2 | 2-1 | 2-2 | ||||
| Temp.(°C) | +30 | -30 | +30 | -30 | +30 | -30 | +30 | -30 |
| Top | 1.0 | 1.5 | 1.4 | 0.9 | 1.7 | 1.9 | 4.7 | 8.1 |
| Mid | 5.1 | 6.0 | 2.6 | 1.7 | 5.3 | 5.5 | -* | -* |
| Bot | 7.4 | 9.2 | 1.8 | 2.2 | 5.8 | 6.0 | -* | -* |
Case 1의 경우 +30°C일 때 벽체 깊이가 깊어질수록 지반반력의 영향과 말뚝의 저항력으로 인하여 변위값은 점점 감소하였다. -30°C일 때는 지반반력이 작용하지 않으나 말뚝의 저항력으로 인하여 벽체 깊이가 깊어짐에 따라 변위값은 감소하였다. 단, +30°C의 경우보다 -30°C의 변위 감소폭은 작다. Case 2의 경우는 +30°C, -30°C 모두 지반반력이 작용하므로 벽체 깊이가 깊어질수록 변위값이 감소하였다.
Table 9에서 보는 바와 같이 Case 1의 경우에는 모델 2와 모델 3의 거동 형상은 상대오차 9.2%(변위차 0.2mm) 이내로 유사하였고 해석 프로그램간 오차도 2.6% 이내로 미소하였다. 반면, Case 2의 경우는 모델 2와 모델 3의 거동 형상은 상대오차 6.0%(변위차 0.1 mm) 이내로 유사하였으나 해석 프로그램간 상대오차는 벽체 깊이가 깊어질수록 증가하였다. 이는 해석 프로그램간 비선형 스프링의 적용 방식에 차이가 있기 때문이다.
6. 결 론
본 연구에서는 shell 요소 기반인 모델 2와 solid 요소 기반인 모델 3의 벽체 깊이에 따른 거동 분석과 해석 프로그램에 따른 비교를 하였다. 이에 대한 결론은 다음과 같다.
1)반일체식 교대 교량은 교량 받침에 의해 상부구조와 하부구조가 분리된 형식으로 교대 벽체 변위에 말뚝의 저항력이 영향을 미치지 않는다. 따라서 지반반력이 작용하지 않는 Case 1, -30°C의 경우 벽체 깊이가 깊어질수록 벽체 변위의 변화는 아주 미소하였다. 반면 지반반력이 작용하는 Case 1, +30°C와 Case 2 조건에서는 벽체 깊이가 깊어질수록 벽체 변위는 감소하였다.
2)완전일체식, 흉벽일체식 교대 교량은 말뚝의 저항력으로 인하여 벽체 깊이가 깊어질수록 변위가 감소하였다.
3)완전일체식 교대 교량의 경우 벽체 깊이에 따른 변위 분석 시 solid 요소 기반 모델인 모델 3이 shell 요소 기반 모델인 모델 2보다 적절하다.
4)해석 프로그램간 비교 결과 Case 1 조건에서는 오차가 미소하였고 Case 2에서는 비선형 스프링 적용 방법 차이로 인하여 오차가 발생하였다.