Induced Charge Distribution Using Accelerated Uzawa Method

Jae-Hyun Kim; Gwanghyun Jo; Youn Doh Ha

doi:10.7734/COSEIK.2021.34.4.191

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 August 2021. 191-197
https://doi.org/10.7734/COSEIK.2021.34.4.191

Induced Charge Distribution Using Accelerated Uzawa Method

가속 Uzawa 방법을 이용한 유도전하계산법

Jae-Hyun Kim¹

Gwanghyun Jo²

Youn Doh Ha³^*

김 재현¹

조 광현²

하 윤도³^*

¹Staff Engineer, DIT Center, Samsung Electronics, Hwaseong, 18448, Korea

²Professor, Department of Mathematics, Kunsan National University, Gunsan, 54150, Korea

³Professor, Department of Naval Architecture and Ocean Engineering, Kunsan National University, Gunsan, 54150, Korea

¹삼성전자 DIT센터 연구원

²군산대학교 수학과 교수

³군산대학교 조선해양공학과 교수

^{*Corresponding Author}

ABSTRACT

To calculate the induced charge of atoms in molecular dynamics, linear equations for the induced charges need to be solved. As induced charges are determined at each time step, the process involves considerable computational costs. Hence, an efficient method for calculating the induced charge distribution is required when analyzing large systems. This paper introduces the Uzawa method for solving saddle point problems, which occur in linear systems, for the solution of the Lagrange equation with constraints. We apply the accelerated Uzawa algorithm, which reduces computational costs noticeably using the Schur complement and preconditioned conjugate gradient methods, in order to overcome the drawback of the Uzawa parameter, which affects the convergence speed, and increase the efficiency of the matrix operation. Numerical models of molecular dynamics in which two gold nanoparticles are placed under external electric fields reveal that the proposed method provides improved results in terms of both convergence and efficiency. The computational cost was reduced by approximately 1/10 compared to that for the Gaussian elimination method, and fast convergence of the conjugate gradient, as compared to the basic Uzawa method, was verified.

Keywords

molecular dynamics

induced charge

saddle point problem

uzawa method

preconditioned conjugate gradient

분자동역학에서의 원자들의 유도전하를 계산하기 위해서는 유도전하를 미지수로 하는 선형방정식을 풀어야 하는데 원자들의 위치가 변화할 때마다 필요한 계산이므로 상당한 계산비용이 요구된다. 따라서 효율적인 유도전하 계산 방법은 다양한 시스템을 해석하기 위해서 필수적이다. 본 연구에서는 constraints가 존재하는 Lagrange 방정식의 해에 대한 선형 시스템, 즉 saddle point를 가지는 문제를 해결하기 위해서 Uzawa method를 도입하였다. Uzawa 매개변수가 수렴 속도에 영향을 미치는 단점을 극복하고 행렬 연산의 효율성을 위해서 Schur complement와 preconditioned conjugate gradient (PCG) 방법을 통해 계산의 효율성을 극대화하는 가속 Uzawa algorithm을 적용한다. 두 금속 나노입자가 전기장에 놓여진 분자동역학 수치모델을 통해서 제시된 방법이 유도전하계산의 수렴성, 효율성 측면에서 모두 향상된 결과를 도출함을 확인하였다. 특히 기존의 가우스 소거법에 의한 계산보다 약 1/10으로 계산비용이 절감되었고, 기본 Uzawa method에 비하여 conjugate gradient (CG)의 높은 수렴성이 입증되었다.

키워드

분자동역학

유도전하

saddle point 문제

Uzawa 방법

Preconditioned conjugate gradient

MAIN

1. 서 론
2. 금속표면 유도전하 가속해석
2.1 최적화를 통한 금속표면 유도전하 계산
2.2 Uzawa method와 PCG를 통한 가속해석
2.3 LAMMPS로의 도입방법
3. 수치 예제
3.1 전기장에 의한 금속나노입자의 전기장해석
3.2 Uzawa method의 효율성 검증
4. 결 론

1. 서 론

나노 입자들의 직접적인 조립 현상은 나노기술에서 중요한 도전과제 중 하나이다. 금속 입자들이 직접 결합하는 현상은 유전영동(dielectrophoresis)으로 인해 변화되는 전기장(Barsotti et al., 2007; Ranjan et al., 2006) 및 균일한 전기장(Pethig, 2016) 하에서 다양한 실험을 통해 관측되었다. 외부 전기장 하에서 금속 나노입자는 자유전자에 의해 자연적으로 극성을 나타낸다. 따라서 이들 간의 인력을 통해 전기장 방향으로 결합하는 pearl chain 형태로 금속 나노입자들이 cold welding하기 때문에 nanorod, nanobeam과 같은 형태를 제작하기에 유리하다.

금속 나노입자들의 cold welding 현상을 전산모사로 정확하게 구현하기 위해서는 first-principle로 페르미 레벨 주변의 density of states를 계산하여 전자적 구조를 계산하는 것이 필수적이다(Han and Ihm, 2000; Kim et al., 2002). 그러나 이러한 방법론은 많은 계산 비용의 요구로 인한 모델 사이즈가 제한되기 때문에 큰 사이즈의 모델 해석을 수행하기가 어렵다(Mayer, 2005). 반면에 분자동역학은 first-principle에 비하여 화학적 구조를 정확하게 관찰하지는 못하지만 보다 상대적으로 큰 스케일의 근사화된 해석을 수행할 수 있기 때문에 다양한 연구에 활용되고 있다(Marx and Hutter, 2000). 분자동역학 해석을 통해 금속나노입자의 유도전하를 계산하기 위해 Djurabekova 등(2011)은 입자가 존재하는 도메인을 mesh의 형태로 나누어 Laplace 방정식을 풀고 계산된 해에 대응되도록 원자에 가해지는 유도전하(induced charge)를 가우스법칙으로 추적하는 방식을 제안하였다. 이 방법에서는 금속 원자가 존재하는 곳 이외의 모든 도메인에 대해 전기장이 계산된다. Ben과 Park(2014)은 금속 원자의 유도 전하와 극성을 모두 고려하여 유도전하를 엄밀하게 계산하는 방법론을 개발하였다. 다만 이 방법에서는 도메인 내의 모든 금속 원자의 전하(charge)와 극성(dipole)에 대한 선형방정식을 입자의 위치가 변화할 때마다 풀어내야 하기 때문에 매우 많은 계산비용이 요구된다. Kim 등(2020)은 금속 표면 원자만을 선형방정식에 포함시키고 극성(dipole)은 제외한 유도전하만을 고려하여 계산비용을 매우 낮추어 계산하는 방법론을 제안하고 실험적으로 확인된 금 나노 입자들의 cold welding 현상을 시뮬레이션하였다.

본 연구에서는 Kim 등(2020)에서 제시된 금속 입자의 유도전하 계산 시스템이 saddle point 문제 특성을 가진다는 것에 착안하여 시스템을 분석하고 효율적인 계산 방법을 연구한다. saddle point 문제를 해석하는데 효율적인 Uzawa type algorithm을 적용하고, preconditioned conjugate gradient(PCG) 방법을 통해 가속한다. 두 개의 금속 입자가 전기장에 놓여졌을 때 유도전하를 계산하는데 계산 비용과 효율성 측면에서 제안된 방법론을 검증한다.

2. 금속표면 유도전하 가속해석

2.1 최적화를 통한 금속표면 유도전하 계산

외부 전기장에 의해서 발생되는 금속 자유전자들의 재배치는 시스템의 전기적 상태에 대한 양자역학적 접근방법을 통해 정확히 계산할 수 있다(Han and Ihm, 2000). 하지만 계산 비용이 매우 많이 들어 상당히 제한적인 시스템에 적용할 수밖에 없다. 따라서 Kim 등(2020)은 분자동역학 해석을 통한 근사계산법으로 금속나노 입자 결합 현상을 설명할 수 있는 방법론을 제시하였다.

N개의 원자로 구성된 금속 입자 시스템의 전체 전기에너지는 다음과 같이 계산된다.

(1)

E = \frac{1}{2} \sum_{i, j}^{N_{s}} q_{i} T_{i j} q_{j} + \sum_{i = 1}^{N_{s}} q_{i} V .

여기서, $N_{s}$ 는 금속 입자의 표면 원자의 개수, $T_{i j}$ 는 쿨룽 계수(Coulombic coefficient), $V$ 는 외부 전압, 그리고 $q_{i}$ 는 원자에 유도된 전하량을 의미한다. 표면 원자는 금속 내부 원자와 구별되는 의미로서 금속 내부의 자유전자들이 모이는 금속 입자의 표면에 위치하는 원자들을 의미한다. 표면 원자와 내부 원자는 원자의 금속결합 에너지를 계산하고 비교하여 구별할 수 있다. 금속 입자들은 금속 결합으로 인접한 원자들끼리의 결속을 유지하게 되는데 각 원자들의 금속결합 에너지를 계산해 보면 내부에 존재하는 원자들이 낮고 항상 일정한 에너지를 갖는 것에 비하여 표면에 위치하는 원자들은 그보다 더 높은 에너지를 가지게 된다. 이는 표면에 위치한 원자들의 결합의 개수가 부족하기 때문에 발생하는데 이러한 성질을 이용하면 표면 원자와 내부 원자를 정확하게 구별할 수 있다. 표면 원자와 내부 원자를 구분하는 금속결합에너지는 신중하게 결정되어야 하는데 그 기준값이 너무 높다면 표면 원자를 너무 적은 개수만을 포함시켜서 정확한 해석을 기대하기 어렵게 되고 반면에 기준값이 너무 낮다면 표면 원자뿐만 아니라 금속결합 격자의 뒤틀림같은 결함이 발생되는 주변의 원자들도 표면원자로 인식될 수 있다는 문제가 발생할 수 있다.

금속 입자 전체의 전기 에너지에서 쿨룽계수는 각각의 입자들이 점전하(point charge)라는 가정을 통해서 $T_{i j} = (1 / 4 π ϵ_{0}) / r_{i j}$ 라고 고려할 수 있다. 이 때 $ϵ_{0}$ 는 진공유전율을 의미한다. 그러나 실제 원자에 소속되어 있는 전자에 대한 전위는 점전하가 아닌 가우시안 분포를 가지는 전하 분포로 고려되어야 하기 때문에 입자 사이의 거리인 $r_{i j}$ 를 $r_{i j} / e r f (r_{i j} / R \sqrt{2})$ 로 대체하게 된다. 이를 통해서 두 개의 가우시안 전하 밀도 사이의 전기 에너지를 정확하게 표현할 수 있게 된다(Mayer, 2005).

고전 전기역학(Jackson, 1999)에 근거하여 외부 전기장이 가해질 때 금속 입자의 표면 원자에 유도되는 전하는 금속 입자 내부의 전기장이 최소가 되도록 재분배가 된다고 가정하였다. 이를 최적화 문제로 접근해 보면 다음과 같은 문제 설정이 가능하다.

(2)

\min \int_{Ω} | E (x) | d V .

여기서, $Ω$ 는 금속 입자의 내부의 부피 공간을 의미하며, $E (x)$ 는 외부 전기장을 뜻한다. $x_{i}$ 라는 위치에서 유도된 전하들에 의해서 받는 전기장의 크기는 다음과 같이 계산된다.

(3)

E (x_{i}) = \sum_{j = 1, j i}^{N_{s}} C_{i j} q_{j}^{} + E_{e x} (x_{i}) = A q + E_{e x} .

$C_{i j}$ 는 고전적 전기학에서는 $(1 / 4 π ϵ_{0}) r_{i j} | r_{i j} |^{3}$ 을 의미하지만 가우시안 분포를 가지는 전하 밀도에 대해서는 아래와 같이 수정된다.

(4)

C_{i j} = \frac{1}{4 π ϵ_{0}} \frac{r_{i j}}{| r_{i j} |^{3}} [e r f \frac{r_{i j}}{R} - \frac{2 r_{i j}}{R \sqrt{π}} \exp (- \frac{r_{i j}^{2}}{R^{2}})] .

여기서, $R$ 은 전기용량으로부터 얻어지는 각 원자들마다 다른 전하 밀도의 폭을 의미한다.

자유 전자들은 금속 입자 내부에서 자유롭게 움직이기 때문에 외부 전기장이 가해졌을 때 자유롭게 금속 입자의 표면까지 이동한다. 그리고 금속 입자의 내부의 전기장이 0이 되어 완전히 안정화되었을 때 자유 전자들의 움직임이 멈추게 된다. 이러한 특성을 이용해서 식 (1)과 같은 문제가 설정된다. 반면에 금속 입자 내부에 있는 자유 전자들이 외부로 도망가거나 유입되지 않기 때문에 $\sum_{j}^{N_{s}} q_{j} = 0$ 을 만족해야 한다. 따라서 본 문제는 라그랑지안을 다음과 같이 설정할 수 있다.

(5)

L (q, λ) = ∥ A q + E_{e x} ∥ + λ^{T} T .

여기서, $λ$ 는 라그랑지 승수이며, $T_{i}$ 는 $i$ 번째 입자가 가지는 총 전하 $Q_{i}$ 가 보존되어야 한다는 제약조건을 의미한다.

(6)

T_{i} = \sum_{j = 1}^{N_{s}} q_{j} - Q_{i} .

식 (5)에 대한 쿤터커(Kuhn-Tucker) 최적조건은 다음과 같이 얻어진다.

(7)

\frac{\partial L}{\partial q} = 2 A^{T} A q + 2 A^{T} E_{e x} + λ = 0,

그리고

(8)

\frac{\partial L}{\partial λ_{i}} = \sum_{j = 1}^{N_{s}} q_{j} - Q_{i} = 0 .

$K = 2 A^{T} A$ 라고 하고 $B = - 2 A^{T} E_{e x}$ 라고 한다면, 식 (7)과 (8)은 하나의 시스템으로 다음과 같이 표현할 수 있다.

(9)

(\begin{matrix} K & B_{1}^{T} & B_{2}^{T} \\ B_{1} & 0 & 0 \\ B_{2} & 0 & 0 \end{matrix}) (\begin{matrix} q \\ λ_{1} \\ λ_{2} \end{matrix}) = (\begin{matrix} B \\ Q_{1} \\ Q_{2} \end{matrix})

여기서, $B$ 는 $N_{s}$ 의 사이즈를 갖는 벡터이며 그 성분으로는 0 또는 1의 값을 갖는데 $\sum_{i} B_{i} = I$ 를 만족한다. 여기서, $I$ 는 모든 성분이 1인 ones-vector이다. 각각의 원자들이 어느 금속 입자에 소속되어 있는지를 결정한다. $B$ 는 입자가 서로 결합하거나 분리되면 스스로 그 성분이 변화되어 자연스럽게 원자의 소속을 결정하게 된다. $B$ 를 결정하는 과정은 유도 전하 분포를 계산하기 전에 항상 수행되는 과정이며, 전체 계산 비용은 다음과 같이 결정된다.

(10)

C_{c l a s s i f i c a t i o n} N \times n + K (N + K / 2)

여기서, $N$ 은 시스템의 총 원자의 개수, $n$ 은 한 원자의 금속결합을 이루는 주변 원자의 개수를 의미한다. 또한 $K$ 는 다른 입자에 소속된 원자와 인접한 원자의 개수를 의미한다.

$B$ 가 결정되고, 식 (9)를 통해서 표면 유도 전하를 계산하면 시스템 전체에 발생되는 전기장을 계산할 수 있고, 원자에 소속된 전하를 이용해서 입자들이 받는 총 전기력을 계산할 수 있다. 이를 이용하면 전기장이 존재할 때 입자들이 결합하거나 정렬되는 다양한 현상들을 전산 모사할 수 있다(Cha et al., 2019).

식 (9)는 유도 전하를 계산하기 위해 꼭 필요하지만, 분자동역학 해석에서 지속적으로 위치가 변화하는 입자들에 대해 식 (9)를 푸는 과정을 반복하는 것은 전산 계산량에 상당한 부담이 된다. 모든 원자를 사용하는 기존의 유도 전하 계산법(Djurabekova et al., 2011)에 비해서 표면 원자만을 계산식에 포함시켜 계산 행렬의 크기를 대폭 감소시켰음에도 불구하고 전체 분자동역학 해석 과정에서 유도 전하 계산에 할당되는 계산량이 상당히 크기 때문에 이 부분을 개선하는 것이 필수적이다.

2.2 Uzawa method와 PCG를 통한 가속해석

식 (9)는 SPD(Symmetric positive definite) 행렬 $K$ 에 대해 구성되는 선형 시스템으로서 아래와 같은 형식을 구성하는 saddle point 문제가 된다(Benzi et al., 2005).

(11)

(\begin{matrix} K & B^{T} \\ B & 0 \end{matrix}) (\begin{matrix} q \\ λ \end{matrix}) = (\begin{matrix} F \\ Q \end{matrix})

Saddple point 시스템의 Schur complement, S:= $B K^{- 1} B^{T}$ 를 이용해서, 식 (11)에서 변수 $q$ 를 제거하고 다음의 변수 $λ$ 에 대한 식을 만들 수 있다.

(12)

S λ = B A^{- 1} F - Q

이 때 Schur complement의 역함수를 구하는 대신에 iterative 한 방법으로 $q$ 와 $λ$ 를 구하는 Uzawa 방법을 사용하면 빠르게 해를 구할 수 있게 된다. 다음 Algorithm 1은 가장 간단한 형태의 Uzawa algorithm이다.

Algorithm 1(Basic Uzawa algorithm)

1.Set $q^{0} = 0, λ^{0} = 0$ .

2. Find $q^{k + 1}, λ^{k + 1}$ from $q^{k}, λ^{k}$

2.1 $q^{k + 1} = K^{- 1} (F - A q^{k} - B^{T} λ^{k})$

2.2 $λ^{k + 1} = λ^{k} + α B q$

Algorithm 1은 parameter에 의존적이고 속도가 느리다는 단점이 있다. 그래서 다양한 종류의 Uzawa algorithm의 변형이 알려져 있다. 본 연구에서는 식 (12)에 conjugate gradient(CG) 방법을 적용하여 유도된 Accelerated Uzawa algorithm을 사용한다.

먼저 식 (12)에 CG 방법을 적용하면 다음과 같은 algorithm이 유도된다.

Algorithm 2(CG for Schur complement)

1. Set $r^{0} : = B A^{- 1} F - Q - S λ^{0}, p^{0} : = r^{0}$ ,

2. Find $λ^{k + 1}$ from $λ^{k}$

2.1 $α : = \frac{(r_{k}, r_{k})}{(p^{k}, S p^{k})}$

2.2 $λ^{k + 1} = λ^{k} + α p^{k}$

2.3 $r^{k + 1} = r^{k} - α S λ^{k}$

2.4 $β = \frac{(r^{k + 1}, r^{k + 1})}{(r^{k}, r^{k})}$

2.5 $p^{k + 1} = r^{k + 1} + β p^{k}$

Algorithm 2가 잘 작동하기 위한 필요 조건은 Schur complement, S가 SPD인 조건 뿐이며 식 (11)의 수렴 속도는 S의 condition number에 의존적이다. 다만 S를 직접 계산하여 저장하는 것은 매우 어려운 일이다. 따라서 다음과 같은 방법을 통해 Algorithm 2를 효율적으로 구현해야 한다. 다음의 계산은 모든 k-step에 대해서 $q^{k}, p^{k}$ 가 $A u^{k} + B λ^{k} = F$ 을 만족하고 있다는 가정 안에서 이루어진다.

1) $α$ 계산하기:

1.1) $h = K^{- 1} B^{T} p^{k}$ .

1.2) $S p^{k} = B h$ .

1.3) $α = \frac{(r_{k}, r_{k})}{(p^{k}, S p^{k})} = \frac{(r_{k}, r_{k})}{(h, B^{T} p^{k})}$

2) $q^{k + 1}$ 계산하기:

$q^{k + 1} = K^{- 1} (F - B^{T} p^{k + 1}) = K^{- 1} (F - B^{T} p^{k} - α B^{T} p^{k}) = q^{k} - α K^{- 1} B^{T} p^{k} = q^{k} - α h$

3) $r^{k + 1}$ 계산하기:

$r^{k + 1} = B K^{- 1} F - Q - S λ^{k + 1} = B K^{- 1} (K q^{k + 1} + B^{T} λ^{k + 1}) - S λ^{k + 1} = B q^{k + 1} + S λ^{k + 1} - S λ^{k + 1} = B q^{k + 1}$

위의 계산법을 사용하여 다음과 같은 가속 Uzawa algorithm를 구성할 수 있다.

Algorithm 3(Accelerated Uzawa algorithm)

1. Set $q^{0} = K^{- 1} F, r^{0} = B q^{0}, p^{0} = r^{0}$ ,

2. Repeat the process k=0,1,2,3...

2.1 $h = K^{- 1} B^{T} p^{k}$

2.2 $α = \frac{(r^{k}, r^{k})}{(h, B^{T} p^{k})}$

2.3 $λ^{k + 1} = λ^{k} - α p^{k}$

2.4 $q^{k + 1} = q^{k} - α h$

2.5 $r^{k + 1} = - B q^{k + 1}$

2.6 $β = \frac{(r^{k + 1}, r^{k + 1})}{(r^{k}, r^{k})}$

2.7 $p^{k + 1} = r^{k + 1} + β p^{k}$

Remark

1. 가속 Uzawa algorithm은 Shur complement의 CG 버전이기 때문에, Shur complemement의 condition number에 반복 계산 횟수가 의존적이다.

2. 계산 시간이 가장 많이 걸리는 단계는 K의 역함수를 구하는 단계이다. 따라서 K의 역함수를 효율적으로 구하기 위해서 보통 PCG scheme을 사용한다. 본 연구에서는 QR decomposition을 통해 preconditioner를 구성하였다.

2.3 LAMMPS로의 도입방법

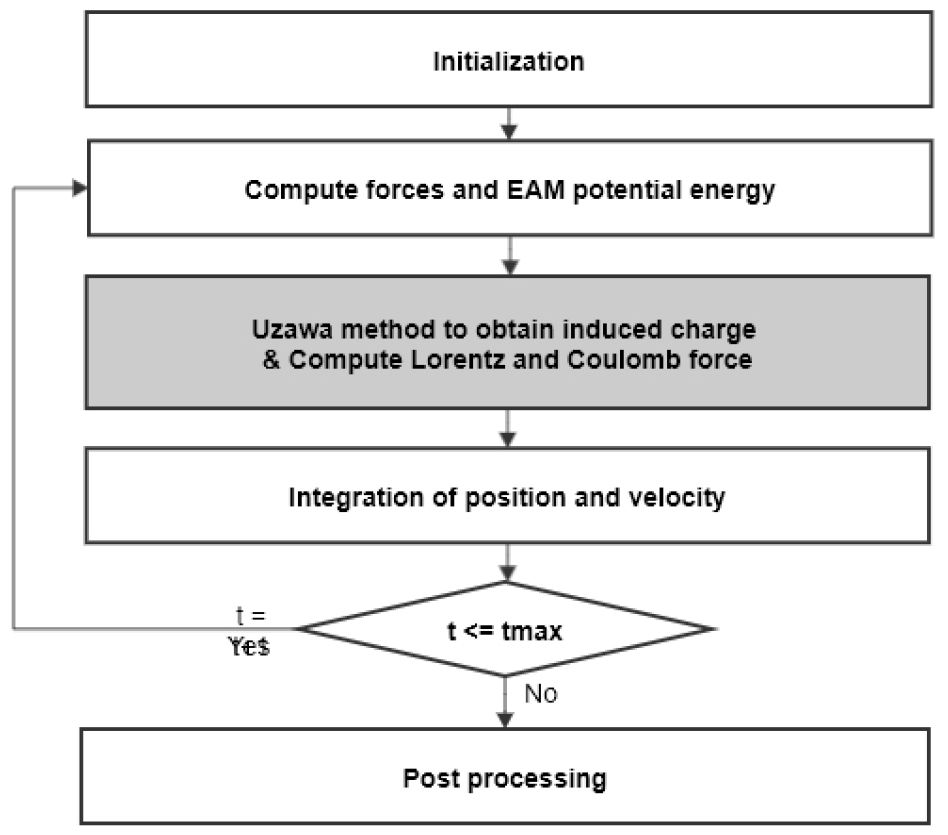
본 연구에서는 위의 유도전하계산법을 잘 알려진 분자동역학 시뮬레이터인 LAMMPS에 도입하여 LAMMPS 시뮬레이션에서 활용할 수 있도록 하였다. Fig. 1은 전체적인 분자동역학의 흐름에서 Uzawa scheme이 어디에 도입되는지를 보여준다. 그리고 내부의 알고리즘은 다음과 같은 순서로 이루어진다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-04/N0040340403/images/Figure_jcoseik_34_04_03_F1.jpg

Fig. 1.

Flow chart for overall MD procedures and Uzawa scheme

1. 금속 결합 에너지를 계산하여 표면 전하와 내부 전하를 구분한다.

2. 금속 입자들을 구분하고 각 입자에 소속되어 있는 금속 원자들을 추적하여 $B$ 벡터를 결정한다.

3. $A$ 를 구성하여 $K$ 에 대한 식 (9)를 풀어내기 위한 Algorithm 1,2,3을 도입하여 유도전하를 계산한다.

4. 유도 전하를 이용하여 쿨룽힘과 로렌츠힘을 계산한다.

개발된 방법론은 EAM potential에 의해서 결정되는 금속결합에너지를 이용하여 표면전하를 구분하기 때문에 LAMMPS 내부에서 EAM potential을 계산한 이후에 계산이 이루어져야 한다. 따라서 개발된 방법론을 이용하여 쿨룽힘과 로렌츠힘이 계산되면 먼저 계산되어 있었던 각각의 입자들에 가해진 힘에 더해줘 전하에 의한 힘을 반영해 준다.

3. 수치 예제

3.1 전기장에 의한 금속나노입자의 전기장해석

본 연구에서는 금속 나노입자의 유도전하계산 방법론의 효율성을 검증하기 위하여 두 개의 나노입자를 약 7nm만큼 떨어뜨려 배치시키고 x축 방향으로 $0.02 V / \dot{A}$ 의 전기장을 가해주었다. 3857개의 원자들로 이루어진 5nm의 직경을 가진 금나노입자 두 개를 약 20도정도 x축 방향에서 경사를 가지도록 모델링하였다. 표면원자와 내부원자를 구별하기 위한 금속결합에너지는 –3.75eV로 설정하였고 분자동역학 전산모사에서 금원자 사이의 결합은 EAM potential로 모델링하였다. 금원자의 벌크 금속 결합에너지는 –3.93eV로 알려져 있다. 또한 내부 금속 결합의 결함을 표면원자에 포함시키지 않기 위해서 결함 주변의 원자들의 에너지가 (111), (100), (110) 표면에서 각각 –3.6eV, -3.49eV, -3.36eV임을 감안하여 –3.75eV가 선택되었다.

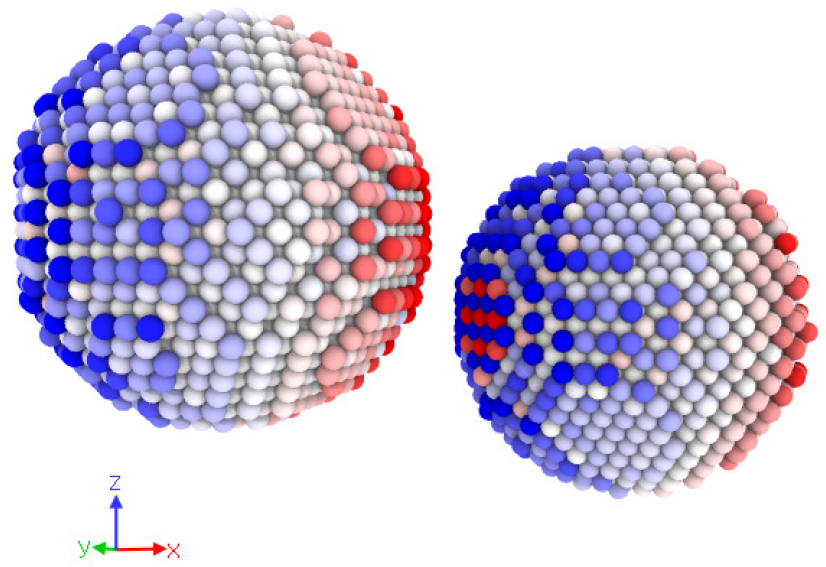
Fig. 2은 전기장에 의해 유도된 유도전하들을 개발된 방법론으로 계산한 결과를 보여준다. 입자들의 색깔은 파란색이 음전하, 빨간색이 양전하를 뜻한다. 금나노입자는 위치에 상관없이 그리고 결합유무에 상관없이 금나노입자 내부가 전기장이 최소가 되도록 만드는 표면 유도전하를 계산한다. 이러한 결과는 Fig. 3에서 더 정확하게 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-04/N0040340403/images/Figure_jcoseik_34_04_03_F2.jpg

Fig. 2.

Induced charges of surface atoms on gold nanoparticles under external electric fields(color on each atom indicates the value of induced charges. Blue means negative charge and red means positive charge)

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-04/N0040340403/images/Figure_jcoseik_34_04_03_F3.jpg

Fig. 3.

Electric fields around gold nanoparticles on y-directional plane

Fig. 3는 입자의 내부를 확인할 수 있도록 y축 평면으로 잘라서 y축평면에서의 입자주변의 전기장을 보여주고 있다. 입자의 주변에는 전기장이 존재하고, 특히 입자와 입자 사이의 공간에는 가해진 전기장의 약 4배에 해당하는 전기장이 존재하는 것을 확인할 수 있지만 입자의 내부에는 거의 전기장이 0이 되도록 유도전하가 잘 분포됨을 확인할 수 있다.

3.2 Uzawa method의 효율성 검증

기존의 유도전하계산법은 LINPACK library에 있는 DGEFA를 이용한 matrix factorization을 통해 계산되었다. 이 방법은 $K = A^{T} A$ 를 직접 계산하기 때문에 상당히 비효율적인 계산법이다. 예를 들어 A의 행의 개수가 17268이고, 열의 개수가 1848일 경우 전체 계산 비용의 약 99.7%가 $K = A^{T} A$ 를 계산하는데 시간이 소요된다는 것이 확인되었다. 따라서 기존의 방법론에서 계산 비용은 다음과 같이 $A^{T} A$ 를 계산하는데 필요한 비용으로 계산된다.

(13)

C_{\in v e r s e} ≃ n_{l} \times n_{c}^{2}

여기서, $n_{l}$ 은 $A$ 의 행의 개수를 뜻하며 내부금속원자의 개수×3(차원)으로 나타난다. 또한 $n_{c}$ 는 $A$ 의 열의 개수이며 표면금속원자의 개수를 의미한다. 이러한 불필요한 계산비용을 효율적으로 개선하기 위해 개발된 QR decomposition을 이용한 가속 Uzawa algorithm과 PCG scheme은 $A^{T} A$ 를 직접 계산하지 않으면서 식 (9)의 해를 효율적으로 계산할 수 있다.

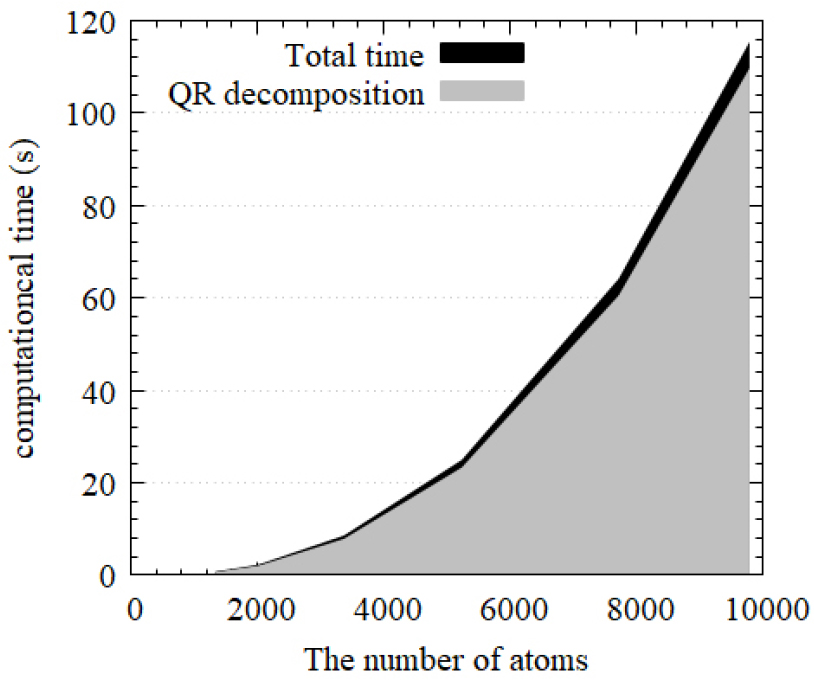
Fig. 4은 제안된 방법의 전체 계산비용에서 QR decomposition이 차지하는 비율을 보여준다. 대부분의 계산비용은 QR decomposition에서 소요되는 것을 확인할 수 있고, 그 이후에 Uzawa iteration과 PCG iteration은 대부분 1번이나 두 번만에 수렴하기 때문에 계산비용을 상당히 절감시킨다는 것을 알 수 있다. 따라서 개발된 방법은 아래와 같이 QR decomposition에 필요한 계산비용으로 근사할 수 있다(Golub and Van Loan, 2013).

(14)

C o s t ≃ 2 (n_{l} - n_{c} / 3) ∙ n_{c}^{2}

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-04/N0040340403/images/Figure_jcoseik_34_04_03_F4.jpg

Fig. 4.

The ratio of QR decomposition to total computational cost from the accelerated uzawa algorithm

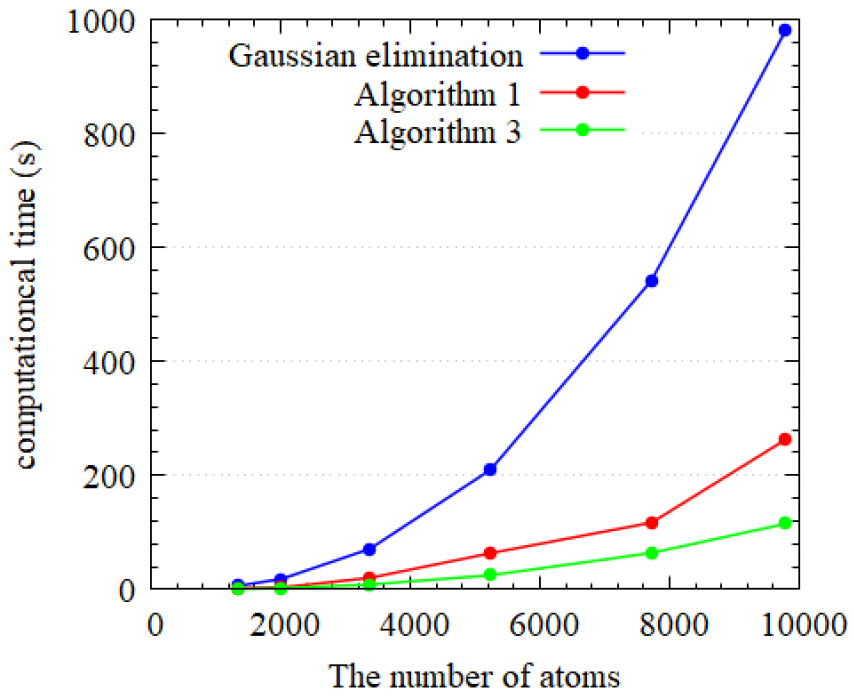
따라서 개발된 방법론은 $A$ 행렬의 열과 행간의 관계, $(n_{l} - n_{c} / 3)$ 가 작아질수록 더 효율적으로 계산될 수 있음을 알 수 있다. 또한 $(n_{l} - n_{c} / 3)$ 가 같은 모델일 경우 시스템의 사이즈가 변화하더라도 기존의 방법에 비해서 일정한 비율로 계산비용이 감소하는 시스템이라는 것을 알 수 있다. 기존의 방법과 개발된 방법간의 효율성 비교는 Fig. 5에서 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-04/N0040340403/images/Figure_jcoseik_34_04_03_F5.jpg

Fig. 5.

Comparison of calculation cost according to system size change between the existing Gaussian elimination method and the uzawa algorithms

가우스 소거법을 이용한 방법에 비해서 Uzawa algorithm (algorithm 1과 2)는 본 문제에 대해서 1/3이상의 계산비용 절감효과가 나타나는 것을 확인할 수 있다. 또한 가속 Uzawa algorithm(algorithm 3)은 가우스 소거법에 비하여 약 1/10의 계산 비용 만을 필요로 하여 상당한 계산효율의 증대를 가져온다. 이러한 효율성은 가속 Uzawa algorithm의 수렴성과도 관련이 있는데 본 모델은 식 (11)에서 $λ$ 의 개수가 2개였고, 가속 Uzawa algorithm은 모든 계산에서 단 1번의 계산으로 이미 충분한 수렴성을 보이며 반복계산을 마쳤다. 또한 각각의 Uzawa iteration step에서 PCG 또한 반복계산 2번 만에 수렴하는 결과를 보여주며 계산효율의 향상을 가능하게 하였다. 반면에 Fig. 6에서 볼 수 있듯이 기본 Uzawa algorithm(algorithm 1)에서는 Uzawa iteration이 한번만에 수렴하였으나 그 내부에서 100회 이상의 CG 반복계산이 이루어졌다. 그럼에도 불구하고 근사해의 잔차(residual)은 가속 Uzawa algorithm에 비하여 훨씬 부족한 결과를 보여주었다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-04/N0040340403/images/Figure_jcoseik_34_04_03_F6.jpg

Fig. 6.

Comparison of convergence and conjugate gradient iteration between the basic Uzawa algorithm (algorithm 1) and the accelerated Uzawa algorithm (algorithm 3)

4. 결 론

본 연구에서는 분자동역학의 금속나노입자의 유도전하를 계산하는 방법의 효율성을 개선하고 검증하였다. Saddle point를 가지는 densed normal matrix system에 대한 효율적인 계산을 위하여 가속 Uzawa algorithm를 적용하였다. 두 개의 금나노입자가 외부의 전기장 아래 놓여 있는 모델에 대한 수치예제를 통해서 금속나노입자의 표면에 유도되는 전하를 계산하고 가속 Uzawa algorithm의 효율성과 수렴성을 가우스 소거법과 Uzawa algorithm과의 비교를 통해서 검증하였다. 가속 Uzawa algorithm은 다른 방법에 비해 높은 수렴성과 효율성을 가진다는 것을 확인했으나 QR decomposition에 많은 계산비용이 소모된다는 점은 이후의 개선이 필요한 부분으로 보여진다. 해당 부분에 대한 개선을 위하여 $A^{T} A$ 형태의 normal 방정식에 대해 incomplete QR decomposition 혹은 Cholesky decomposition을 통한 preconditioner를 생성하는 방안을 향후 연구할 계획이다.

Acknowledgements

본 연구는 정부(교육부) 재원으로 한국연구재단이 주관하는 기본연구지원사업(No. 2021R1F1A104563511)의 지원을 통해 수행되었습니다.

References

Barsotti Jr, R.J., Vahey, M.D., Wartena, R., Chiang, Y.M., Voldman, J., Stellacci, F. (2007) Assembly of Metal NanoParticles into Nanogaps, Small, 3(3), pp.488~499. 10.1002/smll.20060033417290481

Ben, X., Park, H.S. (2014) Atomistic Simulations of Electric Field Effects on the Youngʼs Modulus of Metal Nanowires, Nanotechnol, 25(45), p.455704. 10.1088/0957-4484/25/45/45570425337694

Benzi, M., Golub, G.H., Liesen, J. (2005) Numerical Solution of Saddle Point Problems, Acta Numer., pp.1~137. 10.1017/S0962492904000212

Cha, S.H., Kang, S.H., Lee, Y.J., Kim, J.H., Ahn, E.Y., Park, Y., Cho, S. (2019) Fabrication of Nanoribbons by Dielectrophoresis Assisted Cold Welding of Gold Nanoparticles on Mica Substrate, Sci. Rep., 9(1), pp.1~12. 10.1038/s41598-019-40248-830842622PMC6403349

Djurabekova, F., Parviainen, S., Pohjonen, A., Nordlund, K. (2011) Atomistic Modeling of Metal Surfaces under Electric Fields: Direct Coupling of Electric Fields to a Molecular Dynamics Algorithm, Phys. Rev. E., 83(2), p.026704. 10.1103/PhysRevE.83.02670421405927

Golub, G.H., Van Loan, C.F. (2013) Matrix Computations (Vol. 3), JHU Press.

Han, S., Ihm, J. (2000) Role of the Localized States in Field Emission of Carbon Nanotubes, Phys. Rev.B, 61(15), p.9986. 10.1103/PhysRevB.61.9986

Jackson, J.D. (1999) Classical Electrodynamics, Am. J. Phys., 67(9), pp.841~842. 10.1119/1.19136

Kim, C., Kim, B., Lee, S.M., Jo, C., Lee, Y.H. (2002) Electronic Structures of Capped Carbon Nanotubes under Electric Fields, Phys. Rev. B, 65(16), p.165418. 10.1103/PhysRevB.65.165418

Kim, J.H., Cha, S.H., Kang, S.H., Park, Y., Cho, S. (2020) Atomistic Simulation of Agglomeration of Metal Nanoparticles Considering the Induced Charge Density of Surface Atoms, Int. J. Mech. & Mater. Des., 16(3), pp.475~486. 10.1007/s10999-020-09489-8

Marx, D., Hutter, J. (2000) Ab Initio Molecular Dynamics: Theory and Implementation, Mod. Methods & Algorithms Quantum Chem., 1(301-449), p.141.

Mayer, A. (2005) Polarization of Metallic Carbon Nanotubes from a Model that Includes both Net Charges and Dipoles, Phys. Rev. B, 71(23), p.235333. 10.1103/PhysRevB.71.235333

Pethig, R. (2016) Where is Dielectrophoresis (DEP) going?, J. Electrochem. Soc., 164(5), B3049. 10.1149/2.0071705jes

Ranjan, N., Vinzelberg, H., Mertig, M. (2006) Growing One‐Dimensional Metallic Nanowires by Dielectrophoresis, Small, 2(12), pp.1490~1496. 10.1002/smll.20060035017193011

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Induced Charge Distribution Using Accelerated Uzawa Method

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

Fig. 1.

Flow chart for overall MD procedures and Uzawa scheme

Fig. 2.

Induced charges of surface atoms on gold nanoparticles under external electric fields(color on each atom indicates the value of induced charges. Blue means negative charge and red means positive charge)

Fig. 3.

Electric fields around gold nanoparticles on y-directional plane

(13)

(14)

Fig. 4.

The ratio of QR decomposition to total computational cost from the accelerated uzawa algorithm

Fig. 5.

Comparison of calculation cost according to system size change between the existing Gaussian elimination method and the uzawa algorithms

Fig. 6.

Comparison of convergence and conjugate gradient iteration between the basic Uzawa algorithm (algorithm 1) and the accelerated Uzawa algorithm (algorithm 3)

Acknowledgements

References