Optimal Sensor Placement for Improved Prediction Accuracy of Structural Responses in Model Test of Multi-Linked Floating Offshore Systems Using Genetic Algorithms

Kichan Sim; Kangsu Lee

doi:10.7734/COSEIK.2024.37.3.163

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 June 2024. 163-171
https://doi.org/10.7734/COSEIK.2024.37.3.163

Optimal Sensor Placement for Improved Prediction Accuracy of Structural Responses in Model Test of Multi-Linked Floating Offshore Systems Using Genetic Algorithms

다중연결 해양부유체의 모형시험 구조응답 예측정확도 향상을 위한 유전알고리즘을 이용한 센서배치 최적화

Kichan Sim¹

Kangsu Lee²³^*

심 기찬¹

이 강수²³^*

¹Graduate Student, Korea Research Institute of Ships & Ocean Engineering School, University of Science & Technology, Daejeon, 34113, Korea

²Professor, Korea Research Institute of Ships & Ocean Engineering School, University of Science & Technology, Daejeon, 34113, Korea

³Principal Researcher, Department of Eco-friendly Ocean Development Research Division, Korea Research Institute of Ships & Ocean Engineering, Daejeon 34103, Korea

¹과학기술연합대학원대학교 선박해양플랜트연구소스쿨 박사과정

²과학기술연합대학원대학교 선박해양플랜트연구소스쿨 교수

³선박해양플랜트연구소 친환경해양개발연구본부 책임연구원

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/3.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Structural health monitoring for ships and offshore structures is important in various aspects. Ships and offshore structures are continuously exposed to various environmental conditions, such as waves, wind, and currents. In the event of an accident, immense economic losses, environmental pollution, and safety problems can occur, so it is necessary to detect structural damage or defects early. In this study, structural response data of multi-linked floating offshore structures under various wave load conditions was calculated by performing fluid-structure coupled analysis. Furthermore, the order reduction method with distortion base mode was applied to the structures for predicting the structural response by using the results of numerical analysis. The distortion base mode order reduction method can predict the structural response of a desired area with high accuracy, but prediction performance is affected by sensor arrangement. Optimization based on a genetic algorithm was performed to search for optimal sensor arrangement and improve the prediction performance of the distortion base mode-based reduced-order model. Consequently, a sensor arrangement that predicted the structural response with an error of about 84.0% less than the initial sensor arrangement was derived based on the root mean squared error, which is a prediction performance evaluation index. The computational cost was reduced by about 8 times compared to evaluating the prediction performance of reduced-order models for a total of 43,758 sensor arrangement combinations. and the expected performance was overturned to approximately 84.0% based on sensor placement, including the largest square root error.

Keywords

multi-linked floating offshore structure

hydrodynamic-structure coupled analysis

distortion base mode

genetic algorithm

sensor arrangement

본 논문에서는 다목적 구조물인 다중연결 해양부유체를 대상으로 변형 기반 모드 차수축소법을 적용하고 차수축소모델의 구조응답 예측 성능을 향상시키기 위해 유전 알고리즘 기반의 센서 배치 최적화를 수행하였다. 다중연결 해양부유체의 차수축소모델 생성에 필요한 변형 기반 모드 데이터를 얻기 위해 다양한 규칙파랑하중조건에 대한 유체-구조 연성 수치해석을 수행하고 변형 기반 모드의 직교성, 자기상관계수를 이용하여 주요 변형 기반 모드를 선정하였다. 다중연결 해양부유체의 경우 차수축소모델의 구조응답 예측 성능이 계측 및 예측 구조응답 위치에 따라 민감하기 때문에 유전 알고리즘 기반의 최적화를 수행하여 최적의 센서 배치를 도출하였다. 최적화 결과, 모든 센서 배치 조합에 대한 차수축소모델 생성 및 예측 성능 평가 대비 약 8배의 계산 비용을 절감하였으며, 예측 성능 평가 지표인 평균 제곱근 오차가 초기 센서 배치보다 84% 감소하였다. 또한, 다중연결 해양부유체 모형시험 결과를 이용하여 불규칙파랑하중에 대한 최적화된 센서 배치의 차수축소모델의 구조응답 예측 성능을 평가 및 검증하였다.

키워드

다중연결 해양부유체

유체-구조 연성 수치해석

변형 기반 모드

유전 알고리즘 기반 최적화

센서 배치

MAIN

1. 서 론
2. 다중연결 해양부유체 계측센서 배치 최적화
2.1 다중연결 해양부유체 유체-구조 연성 수치해석
2.2 축소전환행렬 기반 구조응답 평가
2.3 가상 센서 배치 최적화
2.4 센서 배치 최적화 결과
2.5 모형시험 계측 결과 비교
3. 결 론

1. 서 론

선박, 해양구조물에 대한 구조 건전성 모니터링은 다양한 측면에서 중요성을 지니고 있다. 선박, 해양구조물은 파도, 바람, 해류 등의 다양한 해상환경에 지속적으로 노출되며 사고 발생시 매우 큰 경제적 손실, 환경 오염, 안전 문제가 발생할 수 있기 때문에 이에 따른 손상이나 결함을 조기에 감지할 필요가 있다. 또한, 구조 건전성 모니터링을 통한 구조물의 손상 정도를 정확히 파악하고 이를 토대로 효과적인 유지보수 계획을 수립하여야 한다. 사고나 재난 상황에 신속히 대응하고 비용 효율적인 유지보수를 하기 위해서는 시간에 따라 불규칙하게 변화하는 해상환경에 따른 구조물의 응력 및 변형 상태를 단시간 안에 높은 정확도로 평가가 가능한 실시간 모니터링 기술이 요구된다.

최근 실시간으로 계측한 데이터를 가상의 모델에 입력하여 실제 구조물의 구조응답을 예측 및 평가하는 디지털 트윈 기술에 관한 다양한 연구가 수행되고 있다. 특히, 정밀한 구조응답 계산이 가능하지만 많은 계산비용이 요구되는 수치해석의 모델의 차수를 축소하여 빠른 구조응답 평가 및 예측이 가능한 차수축소법(Order reduction method)에 대한 연구가 활발히 진행되고 있다. Han과 Kim(2023)은 자동차 주행으로 인한 동하중이 작용하는 거더 다리를 대상으로 전체 구조물의 시스템 행렬을 크리로프 부공간(Krylov subspace)에 투영하여 약 6만개의 자유도를 5개 자유도로 축소된 축소차수모델을 생성하고 과도응답해석을 수행하였으며, 약 세배 빠른 계산시간으로 높은 정확도의 구조응답을 계산하였다. Lee 등(2021)은 비선형 시스템에 대한 요소별 강성 평가 절차 기반 차수축소기법에 초감소 방법(Hyper-reduction method)를 적용하여 차수축소기법의 계산 속도를 약 5배 향상시켰다. Lee(2022)는 컨테이너 선박을 대상으로 다양한 파랑하중에 따른 변형 기반 모드 중 가장 영향력이 큰 성분들을 선정하여 모드중첩법과 같이 실제 계측된 구조응답 데이터를 통해 원하는 위치의 구조응답을 평가 및 예측하는 차수축소기법을 적용하였다.

차수축소법 등의 실시간 구조 건전성 모니터링을 통한 구조응답 평가 및 예측 정확도를 향상시키기 위해서 구조물에 설치된 센서의 계측 데이터가 구조물의 응답 특성을 잘 반영하여야 한다. 또한, 구조물의 전체 특성을 반영하기 위해서는 다양한 위치에서의 계측 값이 필요하다. 그러나 비용 등의 문제로 설치하는 센서 수가 한정되기 때문에 응답 특성을 효과적으로 계측하기 위한 센서 배치가 필요하다(Lee et al., 2023a). Bruggi와 Mariani(2013)은 미세 전기 기계 시스템(Micro electro-mechanical systems, MEMS)를 대상으로 손상의 영향과 손상 자체에 대한 탐지능력을 목적함수로 최적화를 수행하여 최적의 속도계 배치를 도출하였다. 또한, Sajedi와 Liang(2021)은 기계학습 모델과 베이지안(Bayesian) 최적화를 결합하여 구조물의 손상 감지를 위한 센서 배치를 최적화하는 기법을 연구하였다.

본 연구에서는 선박 및 해양구조물과 같이 매우 복잡한 대형 구조물에 대한 수치해석 시 발생하는 많은 계산 비용을 절감하며 원하는 구조응답을 빠르게 계산하기 위해 변형 기반 모드 축소전환행렬을 적용하였다. 본 연구의 대상구조물인 다중연결 해양부유체의 경우 초대형 구조물로 확장시 수백만~천만개의 유한요소 수를 가지기 때문에 보 요소로 구성되어 있음에도 불구하고 많은 계산비용이 소요된다. 따라서 적은 계산비용으로 보다 빠른 구조응답 예측을 하기 위해 변형 기반 모드 축소전환행렬기법을 적용하였다. 변형 기반 모드 축소전환행렬의 경우, 계측 센서 데이터를 이용하여 미지 영역에 대한 구조응답 예측이 가능한 장점이 있으며, 축소전환행렬의 구조응답 예측 정확도를 높이기 위해 유전 알고리즘 최적화 기법을 활용하여 제한된 수의 센서에 대한 계측 지점의 조합을 도출하였다.

2. 다중연결 해양부유체 계측센서 배치 최적화

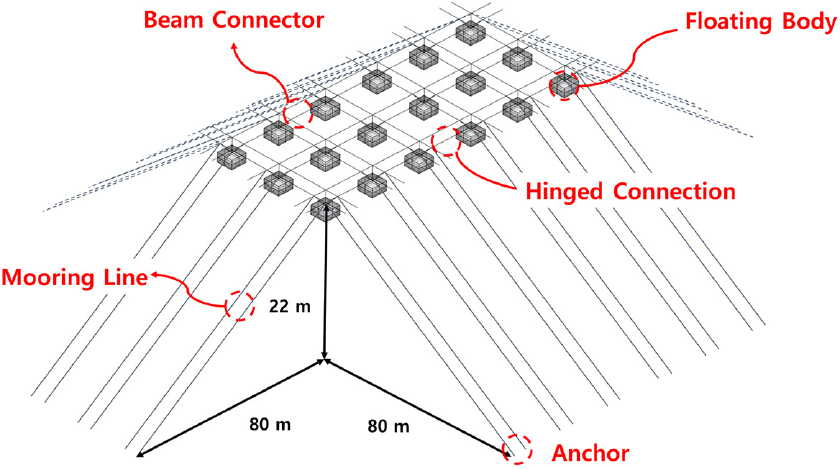
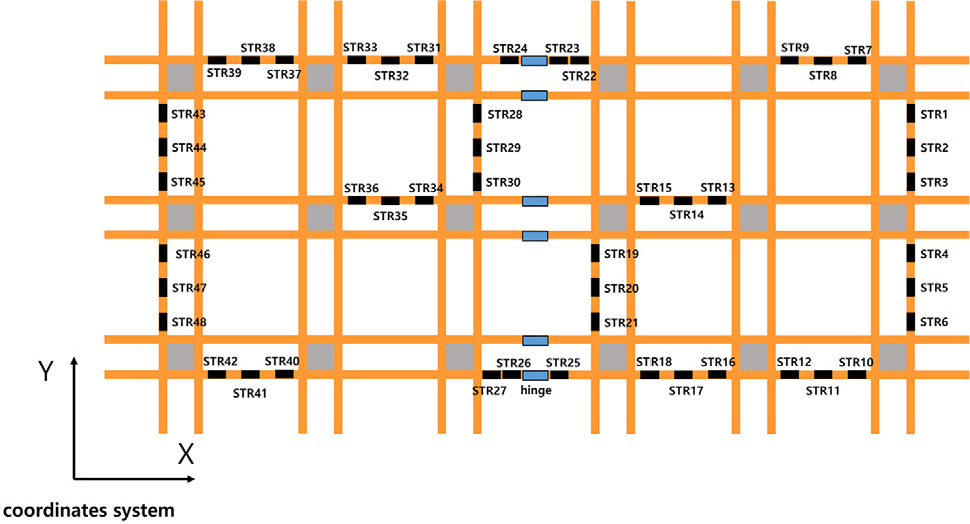
다중연결 해양부유체(Multi-linked floating offshore structure)란, 다수의 단위 부유구조물(unit floating structure)을 보(beam) 형식의 구조부재로 연결된 하나의 해양구조물이다. 이와 같은 형태의 구조물은 확장에 용이하기 때문에 넓은 면적을 필요로 하는 수상 및 해상 태양광 발전 시스템 등의 대규모 단지 조성에 활용 가능하다. 선박해양플랜트연구소(Korea Research Institute of Ships & Ocean Engineering, KRISO)는 Fig. 1과 같이 자체개발한 다중연결 해양부유체 단위구조물이 힌지 연결부로 연결되어 확장된 2.2MW급 태양광 발전 시스템을 대상으로 다수 부유체로 이루어진 구조물에 대한 수치해석 기법을 개발하였으며 모형시험을 통해 수치해석 기법의 검증, 다중연결 해양부유체에 대한 구조안전성 평가를 수행하였다(Kim, 2023). 본 연구에서는 Fig. 2와 같이 두 개의 다중연결 해양부유체 단위 구조물이 힌지 연결부로 연결된 하나의 모듈을 대상으로 센서 배치 최적화 기법에 관한 연구를 수행하였다(Sim et al., 2023).

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F1.jpg

Fig. 1.

Model test for photovoltaic system with multi-linked floating offshore structure (Kim, 2023)

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F2.jpg

Fig. 2.

Numerical model of 1 module structure

2.1 다중연결 해양부유체 유체-구조 연성 수치해석

파랑하중에 대한 다중연결 해양부유체의 구조응답을 평가하기 위한 수치해석은 선박해양플랜트연구소에서 자체 개발한 유체-구조 연성 수치해석 in-house 코드를 이용하여 수행하였다. 다중연결 해양부유체의 운동해석을 위해 부력체는 고차경계요소로 수치모델링을 수행하였으며, 구조해석의 경우 다중연결 해양부유체의 1차 부재는 H 단면을 갖는 보 형식으로 구성되어 있어 3차원 보 유한요소로 구성된 수치모델에 대하여 수행하였다. 부유체에 작용하는 파랑유동의 포텐셜은 입사파, 산란파, 방사파로 구분할 수 있으며, 파랑하중조건에서의 선박 및 해양구조물의 운동 특성, 파랑압력 분포를 계산하기 위해 고차경계요소법(High order boundary element method, HOBEM) 기반의 운동해석을 수행하였다(Lee et al., 2023b). 고차경계요소법을 통해 다수의 부유체에 작용하는 식 (1)의 유체동역학적 특성 및 파랑하중을 효과적으로 계산할 수 있다(Kim et al., 2013).

(1)

\begin{aligned} (- ω^{2} [{\bar{M}}_{B} + {\bar{M}}_{add} (ω)] - i ω [{\bar{C}}_{B} (ω)] + [{\bar{K}}_{B}]) \vec{x} (ω) = {\vec{f}}_{wave} (ω) \end{aligned}

여기서, $[M_{B}]$ , $[M_{a d d}]$ 는 각각 부유체 질량 및 부가질량, $[C_{B}]$ 는 유체동역학적 감쇠, $[K_{B}]$ 는 유체동역학적 복원강성을 의미하며, $x (ω)$ , $f_{w a v e} (ω)$ 는 파주파수 𝜔에 따른 부유체 운동, 파랑하중을 의미한다. 식 (1)과 같이 주파수 영역에서 계산한 부유체의 6자유도 운동은 식 (2)의 컨볼루션(convolution)를 통해 시간 영역으로 변환할 수 있다(Cummins, 1962). 여기서 식 (2)의 $g, h$ 는 입력하중, 임펄스(impulse) 응답을 의미한다. 시간 영역으로 변환된 유체동역학적 특성 및 파랑하중은 유한요소모델에 하중 조건으로 적용하여 최종적으로 식 (3)와 같이 운동방정식을 통해 시간영역에서의 구조해석을 수행하였다(Kim et al., 2016). 대상구조물은 9개의 부유체가 보로 엮여있는 2개의 단위구조물이 힌지 연결부로 연결되어 있으며, 구조물의 보 끝단에 계류선이 연결되어 있는 구조로 제원은 Table 1과 같다.

Table 1

Properties of multi-linked floating offshore structure

Item	Property
Beam connector	Material	Aluminum
	Elastic modulus (GPa)	69.60
	Sectional dimension of H beam (m)	Width = 0.34 Height = 0.38 Thickness = 0.03
Buoy	Material	Aluminum
	Dimension (m)	B × L × H = 1.8 × 1.8 × 1.72
	Draft (m)	1.005
Mooring line	Material	Polyester rope
	Diameter (m)	0.044
	Spring constant (N/m)	62,336.97
Total structure	Dimension (m)	B × L = 18 × 36
Total structure	Mass (kg)	60,082

(2)

\vec{u} (t) = \int_{0}^{t} g (t - τ) h (τ) d τ + \vec{u} |_{t = 0}

(3)

\begin{aligned} [\bar{M} + {\bar{M}}_{B} + {\bar{M}}_{add} (ω)] \vec{\ddot{u}} (t) + [\bar{C} + {\bar{C}}_{B} (ω)] \vec{\dot{u}} (t) + [\bar{K} + {\bar{K}}_{B}] \vec{u} (t) = f_{wave} (t) \end{aligned}

여기서, $[M]$ , $[C]$ , $[K]$ 는 다중연결 해양부유체의 구조 수치 모델의 질량, 감쇠, 강성, $u (t)$ 는 시간영역에서의 구조물의 변위를 의미한다. 시간영역 구조해석은 대표적인 음해법(Implicit method)인 Newmark 적분 알고리즘을 적용하여 수치해석을 수행하였다.

2.2 축소전환행렬 기반 구조응답 평가

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F3.jpg

Fig. 3.

Distortion Base Mode of multi-linked floating offshore structure

수치해석 결과를 바탕으로 다중연결 해양부유체의 변형 기반 모드(Distortion base mode)를 이용한 구조응답 예측기법을 적용하였다. 변형 기반 모드란 Fig. 3과 같이 파랑하중이 작용하여 변형된 구조물의 구조응답의 기저 벡터를 의미한다. 모드 해석을 통해 계산되는 고유 진동 모드와는 달리 파랑하중이 작용할 때의 선박 및 해양구조물에 발생할 수 있는 다양한 변형형상의 조합으로 가정하여 실제 해상환경하중에 대한 운동해석 및 구조해석을 수행하여 계산된 단면력, 응력 등의 구조응답의 조합을 통해 변형 기반 모드를 계산할 수 있다(Bigot et al., 2013; Bigot et al., 2015). 변형 기반 모드로 구성된 전환행렬을 이용하여 구조물에 설치한 센서 계측값을 이용하여 사용자가 원하는 위치에서의 구조응답을 평가할 수 있으며, 여기서 구조응답은 구조물에 작용하는 굽힘모멘트 등의 하중, 구조물의 국부 응력 등을 의미한다. 변형 기반 모드는 모드 중첩법 가정을 따르며, 식 (4), (5)와 같이 구조응답은 변형 기반 모드 $S$ 와 모드 진폭 벡터 𝜉로 표현할 수 있다.

(4a)

S_{i n} = [S_{i n, 1}, S_{i n, 2}, \dots, S_{i n, N_{i n}}]

(4b)

S_{o u t} = [S_{o u t, 1}, S_{o u t, 2}, \dots, S_{o u t, N_{o u t}}]

(5a)

S_{i n} = ξ_{1} S_{i n}^{1} + ξ_{2} S_{i n}^{2} + \dots + ξ_{N_{m}} S_{i n}^{N_{m}} = B ∙ ξ

(5b)

S_{o u t} = ξ_{1} S_{o u t}^{1} + ξ_{2} S_{o u t}^{2} + \dots + ξ_{N_{m}} S_{o u t}^{N_{m}} = M ∙ ξ

여기서, $S_{i n}$ 은 $N_{i n}$ 개의 센서에서 계측한 구조응답, $S_{o u t}$ 은 $N_{o u t}$ 개의 위치에서의 예측 구조응답을 의미하며, $N_{i n}$ 개의 변형 기반 모드와 모드 진폭 벡터를 이용하여 표현할 수 있다. 식 (5a), (5b)의 $B$ , $M$ 은 주요 변형 기반 모드로 구성된 행렬을 의미하며 모드 진폭 벡터와의 선형 조합을 통해 계측 및 예측 위치에서의 구조응답을 표현할 수 있다. 최종적으로 $B$ , $M$ 행렬과 모드 진폭 벡터와의 관계를 이용하여 계측 및 예측 구조응답의 관계를 나타내는 전환행렬 $A$ 를 도출할 수 있다. 전환행렬 $A$ 를 구성하는 행렬 $B$ 와 $M$ 의 역행렬은 정사각행렬이 아니므로 무어-펜로즈 유사 역행렬(Moore-Penrose pseudo inverse matrix)을 이용하여 계산하였다(Bjerhammar, 1951; Moore, 1920).

(6)

S_{o u t} = B ∙ M^{+} S_{i n} = A S_{i n}

전환행렬을 통한 예측 구조응답의 정확도는 전환행렬을 구성하는 변형 기반 모드 및 개수에 민감하며 식 (6), (7)과 같이 모드직교성, 자기상관계수를 이용한 모드 선정 알고리즘을 통해 주요 변형 기반 모드를 선정하였다.

(6a)

N_{c a s e} = N_{β} \times N_{ω} \times N_{ϕ}

(6b)

Q_{i j} = {\{\max [S_{o u t}^{i} | 1 \leq i \leq N_{c a s e}]\}}^{- 1} δ_{i j}

(6c)

C S_{1} = \{\begin{matrix} S_{o u t}^{i} | (Q ∙ S_{o u t}^{i}) ∙ (Q ∙ S_{o u t}^{i}) \\ \geq C o e f_{1} (Q ∙ S_{o u t}^{m a x}) ∙ (Q ∙ S_{o u t}^{m a x}) \end{matrix}\}

(6d)

C S_{2} = \{\begin{matrix} S_{o u t}^{k} | (Q ∙ S_{o u t}^{k}) ∙ (Q ∙ S_{o u t}^{k}) \\ \geq C o e f_{2} (Q ∙ S_{o u t}^{C S_{1}}) ∙ (Q ∙ S_{o u t}^{C S_{1}}) \end{matrix}\}

(7)

r_{k} = \sum (Q ∙ S_{o u t}^{l}) ∙ (Q ∙ S_{o u t}^{C S_{2}}) S_{o u t}^{l} \in D B M, S_{o u t}^{C S_{2}} \in C S_{2}

여기서, 변형 기반 모드의 총 수 $N_{c a s e}$ 는 파향 $N_{β}$ , 파주파수 $N_{ω}$ , 위상각 $N_{ϕ}$ 에 따른 파랑하중조건의 개수이다. 주요 변형 기반 모드를 선정하기 앞서 알고리즘 수치전산오차를 줄이기 위해 $Q_{i j}$ 행렬을 통해 정규화를 수행한다. 이후 변형 기반 모드의 자기상관계수 중 가장 큰 값을 기준으로 첫 번째 주요 변형 기반 모드 그룹을 선정한다. 다음으로 첫 번째 주요 변형 기반 모드 그룹의 각 원소별로 두 번째 주요 변형 기반 모드를 선정한다. 여기서 $C o e f_{1}$ , $C o e f_{2}$ 는 . 이후 세 번째부터 $N_{m}$ 개까지의 주요 변형 기반 모드는 모드직교성을 이용하여 선정한다. 첫 번째 주요 변형 기반 모드 그룹의 원소별로 생성된 각 주요 변형 기반 모드 그룹 $D B M$ 을 이용하여 전환행렬을 구성한다. 그 중 예측 위치에서의 수치해석 결과, 전환행렬을 통해 예측한 구조응답 $S_{p r e d i c t}$ 의 식 (8)의 평균 제곱근 오차(Root Mean Square Error, RMSE)를 평가하여 가장 작은 값을 가지는 원소의 DBM을 최종 DBM으로 선정한다.

(8)

RMSE = \sqrt{\frac{\sum_{n = 1}^{N_{osese}} {(S_{out} - S_{predict})}^{2}}{N_{case}}}

2.3 가상 센서 배치 최적화

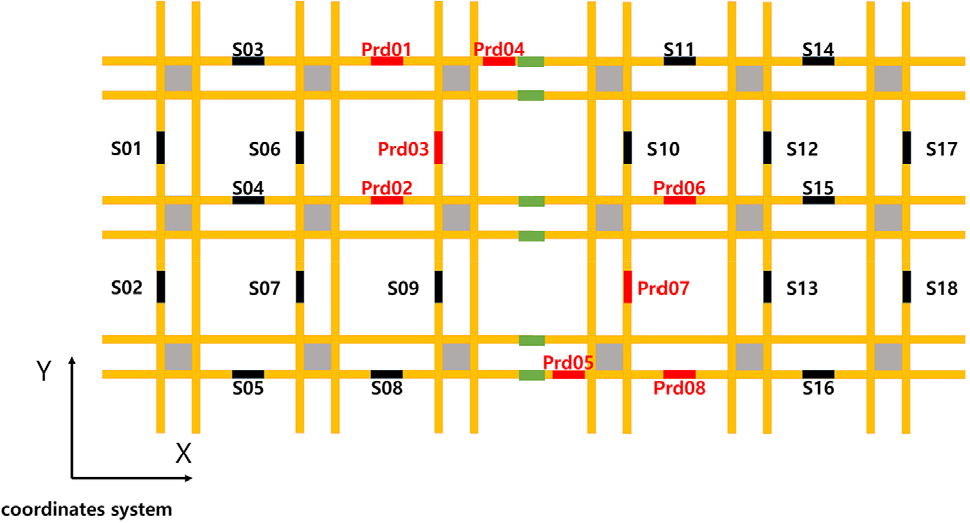
계측 지점에 따른 변형률 센서로부터 수집된 데이터를 입력으로 하는 변형 기반 모드 차수축소법 적용시, 이러한 데이터의 조합이 구조응답 평가 성능에 큰 영향을 미친다. 따라서 본 연구에서는 다중연결 해양부유체에 대한 변형 기반 모드 차수축소법 기반 구조응답 평가에 효과적인 센서 배치 조합을 도출하기 위해 유전 알고리즘 최적화기법을 적용하였다. 유전 알고리즘은 생물학적 진화 원리를 모방하여 최적화 문제를 해결하는 탐색 알고리즘 중 하나로 센서 위치와 같이 불연속적이며, 변수간 상관관계가 매우 복잡한 경우 무작위성을 통해 효과적으로 최적해를 탐색할 수 있는 장점이 있다(Balling et al., 2006; Holland, 1975; Rahami et al., 2008). 초기 해를 무작위로 생성하고, 이를 변형 및 선택하는 과정을 통해 해의 집단을 진화시킴으로써 최적해를 찾아가는 방법으로 Fig. 4과 같이 다양한 계측 위치를 선정하여 예측 위치의 구조응답을 높은 정확도로 예측하는 센서 배치 조합을 탐색 및 최적화하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F4.jpg

Fig. 4.

Position of measured and predicted structural responses

2.3.1 최적화 문제 정식화

설계 변수(Design Variable) $D V$ 는 Fig. 4의 계측(입력) 위치 $S 01$ ~ $S 18$ 의 구조응답 중 8개를 선택하는 조합으로 구성된 염색체로 배열되어 있다. 예측 위치는 Fig. 4의 $P r d 01$ ~ $P r d 08$ 에 해당한다. 다중연결 해양부유체의 경우, 파랑하중이 부유체와 연결된 보 연결체에 전달되며, 이로 인해 수심 방향의 굽힘응력이 크게 발생한기 때문에 계측 위치의 구조응답은 보에 작용하는 굽힘응력으로 선정하였다. 계측 센서의 배치 최적화 문제의 정식화는 식 (9)와 같이 제약조건을 만족하는 계측 센서 배치에 대한 전환행렬의 평균 제곱근 오차 최소화로 정의할 수 있다. 각 세대별 염색체 배열의 수는 100, 세대 수는 50으로 선정하였다.

(9)

\begin{array}{ll} Find & D V = {D V_{1}, D V_{2}, \dots, D V_{7}, D V_{8}} \\ Minimize & RMSE \\ subjectto & 1 \leq D V_{i} \leq 18, 1 \leq i \leq 8 \\ D V_{i} = integer \end{array}

최적화 정식화를 바탕으로 유전 알고리즘 기반 최적화를 진행하며, 목적함수인 평균 제곱근 오차를 평가하기 위한 파랑하중조건에 따른 다중연결부유체의 변형 기반 모드는 KRISO in-house code를 이용한 유체-구조 연성 수치해석을 통해 계산하였으며, 파랑하중조건은 Table 2와 같이 총 2,268개의 규칙파를 사용하였다.

Table 2

Wave load condition for DBM

Item	Case
Heading angle 𝛽 (°)	[0, 15, 30, 45, 60, 75, 90]
Frequency 𝜔 (rad/sec)	[0.13, 0.14, 0.17, 0.18, 0.2, 0.22, 0.25, 0.29, 0.33]
Phase angle 𝜙 (rad)	[0:𝜋/18:36]
Total number of case	2,268

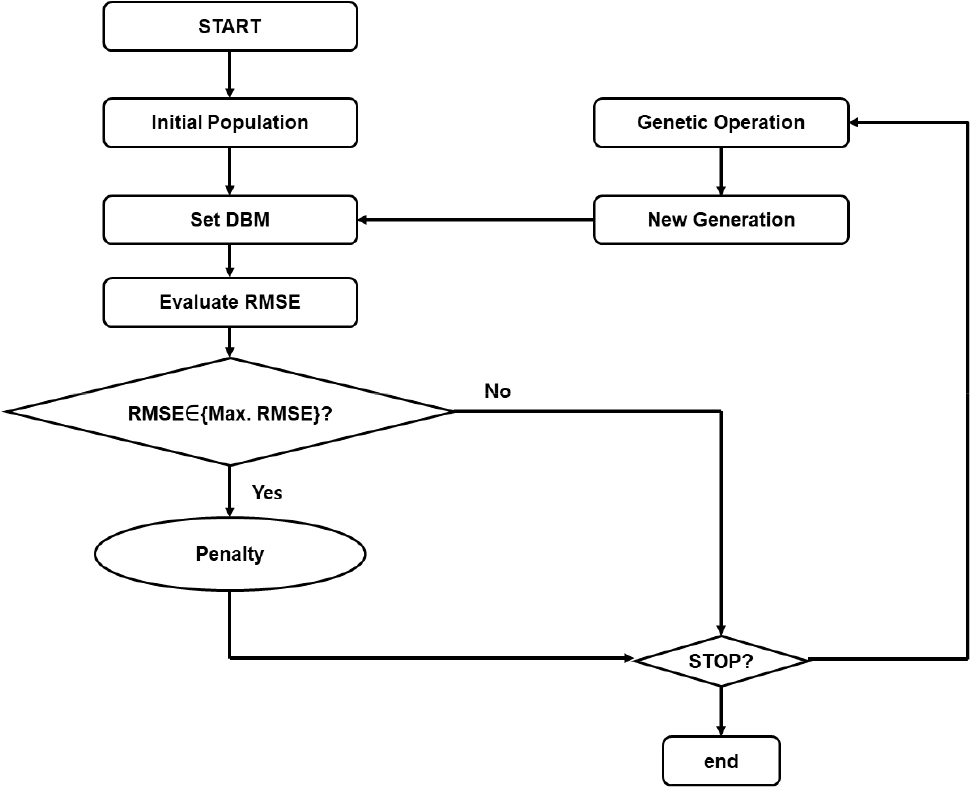
최적화는 상용 프로그램인 Matlab으로 수행하였으며, Fig. 5의 흐름도로 진행된다(Mathworks Inc., 2004). 초기세대가 생성된 이후, 각 설계변수별로 주요 변형 기반 모드 선정 알고리즘을 수행하여 수치해석 결과와 전환행렬을 통한 예측 구조응답의 평균 제곱근 오차를 평가한다. 평균 제곱근 오차가 작을수록 전환행렬의 구조응답 예측성능이 높은 것을 의미하며, 평균 제곱근 오차 크기에 따른 오름차순시 상위 30%의 염색체 배열 집단은 우수염색체(Elite)로 다음 세대에 보존된다. 또한, 하위 20%의 염색체 배열 집단은 목적함수에 패널티를 가하여 다음 세대에 전달되지 않는다. 우수염색체 외 나머지 집단 중 70%는 교차(Crossover) 및 돌연변이(Mutation) 등의 진화 연산을 거쳐 다음 세대를 구성한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F5.jpg

Fig. 5.

Optimization of sensor placement combination flow chart

2.4 센서 배치 최적화 결과

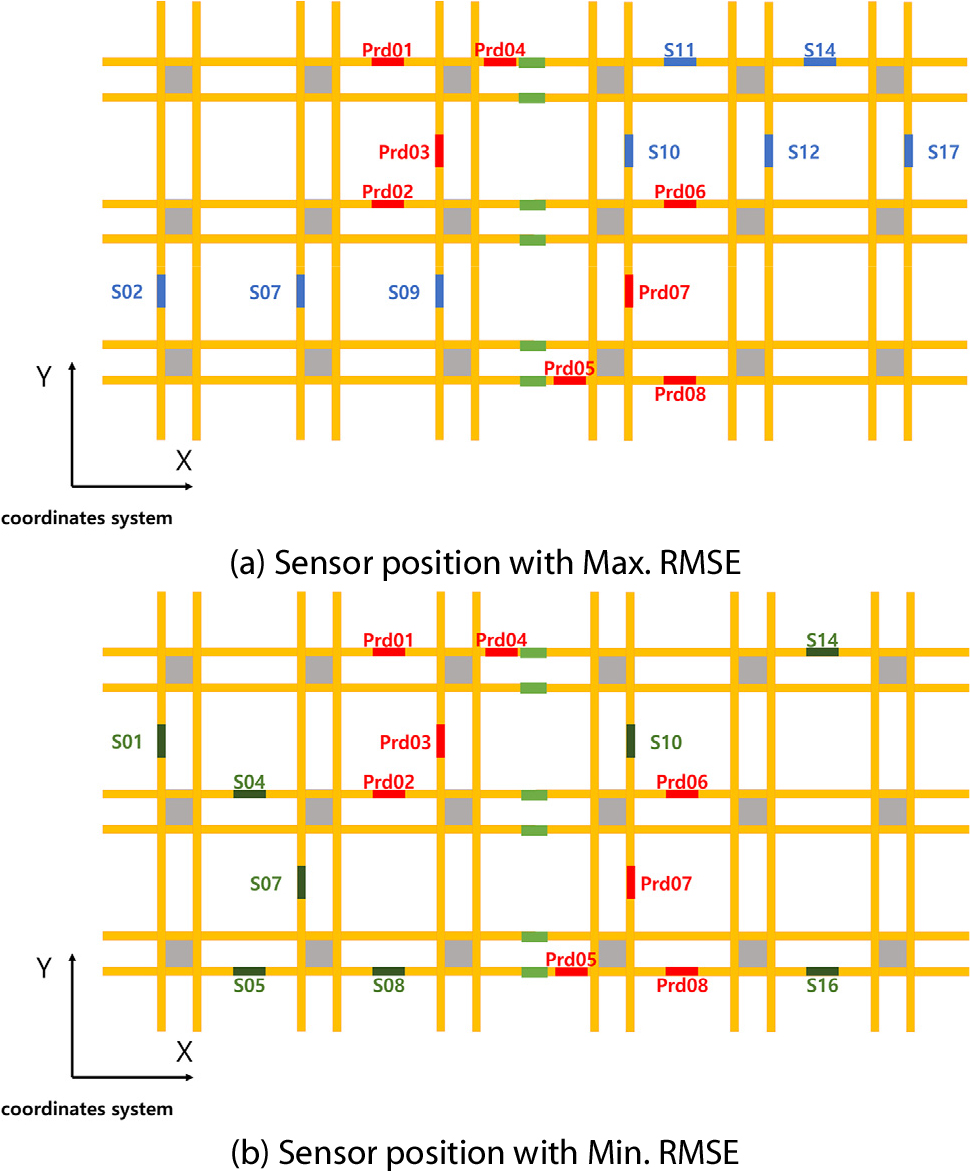
최적화 결과, Fig. 6와 같이 총 50세대를 거치면서 목적함수인 평균 제곱근 오차가 수렴하는 것을 확인하였다. 초기 집단에서의 가장 큰 평균 제곱근 오차는 1.845MPa로 해당 센서 배치는 Fig. 7(a)와 같으며, 수렴 이후 Fig. 7(b)와 같이 가장 작은 값을 가지는 센서 배치를 도출하였다. 다중연결부유체의 경우, 계류선과 근접한 구조물 가장자리의 보 연결체에서 높은 굽힘응력이 발생하지만 최적화된 센서 배치를 보면 가장자리뿐만 아니라 구조물 중앙부 등 비대칭의 형태로 배치되어 있는 것을 확인할 수 있다. 이는 각 변형 기반 모드간 직교성을 만족하며 예측 위치의 구조응답을 표현할 수 있는 변형 기반 모드가 선정되었다고 분석할 수 있다. 최적화된 센서 배치평균 제곱근 오차는 Table 3과 같이 0.296MPa로 약 84.0% 감소한 것을 확인할 수 있다. 또한, 43,785개의 모든 센서 배치 조합의 수에 대해서 변형 기반 모드 선정, 전환행렬 계산 및 예측성능 평가하여 가장 작은 평균 제곱근 오차를 가진 센서 배치를 탐색하는 경우 87,570초(약 24시간)의 계산시간이 소요되는데 반해 유전 알고리즘 기반의 최적화를 통한 센서 배치 탐색은 에 대한 주요 변형 기반 모드 선정 및 평균제곱근 오차 계산시간은 약 24시간이 소요되지만 유전 알고리즘 기반 최적화는 계산시간이 14,800초(약 4시간)으로 계산 비용을 6배 절감하였다. Fig. 8은 최적화를 통해 도출한 계측 센서 배치를 통해 예측한 굽힘응력 결과이다. 8개의 예측 위치에서 시간에 따라 예측한 굽힘응력이 주요 변형 기반 모드로 선정되지 않은 파랑하중조건에서도 수치해석 결과 대비 크기 및 위상차가 잘 일치하는 것을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F6.jpg

Fig. 6.

Convergence history of optimization based on genetic algorithm

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F7.jpg

Fig. 7.

Comparison of sensor position

Table 3

Result of optimization

Item	Result
$D V_{o p t i m i z e d}$	[ $S 01$ , $S 04$ , $S 05$ , $S 07$ , $S 08$ , $S 10$ , $S 14$ , $S 16$ ]
Population size	100
Generation	50
RMSE	0.296MPa
Computing time	14,800seconds (about 4 hours)

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F8.jpg

Fig. 8.

Predicted bending stress for wave load condition, 𝛽 = 45°, 𝜔 = 0.24rad/s

2.5 모형시험 계측 결과 비교

유전 알고리즘을 이용한 최적화를 통해 센서 배치 최적화를 수행한 이후, 수치해석 결과를 바탕으로 전환행렬의 구조응답 예측 성능을 평가하였다. 실제 계측 데이터에 대한 전환행렬의 예측 성능을 평가하기 위해 Fig. 9의 선박해양플랜트연구소에서 수행한 다중연결부유체 1 모듈에 대한 모형시험 계측 데이터와 비교하였다 (Sim and Lee, 2024). 모형시험을 통해 48 개의 1축 변형률 게이지를 통해 모형의 변형률 및 굽힘응력을 계측하였으며, 변형률 게이지 부착 위치는 Fig. 10와 같다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F9.jpg

Fig. 9.

Model test for multi-linked floating offshore structure 1 module

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F10.jpg

Fig. 10.

Layout of 1-axis strain gauge

최적화된 센서 배치 중 변형률 게이지가 $S 04$ , $S 07$ , $S 08$ , $S 10$ 등과 같이 설치되지 않은 곳은 계측 데이터 대신 수치해석 데이터로 대체하였다. 예측성능 평가는 다양한 규칙파의 선형중첩으로 표현되는 불규칙파에 대해서 수행하였으며, Fig. 11과 같이 8개의 예측 위치에서의 굽힘응력 예측 결과가 모형시험 결과와 잘 일치하는 것을 확인할 수 있다. 불규칙파에 대한 구조응답 예측 성능을 비교하기 위해 큰 굽힘응력이 발생하는 구조물 가장자리 위치를 기준으로 선정한 8개의 센서 위치 ( $S 01$ , $S 02$ , $S 03$ , $S 05$ , $S 14$ , $S 16$ , $S 17$ , $S 18$ )에 대한 전환행렬 예측성능(Sim and Lee, 2024)과도 비교를 수행하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370302/images/Figure_jcoseik_37_03_02_F11.jpg

Fig. 11.

Predicted bending stress for wave load condition, 𝛽 = 45°, Hs = 1.0m, Tp = 4.0s

Table 4와 같이 해당 파랑하중조건에 대한 평균 제곱근 오차 비교 결과, 가장자리 위치의 경우 0.7MPa, 최적화된 센서 배치의 경우 0.5MPa로 최적화된 센서 배치에 대한 전환행렬의 예측 성능이 더 높은 것을 알 수 있다. 이는 최적화된 센서 배치의 경우 일부 계측 데이터를 수치해석 데이터로 대체한 것이 영향을 주었으며 다양한 규칙파랑하중조건에서 높은 예측성능을 가지기 때문에 규칙파의 선형중첩으로 표현되는 불규칙파에서도 성능을 유지하는 것으로 분석된다.

Table 4

Comparison of prediction results for model test

Sensor arrangement	Sim and Lee, 2024	$D V_{o p t i m i z e d}$
Wave load condition	Heading angle = 45° Significant wave height Hs = 1.0m Peak period Tp = 4.0s
Measured sensor	[ $S 01$ , $S 04$ , $S 05$ , $S 07$ , $S 08$ , $S 10$ , $S 14$ , $S 16$ ]	[ $S 01$ , $S 05$ , $S 14$ , $S 16$ ]
Virtual sensor(numerical result)	-	[ $S 04$ , $S 07$ , $S 08$ , $S 10$ ]
Predicted position	$P r d 01$ ~ $P r d 08$
RMSE (MPa)	0.7MPa	0.5MPa
Difference of RMSE	0.2MPa(28.6%)

3. 결 론

본 연구에서는 다목적 해양구조물인 다중연결부유체를 대상으로 유체-구조 연성수치해석을 수행하여 다양한 파랑하중조건에서의 구조응답 데이터를 구축하였다. 이를 바탕으로 변형 기반 모드 차수축소법을 이용한 구조물의 구조응답 예측을 수행하였으며, 계측 센서 위치에 민감한 전환행렬의 예측성능을 최적화하고자 유전자알고리즘을 이용한 센서 배치 최적화를 수행하였다. 센서 배치의 총 조합 수는 43,758개로 가장 높은 성능의 전환행렬을 가지는 센서 배치를 도출하기 위해 모든 조합에 대하여 전환행렬을 계산하고 평균 제곱근 오차 계산시 24.3시간의 계산 비용이 발생하지만, 유전 알고리즘 기반 최적화를 통해 모든 센서 배치 조합을 계산하지 않고 4.1시간의 계산비용으로 최적의 센서 배치를 도출하였다. 결과적으로 약 8배의 계산비용을 절감, 예측 성능을 가장 큰 평균 제곱근 오차를 가지는 센서 배치 기준 약 84.0% 향상되었다.

본 논문에서 제시한 유전 알고리즘을 활용한 센서 배치 최적화 방법은 다중연결부유체뿐만 아니라 선박 및 다양한 해양구조물에 적용할 수 있으며, 특히 복잡한 형상을 가지는 해양구조물에서 효과적으로 구조응답은 보다 빠르게 예측할 수 있다. 유전 알고리즘을 이용한 최적화의 경우, 설계변수의 민감도 정보가 필요하지 않아 불연속적 변수에 대하여 수행할 수 있지만, 계측 센서의 수가 늘어나는 경우 염색체 배열의 수가 크게 증가하며 많은 세대를 거쳐야 한다는 단점이 있다. 향후, 인공지능, 딥러닝 기반의 최적화기법 등을 이용한 센서 배치 탐색 등의 연구를 수행할 필요가 있다. 또한, 수치해석 데이터를 기반으로 전환행렬을 계산하기 때문에 수치해석의 정밀도, 정확도에 따라 실제 구조물에 대한 예측성능이 변하며 따라서 수치해석 결과뿐만 아니라 실제 계측 데이터를 활용한 구조물의 차수축소모델 생성 연구를 수행할 필요가 있다.

Acknowledgements

본 논문은 선박해양플랜트연구소 기본사업 “불확실성을 고려한 유탄성 기반 해양구조물 구조손상도평가 핵심기술 개발(5/5)”[PES5150]과 산업통상자원부 및 산업기술평가관리원(KEIT) 지원[20024292]에 의한 연구로 수행된 연구결과입니다.

References

Balling, R.J., Briggs, R.R., Gilman, K. (2006) Multiple Optimum Size/Shape/Topology Designs for Skeletal Structures Using a Genetic Algorithm, J. Struct. Eng., 132(7), pp.1158~1165.

10.1061/(ASCE)0733-9445(2006)132:7(1158)

Bigot, F., Derbanne, Q., Baudin, E. (2013) A Review of Strains to Internal Loads Conversion Methods in Full Scale Measurements, In Proceedings of the PRADS2013, Changwon, Republic of Korea, 20-25 October 2013, pp.259~266.

Bigot, F., Sireta, F.X., Baudin, E., Derbanne, Q., Tiphine, E., Malenica, S. (2015) A Novel Solution to Compute Stress Time Series in Nonlinear Hydro-Structure Simulation. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John's, NL, Canada, 31 May-5 June 2015, pp.1~11.

10.1115/OMAE2015-42014

Bjerhammar, A. (1951) Application of Calculus of Matrices to Method of Least Squares: With Special References to Geodetic Calculations, Trans. Roy. Inst. Tech. Stockh., 49, pp.1~86.

10.1007/BF02526278

Bruggi, M., Mariani, S. (2013) Optimization of Sensor Placement to Detect Damage in Flexible Plates. J. Eng. Optim., 45(6), pp.659~676.

10.1080/0305215X.2012.690870

Cummins, W.E. (1962) The Impulse Response Function and Ship Motions, Symposium on Ship Theory at the Institut fur Schiffbau der Universitat Hamburg, 47, pp.101~109.

Han, J.S., Kim, S.H. (2023) Automation of Krylov Subspace Model Order Reduction for Transient Response Analysis with Multiple Loading, J. Comput. Struct. Eng. Inst. Korea, 34(2), pp.101~111.

10.7734/COSEIK.2021.34.2.101

Holland, J.H. (1975) Adaptation in Natural and Artificial Systems, The MIT Press, Cambridge, p.217.

Kim, B.W., Hong, S.Y., Sung, H.G. (2016) Comparison of Drift Force Calculation Methods in Time Domain Analysis of Moored Bodies, Ocean. Eng., 126, pp.81~91.

10.1016/j.oceaneng.2016.08.021

Kim, B.W., Sung, H.G., Kim, J.H., Hong, S.Y. (2013) Comparison of Linear Spring and Nonlinear FEM Methods in Dynamic Coupled Analysis of Floating Structure and Mooring System, J. Fluids & Struct.,42, pp.205~227.

10.1016/j.jfluidstructs.2013.07.002

Kim, H.-S. (2023) Efficient Wave Load Calculation Methods for Estimating Structural Responses of Highly Numerous Floating Bodies with Connection Beams, Ph.D dissertation, University of Science and Technology, p.248.

Lee, C., Kim, Y., Jung, H. (2023a) A Study on Robust Optimal Sensor Placement for Real-time Monitoring of Containment Buildings in Nuclear Power Plants, J. Comput. Struct. Eng. Inst. Korea, 36(3), pp.155~163.

10.7734/COSEIK.2023.36.3.155

Lee, D.-Y. (2022) Hull Structural Response Prediction using Distortion Base Mode, Master Thesis, Seoul National University, p.116.

Lee, J., Lee, J., Cho, H., Kim, E., Cho, M. (2021) Hyper Reduction with Element Wise Stiffness Evaluation Procedure Reduced Order Modeling for Nonliner Dynamic Structural Mechanics, J. Comput. Mech., 67(5), pp.523~540.

10.1007/s00466-020-01946-7

Lee, K., Kim H.-S., Kim, B.W. (2023b) A Study on the Global Motion Performance of Floater and Mooring Due to Arrangement of Detachable Mooring System, J. Wind Energy, 14(2), pp.26~33.

Mathworks Inc. (2004) Genetic Algorithm and Direct Search Toolbox for Use with Matlab, p.222.

Moore, E.H. (1920) On the Reciprocal of the General Algebraic Matrix, Bull. Am. Math. Soc., 26, pp.394~395.

10.1090/S0002-9904-1920-03332-X

Rahami, H., Kaveh, A., Gholipour, Y. (2008) Sizing, Geometry and Topology Optimization of Trusses via Force Method and Genetic Algorithm, Eng. Struct., 30(9), pp.2360~2369.

10.1016/j.engstruct.2008.01.012

Sajedi, S., Liang, X. (2022) Deep Generative Bayesian Optimization for Sensor Placement in Structural Health Monitoring, J. Computer-Aided Civil & Infrastruct. Eng., 37(9), pp.1067~1204.

10.1111/mice.12799

Sim, K., Lee, K. (2024) A Comparative Study on the Structural Response of Multi-Linked Floating Offshore Structure between Digital Model and Physical Model Test for Digital Twin Implementation, J. Mar. Sci. Eng., 12(2), p.262.

10.3390/jmse12020262

Sim, K., Lee, K., Kim, B.W. (2023) Structural Response Analysis for Multi-Linked Floating Offshore Structure Based on Fluid-Structure Coupled Analysis, J. Ocean. Eng. Technol., 37, pp.273~281.

10.26748/KSOE.2023.026

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Optimal Sensor Placement for Improved Prediction Accuracy of Structural Responses in Model Test of Multi-Linked Floating Offshore Systems Using Genetic Algorithms

ABSTRACT

MAIN

Fig. 1.

Model test for photovoltaic system with multi-linked floating offshore structure (Kim, 2023)

Fig. 2.

Numerical model of 1 module structure

(1)

Table 1

Properties of multi-linked floating offshore structure

(2)

(3)

Fig. 3.

Distortion Base Mode of multi-linked floating offshore structure

(4a)

(4b)

(5a)

(5b)

(6)

(6a)

(6b)

(6c)

(6d)

(7)

(8)

Fig. 4.

Position of measured and predicted structural responses

(9)

Table 2

Wave load condition for DBM

Fig. 5.

Optimization of sensor placement combination flow chart

Fig. 6.

Convergence history of optimization based on genetic algorithm

Fig. 7.

Comparison of sensor position

Table 3

Result of optimization

Fig. 8.

Predicted bending stress for wave load condition, 𝛽 = 45°, 𝜔 = 0.24rad/s

Fig. 9.

Model test for multi-linked floating offshore structure 1 module

Fig. 10.

Layout of 1-axis strain gauge

Fig. 11.

Predicted bending stress for wave load condition, 𝛽 = 45°, Hs = 1.0m, Tp = 4.0s

Table 4

Comparison of prediction results for model test

Acknowledgements

References