Dynamic Analysis of RC Piloti-Type Building Subjected to Earthquake Loads

Ju-Won Kim

doi:10.7734/COSEIK.2021.34.3.121

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 June 2021. 121-128
https://doi.org/10.7734/COSEIK.2021.34.3.121

Dynamic Analysis of RC Piloti-Type Building Subjected to Earthquake Loads

지진하중이 작용하는 RC 필로티 건축물의 동적해석

Ju-Won Kim¹^*

김 주원¹^*

¹Assistant Professor, Department of Architecture Engineering, Tongmyoung University, Busan, 48520, Korea

¹동명대학교 건축공학과 조교수

^{*Corresponding Author}

ABSTRACT

Piloti-type buildings in Korea are usually composed of lower frames and upper shear wall structures. Piloti-type buildings have been seriously damaged during earthquakes because of the construction of soft and weak stories. Piloti-type buildings with edge cores are two-way unsymmetric planes. This paper analyzed and obtained the dynamic response for structures modeled using a multistory two-way asymmetric system. The numerical results, obtained using the Newmark-β method, show the time-history responses and trends of maximum displacements and shear forces. The purpose of this study is to evaluate the effect of reinforcement on dynamic response when a shear wall or brace is reinforced in the corner opposite the piloti.

Keywords

pohang earthquake

piloti-type

dynamic analysis

vertical and torsional irregularities

본 연구에서는 비틀림비정형성과 수직비정형성을 가진 RC 필로티 건축물의 지진동에 대한 거동을 층강성을 적용하여 간단하게 모델링하는 선형 동적해석 프로그램을 개발하고자 한다. 개발된 동적 해석 프로그램을 적용하여 필로티 건축물의 동적 거동 및 필로티층 각 기둥의 전단력을 분석하고, 필로티층에 전단벽 또는 가새를 보강하였을 때 보강효과를 평가하고자 한다. 모서리코어가 있는 필로티 건축물에서 필로티층의 코어 반대편 모서리를 전단벽이나 K형 가새로 보강하였을 때 변위와 기둥 전단력이 크게 감소하는 것으로 나타났으며, 모서리 양면을 K형 가새로 보강하는 것보다 한 면을 전단벽으로 보강하는 것이 보강효과가 큰 것으로 나타났다.

키워드

포항지진

필로티 건축물

동적 해석

비틀림비정형성

수직비정형성

MAIN

1. 서 론
1.1 연구배경 및 목적
1.2 연구의 범위 및 방법
2. 구조물의 동적해석방법
2.1 비대칭 평면의 강성행렬과 질량행렬
2.2 구조물의 시간이력 해석
3. 구조물의 동적 거동 해석 및 분석
3.1 적용 건물
3.2 필로티 건물의 동적 거동 분석
3.3 전단벽 또는 가새 보강 효과에 대한 분석
4. 결 론

1. 서 론

1.1 연구배경 및 목적

2017년 11월 15일 경상북도 포항시 북구 북쪽 8km 지역에 지원 깊이 7km, 규모 5.4의 지진이 발생하였다. 포항지진에 의해 경상북도를 포함한 전국에서 지진동이 감지되었으며, 지진의 진도는 경북이 6~7, 울산 ‧ 대구 ‧ 부산 ‧ 경남 ‧ 충북 ‧ 강원도가 4로 관측되었다(Kim et al., 2019).

포항지진에 의하여 저층 RC 필로티 건축물에 많은 피해가 발생하였다. 이는 필로티 건축물이 집중되어 있는 지역이 진앙에서 가까운 곳에 위치하였고, 필로티 건축물의 내진성능이 일반 건축물과 비교하여 탁월하지 않기 때문인 것으로 판단된다. 국내 저층 건축물에 많이 사용되는 필로티(Pilotis) 구조는 주차공간을 확보하기 위하여 저층부는 보와 기둥을 사용한 골조형식을, 주거용도로 사용되는 상층부는 내력벽 형식을 적용하고 있다. 상층부의 벽식 구조에 비하여 저층부 골조 구조는 강성과 내력이 상부에 비해 상대적으로 낮아 지진동 발생 시에 저층부에 응력이 집중하게 되며, 횡력저항시스템이 수직적으로 불연속이 되는 구조적 특징을 가지며, 내진성능이 취약해진다(Moon et al., 2019). 또한 1층과 상층부의 강성 비정형이 생기며 이를 수직비정형이라 한다.

일반적으로 건물의 필로티 층은 기둥만으로 구성되어 있는 것이 아니라 계단실이 설치된 코어부를 갖는 것이 대부분이며, 코어부가 측면이나 모서리에 위치하여 한방향 또는 양방향 비대칭 평면이 되어, 질량중심과 강성중심이 일치하지 않아 수평하중이 작용할 때 비틀림이 발생하여 심각한 손상이 발생할 수 있다.

이에 국내의 건축구조기준(The Architectural Institute of Korea, 2016)은 내진설계범주 C 혹은 D에 해당하는 건물이 수직비정형이며, 높이가 20m 혹은 6층 미만의 건물이 비틀림비정형을 가지는 경우 등가정적해석을 이용하여 설계할 때 특별지진하중과 비틀림증폭계수를 사용하도록 규정하고 있다. 지진응답해석에 사용되는 Opensees와 CANNY 프로그램은 재료비선형 동적 해석이 가능하지만, 각 층의 부재를 절점으로 연결하므로 상층부 벽의 배치가 복잡한 수직비정형성을 가진 필로티 구조물의 벽을 모델링하기는 어렵다고 할 수 있다. 복잡하게 배치된 벽체가 동적거동에 미치는 영향을 파악하기 위하여 벽체 모델링이 간편한 동적 해석 프로그램 개발이 필요하다.

본 연구에서는 비틀림비정형성과 수직비정형성을 가진 RC 필로티 건축물의 지진동에 대한 거동을 층강성을 적용하여 간단하게 모델링하는 선형 동적해석 프로그램을 개발하고자 한다. 개발된 동적 해석 프로그램을 적용하여 필로티 건축물의 동적 거동 및 필로티층 각 기둥의 전단력을 분석하고, 필로티층을 전단벽 또는 가새로 보강하였을 때 보강효과를 평가하고자 한다.

1.2 연구의 범위 및 방법

본 연구에서는 비틀림비정형성과 수직비정형성을 가진 RC 필로티 건축물의 지진동에 대한 동적 거동을 해석하는 프로그램을 개발한다.

비틀림비정형성과 수직비정형성을 가진 RC 필로티 건축물의 동적해석을 위하여 층당 3개의 자유도를 가진 강성행렬과 질량행렬을 산정하는 방법을 제시하고, 강성행렬을 고유치 해석에 적용하여 구조물의 고유주기와 고유진동 모드를 구한다. 또한, 구조물의 감쇠를 Rayeigh 감쇠로 가정하여 임의의 규정된 모든 감쇠비에 대응하는 감쇠행렬을 산정한다. Newmark-β법을 이용한 수치해석방법을 적용하여 시간에 따른 구조물의 응답을 구한다(Paz, 1985).

2017년에 발생한 포항 지진에 의해 실제 피해를 입은 비틀림비정형성과 수직비정형성을 가진 RC 필로티 건물에 적용하여 동적해석을 실시한다. 대상 건축물은 집중 질량으로 치환하고, 감쇠비 5%를 적용한다. 또한, 재료는 탄성 범위내에서만 변형을 일으키는 것으로 가정하고 재료비선형은 고려하지 않는다.

2. 구조물의 동적해석방법

2.1 비대칭 평면의 강성행렬과 질량행렬

본 연구에서는 비틀림비정형성과 수직비정형성을 가진 필로티 건축물의 동적 해석을 위하여 층당 $x$ 방향 변위, $y$ 방향 변위, $z$ 방향 회전각의 3개의 자유도를 적용한 강성행렬, 질량행렬, 감쇠행렬을 산정하여 동적 해석을 실시한다.

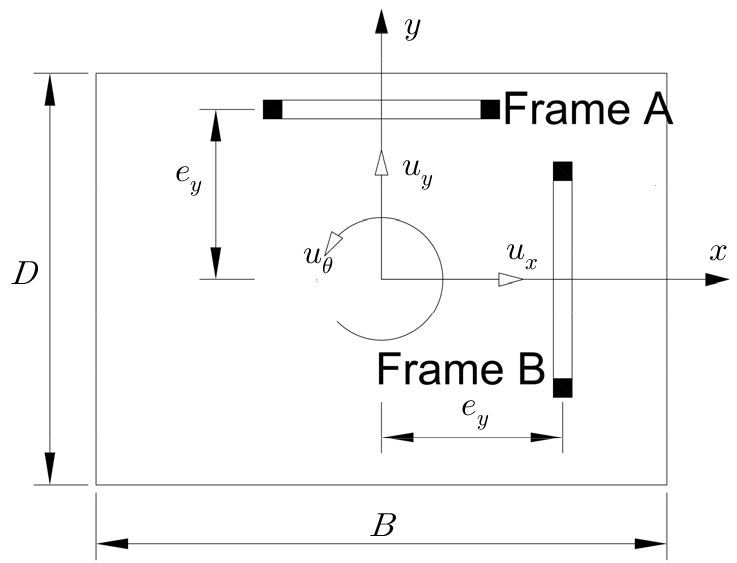
Chopra(2001)의 한방향 비대칭 평면에 대한 강성 계산 방법을 이용하여 Fig. 1과 같은 양방향 비대칭 평면의 강성을 산정할 수 있다. Frame A의 $x$ 방향 변위 $u_{A}$ , Frame B의 $y$ 방향 변위 $u_{B}$ 와 층변위 $u_{x}$ , $u_{y}$ , $u_{θ}$ 의 관계를 다음 식과 나타낼 수 있다.

(1a)

u_{A} = u_{x} - e_{y} u_{θ}

(1b)

u_{B} = u_{y} + e_{x} u_{θ}

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F1.jpg

Fig. 1.

Two-way unsymmetric plan

위 식을 행렬 형태로 표기하면 아래와 같다.

(2a)

u_{A} = [1 0 - e_{y}] \{\begin{matrix} u_{x} \\ u_{y} \\ u_{θ} \end{matrix}\}

(2b)

u_{B} = [1 0 e_{x}] \{\begin{matrix} u_{x} \\ u_{y} \\ u_{θ} \end{matrix}\}

식 (2)를 이용하여 Frame A의 $x$ 방향 변위 강성 $k_{A, x}$ 와 Frame B의 $y$ 방향 변위 강성 $k_{B, y}$ 를 층강성으로 치환하면 다음 식과 같다.

(3a)

k_{A, g} = \{\begin{matrix} 1 \\ 0 \\ - e_{y} \end{matrix}\} k_{A, x} [\begin{matrix} 1 & 0 & - e_{y} \end{matrix}] = k_{A, x} [\begin{matrix} 1 & 0 & - e_{y} \\ 0 & 0 & 0 \\ - e_{y} & 0 & e_{y}^{2} \end{matrix}]

(3b)

k_{B, g} = \{\begin{matrix} 1 \\ 0 \\ e_{x} \end{matrix}\} k_{B, y} [\begin{matrix} 1 & 0 & - e_{x} \end{matrix}] = k_{B, y} [\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & e_{x} \\ 0 & e_{x} & e_{x}^{2} \end{matrix}]

Fig. 1과 같은 평면의 층강성행렬은 식 (3)의 Frame A와 Frame B의 강성을 합하여 다음 식과 같이 된다.

(4)

k_{g} = [\begin{matrix} k_{A, x} & 0 & - e_{y} k_{A, x} \\ 0 & k_{B, y} & e_{x} k_{B, y} \\ - e_{y} k_{A, x} & e_{x} k_{B, y} & e_{y}^{2} k_{A, x} + e_{x}^{2} k_{B, y} \end{matrix}]

다층 구조물의 $i$ 층 강성행렬은 기둥과 전단벽의 강성을 적용하여 아래 식으로 나타낼 수 있다.

(5a)

k_{g} = [\begin{matrix} k_{x x, i} & 0 & k_{x θ, i} \\ 0 & k_{y y, i} & k_{y θ, i} \\ k_{x θ, i} & k_{y θ, i} & k_{θ θ, i} \end{matrix}]

(5b)

k_{x x, i} = Σ k_{c o l, x} + Σ k_{w}, x

(5c)

k_{x θ, i} = - Σ e_{y} k_{c o l, x} - Σ e_{y} k_{w, x}

(5d)

k_{y} y, i = Σ k_{c o l, y} + Σ k_{w}, y

(5e)

k_{y θ, i} = Σ e_{x} k

(5f)

k_{θ θ, i} = Σ (e_{y}^{2} k_{c o l, x} + Σ e_{x}^{2} k_{c o l, y}) + Σ e_{y}^{2} k_{w, x} + Σ e_{x}^{2} k_{w, y}

여기서, $k_{c o l}$ 은 기둥의 강성이고 $k_{w}$ 은 전단벽의 강성이다. 기둥은 $x$ 방향과 $y$ 방향 강성을 가지며, 전단벽은 벽의 방향에 따라 $x$ 방향 또는 $y$ 방향 강성을 가진다.

다층 구조물의 $i$ 층 질량행렬은 다음 식과 같다(Chopra, 2001).

(6a)

m_{i} = [\begin{matrix} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & I_{o} m \end{matrix}]

(6b)

I_{o} = \frac{B^{2} + D^{2}}{12}

여기서, $m$ 은 $i$ 층의 총질량이고 $B$ 와 $D$ 는 평면의 치수이다.

층별 평면의 치수가 기준층과 다르면 질량 중심이 달라지므로 층질량 행렬을 식 (6a)이 아니라 기준층의 질량 중심과의 거리 $c_{x}$ 와 $c_{y}$ 를 적용하여 변환한 아래의 식을 사용한다.

(7)

m_{i} = [\begin{matrix} m & 0 & - c_{y} m \\ 0 & m & c_{x} m \\ - c_{y} m & c_{x} m & I_{o} m + c_{y}^{2} m + c_{x}^{2} m \end{matrix}]

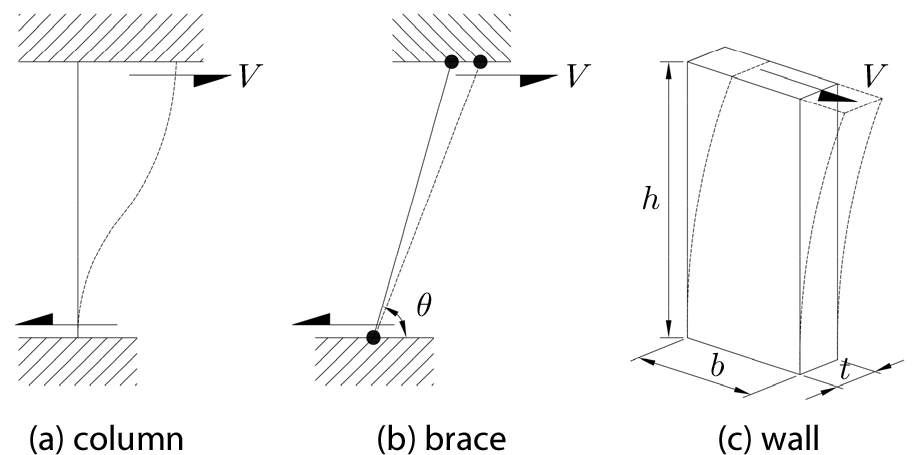
Fig. 2의 기둥, 가새, 전단벽의 강성은 다음 식으로 계산한다(Naeim, 2001).

(8a)

k_{c o l} = \frac{12 E I}{L^{3}}

(8b)

k_{b r a c e} = \frac{A E}{L} \cos^{2} θ

(8c)

k_{w} = \frac{3 E I}{h^{3} [1 + 0.6 (1 + ν)] {(\frac{b}{h})}^{2}}

여기서, $I$ 는 단면2차모멘트, $L$ 은 부재길이, $ν$ 는 포아송비이다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F2.jpg

Fig. 2.

Stiffness

각 층에 작용하는 유효지진하중은 질량행렬에 지반가속도를 곱하여 산정한다. 평면의 치수가 기준층과 같은 층은 식 (9a)을 평면의 치수가 기준층과 다른 층은 식 (9b)을 사용한다.

(9a)

\{\begin{matrix} F_{x} \\ F_{y} \\ T \end{matrix}\} = - [\begin{matrix} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & I_{o} m \end{matrix}] \{\begin{matrix} {\ddot{u}}_{g, x} \\ {\ddot{u}}_{g, y} \\ 0 \end{matrix}\}

(9b)

\{\begin{matrix} F_{x} \\ F_{y} \\ T \end{matrix}\} = - [\begin{matrix} m & 0 & - c_{y} m \\ 0 & m & c_{x} m \\ - c_{y} m & c_{x} m & I_{o} m + c_{y}^{2} m + c_{x}^{2} m \end{matrix}] \{\begin{matrix} {\ddot{u}}_{g, x} \\ {\ddot{u}}_{g, y} \\ 0 \end{matrix}\}

비틀림비정형성과 수직비정형성을 가진 필로티 건축물의 층강성행렬은 식 (5), 층질량행렬은 식 (7), 층지진하중은 식 (9)으로 산정한다.

2.2 구조물의 시간이력 해석

동적해석을 하기 위한 기본 운동방정식은 다음과 같다(Paz, 1985).

(10)

[M] \{\ddot{y}\} + [C] \{\dot{y}\} + [K] \{y\} = \{F\}

여기서, $\{F\}$ 는 구조물에 작용하는 외력 벡터이고, $\{\ddot{y}\}$ , $\{\dot{y}\}$ , $\{y\}$ 는 각각 가속도, 속도, 변위 벡터이다. 다층 구조물의 질량행렬 $[M]$ 과 강성행렬 $[K]$ 는 식 (7)의 층질량과 식 (5)의 층강성을 조합하여 산정하고, 구조물의 감쇠를 Rayleigh 감쇠로 가정하여 임의의 규정된 모든 감쇠비에 대응하는 감쇠행렬 $[C]$ 을 산정한다(Paz, 1985).

구조물의 동적 해석을 하기 위해 식 (10)의 운동방정식을 순차적인 과정으로 수치적분하여야 한다. 임의의 시간 $t_{i}$ 에서 $∆ t$ 만큼 시간이 경과하였을 때의 운동방정식은 아래와 같다(Paz, 1985).

(11)

[M] \{∆ {\ddot{y}}_{i}\} + [C] \{∆ {\dot{y}}_{i}\} + [K] \{∆ y_{i}\} = \{∆ F_{i}\}

본 연구에서는 식 (11)의 운동방정식을 일반적인 수치적분방법으로 많이 사용되고 있는 Newmark-β법을 이용하여 동적 해석을 한다.

1층에 작용하는 전단력과 비틀림 모멘트는 식 (5)로 계산한 1층 강성과 시간이력해석 결과 산정된 1층 변위를 곱하여 아래 식으로 산정한다.

(12)

\{\begin{matrix} V_{x, 1} \\ V_{y, 1} \\ T_{1} \end{matrix}\} = [\begin{matrix} k_{x x, 1} & 0 & k_{x θ, 1} \\ 0 & k_{y y, 1} & k_{y θ, 1} \\ k_{x θ, 1} & k_{y θ, 1} & k_{θ θ, 1} \end{matrix}] \{\begin{matrix} u_{x, 1} \\ u_{y, 1} \\ u_{θ, 1} \end{matrix}\}

1층의 각 기둥에 작용하는 전단력은 다음 식으로 산정한다.

(13)

\{\begin{matrix} V_{c o l, x} \\ V_{c o l, y} \end{matrix}\} = [\begin{matrix} k_{c o l, x} & 0 & - e_{y} k_{c o l, x} \\ 0 & k_{c o l, y} & e_{x} k_{c o l, y} \end{matrix}] \{\begin{matrix} u_{x, 1} \\ u_{y, 1} \\ u_{θ, 1} \end{matrix}\}

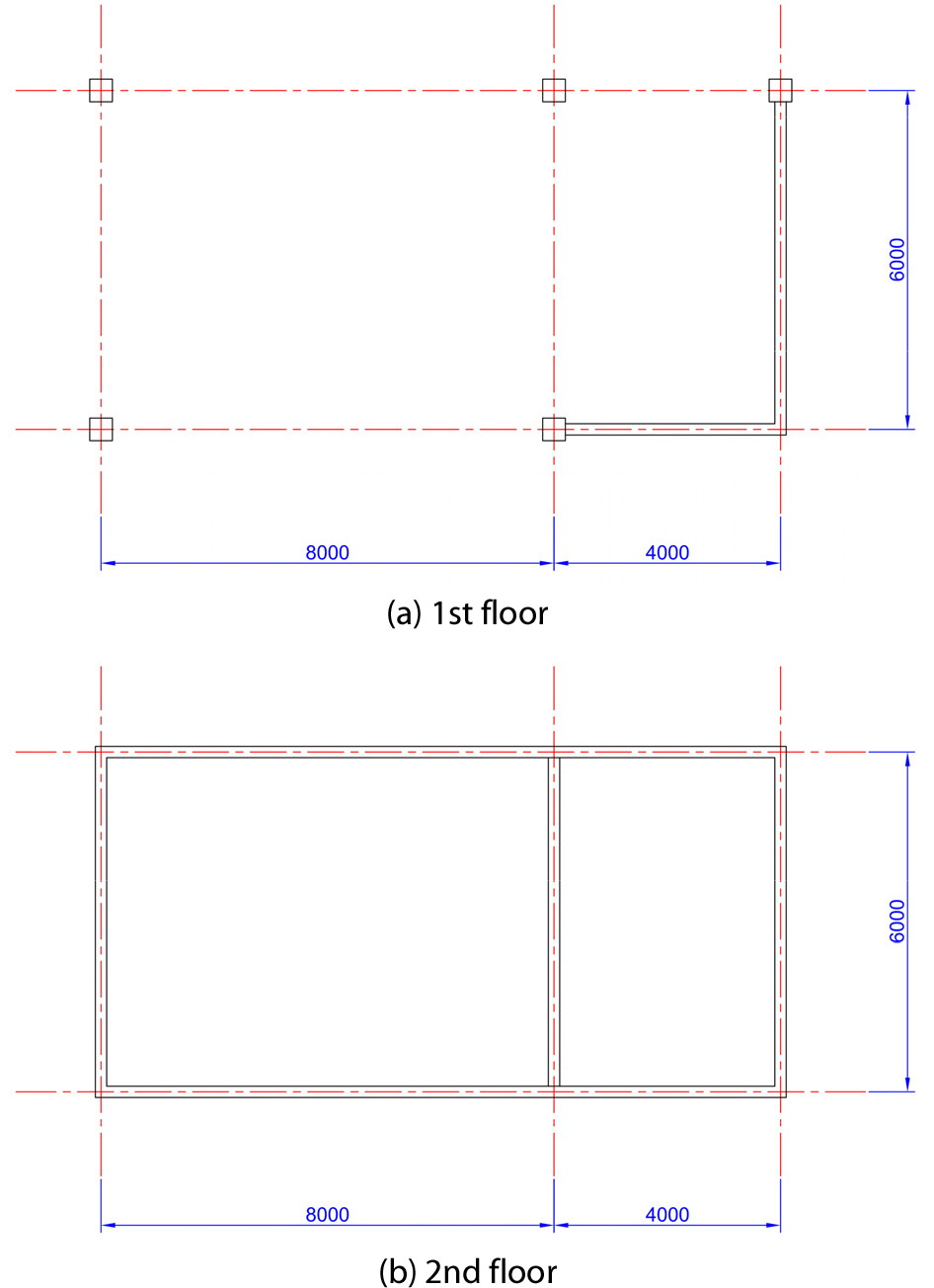
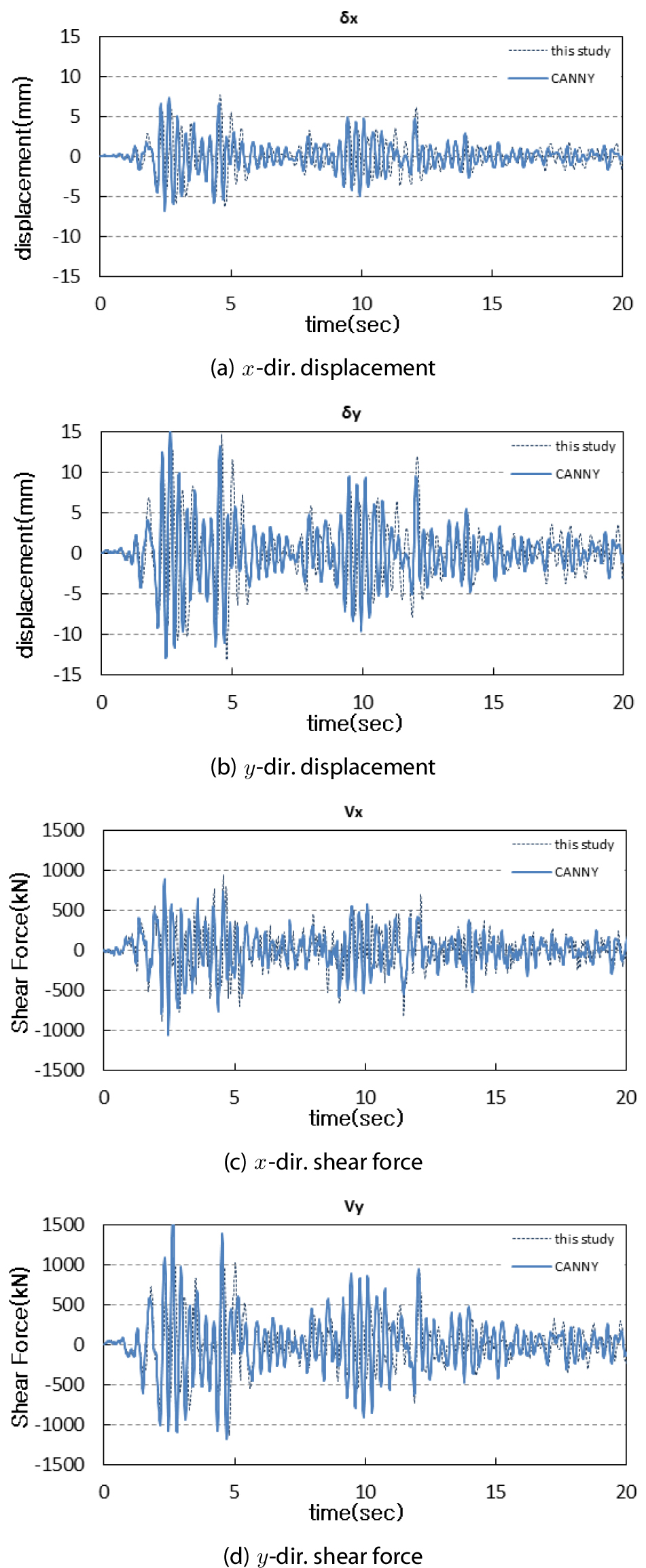
본 연구에서 개발한 비틀림비정형성과 수직비정형성을 가진 필로티 건축물의 동적 해석 프로그램 흐름도는 Fig. 3과 같다. 개발된 해석 프로그램의 신뢰성을 검증하기 위하여 Fig. 4의 평면을 가진 2층 건축물의 해석결과를 CANNY2010(이하 CANNY) 프로그램의 해석 결과와 비교하였다. 예제 건축물의 기둥치수는 400×400, 벽두께는 200mm, 층고는 4m이다. 콘크리트 C21을 적용하여 산정한 탄성계수 24,834MPa을 사용하여 강성을 계산하였다. $x$ 방향으로는 ElCentro EW를 $y$ 방향으로는 ElCentro NS를 작용시켜 해석을 실시하였다. CANNY에서 복원력 모델은 이선형모델을 사용하였고, 탄성내 거동을 하도록 설정하였다. 해석한 결과 중에서 1층 변위와 전단력을 Fig. 5에 나타내었고, 1차모드 주기와 1층의 최대변위 및 최대전단력을 Table 1에 나타내었다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F3.jpg

Fig. 3.

Flow chart for program

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F4.jpg

Fig. 4.

Plan of building with unsymmetric plan

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F5.jpg

Fig. 5.

Responses of 1st floor

Table 1.

Dynamic responses of building

Dynamic values		CANNY	this study
1st mode Natural Period(sec)		0.3145	0.3748
$d_{\max}$ (mm)	$x$ -dir	7.30	7.73
$d_{\max}$ (mm)	$y$ -dir	15.27	14.61
$V_{\max}$ (kN)	$x$ -dir	1059	1043
$V_{\max}$ (kN)	$y$ -dir	1651	1246

본 연구의 해석결과가 1차 모드 주기는 16% 작고, 최대변위와 최대전단력은 $y$ 방향이 각각 4.5%, 32% 작은 것으로 나타났다. 해석 결과에 차이가 생기는 이유는 전단벽의 강성을 본 연구에서는 식 (8c)으로 계산하였는데 CANNY에서는 휨/전단/축력 스프링을 가지는 기둥으로 모델링하기떄문에 강성 차가 생기는 것으로 판단된다. Fig. 5에서 1층의 변위와 전단력 응답이 CANNY의 결과와 유사하게 나오므로 본 연구에서 개발한 비틀림비정형성과 수직비정형성을 가진 필로티 건축물의 동적 해석 프로그램에 대한 신뢰성이 검증되었다.

3. 구조물의 동적 거동 해석 및 분석

3.1 적용 건물

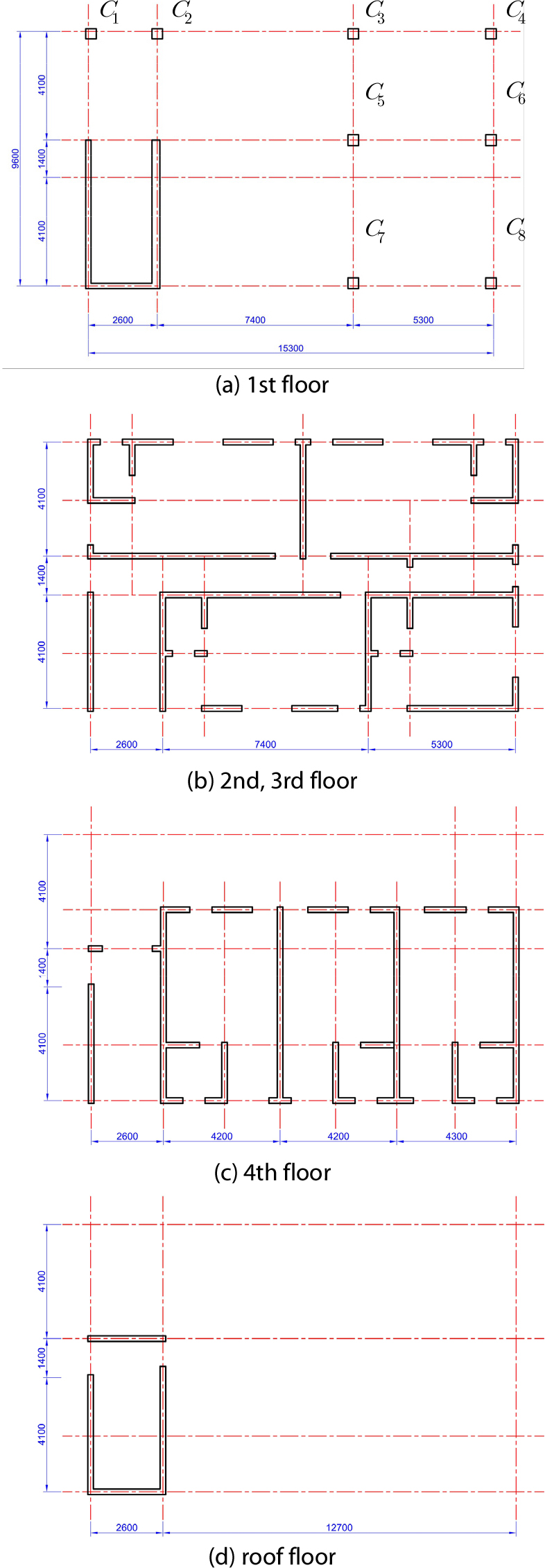
본 연구에서 개발한 비틀림비정형성과 수직비정형성을 가진 필로티 건축물의 지진동에 대한 동적 거동 해석 프로그램에 적용할 구조물은 포항지진 발생시 피해를 입은 필로티 건축물 중에서 코어가 모서리에 위치한 양방향 비대칭 평면을 가진 오OO빌라를 선정하였다. Fig. 6은 경상북도 포항시에 위치한 오OO빌라의 평면도이다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F6.jpg

Fig. 6.

Plan

평면도를 보면 오OO빌라는 필로티층인 1층에 8개의 기둥이 있으며 좌측하단 모서리에 코어가 있는 구조물이다. 오OO빌라는 포항지진시에 코어와 가장 먼 위치에 있는 $C_{4}$ 기둥이 파손되었으며 1층 기준으로 바닥면적 약 151.9㎡ 이며 옥탑층을 포함하여 5층 규모의 소규모 빌라이다.

오OO빌라를 해석 구조물로 선정한 이유는 포항지진으로 인하여 실제 구조적인 피해가 발생하였으며, 지진에 가장 취약한 건물의 대표적인 형태이기 때문이다. 고정하중으로 계산한 층질량과 식 (5)로 계산한 층강성은 Table 2에 나타내었다. 콘크리트 C21을 적용하여 산정한 탄성계수 24,834MPa을 사용하여 강성을 계산하였다.

Table 2.

Stiffness & mass

floor		1st	2ed~3rd	4th	roof
s t i f f n e s s	$k_{x x}$ (kN/m)	3.43×10⁵	1.55×10⁷	9.66×10⁵	1.16×10⁶
	$k_{y y}$ (kN/m)	2.86×10⁶	6.87×10⁶	1.54×10⁷	3.06×10⁶
	$k_{x θ}$ (kN)	1.18×10⁶	-6.21×10⁶	5.92×10⁵	2.10×10⁶
	$k_{y θ}$ (kN)	-1.75×10⁷	-1.41×10⁷	6.04×10⁶	-1.92×10⁷
	$k_{θ θ}$ (kN·m)	1.27×10⁸	2.89×10⁸	4.17×10⁸	1.38×10⁸
mass (kN/m/s²)		123.56	181.12	136.16	29.27

3.2 필로티 건물의 동적 거동 분석

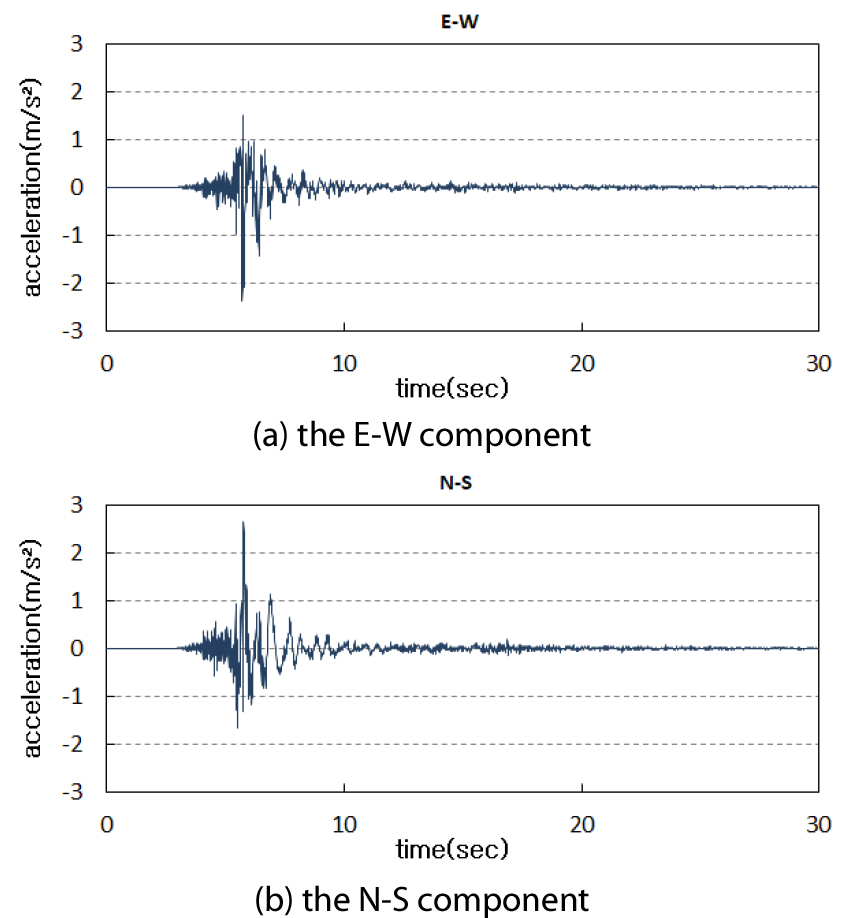
모서리코어가 있는 필로티 건물은 양방향 비대칭평면이므로 양방향 하중을 적용하여 비틀림의 영향을 고려할 필요가 있다. Fig. 7은 2017년 11월 15일에 발생한 포항지진의 관측소 가속도이다. 지진파의 E-W성분은 건물의 $x$ 방향 지반 진동으로, N-S 성분은 $y$ 방향 지반 진동으로 해석에 적용하였으며, 감쇠비는 0.05를 사용하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F7.jpg

Fig. 7.

Pohang earthquake

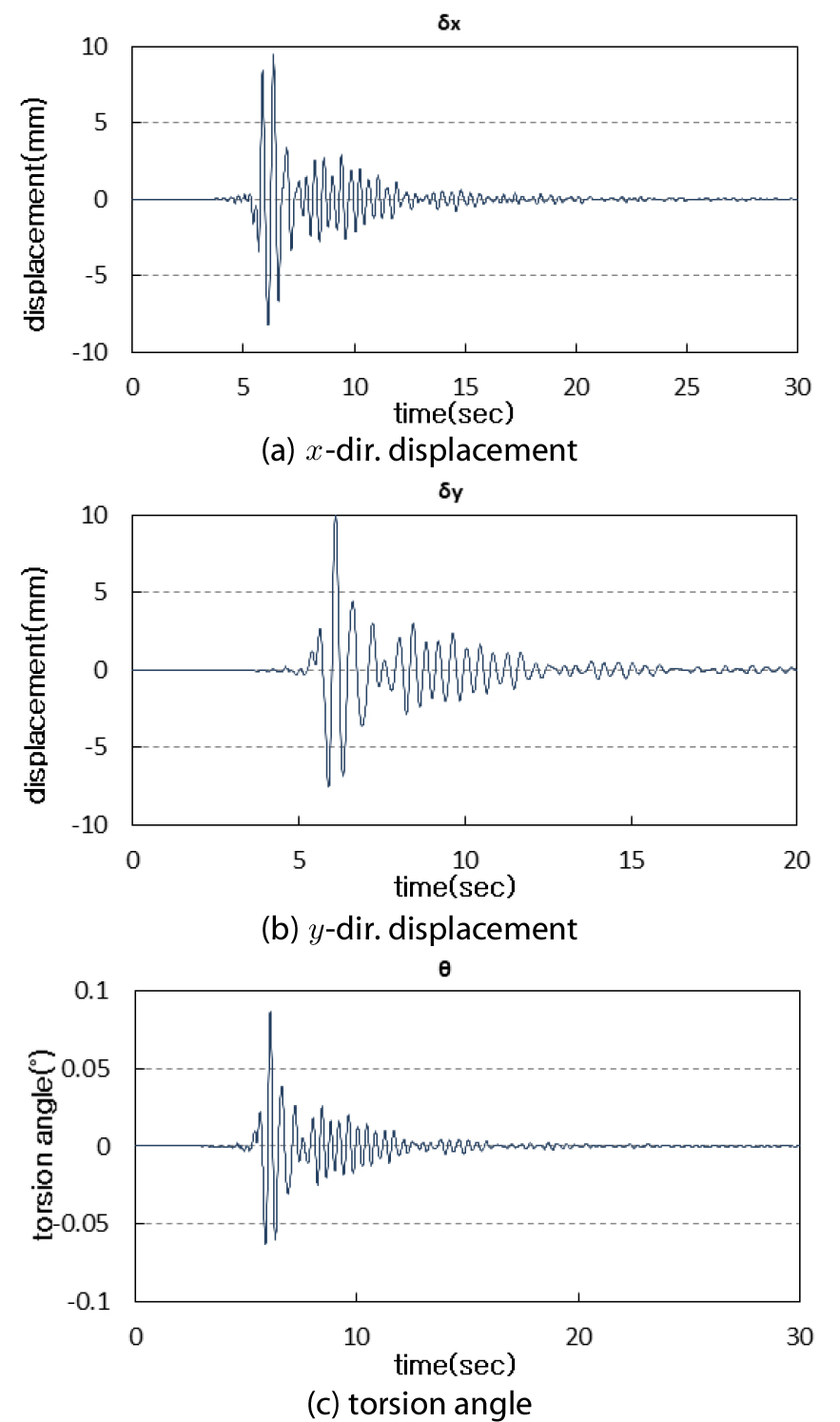
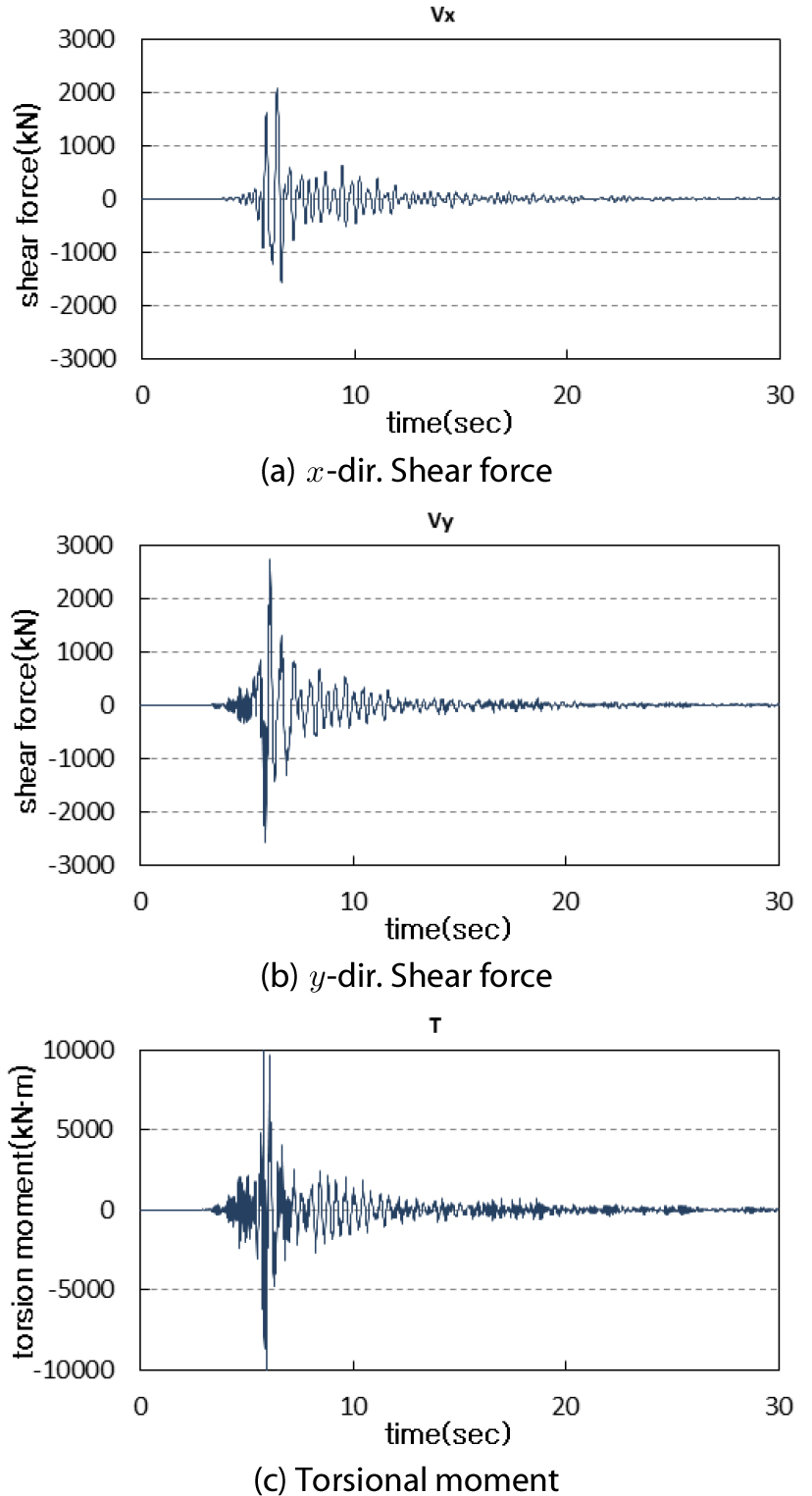
적용 건물의 동적해석을 실시한 결과 중 1층의 변위 및 비틀림각은 Fig. 8에, 1층 전단력 및 비틀림모멘트는 Fig. 9에 나타내었다. $x$ 방향 최대변위는 9.52mm, $y$ 방향 최대변위는 10.11mm, 최대비틀림각은 0.087°로 나타났다. 1층에 작용하는 전단력과 비틀림모멘트는 식 (12)으로 계산하여 Fig. 9에 나타내었다. $y$ 방향 강성이 크므로 $x$ 방향 전단력에 비하여 $y$ 방향 전단력이 커지는 것을 알 수 있다. $x$ 방향 최대전단력은 2076kN, $y$ 방향 최대전단력은 2725kN, 최대비틀림모멘트는 10731kN⋅m로 나타났다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F8.jpg

Fig. 8.

Displacement of 1st floor

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F9.jpg

Fig. 9.

Reaction of 1st floor

기둥에 작용하는 전단력은 식 (13)으로 계산하며, Fig. 6(a) 도면의 1층 각 기둥에 작용하는 전단력 중에서 $x$ 방향 전단력 $V_{x}$ 와 $y$ 방향 전단력 $V_{y}$ 의 합력이 최대일 때를 Table 3에 나타내었다. 편심의 영향이 가장 큰 $C_{4}$ 기둥의 전단력이 최대였으며, 측면 기둥인 $C_{3}$ , $C_{6}$ , $C_{8}$ 기둥도 전단력이 크게 작용하는 것을 알 수 있다.

Table 3.

Shear force of column(kN)

no.	$V_{x}$ (kN)	$V_{y}$ (kN)	$\sum_{}^{} (V_{x} + V_{y}), \max$
$C_{1}$	152.60	13.58	153.21
$C_{2}$	152.60	25.16	154.66
$C_{3}$	152.60	135.42	204.02
$C_{4}$	152.12	215.27	263.59
$C_{5}$	70.65	135.42	152.74
$C_{6}$	69.47	215.27	226.20
$C_{7}$	7.86	135.63	135.86
$C_{8}$	7.86	215.27	215.41

3.3 전단벽 또는 가새 보강 효과에 대한 분석

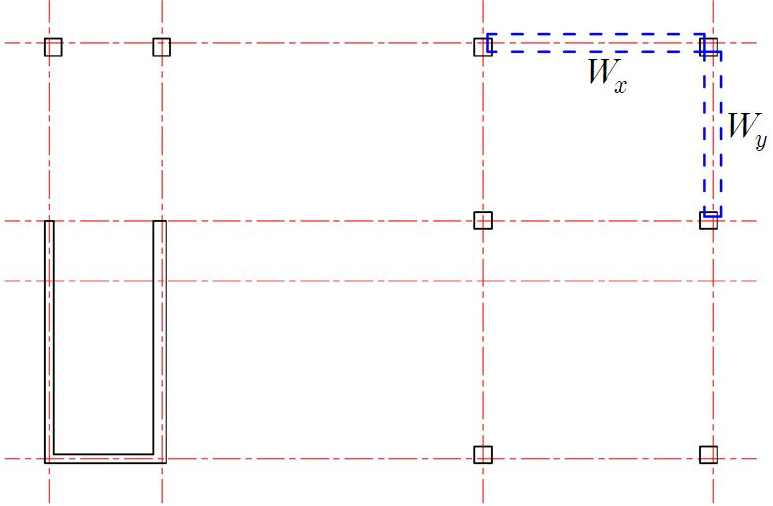
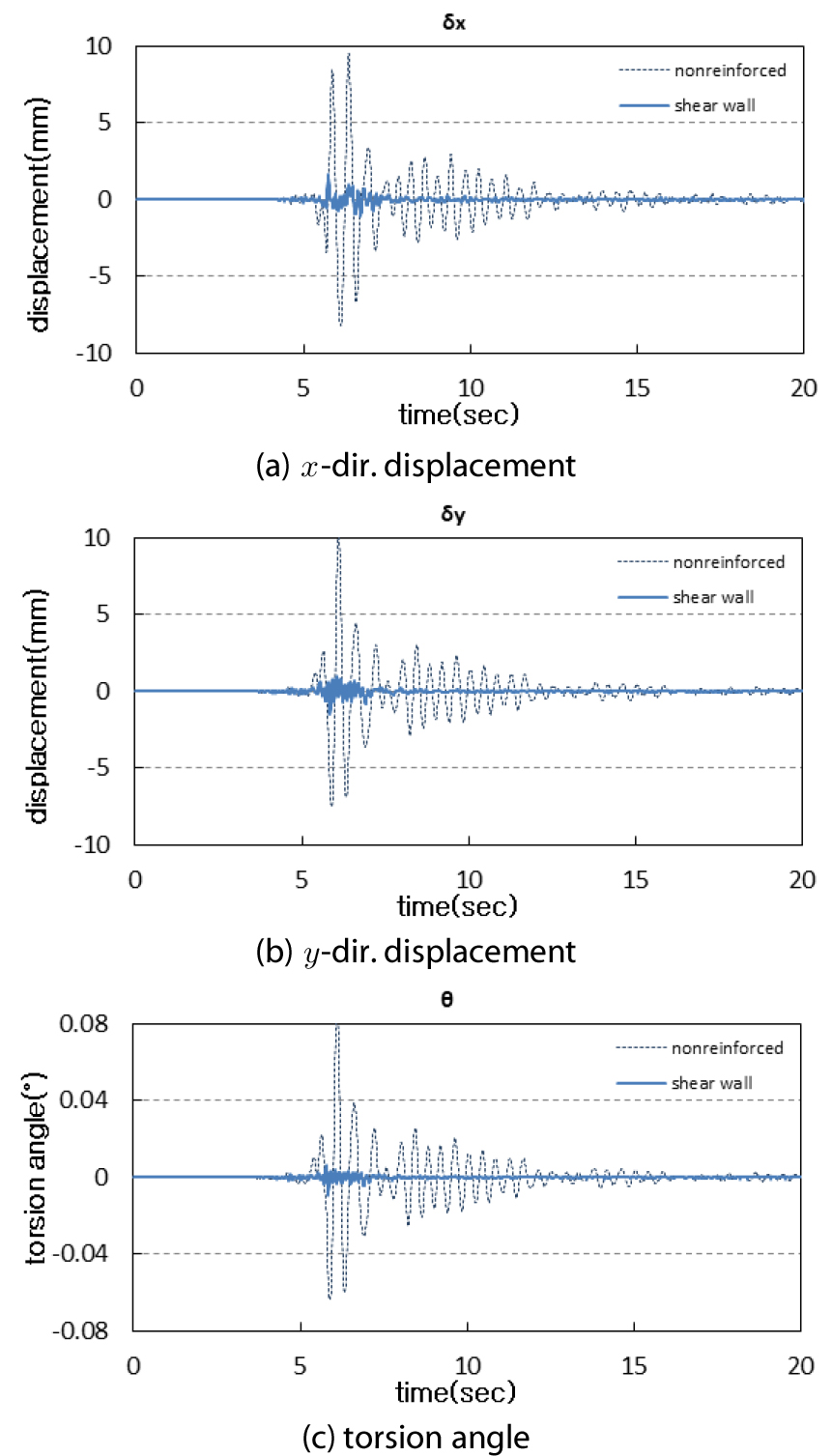
측면코어에 의한 큰 비틀림모멘트 발생을 방지하기 위하여서 콘크리트 전단벽 또는 H형강을 사용한 K형 가새로 보강했을 때의 보강효과를 알아보기 위하여 Fig. 10의 점선으로 표시한 구간을 보강한 건물에 양방향 지진파를 적용하여 동적해석을 실시하였다. Fig. 10에 점선으로 표시한 $W_{x}$ 와 $W_{y}$ 구간에 두께 200mm의 전단벽을 보강한 건물 1층의 동적 응답을 Fig. 11에 나타내었다. Fig. 11의 비보강은 Fig. 5의 원건물을 나타낸다. 해석결과 비보강 건물에 비하여 보강한 건물의 응답이 줄어드는 것을 알 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F10.jpg

Fig. 10.

Reinforcement position

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340301/images/Figure_jcoseik_34_03_01_F11.jpg

Fig. 11.

Dynamic responses of reinforced shear wall

콘크리트 전단벽 또는 H형강을 사용한 K형 가새로 보강한 건물의 최대변위와 감소비율을 Table 4에 나타내었다. $W_{x}$ 와 $W_{y}$ 구간에 두께 200mm의 전단벽 보강한 건물( $W_{x}$ & $W_{y}$ 보강), $W_{x}$ 구간에 두께 200mm의 전단벽 보강한 건물( $W_{x}$ 보강), $W_{x}$ 구간에 두께 200mm의 전단벽 보강한 건물( $W_{y}$ 보강), $W_{x}$ 와 $W_{y}$ 구간에 H-300×300×300×10×15를 사용한 K형 가새로 보강한 건물(K-brace)의 보강효과를 분석하면 가새보다는 전단벽이 보강효과가 크며, 전단벽의 한면만 설치하더라도 가새보다 보강효과가 큰 것을 알 수 있다. 시공적 측면에서도 가새로 보강하는 것보다 한쪽 면을 전단벽으로 보강하는 것이 유리할 것으로 판단된다.

Table 4.

Dynamic responses of reinforced building

building type		displasement(mm)		reduced ratio(%)
building type		$d_{x}$	$d_{y}$	$d_{x}$	$d_{y}$
nonreinforced		9.52	10.11	-	-
shear wall	$W_{x}$ , $W_{y}$	1.65	1.54	82.67	84.77
	$W_{x}$	1.36	2.28	85.71	77.45
	$W_{y}$	5.63	1.27	40.86	87.44
K-brace		6.20	3.99	34.87	60.53

기둥 전단력에 대한 보강효과를 알아보기 위하여 원건물에서 가장 전단력이 큰 $C_{4}$ 기둥의 최대 전단력과 보강에 의한 전단력 감소비율을 Table 5에 나타내었다. 변위보다 기둥 전단력 감소비율 더 크게 나타났으며, 변위와 동일하게 한면만 전단벽을 설치한 보강이 가새보다 보강효과가 큰 것을 알 수 있다.

Table 5.

Shear force of $C_{4}$

building type	Shear force(kN)			reduced ratio(%)
building type	$V_{x}$	$V_{y}$	$V$	$V_{x}$	$V_{y}$	$V$
non	153	215	264	-	-	-
$W_{x}$ , $W_{y}$	17	27	28	88.89	87.44	89.39
$W_{x}$	20	46	50	86.93	78.60	81.06
$W_{y}$	62	28	67	59.48	86.98	74.62
K-brace	85	82	107	44.44	61.86	59.47

본 연구에서 개발한 비틀림비정형성과 수직비정형성을 가진 건축물의 동적 프로그램은 모서리코어를 가진 필로티 건물 해석에 적용가능하며, 필로티층의 기둥 설계에 기초자료를 제공할 수 있을 것으로 기대된다. 또한, 모서리코어가 있는 필로티층의 양방향 편심의 영향을 줄이기 위하여 전단벽이나 K형 가새로 보강하였을 때 보강효과 큰 것을 알 수 있다. 재료비선형을 적용한 동적 해석 프로그램의 개발을 진행할 예정이다.

4. 결 론

본 연구에서는 비틀림비정형성과 수직비정형성을 가진 건축물의 지진동에 대한 동적 거동을 해석할 수 있는 프로그램을 개발하였고, 모서리 코어가 있는 필로티 건물의 동적 거동을 해석하여 다음과 같은 결론을 얻었다.

1)비틀림비정형성과 수직비정형성을 가진 건축물에 양방향 지진동을 적용하여 해석한 결과를 CANNY 프로그램의 해석 결과와 비교하여 개발한 프로그램의 탄성 동적거동에 대한 신뢰성을 검증하였다.

2)모서리 코어가 있는 필로티 건축물의 필로티층 기둥 전단력 해석 결과를 기둥 설계 기초 자료로 활용할 수 있을 것으로 판단된다.

3)모서리코어가 있는 필로티 건축물에서 필로티층의 코어 반대편 모서리를 전단벽이나 K형 가새로 보강하였을 때 변위와 기둥 전단력이 크게 감소하는 것으로 나타났으며, 모서리 양면을 K형 가새로 보강하는 것보다 한 면을 전단벽으로 보강하는 것이 보강효과가 큰 것으로 나타났다.

References

Chopra, A.K. (2001) Dynamics of Structures, Prentice Hall, New Jersey, p.844.

Kim, J.C., Shin, S.H., Oh, S.H. (2019) Damage Investigation of Pilotis Structures and Analysis of Damage Causes by Pohang Earthquake, Archit. Inst. Korea, 35(3), pp.3~10.

Moon, E.C., Baek, E.R., Lee, S.H. (2019) Study on the Seismic Performance for Low-rised RC Building with Vertical and Torsional Irregularities, J. Archit. Inst. Korea Struct. & Constr., 35(12), pp.137~148.

Naeim, F. (2001) The Seismic Design Handbook, Springer, New York, p.830. 10.1007/978-1-4615-1693-411780701

Paz, M. (1985) Structural Dynamics. Van Nostrand Reinhold, New York, p.626.

The Architectural Institute of Korea (2016) Korean Building Code and Commentary.

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Dynamic Analysis of RC Piloti-Type Building Subjected to Earthquake Loads

ABSTRACT

MAIN

(1a)

(1b)

Fig. 1.

Two-way unsymmetric plan

(2a)

(2b)

(3a)

(3b)

(4)

(5a)

(5b)

(5c)

(5d)

(5e)

(5f)

(6a)

(6b)

(7)

(8a)

(8b)

(8c)

Fig. 2.

Stiffness

(9a)

(9b)

(10)

(11)

(12)

(13)

Fig. 3.

Flow chart for program

Fig. 4.

Plan of building with unsymmetric plan

Fig. 5.

Responses of 1st floor

Table 1.

Dynamic responses of building

Fig. 6.

Plan

Table 2.

Stiffness & mass

Fig. 7.

Pohang earthquake

Fig. 8.

Displacement of 1st floor

Fig. 9.

Reaction of 1st floor

Table 3.

Shear force of column(kN)

Fig. 10.

Reinforcement position

Fig. 11.

Dynamic responses of reinforced shear wall

Table 4.

Dynamic responses of reinforced building

Table 5.

Shear force of C4

References

Shear force of $C_{4}$