1. 서 론
2. 부유식 LMU 초기설계
2.1 엘라스토메릭 스택 설계
2.2 리셉터 설계
2.3 경계 조건 및 수치해석 모델
2.4 LMU 초기설계의 수치해석 결과
3. 부유식 LMU 최적설계
3.1 설계 변수 정의
3.2 샘플링 기반 설계민감도해석
3.3 LMU 최적설계
4. 결 론
1. 서 론
육지와 가까워 수심이 얕아 상대적으로 채굴이 쉬운 근해의 석유 자원이 고갈되어감에 따라 수심이 깊은 원해에서의 원유 및 천연가스 채굴에 대한 수요가 꾸준히 증가하고 있다. 원해의 석유자원은 수심이 깊어 고정식 해양구조물의 활용이 어렵기 때문에 채굴을 위한 장비와 이를 정제하거나 저장하기 위한 설비 등으로 구성된 상부구조물이 부유식 해양구조물에 설치되어 수행된다. 이러한 해양구조물을 설치하는 공법은 Fig. 1과 같이 그 방법에 따라 크게 두 가지로 나눌 수 있다. 하나는 해상 크레인을 활용하여 상부구조물의 모듈 또는 전체를 하부지지구조물에 설치하는 리프팅(lifting) 설치 공법이며, 다른 하나는 상부구조물과 하부지지구조물을 각각 제작하여 설치 장소로 운송한 후 바지선 등을 활용하여 상부구조물을 하부지지구조물 위에 얹는 플로트오버(float-over) 설치 공법이다. 플로트오버 설치 공법은 리프팅 설치 공법과 비교하였을 때 해상에서 수행되는 작업이 적고 바지선을 용선하는 비용이 해상 크레인의 비용보다 저렴하기 때문에 경제성이 높을 뿐만 아니라 훅업(hook-up)이나 모듈의 조립 작업이 필요 없어 상대적으로 안전한 공법으로 알려져 있다(Seji and Groot, 2007). 플로트오버 설치 공법을 활용한 해양구조물의 설치 과정에서 상부구조물과 하부지지구조물은 다양한 외력에 영향을 받을 수 있기 때문에 각 구조물을 보호하고 안전한 결합을 위해서는 LMU(Leg Mating Unit), DSU(Deck Support Unit), DSF(Deck Support Frame), 그리고 휀더(fender)와 같은 장비들의 활용이 필수적이다(Tan et al., 2008). LMU는 상부 구조물과 하부지지구조물 사이에 설치되는 장비로써 각 구조물에 작용하는 하중을 저감하기 위한 엘라스토메릭 스택(elastomeric stack)과 원활한 결합을 유도하기 위한 리셉터(receptor) 부분으로 구성된다.
해양구조물은 설치 위치와 목적에 따라 각기 다른 특성을 갖기 때문에 각 부분을 최적화 하여 경쟁력을 높이는 등의 상세 과정 및 내용은 기업의 기밀 사항에 해당되어 문헌으로 공개된 내용이 많지 않다. Yuan 등(2012)은 플로트오버 설치 공법에서 사용되는 LMU를 설계할 때 고려되어야 하는 설계 조건들에 대해 소개하고 유한요소 기반 수치해석 결과와 실 스케일 모형 시험 결과를 비교하였다. Lee 등(2015)은 플로트오버 결합 과정에서 재료 비선형 해석을 통해 LMU의 엘라스토메릭 스택의 반발력을 추정하였으며, 이어서 엘라스토메릭 스택의 요구 반발력을 만족하는 재료 상수들을 역설계를 통해 도출하는 연구를 수행하였다(Lee et al., 2016). Lee 등(2018)은 최적설계를 활용하여 고정식 하부지지구조물과 상부구조물의 플로트오버 설치 과정에서 사용되는 LMU를 개발하였다. Kim 등(2019)은 파라메트릭 스터디를 통해 부유식 하부지지구조물의 플로트오버 설치에서 사용될 수 있는 LMU의 엘라스토메릭 패드(pad)에 대한 각 인자들의 영향을 조사하였다. 초탄성재료의 물성치는 시험을 통해서도 추정될 수 있는데, Song 등(2019)은 압입시험과 유한요소해석 기반 회귀식을 바탕으로 초탄성재료의 물성치를 평가하는 방법을 제안하였다.
본 연구에서는 부유식 해양구조물의 플로트오버 설치 과정에서 사용되는 LMU에 대해 중량을 목적함수로 하면서 허용 응력과 반발력을 제약조건으로 하는 최적설계를 수행하여 성능이 개선된 설계를 제안한다. 부재들의 두께, 높이, 그리고 너비 등과 같은 기하 변수들뿐만 아니라 부재들의 각도와 개수 등 구성(configuration) 변수들 또한 설계 변수로 고려하였으며, 설계민감도해석을 통해 중요도에 따라 선별하였다.
2. 부유식 LMU 초기설계
2.1 엘라스토메릭 스택 설계
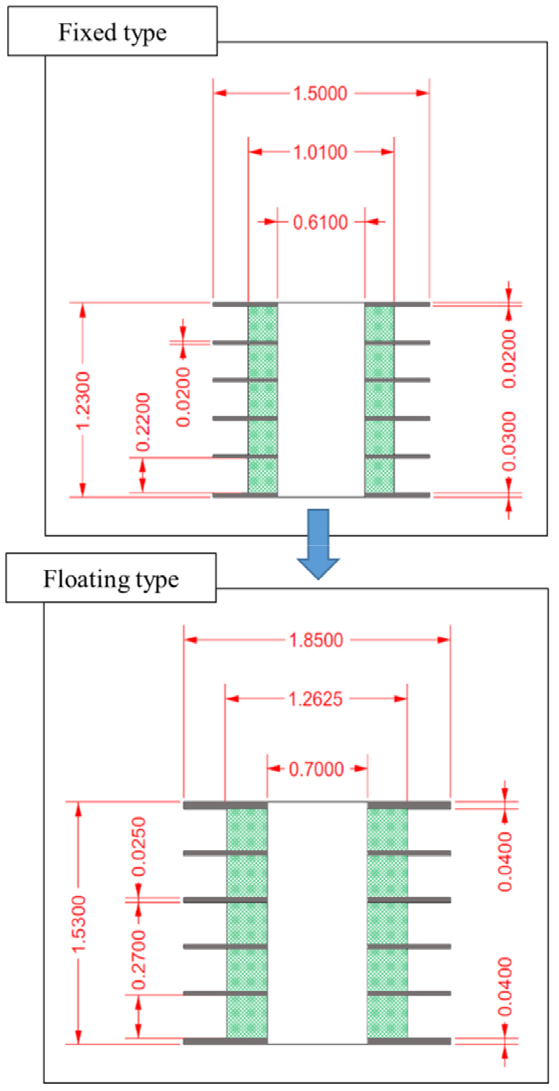
LMU의 엘라스토메릭 스택은 하중을 저감하고 충격을 흡수하는 역할을 하며 초탄성재료인 엘라스토머(elastomer)와 스페이서(spacer)로 구성된다. 본 연구에서는 Fig. 2와 같이 고정식 하부지지구조물에 설치될 수 있도록 개발된 LMU의 제원과 부유식 하부지지구조물에서 LMU가 설치될 위치를 고려하여 엘라스토메릭 스택의 초기 제원을 결정하였다.
엘라스토머의 변형 에너지 밀도 함수(strain energy density function) 를 식 (1)과 같이 2 파라미터 Mooney-Rivlin 모델을 활용하여 표현하였다(Mooney, 1940; Rivlin, 1948).
여기서, , , , , , 그리고 은 각각 1차, 2차 변형률 불변량(deviatoric strain invariant), 재료 상수들, 탄성 체적비(elastic volume ratio), 그리고 비압축성 파라미터(incompressibility parameter)이다. 본 연구에서 활용한 엘라스토머와 스페이서 등 구조용 강철들의 영률과 포아송 비(Poisson’s ratio)는 Table 1에 정리하였으며(Cambridge University, 2003; Harris and Piersol, 2002), 초탄성재료의 재료 상수들은 Table 2와 같다. 아울러 엘라스토머는 비압축성으로 고려하였다.
Table 1.
Material properties of steel and elastomeric pad
2.2 리셉터 설계
LMU의 리셉터는 상부구조물과 하부지지구조물의 원활한 결합을 유도하는 역할을 한다. 리셉터의 초기설계는 Fig. 3과 같이 결합을 위한 깔때기 모양의 리셉터, 수평 및 수직 방향 보강 판들로 구성되어 있다. 이 때 제원은 Table 3에 나타내었다.
Table 3.
Initial dimension of receptor for floating type LMU
2.3 경계 조건 및 수치해석 모델
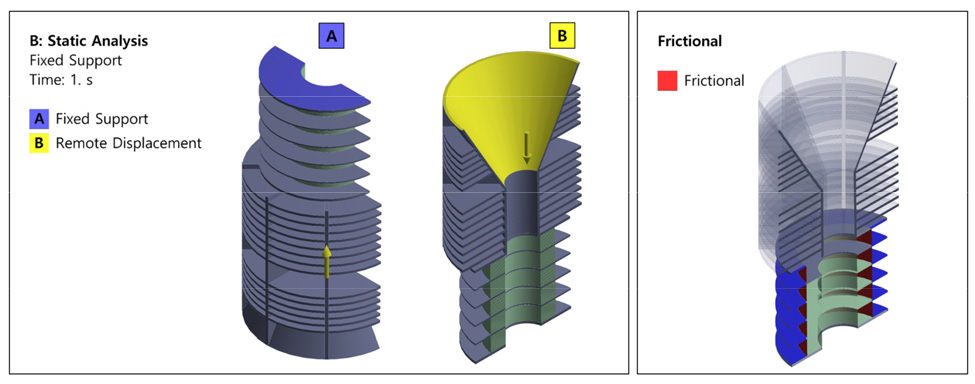
부유식 해양구조물의 플로트오버 설치를 위한 LMU의 경계조건은 Fig. 4와 같다. LMU의 엘라스토머 스택 최하단에 고정 경계조건을 부여하였고, 부유식 해양구조물의 플로트오버 설치에서 설계 조건인 수직 아래 방향 변위 하중 500mm를 리셉터 부분에 인가하였다. 또한 초탄성재료인 엘라스토머와 구조용 강철인 스페이서 사이 접촉을 구현하기 위해 마찰계수 0.3의 마찰 조건(frictional)을 부여하였다.
LMU 수치해석 모델은 ANSYS DesignModeler 2019 R2를 사용하여 모델링하였으며, 20 절점 헥사헤드론(20 node hexahedron, Hex20) 요소를 활용하였다. LMU 초기설계의 수치해석 모델은 264,312개의 절점과 50,928개의 요소로 구성된다.
2.4 LMU 초기설계의 수치해석 결과
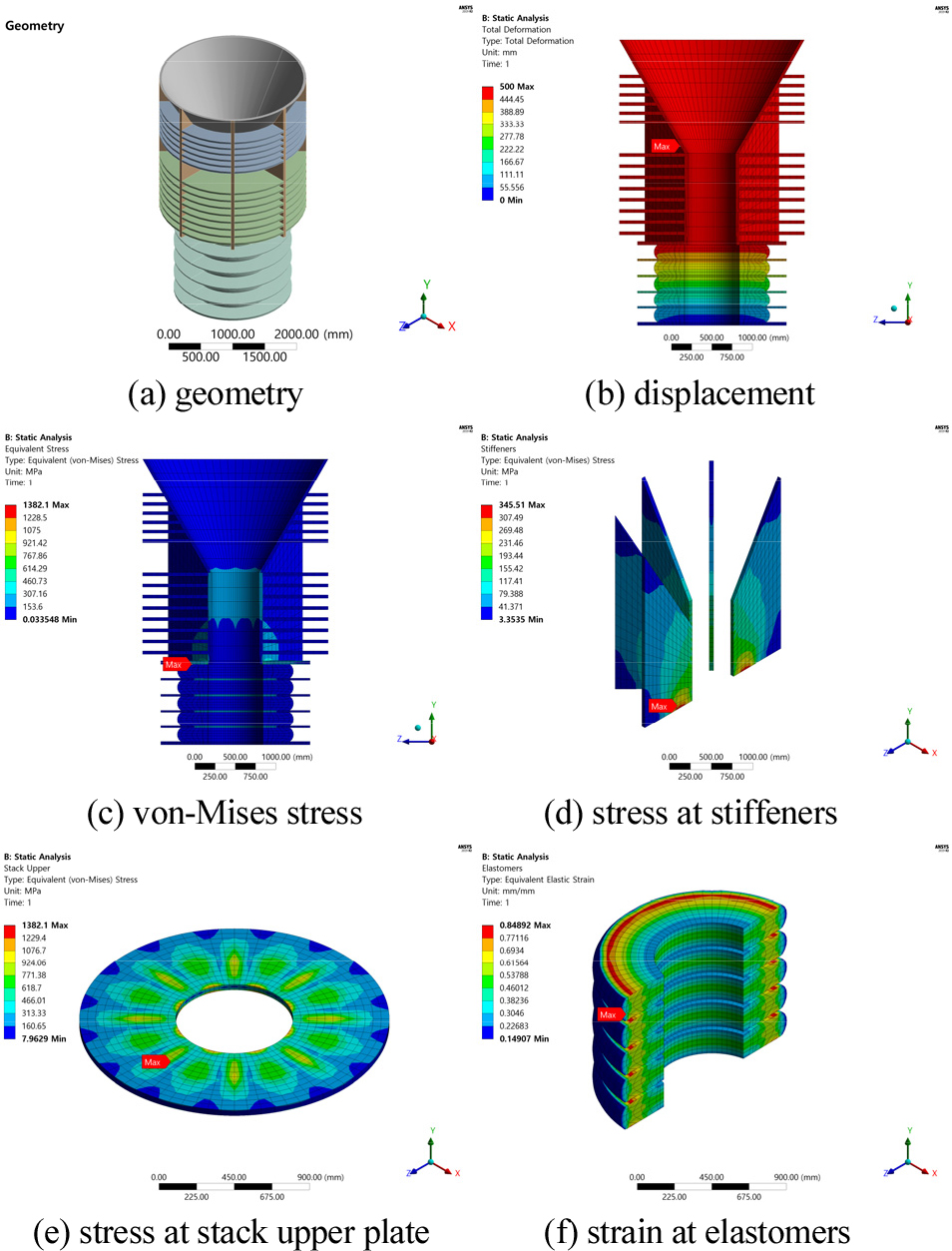
LMU 초기설계의 성능을 확인하기 위해 ANSYS Mechanical 2019 R2를 활용하여 대변형을 고려한 유한요소해석을 수행하였다. LMU 초기설계의 수치해석 결과는 Fig. 5에 도식하였으며, 총 질량, 최대 폰-미세스(von-Mises) 응력, 그리고 반발력은 Table 4에 정리하였다. 아울러 해양구조물에 대한 선급 규정에서는 일반적으로 구조용 강철에 대해 수치해석 결과 350MPa 이하의 폰-미세스 응력이 작용하도록 규정하고 있다. 아울러 본 연구에서 고려한 상부구조물의 무게와 플로트오버 설치 공법에서 부유체 운동해석 결과로 도출된 하중 및 안전계수를 고려하였을 때 각 LMU에서 7,500ton 이상의 반발력이 필요하다. LMU 초기설계에 대한 수치해석 결과를 살펴보면, 최대 응력은 엘라스토머 스택의 상판에서 1,382MPa이 도출되었으며, 반발력은 4,900ton으로 나타난다. 이는 LMU의 응력 허용 조건과 반발력 요구 조건을 만족시키지 못하는 설계로 최적설계를 통해 설계 조건을 만족하면서 성능이 향상된 LMU 최적설계(안)의 도출이 필요하다.
3. 부유식 LMU 최적설계
3.1 설계 변수 정의
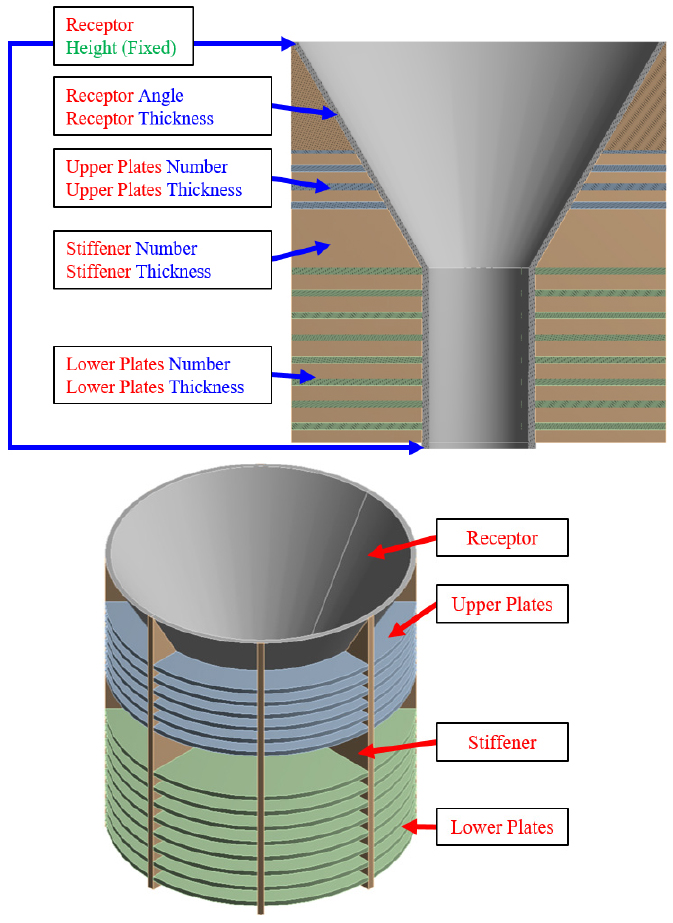
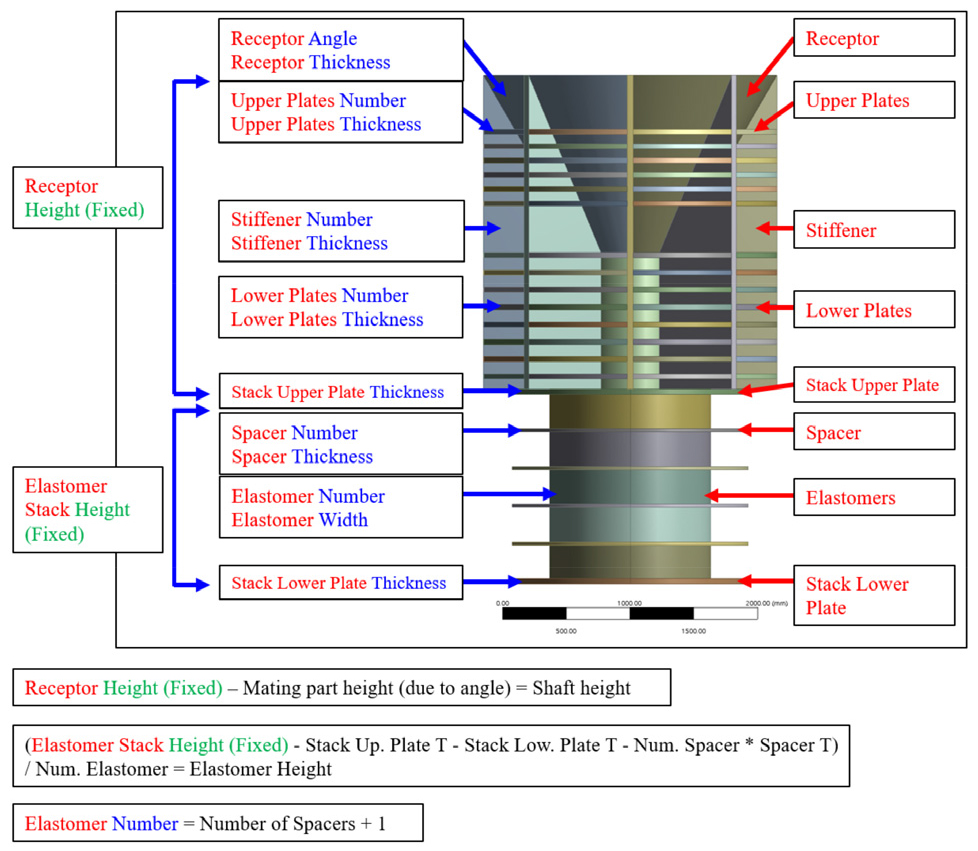
LMU의 성능을 향상하고 설계 요구 조건을 만족하기 위한 최적설계를 수행하기 위해 설계 변수를 정의하였다. 설계 변수는 부재들의 두께, 높이, 그리고 너비와 같은 기하 변수들과 리셉터의 각도 및 보강재들과 엘라스토머의 개수 등 구성 변수들을 포함한다. 다만, 설치 조건을 만족하기 위해 리셉터와 엘라스토머 스택의 높이는 고정되는 제약 조건이 부여되고, 이로 인하여 결합(mating) 부와 샤프트(shaft)의 길이 그리고 엘라스토머 스택을 구성하는 부재들을 매개화하였다. 뿐만 아니라 엘라스토머와 스페이서의 관계 또한 매개화 될 수 있다. 설계 변수들과 매개화된 결과는 Fig. 6에 정리하였다. 또한 Fig. 6에 설계 변수는 파란색으로, 부재들의 이름은 붉은색으로 표기하였으며 설치 조건으로 인해 고정된 값은 녹색으로 명시하였다. 본 연구에서 고려된 설계 변수는 총 13개이다. 설계 변수들의 초기 값과 하한 및 상한 값은 Table 5에 정리하였다.
Table 5.
Design variables and bounds
3.2 샘플링 기반 설계민감도해석
본 연구에서 고려하는 LMU의 성능 함수는 구조물의 총 중량, 구조물에 작용하는 최대 폰-미세스 응력, 그리고 경계 조건에서의 반발력이다. 앞서 정의한 13개의 설계 변수들에 대하여 각 성능 함수들에 대한 영향력을 Advanced Latin hypercube 샘플링 방법을 활용하여 설계민감도해석을 수행하여 분석하였다. 총 200개의 샘플링이 수행되었으며, 설계민감도해석 결과는 Table 6과 같다. 설계민감도해석 결과의 정확도는 CoP(Coefficient of Prognosis)로 표현되며, 이 때 각 설계 변수들의 영향 또한 CoP를 통해 알 수 있다. Table 6의 설계민감도해석 결과를 살펴보면, 모든 성능 함수들에 대한 CoP가 99% 이상으로 매우 높은 정확도를 가지고 설계민감도해석이 수행되었음을 알 수 있다. 반발력에 가장 큰 영향을 미치는 설계 변수는 엘라스토머의 너비임을 알 수 있고 최대 폰-미세스 응력은 엘라스토머 스택의 상판의 두께와 수직 보강재(stiffener)의 개수에 가장 큰 영향을 받는 것을 알 수 있다. 설계 변수들의 CoP 합계는 각 성능 함수의 전체 CoP와 다를 수 있다. 이는 설계 변수들의 상관관계에 의한 영향으로 현재 중량에서는 약 3%, 반발력에서는 약 1%, 그리고 최대 폰-미세스 응력에서는 약 40%의 설계 변수 상호 작용이 있는 것으로 분석된다. 아울러 설계민감도해석 결과 각 성능함수에 영향이 미미한 것으로 분석된 리셉터 각도와 엘라스토머 스택의 하판 두께는 필터링하여 총 11개의 설계 변수를 사용하여 최적설계를 수행하였다.
Table 6.
Design sensitivity analysis results
3.3 LMU 최적설계
LMU의 최적설계는 앞서 수행한 설계민감도해석 결과를 바탕으로 진화 알고리듬(evolutionary algorithm)을 활용하여 ANSYS workbench 2019 R2와 결합된 Dynardo optiSLang 7.4.1을 사용하여 수행되었다. 최적설계의 정식화는 식 (2)와 같이 하였으며, 목적함수는 LMU의 총 중량이고 제약 조건은 허용 응력과 요구 반발력이다. 이 때 허용 응력 제약 조건에 5%의 안전 계수를 부여하여 LMU에 작용하는 최대 폰-미세스 응력이 330MPa 이하가 되도록 하였다.
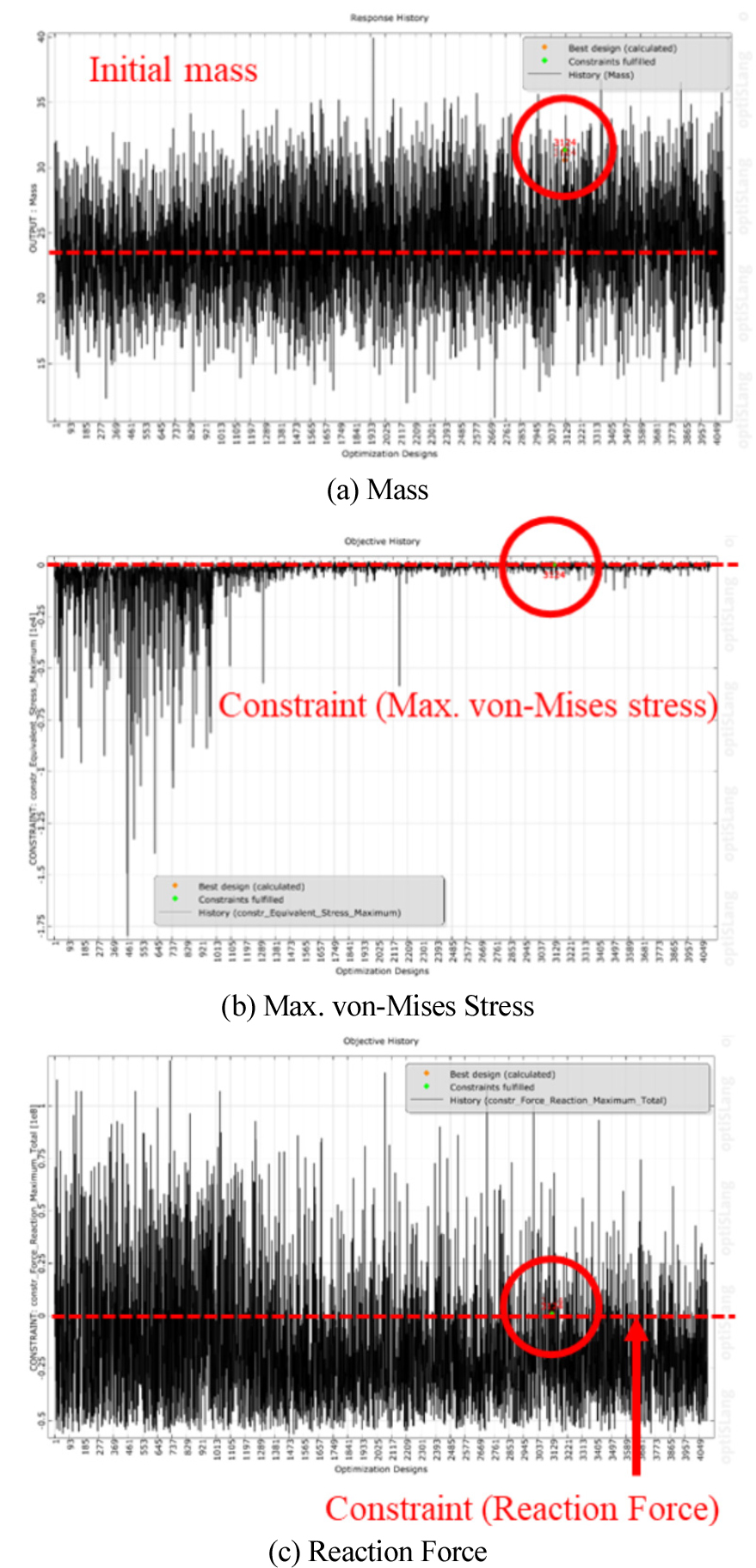
LMU의 각 성능함수들에 대한 최적설계 이력은 Fig. 7에 도식하였다. 총 4,100 번의 설계 생성을 거쳐 수렴하였으며, 3124 번째 설계가 최적의 해로 도출되었다.
최적설계 결과는 Table 7에 정리하였다. 이 때 LMU 초기설계에서의 응력 과다로 인하여 목적함수인 중량은 감소되지 못하고 약 30% 증가하였으며, LMU에 작용하는 최대 폰-미세스 응력은 307.18MPa로 약 78% 저감되었다. 뿐만 아니라 LMU 최적해의 반발력은 약 7,900ton으로 요구 반발력 조건인 7,500ton을 만족하는 것을 알 수 있다.
Table 7.
Design optimization results
| Response | (a) Initial design | (b) Optimal design | (c) (b)/(a)(%) |
| Mass(ton) | 23.32 | 30.58 | 131.13 |
| Max. von-Mises stress(MPa) | 1,382 | 307 | 22.21 |
| Reaction force(ton) | 4,900 | 7,878 | 160.78 |
최적설계로 도출된 LMU의 최적해와 초기설계를 비교하여 각 설계 변수들의 변화를 Table 8에 정리하였다. 결과를 살펴보면, 초기설계에서 최대 폰-미세스 응력이 작용하던 엘라스토메릭 스택의 상판 두께가 최적 해에서 약 4배 증가한 것을 알 수 있다. 두 번째로 영향이 컸던 스티프너의 개수는 해당 설계 변수의 상한인 8개 그대로 유지되었으며, 엘라스토머의 너비와 스페이서의 개수의 변화량은 미미하였다. 이는 해당 설계 변수들이 LMU의 반발력에도 영향을 주기 때문에 허용 응력 조건과 요구 반발력 조건을 동시에 만족시키는 형태로 최적화 된 것으로 분석된다. 다만 대부분의 부재들의 두께가 증가하였는데, 이는 LMU에 작용하는 폰-미세스 응력이 허용 응력 조건을 만족하도록 하기 위함인 것으로 분석된다. 때문에 LMU 최적해의 중량은 초기설계에 비해 증가하였으나, 최대한 중량을 낮추기 위해 상대적으로 영향이 큰리셉터 상하부 보강판의 개수가 감소한 것을 알 수 있다.
Table 8.
Comparison of design variables
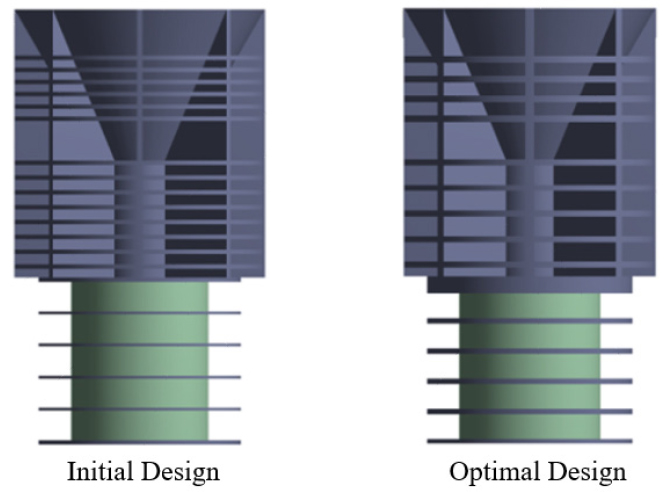
LMU의 초기설계와 최적설계 결과 도출된 최적설계(안)의 형상은 Fig. 8에 비교 및 도시하였다. 최적설계 결과 설치 조건을 만족하기 위해 LMU의 높이는 변함이 없으나, 초기설계에서 최대 폰-미세스 응력이 작용하던 엘라스토메릭 스택의 상판 두께가 증가한 것을 알 수 있다. 또한 리셉터 부의 상하부 보강판의 개수 또한 감소한 것을 확인할 수 있으며 엘라스토머의 폭이 증가하고 높이가 감소한 것을 알 수 있다.
엘라스토머는 고무와 같은 초탄성재료로 성분의 배합과 제조 과정에 따라 그 특성이 영향을 받는다. 때문에 이러한 초탄성재료의 거동을 표현하는 재료 상수를 설계 변수로 두고 최적설계를 통해 도출된 특정 물성을 갖는 초탄성재료를 제조하는 것은 현실적으로 매우 어렵다. 본 연구에서는 시장에서 기성품으로 존재하는 초탄성재료의 물성을 초기설계에서 활용하면서, 엘라스토메릭 스택의 매개화된 설계 변수들을 변화시켜 요구 반발력 조건을 만족시켰다. 엘라스토머의 너비가 증가하고 스페이서들의 두께가 증가함에 따른 엘라스토머의 높이 변화와 LMU의 초기설계 및 최적설계 결과에서 반발력을 Table 9에 정리하였다. 설계 요구 조건에 의해 엘라스토메릭 스택의 높이가 고정되어 있기 때문에 엘라스토메릭 스택의 상하판 두께, 스페이서 두께, 엘라스토머 높이, 스페이서 개수, 그리고 엘라스토머 개수의 설계 변수들이 매개화되어 있다. 결과를 살펴보면 이러한 매개화를 통해 결정된 초탄성재료의 물성 변경 없이도 LMU의 요구 반발력을 만족하는 최적설계를 도출할 수 있음을 알 수 있다.
Table 9.
Comparison of elastomeric stack dimension and reaction force
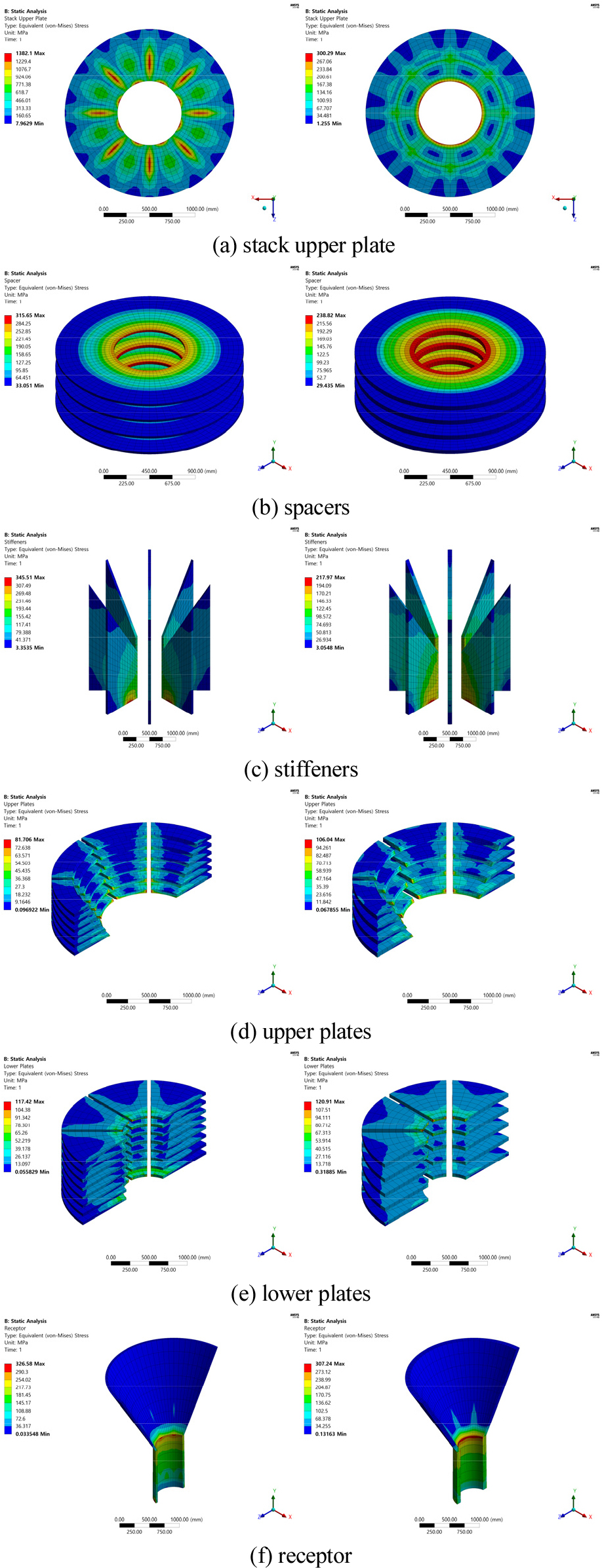
Fig. 9에서는 LMU의 초기설계와 최적설계로 도출된 최적설계(안)의 각 부재들에 대한 폰-미세스 응력을 도식하여 비교하였다. 또한 Table 10에서 각 부재별 최대 폰-미세스 응력을 비교하여 최적설계의 효용성을 확인하였다. 표를 살펴보면 최적설계의 결과로 최대 폰-미세스 응력이 작용하던 엘라스토머 스택 상판에서의 응력이 허용 응력 이하 수준으로 저감된 것을 알 수 있으며, 스페이서와 보강재에서도 약 25~35% 정도 최대 폰-미세스 응력이 감소된 것을 알 수 있다. 다만 리셉터 부의 상부 보강판의 경우 최대 폰-미세스 응력이 약 30% 증가하였으나 허용 응력 조건을 만족하였다. 그리고 리셉터 부의 하부 보강판과 리셉터의 경우에는 초기설계와 비슷한 수준의 응력이 작용하는 것으로 확인된다.
4. 결 론
본 연구에서는 부유식 해양구조물의 플로트오버 설치 과정에서 구조물에 작용하는 하중을 저감하고 원활한 결합이 될 수 있도록 유도하는 LMU에 대해 최적설계를 수행하여 선급 규정에서 정의하고 있는 허용 응력 조건과 요구 반발력 조건을 만족하는 설계를 개발하였다. 설계 변수는 부재들의 기하학적 변수들뿐만 아니라 각도와 개수 등 구성 변수들도 포함하여 정의되었으며, 설계 요구 조건을 만족하기 위해 매개화하였다. 설계민감도해석을 통해 중요도를 기준으로 선별하였으며, 진화 알고리듬을 활용하여 최적설계를 수행하였다.
최적설계 결과 LMU 초기설계와 비교하여 LMU에 작용하는 최대 폰-미세스 응력은 약 80% 저감되었으며 LMU의 성능을 평가할 수 있는 지표인 반발력은 약 60% 개선되어 고정식 해양구조물의 경우를 참조한 LMU 초기설계가 만족하지 못하던 허용 응력 조건과 요구 반발력 조건을 모두 만족할 수 있는 최적설계(안)을 도출할 수 있었다. 다만, 초기설계에서 과도한 응력 집중이 있었기 때문에 LMU의 중량은 초기설계에 비해 증가하였다. 아울러 본 연구에서 활용한 진화 알고리즘은 근사 최적설계 방법론으로, 예측된 값과 최적설계 검증 해석에 오차가 발생할 수 있다. 때문에 최적설계로 도출된 최적해의 응력 및 반발력 등 제약 조건이 정식화 과정에서 설정한 값과 차이가 있다. 이는 도출된 근사 최적해를 시작점으로 하여 직접 최적설계를 수행함으로써 수렴성을 개선할 수 있으며 추가적인 중량 감소 효과 또한 기대할 수 있다. 다만, 본 연구에서는 추가 최적설계를 수행하지 않았으며, 추후 보완을 통해 최적설계 결과를 개선할 계획이다.