Comparison of the Applicability of Bayesian Filters for System Identification of Sudden Structural Damage

Se-Hyeok Lee; Minkyu Kim; Sang-ri Yi

doi:10.7734/COSEIK.2024.37.4.283

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 August 2024. 283-293
https://doi.org/10.7734/COSEIK.2024.37.4.283

Comparison of the Applicability of Bayesian Filters for System Identification of Sudden Structural Damage

급격한 구조손상탐지를 위한 베이지안 필터 적용가능성 비교 검토 연구

Se-Hyeok Lee¹^†

Minkyu Kim²

Sang-ri Yi³

이 세혁¹^†

김 민규²

이 상리³

¹Senior Researcher, Department of Structural Engineering Research, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

²Postdoctoral Researcher, Structural and Seismic Safety Research Division, Korea Atomic Energy Research Institute, Daejeon, 34057, Korea

³Assistant Project Scientist, Department of Civil and Environmental Engineering, University of California, Berkeley, CA, USA

¹한국건설기술연구원 구조연구본부 수석연구원

²한국원자력연구원 구조･지진안전연구부 박사후연구원

³University of California, Berkeley 박사후연구원

^{†Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In this study, advanced unscented Kalman filter (UKF) and particle filter (PF) implementations are introduced and applied to perform system identification (SI) for sudden structural damage induced by seismic loading. These two methods are then compared to validate their applicability to SI tasks. For this validation, the Bouc– Wen model is used to simulate the nonlinear shear-building response, and an adaptive rule (i.e., an adaptive tracking method) is applied to the two filter methods to improve their tracking performance during sudden changes in system properties. When the original UKF and PF are applied to an earthquake scenario, both methods fail to estimate the damage initiation time and post-damage parameter values. After applying the adaptive tracking method, it is found for both methods that although the occurrence time is identified, the estimation of the damage state is still not accurate. To improve the accuracy, an adjusted adaptive tracking method is applied, and the two methods then derive accurate estimates. Finally, when considering the computation time, UKF is promoted as a better choice for practical applications, provided that a proper adaptive tracking method is implemented.

Keywords

unscented kalman filter

particle filter

system identification

sudden structural damage

bouc-wen model

본 논문에서는 지진 하중으로 인한 급격한 구조손상탐지를 수행하기 위해 분산점 칼만필터(Unscented Kalman Filter, UKF)와 파티클 필터(Particle Filter)를 소개하고 지진 손상 시나리오에 적용 및 비교･검토하였다. 이때, 비선형 전단 빌딩을 모사하기 위해 Bouc-Wen 모델을 사용하였고, 급격한 변화를 추정하기 위해 추가적으로 적응형 기법(Adaptive rule)인 Adaptive Jumping Method를 두 필터 모두에 적용하였다. 적용 결과 두 오리지날 필터 모두 급격한 손상 시점과 정도를 파악하지 못하였고, 적응형 기법을 반영하였을 경우에만 시점 파악이 가능하였다. 하지만, 여전히 손상 정도를 정확히 파악하지 못하였고, 두 방법 모두 제안된 적응형 기법을 새로이 조정하였을 경우에 정확한 추정이 가능함을 확인하였다. 최종적으로 계산시간을 고려하였을 때, 새로운 형태의 적응형 기법을 적용한 UKF 사용을 제안하는 것으로 비교 검토를 수행하였다.

키워드

분산점 칼만필터

파티클 필터

구조손상탐지기법

급격한 구조 손상

Bouc-Wen 모델

MAIN

1. 서 론
2. 비선형을 고려한 State-space 모델
3. 급격한 구조손상탐지를 위한 베이지안 필터
3.1 분산점 칼만필터(Unscented Kalman Filter)
3.2 파티클 필터(Particle Filter)
3.3 적응형 기법: Adaptive Tracking Method
4. 수치 예제 적용
4.1 오리지날 및 적응형 분산점 칼만필터 적용 결과
4.2 오리지날 및 적응형 파티클 필터 적용 및 결과
5. 결 론

1. 서 론

베이지안 필터(Bayesian Filter)는 측정된 시계열 데이터를 이용하여 대상 시스템의 주요 변수(예: 강성, 감쇠, 질량 등)들의 확률 분포 함수를 실시간으로 추정하고 업데이트할 수 있는 방법론으로서 크게 예측과 보정 두 단계로 이루어진다(Lee and Song, 2020; Yi and Song, 2018). 예측 단계는 시간의 흐름에 따른 대상 시스템의 변화를 주어진 함수 모델을 이용하여 예측하며, 보정 단계에서는 앞서 예측된 시스템의 추정 상태를 측정 데이터를 기반으로 수정 및 조정하게 된다. 이 두 단계가 반복적으로 수행될 경우 베이지안 필터로 불리며 대표적인 예로는 칼만 필터(Kalman Filter)가 있다. 칼만 필터는 측정된 데이터를 이용하여 대상 시스템을 편향되지 않고(Unbiased), 최소 분산(Minimum variance)을 갖도록 추정하며, 상태 예측 및 적응 제어 등 다양한 분야에서 활용되고 있다(Kalman, 1960; Lee and Song, 2020; Lee et al., 2023; Nguyen et al., 2022).

이러한 필터 방법론을 적용하기 위해서는 대상 동적 시스템을 수학적 모델인 State-space 모델로 표현해야 하며, 해당 모델의 비선형성 여부와 정도에 따라 적용하는 방법이 달라지게 된다. 비선형성을 고려할 수 있는 고전적인(Classical) 방법으로는 확장 칼만 필터(Extended Kalman Filter, EKF)와 분산점 칼만 필터(Unscented Kalman Filter, UKF)가 있다. EKF는 테일러 근사(Taylor expansion)에 기반한 1차(선형) 근사를 활용하며, UKF는 분산점들(Sigma-points)을 이용한 Unscented Transformation을 기반으로 2차 다항 근사의 정확도를 도출한다. 대상 시스템의 변수가 매우 많거나, 시스템 모델 자체의 계산 비용이 매우 큰 경우를 제외하고는 일반적으로 UKF를 사용하는 것이 효과적이며, 최근 다중 분산점을 활용하여 UKF의 자체 파라미터 설정 문제를 완화하려는 노력이 이루어진 바 있다(Lee et al., 2023).

한편 칼만 필터류의 널리 알려진 고질적인 문제로는 자체 파라미터인 두 가지 인공오차를 설정하는 것에 대한 어려움이 있다. 적절한 인공오차들이 설정될 경우 최적의 해가 추정될 수 있지만, 그렇지 못할 경우 해가 발산하거나 수치 문제로 인해 알고리즘이 도중에 중단될 수 있다(Lee et al., 2024). 이에 반해, 현대적인(Modern) 베이지안 필터 방법으로 알려진 파티클 필터(Particle Filter, PF)는 샘플링을 기반으로 예측･보정을 수행하여 대상 시스템의 상태를 추정한다. 파티클 필터 또한 인공오차를 설정해야 하지만, 해당 인공오차는 샘플링 함수의 분포를 결정하게 되며 직관적인 설정이 가능하다.

최근 다양한 베이지안 필터 방법론들을 이용하여 외부하중으로 인해 초래된 구조 손상과 같이 구조적 특성이 변화된(Time-variant) 동적 시스템 상태를 추정하는 연구들이 수행되었다(Lee and Song, 2020; Lee et al., 2023; 2024; Nguyen et al., 2022; Papakonstantinou et al., 2020; Yi and Song, 2018). 이러한 연구들은 계측된 가속도를 기반으로 대상 시스템의 구조적 정보(강성, 감쇠 등)를 역 추정하는 것을 목적으로 칼만 필터 또는 파티클 필터를 이용하였다. 본 연구에서는 지진 하중으로 인해 급격한 구조손상을 겪는 구조물을 모사하는 비선형 모델을 활용하여 UKF와 파티클 필터의 적용성을 비교 분석하는 것을 목표로 한다. 이때, 급격한 구조 손상을 추정하기 위해 개발된 Adaptive Tracking Method를 소개하고(Liu et al., 2005; Yang et al., 2006), 두 방법론에 동일하게 적용하여 추정을 수행한다.

2장에서는 베이지안 필터 적용을 위해 필요한 동적 시스템을 이산화하는 State-Space 모델과 함께 비선형성 고려를 위해 도입된 Bouc-Wen 모델을 간략히 설명한다. 3장에서는 각각 UKF와 파티클 필터에 대해 소개하고, 급격한 구조손상탐지를 위해 Adaptive Tracking Method를 도입한다. 4장에서는 지진으로 인한 여러 구조손상 시나리오들을 가정하고 소개된 두 가지 방법을 수행한다. 최종적으로, 수행된 결과들을 바탕으로 두 방법론의 장단점을 파악하고 실제 구조손상탐지 적용가능성을 검토하도록 한다.

2. 비선형을 고려한 State-space 모델

베이지안 필터 방법론을 적용하기 위해서는 대상 동적 시스템을 이산화하는 수학적 모델을 구축해야 하며, 이를 State-space 모델이라 한다(Chatzi and Smyth, 2009; Lee and Song, 2020; van der Merwe and Wan, 2001; Yi and Song, 2018). State-space 모델은 시간의 흐름에 따라 대상 시스템의 상태 예측을 수행하는 System-process 예측 모델과, 예측된 상태를 수정 및 조정하는 Measurement-output 보정 모델로 구성되며 각각 다음 수식 (1), (2)와 같다.

(1)

x_{t + 1} = f (x_{t}) + w_{t}, ∵ w_{t} ~ N ({0, Q}_{t})

(2)

z_{t + 1} = h (x_{t + 1}, u_{t + 1}) + v_{t + 1}, ∵ v_{t + 1} ~ N ({0, R}_{t + 1})

위 식에서 벡터 $x_{t}$ 는 강성 및 감쇠계수와 같은 대상시스템의 상태를 나타낼 수 있는 변수들을 의미하며, $u_{t + 1}$ 은 입력 벡터를 의미한다. $f (∙)$ 와 $h (∙)$ 는 각각 예측, 보정 모델을 대표하는 함수들이며, $z_{t + 1}$ 는 예측된 시스템 상태벡터를 기반으로 보정 모델을 통해 산정된 시스템 거동(예: 가속도) 벡터를 의미한다. 마지막으로 $w_{t}$ 와 $v_{t + 1}$ 는 각각 시스템 인공오차, 측정 인공오차를 의미한다. 가우시안 랜덤 변수인 두 벡터는 평균이 0이고 사전에 설정된 인공오차 $Q_{t}$ , $R_{t + 1}$ 로부터 생성된다. 베이지안 필터를 이용하여 최적의 예측을 수행하기 위해서는 적절한 인공오차 공분산들을 설정해야 하며, 대게 경험적인 방법이 많이 사용되지만 전역 최적화와 같은 방법을 통해 산정한 연구가 진행된 바 있다(Lee and Song, 2020).

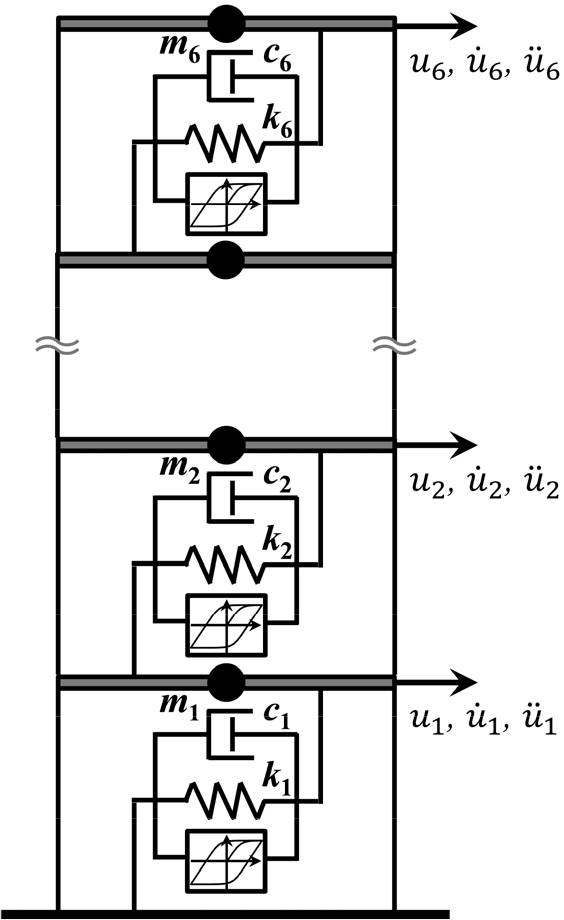
본 연구에서는 대상 시스템의 강성을 추정하고자 하였고, 따라서 예측 모델 함수 $f (∙)$ 는 $x_{t + 1} = x_{t} + w_{t}$ 와 같이 간단하게 정의될 수 있다. 반면, 시스템의 거동을 산정하는 보정 모델 함수 $h (∙)$ 는 뉴마크(Newmark) 동해석 기법 등이 활용될 수 있으며, 본 연구에서는 지진으로 인한 비선형 이력 거동을 모사하기 위해 Bouc-Wen 모델을 도입하기로 한다(Song and Der Kiureghian, 2006; Vaiana et al., 2018). Bouc-Wen 모델은 1967년 Bouc이 제안하고 1976년 Wen에 의해 개선되었으며, 외부 진동에 의한 구조물의 이력현상(Hysteresis)을 부드러운 곡선으로 표현하는 효율적인 모델로 알려져 있다(Baber and Noori, 1984; Baber and Wen, 1981; Foliente et al., 1996; Noori et al., 1986; Wang and Wen 1998). Fig. 1은 Bouc-Wen 모델을 설명하기 위한 단자유도 모델이다.

Fig. 1과 같이 지진하중을 받는 Bouc-Wen 모델이 적용된 시스템의 평형 방정식은 다음과 같다(Fujimura and Der Kiureghian, 2007; Yi et al., 2017).

(3)

m \ddot{u} (t) + c \dot{u} (t) + k_{0} [α_{B W} u (t) + (1 - α_{B W}) z (t)] = F (t)

이때, $m$ , $c$ , $k_{0}$ , $\ddot{u} (t)$ , $u (t)$ , $F (t)$ 는 일반적인 평형 방정식과 같이 질량, 감쇠 계수, 강성, 가속도, 속도, 변위, 지진 하중( $F (t)$ $= m {\ddot{u}}_{g} (t)$ )을 의미한다. 이 외에 변수들은 Bouc-Wen 모델 도입을 위해 추가된 변수들이며, $α_{B W}$ 는 항복 후 강성비로 본 연구에서는 0.1을 사용하였다. $z (t)$ 는 보조 변수로서 다음의 Bouc-Wen 모델 수식을 따른다.

(4)

\dot{z} (t) = \dot{u} (t) \{A - [γ s i g n (z (t) \dot{u} (t)) + η] | z (t) |^{n}\}

위 식에서 거동과 관련된 변수 $z (t)$ , $u (t)$ 를 제외한 나머지 변수들은 이력곡선의 형상을 결정한다. 각 변수의 상세 수치는 4장에서 소개될 수치 예제에서 설명하도록 한다. 최종적으로 보정 모델 함수 $h (∙)$ 는 식 (3)과 (4)로 표현된 Bouc-Wen 모델을 이산화하여 지진 거동 이력을 산정하며, 다음장에서는 비선형을 고려한 State-space 모델을 이용하는 두 가지 베이지안 필터 방법론들을 간략히 소개한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F1.jpg

Fig. 1.

SDOF Oscillator considering Bouc-Wen Model

3. 급격한 구조손상탐지를 위한 베이지안 필터

앞서 2장에서는 지진 하중으로 인한 비선형 이력곡선을 고려하기 위해 Bouc-Wen 모델이 도입된 State-space 모델을 소개하였다. 다음으로는 이러한 비선형성을 고려할 수 있는 칼만필터인 UKF와 파티클 필터의 알고리즘을 설명한다. 또한 급격한 상태 변화를 탐지하기 위해 제안된 Adaptive Tracking Method를 소개하고 각 방법에 적용하도록 한다.

3.1 분산점 칼만필터(Unscented Kalman Filter)

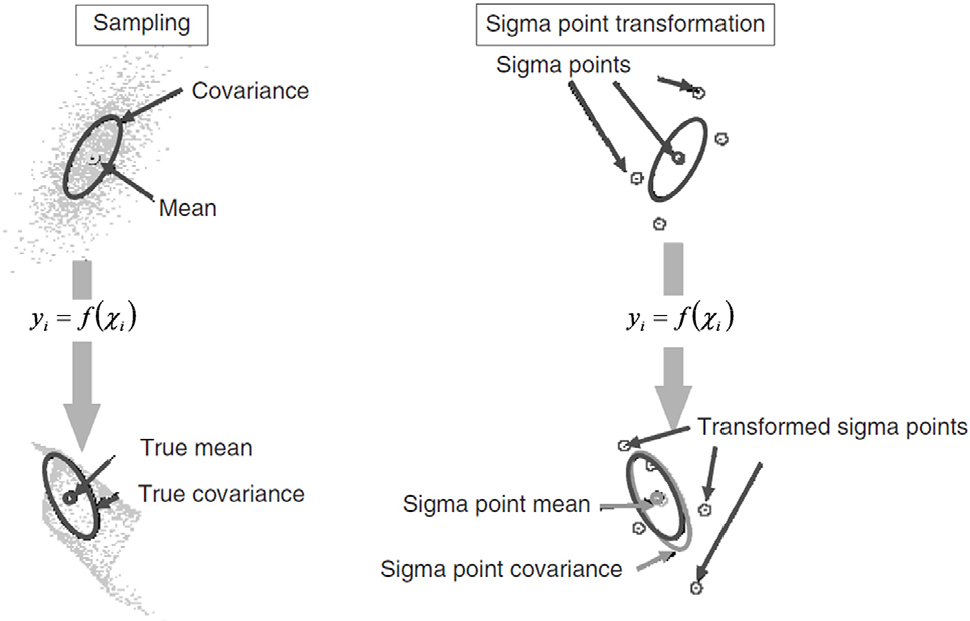
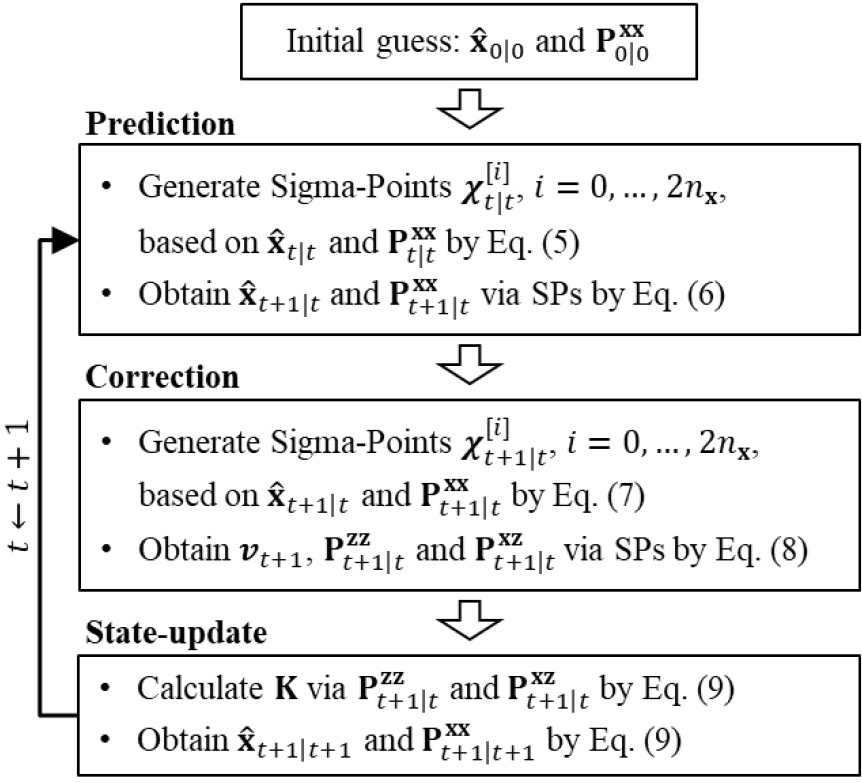
분산점 칼만필터(Unscented Kalman Filter, UKF)의 특징은 Fig. 2와 같이 Unscented Transformation을 이용하여 비선형성을 고려하는 것이며, 이는 시그마 포인트(Sigma-points, SP)를 이용하여 State-space 모델의 비선형성을 2차 선형 근사화 하는 것으로 알려져 있다. Fig. 3은 UKF의 알고리즘을 나타내며, ${\hat{x}}_{t | t}$ , $P_{t | t}^{xx}$ 는 시간 t에서의 평균 상태(State) 벡터와 공분산(Covariance) 행렬을 의미한다. 알고리즘의 예측(Prediction)단계에서는 SP를 생성하고 예측 모델을 이용하여 상태벡터를 업데이트 한다. 다음은 SP를 계산하는 과정이다(Lee and Song, 2020; Lee et al., 2023).

(5)

\begin{aligned} χ_{t ∣ t}^{[0]} = {\hat{x}}_{t ∣ t} \\ χ_{t ∣ t}^{[i]} = {\hat{x}}_{t ∣ t} + {(\sqrt{(n_{x} + λ) P_{t ∣ t}^{xx}})}^{i}, i = 1, \dots, n_{x} \\ χ_{t ∣ t}^{[i]} = {\hat{x}}_{t ∣ t} + {(\sqrt{(n_{x} + λ) P_{t ∣ t}^{xx}})}^{i - n_{x}}, i = n_{x} + 1, \dots, 2 n_{x} \end{aligned}

위 수식에 따르면, $2 n_{x} + 1$ 개의 SP( $χ_{t | t}^{[i]}$ )들이 생성된다. 여기서, $n_{x}$ 와 𝜆는 각각 상태 벡터에 해당하는 변수의 개수와 자체 파라미터이다. 이때, $λ = α^{2} (n_{X} + κ) - n_{X}$ 와 같은 관계를 가지며, 𝛼와 𝜅는 스케일링 파라미터이다. 보통 𝛼에 의해 SP의 분포도가 결정되며, 𝜅는 고차 모멘트(예: 뒤틀림, 첨도 등)를 고려할 때 사용되는 값으로 본 연구에서는 0으로 고정하였다. 행렬 제곱근을 계산하기 위해 Cholesky Factorization이 사용되며(van der Merwe and Wan, 2001), $(∙)^{i}$ 는 괄호 안 행렬의 i번째 열 벡터이다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F2.jpg

Fig. 2.

Schematic Diagram of Unscented Transformation

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F3.jpg

Fig. 3.

Algorithm of Unscented Kalman Filter

식 (5)에서 산정된 SP들은 2장에서 소개된 예측 모델 함수 $f (∙)$ 를 통해 업데이트되며 식 (6)과 같이 업데이트 된다.

(6)

\begin{aligned} χ_{t + 1 ∣ t}^{[i]} = f (χ_{t ∣ t}^{[i]}), i = 0, \dots, 2 n_{x} \\ {\hat{x}}_{t + 1 ∣ t} = \sum_{i = 0}^{2 n_{x}} W_{m}^{i} χ_{t + 1 ∣ t}^{[i]} \\ P_{t + 1 ∣ t}^{xx} = \sum_{i = 0}^{2 n_{x}} W_{c}^{i} [χ_{t + 1 ∣ t}^{[i]} - {\hat{x}}_{t + 1 ∣ t}] {[χ_{t + 1 ∣ t}^{[i]} - {\hat{x}}_{t + 1 ∣ t}]}^{T} + Q_{t} \end{aligned}

위 식에서 $i \neq 0$ 인 경우 가중치는 $W_{m}^{i} = W_{c}^{i} = 1 / 2 (n_{x} + λ)$ 와 같이 정의되며, SP의 평균 값을 계산할 경우( $i$ =0)에만 $W_{m}^{0} = λ / (n_{x} + λ)$ , $W_{c}^{0} = W_{m}^{0} + (1 - α^{2} + β)$ 로 정의된다. 상태 벡터의 분포 형태를 결정하는 𝛽는 2가 사용되었으며(van der Merwe and Wan, 2000), 이로부터 최종 예측 값인 ${\hat{x}}_{t + 1 | t}$ 와 $P_{t + 1 | t}^{xx}$ 가 계산된다. 해당 값들은 상태 벡터와 공분산의 평균값을 의미하며 다음 보정 단계에서 측정된 정보를 기반으로 수정 및 조정된다.

예측 단계와 마찬가지로 보정 단계에서도 다음 식 (7)과 같이 SP를 생성한다. 이때 SP들의 분포 조정은 필요하지 않으므로 이와 관련된 파라미터들은 생략된다.

(7)

\begin{aligned} χ_{t + 1 ∣ t}^{[0]} = {\hat{x}}_{t + 1 ∣ t} \\ χ_{t + 1 ∣ t}^{[i]} = {\hat{x}}_{t + 1 ∣ t} + {(\sqrt{P_{t + 1 ∣ t}^{xx}})}^{i}, i = 1, n_{x} \\ χ_{t + 1 ∣ t}^{[i]} = {\hat{x}}_{t + 1 ∣ t} + {(\sqrt{P_{t + 1 ∣ t}^{xx}})}^{i - n_{x}}, i = n_{x} + 1, \dots, 2 n_{x} \end{aligned}

계산된 SP는 보정 모델 함수 $h (∙)$ 를 통해 대상 시스템의 예측 거동 값을 계산하는데 사용된다. 계산된 값들을 이용하여 다음 식 (8)의 과정에서 표현된 것과 같이 두 가지 공분산이 산정된다.

(8)

\begin{aligned} ζ_{t + 1 ∣ t}^{[0]} = h (χ_{t + 1 ∣ t}^{[i]}), i = 0, \dots, 2 n_{x} \\ {\hat{z}}_{t + 1 ∣ t} = \sum_{i = 0}^{2 n_{x}} W_{m}^{i} ζ_{t + 1 ∣ t}^{[i]} \\ v_{t + 1} = z_{t + 1} - {\hat{z}}_{t + 1 ∣ t} \\ P_{t + 1 ∣ t}^{xx} = \sum_{i = 0}^{2 n_{x}} W_{c}^{i} [ζ_{t + 1 ∣ t}^{[i]} - {\hat{z}}_{t + 1 ∣ t}] {[ζ_{t + 1 ∣ t}^{[i]} - {\hat{z}}_{t + 1 ∣ t}]}^{T} + R_{t + 1} \\ P_{t + 1 ∣ t}^{xz} = \sum_{i = 0}^{2 n_{x}} W_{c}^{i} [χ_{t + 1 ∣ t}^{[i]} - {\hat{x}}_{t + 1 ∣ t}] {[ζ_{t + 1 ∣ t}^{[i]} - {\hat{z}}_{t + 1 ∣ t}]}^{T} \end{aligned}

위 식에서 $ζ_{t + 1 | t}^{[i]}$ 는 $χ_{t + 1 | t}^{[i]}$ 에 대응하는 가속도와 같은 거동과 관련된 벡터이며, ${\hat{z}}_{t + 1 | t}$ 는 평균 값이다. $z_{t + 1}$ 는 현 시점에서 계측된 가속도 데이터이며, $v_{t + 1}$ 는 실제 데이터와 예측된 거동 값의 이론적 잔차(Innovation)를 의미한다. $P_{t + 1 | t}^{xx}$ 와 $P_{t + 1 | t}^{xz}$ 는 각각 예측된 거동의 공분산과, 상태 벡터와 거동 벡터의 교차 공분산(Cross-covariance)을 의미한다.

다음 식 (9)와 같이 두 공분산을 이용하여 칼만 게인(Kalman gain)이 산정되며, 칼만 게인 $K$ 는 예측된 값을 보정하는데 사용된다.

(9)

\begin{aligned} K = P_{t + 1 ∣ t}^{xz} {(P_{t + 1 ∣ t}^{zz})}^{- 1} \\ {\hat{x}}_{t + 1 ∣ t + 1} = {\hat{x}}_{t + 1 ∣ t} + K v_{t + 1} \\ P_{t + 1 ∣ t + 1}^{xx} = P_{t + 1 ∣ t}^{xx} - {KP}_{t + 1 ∣ t}^{zz} K^{T} \end{aligned}

최종적으로 보정된 ${\hat{x}}_{t + 1 | t + 1}$ 와 $P_{t + 1 | t + 1}^{xx}$ 는 현 시점에서의 최종 추정값이며, 해당 값은 Fig. 3과 같이 다음 시간 스텝의 예측 단계 초기값으로 사용된다. 최적의 성능을 보이는 UKF를 도출하기 위해서는 인공 오차 공분산 $Q_{t}$ 와 $R_{t + 1}$ 를 적절하게 선정해야 한다. 본 연구에서는 측정 센서의 규격을 통해 $R_{t + 1}$ 를 결정할 수 있을 것으로 가정하고, 시행착오(Trial and error)를 통해 $Q_{t}$ 값을 선정하는 방법을 사용하였다. 소개된 UKF는 3.3절에서 소개될 Adaptive Tracking Method과 함께 급격한 구조손상탐지를 모사하는 수치 예제에 적용하고 적용가능성에 대해 검토하도록 한다.

3.2 파티클 필터(Particle Filter)

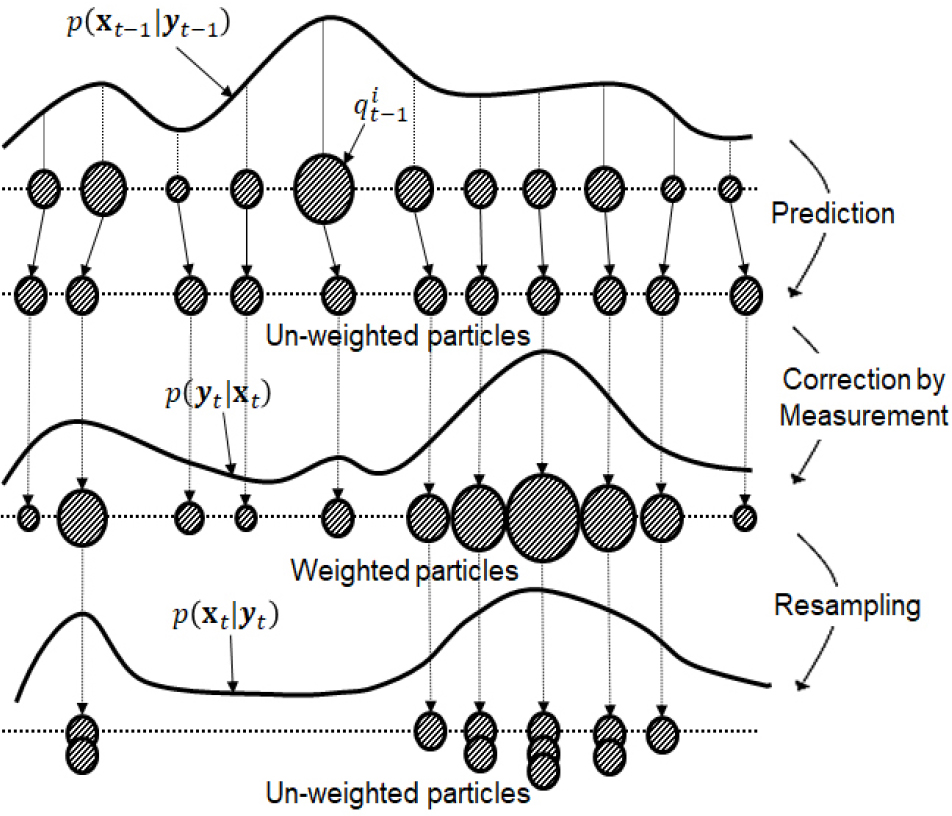
$2 n_{X} + 1$ 개의 샘플을 생성하여 예측과 보정을 수행하는 UKF와 달리 파티클 필터는 보다 많은 수의 샘플을 생성하여 Fig. 4와 같이 예측･보정을 수행한다(Candy, 2006; Kim, 2019). 이때 생성된 샘플을 파티클이라고 하며, 많은 파티클 덕분에 함수를 사용하는 대신 샘플링 기반의 근사 분포를 직접적으로 사용하여 다양한 확률 분포 형태를 모사할 수 있다. 이 덕분에 칼만 필터 방법들보다 비선형성, 비가우시안(non-Gaussian) 문제에 적합한 것으로 알려져 있다(Candy, 2006; Kim, 2019; Yi and Song, 2018). 파티클 필터는 샘플링에 기반하여 수행되기 때문에 Sequential Monte Carlo 방법으로 불리기도 하며, 다음과 같은 State-space 모델이 사용된다.

(10)

x_{t + 1} = f (x_{t}, w_{t})

(11)

y_{t + 1} = h (x_{t + 1}, u_{t + 1}, v_{t + 1})

앞서 UKF에서 사용된 State-space 모델과는 달리, 파티클 필터는 많은 수의 샘플들을 통해 확률 분포가 직접적으로 정의되기 때문에 랜덤 변수 $w_{t}$ 와 $v_{t + 1}$ 이 예측 및 보정 모델 함수들 안에 내포되어 각 파티클이 함수들을 통해 전이(Transition)될 때 마다 랜덤하게 생성된다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F4.jpg

Fig. 4.

Schematic Algorithm of Particle Filter

다음으로 파티클 필터 또한 예측, 보정단계에 따라 대상 시스템의 상태 벡터를 추정하게 되며, 이를 수행하기 위해서는 다음 식 (12)와 같이 결합 확률분포함수(Joint Probability Density Function, JPDF) 개념을 기반으로 한다.

(12)

p (x_{t} | y_{t}) = c ∙ L (y_{t} | x_{t}) p (x_{t})

위 수식은 일반적인 베이지안 업데이팅(Bayesian updating)을 나타낸다. $L (y_{t} | x_{t})$ 는 식 (11)의 보정 모델 함수에 기반한 가능도(Likelihood) 함수이며, $p (x_{t})$ 는 식 (10)을 이용한 예측단계에서 얻어진 사전 분포(Prior distribution) 함수이다. 여기서 $c$ 는 정규화 상수로, 샘플링 기법 적용시 계산을 필요로 하지 않는다(Lee and Song, 2017).

예측 단계는 예측 모델 함수 $f (∙)$ 를 이용하여 사전 분포로부터 랜덤하게 생성된 $N_{p}$ 개의 파티클을 전이시킨다. 전이된 파티클은 $x_{t}^{i} = f (x_{t - 1}^{i}, w_{t - 1}^{i})$ 과 같이 생성되며, $i = 1, 2, \dots, N_{p}$ 이다. 다음 스텝으로 전이된 파티클은 다음 수식과 같이 가능도 함수를 기반으로 하여 가중치를 결정한다.

(13)

q_{t} = \frac{L (y_{t}^{i} ∣ x_{t}^{i})}{\sum_{i = 1}^{N} L (y_{t}^{i} ∣ x_{t}^{i})} \propto \frac{\exp (- \frac{1}{2} {[y_{t}^{m} - y_{t}^{i}]}^{T} R^{- 1} [y_{t}^{m} - y_{t}^{i}])}{\sqrt{| R | (2 π)^{N_{m}}}}

이때, $y_{t}^{i} = h (x_{t}^{i}, u_{t}, v_{t}^{i})$ 와 같이 보정 모델 함수를 이용하여 전이된 파티클 기반으로 거동을 예측할 수 있으며, 측정된 거동 값이 정규 분포를 따를 경우 가중치는 식 (13)의 우변과 같이 근사하여 계산할 수 있다. 이때 $y_{t}^{m}$ 는 측정된 거동(즉, 가속도)이며 $R$ 은 측정오차의 공분산을 의미한다.

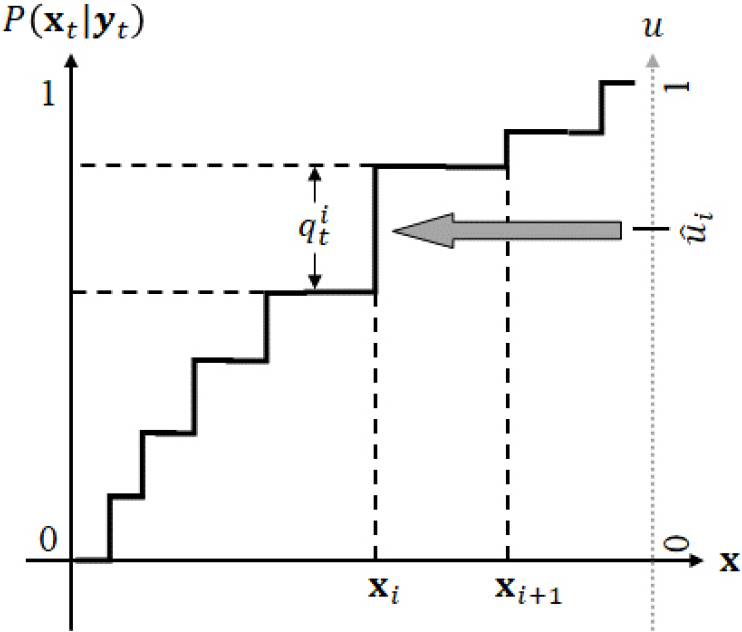
계산된 가중치는 파티클을 리샘플링(Resampling)하는 과정에 사용된다. 리샘플링 과정을 통해 높은 가중치를 갖는 파티클은 복제되고, 낮은 가중치를 갖는 파티클은 제거되며, 이 과정에서 파티클의 개수는 유지된다. 알려진 리샘플링 방법으로는 ‘Multinomial’, ‘Residual’, ‘Systematic’ 방법 등이 있으며 본 연구에서는 Systematic 방법을 적용한다. Systematic 리샘플링 과정은 다음과 같다(Candy, 2006; Kim, 2019). (1) $\{x_{t}^{i}, q_{t}^{i}\}$ , $i = 1, \dots, N_{p}$ 과 같이 파티클과 대응되는 가중치 집합을 순서대로 나열한다. (2) 나열된 $i$ 번째 파티클의 복제여부를 결정하는 오름차순 랜덤변수를 다음 식 (14)와 같이 생성한다.

(14)

{\hat{u}}_{i} = u_{i} + (i - 1) / N_{p}, ∵ u_{i} ~ U (0, 1 / N_{p})

여기서, $U (∙)$ 는 등분포 함수를 의미한다. (3) 생성된 랜덤변수 ${\hat{u}}_{i}$ 를 이용하여 다음 식 (15)와 같이 복제 여부를 결정한다.

(15)

{\hat{x}}_{t}^{i} = \{\begin{cases} x_{t}^{i} if {\hat{u}}_{i} > \sum_{j = 1}^{i} q_{t}^{j} \\ {\hat{x}}_{t}^{i - 1} otherwise \end{cases}

리샘플링 과정이 끝나고 난 후 모든 파티클들의 가중치는 $q_{t}^{i} = 1 / N_{p}$ 로 등분포화 된다. Fig. 5는 Systematic 리샘플링 과정을 도해화 한 것이며, 해당 그림에서 $q_{t}^{i}$ 폭이 클수록 해당 파티클이 복제될 가능성이 높음을 의미한다. 최종적으로 사후분포(Posterior distribution), $p (x_{t} | y_{t})$ 는 다음 식 (16)과 같이 근사하여 표현할 수 있다.

(16)

p (x_{t} | y_{t}) ≅ p (x_{t}) = \sum_{i = 1}^{N_{p}} q_{t}^{i} δ (x_{t} - {\hat{x}}_{t}^{i})

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F5.jpg

Fig. 5.

Schematic Diagram of Systematic Resampling

도출된 사후분포는 다음 시간 스텝에서의 사전분포로 사용되며 Fig. 6은 파티클 필터 알고리즘을 나타낸다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F6.jpg

Fig. 6.

Algorithm of Systematic Resampling

3.3 적응형 기법: Adaptive Tracking Method

지진과 같은 외부 하중이 구조물에 재하될 경우, 짧은 시간내에 강성과 같은 시스템 인자가 급격히 변화하는 손상이 발생할 수 있다. 이러한 급격한 구조 손상 시나리오는 대게 강성이 급격히 감소하는 형태로 표현되며, 앞서 두 가지 방법 모두 적용된 연구가 진행된 바 있다(Kim, 2019; Lee and Song, 2020; Lee et al., 2023). 이때 두 가지 방법 모두 급격한 변화가 발생하는 지점에서 빠르게 추정하지 못함이 확인되었고, 빠른 추정을 위해서는 추가적인 기법 도입이 필요하다. 이러한 기법을 대게 적응형 기법(Adaptive rule)이라고 하며, 본 연구에서는 다양한 기법들 중 Adaptive Tracking Method(ATM)를 적용하고자 한다(Kim, 2019; Liu et al., 2005; Yang et al., 2006).

ATM의 핵심 아이디어는 필터 방법론들이 대상 동적 시스템을 추정하고 있을 때, 급작스러운 변화가 생길 경우 이론적 잔차(Innovation)에 이상치(Outlier)가 발생함을 파악하고 다음 시간 스텝에 반영하는 것이다. 이상치가 발생하는 이유는 예측된 거동과 실제 측정된 거동의 차이가 많음을 의미하는 것이며, 이는 곧 시스템의 변화가 크다는 것을 뜻한다. ATM은 이러한 경우에 대해 다음 시간 스텝의 예측 단계에서, 추가 변수를 도입하여 상태 벡터 추정 값의 급격한 전이를 유도한다. 이때, 추가 상수는 잔차들의 시간이력을 기반으로 산정되며 다음 식 (17), (18)과 같다.

(17)

λ_{0} = tr [V_{t}] / tr [M_{t}]

(18)

λ_{0, t + 1} = \{\begin{cases} λ_{0} if λ_{0} > 1 \\ 1 if λ_{0} \leq 1 \end{cases}

여기서, $λ_{0, t + 1}$ 은 점핑 파라미터(Jumping parameter)이며, $tr [∙]$ 은 행렬의 대각 성분들의 합을 의미하는 연산자이다. $V_{t}$ 와 $M_{t}$ 는 각각 이론적 잔차와 실제 잔차의 공분산 행렬을 의미하며 다음 식 (19), (20)과 같이 계산된다. 여기서는 편의상 잔차들을 필수적으로 계산하는 UKF 기준으로 설명하도록 한다.

(19)

V_{t} = \frac{1}{ρ} [ρ V_{t - 1} + \frac{1}{N_{S P}} \sum_{i = 1}^{N_{S P}} v_{t} (v_{t})^{T}]

(20)

M_{t} = \frac{\sum_{t = 0}^{N_{t}} \sum_{i = 1}^{N_{S P}} [{{\hat{z}}_{t | t - 1} - ζ}_{t | t - 1}^{[i]}] [{{\hat{z}}_{t | t - 1} - ζ}_{t | t - 1}^{[i]}]^{T}}{N_{t} ∙ N_{SP}}

위 식에서 𝜌는 망각 변수(Forgetting parameter)이며 대게 0.95 값이 사용된다(Liu et al., 2005). $N_{t}$ 와 $N_{SP}$ 는 각각 현 시점까지의 이산화 된 시간 스텝 수와 시그마 포인트의 수를 의미한다.

그런데 최근 다자유도 전단 빌딩 구조물의 급격한 손상정도와 위치를 정확히 추정하기 위해서는 새로운 형태의 이론적 잔차가 필요함이 확인되었다(Lee et al., 2024). 다음은 취약도 곡선 도출 시 많이 정의되는 층간 상대 변위율(Inter-story drift ratio)을 착안하여 최근 제안된 이론적 잔차이다.

(21)

{\tilde{v}}_{t}^{[k]} = \{\begin{cases} v_{t}^{[k]} / h_{k} ∵ k = 1 \\ (v_{t}^{[k]} - v_{t}^{[k - 1]}) / h_{k} ∵ k \geq 2 \end{cases}

여기서, $k$ 와 $h_{k}$ 는 다자유도 전단 빌딩의 층 수와 층간 높이를 의미한다. 다음으로 새로운 이론적 잔차 정의와 함께 알고리즘의 효율성을 높이기 위해 간략화 된 $V_{t}$ 와 $M_{t}$ 이 다음과 같이 제안되었다.

(22)

V_{t} = \frac{1}{N_{SP}} \sum_{i = 1}^{N_{SP}} v_{t} (v_{t})^{T}

(23)

M_{t} = \frac{1}{N_{t - 1} ∙ N_{SP}} \sum_{t = 0}^{N_{t - 1}} \sum_{i = 1}^{N_{SP}} v_{t} (v_{t})^{T}

$V_{t}$ 의 경우 이전 시간 스텝과 관련된 항이 삭제되었다. 또한 $M_{t}$ 의 경우, 본래는 실제 잔차를 이용하여 계산해야 하지만, 그럴 경우 많은 값들을 저장해야 하는 번거로움이 있다. 따라서, 이전 시간 스텝에서의 이론적 잔차는 실제 잔차와 거의 동일하다는 가정을 이용하여 식 (20)에서 식 (23)과 같이 간략화 할 수 있다. 최종적으로 계산되는 점핑 파라미터 $λ_{0, t + 1}$ 는 UKF와 파티클 필터의 인공오차에 곱해져야 하므로 다음 식 (24)와 같이 스칼라(Scalar)가 아닌 행렬 형태로 계산되어야 한다.

(24)

λ_{0, t + 1} = diag [V_{t + 1} / M_{t + 1}]

위 식에서 $diag [∙]$ 은 대각 성분으로 이루어지는 행렬을 의미하며, 각 성분 값이 1보다 작을 경우는 1로 치환된다. 최종적으로 계산된 행렬은 예측 단계에서 사용되며, UKF의 경우에는 식 (6)의 $Q_{t}$ 에 곱해진다. 이때 곱해진 값으로 인해 생성되는 시그마 포인트의 분포가 넓어지게 되고, 이는 칼만 게인을 크게 만들어 급격한 전이를 가능하게 한다. 파티클 필터의 경우에는 식 (10)을 이용한 전이된 파티클 계산 시 필요한 인공 오차 $w_{t}$ 를 생성할 때, 샘플링 함수의 공분산을 $λ_{0, t + 1} Q_{t}$ 와 같이 증폭하여 파티클들의 샘플 범위를 넓히게 된다. 다음 장에서는 ATM 방법을 적용한 UKF와 파티클 필터를 급격한 구조손상 시나리오에 대해 적용하도록 한다.

4. 수치 예제 적용

본 장에서는 적응형 기법을 고려한 두 가지 베이지안 필터 방법들을 검증하기 위해 Bouc-Wen 모델이 적용된 6자유도 전단 빌딩(Shear-Building)과 지진 시나리오를 가정한다. 검증을 위해 규모 6.5, Strike-Slip 메커니즘의 1942년 Borrego 지진을 사용하였다. Fig. 7은 사용된 6자유도 전단빌딩을 나타내며, 각 층의 질량은 절점 질량으로 가정하고 3 × 10⁴kg의 값을 사용하였다. 각 층의 강성과 적용된 Rayleigh 감쇠율은 $k =$ [7.5, 7.0, 6.5, 5.5, 4.0, 2.0] × 10⁴kN/m, 5%로 각각 가정하였다. Bouc-Wen 모델의 형상을 결정하는 $A$ 와 $n$ 은 각각 1과 3으로 가정하고, 𝛾와 𝜂는 $γ = η = 1 / (2 u_{y}^{n})$ 의 관계를 가지며 이때 항복 변위 $u_{y}^{n}$ 는 0.0153m로 가정되었다. 다음으로 급격한 손상탐지 가능 여부를 검증하기 위해 Table 1과 같이 두 가지 시나리오를 가정하였다. 이때 전 층에서의 가속도를 계측 값으로 설정하고, SNR(Signal-to-Noise Ratio) 13dB의 백색 잡음(White Noise)를 생성하여 추가하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F7.jpg

Fig. 7.

6-dof Shear-Building considering Bouc-Wen Model

Table 1.

Sudden Damage Scenarios for Borrego Earthquake

	Damage Description
Scenario 1	Stiffness k₁ decreases suddenly by 40% at 4.96sec
Scenario 2	Stiffness k₃ decreases suddenly by 40% at 4.99sec à k₃ decreases suddenly by 60% at 14.91sec

4.1 오리지날 및 적응형 분산점 칼만필터 적용 결과

UKF를 수행하기 위한 초기설정으로, ${\hat{x}}_{0} = k_{0}$ , $P_{0}^{xx} = diag [k_{0} ∙ 10^{- 2}]$ 을 사용하였고, 측정 인공오차의 공분산은 $R_{t} = diag [RMS ({\ddot{u}}_{0 : d t : T})]$ 로 가정하였다. 여기서, $RMS (∙)$ 는 Root-Mean-Square를 의미한다. UKF의 최적 성능을 결정하는 시그마 포인트의 스케일링 파라미터 𝛼는 0.1로 설정하였으며, 시스템 인공오차는 시행착오를 통해 $diag (Q_{t}) = k_{0} \times 10^{- 3.8}$ 로 설정하였다. 다음 Fig. 8은 시나리오1에 대해 오리지날 UKF와 적응형 UKF를 적용한 결과이다. 오리지날 UKF는 정확한 손상 시점을 파악하지 못하고 발산하였으며, 적응형 UKF의 경우 손상 시점은 파악하였지만 정확한 손상 정도를 추정하지 못하고 발산함을 확인하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F8.jpg

Fig. 8.

Results of Original UKF (Top) and Adaptive UKF (Bottom): Scenario 1

이러한 결과의 의미는 UKF를 이용한 급격한 구조손상을 탐지하기 위해서는 적응형 기법이 필수적이나, 본 연구에서 사용된 적응형 기법으로는 한계가 있음을 의미한다. 따라서 이러한 한계를 극복하기 위해서는 개선된 적응형 기법이 필요하며, Fig. 9는 적응형 UKF가 손상 시점에서 계산한 점핑 파라미터 행렬( $λ_{0, t + 1}$ ) 중 가장 큰 값을 순차적으로 키우면서 최종적으로 2400으로 조정하였을 때의 결과이다. 이때 점핑 파라미터 행렬에서 가장 큰 수치에 해당하는 좌표는 구조 손상이 발생한 자유도를 의미한다. 도출된 결과를 보면 손상 시점과 그 정도를 정확히 추정함을 확인할 수 있다. 이러한 결과로부터, 적응형 UKF는 인위적으로 적정 파라미터 값을 찾아내야만 하는 번거로움을 확인하였고, 적정 파라미터를 자동으로 찾아내기 위한 추가 연구가 필요함을 알 수 있다. 다음으로 같은 시나리오1에 대해 파티클 필터를 수행하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F9.jpg

Fig. 9.

Result of Adaptive UKF with Adjusted $λ_{0, t + 1}$ : Scenario 1

4.2 오리지날 및 적응형 파티클 필터 적용 및 결과

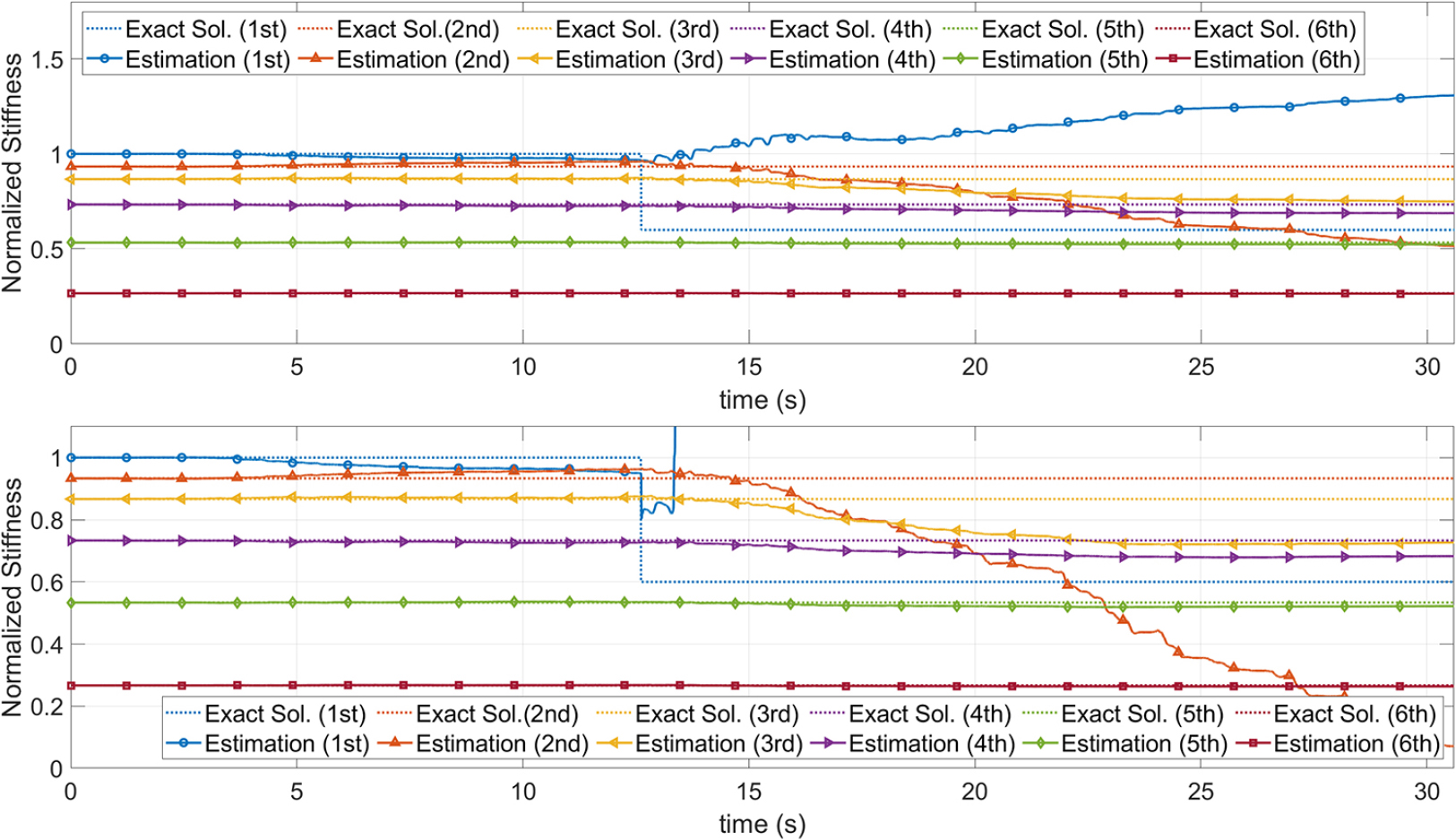
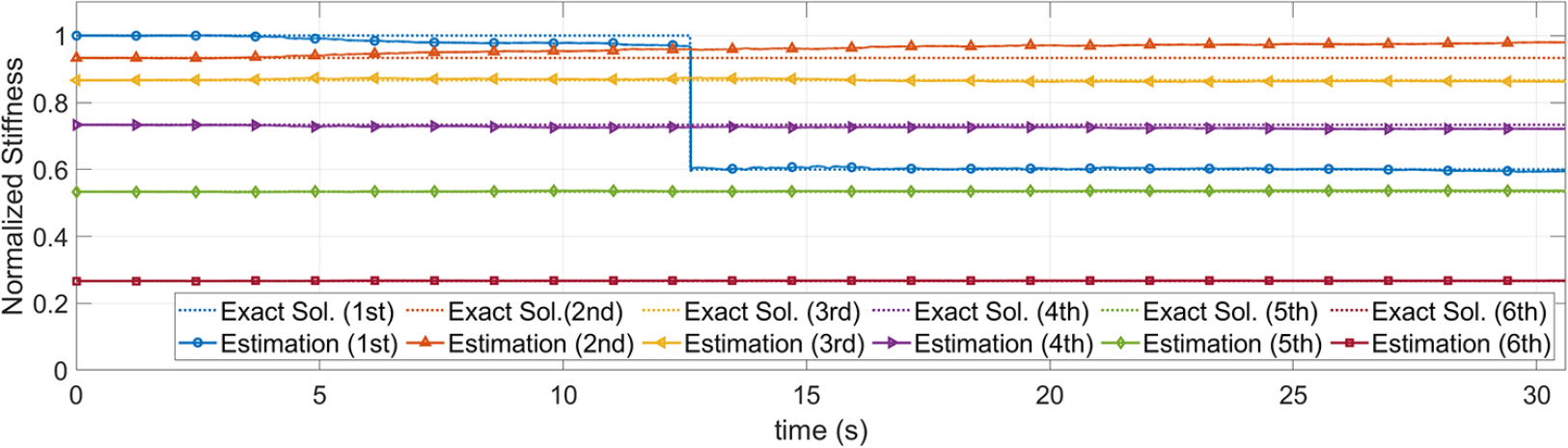
UKF와 마찬가지로 오리지날 파티클 필터와 적응형 파티클 필터를 수행하였다. 이때 파티클의 개수는 100개로 설정하였으며, 시스템 상태 벡터의 초기 샘플링은 초기 강성, $k_{0}$ 의 99%에서 101%를 범위로 하는 등분포 함수에서 생성하였다. Fig. 10은 오리지날 파티클 필터와 적응형 파티클 필터를 시나리오1에 대해 수행한 결과이다. 이때, 파티클 필터의 추정 값은 각 시간 스텝에서 구해진 사후분포의 평균값으로 계산되었다. 오리지날 파티클 필터 적용 결과를 보면, 손상시점을 정확히 파악하지 못하고 지진이력 내에 정해에 도달하지 못함을 확인할 수 있다. 이에 반해 적응형 파티클 필터는 손상시점을 정확히 파악하는 것을 확인하였다. 하지만, 여전히 손상 정도를 정확히 파악하지 못하며, 이 때문에 다른 층의 강성 값들의 추정치가 부정확해지는 것을 확인할 수 있다.

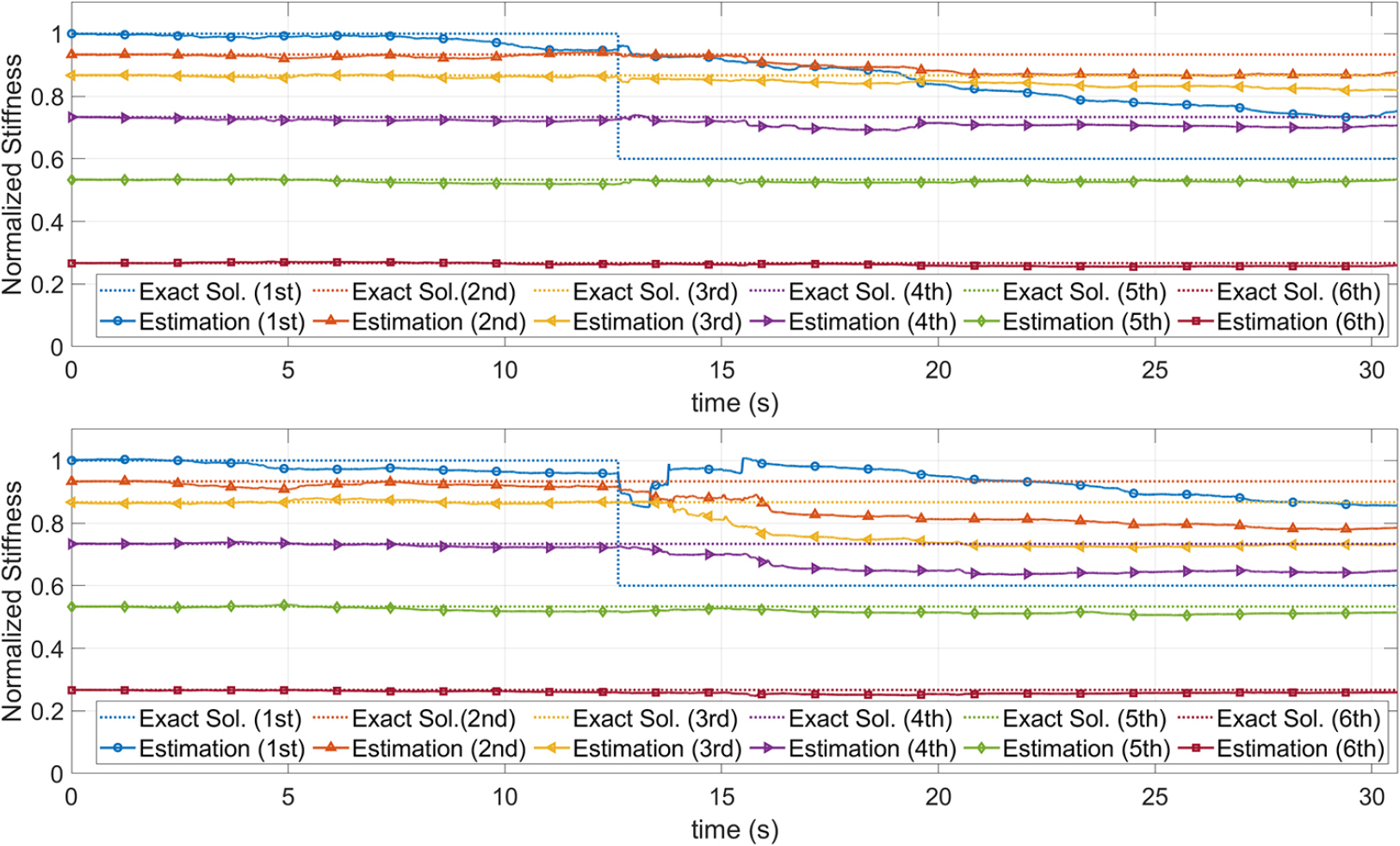
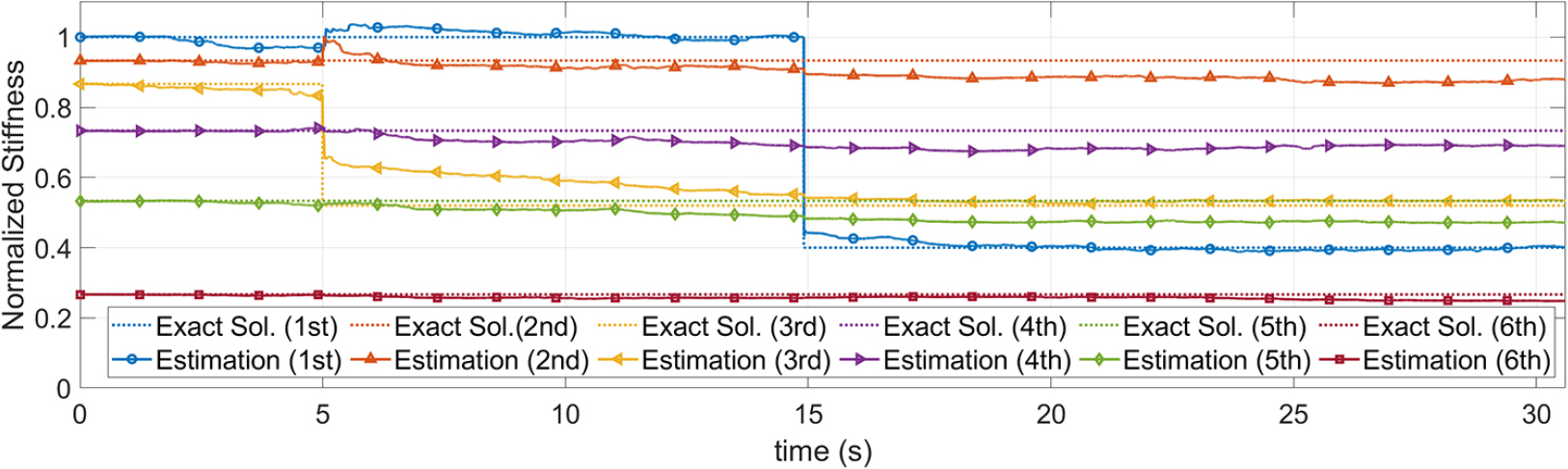
이러한 현상의 이유는 적응형 UKF와 마찬가지로, 적응형 기법에서 산정된 점핑 파라미터의 행렬( $λ_{0, t + 1}$ )이 예측 보정 모델의 인공오차, 즉 공분산을 적절히 증폭시키지 못하여 상태 벡터의 급격한 전이가 이루어지지 못했기 때문이다. 이를 극복하기 위해 ${\hat{λ}}_{0, t + 1} = [λ_{0, t + 1}]^{3}$ 과 같이 크기를 증폭시켜 큰 폭의 천이를 유도하는 조정된 점핑 파라미터 행렬을 적용하였다. 여기서 $[∙]^{3}$ 은 행렬 각 성분의 지수 승을 의미한다. Fig. 11과 Fig. 12는 각각 시나리오1과 2에 대해 조정된(Adjusted) 점핑 파라미터 행렬을 적용한 결과이며, 점핑 파라미터 행렬을 조정하기 전 결과보다 정확성이 크게 향상된 것을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F10.jpg

Fig. 10.

Results of Original PF (Top) and Adaptive PF (Bottom): Scenario 1

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F11.jpg

Fig. 11.

Result of Adaptive PF with Adjusted $λ_{0, t + 1}$ : Scenario 1

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-04/N0040370408/images/Figure_jcoseik_37_04_08_F12.jpg

Fig. 12.

Result of Adaptive PF with Adjusted $λ_{0, t + 1}$ : Scenario 2

5. 결 론

본 연구에서는 분산점 칼만필터(Unscented Kalman Filter, UKF)와 파티클 필터(Particle Filter)를 이용한 급격한 구조손상탐지 가능성을 검토하였다. 이때, 선행연구로부터 두 가지 방법 모두 급격한 변화를 잘 추정하지 못함을 확인하였고, 이를 보완하기 위해 적응형 기법(Adaptive rule)인 Adaptive Tracking Method를 도입하였다. 대상 동적 시스템으로는 Bouc-Wen 모델을 고려한 6자유도 전단 빌딩을 가정하였다. 급격한 손상을 모사하는 지진 시나리오를 가정하고, 오리지날 방법들과 적응형 기법을 적용한 방법들에 대해 결과를 도출하였다. 두 오리지날 방법 모두 손상 시점을 명확히 파악하지 못하고, 발산함을 확인하였다. 반면에 적응형 기법을 적용한 경우, 손상시점을 명확히 파악할 수 있음을 확인하였다. 하지만 여전히 손상 정도를 정확히 추정하지 못하였는데, 이는 적응형 기법이 예측단계에서 상태 벡터를 충분한 전이를 시키지 못함을 의미한다. 따라서, 소개된 적응형 기법의 자체 파라미터를 조정하였을 때, 손상 정도를 정확히 추정할 수 있음을 확인하였다.

적응형 UKF의 경우 점핑 파라미터( $λ_{0, t + 1}$ )를 지진 시나리오마다, 그리고 손상정도에 따라 적합한 값을 인위적으로 설정해야만 정확한 추정이 가능하다. 반면에 적응형 파티클 필터의 경우 점핑 파라미터를 일률적으로 조정함으로써 여러 지진 시나리오들의 가정과 상관없이 일관성 있게 추정 가능함을 확인하였다. 하지만, 적응형 UKF의 수행시간은 일반 개인 PC(CPU: Intel i9, 2.0GHz) 기준으로 약 54초이고, 파티클 필터의 경우 약 770초가 소요되었다. 이때, 파티클 필터 수행 시 사용된 파티클 개수는 100개로, 일반적인 문헌에서 사용되는 개수보다 적은 편이다. 이러한 계산시간은 주어진 시스템이 거대하고 더욱 복잡해질수록 격차가 심해질 것으로 예상할 수 있다. 결론적으로, 일관성 있는 적응형 기법 적용 측면에서는 파티클 필터가 용이하지만, 실적용을 위해서는 빠른 수행이 가능한 UKF가 적합하다. 따라서, 새로운 적응형 기법을 탑재한 UKF가 현 시점에서 가장 타당한 구조물 손상탐지 기법인 것으로 판단되며, 추후 하드웨어의 발전에 따라 파티클 필터의 효용성이 높아질 것으로 생각된다. 이러한 기법의 개발은 충분한 검증을 바탕으로 지진과 같은 외부하중으로 인한 대형설비의 손상과 더불어 누출로 인한 상태 변화를 빠르게 파악 가능할 것으로 기대된다.

Acknowledgements

본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었습니다(과제번호: RS-2021-KA163162).

References

Baber, T.T., Noori, M.N. (1984) Random Vibration of Pinching Hysteretic Systems, J. Eng. Mech., 110(7), pp.1036~1049.

10.1061/(ASCE)0733-9399(1984)110:7(1036)

Baber, T.T., Wen, Y.K. (1981) Random Vibration Hysteretic, Degrading Systems, J. Eng. Mech. Div., Am. Soc. Civil Eng., 107(6), pp.1069~1087.

10.1061/JMCEA3.0002768

Candy, J.V. (2006) Bayesian Signal Process: Classical, Modern, and Particle Filtering Methods, John Wiley & Sons, Inc.: Hoboken, NJ, USA.

Chatzi, E.N., Smyth, A.W. (2009) The Unscented Kalman Filter and Particle Filter Methods for Nonlinear Structural System Identification with Non-Collocated Heterogeneous Sensing, Struct. Control & Health Monit., 16, pp.99~123.

10.1002/stc.290

Foliente, G.C., Singh, M.P., Noori, M.N. (1996) Equivalent Linearization of Generally Pinching Hysteretic, Degrading Systems, Earthq. Eng. & Struct. Dyn., 25, pp.611~629.

10.1002/(SICI)1096-9845(199606)25:6<611::AID-EQE572>3.0.CO;2-S

Fujimura, K., Der Kiureghian, A. (2007) Tail-Equivalent Linearization Method for Nonlinear Random Vibration, Probab. Eng. Mech., 22, pp.63~76.

10.1016/j.probengmech.2006.08.001

Kalman, R.E. (1960) A New approach to Linear Filtering and Prediction Problems, J. Basic Eng.-T. ASME, 82(1), pp.35~45.

10.1115/1.3662552

Kim, M. (2019) Parameter Identification of Structures under Earthquake Excitations Using Adaptive Particle Filter and Ensemble Learning Method, Seoul National University, Master Thesis.

Lee, S.-H., Kim, M., Yi, S.-R. (2024) Identification of Sudden Structural Damage using Unscented Kalman Filter with Enhanced Algorithmic Adaptive Jumping Method, submitted.

Lee, S.-H., Song, J. (2017) System Identification of Spatial Distribution of Structural Parameters Using Modified Transitional Markov Chain Monte Carlo Method, J. Eng. Mech., 143(9), p.04017099.

10.1061/(ASCE)EM.1943-7889.0001316

Lee, S.-H., Song, J. (2020) Regularization-Based Dual Adaptive Kalman Filter for Identification of Sudden Structural Damage Using Sparse Measurements, Appl. Sci., 10(850). DOI: 10.3390/app10030850.

10.3390/app10030850

Lee, S.-H., Yi, S.-R., Lee, J.H. (2023) Unscented Kalman Filter with Multiple Sigma Points for Robust System Identification of Sudden Structural Damage, J. Comput. Struct. Eng. Inst. Korea, 36(4), pp.233~242.

10.7734/COSEIK.2023.36.4.233

Liu, M., Zang, S., Zhou, D. (2005) Fast Leak Detection and Locations of Gas Pipelines Based on an Adaptive Particle Filter, Int. J. Appl. Math. Comput. Sci., 15, pp.541~550.

Nguyen, V.H., Lee, S.-H., Lee, J.H. (2022) Application of the Unscented Kalman Filter to Estimate the Material Properties of a Layered Half-Space, Int. J. Appl. Mech., 15(2), p.2350005.

10.1142/S1758825123500059

Noori, M.N., Choi, J., Davoodi, H. (1986) Zero and Nonzero Mean Random Vibration Analysis of a New General Hysteresis Model, Probab. Eng. Mech., 1(4), pp.192~201.

10.1016/0266-8920(86)90012-3

Papakonstantinou, K.G., Amir, M., Warn, G.P. (2020) A Scaled Spherical Simplex Filter (S3F) with a decreased n + 2 sigma points set size and equivalent 2n + 1 Unscented Kalman (UKF) accuracy, Mech. Syst. & Signal Process., 163(2022), p.107433.

10.1016/j.ymssp.2020.107433

Song, J., Der Kiureghin, A. (2006) Generalized Bouc-Wen Model for Highly Asymmetric Hysteresis, J. Eng. Mech., 123(6), pp.610~618.

10.1061/(ASCE)0733-9399(2006)132:6(610)

Vaiana, N., Sessa, S., Marmo, F., Rosati, L. (2018) A Class of Uniaxial Phenomenological Models for Simulating Hysteretic Phenomena in Rate-Independent Mechanical Systems and Materials, Nonlinear Dyn., 93(3), pp.1647~1669.

10.1007/s11071-018-4282-2

Van der Merwe, R., Wan, E. (2001) The Square-Root Unscented Kalman Filter for State and Parameter-Estimation, 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Proceedings (Cat. No.01CH37221). Salt Lake City, UT, USA, 7-11 May 2001, 6, pp.3461~3464.

10.1109/ICASSP.2001.940586

Wang, C.-H., Wen, Y.K. (1998) Reliability and Redundancy of Pre-Northridge Low-Rise Steel Building Under Seismic Excitation, Rep. No. UILU-ENG-99-2002, Univ. Illinois at Urbana-Champaign, Champaign, Ill.

Yang, J.N., Lin, S., Huang, H., Zhou, L. (2006) An Adaptive Extended Kalman Filter for Structural Damage Identification, Struct. Control. Health Monit., 13, pp.849~867.

10.1002/stc.84

Yi, S.-R., Song, J. (2018) Particle Filter Based Monitoring and Prediction of Spatiotemporal Corrosion Using Successive Measurements of Structural Responses, Sens., 18(3909). DOI: 10.3390/s18113909.

10.3390/s1811390930428593PMC6263897

Yi, S.-R., Wang, Z., Song, J. (2017) Bivariate Gaussian Mixture-based Equivalent Linearization Method for Stochastic Seismic Analysis of Nonlinear Structures, Earthq. Eng. Struct. Dyn., 2018(47), pp.678~696.

10.1002/eqe.2985

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Comparison of the Applicability of Bayesian Filters for System Identification of Sudden Structural Damage

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

Fig. 1.

SDOF Oscillator considering Bouc-Wen Model

(5)

Fig. 2.

Schematic Diagram of Unscented Transformation

Fig. 3.

Algorithm of Unscented Kalman Filter

(6)

(7)

(8)

(9)

(10)

(11)

Fig. 4.

Schematic Algorithm of Particle Filter

(12)

(13)

(14)

(15)

(16)

Fig. 5.

Schematic Diagram of Systematic Resampling

Fig. 6.

Algorithm of Systematic Resampling

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

Fig. 7.

6-dof Shear-Building considering Bouc-Wen Model

Table 1.

Sudden Damage Scenarios for Borrego Earthquake

Fig. 8.

Results of Original UKF (Top) and Adaptive UKF (Bottom): Scenario 1

Fig. 9.

Result of Adaptive UKF with Adjusted λ0,t+1: Scenario 1

Fig. 10.

Results of Original PF (Top) and Adaptive PF (Bottom): Scenario 1

Fig. 11.

Result of Adaptive PF with Adjusted λ0,t+1: Scenario 1

Fig. 12.

Result of Adaptive PF with Adjusted λ0,t+1: Scenario 2

Acknowledgements

References

Result of Adaptive UKF with Adjusted $λ_{0, t + 1}$ : Scenario 1

Result of Adaptive PF with Adjusted $λ_{0, t + 1}$ : Scenario 1

Result of Adaptive PF with Adjusted $λ_{0, t + 1}$ : Scenario 2