1. 서 론
2. 폭압의 종류 및 폭압 산정법
2.1 폭압 산정법
2.2 TNT 등가량 환산법
2.3 멀티에너지법
3. 폭발 사례를 적용한 폭압 산정법 검증
3.1 Case 1: Buncefield Explosion
3.2 Case2: Jaipur Explosion
3.3 Case3: Amuay Refinery Explosion
4. 결 론
1. 서 론
최근 전 세계적으로 플랜트 산업의 형태가 고도화 및 고령화로 진행됨에 따라 플랜트에서 발생되는 재난 및 재해가 증가하고 있고 이 중에서 폭발사고는 경제적 손실뿐만 아니라 인명피해를 유발하며 특히 석유화학을 이용한 산업플랜트의 경우 막대한 폭발을 일으킬 수 있는 탄화수소와 관련 연료를 취급하고 있어 위험성이 크다(Zhu et al., 2020).
CCPS(1996)에서는 폭발로 인한 플랜트 구조물의 평가를 위한 가이드라인을 제시하고 있으며, ASCE(2010)에서는 석유화학 플랜트에 대한 방폭설계 방법을 제시하고 있다. Assael와 Kakosimos(2010)는 1984년에 발생한 PEMEX LPG 폭발 사고를 적용한 다양한 폭압 산정법을 보여준다.
플랜트 폭발의 대표적 유형은 증기운 폭발이다. 플랜트에서 발생하는 증기운 폭발의 폭압을 예측하기 위하여 주로 TNT 등가량 환산법(TNT-equivalent method)과 Van den Berg(1985)가 제시한 멀티에너지법(multi-energy method)이 사용된다. Ngo 등(2015)은 5,000kg의 TNT를 사용한 자유장(free-field) 실험과 TNT 등가량 환산법과의 비교를 통하여 원거리(far-field)의 경우 TNT 등가량 환산법의 폭압이 과소평가됨을 확인하였다. Assael와 Kakosimos(2010)는 증기운 폭발을 예시로 TNT 등가량 환산법과 멀티에너지법의 최대 폭압을 비교하였으며, 원거리(far-field)에서 TNT 등가량 환산법은 과소평가를 나타내고 멀티에너지법은 실제 최대 폭압과 유사한 결과를 나타낸다고 하였다. TNT 등가량 환산법과 멀티에너지법의 큰 차이는 TNT 등가량 환산법은 개방공간에서의 폭굉(detonation)을 전제로 계산되며, 멀티에너지법은 폭연(deflagration)을 전제로 계산된다.
멀티에너지법은 폭발강도계수(charge strength)의 영향을 크게 받는다. 따라서 CPR14E(2005)에서 제시하고 있는 폭발강도계수 가이드라인의 적절성을 확인하고 초기 과압의 영향성에 대한 분석이 필요하다. 현재 증기운 폭발 메커니즘을 규명하기 위한 연구가 진행 중이지만, 대규모의 증기운 폭발 실험이 어려우므로 실제 증기운 폭발 사례를 분석하여 각각의 폭압 산정법의 합리성을 살펴보고자 한다.
따라서, 본 연구에서는 증기운 폭발에서 TNT 등가량 환산법과 멀티에너지법을 적용한 폭압이 구조물에 미치는 거동을 분석하여 합리성과 정확성을 제시한다. 증기운 폭발 사례의 피해 구조물을 선정하여 피해 정도와 폭발 정보를 추정한 후, 폭압을 도출하기 위해 TNT 등가량 환산법과 멀티에너지법의 다양한 변수를 생성하여 비교 및 검토한다. 폭압에 따른 구조물의 피해 및 거동의 분석을 위하여 단자유도 해석과 비선형 동적 해석에 따른 변형 및 손상 정도를 비교한다. 과거 플랜트 증기운 폭발사고를 통하여 TNT 등가량 환산법과 멀티에너지법의 정확성과 영향성을 비교하며, 멀티에너지법의 전반적인 적절한 폭발강도계수를 제시한다.
본 연구의 결과는 폭압 산정법에 따른 폭발 위험도 평가 및 방폭 설계의 폭압 모델 개발에 활용될 수 있다.
2. 폭압의 종류 및 폭압 산정법
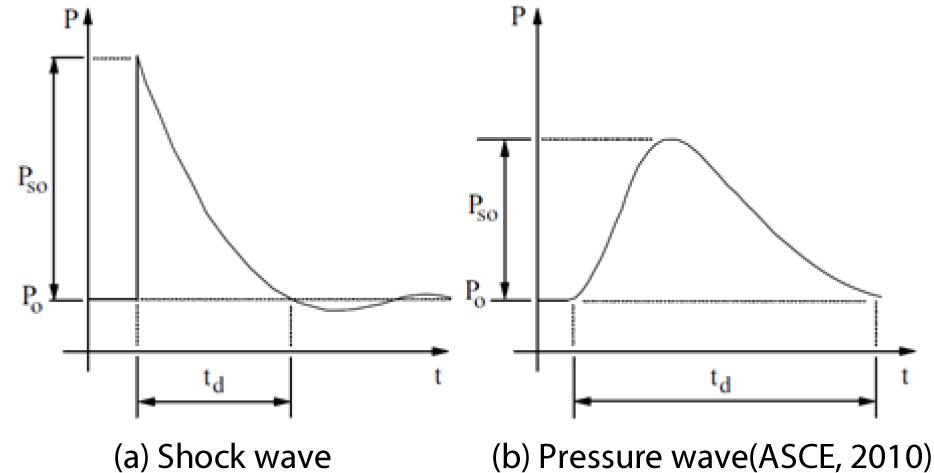
ASCE(2010)에서 폭압 특성을 고려하여 Fig. 1과 같이 시간에 따른 폭압의 형상을 충격파(shock wave)와 압력파(pressure wave)로 구분하여 제시하였다. 충격파는 급격히 과압이 증가하며, 높은 과압과 짧은 지속시간을 특징으로 하고 대체로 구조물에 큰 피해를 입힌다. 일반적으로 TNT 또는 폭발성 물질 등의 경우에서 나타나며, 폭굉(detonation) 형태를 나타낸다. 압력파는 점진적인 과압의 증가와 상대적으로 긴 지속시간을 특징으로 한다. 이는 플랜트 폭발의 경우 많이 발생하며, 폭연(deflagration) 형태를 나타낸다.
플랜트 폭발로 발생하는 폭압을 충격파로 환산하여 폭압을 산정하는 것은 결과적으로 과대평가 또는 과소평가를 초래할 수 있다. 플랜트 폭발의 특성을 보다 정확하게 반영하기 위해서는 증기운 폭발 메커니즘을 이해하여 정확한 폭압 산정법을 선정하여야 한다.
2.1 폭압 산정법
폭압을 산정하는 다양한 방법이 있으며 대표적인 폭압 산정법은 많은 실험과 자료를 통해 개발된 TNT 등가량 환산법(TNT-equivalent method)과 유럽권역에서 많이 연구된 멀티에너지법(multi-energy method)을 사용할 수 있다.
2.2 TNT 등가량 환산법
TNT 등가량 환산법은 UFC3-340-02(2008)에서 다양한 변수를 조정 및 환산계수를 사용하여 정립시킨 방법으로 다양한 폭발물질에 대하여 TNT 등가량을 환산한 후 TNT의 폭압을 이용하여 증기운 폭발의 폭압을 산정하는 방법이다. 이는 CCPS(1996) 및 ASCE(2010)에서 환산된 값을 바탕으로 가스 및 플랜트 폭발에 대하여 TNT와 같은 폭발과 유사하다는 가정에 기초한 방법이다. TNT 등가량 환산법은 식 (1)을 통하여 TNT 등가량을 산정한다.
여기서, 는 TNT 등가량(kg), 는 폭발물질의 연소열(kJ/kg), 는 TNT 연소열(kJ/kg), 는 폭발물질의 질량(kg), 는 수율 계수(yield factor)이다.
TNT 등가량은 수율 계수의 영향을 많이 받으며, 일반적으로 0.03~0.05를 적용한다. 하지만 CPR14E(2005)에서 연구자들은 수율 계수를 0.02~0.3 등의 다양한 의견을 제시하고 있으며, Rashid 등(2015)은 Flixborough 폭발사고에 대하여 수율 계수를 변화시키면서 거리에 따른 차이를 보여주는 등, 정립되지 않는 수율 계수를 보여주고 있다. 따라서 수율 계수의 영향으로 TNT 등가량이 크게 변할 수 있다.
TNT 등가량을 산정한 후, 폭원과의 거리에 따른 효과를 반영하여야 하며 대표적으로 식 (2)의 Hopkinson-Cranz 환산 거리 방정식을 사용한다.
여기서, : 거리(m), : 환산 거리(m/kg1/3)이다.
산정된 TNT 등가량과 환산 거리를 이용하여 Kingery & Bulmash 식을 적용하여 폭압과 지속시간을 도출하게 된다. 폭압과 지속시간은 Fig. 1의 (a)와 같으며, 최대 과압과 임펄스를 고정한 후 삼각형 형상으로 하중이 작용하도록 지속시간을 감소시키면 폭압의 이상화 및 단순화가 가능하다.
2.3 멀티에너지법
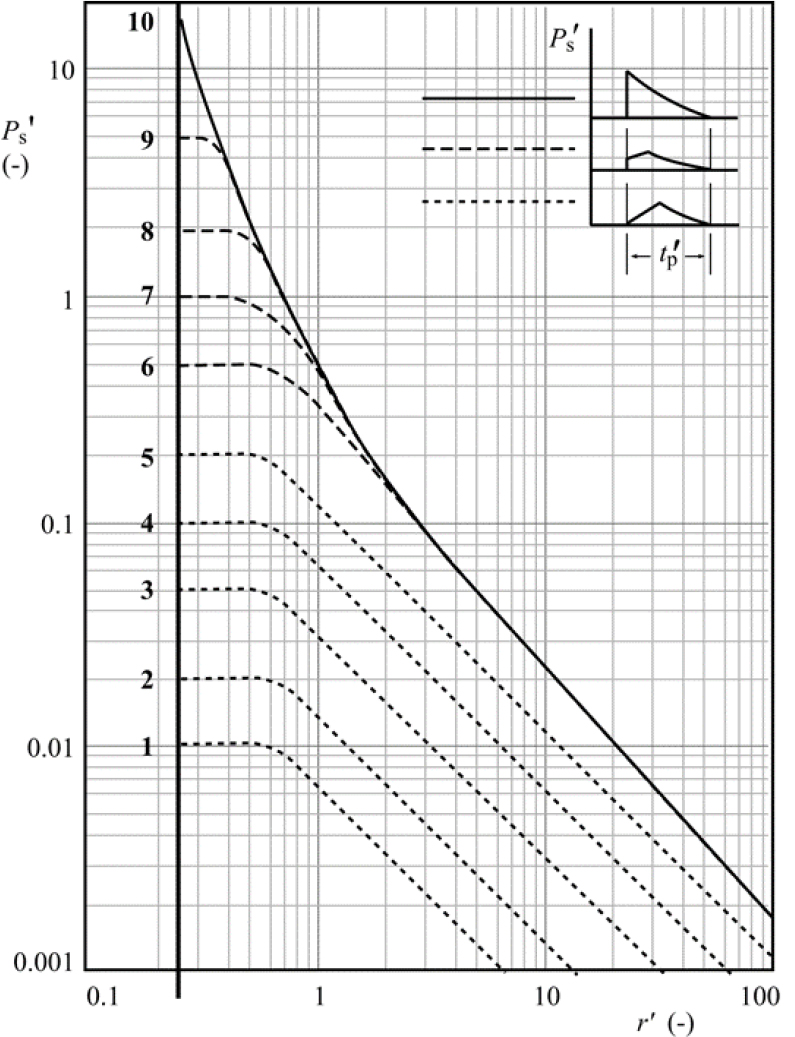
과거 연구자들이 주요 증기운 폭발사고 형태를 연구한 결과, 충격파와 압력파의 양상이 다르다는 점을 고려하여 개발된 방법이다. 멀티에너지법은 Van den Berg(1985)가 제안한 방법으로 증기운 폭발을 예측하기 위한 기본 도구로 이상화된 가스 폭발을 사용한다. 증기운 폭발의 강도와 관련하여 공간 밀집도, 장애물, 점화원 등의 환경조건의 중요성을 고려하여 개발되었으며 특성 곡선은 Fig. 2와 같고 이를 통해 폭압과 지속시간을 도출한다.
특성 곡선 식을 이용한 폭압과 지속시간을 구하는 과정은 식 (3), (4), (5), (6)과 같다.
여기서, 는 폭발에너지(MJ), 는 증기운 부피(m3), 는 연소열(kJ/kg), 는 물질 밀도, 는 공기와 폭발물질 비율, 은 거리(m), 은 환산 거리, 은 대기압(kPa), 은 최대 과압(kPa), 은 환산 최대 과압, 은 지속시간(ms), 은 환산 지속시간, 은 음속(m/s)을 의미한다.
특성 곡선을 이용하여 폭압과 지속시간을 찾는 방법은 Alonso 등(2006)이 제시한 회귀방정식을 적용하는 방법이 있다. 본 논문에서도 제안된 방정식을 사용하여 폭압과 지속시간을 산정한다.
Fig. 2의 오른쪽 상단은 폭압 형상을 나타내며, 폭발강도계수 1~5는 점선으로서 초기 과압이 0으로 시작하는 느린 폭연 형상이고, 폭발강도계수 10은 실선으로서 폭굉처럼 초기 과압이 최대 과압인 충격파 형태를 나타낸다. 폭발강도계수 6~9는 파선으로 초기 과압이 0과 최대 과압 사이에 존재하는 것으로서 폭연 형태이다. 하지만 초기 과압 산정에 대한 명확한 분석이나 문헌이 없는 실정이다. 이에 따라서 초기 과압의 영향을 분석하기 위하여 임펄스를 동일한 크기로 고정한 후, 최대 과압 대비 초기 과압()을 0~50% 6가지로 구분하여 분석한다. 또한, 멀티에너지법의 폭압의 형태는 폭발강도계수가 10 이외의 경우 상승시간(rising time)과 하강시간(decaying time)이 구분되어야 하는데, Weidlinger(2009)에 의하면 3:7 비율로 산정한다.
멀티에너지법은 공간의 밀집도, 장애물, 점화원 등의 영향성을 폭발강도계수 분류로 나누고 있으며, 폭압을 보다 보수적으로 볼 것인지 등의 판단을 적용하여 CPR14E(2005)에서 다양한 연구진들이 표 형식으로 적절한 폭발강도계수를 선정하는 가이드라인을 제시하고 있다.
3. 폭발 사례를 적용한 폭압 산정법 검증
TNT 등가량 환산법과 멀티에너지법의 폭압 산정을 이용한 구조물의 피해 양상을 비교하기 위해서 Case 1~3의 3가지 플랜트 폭발 피해 사건을 분석한다.
Case 1(Buncefield)과 Case 2(Jaipur) 폭발은 일방향 구조이므로 단자유도 해석을 수행하였으며, Case 3(Amuay) 폭발은 이방향구조와 개구부의 영향을 고려하여 비선형 동적 유한요소 해석을 수행하였다.
단자유도 해석은 실험 결과와의 비교 검증을 거친 RCBlast (Jacques et al., 2013)를 사용하여 단자유도 시스템의 시간에 따른 변형을 계산한다. 비선형 동적 유한요소 해석은 폭발이나 충격과 같은 비정상 하중에 대한 해석이 가능한 Autodyn (2005)을 사용하였다. Autodyn은 짧은 시간에 발생하는 높은 폭압에 대한 철근콘크리트 부재의 초기 거동을 비교적 잘 묘사하는 특징이 있으며, 이를 이용하여 손상 및 변형 등 다양한 지표를 분석하였다.
3.1 Case 1: Buncefield Explosion
3.1.1 폭발사건 개요
RR718(2009)과 RR1113(2017) 등에 의하면 2005년 12월 11일에 영국의 번스필드(Buncefield,UK)에서 석유 관련 플랜트의 탱크 공정 표시기와 자동 차단 시스템이 미작동하여 탱크에서 가솔린이 총 23분간 약 550~900m3/hr 속도로 누출되었다. 대부분의 외부 산업용지에 증기 구름이 퍼져나갔으며 최대 범위는 500m×350m이었고, 증기 구름 높이는 약 2m였다.
RR718(2009)은 대표적인 피해 구조물 중 하나인 Northgate Building의 피해와 점화원을 제시하였다. 건물은 폭원으로부터 약 135m 거리에 있었으며, 폭압에 따른 건물 피해는 Fig. 3에 제시되어 있다. 피복 패널의 파괴 및 변형이 발생한 것을 볼 수 있으며, 최상단에 있는 피복 패널의 영구변형은 약 200mm가 발생하였고, 이를 비교·분석한다.
3.1.2 폭압 산정
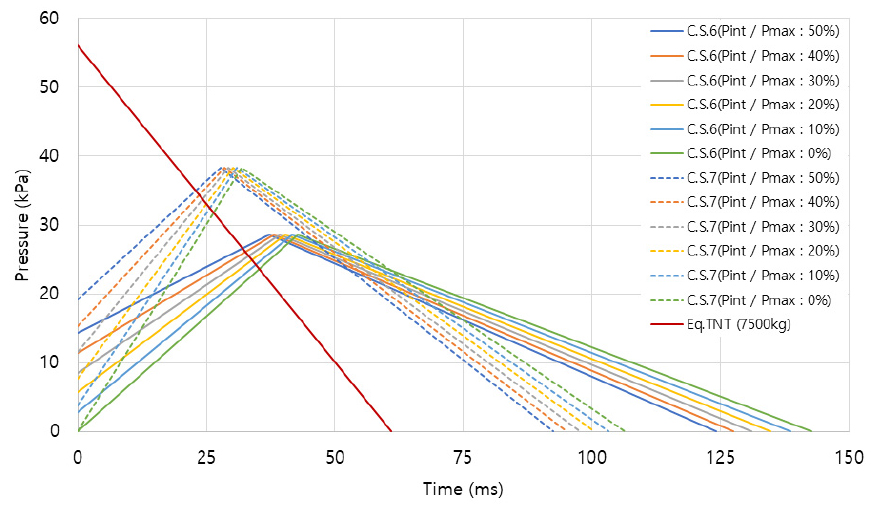
TNT 등가량 환산법을 사용하기 위한 정보인 TNT 등가량은 RR718(2009)에서 제시한 7,500kg을 적용한다. 하중을 이상화할 경우 최대 과압은 56.1kPa, 지속시간은 61ms이며, Fig. 4의 Eq.TNT(7500kg) 그래프와 같다.
멀티에너지법의 경우 RR512(2007)에서 폭발에 관여하는 Vcloud는 60,000m3이며, 폭발강도계수는 가이드라인에 따라 6(C.S.6) 또는 7(C.S.7)로 적용하였으며, 각각 최대 과압은 28.6kPa, 38.3kPa이며, 지속시간은 142ms, 106ms이다. 초기 과압의 영향을 분석하기 위하여 최대 과압 대비 초기 과압비 의 그래프는 Fig. 4에 나타내었다.
3.1.3 패널 모델링
Buncefield 폭발은 단자유도 해석을 수행하여 시간에 따른 변형과 영구변형을 비교·분석하였다.
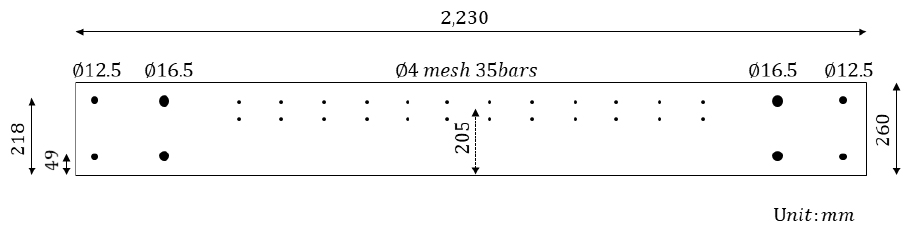
Northgate Building 패널에 관한 단면 및 재료 물성치 정보는 Weidlinger(2009)의 자료를 참고하였다. 해석 모델은 경간 7,000mm, 높이 2,230mm, 폭 260mm이며, 철근 직경이 12.5mm, 16.5mm와 인장면에 와이어메쉬 직경 4mm를 사용한다. 단자유도 해석은 Jacques 등(2013)에 근거하여 질량은 약 10,000kg이며, 질량계수는 0.33으로 적용하고 감쇠비 4%이며, 단순지지이다. 단면 상세는 Fig. 5와 같고 재료 물성치는 Table 1과 같다.
Table 1.
Material properties of cladding panel
3.1.4 패널 해석 결과
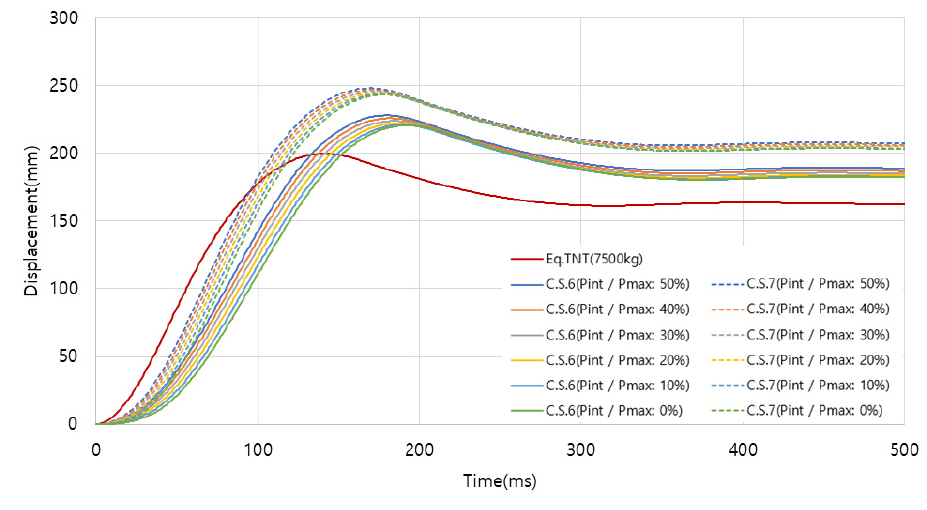
Northgate Building 패널의 영구변형은 약 200mm였으며, 고유주기는 약 70ms이다. 다양한 폭압 산정법에 대한 시간에 따른 변형을 Fig. 6에 나타내었다.
각각의 폭압에 대한 영구변형과 실제 영구변형을 비교·분석한 것이 Table 2이며, TNT 등가량 환산법은 실제 영구변형과 19% 차이가 발생하여 영구변형을 과소평가하는 양상을 보인다. 멀티에너지법(C.S.6)과 멀티에너지법(C.S.7)을 적용할 경우 최소 차이는 각각 5.5%, 1.5%로서 실제 영구변형과 유사함을 알 수 있다. 또한, 초기 과압의 영향을 분석한 결과, 초기 과압이 증가할수록 변형 또한 증가하지만, Pint/Pmax가 0%와 50%의 차이가 최대 약 3.5%로서 미미한 차이가 발생하여 전반적인 양상은 비슷함을 알 수 있다.
Table 2.
Displacement analysis of each method
3.2 Case2: Jaipur Explosion
3.2.1 폭발사건 개요
2009년 10월 29일에 인도 자이푸르(Jaipur, India)의 휘발유 정제 플랜트에서 휘발유 탱크 밸브가 오작동하여 가연성 물질이 액체와 함께 솟구쳤다. 바람은 불지 않았고 75~90분 동안 증기 구름이 사방으로 퍼져 약 700×700m 범위로 퍼져나갔다(RR1113, 2017).
Sharma 등(2013)은 Jaipur Explosion의 폭원과 피해 구조물 중 하나인 Administration Building의 피해 정도를 Fig. 7의 사진으로 제시하였다. 구조물은 폭원으로부터 약 252m 거리에 위치하였다.
빨간 실선으로 표시한 1층 기둥의 중앙부에 균열이 발생하였음을 알 수 있다. PDC-TR 06-08(2008)과 ASCE(2010) 등은 손상 기준으로 영구변형과 겉보기 손상 정도 등을 제시하였다. 이에 따르면 미세 균열이 있지만 특정한 영구변형이 없을 경우, Superficial Damage 수준으로 부재의 항복 이전과 연성비 1 이하를 뜻한다. 이 기둥의 손상 정도 평가는 항복 이전 수준으로 판단된다.
3.2.2 폭압 산정
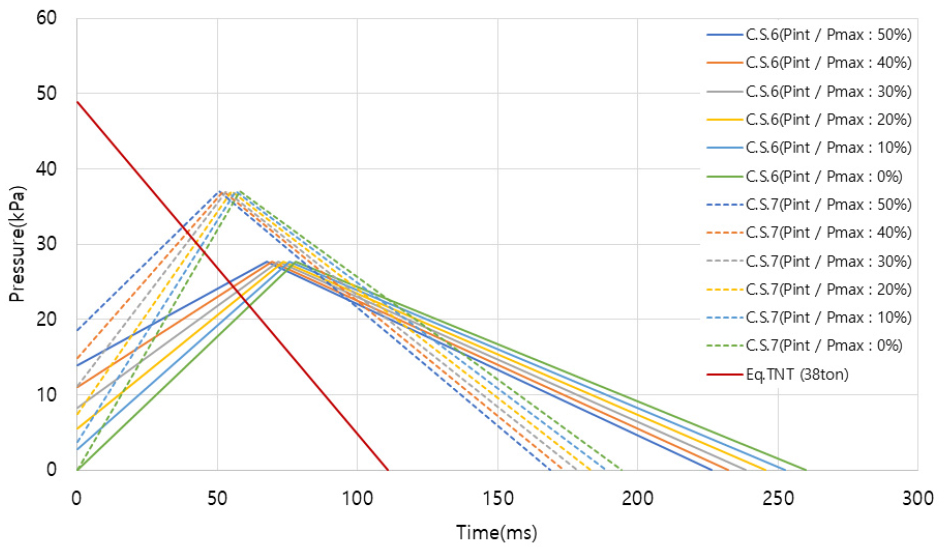
폭원에서 피해 건물까지 거리(R)는 약 252m이며, TNT 등가량 환산법을 사용하기 위한 정보인 TNT 등가량은 Sharma 등(2013)이 제시한 38ton을 적용하였다. 하중을 이상화할 경우 최대 과압은 48.9kPa, 지속시간은 110.9ms이며, Fig. 8의 Eq.TNT(38ton) 그래프와 같다.
멀티에너지법의 경우 Sharma 등(2013)은 폭발에 관여하는 Vcloud를 360,000m3 추정하였다. 폭발강도계수는 가이드라인에 따라 6(C.S.6) 또는 7(C.S.7)로 적용하였으며, 각각 최대 과압은 27.7kPa, 37.1kPa이며, 지속시간은 260ms, 194.2ms이다. 최대 과압 대비 초기 과압비 의 그래프는 Fig. 8에 나타내었다.
3.2.3 기둥 모델링
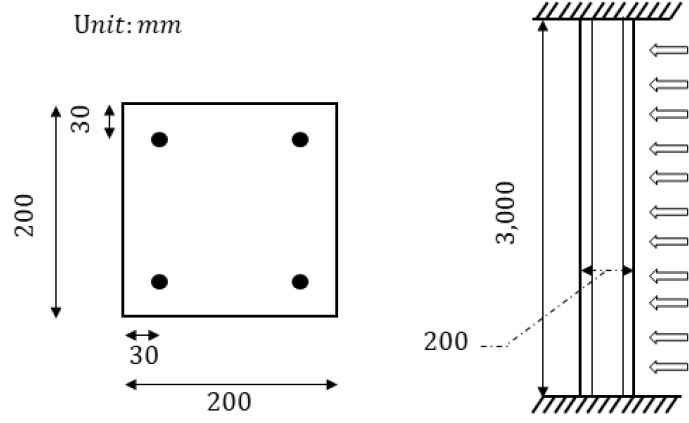
Jaipur 폭발은 단자유도 해석을 수행하여 시간에 따른 변형을 비교·분석하였다. 기둥의 상세 정보가 없으므로 Fig. 7을 바탕으로 추정하였다. 기둥 두께만큼의 조적 벽돌을 사용함에 따라 단면이 200mm×200mm 및 높이는 3,000mm이고 작용하는 축력을 200kN으로 가정하였으며, 단면 상세는 Fig. 9와 같이 가정하였다. 단자유도 해석은 Jacques 등(2013)에 근거하여 질량은 약 300kg이며, 질량계수는 0.33으로 적용하고 감쇠비 4%이며, 양단 고정이다. 재료는 Table 3와 같고 시대적 건축 자료를 근거로 콘크리트의 압축강도 24MPa, 인장강도는 압축강도의 10%인 2.4MPa 추정한다. 철근은 인도 철근콘크리트 기준(IS456)에 근거하여 항복강도를 250MPa(Mild Steel GradeⅠ)로 가정하였으며, 단면이 작고 저층 구조물에 따른 피복두께는 30mm, 철근비 약 1.3%로 가정하였다.
Table 3.
Material properties of column
| Concrete | ||
| Compressive Strength | Tensile Strength | Elastic Modulus |
| 24MPa | 2.4MPa | 25,800MPa |
| Steel Reinforcement | ||
| Yield Strength(Elastic – Perfect Plasticity) | Elastic Modulus | |
| 250MPa(Φ13) | 200GPa | |
3.2.4 기둥 해석 결과
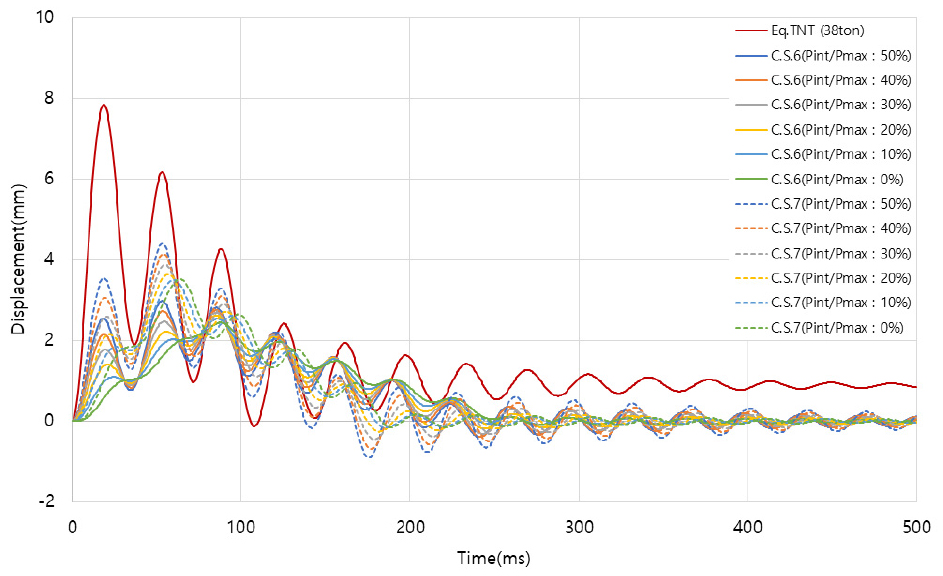
Administration Building 기둥의 고유주기는 약 40ms, 항복 이전의 손상 수준을 나타내며 다양한 폭압 산정법에 대하여 시간에 따른 변형을 비교·분석한 결과를 Fig. 10에 나타내었다. TNT 등가량 환산법은 부재가 항복 이후의 중앙부 영구변형이 1.4mm 발생하였지만, 멀티에너지법은 모두 탄성의 결과를 보여준다. Superficial Damage의 손상 기준에 근거할 경우 TNT 등가량 환산법에 비해 멀티에너지법이 실제 피해에 더욱 근접한 결과를 보여준다.
3.3 Case3: Amuay Refinery Explosion
3.3.1 폭발사건 개요
2012년 8월 25일에 베네수엘라 팔콘(Falcon State, Venezuela)에 있는 정유 공장에서 폭발사고가 발생하였다. RR1113(2017)에 의하면 탄화수소를 취급하는 펌프에서 누출이 발생하였고, 폭발 발생 전날 바람이 거의 없어 높은 수준의 가연성 증기가 최대 1100m×800m 범위와 135~ 180°의 부채꼴 모양으로 확산되었다. Mishra 등(2014)은 피해 사례 일부를 Fig. 11과 같이 제시하였다.
단층의 건축물로 개구부가 있는 벽체의 피해 양상은 기둥과 보에 인접한 부근에 균열이 형성되었으며 벽체의 좌측 하단부는 사선의 균열 형태를 볼 수 있다. 장애물과 밀집도 등의 환경적 변수 및 정중앙이 아닌 개구부 위치의 영향으로 인해 좌우대칭이 아닌 균열 및 영구변형이 발생하였음을 추정할 수 있다.
3.3.2 폭압 산정
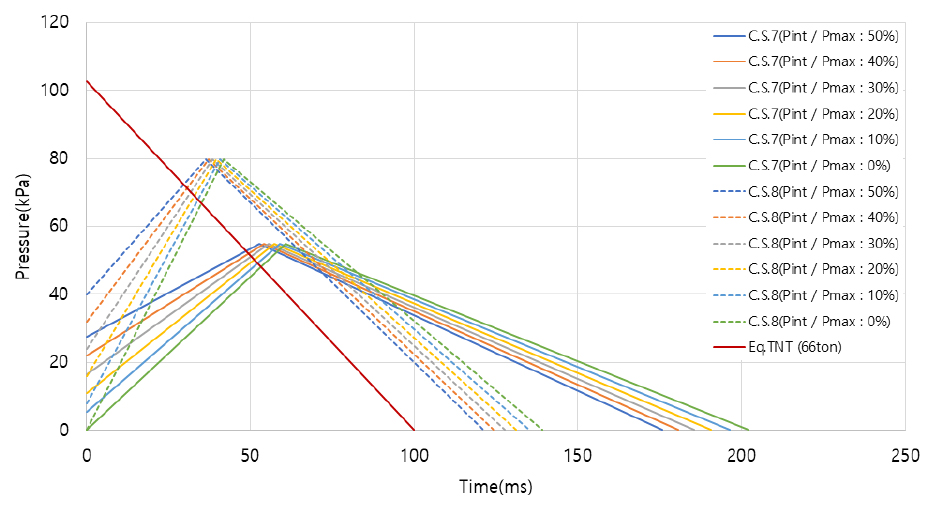
폭원에서 피해를 입은 구조물까지의 거리(R)는 약 200m이며, RR1113(2017)에서 제시하는 표를 사용하여 TNT 등가량은 약 66ton으로 추정하였다. 하중을 이상화할 경우, 최대 과압은 102.77kPa, 지속시간은 99.89ms이며, Fig. 12의 Eq.TNT(66ton) 그래프와 같다.
멀티에너지법의 경우 Vcloud는 480,000m3으로 적용하였으며 폭발강도계수는 이전 2가지 폭발과 다르게 점화원의 강도가 높았기 때문에 7(C.S.7) 또는 8(C.S.8)로 적용하여 각각 최대 과압은 54.95kPa, 79.86kPa이며 지속시간은 202.25ms, 139.17ms이다. 해석에 사용된 최대 과압 대비 초기 과압비 는 Fig. 12에 나타내었다.
3.3.3 개구부가 있는 벽체 모델링
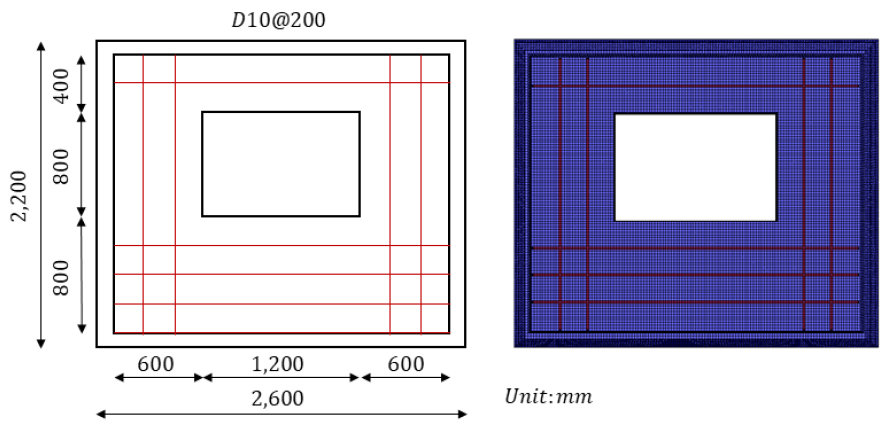
Amuay 폭발 사례는 이방향구조 및 개구부를 고려하여 비선형 동적 유한요소 해석(Autodyn, 2005)을 수행하였다. 개구부가 있는 비내력 벽체에 대한 자세한 도면 및 정보를 얻을 수 없어 Fig. 11을 참고하여 해석 모델을 작성하였다. 벽체는 폭 2,400mm, 높이 2,000mm, 깊이 100mm, D10@200 철근이 중앙부에 배근된 것으로 가정하였다. 벽체와 연결된 보 및 기둥을 나타내기 위하여 Fig. 13과 같이 벽체 사변에 폭 100mm, 깊이 300mm의 요소를 추가하였다. 콘크리트는 입체 요소, 철근은 보 요소를 이용하였으며, 철근과 콘크리트는 완전 결합으로 모델링하였다. 요소의 크기를 20mm로 하여 총 82,500개의 요소를 사용하였다.
재료 물성치는 Table 4와 같고 콘크리트 모델은 취성재료가 동적하중을 받을 때 거동을 표현하기 위해 만들어졌으며, 소성 및 전단에 의한 손상 고려가 가능한 RHT 콘크리트 모델을 적용하였다(Autodyn, 2005). 철근은 속도 의존적 특성과 대변형을 표현할 수 있는 Piecewise Linear Johnson-Cook을 적용하였다(Kim et al., 2014).
Table 4.
Material properties of wall
3.3.4 개구부가 있는 벽체 해석 결과
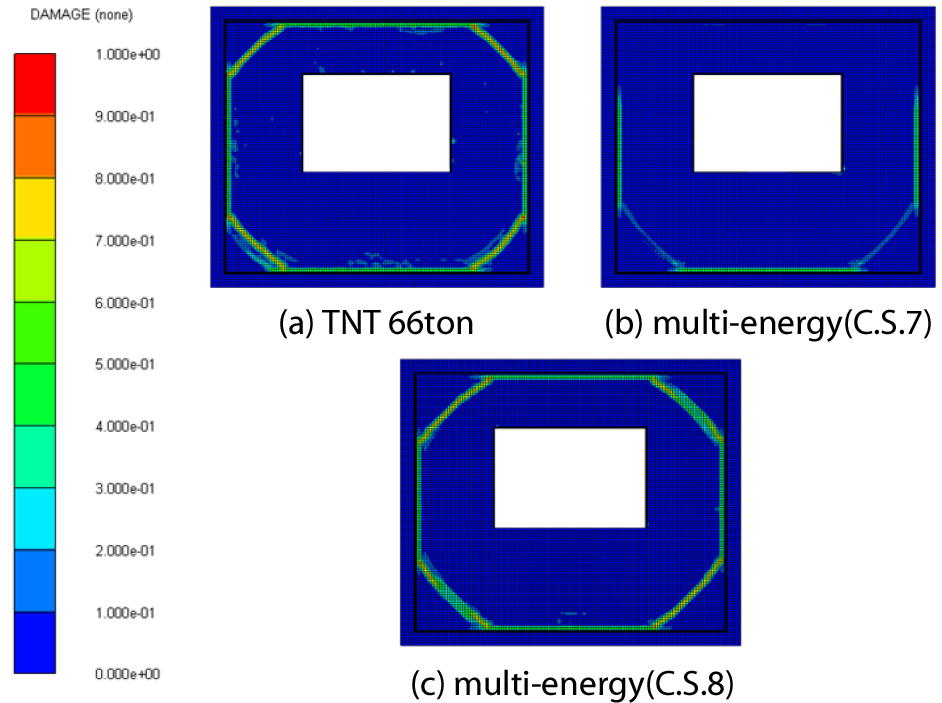
TNT 등가량 환산법과 멀티에너지법으로 산정된 폭압의 손상 분포(Damage Contour)를 Fig. 14에 나타내었다.
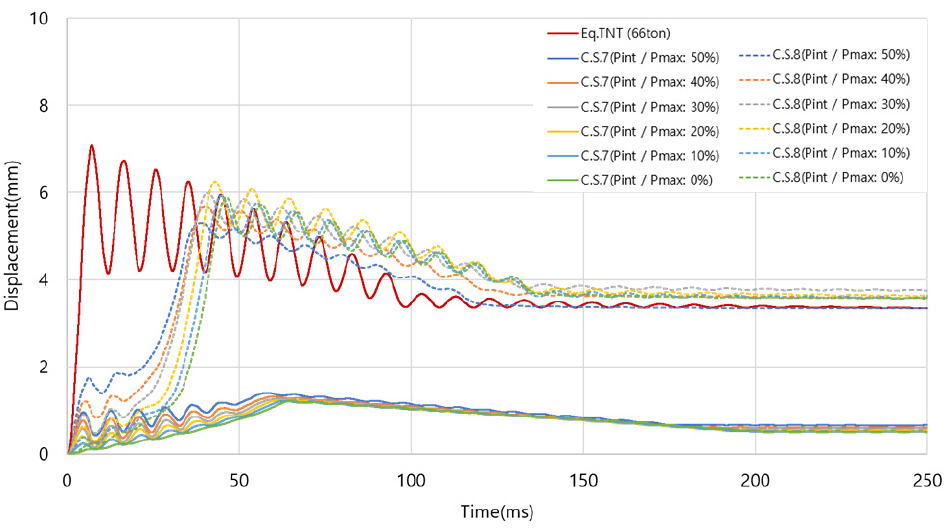
중앙부와 하부의 균열은 실제 피해와 유사하지만, 상부 균열은 차이를 보인다. 이는 실제 벽체에 발생한 크리프나 건조 수축에 의한 균열을 폭파해석에서는 재현하지 못하기 때문으로 추정된다. 멀티에너지법(C.S.7)은 손상 양상이 적절하지 못한 과소평가가 나타나고 TNT 등가량 환산법과 멀티에너지법(C.S.8)을 적용할 경우 실제와 비슷한 손상 양상을 보인다. Fig. 15는 폭압에 대한 변형을 나타내며, 약 10ms의 주기가 나타난다. 멀티에너지법(C.S.7)의 영구변형은 0.49~0.66mm로 실제에 비해 과소평가함을 보이지만 TNT 등가량 환산법의 영구변형은 3.34mm와 멀티에너지법(C.S.8)은 3.33~3.75mm로 실제와 유사한 결과를 보인다.
종합적으로 손상 분포와 영구변형을 보아 실제 개구부가 있는 벽체와 유사한 거동을 보이는 것은 TNT 등가량 환산법과 멀티에너지법(C.S.8)로 판단된다. 이전의 2가지 폭발 사례와는 다르게 개구부가 있는 벽체는 이방향구조인 특징과 진동주기가 폭압 지속시간에 비해 약 14배 짧기에 TNT 등가량 환산법과 멀티에너지법(C.S.8)의 폭압 영향 및 구조물의 거동이 큰 차이가 나지 않는다고 분석할 수 있다.
4. 결 론
본 연구에서는 플랜트에서 발생하는 증기운 폭발에 대하여 TNT 등가량 환산법과 멀티에너지법을 이용하여 산정한 폭압의 적절성을 평가하였다. 3가지 플랜트 증기운 폭발 사례에서 피해를 입은 특정 부재를 선정하여 단자유도 해석 또는 비선형 동적 유한요소 해석을 이용하여 분석한 결과, 증기운 폭발 메커니즘에 TNT 등가량 환산법을 적용한 경우에 폭압이 과소 및 과대평가될 수 있음을 확인하였다. 반면에 멀티에너지법은 점화원, 장애물, 밀집도 등의 환경적 변수를 폭발강도계수로써 반영할 수 있기 때문에 더 정확한 폭압을 산정할 수 있었다. 하지만 Amuay 폭발 사례의 개구부가 있는 벽체의 경우에는 이방향구조인 특징과 고유주기가 폭압 지속시간에 비하여 상대적으로 매우 짧기 때문에 TNT 등가량 환산법과 멀티에너지법이 유사함을 보였다.
비록 분석한 사례가 3가지로 제한되어 있지만, 멀티에너지법의 폭발강도계수를 7 또는 8로 가정하면 플랜트 증기운 폭발의 폭압 모델을 비교적 정확하게 산정할 수 있을 것으로 판단된다. 한편, 멀티에너지법에서 최대 과압 대비 초기 과압의 영향은 크지 않은 것으로 분석되었다. 이는 초기 과압 보다는 폭압의 상승과 하강의 지속시간이 더 구조물에 영향을 주는 것으로 판단되며 플랜트 증기운 폭발은 획일적인 폭굉이나 폭연이 아니라 DDT(Deflagration to Detonation Transition) 등 복합적인 메커니즘임을 보여준다.