1. 서 론
2. 비국부 적분 연산기와 페리다이나믹 방정식
2.1 비국부 적분 연산기의 고윳값 성질
2.2 Fractional Laplacian kernel 형태의 페리다이나믹 정식화
2.3 정적 문제의 수치 정식화
3. 수치예제
3.1 Condition number에 대한 의 영향
3.2 Condition number에 대한 의 영향
4. 결 론
1. 서 론
페리다이나믹 해석법(peridynamics)은 horizon으로 표현되는 유한한 영향 영역 내에서 절점 간 상호작용력을 통해 연속체의 거동을 모사하는 절점 해석 기술이다. 페리다이나믹 해석법에서는 변형의 공간 미분을 정의하는 대신 상호작용력을 적분하여 비국부 적분 방정식(nonlocal integral equation)을 사용하기 때문에 균열(crack) 등과 같은 불연속 현상을 모사하기에 적합하다. Silling(2000)에서 제안된 이후, 페리다이나믹 해석법으로 유리, 복합재, 암석재료 등 취성 재료에 대한 파괴 및 동적 손상 해석을 분석하는 다양한 연구들이 수행되었다(Ha and Bobaru, 2011; Ha and Cho, 2011; Hu et al., 2012; Ha et al., 2015; Ha, 2020). Horizon은 또한 페리다이나믹 모델에 비국부 특성을 부여하는 일종의 길이 차원의 파라미터로서 작용한다. 따라서 horizon이 0으로 수렴하는 경우에는 물리적인 비국부 특성이 완전히 사라지게 되며, 연속체역학 문제와 이론적으로 동일해진다고 알려져 있다. 다만 작은 horizon을 사용하게 되면 계산 시간 부담이 많이 증가하기 때문에 실질적인 수치해석에서는 간단한 수렴성 테스트를 통해 적절한 크기의 horizon을 결정하여 사용한다. Horizon과 함께 비국부 적분 영역의 특성을 결정하는 또 다른 매개변수로 영향 함수(influence function)가 있다. Seleson과 Parks(2011)은 다양한 차수의 radial influence function에 대해 간단한 wave equation의 비국부 경향을 explicit 해석을 통해 수치적으로 확인한 바 있다.
정적/준정적 손상 해석 문제를 해석하기 위해서는 implicit 해석이 요구된다(Ni et al., 2019; Hashim et al., 2020). Implicit 정식화에서 대수방정식 형태로 나타나는 비국부 적분 방정식을 수치적으로 효율적으로 풀기 위해서는 condition number가 중요하다. 일반적으로 대수방정식의 condition number가 작을수록 conjugate gradient(CG)나 preconditioned conjugated gradient (PCG)를 적용할 때, CG와 PCG의 iteration 횟수가 줄어드는 것이 알려져 있다. 특히 radial influence 함수 형태의 비국부 적분 연산기(nonlocal integral operator)를 사용하는 비국부 적분 방정식에서 radial influence 함수의 차수가 condition number에 끼치는 영향은 Aksoylu와 Unlu(2014)에서 연구되었다. 본 논문에서는 페리다이나믹 방정식의 비국부 적분 연산기가 radial influence을 kernel로 갖는 fractional Laplacian 형태로 표현될 수 있음을 설명하고, kernel 형상이 condition number에 끼치는 영향을 연구한다. 반면 Aksoylu와 Unlu(2014)에서는 crack이 있는 구체적인 페리다이나믹 문제에 대한 대수 방정식의 condition number에 대한 설명은 이루어지지 않고 있기 때문에, 이러한 이론적인 설명이 실제적인 예제에서 성립하는지를 확인할 필요가 있다. 본 연구에서는 frational Laplacian kernel을 적용한 비국부 방정식 연구를 토대로 구체적인 페리다이나믹 문제에서 radial influence function의 차수(형상), horizon 크기, meshsize가 대수방정식의 condition number와 PCG 해석 시간에 어떠한 영향을 끼치는지를 확인하려 한다.
본 논문은 다음과 같이 구성되었다. 2장에서 비국부 적분 연산기를 사용하는 비국부 방정식의 condition number와 페리다이나믹 방정식을 설명한다. 3장에서는 다양한 radial influence 함수와 horizon 크기에 대해서 페리다이나믹의 해석 시간과 대수방정식의 condition number를 비교하며, 4장에서 결론을 제시한다.
2. 비국부 적분 연산기와 페리다이나믹 방정식
본 장에서는 fractional Laplacian kernel을 사용하는 비국부 방정식에서 비국부 적분 연산기의 condition number 및 고윳값의 성질을 분석한다. 또한 페리다이나믹 방정식을 적절한 영향 함수을 사용하여 fractional Laplacian kernel 형태로 정식화한다.
2.1 비국부 적분 연산기의 고윳값 성질
정의역 가 d차원에서 주어졌다고 하자. 비국부 연산기의 horizon 사이즈가 일 때, 정의역을 horizon의 크기만큼 확장한 domain을 이라 하자. 다음의 형태의 비국부 적분 연산기를 생각할 수 있다. 그러면 일반적으로 fractional Sobolev 공간 안에 있는 에 대해서 다음과 같은 fractional Laplacian kernel 형태의 비국부 적분 방정식을 정의할 수 있다.
위와 같이 정의되는 문제 를 weak formulation을 통하여 표현할 때, 다음의 bilinear form이 등장하게 된다(Aksoylu and Park, 2011).
페리다이나믹 해석법을 통한 손상 해석을 할 때, 계산 시간에 영향을 끼치는 요소는 bilinear form을 통하여 등장하는 대수 방정식의 condition number이다. Aksoylu와 Unlu(2014) 연구에서 증명된 다음의 결과는 가 의 고윳값에 어떠한 영향을 끼치는지를 설명하고 있다. 아래에서 h는 이산화의 크기(예: 절점 간격)를 의미한다.
Proposition 1.의 가장 고윳값은 다음에 의해서 상한과 하한이 결정된다:
Proposition 1을 통하여 의 가장 작은 고윳값은 이며, 에 대해서는 영향을 받지 않는다. 반면, 의 가장 큰 고윳값은 모두에 영향을 받는다(Aksoylu and Unlu, 2014). 만약 이고, 라면, 다음이 성립하게 되며
이것은 비국부 적분 연산기을 통하여 등장하는 대수 방정식의 condition number가 1) factor가 크면 클수록, 2) 값이 작으면 작을수록, 작아진다는 것을 의미한다. 따라서 만약 factor가 고정되어 있다면, 비국부 연산기의 kernel이 중점으로부터 멀어질 때 천천히 작아지는 경우, 대수 방정식의 condition number가 작으며, 대수 방정식이 빨리 풀릴 수 있음을 알수 있다.
2.2 Fractional Laplacian kernel 형태의 페리다이나믹 정식화
시간 에서 물체 에 속하는 절점 의 위치를 로 정의할 때, 이에 대한 페리다이나믹 운동방정식은 다음과 같이 정의된다(Silling, 2000).
여기서, 는 재료 밀도이고 는 체적력 밀도를 의미한다. 는 절점 와 일정 거리() 내에서 상호작용하는 의 집합으로 다음 식과 같이 정의되는 비국부 영역이다.
페리다이나믹 이론은 내에서 유효한 상호작용력을 적분하여 운동방정식 (4)에서 응력의 미분을 대신한다. 결합 기반 페리다이나믹 모델에서는 절점 와 의 상호작용력을 스프링 구조와 유사하게 다음과 같이 정의한다.
여기서, 는 스칼라 함수로 변위 에 의한 변형 후 위치 와 원래 위치 와 의 관계로 다음과 같이 표현할 수 있다.
여기서, 는 micromodulus 상수이며 는 결합 인장(bond extension)으로 다음과 같이 정의된다.
여기서, , 이다. 또한 는 비국부 상호작용을 조절하는 일종의 영향 함수로 fractional Laplacian kernel 형태의 비국부 방정식을 구성하기 위해 다음과 같은 radial function을 사용한다.
여기서, 이다. 식 (7)과 (9)를 (2)에 대입하면 식 (1)과 유사한 비국부 적분 연산기의 형태로 페리다이나믹 정식화가 가능하다. 결합 변형률(bond strain) 를 정의하면 페리다이나믹 변형 에너지는 다음과 같다.
페리다이나믹 변형 에너지를 균질 변형(homogeneous deformation, =constant) 상의 일반적인 선형탄성 변형 에너지에 대해 표현하면, 미소탄성 균질 등방성 재료에 대한 micromodulus 상수를 계산할 수 있다. 본 연구에서는 2차원 문제(d=2)에 대해 정식화한다.
여기서, 는 2차원 평판의 두께이다. 위 식의 적분은 다음과 같이 정리된다.
따라서 micromodulus는 다음과 같이 유도된다.
여기서,
위에서 는 Young’s modulus이고, 는 Poisson ratio이다. 페리다이나믹 모델에서의 재료 손상은 연결된 결합 간의 상호작용을 삭제하는 것으로 표현할 수 있으며, 다음과 같은 스칼라 함수를 식 (7)에 추가한다. 일단 손상된 결합은 다시 복구되지 않으며 해당 결합 사이에는 어떠한 힘도 작용하지 못한다(Silling and Askari, 2005).
여기서, 는 critical bond strain이다.
2.3 정적 문제의 수치 정식화
본 연구에서는 식 (4)를 2차원 정적 비선형 문제에 대해 다음과 같이 수치 정식화를 한다. 이때 는 크기의 사각격자로 분할하였으며, 시스템은 총 N개의 절점으로 구성된다. 로 정하면 Section 2.1과 같이 의 관계를 구성할 수 있다.
이때,
이고, 는 절점 i의 부피(면적)이다.
비선형 방정식을 풀기 위해서 Newton-Raphson method을 사용하면, 다음과 같은 1차 Talor expansion을 구성할 수 있다.
여기서, 는 Newton-Raphson의 초기값이며 는 보정항이다. 최종적으로 식 (16)의 선형화된 시스템은 다음과 같다.
여기서, 1차 미분 기울기는 다음과 같다.
이때 에서는 이 사라지고, 에서는 인 경우를 제외한 모든 항이 사라지게 된다. 최종적으로 는 각 결합 i, j에 대해서 2×2 행렬 형태를 구성한다. (19)-(20)을 정리하면 결과적으로 형태의 대수 방정식이 만들어지게 된다. 이러한 대수 방정식은 symmetric positive definite system이며 따라서 preconditioned conjugate gradient로 효과적으로 풀릴 수 있다. Newton-Raphson의 초기값 은 zero vector을 사용하였다. 또한 으로부터 만들어진 tangent 행렬을 풀어서 만들어진 해를 이라 할 때, 우리는 과 의 차이가 어떤 허용범위보다 작아질 때까지 작업을 반복해서 수렴된 해를 찾는다.
3. 수치예제
2 단원에서 비국부 적분 연산기에 따라서 발생하는 대수방정식의 condition number 가 달라짐을 보고하였다. 하지만 Proposition 1의 결과는 페리다이나믹 방정식에 그대로 적용할 수 없는 몇 가지 이유가 있다.
(1)도메인에 균열(crack)이 있을 경우, condition number가 어떻게 달라질지 알 수 없으며,
(2)매개변수 가 의 범위를 넘어 설 경우, condition number가 어떻게 달라지는 지를 알기가 힘들다.
본 단원에서는 균열이 있는 페리다이나믹 모델에서 매개변수 와 을 바꾸며 발생하는 대수 방정식이 풀리는데 걸리는 시간을 비교한다. 이때 대수 방정식을 풀기 위해 CG, PCG와 MG-PCG(multigrid method with PCG) 해석기들을 적용하고 결과를 비교하였다. 가 작을수록 그리고 R이 클수록 condition number가 작아지게 됨으로, PCG 반복수는 작아지는 경향이 있다. 반면 절대적인 CPU-time의 경우 R이 커지면 증가하는 것을 확인할 수 있다. MG-PCG는 본 연구팀이 개발한 multigrid 알고리즘을 이용한 preconditioner를 적용하는 PCG 해석기로서 균열이 있는 domain에 대한 페리다이나믹 해석을 위해 개발되었으며, 자유도 N 증가에 대해 iteration 증가가 없이 을 만족하는 효율적인 행렬 해석 기술이다(Jo and Ha, 2021).
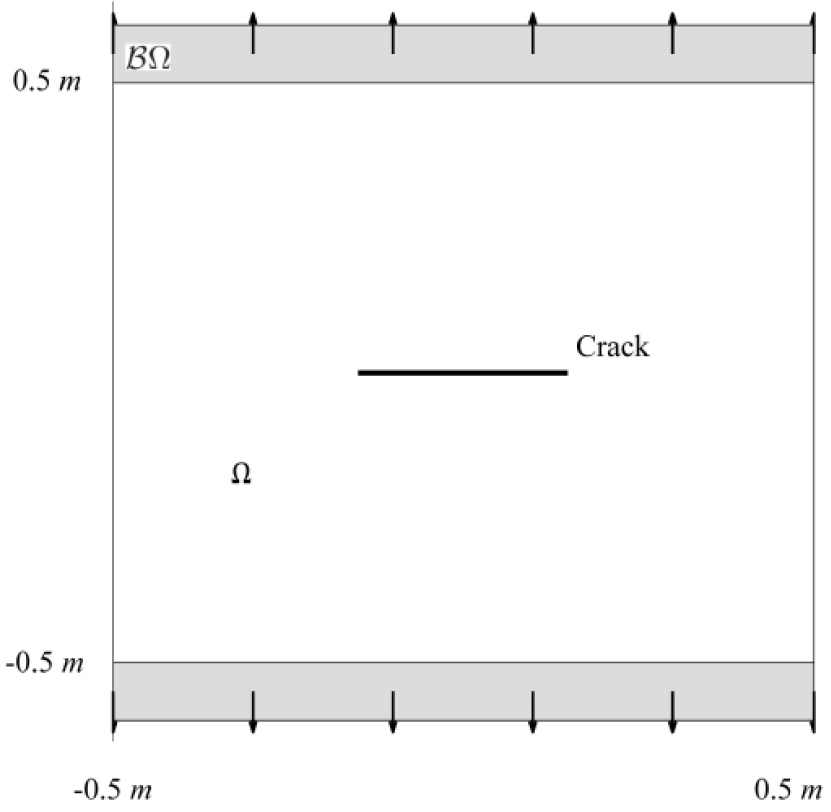
수치 예제의 domain은 (m-unit)이며, 을 수직 방향으로 인장시키는 조건이 주어진다. 또한 의 중앙에 크기가 0.3m인 균열이 주어져 있다(Fig. 1). Young’s modulus는 이며, Poisson ratio는 1/3이다. 수치 테스트 환경은 Intel(R) i9-10940X CPU @ 3.30GHz가 사용되었으며, 모든 해석 모델 및 solver는 c++로 구현되었다. Newton-Raphson 방법으로 대수 방정식을 풀기 위한 stopping 조건은 대수 방정식의 에러가 초기값에 비해서 이하로 작아지는 것으로 하였다.
3.1 Condition number에 대한 의 영향
3.1 절에서는 고정된 R 값에 대해서() 가 변할 때, 대수 방정식의 condition number와 여러 해석기들의 CPU-time을 보고한다. 편의상 첫번째 Newton-iteration에서 등장하는 대수 방정식을 푸는데 걸리는 시간을 보고하는데, 이것은 두 번째, 세 번쨰 Newton-iteration에서의 결과가 큰 차이가 없기 때문이다. Table 1은 대수방정식의 condition number 를 보여 준다. 여기서, 는 매개변수 에 따라 달라지는 대수 방정식의 행렬을 의미한다. Table 1에서 우리는 가 커질수록, condition number가 커짐을 알수 있다. 또한 동일한 에 대해서는 가 작아질 때 condition number가 4배 커짐을 확인 할 수 있다.
Table 1.
Condition numbers of algebraic equations
| 5.19E+1 | 5.72E+1 | 6.80E+1 | 1.53E+2 | 4.47E+2 | 1.10E+3 | |
| 1.95E+2 | 2.16E+2 | 2.59E+2 | 5.90E+2 | 1.77E+3 | 4.46E+3 | |
| 7.54E+2 | 8.40E+2 | 1.01E+3 | 2.31E+3 | 7.03E+3 | 1.80E+4 | |
| 2.96E+3 | 3.30E+3 | 4.00E+3 | 9.18E+3 | 2.81E+4 | 7.23E+4 |
Tables 2, 3, 4는 CG, D-PCG, MG-PCG로 대수 방정식을 풀 때 stopping 조건까지 대수 방정식의 상대 잔류(relative residual)가 줄어드는데 걸리는 수(N)와 CPU-time(CT)을 보고한다. 이때 D-PCG는 행렬의 diagonal을 preconditioner로 사용한 PCG solver를 의미하며, MG-PCG는 multigrid를 preconditioner로 사용한 PCG를 의미한다.
Table 2.
Numerical performance of CG with varying : Iteration numbers (N) and computational time (CT)
Table 3.
Numerical performance of D-PCG with varying : Iteration numbers (N) and computational
Table 4.
Numerical performance of MG-PCG with varying : Iteration numbers (N) and computational time (CT)
Tables 2, 3, 4에 보고된 결과를 보면, 모든 solver에 대해서 가 작을수록 더 작은 수의 iteration 수와 CPU-time으로 대수 방정식이 풀리는 것을 확인할 수 있다. 반면 고정된 에 대해서는 가 2배 작아질 때 CG, D-PCG의 경우 CPU-time이 8배 증가하는 것을 볼수 있는데, 이것은 대수 방정식을 푸는데 걸리는 시간이 임을 의미 한다. 한편 모든 비율에 대해서 MG-PCG의 경우 가 2배 작아질 때, CPU-time이 4배 증가하는데, 이것은 MG-PCG이 알고리즘을 의미한다. 따라서 MG-PCG의 경우 의 비율과 상관없이 성능이 robust 함을 확인할 수 있다.
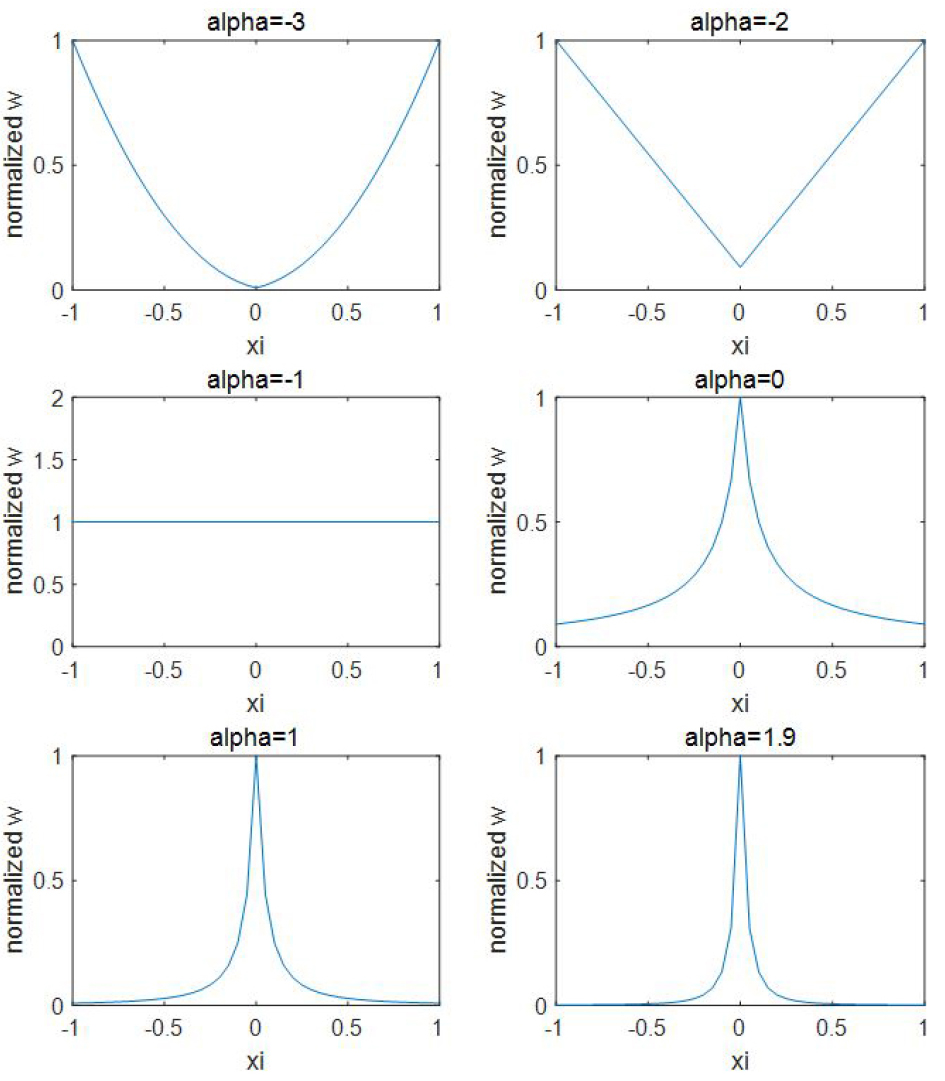
Fig. 2는 정규화된 영향 함수 를 에 대해서 표현한 것이다. 이때 페리다이나믹 상호작용력을 micromodulus 와 bond strain 의 관계식으로 다음과 같이 명시적으로 표현하면, 는 상호작용력을 구성하는 결합 간 비국부 특성을 보여준다.
식 (9)에 의해 에서 가 증가하면 미분의 fractional 차수가 높아지게 되어 condition number가 커지는 결과를 얻을 수 있다. 또한 Fig. 2에서 볼 수 있듯이 페리다이나믹 모델의 결합 간 비국부 특성이 급격히 줄어드는 것을 확인할 수 있다.
3.2 Condition number에 대한 의 영향
3.2 절에서는 고정된 에 대해서 가 변할 때, 대수 방정식의 condition number와 여러 solver들의 CPU-time을 보고한다. Tables 5, 6, 7에서 각각 CG, D-PCG, MG-PCG의 iteration 수와 CPU-time을 보고 한다. 여기서, 가 클수록 대수 방정식의 condition number가 작아지기 때문에 iteration 횟수가 줄어드는 것을 확인 할 수 있다. 반면 절대적인 CPU 시간의 경우 이 작을수록 줄어드는 것을 볼 수 있는데, 이것은 이 커지면 행렬의 density가 증가하기 때문이다. 예를 들어 이 두 배가 되면 horizon에 들어가는 node의 수가 약 4배(2차원 모델)가 되어서 tangent 행렬의 density가 4배가 된다.
Table 5.
Numerical performance of CG with varying R: Iteration numbers (N) and computational time (CT)
| N | CT | N | CT | N | CT | |
| 47 | 0.14 | 30 | 0.37 | 20 | 0.73 | |
| 91 | 1.99 | 55 | 3.12 | 34 | 6.92 | |
| 177 | 10.17 | 106 | 26.00 | 62 | 57.80 | |
| 349 | 83.06 | 205 | 204.59 | 118 | 460.77 | |
4. 결 론
비국부 적분식으로 표현되는 페리다이나믹 방정식의 implicit 정식화 과정에서 나타나는 대수 방정식의 condition number는 해석 시간에 직접적인 영향을 주는 주요한 요소가 된다. 본 연구에서는 비국부 적분식의 형태를 fractional Laplacian으로 표현할 수 있다는 이론에 근거하여, 페리다아니믹의 연산기를 radial function을 kernel로 갖는 fractional Laplacian으로 표현하고 radial function의 차수에 따른 condition number의 경향성을 조사하였다. 수치 실험은 이론적 설명을 뒷받침 하는데, meshsize가 동일하다면 kernel의 radial function의 차수가 클수록(가 작을수록) 그리고 horizon size가 작을수록(이 클수록) 대수방정식의 condition number가 작음을 확인할 수 있다. 따라서 CG와 PCG의 iteration 횟수가 가 작을수록 이 클수록 작아진다. 반면 절대적인 해석 시간에 대해서는 가 작을수록 이 작을수록 CPU time이 줄어드는 경향을 확인할 수 있었다.