1. 서 론

기후변화로 인한 재난의 강도 및 빈도의 증가는 기존 설계기준으로 건설된 인프라 시설의 안전을 더욱 위협하고 있으며, 이로 인해 구조물의 파괴와 붕괴 위험이 증대하고 있다. 더 나아가 도시의 고밀도화 및 재난 재해 관련 불확실성의 증가로 인해 이를 구성하는 토목 인프라 시설물의 재난 리스크 예측이 어려워져 확률론적 개념을 도입하여 구조시스템의 리스크를 평가해야 할 필요성이 증가하고 있다. 특히 근래의 재난 위험 관리 프레임워크는 재난 및 구조물에 내재된 불확실성의 정량화와 함께 단순 재난에 대한 구조물의 안전성 관리를 넘어 파괴 및 붕괴 시 원래의 상태를 회복하는 “회복력”을 포괄하는 리질리언스(Resilience) 개념을 적극 도입하고 있다.

리질리언스는 라틴어 “resilire”를 어원으로 하며 “원래 상태로 되돌아가는”이라는 의미를 지니고 있다(Holling, 1973). 공학에서 리질리언스는 외부 및 내부의 충격이 발생하여도 시스템의 원래 기능을 지속하게 하는 역량과 시스템의 기능이 중단 혹은 손상되었을 경우 완전히 그리고 신속하게 기능을 회복할 수 있게 하는 종합적인 역량으로 정의된다(ASME, 2009). 이러한 종합적인 역량을 정량적 및 수치적으로 평가하기 위해 다양한 연구가 수행되고 있다.

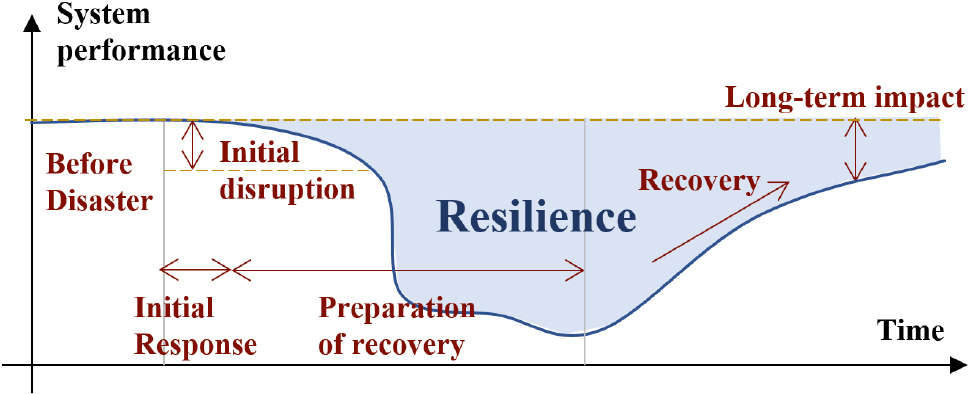
그 중 Bruneau 등(2003)이 제시한 리질리언스 평가 개념이 토목공학 분야에서는 전 세계적으로 가장 빈번히 사용되고 있으며, 제안된 프레임워크는 리질리언스를 견고성(Robustness), 여용성(Redundancy), 자원 활용성(Resourcefulness), 신속성(Rapidity)의 네 가지 “R”로 설명하였다. 특히 Fig. 1과 같은 리질리언스 삼각형 모델을 네 가지 “R”과 함께 제시함으로써 회복 시간에 따른 토목 구조시스템의 성능 변화를 직관적으로 이해할 수 있도록 하였다. 시간에 따른 성능 감소량(Fig. 1의 파란색 음영 면적)을 활용하여 리질리언스 성능을 정량화하였고, 의사 결정자는 파란색 음영 면적을 최소화하기 위한 최적의 보수 및 보강 전략을 수립해야 한다.

Fig. 1.

Resilience triangle model (Bruneau et al., 2003)

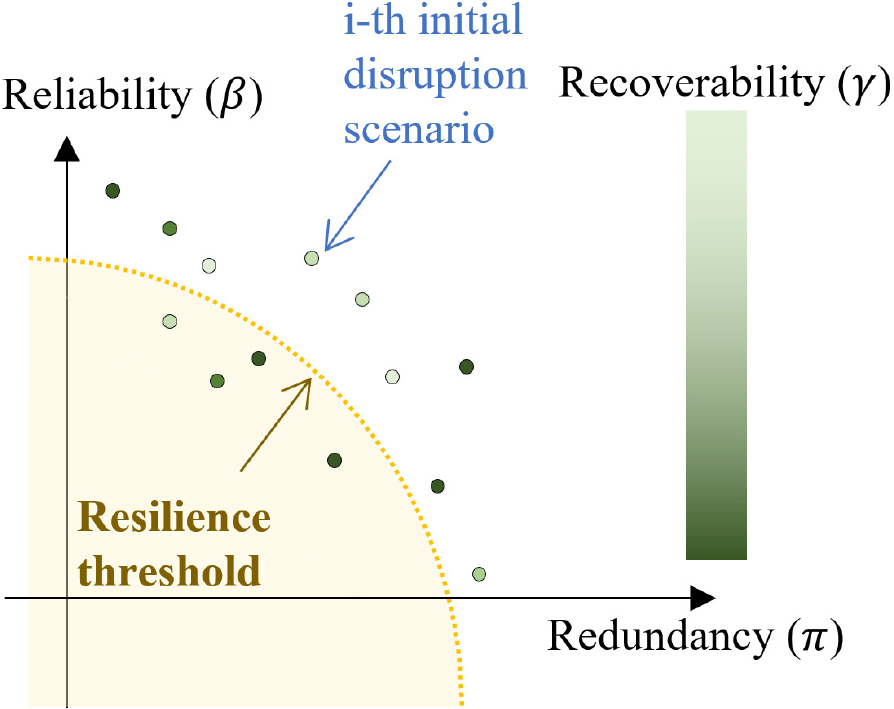
하지만 Bruneau 등(2003)의 모델은 시스템의 성능(즉, 리질리언스 삼각형 모델의 y축 값)의 정의가 공학자마다 다를 수 있으며, 외력 및 구조시스템 내에 잠재하고 있는 불확실성을 적절히 고려하지 못하는 한계를 보인다. 더 나아가 구조 시스템을 구성하는 요소의 성능과 시스템의 성능을 동시에 분석하는데 한계가 있다. 이러한 문제를 해결하기 위하여 Lim 등(2022)은 시스템 신뢰성 관점에서 새로운 재난 리질리언스 개념을 제안하였다. 제안된 프레임워크에서는 리질리언스를 신뢰성(Reliability), 여용성(Redundancy), 회복력(Recoverability)의 세 가지 “R”로 설명하며, 신뢰성과 여용성을 수학적으로 산정할 수 있는 지수를 제안하였다. 더불어, 신뢰성과 여용성을 각 축으로 하며, 회복력의 정도를 색상으로 표현한 𝛽-𝜋 도표를 제시하였다(Fig. 2 참조). 이때 신뢰성, 여용성, 회복력 지표는 구조물의 파괴 시나리오 마다 계산하고, 그 결과를 미리 설정된 리질리언스 한계 상태(Resilience threshold)와 비교하여 리질리언스 성능을 평가한다.

Fig. 2.

Concept of 𝛽-𝜋 diagram (Lim et al., 2022)

Lim 등(2022)은 정하중에 대한 구조물의 리질리언스 성능 평가 방법론을 제안하였고, 이를 기반으로 Yi와 Kim(2023)은 전확률분포(Total probability theorem) 및 구조물의 취약도 곡선(Fragility curve)을 활용하여 지진, 바람 등과 같은 불규칙 진동(Random vibration)에 대한 구조물의 리질리언스 평가 방법론을 제안하였다. 해당 방법론에서는 대상 재해가 지진인 경우 내재적 불확실성(Aleatoric uncertainty)을 고려하기 위해 고전 지진 취약도 해석방법과 유사하게 지진동 기반 시간이력해석을 수행하며, 이를 위해 설계기준에서 제시하는 설계응답스펙트럼(Design response spectrum)을 기준으로 그에 상응하는 인공지진동을 생성하거나 계측된 지진동을 분석하여 적절히 선택하는 과정을 거친다(Kim et al., 2021a).

고전 취약도 해석의 경우, 많은 선행연구로부터 시간이력해석에 사용하는 지진동 모음으로 표현되는 내재적 불확실성의 특성에 따라 구조물의 취약도 성능에 차이가 있음이 알려져 있다(Kwon et al., 2024; Park et al., 2023). 한편 그러한 내재적 불확실성이 리질리언스 평가 결과에 미치는 영향은 명확히 연구된 바 없다. 이에 본 연구에서는 Yi와 Kim(2023)에서 제시한 프레임워크를 적용하여 지진동의 지역 특성 변화에 따른 리질리언스 성능의 차이를 정량적으로 분석하고자 한다. 본 연구는 선행연구를 따라 회복력을 제외한 신뢰성과 여용성의 변화만을 평가하여 외부 요인을 제외한 내재적 리질리언스 평가에 초점을 둔다. 지역적 차이를 반영하기 위해 국내의 설계응답스펙트럼과 캐나다 서부의 설계응답스펙트럼을 목표응답스펙트럼으로 설정하여 지진동을 생성, 보정한다. 대상 구조물은 6층 철골 구조물으로 선정하여 OpenSees(McKenna, 2011)를 통해 모델링하고, 증분동적해석(Incremental Dynamic Analysis, IDA)를 수행하여 신뢰도 및 여용성 곡선을 계산한다. 참고로 리질리언스 성능 평가 시 IDA이외에 다중 띠 분석(Multiple Stripe Analysis, MSA) 등 다양한 취약도 산정 기법을 적용할 수 있다.

2절에서는 시스템 신뢰성 기반 리질리언스 평가법을 소개한다. 3절에서는 설계응답스펙트럼에 따른 지진동 생성이론을 요약한다. 4절에서는 6층 철골 수치모델을 대상으로 3절에서 생성한 지진동을 활용하여 리질리언스 성능을 평가하고 이를 𝛽-𝜋 도표에 도식화한다. 지진동 모음에 따른 리질리언스 성능을 비교하여 응답 스펙트럼 변화와 리질리언스 성능의 관계를 정량적으로 분석한다. 본 연구를 통해 응답스펙트럼에 따른 취약 파괴모드를 정량적으로 분석함으로써 향후 리질리언스 기반 보수/보강 의사결정의 기초기술로 활용될 수 있다.

2. 시스템 신뢰성 기반 리질리언스 성능 평가

2.1 정하중에 대한 리질리언스 성능 평가

Lim 등(2022)에 따르면 신뢰성은 재난재해 사건이 발생했을 때 외부의 충격을 견디는 능력을, 여용성은 재난재해로 인해 시스템 구성요소의 일부가 손상되었음에도 시스템이 제 기능을 수행하고 순차적 파괴를 막는 능력을, 회복력은 재난재해로 인해 시스템 구성요소의 일부가 손상되거나 기능이 저감되었을 때 시스템의 성능을 신속하고 완전하게 복구할 수 있는 능력을 의미한다. 언급한대로 시스템 신뢰성 기반 리질리언스 성능 평가 방법론은 위의 세 척도를 각 파괴 시나리오 마다 산정한다.

재해(H)에 대한 i-번째 파괴모드(Fi)의 신뢰성(βi)과 여용성(πi) 지수는 각각 다음의 확률계산으로 산정된다.

여기서, -Φ-1(∙)은 표준정규분포(Standard normal distribution)의 역누적분포함수(Inverse cumulative distribution function)를, Fsys는 시스템 파괴를 의미한다. Fig. 2의 각 점들은 파괴모드마다 계산된 𝛽와 𝜋값을 나타낸다.

각 파괴 시나리오가 상호 배타적이며 전체포괄(Mutually Exclusive and Collectively Exhaustive; MECE) 사건의 집합으로 구성되어 있다면 시스템 파괴확률(P(Fsys))은 다음과 같이 표현될 수 있다.

여기서, PFsys,i는 i번째 시나리오에 따른 시스템의 연간 파괴 확률을 의미하며, NF는 구조물의 모든 파괴 시나리오의 수를 나타내고λH 는 재해의 연간 발생 확률을 의미한다. Lim 등(2022)에서는 de minimis 리스크(Pdm) 개념을 도입하여 리질리언스 성능 평가를 위한 한계상태로 사용하였다. 여기서 de minimis 리스크란 사회가 규제를 부여하지 않은 리스크 수준 상태를 의미하며 토목 구조물의 경우 10-7/yr가 일반적으로 사용된다(Paté-Cornell, 1994). Lim 등(2022)의 방법론을 기반으로 향상된 리질리언스 성능 평가 기법을 후속절에서 기술하고자 한다.

2.2 불규칙 진동에 대한 리질리언스 성능 평가

지진동에 따른 구조물 응답의 변동성을 고려하기 위하여 Yi와 Kim(2023)은 전확률분포 개념을 활용하여 다음과 같이 부재 및 시스템 파괴 확률을 정의하였다.

여기서, im은 지진강도척도(Intensity Measure; IM)을 의미한다. 식 (4)와 (5)를 각각 식 (1)과 (2)에 대입하게 되면 불규칙진동의 불확실성을 고려한 신뢰성 및 여용성 지표 산정이 가능하다.

de minimis 개념을 활용한다면 식 (3)의 시스템 파괴확률은 de minimis 리스크(Pdm) 보다 작아야 한다. 각 파괴 시나리오에 같은 리스크가 부여된다고 가정한다면 i-번째 파괴모드(Fi)의 신뢰성과 여용성은 다음 식 (6)의 리질리언스 한계상태(Pdm/(λH∙NF))를 만족해야 한다.

리질리언스 한계상태는 𝛽-𝜋 도표(Fig. 2)에서 점선으로 표현된 원호이며, Fig. 2에서 노란색 음영(원점을 기준으로 원호 안쪽)에 도시된 점들은 리질리언스 한계상태를 만족하지 못한 파괴 시나리오이다. 따라서 원점을 기준으로 한계상태 바깥에 위치한 점들은 리질리언스 한계상태를 만족한 파괴 시나리오이다. 제안된 방법론은 정량적 및 시각적으로 구조물의 리질리언스 성능을 파악하는 데 도움을 준다.

3. 설계응답스펙트럼 및 지진동 생성

3.1 설계응답스펙트럼

지진에 대한 선형 구조시스템의 응답은 지진동의 주파수성분과 구조시스템의 주기의 함수로 결정된다. 이에 설계(가속도)응답스펙트럼은 지반조건을 고려하여 고유진동수에 따라 관심 지역에서 관측된 평균적인 지진에 대한 구조물의 최대 가속도 응답을 나타낸다. 지역특성에 따라 예상되는 지반운동이 다르기 때문에 각국의 설계기준은 서로 다른 설계응답스펙트럼 공식을 제공하고, 이에 따라 같은 구조물이라도 서로 다른 응답 값이 예측될 수 있다.

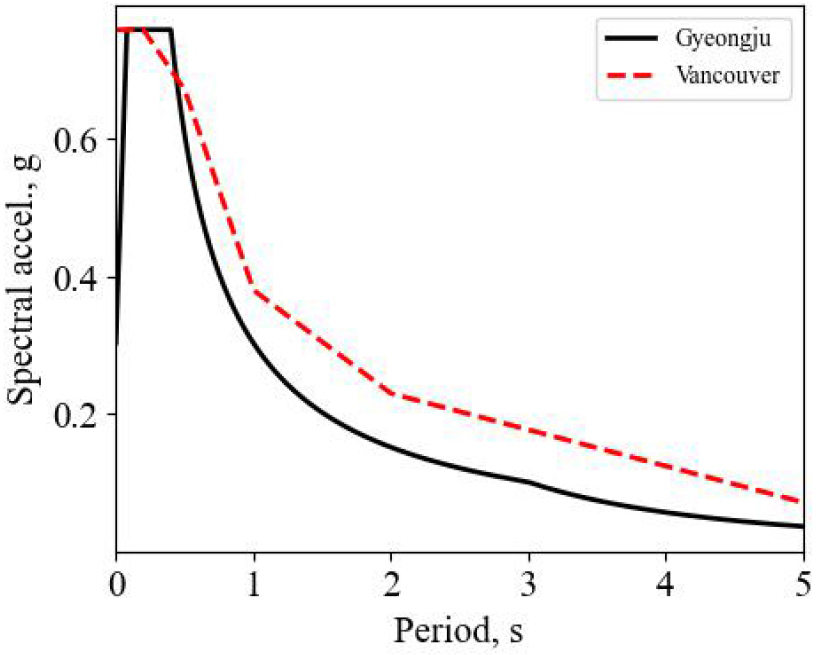
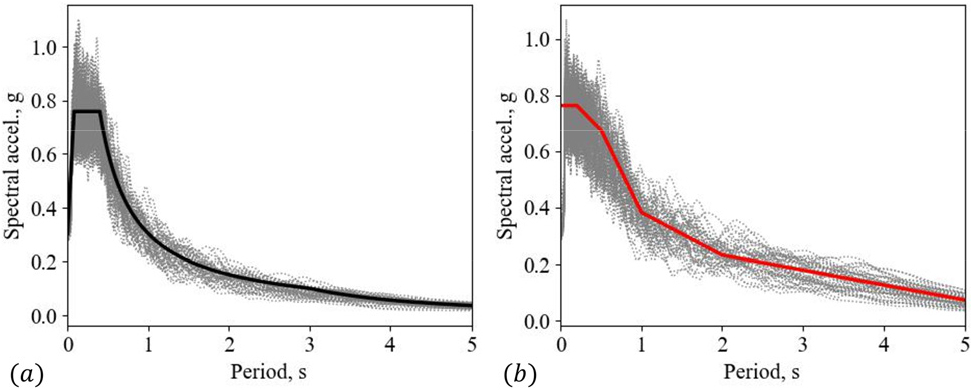
Fig. 3은 2,400년 재현주기의 한국 경주지역(I구역 특등급 구조물의 붕괴방지 성능 수준)과 2,475년 재현주기의 캐나다 밴쿠버(Vancouver, Canada) 지역의 응답스펙트럼을 도시하였다(KMOLIT, 2018; NRC, 2020). 두 지역의 상이한 지반 특성을 반영하여 경주는 S2(얕고 단단한 지반) 지반조건을, 밴쿠버는 C(매우 빽빽한 흙과 부드러운 바위로 구성) 지반조건을 가정하였다. 두 스펙트럼의 비교를 위하여 밴쿠버의 단주기 스펙트럼 값이 경주의 값과 같은 값을 같도록 밴쿠버 스펙트럼 전체에 약 0.9를 곱해 주었다. 참고로 리질리언스 해석 과정 중 얻어지는 신뢰도 곡선과 여용성 곡선의 경우 가진 강도에 대한 조건부 확률을 다루기 때문에 이와 같은 조정은 계수에 영향을 받지 않는다.

Fig. 3.

The design response spectrums of Korea and Canada

미국 서부와 마찬가지로 캐나다 서부의 기반암 깊이는 한국보다 깊기 때문에 장주기 특성을 반영하도록 설계스펙트럼이 제시된 것을 확인할 수 있다. 이에 반해 기반암 깊이가 얕은 국내의 경우 단주기 대역에서 지진의 증폭이 예상되므로 이를 반영한 내진설계용 설계응답스펙트럼이 제시되어 있다(Cho et al., 2016). 후속절에서는 응답스펙트럼 맞춤 지진동 생성기법을 기반으로 각 지역 특성을 대표할 수 있는 지진동 모음을 생성하고자 한다.

3.2 설계응답 맞춤 지진동 생성

응답스펙트럼에 상응하는 지진동 생성을 위하여 Kim 등(2021b)이 제안한 방법론을 사용하고자 한다. 제안된 방법론은 스펙트럼 표현법(Spectral representation)을 기반으로 생성할 지진동의 파워스펙트럼밀도(Power spectrum density)와 보정 파워스펙트럼밀도를 합하여 목표스펙트럼에 상응하는 지진동을 생성한다. 공식 및 생성 시 사용한 변수 설정은 Kim 등(2021b)을 따른다.

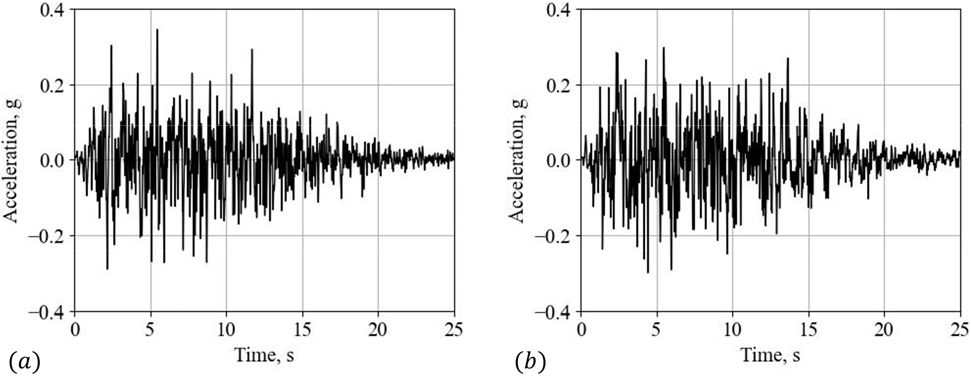
각 응답스펙트럼에 대하여 50개의 지진동을 개별적으로 생성하였다. 대표적인 지진동을 Fig. 4에 도시하였으며, 해당 지진동 샘플의 응답스펙트럼을 Fig. 5에 나타내었다. 그림에서 볼 수 있듯이 생성된 지진동은 응답스펙트럼에서 발견되는 장주기/단주기 특성을 반영하는 것을 확인할 수 있으며, 시간개형 또한 기록된 지진과 비슷하게 나타난다. 생성된 지진동 모음을 활용하여 4절에서는 시스템 신뢰성 기반 리질리언스 해석을 진행하고자 한다.

Fig. 4.

Examples of generated ground motion acceleration time history: (a) Korea, (b) Canada

Fig. 5.

Response Spectra of the generated ground motions: (a) Korea, (b) Canada

4. 시스템 신뢰성 기반 리질리언스 해석

4.1 구조시스템

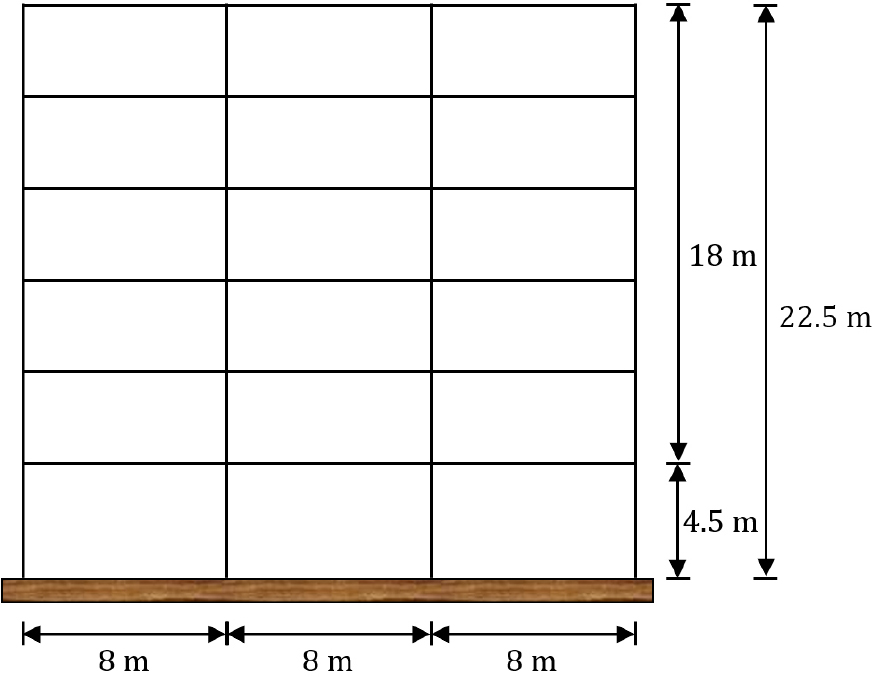
Gómez 등(2015)에서 제안한 철골 구조물을 활용하여 리질리언스 성능평가 수치해석 구조물을 활용하고자 한다(Fig. 6 참조). 구조물은 6층 모멘트 저항 골조로서 OpenSees(McKenna, 2011)로 모델링되었으며 탄성계수 200GPa, 항복강도 379MPa, 그리고 항복 후 강성비 0.3으로 재료 정보를 가정하였다. 각 부재의 단면정보는 Table 1에 정리되어 있다. 리질리언스 평가 시 유한요소해석(혹은 구조해석)에 소요되는 계산시간을 최소화하기 위하여 구조물 모델링 시 보와 기둥을 고려하였으며 패널존 및 접합부 상세 모델링은 생략하였다. Fig. 6의 우측 끝에는 P-delta 기둥을 배치하여 구조해석시 P-delta 효과를 고려하였으며, 그 외 자세한 모델링 정보는 Gómez 등(2015)과 Kim 등(2023)에 제공되어 있다. 개발한 모델의 1차, 2차, 3차 주기는 각각 2.61초, 1.05초, 0.56초이다.

Fig. 6.

Reference structure: six-story steel moment-resistance frame

4.2 부재 및 시스템 파괴모드 정의

구조물 부재의 파괴는 층간 상대변위를 기준으로 설정하였다. i층의 파괴는 층간 상대 변위각(δj)이 한계 변위각(δtr,j)을 초과하는 사건으로 정의한다(식 (7)).

이로부터 MECE 조건을 만족하는 파괴모드 집합을 다음 식 (8)과 같이 도출한다.

이때 C¯j는 j층의 변위가 파괴하지 않는 사건을 나타낸다. 한편 구조물의 전역 파괴는 구조물의 최상단 변위각(δroof)이 한계 변위각(δth,roof)을 초과하는 사건으로 정의한다(식 (9)).

기존 연구를 바탕으로 본 연구에서 δth,roof = 0.07 와 δth,j = 0.02로 설정하였다(Yi and Kim, 2023). 추가로 여용성 평가를 위해 손상부재의 유효 강성이 절반으로 감소하는 것으로 가정하였다.

4.3 신뢰도 곡선 및 여용성 곡선

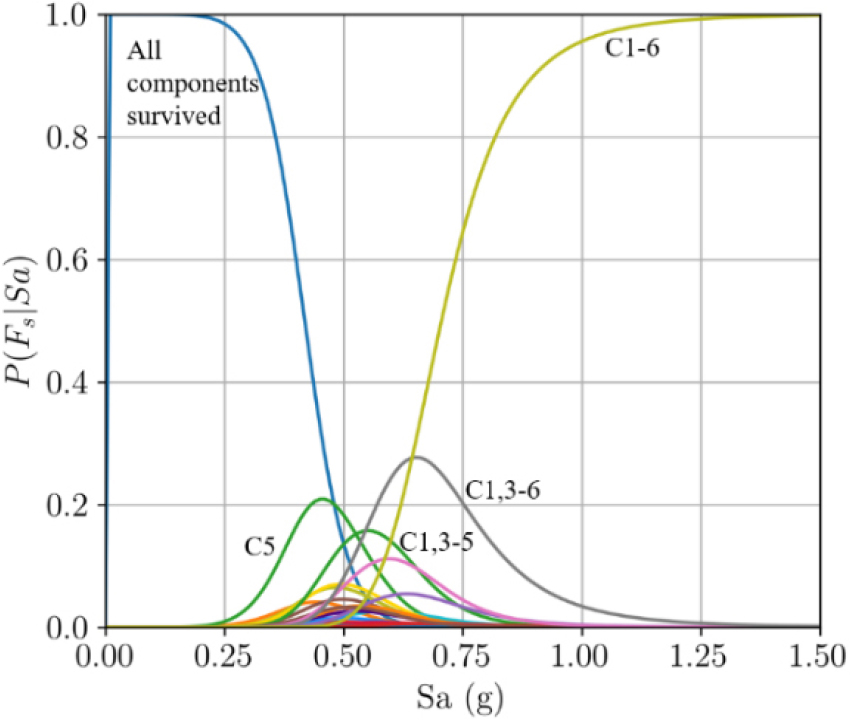
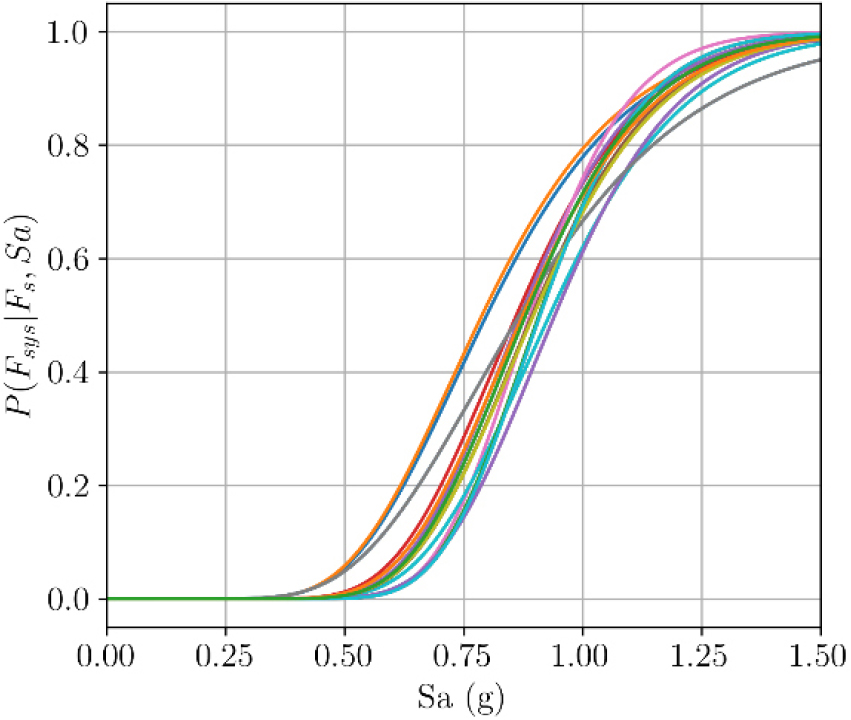
파괴 시나리오 별 신뢰성 지수의 평가를 위해 경주지역에 맞게 생성된 50개의 지진동에 증분 동적해석을 수행하였고, 총 450회의 비선형 동해석 결과로부터 파괴 모드 관측 결과와 T = 2.61초에서의 스펙트럼 가속도(Sa) 샘플을 수집하였다. 이로부터 로지스틱 회귀 기법(Yi and Kim, 2023)을 사용하여 신뢰도 곡선을 Fig. 7과 같이 도출하였다. 신뢰도 곡선은 특정 가진 강도에서 서로 다른 파괴모드가 초래될 확률을 보여주는 곡선으로 일반적으로 가진 강도가 작을 경우 모든 부재가 파괴되지 않는 사건이 지배적이며, 강도의 증가에 따라 주요 파괴모드가 변화하고 가진 강도가 매우 강할 경우 모든 부재의 파괴로 수렴하는 양상을 보인다. Fig. 7에 따르면 대상 구조물이 강-중 가진에 노출되었을 때 주요 파괴모드는 1층 파괴 (C5), 1,3,4,5 층의 동시 파괴 (C1,3-5), 그리고 1층과 3-6층의 동시 파괴 (C1,3-6) 임을 알 수 있다.

Fig. 7.

Reliability curves for Gyeongju, South Korea

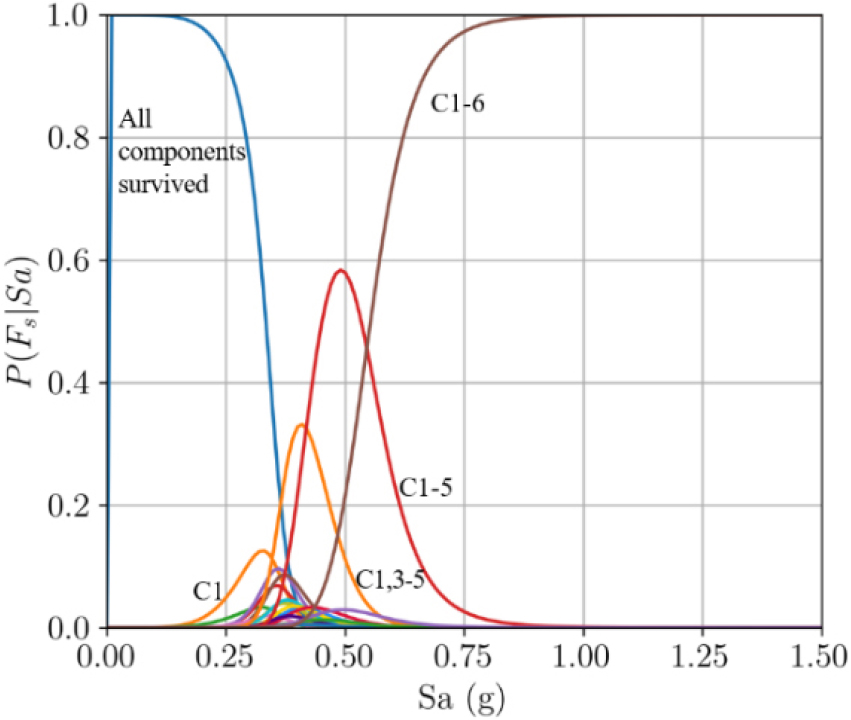
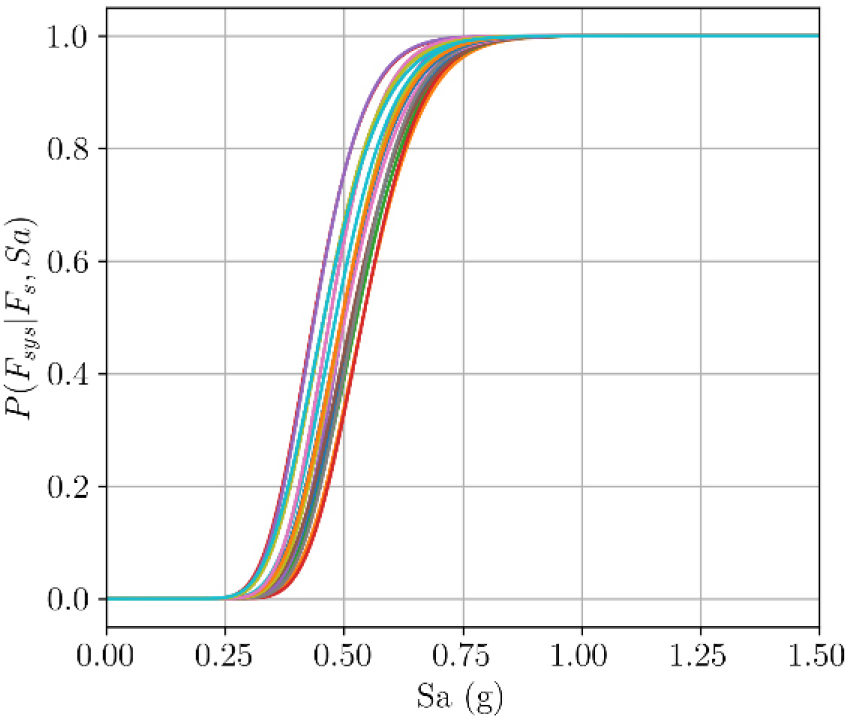
대상 구조물에 밴쿠버 지역에 대해 생성된 지진동을 적용하여 동일한 해석을 반복해 얻어진 신뢰도 곡선을 Fig. 8에 나타내었다. 전반적으로 Fig. 7과 비슷한 양상을 보이나 더 낮은 강도에서부터 구조물의 파괴가 발생하기 시작하고, 전 부재 파괴(C1-6)가 지배하기 시작하는 가진 강도 또한 낮은 것을 확인하였다. 이는 벤쿠버 지역의 응답스펙트럼이 경주 지역의 응답스펙트럼보다 천천히 감소하는 형상을 띄며 장주기에서 증폭되는 것에서부터 예측 가능하다. 즉, T=2.61초에서 더 큰 응답스펙트럼 값을 가지므로 이러한 지진특성이 구조물의 손상을 초래함을 추론할 수 있다.

Fig. 8.

Reliability curves for Vancouver, Canada

저자의 기존 연구(Yi and Kim, 2023)를 바탕으로 경주와 벤쿠버 지역에 대해 여용성 해석을 수행하였다. 신뢰도 지수 산정 시 수행한 증분 동적해석에서 관측되었던 28개와 20개의 파괴모드를 대상으로 해당 파괴모드가 시스템의 파괴로 이어질 확률을 계산하고, 이에 대한 결과를 Fig. 9와 Fig. 10에 각각 나타내었다. 여용성 곡선은 일반적인 취약도 해석 기법을 적용하되 초기조건에 구조물의 초기 손상상태를 반영하여 도출할 수 있으며, 본 연구에서는 여용성 곡선을 산출하기 위하여 IDA해석을 수행하였다. 해석 결과를 비교하였을 때 선택된 지진동의 차이가 구조물의 강건도 산정 결과에 큰 영향을 미치는 것을 확인할 수 있다. 신뢰도 곡선과 마찬가지로 벤쿠버의 경우가 손상 후 시스템의 파괴로 이어지는 사건이 더 낮은 가진강도에서 빈번히 관측되는 것을 확인할 수 있다.

Fig. 9.

Redundancy curves for Gyeongju, South Korea

Fig. 10.

Redundancy curves for Vancouver, Canada

4.4 𝛽-𝜋 도표 분석

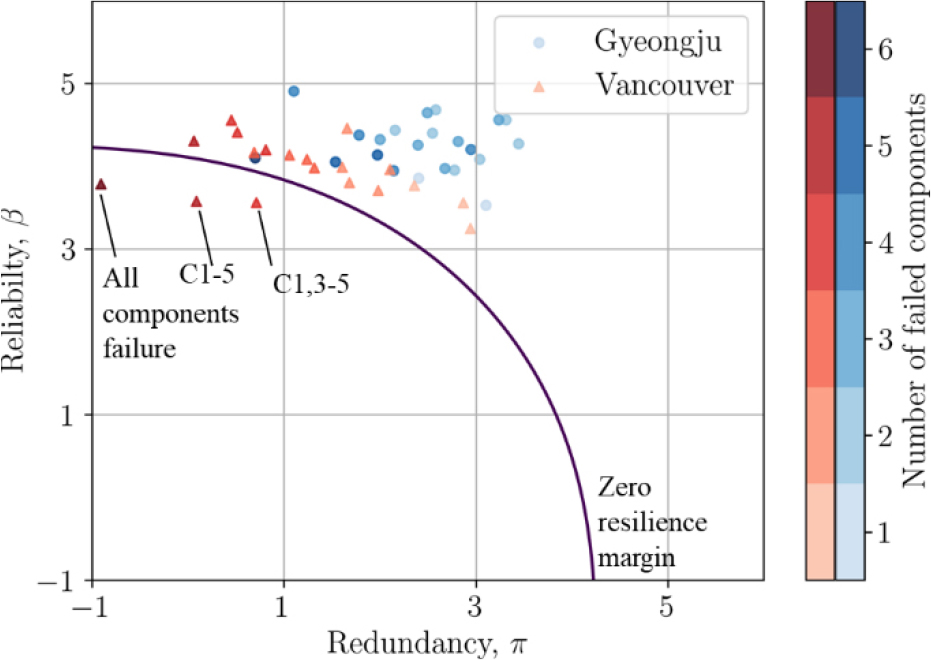
얻어진 신뢰도 곡선과 여용성 곡선을 각각 식 (4)와 (5)에 대입하여 각 파괴 시나리오 별 신뢰성 지수와 여용성 지수를 도출할 수 있으며, 그 결과를 Fig. 11에 나타내었다. 경주와 벤쿠버 지역에 위치한 구조물의 신뢰성-여용성 지수를 각각 빨강과 파란색 점으로 나타내었고, 색상의 명도를 통해 파괴 시나리오에 따라 파괴된 부재의 수를 표현하였다. 선행연구에서 파괴된 부재의 수를 대략적인 회복력 지표로 사용한 바 있다(Lim et al., 2022). 리질리언스 평과 결과와 함께 Pdm/(λH∙NF)=10-5를 가정하였을 때의 리질리언스 한계상태를 보라색 실선으로 나타내었다.

Fig. 11.

𝛽-𝜋 diagram for Gyeongju and Vancouver

같은 구조물에 대한 리질리언스 평가를 수행하였음에도 전반적으로 경주에 비해 벤쿠버 지역에서의 구조물의 여용성이 크게 낮음 확인할 수 있으며, 신뢰성 역시 비교적 낮게 나타난다. 더불어 예시로 제시한 리질리언스 한계상태를 벗어나는 시나리오는 벤쿠버 지역에서만 관찰되었다. 이는 구조부재가 파괴되었을 때 증가하는 구조물의 고유주기의 영향으로 파악된다. 즉 밴쿠버의 응답스펙트럼 곡선이 장주기 부분에서 경주의 응답스펙트럼 곡선보다 높은 값을 가지기 때문이다.

두 지역에서 공통적으로 다수의 부재가 함께 파괴되는 시나리오들(예: C1-5, C1,3-5, C1-6)이 리질리언스 지수가 가장 낮은 파괴모드에 해당하는 것으로 나타났다. 이러한 해석 결과를 통해 구조물의 국부적인 보강보다는 전반적인 보강이 유리한 것을 알 수 있다. 더불어 본 수치 해석을 통해 지역 특성을 반영하는 응답스펙트럼의 선택이 리질리언스 해석 결과에 유의미한 차이를 만들 수 있음을 확인하였다.

5. 결 론

본 연구에서는 최근 제안된 신뢰도기반 리질리언스 평가 방법론을 활용하여 지역의 지진 특성으로 발현되는 내재적 불확실성이 구조물의 리질리언스에 미치는 영향을 정량적으로 평가하였다. 이를 위해 대한민국의 경주와 캐나다의 벤쿠버를 대상 지역으로 선정하여 동일 구조물에 대해 리질리언스 평가를 수행하였다. 각 지역의 지반 특성을 반영하기 위해 먼저 설계 응답 스펙트럼을 구축하였고 이어 스펙트럼 맞춤 지진동을 생성하였다. 해석 결과, 두 지역의 신뢰도 곡선과 여용성 곡선에 유의미한 차이를 확인하였고, 이는 𝛽-𝜋 도표를 통해 확인 가능한 종합적인 성능차이로 이어졌다.

본 연구의 결론은 다른 구조물에 대해서도 유사하게 적용될 것으로 기대되나, 정량적 영향 평가를 위해서는 체계적인 수치해석을 통한 추가 연구가 필요할 것이다. 또한 향후 수치해석의 해상도를 높이기 위하여 파괴 시나리오를 층별 파괴 사건이 아닌 구조부재(기둥, 보, 접합부 등) 단위로 재정의할 필요가 있다. 이러한 경우 𝛽-𝜋 도표가 보다 실용적인 보수 및 보강 정보를 제공할 수 있을 것으로 기대된다.