1. Introduction
1.1 Background of the Soft Actuator
2. Methodology
2.1 Experimentation of K-loop and P-loop
2.2 Constitutive Model
2.3 Numerical Model
2.4 Results
3. Conclusion
1. Introduction
SMA-textile-based materials are nowadays used to create many flexible actuators for different applications. These actuators have many applications in the field of soft robotics to biomedical devices. Usually, SMA wires are wrapped in textile fibers, actuation sheets are created by knitting the SMA wires in the form of loops. When an electric potential is applied to these sheets, they actuate according to their loop arrangement. The conventional method of knitting is used to make these actuation sheets which take a lot of time and need extra expertise. To analyze the actuation of K-loop and P-loop and their combinations needs to knit them to observe the actuation. The SMA material exhibits the ability to undergo large deformation and recover its original shape. Soft actuators are cutting-edge robotics devices that use soft materials and advanced mechanics to enable accurate dynamics, and biomimetic movements with a wide range of applications.
In this paper, SMA-textile-based actuators using K-loop and P-loop are knitted to analyze the actuation, when 15.6 volts are applied to SMA wires. The numerical approach is then adopted to analyze the same experimental actuation by creating a novel method called the equivalent unit cell (EUC) model.
1.1 Background of the Soft Actuator
In recent years, robotics and automation have seen tremendous transitions due to soft actuators (Asaka and Okuzaki, 2019; Chen et al., 2023; Katzschmann et al., 2016). Traditional rigid actuators, which enable precise and controlled motion, have long formed the backbone of robotic systems (Zhang et al., 2023). The rigid actuators are composed of many parts and give limited freedom of motion (Rodrigue et al., 2016; Tang et al., 2022). Recently, SMA-textile-based actuators were created by knitting the SMA wire. Two basic types of arrangements were used P-loop and K-loop. These combinations have been used to actuate four types of patterns plain pattern, rib pattern, seed pattern, and garter pattern (Han and Ahn, 2017). Then morphing of lily-like, daffodil-like, and gamopetalous morphing flowers was actuated using the SMA-textile-based actuator. This validates the mimic behavior of knitted basic patterns which can actuate the biological movements of these flowers. This study has been expanded with a soft gripper design, which consists of a P-loop and can lift lightweight objects and the maximum deflection of material has been analyzed (Shin et al., 2023). Previously, many numerical methods were used to analyze the mechanical behavior of the material and compared with experimental studies (Khalid and Kim, 2019). Therefore, actuation analysis for different patterns and their combinations is now one of the challenges that can be solved by using the finite element analysis and compared with the experimental analysis.
This study aims to analyze the SMA-textile-based actuator deformation. The main objective of this study is to develop the EUC model using the linear constitutive equation for SMA material. As SMA material is highly nonlinear, it is difficult to create an analytical model to predict the large deformation of SMA actuators. The estimation of strain is done using the ABAQUS. For large deformation, a nonlinear geometry feature has been used in ABAQUS which gives approximately the same deformations of K-loop and P-loop. The experimental study and numerical approach have been compared for the desired deformations of K-loop and P-loop. The basic K-loop and P-loop patterns are studied with basic bending actuation. The EUC cell model shows a similar actuation as compared to the experimental study.
2. Methodology
This study aims to enhance the comprehension and predictive capabilities of SMA-textile-based actuators by employing EUC modeling. EUC modeling is a robust computational method that simulates macroscopic behavior by simplifying the representation of material microstructures into unit cells. By applying this technique to the distinctive amalgamation of SMAs and textiles, our objective is to uncover the fundamental mechanics governing actuation deformation in these innovative actuators. The focus of this research lies in modeling EUC models of K-loop and P-loop, demonstrating analogous actuation to experimentally performed knitted SMA-textile-based patterns. To mathematically estimate the actuation of K-loop and P-loop patterns, we obtained values for normal strain and shear strain, induced by an electric potential input, and soft material properties, mimicking the actuation observed in the EUC model. The linear equivalent constitutive equation was implemented in ABAQUS using the Fortran compiler. In the ABAQUS environment, bending actuators were designed, comprising two layers of soft material stacked with thin, flexible polyethylene terephthalate (PET) material. The application of opposite polarities to the two sheets induced bending actuation, resulting in significant strains in both P-loop and K-loop configurations when the geometric nonlinearity feature is considered during the analysis. Geometric nonlinearity helps to analyze the actuation of the K-loop and P-loop for the pure bending strain. For large deformation, the nonlinear geometry feature in the numerical study is beneficial to analyze the basic K-loop and P-loop bending in which sheet deformation was like the experimental deformations.
2.1 Experimentation of K-loop and P-loop
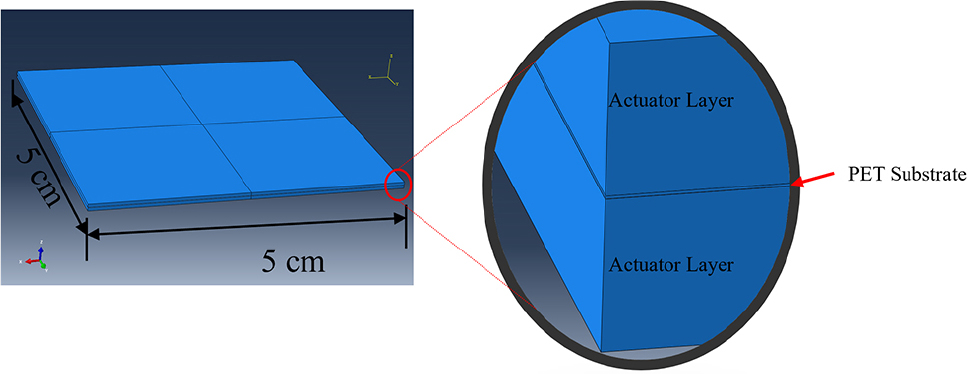
During the experimental phase, the focus was on making soft actuator sheets using a specific knitting pattern called P-loop and K-loop patterns using SMA wires, which are characterized by their plain design. These patterns were carefully chosen to enable a detailed analysis of the actuation process. The sheets were manufactured to be 5cm × 5cm in size, providing a manageable yet representative sample for testing. To create these sheets, SMA wires were employed in the knitting process. SMA wires are known for their unique ability to undergo significant deformation and recover their original shape upon exposure to certain stimuli, such as changes in temperature or applied voltage. In the experimental setup, an initial voltage of 15.6 volts was applied to the P-loop and K-loop knitted sheets. Upon applying 15.6 volts, the SMA wires heat up, causing a phase transformation from martensite to austenite. This transformation induces a shape change as the SMA attempts to return to its pre-programmed shape. This voltage changes in temperature within the SMA wires, prompting the material to undergo actuation. As the SMA wires contract, they generate significant mechanical force. This force is transmitted to the textile fibers, causing them to deform. As a result of this actuation process, the material within the P-loop patterns deformed into a bending shape. It’s worth noting that another type of knitting pattern called K-loop patterns was utilized in addition to the P-loop patterns. The K-loop and P-loop are two basic patterns used in this study. The K-loop consists of two loops in which the lower loop head (blue color) passes below the legs of the above loop. Similarly, the P-loop consists of loops arranged in such a way that the lower loop head (blue color) passes above the legs of the second loop (red color). The bending deformation is formed when an electric voltage is applied to the SMA wires externally. The K-loop and P-loop can be distinguished as shown in Fig. 1.
The K-loop and P-loop sheets are knitted by the conventional process of knitting. The SMA wire is wrapped in insulation material to avoid short-circuiting. The SMA wires and simple textile fiber are rolled together and knitted into sheets. Fig. 2 shows the pink and grey color thread. The grey wire is of SMA material which SMA material wire is wrapped in grey color insulation material. The pink color fiber is simple textile fiber which is a commercially available fiber used in the textile industry. Both SMA wires and textile fiber are wrapped with each other and knitted into K-loop and P-loop. The SMA wires are attached to an external source, which gives electric voltage and causes the SMA wires to deform.
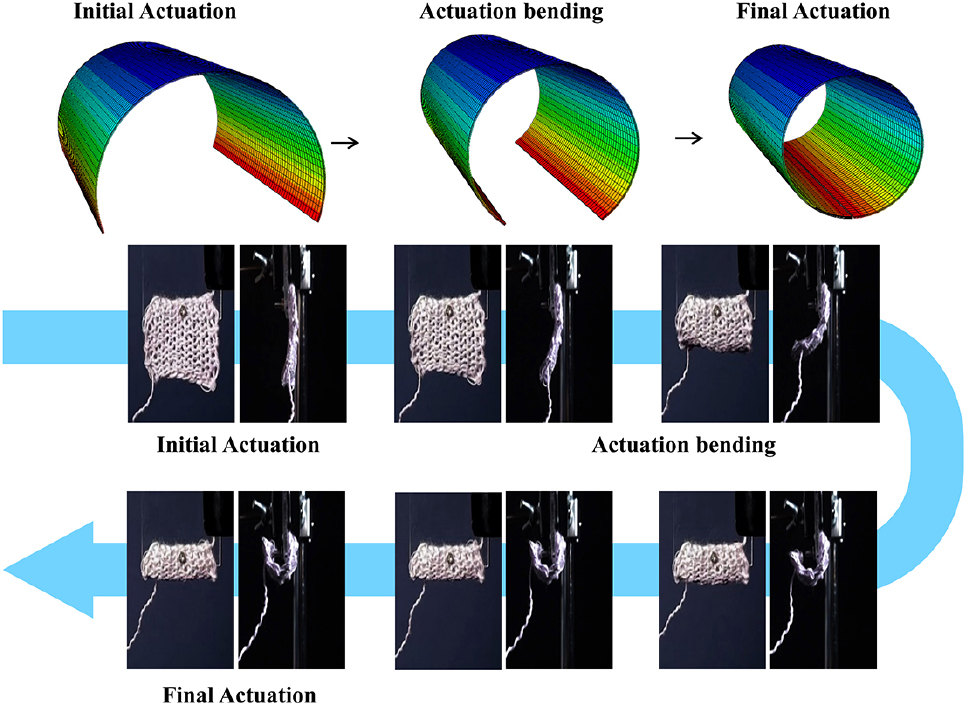
Interestingly, while the P-loop patterns exhibited downward deformation during actuation due to the bending of loop heads towards the legs, the K-loop patterns responded with upward deformation, characterized by a circular geometry, or rolling motion. This is because P-loop and K-loop are similar knitted patterns with loop heads at opposite faces of the sheets. The knitted P-loop sheets are fixed from one end and attached to the acrylic sheet. 15.6 volts are applied to the SMA wire to initialize the actuation. The experimentation results of the P-loop bending are shown in Fig. 3.
2.2 Constitutive Model
The constitutive equation below is the equivalent linear behavior of the SMA-textile actuator. This linear constitutive equation is used to analyze the behavior of SMA material which is highly non-linear. The equation is derived from the piezoelectric material with the material stiffness matrix and the strain constant (Chopra, 2002). The equivalent linear constitutive equations used for an SMA-textile-based actuator involve relating the strain tensor (εij), the electric field vector (Ej), and the stress tensor (σij). The linear constitutive equation is used to analyze the actuation of the K-loop and P-loop as shown in Equation (1). The equation has been used to conduct numerical analysis using ABAQUS.
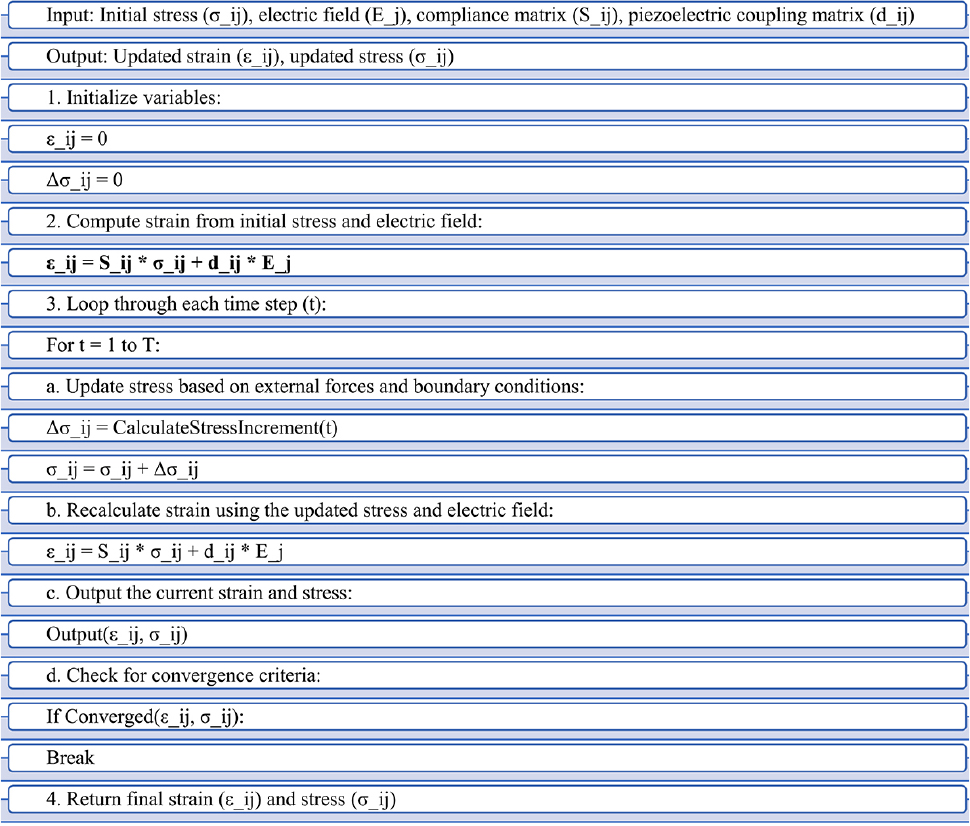
The UMAT subroutine followed for the above equation has been represented in Fig. 4. The initialization of the UMAT subroutine is started by defining the material properties and the output strain vector is determined. Equation (1) is computed iteratively where an electric field is applied and the strain values for each step are saved in the strain vector. The strain is a (6 × 1) vector in which normal and shear strain vectors are calculated. The compliance matrix (6 × 6) and strain constant (6 × 3) are the soft material properties used in this study and are given in Table 1. The brief algorithm steps are shown below in Fig. 4.
Table 1.
Equivalent Unit cell model material properties (Chopra, 2002; Ikonomidou et al., 2013).
2.3 Numerical Model
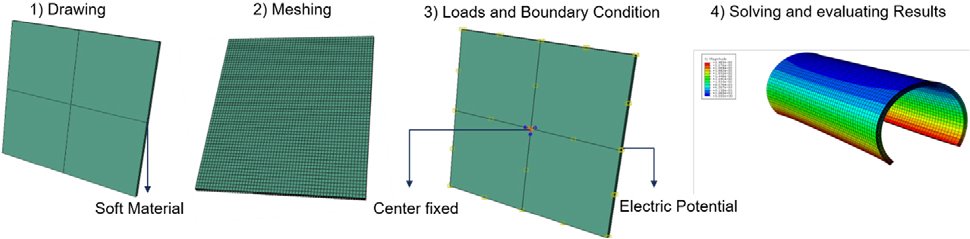
Initially, ABAQUS software was utilized for the 3D modeling of SMA-textile actuator sheets. To address significant deformation and nonlinear effects during motion, the UMAT subroutine with a linear constitutive equation (as described in Equation (1)) was employed, along with an EUC model incorporating elastic stiffness properties (Sij) and strain constants (dij) with a density of 7750kg/m3. The SMA material is highly nonlinear due to which the UMAT subroutine helps to analyze the strain of the SMA-textile-based actuator using a linear constitutive equation as given above in Equation (1). As UMAT can be used to make any material model, so EUC model, which consists of a linear stress-strain relationship constitutive equation is employed in our model using the UMAT subroutine. This helps to create a similar actuation of the soft actuator using the SMA material. The simulation model’s initial increment was adjusted to 0.01, and each analysis step lasted 1 second, with the simulation time step automatically adjusted. The electric potential applied for actuation was 15.6V, consistent with the experimental study. The actuator sheet, with the fixed center, was square in dimension. The schematic model of SMA-textile actuator sheets in Abaqus is illustrated in Fig. 5.
Pure bending in a bimorph structure occurs when a uniform electric field is applied to a symmetrically constructed bimorph, consisting of two actuation layers bonded to either side of a central PET substrate as shown in Fig. 5. The actuation layers, poled in opposite directions, experience differential strain, creating a bending moment around the neutral axis without inducing shear or twisting. Uniform material properties and proper boundary conditions, such as center fixed actuation sheets, ensure consistent bending. For numerical study, an SMA-textile-based actuator is considered for the P-loop as shown in Fig. 2. The K-loop actuates opposite to the P-loop pattern due to the opposite direction of the loop. An EUC model has been created for K-loop and P-loop. These are the estimated soft material properties used to analyze the actuation of P-loop and K-loop. The physical properties used in the UMAT subroutine in ABAQUS are shown in Table 1.
The bimorph structure designed in the ABAQUS environment assigned the soft material properties as shown in Fig. 6. The center of the bimorph sheet is fixed and opposite volts are applied on both sides. A finer mesh usually leads to more accurate results, especially when dealing with complex geometries and nonlinear materials. Given the soft material and the expected large deformations, a fine mesh was likely used to capture the detailed behavior of the bimorph under applied voltages. To induce bending, opposite voltages were applied to both sides of the bimorph. The bending of the P-loop is analyzed and compared with the experimental results.
2.4 Results
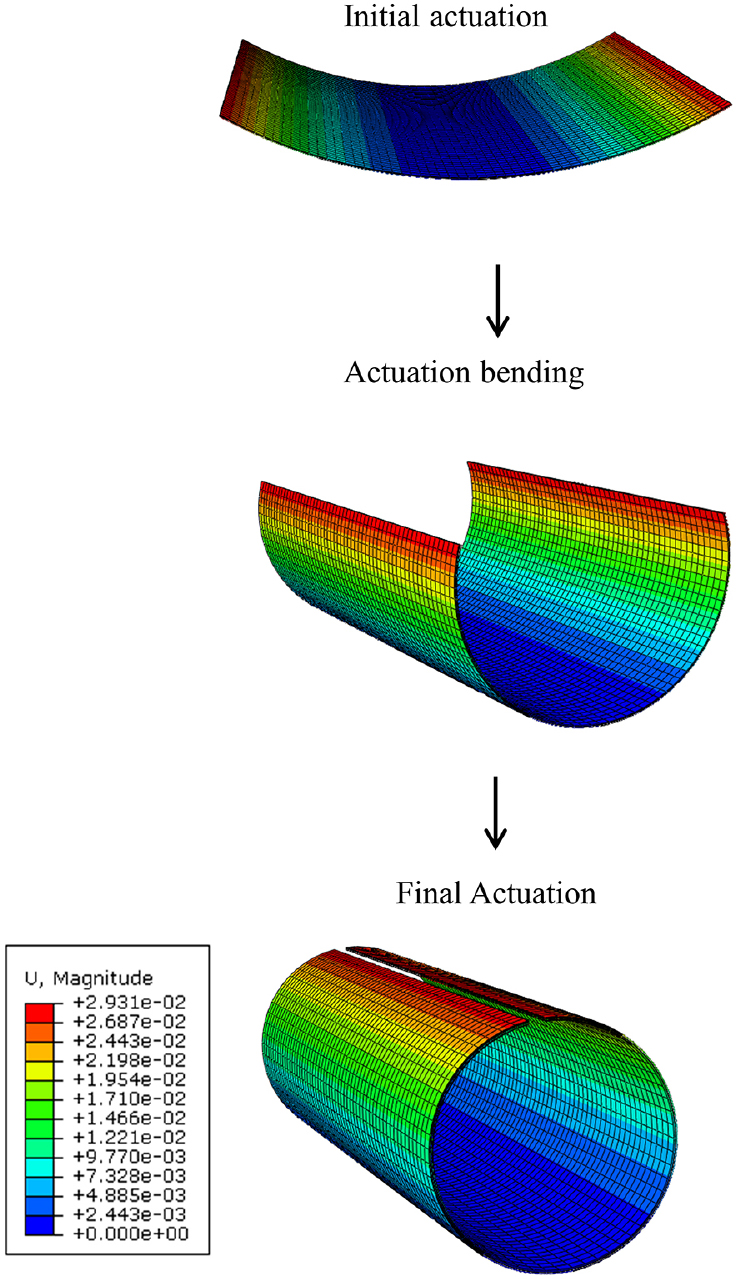
Pure bending deformation has been observed for the K-loop and P-loop. The K-loop and P-loop are knitted with SMA wires and transformed into square actuation sheets. The SMA-textile fiber also deformed into a circular shape when electric volts are applied. The deformation is due to the rolling motion of the loop geometry. Similar actuation has been gathered by using the proposed method. The K-loop and P-loop show the simple circular bending deformation due to the same electric fields applied on the bimorph layer with opposite polarity. Using the nonlinear geometry allows the edges of the EUC model to deform in circular geometry as nodes follow the rotational effect in ABAQUS, otherwise if the linear geometry were used, it shows no bending or curvature at the edges due to the no rotation at the edge’s nodes. This is because when bimorph structures, consisting of layers of piezoelectric material such as PVDF, are affixed to a flexible sheet and subjected to an applied voltage, they undergo bending owing to the piezoelectric effect. In our study, PVDF material property is used for the soft material properties. The soft material properties are assigned to the actuation layer of the bimorph structure. This phenomenon arises from the material’s ability to convert electrical energy into mechanical strain and vice versa. Asymmetrically configured with layers oriented oppositely, the structure experiences compression and tension, prompting it to bend. The direction and degree of bending can be controlled by adjusting the voltage polarity and magnitude, offering precise manipulation of mechanical motion. If the material properties are of soft material, then bending deformation can also be achieved in numerical analysis. Widely applied in actuators, sensors, and microelectromechanical systems, this bending capability enables intricate control and adaptation in various technological domains. As a result, it is observed that the P-loop and K-loop deform when different volts are applied to the actuation sheets. The EUC shows sufficient results as compared to the experimentation results. The deformation is due to bending towards the center of the actuator layer. The rolling motion of experimental results and the EUC model are seen in Fig. 7 as the loop head deforms toward its legs due to bending. The P-loop bending is shown in Fig. 7 and the K-loop bending in Fig. 8. The deformation is prominent as compared to the experimental results.
3. Conclusion
This study utilizes linear equivalent constitutive equations to predict the actuation behavior of K-loop and P-loop patterns, constructed from highly nonlinear SMA-textile-based actuators. The bending result of employing ABAQUS with the Fortran compiler, the UMAT subroutine is utilized to analyze the actuation of these soft actuators. A comparison between the actuation of the P-loop and K-loop pattern and experimental data from laboratory tests is conducted. The bimorph structure EUC model can be used to analyze any bending actuation. This EUC model has been compared with the experimental study. The actuation sheet can be used where bending is required for different applications. Further applications can be made using the SMA-textile-based wires, which can benefit medical devices and rehabilitation purposes. The validation of the EUC model developed in ABAQUS stands out as a significant outcome, offering valuable insights for design considerations and observation of actuation in various applications employing K-loop and P-loop soft actuators.
When actuated, the combination of K-loops and P-loops will create a complex deformation pattern. The K-loops provide a stabilizing effect, while the P-loops allow for more flexibility. This results in a wavy or undulating deformation across the sheet. Through this thorough investigation, the research aims to contribute substantially to the comprehension of SMA-textile-based actuators, providing a reliable analytical tool for engineers and researchers in the expanding fields of soft robotics and wearable devices. The proposed model’s consistent ability to predict deformations positions it as an asset in advancing the design and performance assessment of these innovative actuation systems. In the future, the present EUC model can be used to analyze more combinations of K-loop and P-loop. Soft actuator deformation can be easily analyzed using the EUC model based on different applications and complex movements. Further, optimization and artificial intelligence (AI) will be implemented on the EUC model to enhance and improve its strain estimation using the nonlinear geometry analysis.