Automation of Krylov Subspace Model Order Reduction for Transient Response Analysis with Multiple Loading

Jeong Sam Han; Seung Hyun Kim

doi:10.7734/COSEIK.2021.34.2.101

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 April 2021. 101-111
https://doi.org/10.7734/COSEIK.2021.34.2.101

Automation of Krylov Subspace Model Order Reduction for Transient Response Analysis with Multiple Loading

다중 하중 과도응답해석 과정에 대한 크리로프 부공간 모델차수축소법의 자동화

Jeong Sam Han¹^*

Seung Hyun Kim²

한 정삼¹^*

김 승현²

¹Professor, Department of Mechanical & Robotics Engineering, Andong National University, Andong, 36729, Korea

²Researcher, R&D Center, Haneol Solution, Seoul, 05854, Korea

¹안동대학교 기계로봇공학과 교수

²한얼솔루션 연구원

^{*Corresponding Author}

ABSTRACT

In general, several computational resources are required to perform multiple-loading transient response analyses. In this paper, we present the procedure for multiple-loading transient response analysis using the Krylov subspace model order reduction and Newmark’s time integration scheme. We utilized ANSYS MAPDL, Python, and ANSYS ACT to automate the transient response analysis procedure in the ANSYS Workbench environment and studied several engineering numerical examples to demonstrate the feasibility and efficiency of the proposed approach.

Keywords

krylov subspace

model order reduction

transient response analysis

ANSYS ACT

다중 하중 과도응답해석은 시간에 따른 작용 하중에 대한 과도응답을 확인하므로 정교한 시스템 모델링 및 조밀한 시간 간격을 가질수록 해당 시스템에 대한 동특성은 정확하게 나타내지만 이에 따른 계산 시간은 크게 증가하게 된다. 크리로프 부공간 기반 모델차수축소법은 기계 시스템이 가지는 동적 특성과 거의 동일한 결과를 나타내면서 계산 시간을 줄일 수 있기 때문에 효율적인 과도응답해석 방법이다. 본 연구에서는 다중 하중 및 이동 하중을 가지는 수치 예제를 통하여 크리로프 부공간 모델차수축소법 기반 과도응답해석을 수행하고, 이를 통해 초기 시스템 및 축소차수 모델의 정확성 및 효율성을 비교하였다. 또한, 시스템 행렬 추출, 크리로프 부공간의 기저 벡터로 구성되는 변환행렬 생성 및 축소차수모델 생성 그리고 이를 바탕으로 과도응답해석을 하는 절차를 수립하여 상용 유한요소 프로그램인 ANSYS Workbench ACT를 통해 과도응답해석 과정 자동화를 구현하여 그 효용성과 효율성을 보였다.

키워드

크리로프 부공간

모델차수축소법

과도응답해석

ANSYS ACT

MAIN

1. 서 론
2. 크리로프 부공간 기반 모델차수축소법 및 자동화
2.1 뉴마크 적분법 및 크리로프 부공간 기반 모델차수축소법을 이용한 과도응답해석
2.2 모델차수축소법 기반 과도응답해석 자동화 과정
3. 수치 예제
3.1 초소형 충격 스위치
3.2 거더 다리
4. 결 론

1. 서 론

4차 산업혁명의 도래와 디지털 트윈(digital twin)에 대한 주목 및 발전으로 CAE(computer-aided engineering) 역시 새로운 관심을 받고 있다(Nam et al., 2020; Oh et al., 2020; Shin and Park, 2020). 특히, 여러 산업 분야에서 시스템의 동적 거동을 파악하기 위하여 과도응답해석을 통한 분석이 많이 이용되고 있다. 하지만 과도응답해석의 경우, 시간에 따라 작용하는 하중에 대한 응답을 확인하기 때문에 정교한 시스템 모델링 및 조밀한 시간 간격을 가질수록 해당 시스템에 대한 동특성은 정확하게 나타낼 수 있지만 이에 따른 계산 시간은 크게 증가하게 된다. 따라서, 이러한 경우에는 모델차수축소법(model order reduction method, MOR)을 통해 과도응답해석을 수행하여 초기 시스템(full order model, FOM)에 대한 시스템 특성을 유지하면서도 효율적인 계산을 진행할 수 있다(Han, 2010; Amin and Krisnamoorty, 2012; Han, 2013; Han et al., 2016).

크리로프 부공간(Krylov subspace)에 FOM을 투영하여 축소차수모델(reduced order model, ROM)을 생성하는 크리로프 부공간 기반 모델차수축소법은 1980년대 초부터 연구가 시작되어 많은 연구가 꾸준히 진행되고 있다. 연구 초기인 1980~1990년대에는 주로 관련 이론을 정리 및 증명하는 연구 등이 진행되었으며(Saad, 1983; Su and Craig, 1991), 2000년 대에는 높은 자유도를 가지는 기계(Han, 2007) 또는 전기(Freund, 2000) 분야의 시스템, 그리고 음향해석(Goo et al., 2012), 주파수해석(Won and Han, 2014), 다물체해석(Kim and Yoon, 2016), 지진해석(Han, 2020) 등 여러 시스템에 크리로프 부공간 기반 MOR을 적용한 연구가 수행되었다.

이외에 CMS(component mode synthesis) 기법은 모델축소를 위해 모드중첩법에 기반한 모드 형상, 고유주파수를 사용하기 때문에 기계공학(특히 진동) 분야 연구자들에게 친숙한 방법이다. 이에 더하여 부구조법(sub-structuring)을 기본으로 한다는 점에서 여러 구조가 조립된 복잡한 구조체의 모델링에 편리성과 효율적인 해석시간을 추구할 수 있다는 장점이 있다. 다만, 선형 진동 문제만을 다룰 수 있다는 한계가 있어 최근 비선형 모델의 축소를 위해서 데이터에 기반한 POD(proper orthogonal decomposition) 기법이 널리 사용되고 있으며, 크리로프 부공간 기법에 비해 해의 수렴속도가 느리다는 단점이 있다(Kim et al., 2017). POD 기법(Kerschen et al., 2005)은 초기 시스템의 과도해석의 스냅샷(snapshot)의 특이값분해(sigular value decomposition)로 변환행렬을 계산하므로 초기 시스템의 과도해석이 필요한 반면에 크리로프 부공간 기법은 초기 시스템 행렬만으로 변환행렬을 생성할 수 있는 장점이 있다. 따라서, 시스템의 비선형성 및 최종 축소모델을 생성하는데 필요한 소요시간 및 적용 목적 등에 따라서 가장 합리적인 모델축소기법을 선택할 수가 있다.

한편, 기존의 해석 방식에서는 시스템의 조건이 바뀌면 그에 따라 같은 해석 절차라 할지라도 그 과정을 다시 반복하여 진행해야 한다. 따라서, 최근에는 이러한 반복적인 작업을 효과적으로 수행하기 위하여 유한요소해석 모델링과 해석과정 자동화에 대한 연구가 활발히 진행되고 있다(Moon et al., 2018; Kim, 2018; Seo et al., 2020).

이에 본 논문에서는 크리로프 부공간 기반 모델차수축소법을 이용한 다중 하중 과도응답해석 기법을 설명하고, 이를 적용한 수치 예제를 통해 초기 시스템(FOM) 및 축소차수모델(ROM)의 과도응답을 비교하여 ROM의 정확성 및 효율성을 나타내고자 한다. 이를 바탕으로 상용 유한요소프로그램인 ANSYS Workbench(ANSYS, 2018) 환경에서 사용자의 입력을 최소화하여 다중 하중 과도응답해석을 수행하는 크리로프 부공간 기반 모델차수축소법을 이용하는 과도응답해석 자동화 ACT (Application Customization Toolkit)를 제안하고자 한다.

2. 크리로프 부공간 기반 모델차수축소법 및 자동화

2.1 뉴마크 적분법 및 크리로프 부공간 기반 모델차수축소법을 이용한 과도응답해석

일반적으로 유한요소법에 의한 감쇠 기계 시스템의 행렬방정식은 다음과 같이 시간에 대한 이차 상미분 방정식으로 표현된다(Han, 2020).

(1)

M \ddot{x} (t) + C \dot{x} (t) + K x (t) = F u (t) y (t) = L x (t)

여기서 M, C, K∊ℜN×N는 각각 시스템에 대한 질량, 감쇠, 강성 행렬이다. 그리고 F∊ℜ^N×q, u(t)∊ℜ^q, x(t)∊ℜ^N는 각각 하중 행렬 및 하중입력 벡터, 그리고 상태변수 벡터이다. 또한 y∊ℜ^p 및 L∊ℜ^p×N은 출력 벡터 및 출력측정 행렬이다. 출력 벡터는 출력측정 행렬과 상태변수 벡터의 선형 결합으로 나타나며, 이를 통해 관심 위치에서의 응답 결과를 확인할 수 있다(Han, 2010). 그리고 비례 감쇠(proportional damping)인 경우, 감쇠 행렬 C는 다음 식과 같이 질량 및 강성 행렬의 선형 결합으로 나타낼 수 있다.

(2)

C = α M + β K

이때 $α$ 및 $β$ 는 각각 질량감쇠계수 및 강성감쇠계수를 의미한다(Qu, 2004).

식 (1)의 운동방정식에 대한 과도응답을 구하기 위하여 직접적분법 중 암시적 시간 적분 방법인 뉴마크 적분법을 사용한다(Han, 2013). 시간 $t + ∆ t$ 에서 운동방정식은 다음과 같이 나타낼 수 있다.

(3)

M {\ddot{x}}_{n + 1} + C {\dot{x}}_{n + 1} + K x_{n + 1} = F_{n + 1}

여기서, ${\ddot{x}}_{n + 1}$ , ${\dot{x}}_{n + 1}$ , $x_{n + 1}$ 그리고 F_n+1은 각각 시간 $t + ∆ t$ 에서의 가속도, 속도, 변위 그리고 하중을 의미한다. 뉴마크 적분법은 현재 시간 t와 다음 시간 $t + ∆ t$ 에서 변위와 속도를 다음과 같이 가정한다.

(4)

x_{n + 1} = x_{n} + {\dot{x}}_{n} ∆ t + [(\frac{1}{2} - α) {\ddot{x}}_{n} + α {\ddot{x}}_{n + 1}] ∆ t^{2}

(5)

{\dot{x}}_{n + 1} = {\dot{x}}_{n} + [(1 - δ) {\ddot{x}}_{n} + δ {\ddot{x}}_{n + 1}] ∆ t

이때, $α$ 및 $δ$ 는 뉴마크 적분상수이며 시간적분의 정확도 및 수치 안정성을 결정한다. 뉴마크 적분법은 적분상수 $α$ 및 $δ$ 가 다음의 조건을 만족할 때 무조건적으로 안정하다.

(6)

α \geq \frac{1}{4} {(\frac{1}{2} + δ)}^{2} a n d δ \geq \frac{1}{2}

본 연구에서 적분상수 $α$ 및 $δ$ 는 각각 0.25 및 0.5로 하였고, 위 식 (4)와 (5)는 계수 $a_{0} = \frac{1}{α ∆ t^{2}}$ , $a_{1} = \frac{δ}{α ∆ t}$ , $a_{2} = \frac{1}{α ∆ t}$ , $a_{3} = (\frac{1}{2 α} - 1)$ , $a_{4} = (\frac{δ}{α} - 1)$ , $a_{5} = \frac{∆ t}{2} (\frac{δ}{α} - 2)$ , $a_{6} = ∆ t (1 - δ)$ 및 $a_{7} = δ ∆ t$ 를 이용하여 다음 시간 $t + ∆ t$ 의 가속도 및 속도에 대한 식으로 다음과 같이 재배열하여 나타낼 수 있다.

(7)

{\ddot{x}}_{n + 1} = a_{0} (x_{n + 1} - x_{n}) - a_{2} {\dot{x}}_{n} - a_{3} {\ddot{x}}_{n}

(8)

{\dot{x}}_{n + 1} = a_{1} (x_{n + 1} - x_{n}) - a_{4} {\dot{x}}_{n} - a_{5} {\ddot{x}}_{n}

위의 식 (7) 및 (8)을 시스템의 운동방정식인 식 (3)에 대입하여 정리하면 하나의 미지수인 변위 $x_{n + 1}$ 로 표현되는 다음 식으로 나타낼 수 있다.

(9)

(a_{0} M + a_{1} C + K) x_{n + 1} = F_{n + 1} + M (a_{0} x_{n} + a_{2} {\dot{x}}_{n} + a_{3} {\ddot{x}}_{n}) + C (a_{1} x_{n} + a_{4} \dot{x_{n}} + a_{5} {\ddot{x}}_{n})

정리된 뉴마크 적분 연산 과정에 따라서 다음 시간 $t + ∆ t$ 의 변위를 계산할 수 있다.

크리로프 부공간 기반 모델차수축소법은 고차원의 초기 시스템에 대한 상미분 식 (방정식 (1)에서 상태변수 벡터 x(t)를 식 (10)과 같이 V∊ℜ^N×n라는 저차원 부공간의 기저 벡터로 구성되는 변환행렬 V를 통해 이 변환행렬에 관계되는 새로운 저차원 상태변수 벡터 z(t)로 축소할 수 있다. 이때, 변환행렬은 시스템에 작용하는 하중까지 고려되는 크리로프 벡터를 사용하여 기저 벡터를 구성된다.

(10)

x (t) ≅ V z (t) w h e r e z (t) \in R^{n}

이제 상태변수 벡터는 저차원 부공간 변환행렬의 각 열벡터의 선형 결합으로 표현되며, 초기 시스템을 그 부공간에 투영하면 다음과 같은 축소 시스템을 얻을 수 있다.

(11)

M_{r} \ddot{z} (t) + C_{r} \dot{z} (t) + K_{r} z (t) = F_{r} u (t) y (t) = L_{r} z (t)

축소된 시스템 행렬은 각각 M_r=V^TMV, C_r=V^TCV, K_r=V^TKV, F_r=V^TF이며 축소된 출력측정 행렬은 L_r=LV이다. 축소 감쇠행렬은 앞서 비례 감쇠에서 나타낸 것과 같이 C_r= $α$ M_r+ $β$ K_r로 표현할 수 있다. 그리고 축소 시스템을 뉴마크 적분법에 적용하면 다음과 같다.

(12)

(a_{0} M_{r} + a_{1} C_{r} + K_{r}) z_{n + 1} = V^{T} F_{n + 1} + M_{r} (a_{0} z_{n} + a_{2} {\dot{z}}_{n} + a_{3} {\ddot{z}}_{n}) + C_{r} (a_{1} z_{n} + a_{4} \dot{z_{n}} + a_{5} {\ddot{z}}_{n})

초기 시스템과 축소 시스템 사이의 정확도는 변환행렬 V의 열벡터의 수에 의해 결정된다. 초기 조건이 모두 0일 때, 식 (1)을 라플라스 변환하여 비감쇠 시스템에 대한 전달 함수를 입력 벡터와 출력 벡터의 관계로 나타난다. 이를 급수 전개를 통하여 다음의 식과 같이 계수를 K^-1M과 K^-1F의 곱으로 표현할 수 있다. 이때, 계수 $m_{i}$ 를 전달 함수의 모멘트(moment)라고 한다.

(13)

H (s) = \frac{Y (s)}{U (s)} = L (M s^{2} + K)^{- 1} F = \sum_{i = 0}^{\infty} (- 1)^{i `} L (K^{- 1} M)^{i} (K^{- 1} F) s^{2 i} = \sum_{i = 0}^{\infty} m_{i} s^{2 i}

축소 시스템에 대한 전달 함수도 위와 동일한 방법으로 구하면 다음과 같이 표현된다.

(14)

\overset{⏜}{H} (s) = \sum_{i = 0}^{\infty} (- 1)^{i `} L_{r} (K_{r}^{- 1} M_{r})^{i} (K_{r}^{- 1} F_{r}) s^{2 i} = \sum_{i = 0}^{\infty} {\hat{m}}_{i} s^{2 i}

여기서, ${\overset{⏜}{m}}_{i}$ 는 축소 시스템의 전달 함수의 모멘트를 의미하며, $m_{i}$ 및 ${\overset{⏜}{m}}_{i}$ 의 관계를 통하여 초기 시스템과 축소 시스템의 유사도를 나타낸다. 식 (10)의 변환행렬이 아래 식 (15)에 의해 계산되는 n개의 크리로프 부공간의 기저 벡터로 구성되면, 초기 시스템과 축소 시스템은 초기 n개의 모멘트까지 일치함이 알려져 있다(Freund, 2000; Han, 2007).

크리로프 부공간은 전달 함수의 모멘트에서 표현된 질량 행렬, 강성행렬 및 하중 벡터로 구성되며, 아래 식과 같이 변환행렬이 생성된다.

(15a)

Κ_{n} (K^{- 1} M, K^{- 1} F) = s p a n \{K^{- 1} F, (K^{- 1} M) K^{- 1} F, \dots, (K^{- 1} M)^{n - 1} K^{- 1} F\}

(15b)

c o l s p a n \{V\} = K_{n} (K^{- 1} M, K^{- 1} F)

즉, 크리로프 벡터는 다음 점화식(recurrence formula)으로 생성된다.

(16)

r_{1} = K^{- 1} F r_{i + 1} = K^{- 1} M r_{i}

각 크리로프 벡터는 물리적으로 정적 변형 모드(static mode)로 간주할 수 있다. 첫 벡터 r₁=K^-1F는 하중벡터 F에 대한 시스템의 정적 변형이고, 이후에 벡터 r_i+1는 변형 r_i와 연관된 관성력(inertia force)로 인하여 발생하는 정적 변형으로 해석될 수 있다(Su and Craig, 1991).

크리로프 부공간을 구성하는 기저 벡터는 정규 직교한 기저 벡터를 만드는 아놀디 과정(Freund, 2000; Han, 2007)을 통해 가장 효율적인 방법으로 계산된다. 시스템에 작용하는 하중이 각 방향 별로 조합된 하중벡터일 경우 변환행렬은 다음과 같이 구성된다(Han, 2020).

(17a)

Κ_{n} (K^{- 1} M; K^{- 1} F_{x}, K^{- 1} F_{y}, K^{- 1} F_{z}) = (K^{- 1} F_{x}, K^{- 1} F_{y}, K^{- 1} F_{z}, (K^{- 1} M) K^{- 1} F_{x}, (K^{- 1} M) K^{- 1} F_{y}, (K^{- 1} M) K^{- 1} F_{z}, \dots, (K^{- 1} M)^{(n - 1)} K^{- 1} F_{x}, (K^{- 1} M)^{(n - 1)} K^{- 1} F_{y}, (K^{- 1} M)^{(n - 1)} K^{- 1} F_{z})

(17b)

c o l s p a n \{V\} = K_{n} (K^{- 1} M; K^{- 1} F_{x}, K^{- 1} F_{y}, K^{- 1} F_{z})

세 방향의 하중을 모두 고려할 때, 크리로프 부공간의 기저 벡터로 구성된 변환행렬은 x축, y축 및 z축의 방향에 대한 하중을 포함하므로 3의 배수로 구성된다(Han et al., 2016). 아놀디 과정을 통해 최종적으로 계산된 기저 열벡터로 구성된 변환행렬은 정규 직교하기 때문에 V^TV를 계산하면 단위행렬을 가진다(Han, 2020).

2.2 모델차수축소법 기반 과도응답해석 자동화 과정

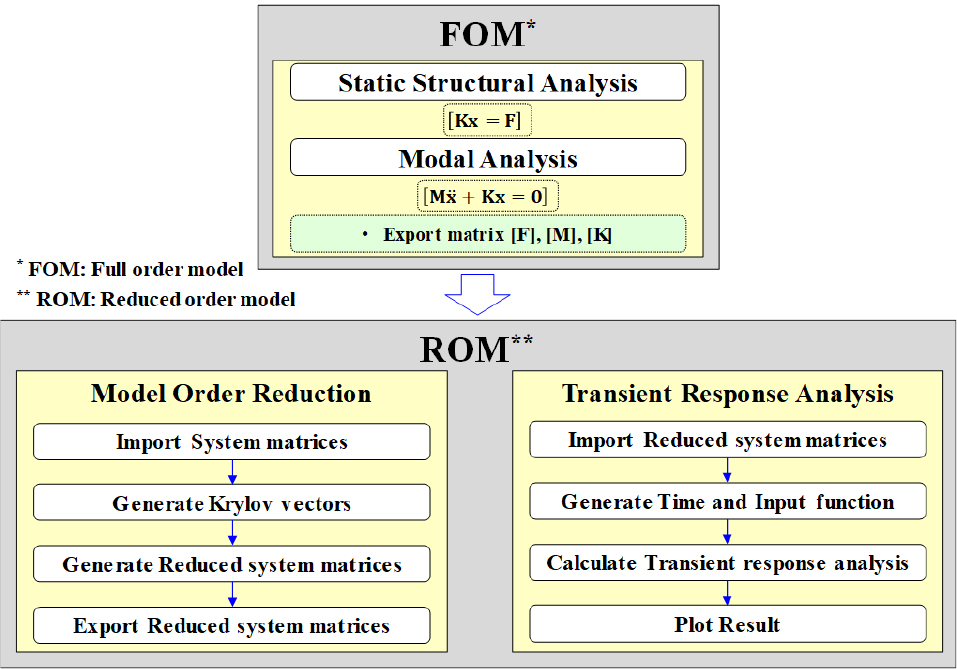
크리로프 부공간 기반 축소차수모델 생성 및 생성된 축소차수모델의 과도응답해석에 대한 진행 과정절차는 Fig. 1에 나타내었다. 먼저, ANSYS에서 정적 구조해석 및 고유진동해석을 통해 시스템 행렬인 M, K, F를 추출한 후 ANSYS MAPDL에서 아놀디 과정으로 초기 시스템의 축소차수모델을 생성한다. 그리고 축소된 시스템 행렬을 이용하여 Python(Python, 2018)에서 뉴마크 적분법 기반의 과도응답해석을 수행하고 결과를 출력한다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F1.jpg

Fig. 1

Transient response analysis procedure based on the model order reduction method

본 논문에서는 이러한 축소모델기반 과도응답해석의 해석 과정을 ANSYS Workbench ACT(ANSYS, 2018)를 통해 자동화 과정으로 구현하였다. ANSYS ACT는 XML(Extensible Markup Language) 및 IronPyhon으로 구성된다. XML파일은 Python함수를 호출하기 위한 사용자 정의 함수 또는 GUI(Graphical User Interface) 등을 정의하고, Python을 통해 XML에서 사용자가 정의한 함수 또는 GUI에 대한 응답을 구현하는 함수를 생성한다.

과도응답해석 자동화 과정은 먼저 ANSYS Workbench에서 유한요소모델링 및 구속조건 정의 후 진행된다. Fig. 2에는 자동화 과정을 통한 축소차수모델 생성 및 과도응답해석을 나타내었다. MOR Process는 프로그램 상단에 정의된 첫 번째 GUI를 눌러 시작되며 첫 번째 과정으로 생성된 유한요소모델에서 하중이 부여되는 위치를 정의한다. 하중 위치는 첫 번째 노란 칸을 활성화한 후 해당 모델의 절점 위치를 마우스로 선택하여 정의할 수 있다. 정의된 절점은 바로 아래 빨간 칸에서 절점 번호를 반환하여 해당 번호를 확인할 수 있고, 또한 이 번호는 나중에 하중 벡터를 추출할 때 해당 위치의 번호가 선택한 순서대로 적용되어 하중 벡터 데이터가 저장된다. 그 아래 세 개의 선택사항이 있는데 이는 정의된 절점에서 x, y, z 방향별 하중벡터의 포함 여부를 결정하는 것이다. 이를 통해 각 방향별로 조합된 하중이 부여된 시스템을 생성할 수 있다. 두 번째 과정은 그 아래에 있는 노란 칸을 활성화한 후 출력측정 절점 위치를 정의하는 것이다. 이 또한 바로 아래 빨간 칸에서 절점 번호를 확인할 수 있으며 출력측정 행렬을 생성할 때 선택된 순서대로 적용되어 데이터가 저장된다. 이 설정들을 마치면 시스템 행렬을 추출할 수 있으며 해당 설정이 하나라도 정의되지 않으면 다음 단계가 진행되지 않는다. 시스템 행렬의 추출은 노란 칸에서 No를 Yes로 변경함으로 Workbench Project창에서 MAPDL이 생성되고 시스템 행렬이 추출된다. 추출 완료 후, 축소모델의 차수 정의 및 질량감쇠계수 D_alpha와 강성감쇠계수 D_beta를 정의하고, 그 아래 노란 칸에 No를 Yes로 바꾸면 Workbench Project창에서 생성된 MAPDL을 통해 축소차수모델이 생성된다. 현재 진행 중인 해석이 저장된 폴더 안에 user_files 폴더가 있으며, 축소차수모델은 user_files폴더 아래에 생성되는 MOR이라는 폴더에 저장된다. 구체적으로, 예를 들어 축소차수가 n=4라면 n4라는 이름의 폴더에 저장된다. 마지막으로 축소차수모델을 이용하여 과도응답해석을 수행하기 위하여 사용자는 자신의 문제에 대한 입력 벡터 및 시간 데이터를 Excel 등을 이용하여 테이블로 데이터를 생성한 후, 축소차수모델이 있는 폴더에 해당 데이터를 저장한다. 그 후 MOR Process 프로그램 상단에 정의된 두 번째 GUI가 클릭되면 정의된 출력측정 절점에서 크리로프 부공간 모델차수축소법 기반 과도응답해석의 결과 데이터 및 그래프가 출력된다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F2.jpg

Fig. 2

The automation procedure of the transient response analysis implemented on ANSYS workbench

3. 수치 예제

3.1 초소형 충격 스위치

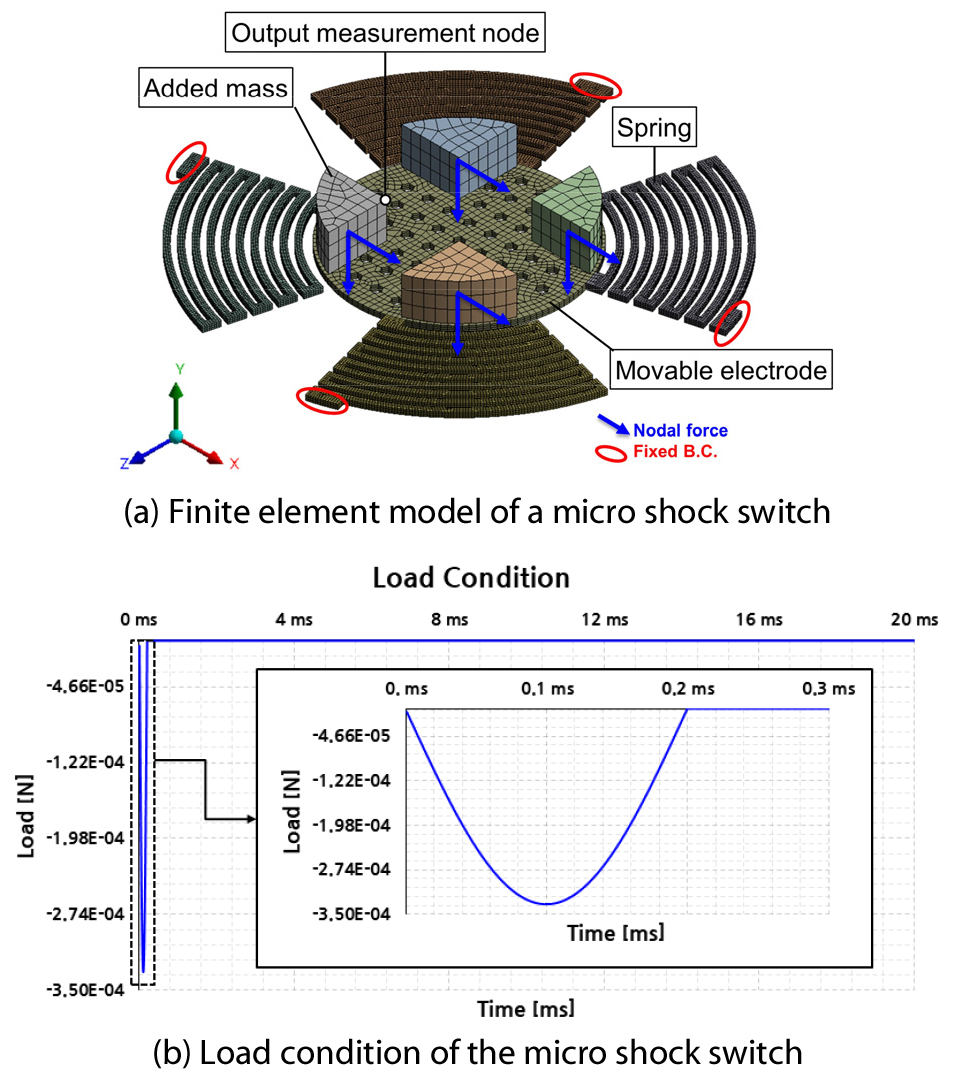
첫 번째 수치예제로 3.0×2.2×0.55mm³의 크기를 가지는 초소형 충격 스위치를 고려하였다(Park et al., 2018). 이 초소형 충격 스위치는 4개의 스프링과 가동전극 그리고 4개의 추가 질량체로 구성되며, 충격이 발생할 때 가동전극 및 추가 질량체가 고정전극에 접촉하여 신호가 발생하는 물리 소자이다(Fig. 3(a) 참고).

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F3.jpg

Fig. 3

Finite element model of a micro shock switch and an analysis condition

ANSYS Mechanical을 통해 유한요소모델을 생성하였으며 SOLID186요소를 이용해 솔리드 요소 35,634개 및 절점 217,802개가 생성되었다. 경계조건으로 가동전극과 연결된 스프링의 끝단 면에서 모든 방향에 대한 자유도를 구속하였다. 해당 모델의 재질은 니켈이며, 사용된 물성치는 탄성계수 E=200GPa, 밀도 ρ=8,908kg/m³, 포아송 비 ν=0.31이다. 이 시스템의 전체 자유도 수(N)는 648,009개이며, 이는 유한요소모델에서 경계조건에 의해 구속된 자유도를 제외한 자유도 수를 의미한다.

하중조건으로 추가 질량체의 무게 중심 절점에 최대 하중이 800G인 반주기의 정현파(half sine shock)를 0.2ms동안 부여하였고, 총 해석 시간은 20ms까지 진행하였다. 이때, 하중은 무게 중심 절점에 x축 및 y축 방향으로 동시에 가해진다고 가정하였다. 비례 감쇠는 감쇠비 ξ=0.02에 대하여 질량감쇠계수 $α$ =0 및 강성감쇠계수 $β$ =1.975×10^-6로 고려하였다. 수치 계산은 3.40GHz Intel(R) Core(TM) i5-4670 CPU 및 16GB의 메모리 용량을 가지는 전산 시스템을 통해 진행하였다.

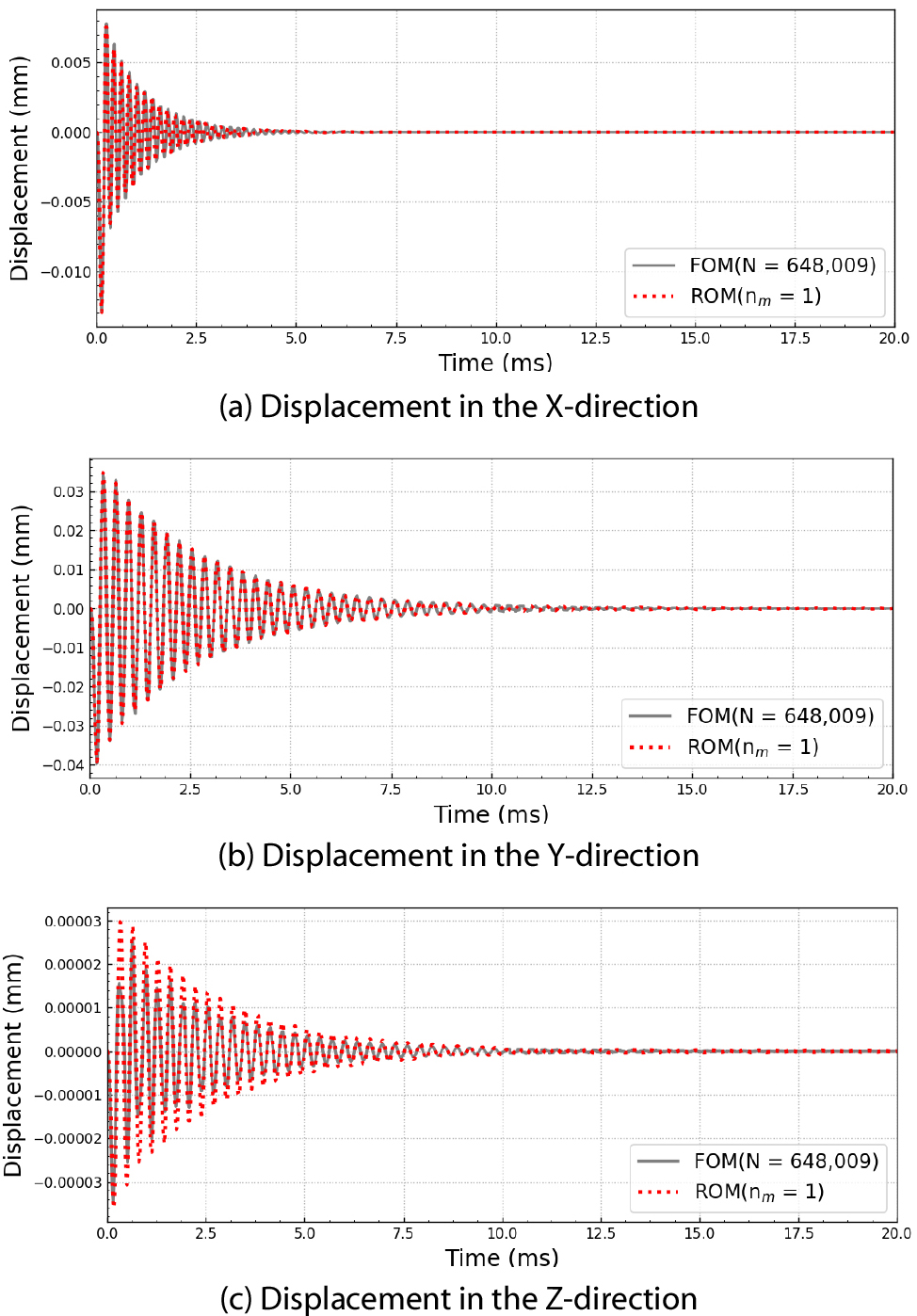
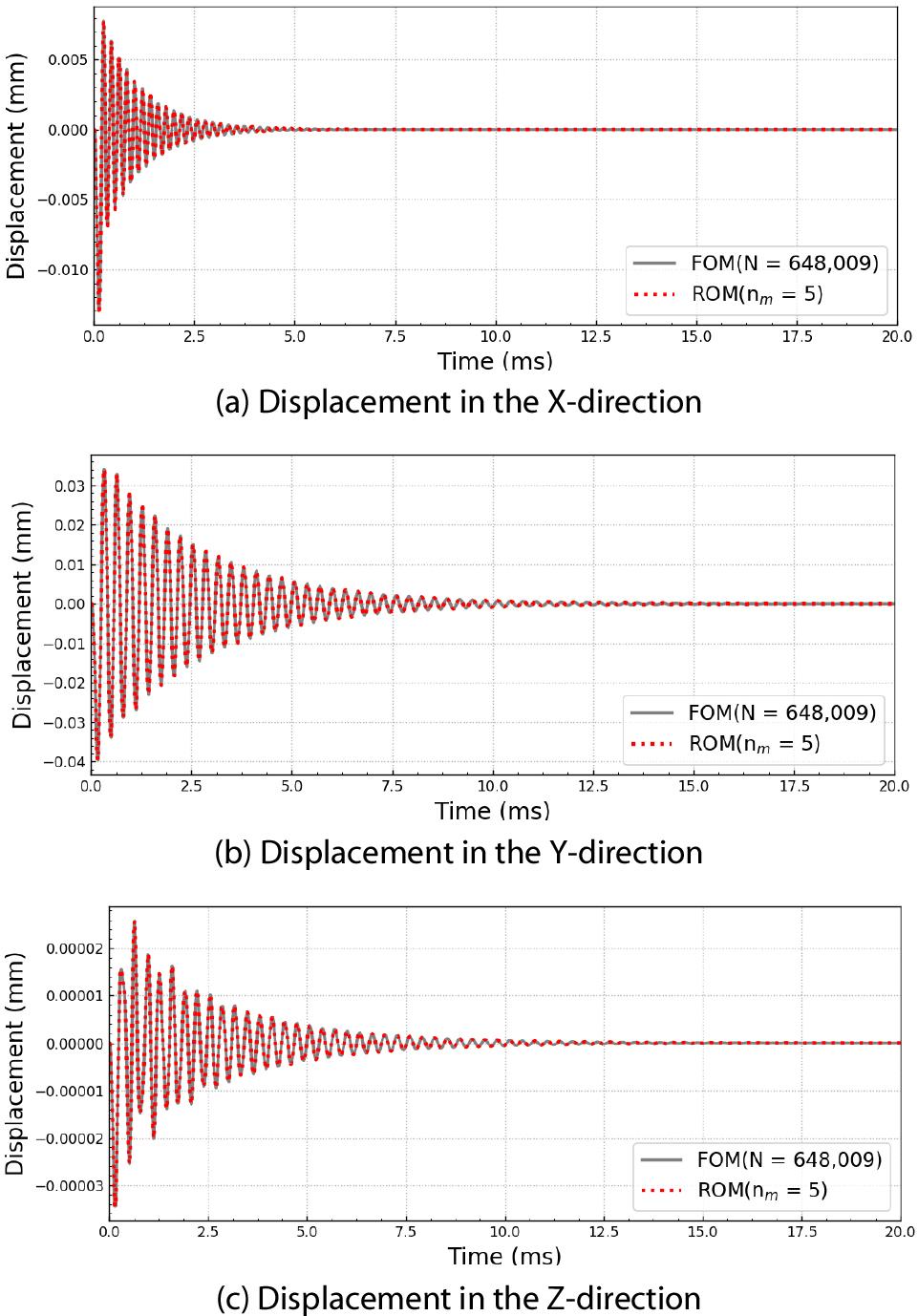
초기 및 축소 시스템의 결과 비교를 위하여 FOM과 1 및 5차 ROM에 대하여 Fig. 3(a)에 표시된 추가 질량체 상단에 위치한 Output 절점에서 시간에 따른 각 방향별 과도응답 결과를 확인하였다. 축소차수 n_m=1과 n_m=5에 대하여 식 (17)로 계산되는 변환행렬 V는 각각 다음과 같다.

(18)

V_{N \times 2 n_{m}} (n_{m} = 1) = [\begin{matrix} | & | \\ v_{x}^{1} & v_{y}^{1} \\ | & | \end{matrix}]

(19)

V_{N \times 2 n_{m}} (n_{m} = 5) = [\begin{matrix} | & | & | & | & | & | \\ v_{x}^{1} & v_{y}^{1} & v_{x}^{2} & v_{y}^{2} & \dots & v_{x}^{5} & v_{y}^{5} \\ | & | & | & | & | & | \end{matrix}] \begin{matrix}  \end{matrix}

이때, $v_{x}^{i}$ , $v_{y}^{i}$ 는 각각 x, y 방향 하중벡터로 생성되는 축소차수(n_m) i차의 크리로프 부공간 기저 벡터를 의미한다. 구체적으로 $v_{x}^{1}$ , $v_{y}^{1}$ 은 각각 x 및 y 방향 하중벡터에 의한 초소형 충격 스위치의 정적 변형이다. 또한 $v_{x}^{2}$ , $v_{y}^{2}$ 은 각각 정적 변형 $v_{x}^{1}$ 및 $v_{y}^{1}$ 와 연관된 관성력으로 인하여 발생하는 정적 변형을 의미한다.

Fig. 4 및 Fig. 5는 각각 n_m=1 및 n_m=5의 방향별 과도응답 결과로 회색 선은 FOM, 빨간 점선은 ROM을 나타낸다. Fig. 4 및 Fig. 5에서 각 방향에 대한 변위를 비교해 보면 크리로프 기저 벡터의 수가 많을수록 축소 시스템은 초기 시스템의 동적 특성을 잘 나타내기 때문에 ROM(n_m=5)의 결과가 ROM(n_m=1)보다 FOM과 더 정확히 일치하는 결과를 나타낸다. 또한, z 방향으로 적용된 하중은 0으로 다른 방향에서 나타나는 변위 응답 결과보다 훨씬 작은 값을 가진다. ROM(n_m=1)의 양상은 FOM과 유사하지만 피크들에서 큰 차이가 나타났는데, 변환행렬을 구성하는 크리로프 기저 벡터들이 FOM의 동적 특성을 반영하기에는 그 수가 부족하기 때문에 발생한 오차이다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F4.jpg

Fig. 4

Transient responses of FOM and ROM(n_m=1) at the output node

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F5.jpg

Fig. 5

Transient responses of FOM and ROM(n_m=5) at the output node

ROM의 차수에 대한 과도응답의 정확성 비교를 위하여 다음의 진상대오차(true relative error, E(n))식을 사용하였다(Han, 2013).

(20)

E (n) = \frac{1}{N_{t}} \sqrt{\sum_{t_{i} = 0}^{N_{t} ∆ t} {(\frac{y_{n} (t_{i}) - y (t_{i})}{y (t_{i})})}^{2}}

(21)

e (n) = \frac{1}{N_{t}} \sqrt{\sum_{t_{i} = 0}^{N_{t} ∆ t} {(\frac{y_{n} (t_{i}) - y_{n + 1} (t_{i})}{y_{n + 1} (t_{i})})}^{2}}

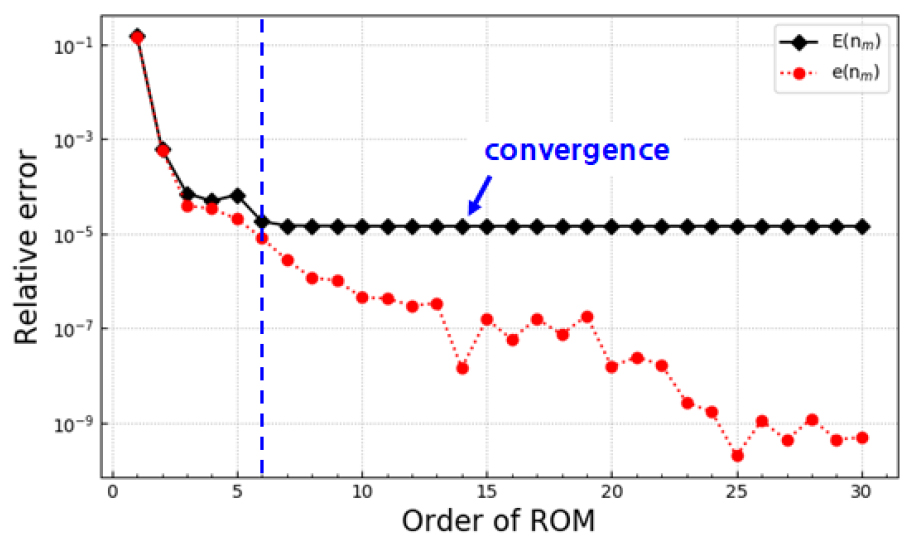
여기서 y_n(t_i) 및 y(t_i)는 각각 시간 t_i에서 축소차수 n을 가지는 ROM과 FOM으로 계산된 과도응답을 나타낸다. 이때 FOM으로 계산되는 y(t_i)는 방대한 계산이 요구되기 때문에 식 (21)과 같이 두개의 연속적인 ROM의 응답으로 계산되는 오차지표(error indicator, e(n))(Han, 2013)를 사용하였다. E(n) 및 e(n)에 대한 결과 그래프를 Fig. 6에 나타내었다. 축소차수 n_m=1의 E(n)은 0.151이고, n_m=5의 E(n)은 6.6×10^-5로 후자의 경우에 오차가 매우 작은 것을 알 수 있다. 또한, Fig. 6의 그래프에서 E(n)과 e(n)는 E(n)이 수렴할 때까지 유사한 경향을 나타내기 때문에 e(n)을 이용하여 ROM의 최적의 차수를 선택할 수 있다. 축소차수 n_m=3의 E(n)은 7.1×10^-5로 n_m=5의 결과와 큰 차이가 나지 않으므로 n_m=3을 사용하여 과도응답해석을 수행하여도 정확한 과도응답 결과를 얻을 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F6.jpg

Fig. 6

Relative error E(n) and error indicator e(n) for the shock switch

ROM의 과도응답 해석의 효율성 비교를 위하여 Table 1과 같이 FOM과 ROM의 과도응답해석 계산 시간을 비교하였다. FOM은 ANSYS를 통하여 진행한 과도응답해석 시간을 측정하였고, ROM은 오차 정도를 고려하여 n_m이 1, 3, 5에 대하여 각각 ROM의 생성 및 과도응답해석 계산 시간을 나타내었다. 표에서 Generation of ROMs는 각 해당 축소차수의 ROM을 생성할 때, Fig. 1에 설명된 ROM 아래의 Model Order Reduction의 4가지 단계를 수행하는데 소요된 총 시간이다. 또한, 표에서 Calculation of transient responses는 각 축소차수의 ROM에 대하여 Python으로 작성된 뉴마크 적분법을 수행하는데 소요된 시간이다. 이에 따라 FOM에서 소요된 총 시간은 17,219초이고, ROM에서는 축소차수에 따라서 각각 142초, 225초, 302초 정도가 소요되어 ROM의 우수한 계산 효율성을 확인할 수 있다.

Table 1.

Computation times for the transient responses using the FOM and ROMs

Computation time(s)	FOM	ROM
Computation time(s)	N=648,009	n_m=1	n_m=3	n_m=5
Generation of ROMs(s)	-	142	225	302
Calculation of transient responses(s)	17,219	0.09	0.12	0.12
Total time(s)	17,219	142	225	302

3.2 거더 다리

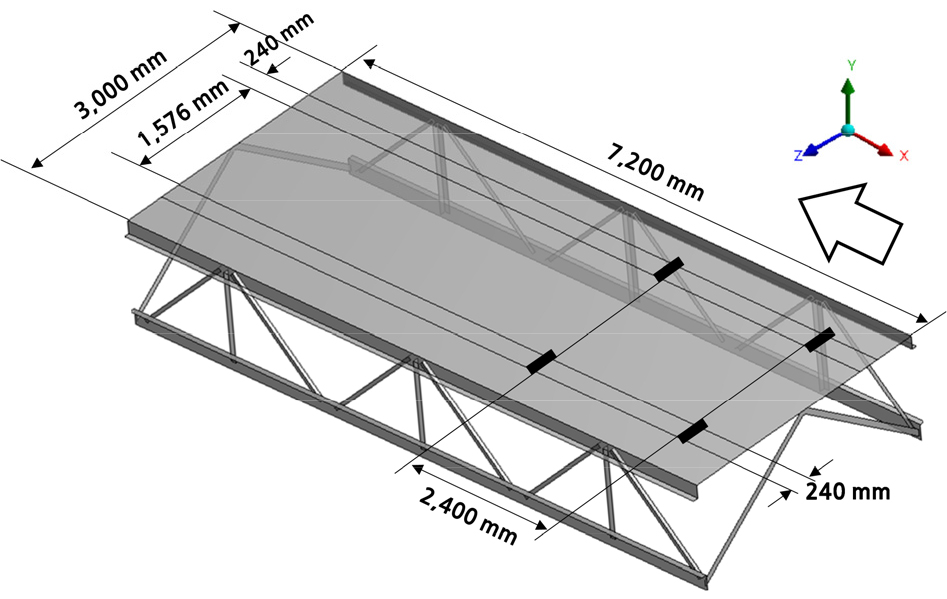
두 번째 수치 예제는 Fig. 7에 표시한 거더 다리이며, 다리 위로 약 40km/h의 일정한 속도로 자동차가 지나는 상황에 대한 과도응답해석을 수행하였다. 다리를 지나가는 자동차의 질량은 900kg이고, 중력 가속도 10m/s²를 적용하였다. 차로의 폭은 3m이며, 이는 도로교통법 규정을 참고하여 반영하였다. 그리고, 해석 수행시 다리 전체에서 7.2m인 일부 구간에서 진행하였다. 자동차의 전폭은 약 2m, 축간 거리 2.4m, 타이어의 단면 폭은 240mm로 설정하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F7.jpg

Fig. 7

Geometric modeling of a girder bridge

유한요소모델링에는 SHELL281요소를 사용하였고, 요소는 3,162개, 절점은 10,599개가 생성되었다. 전체 자유도수(N)는 60,964개이다. 해당 모델의 물성치로는 탄성계수 E=200GPa, 밀도 ρ=7,850kg/m³, 포아송 비 ν=0.3를 사용하였다.

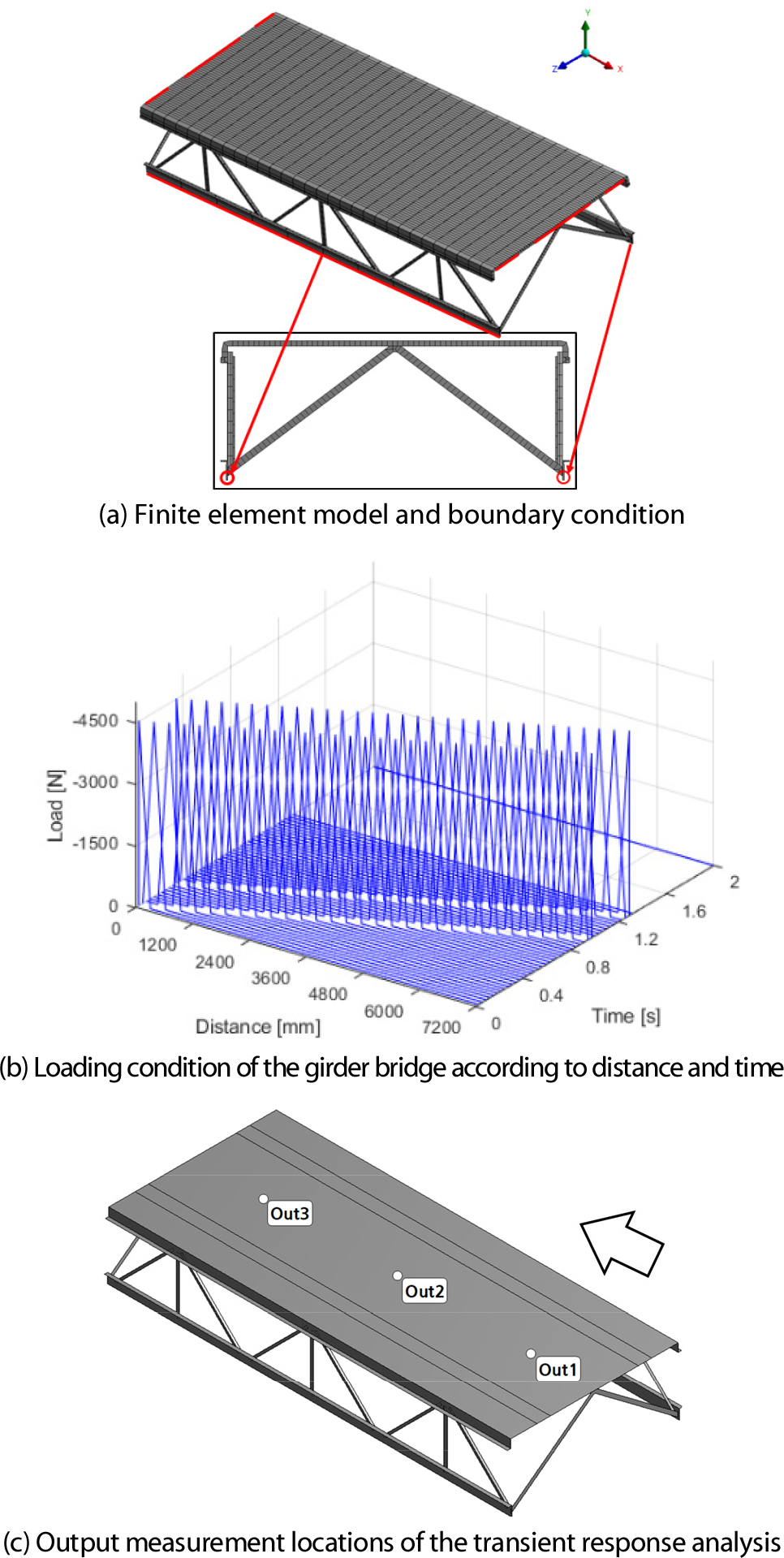
경계조건으로 Fig. 8(a)에 나타낸 바와 같이 도로의 양 끝단 중 타이어 궤적이 아닌 모서리의 x 방향을 구속하였고, 아래 거더의 밑면 모서리의 모든 자유도를 구속하였다. 자동차가 거더 다리의 우측에서 좌측으로 진행하는 동안 자동차의 바퀴를 통해 거더 다리에 가해지는 y 방향 하중을 시간과 진행거리에 따라서 표시하였다(Fig. 8(b) 참고). 자동차는 시간 0초에 앞바퀴가 거더 다리의 우측 끝단에 위치한다고 가정하였고, 시간이 흐르며 앞바퀴, 앞바퀴 및 뒤바퀴, 그리고 뒤바퀴에 의해 거더 다리에 하중이 가해진다. 이러한 자동차의 움직임에 따른 이동 하중을 표현하는데, 총 31개의 y 방향 하중벡터이 부여되었다. 감쇠는 비례 감쇠를 가정하여 감쇠비 ξ=0.01에 대하여 질량감쇠계수 $α$ =0 및 강성감쇠계수 $β$ =2.077×10^-4로 고려하였다. 수치 계산은 3.40GHz Intel(R) Core(TM) i5-4670 CPU 및 16GB의 메모리 용량을 가지는 전산 시스템을 통해 진행하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F8.jpg

Fig. 8

Analysis condition for the girder bridge

이 예제에서 축소차수 n_m=1과 n_m=5에 대한 식 (17)로 계산되는 변환행렬 V는 각각 다음과 같다.

(22)

V_{N \times 31 n_{m}} (n_{m} = 1) = [\begin{matrix} | & | & | & | & | & | \\ v_{y 1}^{1} & v_{y 2}^{1} & v_{y 3}^{1} & \dots & v_{y 29}^{1} & v_{y 30}^{1} & v_{y 31}^{1} \\ | & | & | & | & | & | \end{matrix}] \begin{matrix}  \end{matrix}

(23)

V_{N \times 31 n_{m}} (n_{m} = 5) = [\begin{matrix} | & | & | & | & | & | \\ v_{y 1}^{1} & v_{y 2}^{1} & v_{y 3}^{1} & \dots & v_{y 29}^{5} & v_{y 30}^{5} & v_{y 31}^{5} \\ | & | & | & | & | & | \end{matrix}] \begin{matrix}  \end{matrix}

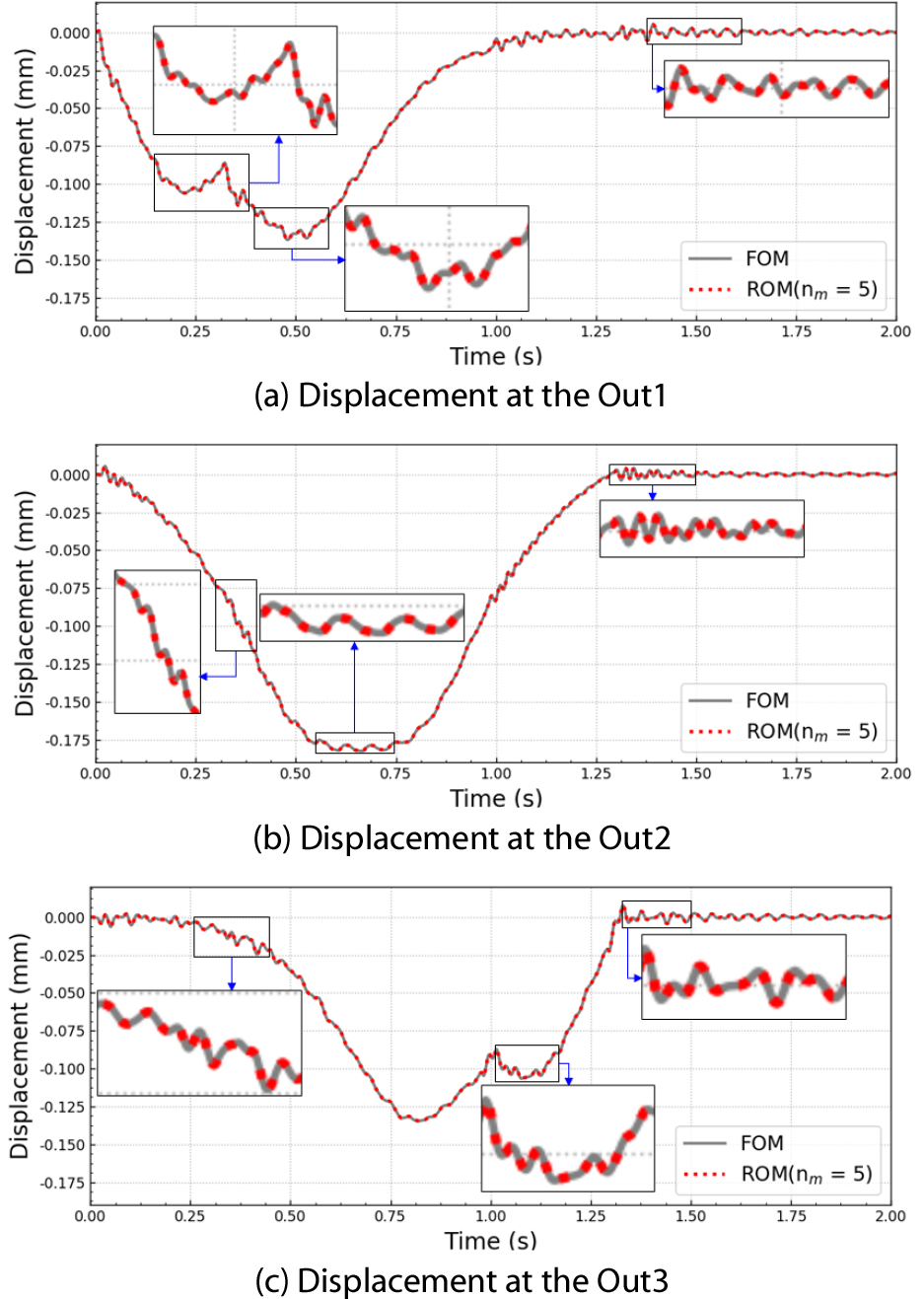
여기서 $v_{y k}^{i}$ 는 y 방향의 k번째 하중에 대한 축소차수 i차 크리로프 부공간 기저 벡터를 의미한다. 과도응답을 확인하기 위하여 도로 위로 자동차가 진입한 지점, 도로 중간 지점, 도로를 나가는 지점 근처의 절점인 Out1, Out2, Out3에서의 y 방향 변위를 확인하였다(Fig. 8(c) 참조).

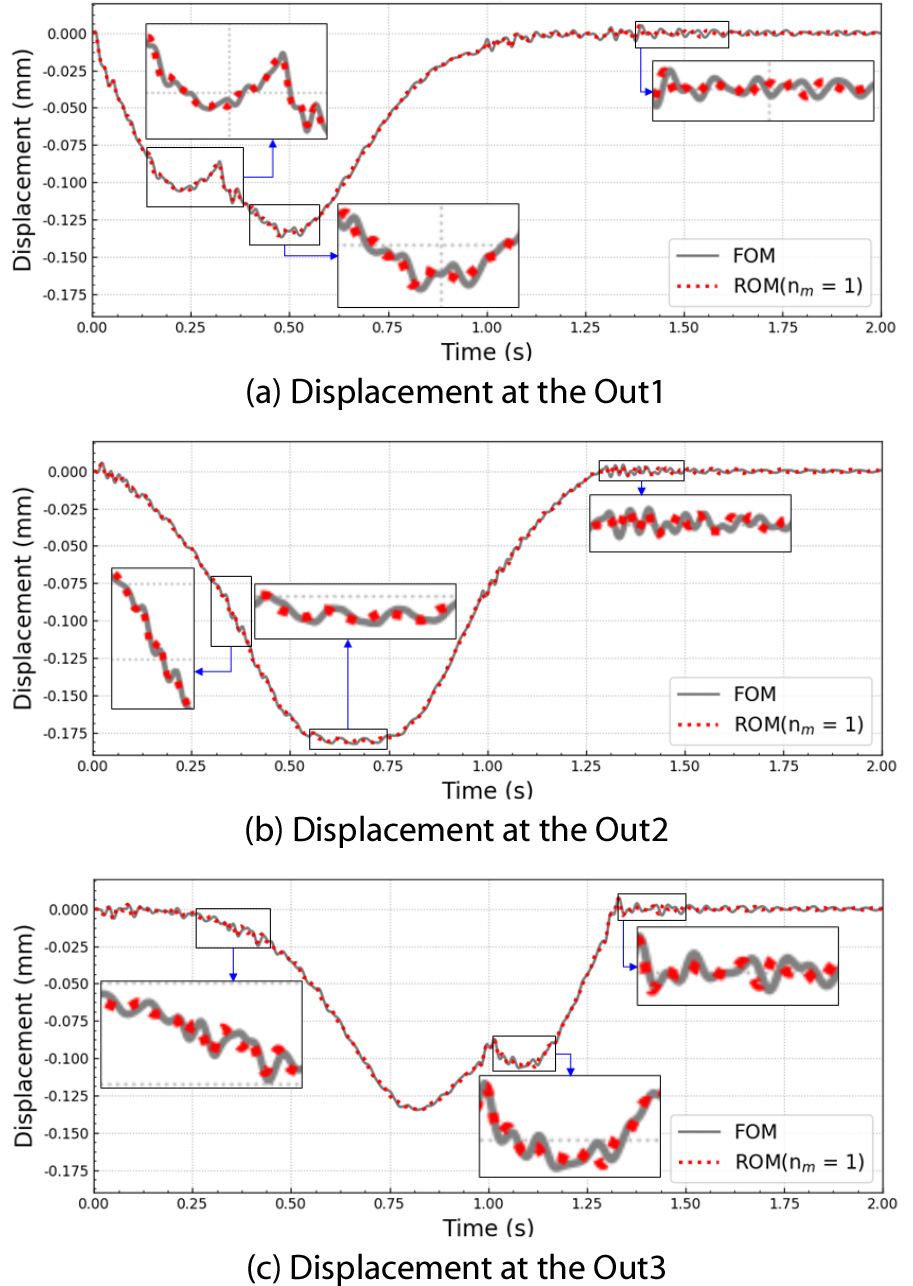
Fig. 9 및 Fig. 10은 각각 축소모델 n_m=1 및 n_m=5의 과도응답 결과로 회색 선은 FOM, 빨간 점선은 ROM을 나타낸다. 각 그래프에서 해당 지점을 지날 때와 자동차가 완전히 다리를 벗어나는 시간에서의 과도응답을 확대하여 나타내었다. ROM(n_m=1)를 이용하여도 초기 시스템의 동적 특성을 충분히 나타낼 수 있는 결과를 얻을 수 있었다. 물론 ROM(n_m=5)의 결과가 ROM(n_m=1)보다 FOM에 더 일치하는 결과를 나타내는 것을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F9.jpg

Fig. 9

Transient response of FOM and ROM(n_m=1) at the output nodes

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F10.jpg

Fig. 10

Transient response of FOM and ROM(n_m=5) at the output nodes

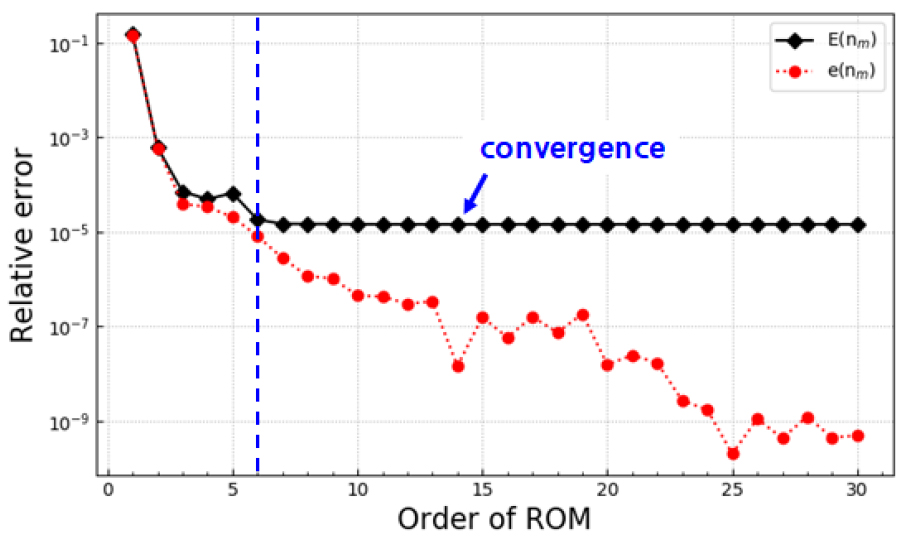
식 (20)으로 계산된 n_m=1의 E(n)은 0.023, n_m=5의 E(n)은 2.77×10^-6으로 n_m=5의 오차가 훨씬 낮았다. 이는 앞에서 설명한 바와 같이 모멘트 일치법에 따라 변환행렬에 크리로프 부공간 기저 벡터가 많이 포함될 수도록 축소모델이 초기 시스템의 동적 특성을 더 잘 표현하기 때문이다. 축소차수에 따른 E(n) 및 e(n)의 비교 그래프를 Fig. 11에 나타내었다. 이 예제의 비교 그래프에서 E(n)과 e(n)은 E(n)이 수렴할 때까지 유사한 경향을 나타내기 때문에 e(n)으로 ROM의 최적의 차수를 선택할 수 있을 것이다. 축소차수 n_m=3까지 오차가 급격히 감소하며, n_m=5 이후부터는 수렴하기 때문에 n_m=5를 최적의 차수로 선택할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-02/N0040340205/images/Figure_jcoseik_34_02_05_F11.jpg

Fig. 11

Relative error and error indicator for the girder bridge

ROM에 대한 과도응답 해석 효율성 비교를 위하여 Table 2와 같이 FOM과 ROM의 과도응답해석 계산 시간을 비교하였다. 각 항목의 구체적인 소요시간은 Table 1에서 설명한 바와 동일하다. FOM은 ANSYS를 통하여 진행한 해석 시간을 측정하였고, ROM은 오차 정도를 고려하여 n_m이 1, 3, 5에 대하여 각각 ROM을 생성하는데 걸린 시간 및 과도응답해석 계산 시간을 나타내었다. FOM에서 소요된 전체 시간은 약 950초이고, ROM에서는 각각 64초, 172초, 304초 정도가 소요되어 본 예제에서도 ROM의 우수한 과도응답 계산 효율성을 확인할 수가 있다.

Table 2.

Computation times for the transient responsesof the FOM and ROMs

Computation time(s)	FOM	ROM
Computation time(s)	N=60,964	n_m=1	n_m=3	n_m=5
Generation of ROMs(s)	-	53	138	238
Calculation of transient responses(s)	955	10.7	33	65.5
Total time(s)	955	64	172	304

이동 하중에 대하여 크리로프 부공간 기반 모델차수축소법을 적용한 사례는 보고된 바가 없었는데, 본 예제를 통하여 이동 하중을 가진 시스템에서도 충분히 크리로프 부공간 기반 모델차수축소법을 적용하여 정확하고 효율적인 과도응답 결과를 얻을 수 있음을 확인하였다.

4. 결 론

본 연구에서는 크리로프 부공간 모델차수축소법 기반 과도응답해석의 자동화를 위한 ANSYS ACT 툴을 개발하고, 각 방향별 다중 하중 및 이동 하중 하에서 수치 예제를 통해 초기 시스템(FOM)과 축소차수모델(ROM)의 과도응답을 비교하였다. 그리고, 두 방법에 대한 해석 결과의 정확성 및 효율성 비교를 위하여 진상대오차(E(n)) 및 오차지표(e(n)), 그리고 해석 소요 시간을 비교하였다. 이를 통하여 크리로프 부공간 모델차수축소법 기반 과도응답해석이 일반적인 과도응답해석과 거의 같은 정확성을 가지면서 계산 시간 측면에서 매우 효율성이 높은 것을 확인하였다. 또한, 본 연구에서는 이러한 과도응답해석 과정을 ANSYS Workbench 환경에서 자동화를 구현하였기 때문에 사용자의 입력을 최소화 하여 반복적인 크리로프 부공간 축소모델 기반 과도응답해석을 간단하고 효율적으로 진행할 수 있을 것으로 기대된다.

Acknowledgements

이 논문은 2020년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2020R1I1A3073275).

References

ANSYS (2018) ANSYS ACT 19.2 Release API and XML Online Reference Guide for Mechanical, SAS IP, Inc.

Amin, N.M., Krisnamoorty, R.R. (2012) Krylov Subspace Model Order Reduction for FE Seismic Analysis, Business, Eng. & Ind. Appl., pp.239~243. 10.1109/ISBEIA.2012.6422877

Freund, R.W. (2000) Krylov-Subspace Methods for Reduced-Order Modeling in Circuit Simulation, J. Comput. & Appl. Math., 123, pp.395~421. 10.1016/S0377-0427(00)00396-4

Goo, S.Y., Kook, J.H., Hyun, J.H., Wang, S.M. (2012) A Comparison Study of Pad Approximation and Model Order Reduction Scheme for Efficient Acoustic Analysis, Trans. Korean Soc. Mech. Eng. Spring & Autumn Conf., pp.455~458.

Han, J.S. (2007) Eigenvalue and Frequency Response Analyses of a Hard Disk Drive Actuator Using Reduced Finite Element Models, Trans. Korean Soc. Mech. Eng. A, 31(5), pp.541~549. 10.3795/KSME-A.2007.31.5.541

Han, J. S. (2010) Direct Design Sensitivity Analysis of Frequency Response Function using Krylov Subspace based Model order Reduction, J. Comput. Struct. Eng. Inst. Korea, 23(2), pp.153~163.

Han, J.S. (2013) Calculation of Design Sensitivity for Large-size Transient Dynamic Problems using Krylov Subspace-based Model Order Reduction, J. Mech. Sci. & Technol., 27(9), pp.2789~2800. 10.1007/s12206-013-0726-2

Han, J.S., Won, B.R., Park, W.S., Ko, J.H. (2016) Transient Response Analysis by Model Order Reduction of a Mokpo- Jeju Submerged Floating Tunnel under Seismic Excitations, Struct. Eng. & Mech., 57(5), pp.921~936. 10.12989/sem.2016.57.5.921

Han, J.S. (2020) Comparison of Model Order Reductions using Krylov and Modal Vectors for Transient Analysis under Seismic Loading, Struct. Eng. & Mech., 76(5), pp.643~651.

Kerschen, G., Golinval, Jc., Vakakis, A.F., Bergman, L.A. (2005) The Method of Proper Orthogonal Decomposition for Dynamical Characterization and Order Reduction of Mechanical Systems: An Overview, Nonlinear Dyn., 41, pp.147~169. 10.1007/s11071-005-2803-2

Kim, J.G., Park, Y.J., Lee, G.H., Kim, D.N. (2017) A General Model Reduction with Primal Assembly in Structural Dynamics, Comput. Methods Appl. Mech. & Eng., 324, pp.1~28. 10.1016/j.cma.2017.06.007

Kim, J.H., Yoon, G.H. (2016) Multi-Component Quasi-Static Ritz Vector (MCQSRV) Method by using Krylov Subspaces and Eigenvectors for Multibody Simulation, Trans. Korean Soc. Mech. Eng. Spring & Autumn Conf., pp.60~61.

Kim, M.C. (2018) Development of Automated Optimization Process for Journal Bearing Analysis in the Driving System of Engine, Trans. Korean Soc. Automot. Eng., pp.83~89.

Moon, S.I., Kang, T., Han, S.W. (2018) Automated Loose-Part Impact Analysis System for Big Data Construction of Nuclear Component, Trans. Korean Soc. Mech. Eng. Spring & Autumn Conf., pp.3145~3150.

Nam, Y.W., Lee, S.H., Lee, D.G., Im, S.J., Noh, S.D. (2020) Digital Twin-based Application for Design of Human-Machine Collaborative Assembly Production Lines, J.Korean Inst. Ind. Eng., 46(1), pp.42~54. 10.7232/JKIIE.2020.46.1.042

Oh, S.I., Park, D.U., Baek, H.W., Kim, S.H., Lee, J.K., Kim, J.G. (2020) Virtual Sensing System of Structural Vibration using Digital Twin, Trans. Korean Soc. Noise & Vib. Eng., 30(2), pp.149~160. 10.5050/KSNVE.2020.30.2.149

Park, B.G., Jeong, J.W., Ko, J.S. (2018) Micro Shock Switch with Additional Mass, Korean J. Air-Cond. & Refrig. Eng., 30(2), pp.586~592. 10.6110/KJACR.2018.30.12.586

Python Software Foundation (2018) Python 3.7 Documentation.

Qu, Z.Q. (2004) Model Order Reduction Techniques: With Application In Finite Element Analysis, Springer Science & Business Media. 10.1007/978-1-4471-3827-3_2

Saad, Y. (1983) Projection Methods for Solving Large Sparse Eigenvalue Problems, Matrix Pencils, 973, pp.121~144. 10.1007/BFb0062098

Seo, H.W., Kim, M.G., Lee, H.M., Han, J.S. (2020) Automation Tool for VDI 2230 Based Structural Analysis and Evaluation of Bolted Joints Using ANSYS and MS Excel, Trans. Korean Soc. Mech. Eng. A, 44(2), pp.149~158. 10.3795/KSME-A.2020.44.2.149

Shin, S.H., Park, M.C. (2020) Implementation of Digital Twin based Building Control System using Wireless Sensor Box, J. Korea Soc. Comput. & Inf., 25(5), pp.57~64.

Su, T.J., Craig, Jr.R.R. (1991) Krylov Model Reduction Algorithm for Undamped Structural Dynamics Systems, J. Guidance, 14(6), pp.1311~1313. 10.2514/3.20789

Won, B.R., Han, J.S. (2014) Comparison of Projection-Based Model Order Reduction for Frequency Responses, Trans. Korean Soc. Mech. Eng. A, 38(9), pp.933~941. 10.3795/KSME-A.2014.38.9.933

Journal of the Computational Structural Engineering Institute of KoreaISSN:1229-3059(Print) 2287-2302(Online)한국전산구조공학회

Preview

Automation of Krylov Subspace Model Order Reduction for Transient Response Analysis with Multiple Loading

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15a)

(15b)

(16)

(17a)

(17b)

Fig. 1

Transient response analysis procedure based on the model order reduction method

Fig. 2

The automation procedure of the transient response analysis implemented on ANSYS workbench

Fig. 3

Finite element model of a micro shock switch and an analysis condition

(18)

(19)

Fig. 4

Transient responses of FOM and ROM(nm=1) at the output node

Fig. 5

Transient responses of FOM and ROM(nm=5) at the output node

(20)

(21)

Fig. 6

Relative error E(n) and error indicator e(n) for the shock switch

Table 1.

Computation times for the transient responses using the FOM and ROMs

Fig. 7

Geometric modeling of a girder bridge

Fig. 8

Analysis condition for the girder bridge

(22)

(23)

Fig. 9

Transient response of FOM and ROM(nm=1) at the output nodes

Fig. 10

Transient response of FOM and ROM(nm=5) at the output nodes

Fig. 11

Relative error and error indicator for the girder bridge

Table 2.

Computation times for the transient responsesof the FOM and ROMs

Acknowledgements

References

Transient responses of FOM and ROM(n_m=1) at the output node

Transient responses of FOM and ROM(n_m=5) at the output node

Transient response of FOM and ROM(n_m=1) at the output nodes

Transient response of FOM and ROM(n_m=5) at the output nodes