1. 서 론
2. 중저준위 방폐물 동굴처분시설 개요
2.1 사일로 구조물
2.2 지반체 및 재료 특성값
3. 지반체의 구성모델 및 철근콘크리트 유한요소
3.1 지반체의 구성 모델
3.2 철근콘크리트 라이너의 유한요소
4. 유한요소해석
4.1 해석영역 및 유한요소망
4.2 사일로 구조물의 건설과정
4.3 2-D 축대칭 모델 및 3차원 모델
5. 해석결과
5.1 쇼크리트 해석결과
5.2 잔류수압을 받는 라이닝 해석결과
6. 결 론
1. 서 론
현재 경주 중저준위 방폐물의 영구처분을 위한 1단계 사일로 타입의 동굴처분시설이 2014년 완공되어 운영되고 있으며, 중저준위 방폐물의 효율적인 관리를 위해 2단계 표층처분시설의 건설이 추진되고 있다(KORAD, 2018). 향후에는 중저준위 방폐물의 지속적인 증가가 예상되어 방폐물 처분장의 3단계 매립형처분시설의 건설도 추진되고 있다.
중저준위 방폐물 처분시설은 건설 및 운영기간 동안 내외부에서 발생가능한 다양한 재난・재해 요인에 대해서도 안전성이 확보되어야 하고, 처분시설의 폐쇄 후에도 장기적인 안전성이 확보되어야 한다(KINS, 2011). 지난 2016년과 2017년에 국내 최대 규모의 지진이 경주와 포항에서 연이어 발생하여 인근 지역에서 가동되고 있는 원자력발전소와 경주 방폐물 처분시설의 내진 안전성 확보에 대한 관심이 매우 높다.
방폐물 처분시설의 방벽설계 주요 목표는 방사성 오염물질과 지하수의 접촉을 최소화하고자 처분시설 외부로 부터 지하수 침입을 차단하는 것이다. 이를 위하여 경주 중저준위 방폐물 처분시설은 3단계의 다중방벽 시스템으로 구축되었다(Park and Park, 2016).
본 논문에서는 경주 방폐물 처분장 1단계 동굴처분시설의 사일로 콘크리트 구조물의 구조적 안전성 검토 수행내용을 제시하였다. 방폐물 처분장의 건설 및 운영과정을 고려하여 사일로의 굴착과 쇼크리트 타설, 철근콘크리트 라이너의 설치, 그리고 잔류수압의 영향 등을 고려하여 단계적으로 유한요소해석을 수행하였다. 사일로 타입 동굴처분시설은 축대칭 형태의 구조물이므로 2차원 축대칭 유한요소해석 만으로 가능하지만 수치해석 결과의 검증을 위해 3차원 유한요소해석도 병행하여 수행하였다. 2차원 축대칭 유한요소 모델링 및 3차원 유한요소 모델링은 SMAP-3D 프로그램을 사용하였다(Comtec Research, 2020).
2. 중저준위 방폐물 동굴처분시설 개요
2.1 사일로 구조물
경주 방폐물 처분장의 지하시설은 사일로, 건설동굴, 운영동굴, 연결동굴, 하역동굴, 수직출입구 등으로 구성되어 있다. 방폐물 처분용기 10만 드럼을 저장하는 사일로는 모두 6개가 건설되어 운영 중에 있으며, 해수면에서 -80m~-130m에 걸쳐 위치한다(Park and Park, 2016).
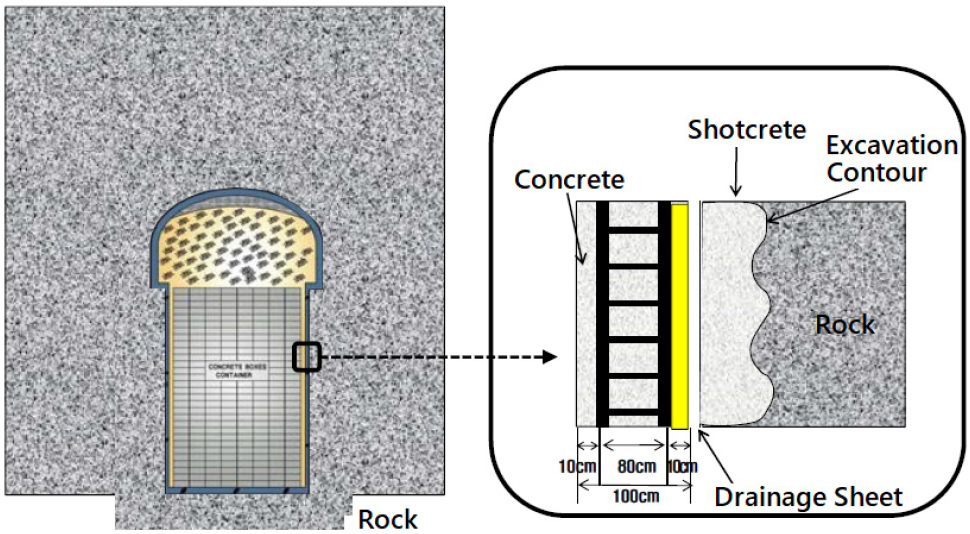
사일로 처분시설은 방폐물 처분 드럼이 저장되는 원통형의 하부(직경 23.6m, 높이 36m)와 폐쇄 후에 잡석으로 채워지는 공간인 돔형의 상부(직경 30m, 높이 17.4m)의 2개 부분으로 구성된다(KINS, 2011). 사일로의 건설과정에서 굴착 직후 암반의 굴착면을 따라 약 50cm의 쇼크리트가 타설되었으며, 내부에는 1m 두께의 철근콘크리트 라이너 구조물이 설치되었다(Fig. 1 참조).
2.2 지반체 및 재료 특성값
경주 방폐물 처분시설의 지반조사결과 사일로 주변 지반체의 측압계수값 K0 (평균 수평응력과 평균수직응력의 비)는 1.17에서 1.92 사이의 값을 나타내는 것으로 발표되었다(Shin and Shin, 2017). 따라서 본 논문에서는 측압계수값을 0.5, 1.0, 2.0 등 3가지 경우에 대해 검토하였다.
지표면~-4.3m는 토사층, 토사층 아래~-9.5m는 풍화암, 그리고 풍화암 아래는 암반층으로 가정하였다. 지반체 및 사일로 구조의 재료 특성값은 문헌조사 및 설계도면자료(Kim et al., 2011; Park et al. 2012)를 토대로 하여 Table 1에 나타낸 바와 같이 가정하였다.
Table 1.
Material Properties used in this study
3. 지반체의 구성모델 및 철근콘크리트 유한요소
3.1 지반체의 구성 모델
지반체의 구성 모델은 Generalized Hoek and Brown(Kim et al., 1987)을 사용하였다. Generalized Hoek and Brown Model의 파괴표면(failure surface)은 아래 식으로 나타낼 수 있다.
식 (1)에서 는 각각 응력불변치(stress invariant)로 아래와 같이 계산할 수 있다.
식 (1a), (1b), (1c), (1d), (1e)에서 는 전응력텐서(total stress tensor)를 의미하고, 는 편차응력(deviatoric stress tensor)을 나타낸다.
식 (1)에서 함수 는 8면체 평면에 투영된 항복표면의 형상을 나타낸다. 지반체 재료의 구성모델에 대한 보다 자세한 내용은 Kim과 Kim(2022)에서 볼 수 있다.
3.2 철근콘크리트 라이너의 유한요소
철근콘크리트 라이너 구조물의 모형화를 위해 축대칭 철근콘크리트 유한요소의 강성행렬을 구성하였다. 콘크리트 유한요소는 축대칭 등매개변수 요소를 사용하였다. 철근 유한요소의 강성행렬은 자오선방향 철근 봉요소의 강성행렬과 원주방향 철근 봉요소의 강성행렬을 중첩하여 구성하였다.
철근콘크리트의 유한요소의 강성행렬은 콘크리트 유한요소의 강성행렬(), 원주(hoop)방향 철근 봉요소의 강성행렬(), 자오선(meridional)방향 철근 봉요소의 강성행렬()을 중첩시켜 아래와 같이 구성하였다.
철근콘크리트 축대칭 유한요소에 대한 보다 추가적인 내용은 Elwi와 Murray(1980)에서 볼 수 있으며, 철근콘크리트 3차원 유한요소에 대한 자세한 내용은 Tamayo 등(2013)에 소개되어 있다. 또한 본 연구에서 검증을 위해 사용된 3차원 철근콘크리트 유한요소의 검증결과는 Comtec Research(2020)에 소개되어 있다.
4. 유한요소해석
4.1 해석영역 및 유한요소망
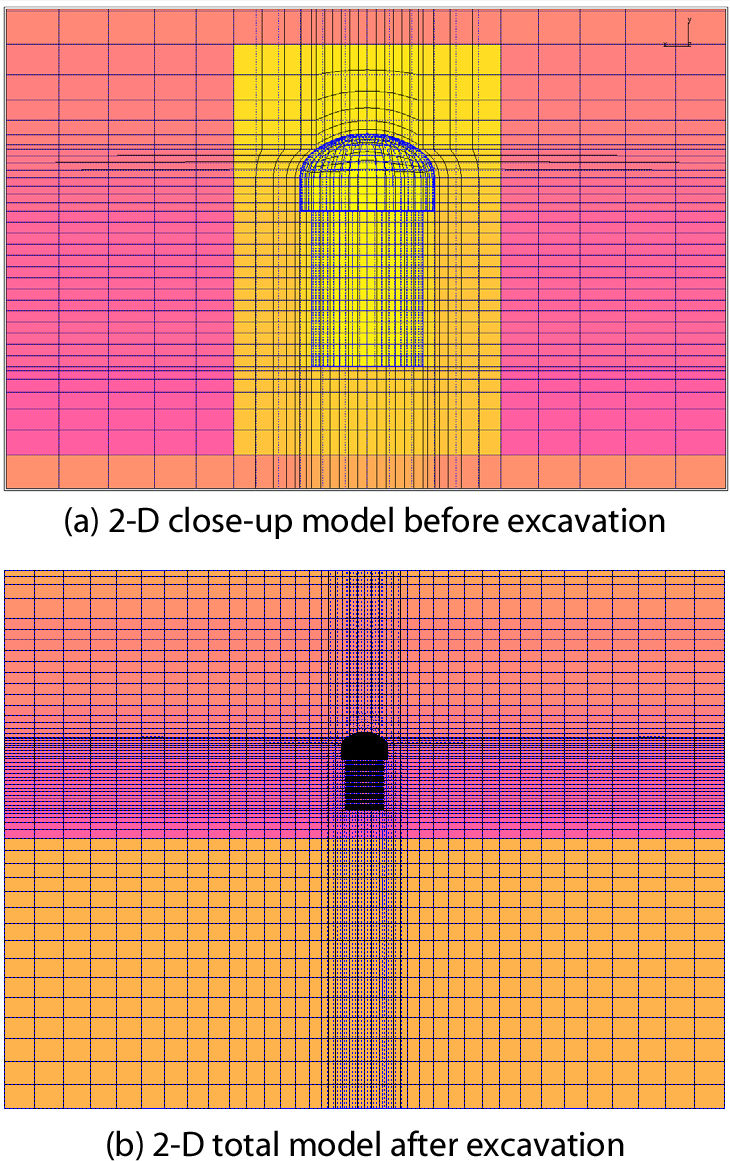
경주 중저준위 방폐물 처분장의 1단계 동굴처분시설은 모두 6개의 사일로 처분동굴이 건설되어 운영 중에 있으나 본 연구에서는 1개의 처분동굴 만을 고려하여 모델링하였다. 처분동굴의 굴착으로 인한 주변 지반체의 응력이완을 충분히 고려하기 위하여 해석영역은 수평방향으로는 처분동굴 직경의 10배까지 고려하였으며, 수직방향으로는 지표면부터 사일로 바닥에서 사일로 높이의 5배까지로 설정하였다. 축대칭요소를 사용하여 사일로 처분동굴의 굴착전 처분동굴 주변 유한요소망을 Fig. 2(a)에 나타내었고, 굴착후 전체 해석모델의 유한요소망을 Fig. 2(b)에 나타내었다.
사일로 처분동굴의 굴착후 3차원해석 유한요소망은 Fig. 3에 나타내었다. 수평방향 및 수직방향 해석영역의 크기는 Fig. 2(b)와 동일하며, 대칭성을 고려하여 두께방향으로는 처분동굴 직경의 10배까지 모델링하였다. 해석모델의 경계조건은 측면 및 하부면은 롤러조건을 적용하였다.
4.2 사일로 구조물의 건설과정
사일로 처분동굴의 건설과정은 전체적으로 Table 2에 나타낸 바와 같이 가정하였다. 사일로 처분동굴의 굴착은 다단계로 진행되었으나 본 논문에서는 한 번에 일괄 굴착을 수행한 것으로 가정하였다. 이 가정은 보수적인 접근으로 사일로 구조물의 구조적안전성 검토에 큰 문제가 없을 것으로 판단된다. Table 2에서 1,2단계와 3단계의 굴착 직후 사일로 주변 지반체에서 발생하는 변형 및 응력분포 결과는 Kim과 Kim(2021)에 제시된 바 있다.
Table 2.
Simulation of construction sequence
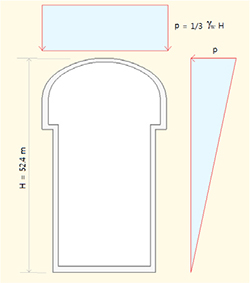
본 논문에서는 3단계에서 굴착직후 50cm 두께의 쇼크리트를 타설하고, 4단계에서 철근콘크리트 라이닝을 설치하는 것으로 가정하여 철근콘크리트 라이닝에서 발생하는 구조거동을 검토하였다. 또한 배수형 터널의 설계에서 사용되는 잔류수압의 크기는 암반 터널인 경우 최대수두를 터널 높이의 1/3로 가정하여 설계하고 있다(KISTEC, 2007). 따라서 5단계에서 철근콘크리트 라이닝에 사일로 높이의 1/3인 17.47m 수두의 잔류수압을 추가로 작용시켜서 가장 보수적 상황에 대한 사일로 구조의 거동 및 안전성을 검토하였다.
4.3 2-D 축대칭 모델 및 3차원 모델
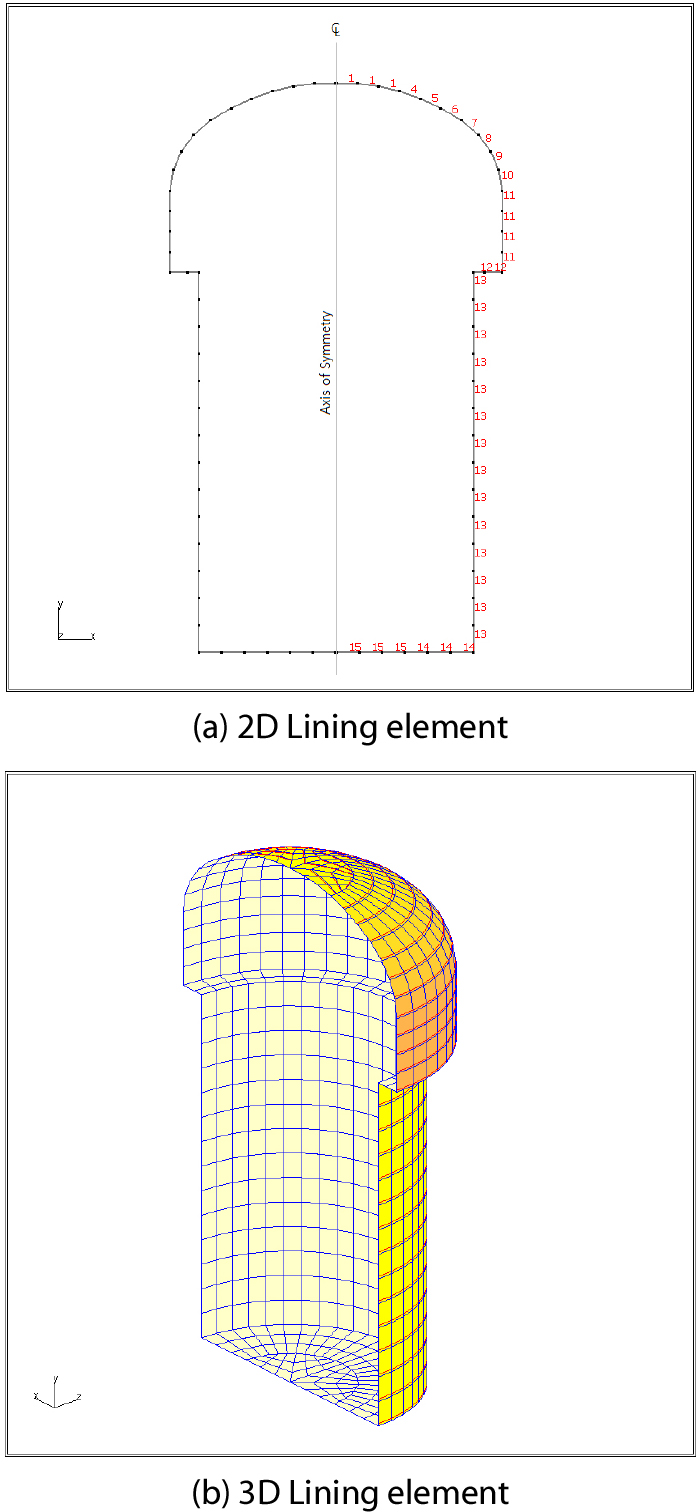
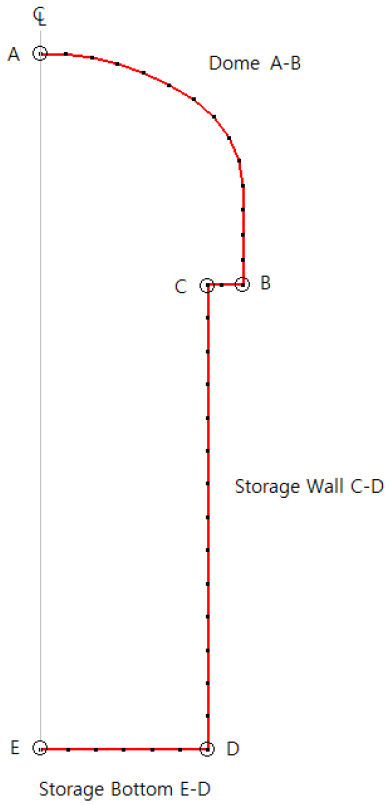
사일로 철근콘크리트 라이닝의 2차원 축대칭 유한요소망과 3차원 유한요소망을 Fig. 4에 나타내었다. 2차원 축대칭 유한요소해석과 3차원 유한요소해석을 수행하여 두 해석결과의 신뢰성을 검증하였으며, Fig. 5에 나타낸 바와 같이 주요 지점으로 판단되는 Dome A-B 구간, Storage Wall C-D 구간, Storage Bottom E-F 구간의 라이닝에서 발생하는 변형 및 응력분포를 검토하였다.
수치해석 결과의 신뢰성을 검증하기 위해서는 현장에서 계측한 자료와 비교분석을 하는 것이 가장 바람직하다. 그러나 현 상황에서 경주 방폐장 사일로 구조물의 변형 및 응력 계측 자료의 수집이 불가능하여 2차원 축대칭해석과 3차원 해석을 병행 수행하였다.
5. 해석결과
5.1 쇼크리트 해석결과
사일로 굴착직후 50cm 두께로 쇼크리트를 타설한 것으로 가정하였다. 측압계수값의 변화(K0=0.5, 1.0, 2.0)에 따른 유한요소해석을 수행하여 쇼크리트에 발생하는 응력값을 Table 3에 나타내었다.
Table 3.
Shotcrete stresses in mid-surface (compression is positive) (Unit: MPa)
쇼크리트의 설계기준강도를 20MPa로 가정하였고, 인장허용강도는 2MPa로 가정하였다. Table 3을 보면 쇼크리트에 발생하는 최대 및 최소 응력값은 모두 자오선 방향에서 발생함을 알 수 있다.
측압계수값 0.5에서 최대압축응력값은 Storage Bottom에서 발생하고, 최대인장응력값은 Storage Wall 상부에서 발생하며, 허용응력값 이내에서 발생하였다. 측압계수값 1.0과 2.0에서 최대압축응력값은 Storage Bottom 모서리에서 발생하고, 최대인장응력값은 Storage Wall 상부에서 발생하며, 허용응력값 이내에서 발생함을 보여주었다.
5.2 잔류수압을 받는 라이닝 해석결과
본 논문의 선행연구결과(Kim and Kim, 2021)를 보면 사일로의 굴착직후 사일로 주변 지반체에서 발생하는 주응력분포를 검토해 본 결과 K0=2의 경우 돔괴 벽체가 만나는 지점의 수평방향 Line에서 평균압력과 편차응력 사이의 관계값은 Mohr- Coulomb 인장모드를 넘어 압축모드에 근접하였으며, 벽체 중앙지점의 수평방향 Line에서 평균압력과 편차응력 사이의 관계값은 Mohr-Coulomb 인장모드에 근접하는 결과를 보여주었다. 따라서 본 논문에는 측압계수 2.0인 경우의 해석결과를 위주로 제시하였다.
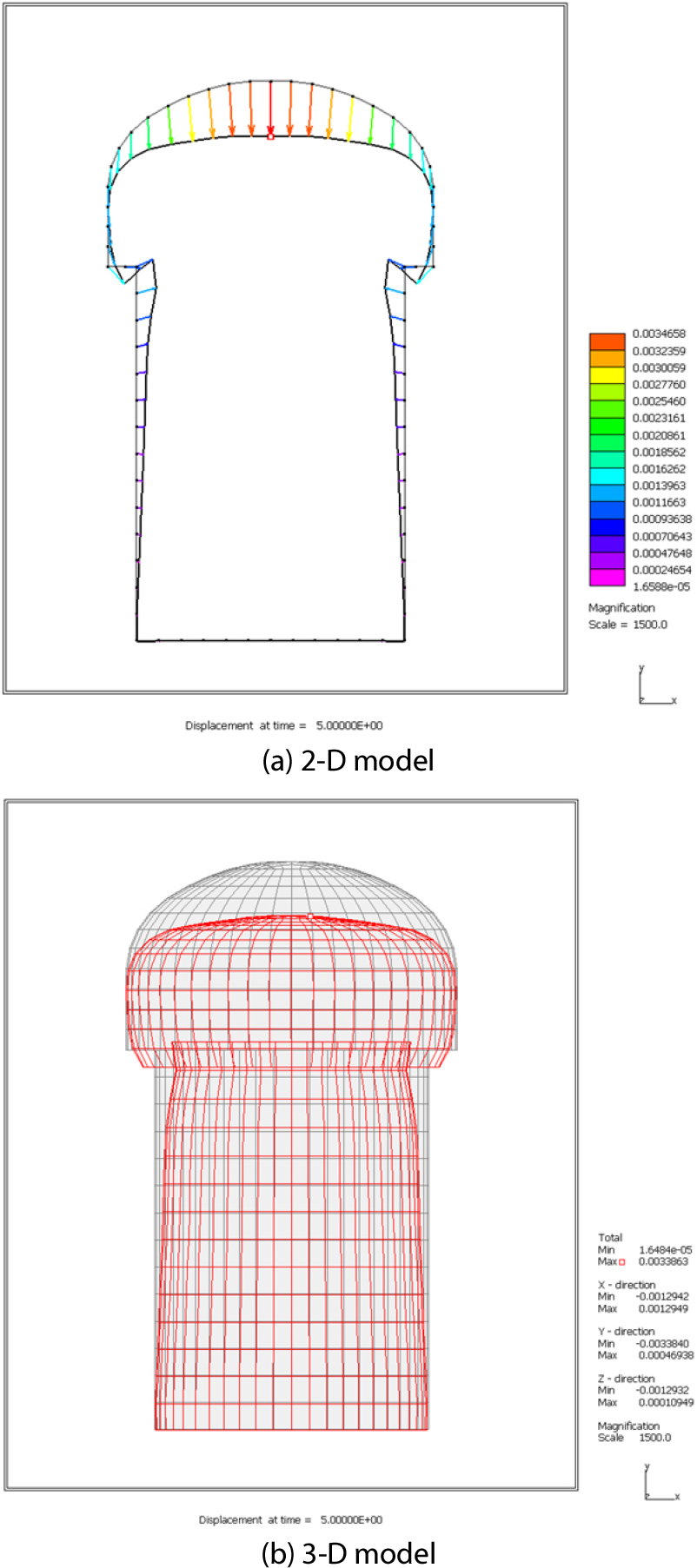
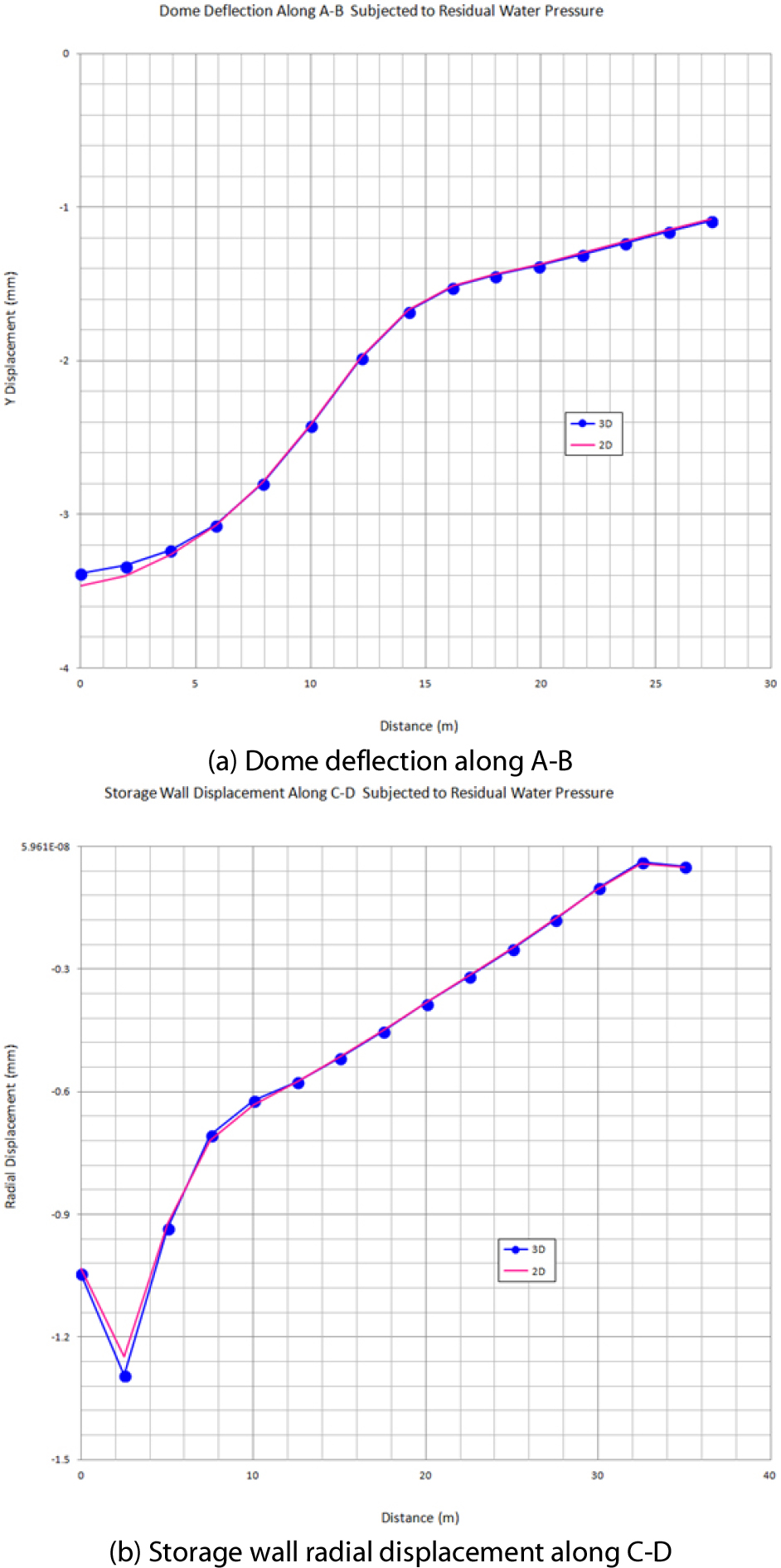
2차원 축대칭 해석과 3차원 해석을 수행하여 얻어진 사일로 구조물의 철근콘크리트 라이닝에 자중과 17.47m 수두의 잔류수압이 작용하는 Table 2의 5단계에서 라이닝의 변형 형상을 Fig. 6에 나타내었다. 그리고 Fig. 5에서 Dome A-B를 따라 발생하는 수직방향 처짐의 분포와 Storage C-D를 따라 발생하는 원주방향 변위의 분포를 Fig. 7에 나타내었다.
Fig. 6과 Fig. 7에서 2차원 축대칭해석 결과와 3차원 해석결과는 철근콘크리트라이닝의 모든 점에서 거의 동일한 값을 보여주어 2가지 해석모델(축대칭 해석모델과 3차원 해석모델)의 신뢰성을 확인할 수 있었다. 또한 수직방향 최대 처짐값은 Dome의 천정부위인 A점에서 발생하였다. 또한 원주방향 최대 변위값은 Dome과 Storage Wall이 만나는 지점 C에서 약 2.5m 아래인 점에서 발생함을 보여주었다.
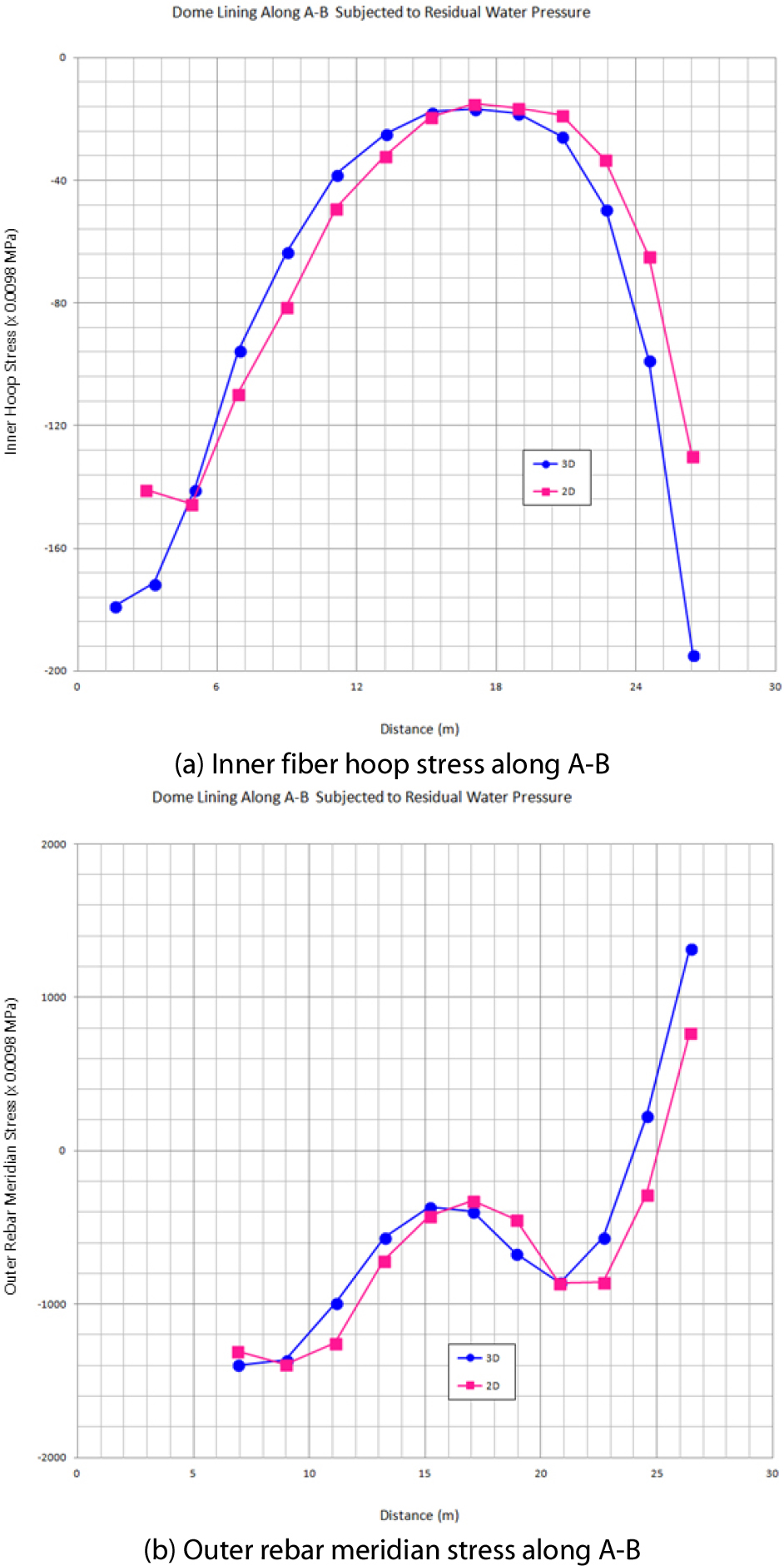
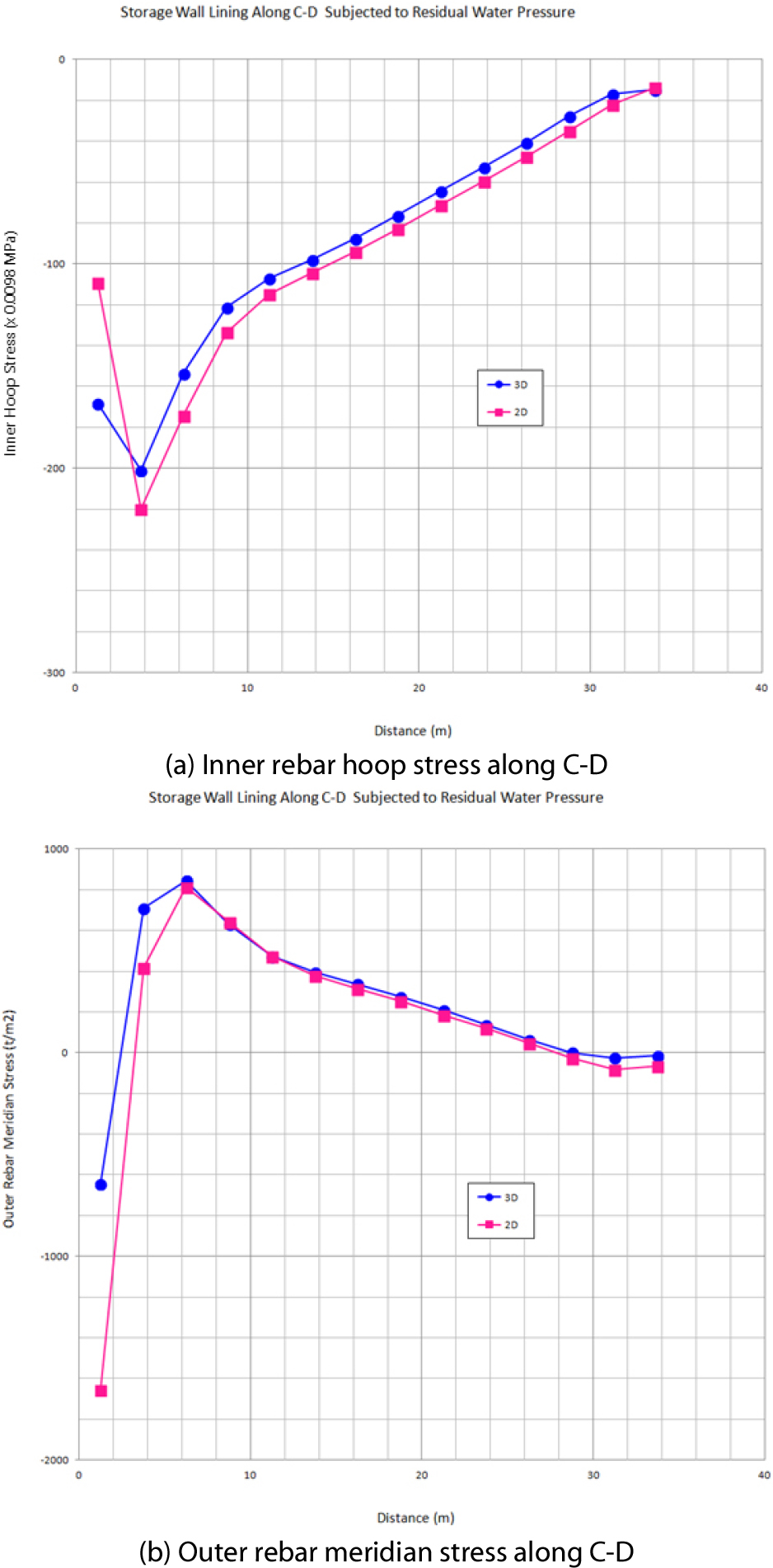
A-B를 따라 라이너 구조물의 안쪽 철근에서 발생하는 후프응력과 바깥쪽 철근에서 발생하는 자오선응력의 분포를 Fig. 8에 나타내었다. C-D를 따라 라이너 구조물의 안쪽 철근에서 발생하는 후프응력과 자오선응력의 분포는 Fig. 9에 나타내었다. 2차원 축대칭 해석결과와 3차원 해석결과는 응력분포에서도 매우 유사한 결과를 보여주었다.
Fig. 8(a)에서 보는 바와 같이 A-B를 따라 라이너 구조물의 안쪽 철근에서 발생하는 후 프응력은 B점 부근에서 가장 큰 값을 보여주었으며, 중심회전축에서 상부 돔 직경의 2/3 떨어진 점 부근에서 가장 적은 값을 보여주었다. 또한 Fig. 8(b)에서 보는 바와 같이 A-B를 따라 라이너 구조물의 바깥쪽 철근에서 발생하는 자오선응력은 A점과 B점 부근에서 인장응력과 압축응력의 가장 큰 값을 각각 보여주었다. Fig. 9(a)에서 보는 바와 같이 C-D를 따라 라이너 구조물 의 안쪽 철근에서 발생하는 자오선응력은 C점에서 4m 아래지점 부근에서 가장 큰 인장응력이 발생하였으며, 사일로의 바닥모서리인 D점에 가까워질수록 발생 응력값은 0에 수렴하였다. 또한 Fig. 9(b)에서 보는 바와 같이 C-D를 따라 라이너 구조물의 바깥쪽 철근에서 발생하는 자오선응력은 C점 부근에서 가장 큰 인장응력이 발생하였고, C점에서 6m 아래 지점 부근에서 가장 큰 압축응력이 발생하였다.
Table 4에 측압계수값이 2.0인 경우 잔류수압을 받고 있는 라이닝에서 발생하는 응력값을 나타내었다. 라이너 콘크리트의 설계기준강도는 38MPa로 가정하였고, 인장허용강도는 3.8MPa로 가정하였다. 또한 철근의 항복강도는 300MPa로 가정하였다.
Table 4.
Lining stresses for p=0.171MPa(17.46t/m2) (compression is positive) (unit: MPa)
콘크리트에서 발생하는 최대압축응력은 Dome 하부에서 발생하며 자오선방향으로 내부 표면에서 발생함을 보여주었다. 또한 최대인장응력은 Storage Wall 상부에서 발생하며 자오선방향으로 내부 표면에서 발생하였다. 콘크리트에서 발생하는 최대압축응력값 및 최대인장응력값은 모두 허용응력 범위 이내임을 보여주었다. 철근에서 발생하는 최대인장응력값은 Storage Wall 상부에서 발생하고, 최대압축응력값은 Dome 하부에서 발생하며, 모두 자오선방향으로 내부 표면에서 발생하였다. 또한 철근에서 발생하는 최대인장응력 및 최대압축응력은 모두 허용응력 범위 이내임을 알 수 있다.
따라서 경주 중저준위 방폐물 처분을 위한 사일로의 철근콘크리트 라이닝은 구조적으로 안전성을 확보하고 있음을 확인할 수 있었다.
6. 결 론
본 연구에서는 중저준위 방폐물 처분 사일로 구조물의 구조거동을 파악하고자 방폐물 처분장의 건설 및 운영과정을 고려하여 사일로의 굴착과 쇼크리트 타설, 철근콘크리트 라이너의 설치, 그리고 잔류수압의 영향 등을 고려하여 단계적으로 유한요소해석을 수행하였다. 사일로 타입 동굴처분시설은 축대칭 형태의 구조물이므로 2차원 축대칭 유한요소해석 만으로 가능하지만 수치해석 결과의 검증을 위해 3차원 유한요소해석도 수행하였다.
사일로 굴착직후 50cm 두께의 쇼크리트를 타설하고, 철근콘크리트 라이닝을 설치하는 것으로 가정하였으며, 철근콘크리트 라이닝에 사일로 높이의 1/3인 17.47m 수두의 잔류수압을 추가로 작용시켜서 가장 보수적 상황에 대한 사일로 구조의 거동 및 안전성을 검토하였다. 본 논문에서 수행한 수치해석 결과를 요약하면 아래와 같다.
1)사일로 굴착직후 50cm 두께의 쇼크리트를 타설하였을 때 측압계수값 변화에 따른 쇼크리트에서 발생하는 응력값의 검토결과, K0=0.5에서 최대압축응력값은 Storage Bottom, 최대인장응력값은 Storage Wall 상부에서 각각 발생하였다. 또한 K0=1.0, 2.0에서 최대압축응력값은 Storage Bottom 모서리, 최대인장응력값은 Storage Wall 상부에서 각각 발생하며, 모든 경우 허용응력값 이내에서 발생함을 보여주었다.
2)2차원 축대칭 해석과 3차원 해석을 수행하여 비교한 결과 모든 점에서 동일한 결과를 얻었으며, 유한요소해석망의 신뢰도를 확인할 수 있었다.
3)잔류수압을 받고 있는 라이닝에서 발생하는 응력값의 검토결과, K0=2.0에서 콘크리트에서 발생하는 최대압축응력은 Dome 하부에서 자오선방향으로 내부 표면에서 발생하였다. 최대인장응력은 Storage Wall 상부에서 자오선방향으로 내부 표면에서 발생하였다. 콘크리트에서 발생하는 최대압축응력값 및 최대인장응력값은 모두 허용응력 범위 이내임을 보여주었다.
수치해석 결과의 신뢰성 검증을 위해서는 현장에서의 계측자료와의 비교검토가 가장 좋은 해법이지만 계측자료 수집의 어려움으로 사일로 동굴처분시설의 3차원 유한요소모델을 구축하고 수치해석을 수행하여 결과의 검증작업을 병행하였다.
본 논문에서 제시한 연구결과는 향후 사일로 동굴처분시설의 안전성 평가를 위한 자료로 활용 가능할 것으로 판단된다.