Functionally Graded Structure Design for Heat Conduction Problems using Machine Learning

Yunho Moon; Cheolwoong Kim; Soonok Park; Jeonghoon Yoo

doi:10.7734/COSEIK.2021.34.3.159

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 June 2021. 159-165
https://doi.org/10.7734/COSEIK.2021.34.3.159

Functionally Graded Structure Design for Heat Conduction Problems using Machine Learning

머신 러닝을 사용한 열전도 문제에 대한 기능적 등급구조 설계

Yunho Moon¹

Cheolwoong Kim²

Soonok Park³

Jeonghoon Yoo⁴^*

문 윤호¹

김 철웅²

박 순옥³

유 정훈⁴^*

¹Graduate Student, Graduate school of Mechanical Engineering, Yonsei University, Seoul, 03722, Korea

²Graduate Student, Graduate school of Mechanical Engineering, Yonsei University, Seoul, 03722, Korea

³Professor, Department of Engineering Automotive, Dong Seoul University, Seongnam, 13117, Korea

⁴Professor, Department of Mechanical Engineering, Yonsei University, Seoul, 03722, Korea

¹연세대학교 대학원 기계공학과 석사과정

²연세대학교 대학원 기계공학과 박사과정

³동서울대학교 기계자동차과 교수

⁴연세대학교 기계공학부 교수

^{*Corresponding Author}

ABSTRACT

This study introduces a topology optimization method for the simultaneous design of macro-scale structural configuration and unit structure variation to ensure effective heat conduction. Shape changes in the unit structure depending on its location within the macro-scale structure result in micro- as well as macro-scale design and enable better performance than using isotropic unit structures. They result in functionally graded composite structures combining both configurations. The representative volume element (RVE) method is applied to obtain various thermal conductivity properties of the multi-material based unit structure according to its shape change. Based on the RVE analysis results, the material properties of the unit structure having a certain shape can be derived using machine learning. Macro-scale topology optimization is performed using the traditional solid isotropic material with penalization method, while the unit structures composing the macro-structure can have various shapes to improve the heat conduction performance according to the simultaneous optimization process. Numerical examples of the thermal compliance minimization issue are provided to verify the effectiveness of the proposed method.

Keywords

functionally graded structure,

topology optimization

heat conduction

representative volume element method

machine learning

solid isotropic material with penalization method

본 연구는 효과적인 열전도를위한 거시적 구조 구성과 단위 구조 변화의 동시 설계를 위한 위상 최적화 방법을 제시한다. 거시적 규모의 구조 내에서 위치에 따른 단위 구조의 형태 변화는 거시적 규모뿐만 아니라 미시적 단위의 설계도 가능하며 등방성 단위 구조를 사용하는 것보다 더 나은 성능을 제공할 수 있다. 이 결과로 두 구성을 결합한 기능적으로 등급의 복합 구조가 생성된다. 대표 체적 요소 (RVE) 방법은 형태 변화에 따른 다중 재료 기반 단위 구조의 다양한 열전도 특성을 얻기 위해 적용된다. RVE 분석 결과를 바탕으로 머신 러닝 기법을 이용하여 특정 형태의 단위 구조물의 물성치를 도출할 수 있다. 거시적 위상 최적화는 기존의 SIMP 방법을 사용하여 수행되며, 거시 구조를 구성하는 단위 구조는 동시 최적화 과정에 따라 열전도 성능을 향상시키기 위한 다양한 형태를 가질 수 있다. 제안된 방법의 효과를 확인하기 위해 열 컴플라이언스 최소화 문제의 수치예가 제공된다.

키워드

기능적 등급구조

위상 최적화

열전도

RVE 방법

머신 러닝

SIMP 방법

MAIN

1. 서 론
2. 단위 구조의 열전도 물성치의 도출
2.1 RVE 방법을 이용한 열전도 계수의 계산
2.2 머신 러닝을 이용한 단위 구조의 열전도 계수
3. 위상 최적설계
3.1 최적설계 알고리즘
3.2 위상 최적설계 정식화
3.3 헬륨홀츠 필터링과 수렴 조건
4. 수치 예제
4.1 단순 밀도법 기반의 위상 최적설계
4.2 제안된 설계 방법을 이용한 위상 최적설계
5. 결 론

1. 서 론

최적화 이론을 기반으로 한 구조물의 형상 최적화의 방법은 변수 최적화, 형상 최적화, 위상 최적화로 구분될 수 있다. 그 중에서도 위상 최적화는 구체적인 초기 형상을 필요로 하지 않고 물리적인 이론만으로는 도출이 어려운 구조를 제시할 수 있는 장점을 가지고 있다. 위상 최적화 방법은 균질화법(homogenization method) 이론을 적용한 방법에서 시작되어(Bendsøe and Kikuchi, 1988) 등방성 물질 기반의 요소의 밀도를 기반으로 한 SIMP (Solid Isotropic Material with Penalization) 방법으로 발전되어 왔으며(Bendsøe and Sigmund, 2003), 탄성, 진동, 열전도 등 다양한 기계적 구조 설계에 적용되었다.

일반적인 밀도법 기반의 위상 최적화에서는 설계 영역을 구성하는 각 요소가 동일한 밀도와 등방성의 물성치를 가지나, 균질화법을 적용한 위상 최적설계에서는 각 요소를 단위 구조(unit structure)로 표시하고 단위 구조의 밀도로써 거시적인 구조물 형상을 나타내고, 구조물에서의 각 요소의 위치에 따라 다른 형태의 단위 구조로 나타내는 거시적-미시적인 구조 설계가 가능하다. 이러한 설계를 기능적 등급 구조 설계(functionally graded structure design)이라고 하며(Lee et al., 2018), 최근에는 설계된 구조물의 구현이 3D 프린팅 기법을 이용하여 가능하게 됨으로써 다양한 관련 연구가 진행되고 있다. 이 방법에서는 단위 구조의 밀도에 따라 일반적인 위상 최적화의 방법과 같이 가시적인 구조물의 형상이 도출되고, 단위 구조의 형상을 정의하는 설계 변수에 따라 각 단위 구조의 형상이 결정된다. 설계 목적 함수의 계산을 위한 물성치는 단위 구조의 형상을 정의하는 설계 변수의 변화에 따라 물질화법을 기반으로 계산하게 된다. 따라서 이를 위해서는 균질화법에 대한 이해와 적용이 필수적이다.

본 연구에서는 이론적으로 복잡한 균질화법의 적용 대신 단위 구조의 형상 변화에 따른 물성치를 머신 러닝 기반의 방법을 이용하여 구하고자 한다. 단위 구조의 형상에 따른 물성치의 계산은 대표 체적 요소(Representative Volume Element, RVE) 방법에 의해 계산할 수 있으며(Sun and Vaidya, 1996), 다양한 형상 변화에 따른 물성치를 계산하여 데이터베이스를 구축하고 이에 머신 러닝 기법을 적용시킴으로써 임의의 형상 설계 변수 값에 따른 해당 단위 구조의 물성치의 회귀함수를 도출하여 이용하게 된다. 또한 기능적 등급 구조 설계의 연구에서 주로 다루고 있는 탄성계수를 이용한 구조물의 설계가 아닌 열전도의 효과를 높이기 위한 구조 설계를 진행하였다. 단위 구조의 형상을 정의하여 설계변수를 설정하고 이의 변화에 따른 단위 구조의 열전도 계수(heat conduction coefficient)를 RVE 방법을 이용하여 계산하고(Jung and Kim, 2016; Iasiello et al., 2019) 데이터베이스를 구축하여 머신 러닝 기법을 적용하였다. 간단한 수치 예제를 통하여 효과적인 열전도를 위한 SIMP 방법 기반의 거시적 구조 설계와 미시적인 단위 구조를 결합한 최적 형상을 도출하여 적용된 방법의 유용성을 검증하였다.

2. 단위 구조의 열전도 물성치의 도출

2.1 RVE 방법을 이용한 열전도 계수의 계산

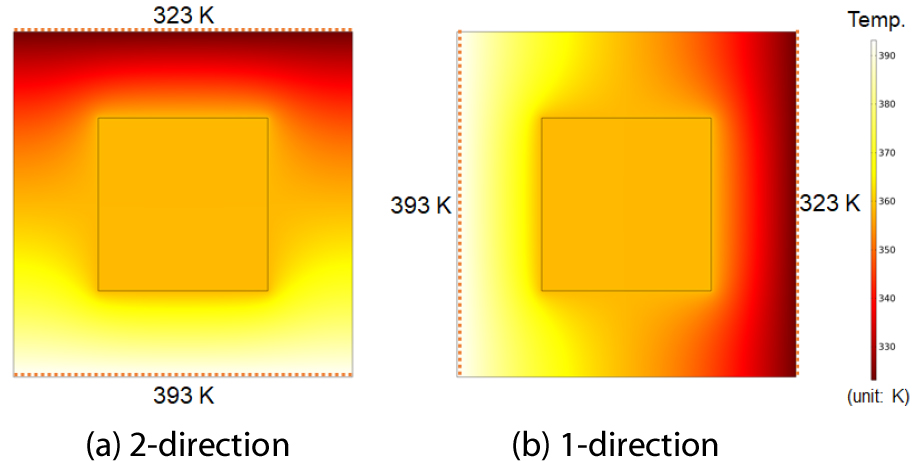
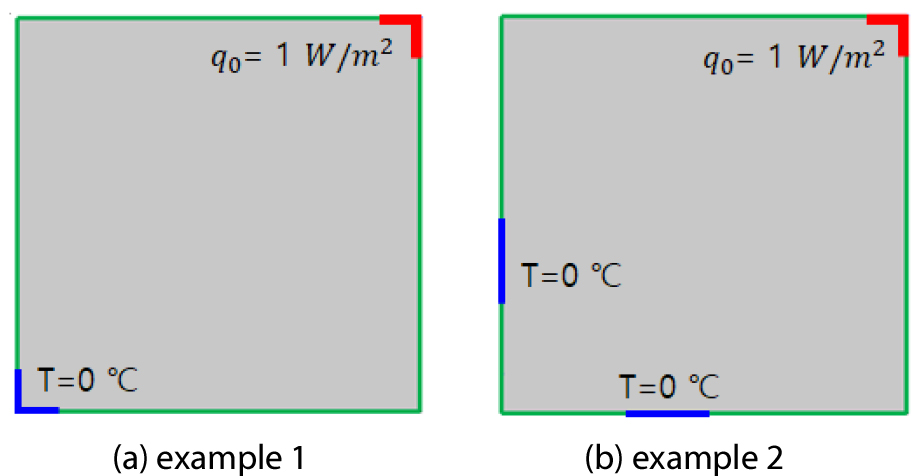
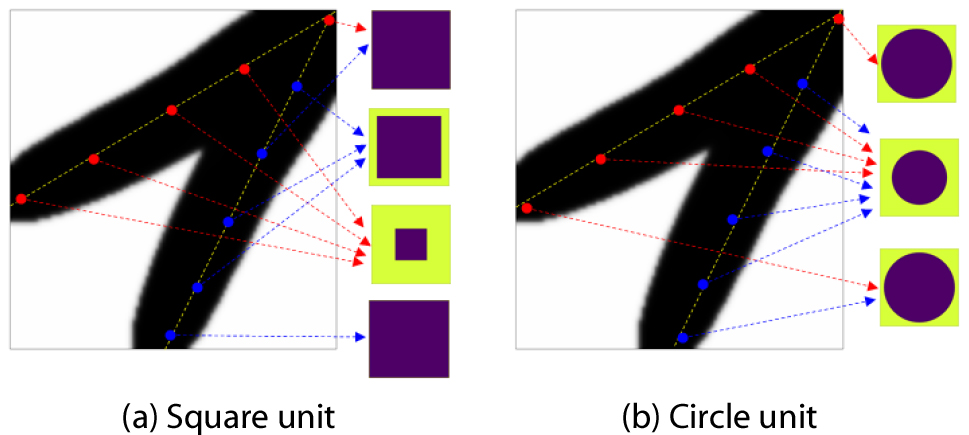
열전도 문제에 대해 등급 구조 설계를 적용하기 위하여 본 설계에 적용한 단위 구조는 등방성의 열전도 특성을 가지도록 Fig. 1에 표시된 바와 같이 다른 물적 특성을 가진 정사각형과 원형의 형상의 이종 물질을 포함하고 있다. Fig. 1의 단위 구조의 안쪽에 위치한 이종 물질의 열전도 계수는 1W/m²K로 설정하고 바깥쪽에 위치한 기저 물질의 열전도 계수는 0.1W/m²K로 설정하였다. 정사각형 단위 구조에서는 형상 변수 B가 0부터 0.01의 간격으로 1까지, 원형의 구조에서는 설계 변수 R이 0부터 0.01의 간격으로 1까지 변하도록 하여 Fig. 1의 1-방향과 2-방향의 열전도 계수를 계산하여 머신 러닝의 적용을 위한 데이터베이스를 구축하고자 하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F1.jpg

Fig. 1.

Shapes of unit structures composed of two different materials

RVE 방법을 이용한 단위 구조의 1-방향 및 2-방향으로의 열전도 계수는 다음의 같은 식을 이용하여 계산된다.

(1)

\bar{q_{i}}'' = \frac{1}{V} \int_{V}^{} q_{i} d V

(2)

\bar{T_{j}} = \frac{1}{V} \int_{V}^{} T_{j} d V

식 (1)은 체적 V에 따른 평균 열유속(heat flux)을 나타내며, 식 (2)는 평균 온도 분포를 나타내고 있다. 단위 구조의 특정 위치에 초기 온도를 설정하여 특정 방향(i 또는 j 방향)으로 열유속을 부여하고 이에 따른 열유속과 온도 분포를 상용패키지 COMSOL을 이용한 유한요소해석(Finite Element Analysis, FEA)을 통하여 계산한다. 단위 구조의 특정 방향의 열전도 계수는 요소 e의 온도 $\bar{T_{e}}$ 와 주변 요소들의 온도 $\bar{T_{j}}$ 를 고려하여 다음과 같이 계산된다.

(3)

k_{i j} = \frac{\bar{q_{i}}}{- (\bar{T_{j}} - \bar{T_{e}})}

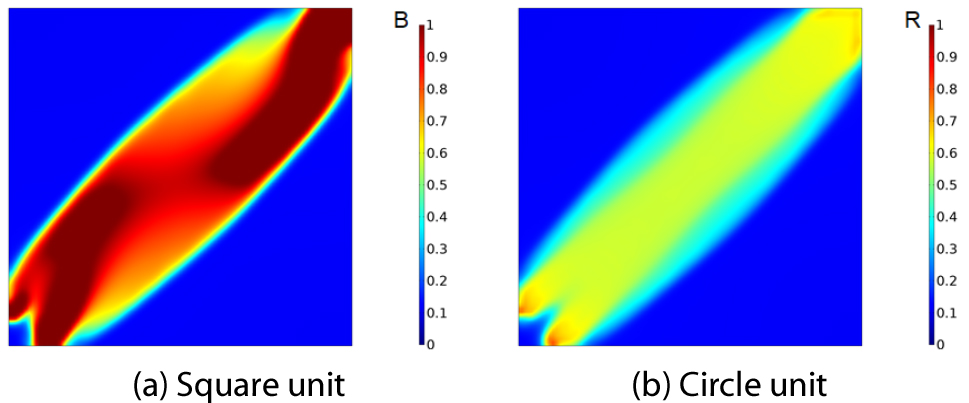
Fig. 2(a)와 (b)는 정사각형의 이종 물질을 지닌 단위 구조에 2-방향과 1-방향으로 120°C와 50°C의 높은 온도와 낮은 온도의 경계를 설정하여 FEA를 수행한 결과를 보여 주고 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F2.jpg

Fig. 2.

Temperature distribution of a unit structure using the finite element analysis

RVE 방법을 이용하여 구한 열전도 계수 값의 유용성을 확인하기 위하여 Fig. 1(a)의 이중 물질을 가진 단위 구조에서 구한 열유속의 평균값과, 동일한 크기의 단위 구조에서 모든 영역이 RVE 방법으로 구해진 일정한 열전도 계수를 가진 균질화한 단위 구조에 대한 열유속 평균값을 비교하였다. 두 개의 단위 구조 모델에 대한 1- 및 2- 방향의 평균 열유속 값을 FEA를 이용하여 도출하고 이에 따른 결과를 Table 1에 나타내었다. 두 결과의 차이는 1-방향으로 0.077%, 2- 방향으로 0.1%으로 나타나며 두 방법의 차이가 거의 없어 RVE 방법으로 구한 열전도 계수의 유용성을 확인할 수 있다.

Table 1.

Comparison of average heat flux between the heterogeneous and the homogeneous unit structure (unit: W/m²)

	Heterogeneous	Homogeneous	difference(%)
1-direction	8.695	8.7017	0.077
2-direction	9.675	9.6848	0.1

2.2 머신 러닝을 이용한 단위 구조의 열전도 계수

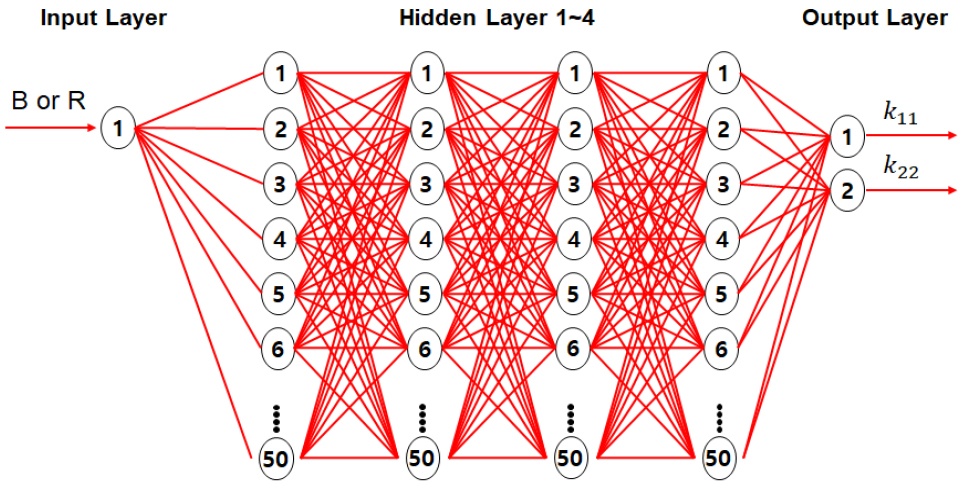
RVE를 이용하여 도출된 단위 구조의 형상에 따른 열전도 계수의 데이터를 이용한 머신 러닝의 구성을 Fig. 3에 나타내었다. 총 데이터의 개수는 사각형 단위 구조의 경우 100개, 원형 단위 구조일 때 50개로 머신 러닝 과정은 MATLAB의 application 모듈을 이용하여 진행하였다. 입력은 설계 변수 B 또는 R이고, 출력은 1- 및 2-방향의 열전도 계수가 된다. 데이터 설정은 training data 70%, validation data 15%, testing data 15%로 무작위로 설정되었다. Hidden layer는 4개로 설정하고 hidden layer의 hidden neuron의 개수는 각각 50개로 설정된다. Hidden layer와 hidden neuron의 개수는 overfitting을 피하기 위한 적합한 개수로 임으로 설정하였다. 학습시킨 머신 러닝 데이터와 RVE 방법으로 도출된 데이터의 비교는 다음의 식 (4)로 표시된 평균제곱오차(Mean Sqaure Error, MSE)를 계산하여 진행하였다. MSE의 값은 0.0056으로 두 데이터가 거의 일치함을 확인할 수 있다.

(4)

M S E = \frac{1}{n} \sum_{i = 1}^{n} (\hat{Y_{i}} - Y_{i})^{2}

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F3.jpg

Fig. 3.

Composition of machine learning process

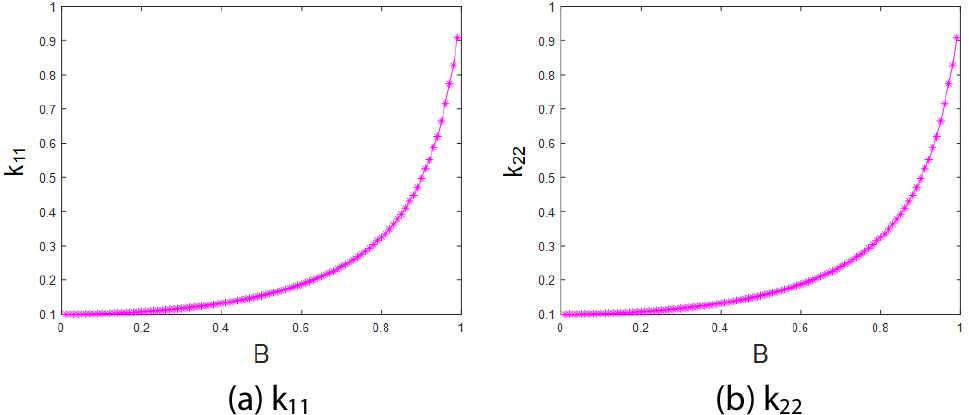
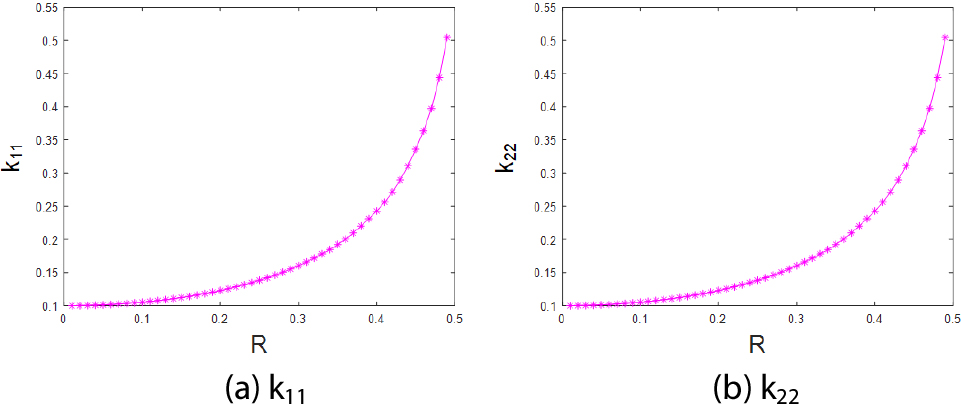
Fig. 1에 제시된 두 개의 단위 구조의 형상 변화에 따른 열전도 계수의 변화량을 머신 러닝에 의해 도출한 그래프를 Fig. 4와 Fig. 5에 나타내었다. 두 단위 구조 모두 $k_{11}$ 과 $k_{22}$ 가 형상 변수 값의 증가에 따라 동일하게 증가하는 것을 확인할 수 있다. 이는 두 단위 구조 모두 1-방향과 2-방향으로 동일한 비율로 증가함에 따로 등방성의 열전도 계수의 특성을 나타냄에 기인한다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F4.jpg

Fig. 4.

Plots of heat conductivity for square type unit structure obtained by machine learning

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F5.jpg

Fig. 5.

Plots of heat conductivity for circle type unit structure obtained by machine learning

3. 위상 최적설계

3.1 최적설계 알고리즘

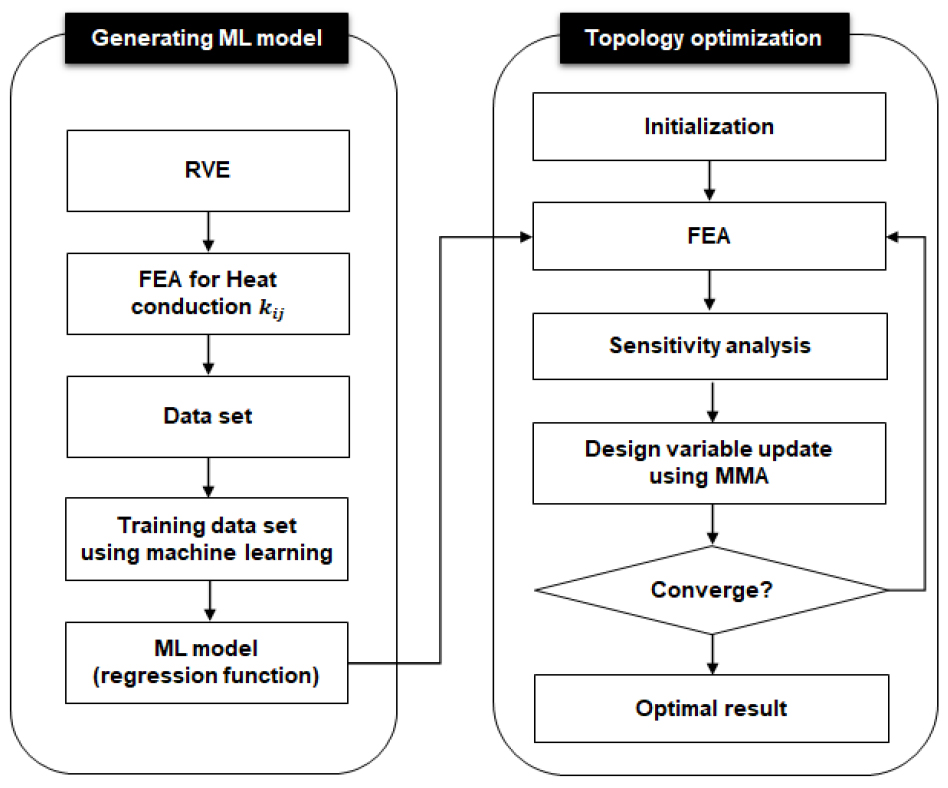
본 연구에서의 최적화 설계의 전체 과정 flowchart를 Fig. 6에 나타내었다. Generating ML model 부분은 2장에서 설명한 RVE와 머신 러닝을 이용하여 단위 구조의 형상 변화에 따른 열전도 계수를 구하는 과정을 보여주고 있다. 단위 구조의 형상 변수 B 또는 R의 변화에 따른 열전도 계수를 회귀방정식(regression function)으로 변환하고 이를 위상 최적설계 부분의 FEA 과정에서의 물성치 정의에 적용한다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F6.jpg

Fig. 6.

Flowchart for the optimization process

위상 최적설계 과정은 거시적 구조의 밀도를 나타내는 설계변수와 더불어 단위 구조의 형상 변수를 설계변수로 설정하여 진행된다. 설계변수의 업데이트는 method of moving asymptotes (MMA) 알고리즘을 이용하여 진행된다(Svanberg, 1987). 변수들의 초기값을 설정하고 FEA, 민감도 계산, MMA 업데이트 방법을 통해 설계 값들이 수렴하면 이에 따른 최적화 형상을 도출하게 된다.

3.2 위상 최적설계 정식화

열전도 효과를 극대화하기 위한 기능적 등급 구조의 위상 최적설계를 위한 최적화 문제는 다음과 같이 정식화된다.

(5)

F i n d : d = (ϕ_{ρ}, ϕ_{B o r R}) \underset{d}{M i n i m i z e} D = \frac{1}{2} \int_{o h m}^{} k (d) (||\nabla T||)^{2} d o h m S u b j e c t t o - \nabla ∙ [k (d) \nabla T] = Q V (ϕ_{ρ}) \leq \bar{V}

위 식에서 설계 변수 d는 거시적 밀도 설계 변수 $ϕ_{ρ}$ 와 단위 구조의 형상 변수 $ϕ_{B or R}$ 이 포함된다.

식 (5)에서 목적함수 D는 설계 변수 d와 상태 변수인 온도 T를 포함하며 이를 최소화함으로써 설게 영역 내에서 열전달률을 극대화하는 또는 열컴플라이언스(thermal compliance) 값을 최소화하는 것을 의미한다. 식 (5)의 설계 제약조건(design constraints)은 각각 물리적 지배 방정식과 설계 영역 내의 부피 제한 조건을 나타낸다. 설계 영역에서 물질에 의해 점유되는 부피는 다음의 식에 의해 계산된다.

(6)

V = \int_{o h m}^{} ρ (ϕ_{ρ}) d V

식 (6)에서 설계영역 내의 총 부피 V는 설계 변수 $ϕ_{ρ}$ 에 의해 결정된 복합 밀도 $ρ$ 에 의해 정의되며 이는 0에서 1 사이의 값을 가진다.

3.3 헬륨홀츠 필터링과 수렴 조건

밀도법에 의해 도출된 위상 최적화의 결과는 체커보드 형상(checkerboard pattern)의 설계 영역을 나타내는 등 유한요소에 의해 좌우되는 결과를 나타낼 수 있으므로, 다음의 편미분 방정식 기반의 Helmholtz 필터를 사용하여 설계 변수를 정규화 하여 매끄럽게 변형된 경계를 도출할 수 있다(Lazarov and Sigmund, 2011).

(7)

- \nabla \cdot (R^{2} \nabla \{\begin{matrix} {\tilde{ϕ}}_{ρ} \\ {\tilde{ϕ}}_{B or R} \end{matrix}\}) + \{\begin{matrix} {\tilde{ϕ}}_{ρ} \\ {\tilde{ϕ}}_{B or R} \end{matrix}\} = \{\begin{matrix} ϕ_{ρ} \\ ϕ_{B or R} \end{matrix}\}

위에서 R은 단위 구조 설계변수에 대한 필터 반경이다. 필터링 된 설계변수 $({\tilde{ϕ}}_{B or R} \in [- 1 . 1])$ 는 다음의 식에 의해 단위 구조 크기 변수 $({\tilde{ϕ}}_{B or R} \in [0 . 1])$ 에 투영된다.

(8)

\{B o r R\} = \frac{1}{2} (\{{\tilde{ϕ}}_{B or R}\} + 1)

(9)

ρ = H_{r} (\tilde{ϕ_{ρ}} (x))

식 (9)의 특성 함수 H_r은 다음과 같이 나타낸다.

(10)

H_{r} ({\tilde{ϕ}}_{ρ}) = \{\begin{matrix} 0 ({\tilde{ϕ}}_{ρ} \leftarrow h) \\ \frac{1}{2} + \frac{15}{16} (\frac{{\tilde{ϕ}}_{ρ}}{h}) - \frac{5}{8} (\frac{{\tilde{ϕ}}_{ρ}}{h})^{3} + \frac{3}{16} (\frac{{\tilde{ϕ}}_{ρ}}{h}) \\ (- h \leq {\tilde{ϕ}}_{ρ} \leq h) \\ 1 (h < {\tilde{ϕ}}_{ρ}) \end{matrix}

식 (10)에서 h는 완전한 복합 영역과 무효 영역 사이의 대역폭을 나타내는 양의 매개변수이다. 좁은 대역폭 h는 필터링에 의해 약화 될 수 있는 경계의 선명도를 향상시킬 수 있다. h는 1에서 시작하여 다음 식 (11)의 수렴 기준이 충족된 후 0.85의 비율로 감소한다. 수렴 조건은 k번째 반복에서의 설계 변수 $Φ^{(k)}$ 의 변화량을 고려하여 다음과 같이 정의된다.

(11)

e r = \frac{||Φ^{(k)}|| - ||Φ^{(k - 1)}||}{||Φ^{(k - 2)}||}

이에 따른 수렴 조건은 $e r \leq \bar{e r} (\bar{e r} = 4 \times 10^{- 4})$ 로 정의된다. $\bar{e r}$ 은 반복 단계에 대한 허용 오차이다. 대역폭 h가 0.1미만으로 감소하면 전체 최적화 과정에서의 수렴 기준이 충족되도록 설정한다.

4. 수치 예제

4.1 단순 밀도법 기반의 위상 최적설계

제안된 위상 최적설계 방법의 효과를 확인하기 위해 Fig. 7에 나타낸 수치 예제에 대하여 최적 형상을 도출하였다. 모든 경우에서 재료의 열전도율과 고정 설계 영역의 초기 구성은 균일한 단위 구조의 분포를 갖는다. 그림에 표시된 설계 영역은 5m $\times$ 5m 정사각형의 형상을 가지며 설계영역은 50 $\times$ 50의 요소로 구성된다. 파란색 경계에는 T=0℃의 온도 분포가, 빨간색 경계에는 열유속 1W/m²이 적용된다. 최적의 형상은 앞의 식 (5)에서와 같이 열 컴플라이언스를 최소화를 목적으로 도출된다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F7.jpg

Fig. 7.

Example model definitions for topology optimization

제안된 설계 방법을 적용하기 전에 일반적인 SIMP 방법 기반의 구조설계를 진행하였다. 각 요소의 열전도 계수 k는 요소의 밀도 ρ에 SIMP 방법을 적용하여 다음의 식으로 계산된다.

(12)

k (ρ) = (0.001 + 0.999 ρ^{p}) k_{0}

여기서, k₀는 ρ=1의 경우의 열전도 계수이며 0.5W/m²K로 설정하였다.

Fig. 8은 부피 제약 조건을 전체 설계 영역의 40%로 설정한 SIMP 방법 기반의 위상 최적설계의 결과를 나타낸다. 모든 경우에서 명확한 위상 최적설계의 형상을 도출하였으며, Fig. 8(a)에서 최적화된 구조의 형상은 열유속 경계 조건이 적용된 오른쪽 상단 모서리에서 온도 조건이 설정된 왼쪽 하단까지 하나로 연결된 구조를 나타낸다. 이에 반하여 Fig. 8(b)에서 도출된 구조는 두 부분으로 설정된 온도 경계 조건으로 갈라지는 구조를 보여주고 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F8.jpg

Fig. 8.

Optimal configurations derived from the ordinary SIMP method

4.2 제안된 설계 방법을 이용한 위상 최적설계

4.1에서 수행된 설계 예제에 대하여 제안된 설계 방법을 적용하여 기능적 등급 구조 기반의 위상최적 형상을 도출하였다. 재료의 열전도율과 고정 설계 영역의 초기 구성은 앞 절과 동일하게 설정하였다. 각 요소의 열전도 계수는 SIMP 방법을 적용하여 다음의 식 (13)과 같이 정의된다. 있는 등방성 재료(SIMP)공식이 수치 예제에 적용된다. SIMP공식에서 열전도 k는 식(13)과 같이 공식화 된다.

(13)

k (ρ) = (0.001 + 0.999 ρ^{p}) k^{D L} (B or R)

여기에서 $k^{D L}$ 은 단위 구조의 설계변수 B 또는 R에 의해 머신 러닝 방법에 의해 도출된 회귀함수를 이용하여 계산된 단위 구조의 열전도 계수이며, 이는 다음의 식으로 표시된다.

(14)

k^{D L} = [\begin{matrix} k_{11} (b y B or R) & 0 \\ 0 & k_{22} (b y B or R) \end{matrix}]

Fig. 9는 Fig. 7의 예제 1에 대해서 Fig. 1의 단위 구조를 적용한 설계 결과를 나타낸다. 부피 제약 조건은 전부 설계영역 면적의 40%로 설정하였다. 거시적인 형상은 두 결과 모두 대각선을 가로지르는 구조를 나타내고 있으나, 단위 구조의 형상에 따라서 미세하게 다른 구조를 나타내고 단위 구조의 설계 변수도 상이한 분포를 보여주고 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F9.jpg

Fig. 9.

Design results of example 1 through the proposed method using different unit structures

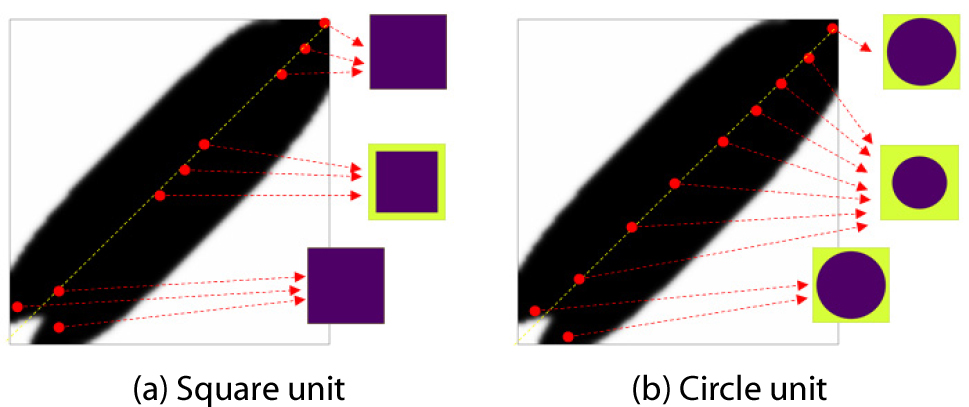
Fig. 10은 Fig. 9의 결과를 기반으로 거시적 구조의 위치에 따른 단위 구조의 형상을 보여주고 있다. 정사각형의 단위 구조는 두 지점을 연결하는 대각선을 따라 단위 구조 안쪽의 높은 열전도 계수를 가진 물질이 거의 채워진 형상을 보여주고 있다. 이에 비해서 원형의 단위 구조는 상대적으로 높은 열전도 계수의 물질이 덜 채워진 분포를 나타낸다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F10.jpg

Fig. 10.

Unit structure distribution of the result of example 1

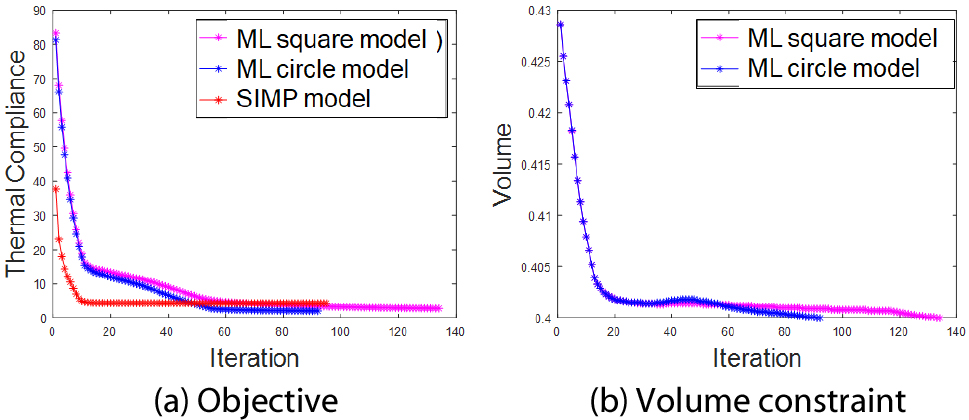
Fig. 11은 예제 1에 대한 설계 이력의 그래프를 나타내고 있다. Fig. 8(a)의 SIMP 적용 결과(SIMP model)와 제시된 방법에 의한 정사각형 단위 구조(ML square model)와 원형 단위 구조(ML circle model)의 적용 결과를 비교할 수 있으며, ML circle 모델의 수렴성이 우수함을 나타내고 있다. 목적 함수의 결과값은 SIMP 모델이 4.87, ML square 모델이 3.16, ML circle 모델이 3.11로 계산된다. SIMP 모델에서 ρ=1의 경우의 열전도 계수를 0.1과 1사이인 0.5로 설정하였음을 고려할 때, 단위 구조를 이용한 기능적 등급 구조 기반의 설계 결과가 더 우수함을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F11.jpg

Fig. 11.

Convergence history plots of example 1 for various cases

Fig. 12는 Fig. 7의 예제 2에 대해서 부피 제약 조건 40%에 대하여 Fig. 1의 단위 구조를 적용한 설계 결과를 나타낸다. 두 형상 모두 우측 상단에서 좌측 하단으로 양 갈래로 나눠지는 형태를 나타내고 있으나 단위 구조의 형상에 따라서 그 분포에서 다른 구조를 나타내고 단위 구조의 설계 변수도 상이한 분포를 보여주고 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F12.jpg

Fig. 12.

Design results of example 2 through the proposed method using different unit structures

Fig. 13은 거시적 구조의 위치에 따른 단위 구조의 형상을 보여주고 있다. 정사각형의 단위 구조에서 위쪽 가지 부분은 고열전도 계수의 정사각형 부분의 크기가 전체 영역의 0.4 정도를 차지하는 반면에 아래쪽 부분은 그 크기가 0.8~1 정도를 차지하고 있다. 원형의 단위 구조의 결과는 양 끝단을 제외하고는 균일하게 높은 열전도도 물질로 차있는 것을 확인할 수 있다. 온도 경계의 위치를 고려할 때 원형의 단위 구조의 결과에서와 같이 대칭적인 결과가 나와야 하지만 정사각형의 단위 구조의 경우는 직교이방성(orthotropic) 물질 특성을 가지고 있어 경사진 구조의 형상에서 이를 반영하지 못하는 것으로 판단된다. 향후의 연구에서는 이러한 한계를 고려한 단위 구조의 설계와 단위 구조의 내부에 위치한 이종 물질의 회전 효과의 고려 등이 요구된다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F13.jpg

Fig. 13.

Unit structure distribution of the result of example 2

Fig. 14는 예제 2에 대한 설계 이력의 그래프를 나타낸다. Fig. 11과 같이 세 개 모델의 적용 결과를 비교할 수 있으며, 전반적으로 ML circle 모델의 수렴성과 결과의 우수성을 보여주고 있다. 목적 함수의 결과값은 SIMP 모델이 4.29, ML square 모델이 2.79, ML circle 모델이 2.07로 계산되며, 단위 구조를 이용한 기능적 등급 구조 기반의 설계 결과가 더 우수함을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340305/images/Figure_jcoseik_34_03_05_F14.jpg

Fig. 14.

Convergence history plots of example 2 for various cases

5. 결 론

본 연구에서는 균질화법이 아닌 머신 러닝 기반의 단위 구조 설계를 이용한 기능적 등급 구조 기반의 위상최적 설계 방법을 제시하였다. 제시된 방법을 열전도 효과의 향상을 위한 예제에 적용한 결과, 단위 구조를 결합한 설계의 결과는 일반적인 SIMP 기반의 밀도법 기반의 결과보다 우수함을 보여 주고 있다. 또한 등방성의 특징을 가진 원형의 고열전도 계수의 물질을 가진 단위 구조가 보다 효과적임을 확인할 수 있다. 일반적인 물질의 열전도 특성을 고려할 때 높은 열전도 계수를 가진 단위 구조의 부분이 인접한 단위 구조의 해당 부분과 서로 연결되는 것이 효과적일 것으로 판단되며, 이를 위해서는 새로운 단위 구조의 제시와 경계 조건의 적용이 요구된다.

Acknowledgements

이 논문은 2019년도 연구재단의 지원과(NRF-2019R1A2B5 B01069788). 2020년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구임(No.2020 4030200010).

References

Bendsøe, M.P., Kikuchi, N. (1988) Generating Optimal Topologies in Structural Design using a Homogenization Method, Comput. Methods Appl. Mech. Eng., 71(2), pp.197~224. 10.1016/0045-7825(88)90086-2

Bendsøe, M.P., Sigmund, O. (2003) Topology Optimization: Theory, Methods and Applications, Springer-Verlag, Berlin, p.370.

Iasiello, M., Bianco, N., Chiu, W.K., Naso, V. (2019) Thermal Conduction in Open-Cell Metal Foams: Anisotropy and Representative Volume Element, Int. J. Therm. Sci., 137, pp.399~409. 10.1016/j.ijthermalsci.2018.12.002

Jung, C.-G., Kim, S.-U. (2016) Study on Material Properties of Composite Materials using Finite Element Method, Compos. Struct., 29(1), pp.61~65. 10.7734/COSEIK.2016.29.1.61

Lazarov, B.S., Sigmund, O. (2011) Filters in Topology Optimization based on Helmholtz‐Type Differential Equations, Int. J. Numer. Methods Eng., 86(6), pp.765~781. 10.1002/nme.3072

Lee, J., Kim, D., Nomura, T., Dede, E.M., Yoo, J. (2018) Topology Optimization for Continuous and Discrete Orientation Design of Functionally Graded Fiber-Reinforced Composite Structures, Compos. Struct., 201, pp.217~233. 10.1016/j.compstruct.2018.06.020

Sun, C., Vaidya, R. (1996) Prediction of Composite Properties from a Representative Volume Element, Compo. Sci. Technol., 56(2), pp.171~179. 10.1016/0266-3538(95)00141-7

Svanberg, K. (1987) The Method of Moving Asymptotes-A New Method for Structural Optimization, Int. J. Numer. Methods Eng., 24(2), pp.379~373. 10.1002/nme.1620240207

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Functionally Graded Structure Design for Heat Conduction Problems using Machine Learning

ABSTRACT

MAIN

Fig. 1.

Shapes of unit structures composed of two different materials

(1)

(2)

(3)

Fig. 2.

Temperature distribution of a unit structure using the finite element analysis

Table 1.

Comparison of average heat flux between the heterogeneous and the homogeneous unit structure (unit: W/m2)

(4)

Fig. 3.

Composition of machine learning process

Fig. 4.

Plots of heat conductivity for square type unit structure obtained by machine learning

Fig. 5.

Plots of heat conductivity for circle type unit structure obtained by machine learning

Fig. 6.

Flowchart for the optimization process

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Fig. 7.

Example model definitions for topology optimization

(12)

Fig. 8.

Optimal configurations derived from the ordinary SIMP method

(13)

(14)

Fig. 9.

Design results of example 1 through the proposed method using different unit structures

Fig. 10.

Unit structure distribution of the result of example 1

Fig. 11.

Convergence history plots of example 1 for various cases

Fig. 12.

Design results of example 2 through the proposed method using different unit structures

Fig. 13.

Unit structure distribution of the result of example 2

Fig. 14.

Convergence history plots of example 2 for various cases

Acknowledgements

References

Comparison of average heat flux between the heterogeneous and the homogeneous unit structure (unit: W/m²)