1. 서 론
2. 본 론
2.1 준-비정상 기법
2.2 형상 및 수치 해석 조건
2.3 격자 독립성과 난류 모델 검증
3. 해석 결과 및 분석
3.1 준-비정상 기법 해석 결과 및 분석
3.2 준-비정상 기법과 비정상 해석 결과 비교
4. 결 론
1. 서 론
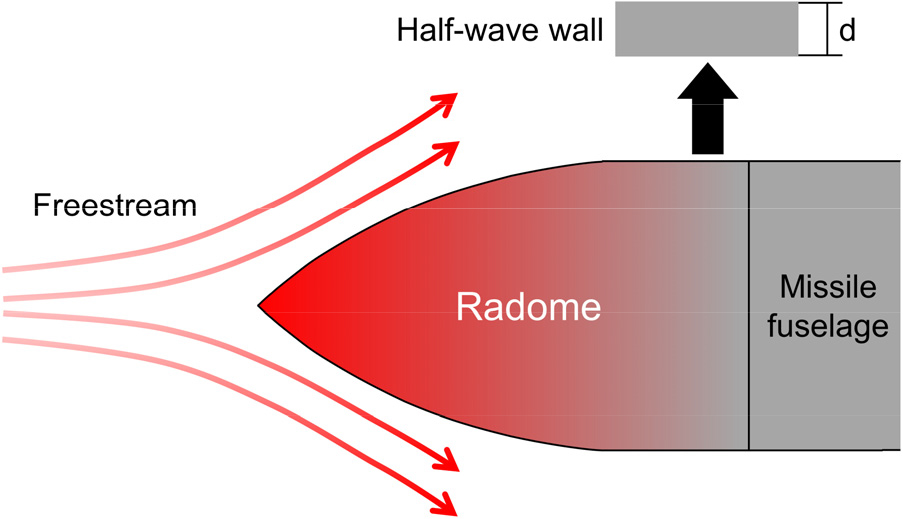
레이돔은 외부 환경으로부터 레이더와 같은 전자장비를 보호하는 장치이다(Crone et al., 1981). 미사일 레이돔은 Fig. 1과 같이 미사일의 첨단부에 설치되어 미사일이 비행하면서 가해지는 공력 가열과 공기역학적 힘, 그리고 빗물의 침식과 같은 요인으로부터 레이더를 보호한다. 특히 초음속 혹은 극초음속으로 비행하는 미사일은 유동의 마찰력으로 인한 영향이 커져 공력 가열에 의해 레이돔이 극심한 열유속에 노출된다(Dhumal et al., 2023). 이러한 열유속에 의해 레이돔 표면의 온도가 소재의 허용 온도 이상으로 상승하면 레이돔의 열적 안정성과 레이더의 성능에 영향을 미칠 수 있으므로 레이돔 설계 과정에서 열전달 특성이 고려되어야 한다.
레이돔의 열전달 특성에 관해서는 실험과 수치 해석을 통해 연구되었다. Dankert와 Otto(2007)은 고엔탈피 충격파 터널에서의 실험을 통해 마하수 6 유동장 내에서의 레이돔 벽의 온도 분포를 도출하였으며, 이를 수치 해석 결과와 비교하여 수치 해석 값을 검증하였다. Hohn 등(2019)은 초음속 풍동 실험을 통해 마하수 3의 유동장 내에서의 레이돔의 온도 분포를 도출하였으며 레이돔 내부 단열재의 영향을 분석하였다. 기존 연구들은 미사일이 비행할 때 비행 시나리오에 따른 속도와 고도 변화를 고려하지 않고 일정한 조건의 유동장 내에서 레이돔의 열전달 특성에 대해 연구하였다. 실제 미사일은 그 사용 목적에 따라 다양한 비행 시나리오 하에서 운용되며 발사 후 속도와 고도가 지속적으로 변한다. 이러한 변화에 따라 미사일에 가해지는 열부하가 변하기 때문에 실제 임무 수행 시 레이돔의 열전달 특성을 분석하기 위해서는 시간에 따른 속도와 고도 변화를 고려해야 한다. 또한 현재 소형 미사일은 최고 속도가 초음속의 범위에서 운용되고 있지만, 극초음속 미사일도 활발히 개발 중이다(Kramer et al., 2023). 미사일의 마하수가 극초음속의 범위로 확장되면 그에 따라 미사일의 구성 요소에 가해지는 열유속은 증가하고 시간에 따른 변화도 커질 것이기 때문에 시간에 따른 변화를 반영한 열전달 특성 분석이 더욱 중요하다.
시간에 따른 미사일의 속도와 고도 변화를 반영하여 레이돔의 열전달 특성을 분석하기 위해서는 대류 열전달과 전도 열전달을 시간에 따라 동시에 계산하는 비정상 복합 열전달 해석(transient conjugate heat transfer analysis)이 필요하다. 또한 미사일이 극초음속까지 가속될 수 있으므로 해석을 수행할 때 초음속 혹은 극초음속 난류 유동의 변화가 고려되어야 한다. 하지만 초음속 혹은 극초음속 난류 유동의 시간 스케일은 매우 작아 해당 시간 스케일에 따른 비행 조건 변화를 모두 고려하여 비정상 복합 열전달 해석을 수행하는 것은 어렵다. 따라서 유동 영역과 고체 영역의 해석을 분리해서 해석을 수행하는 연성 연계 기법(loosely copuled method)가 초음속 비행체의 열전달 특성을 분석하기 위해 사용되고 있다(Zhang et al., 2014). 연성 연계 기법은 일정한 기준에 따라 비행 시나리오의 구간을 나누고 각 구간에 대해서 대류 열전달 해석과 전도 열전달 해석을 분리하여 수행하는 기법이다. 대류 열전달 해석을 수행할 때는 비행체의 표면 온도를 고정하고, 정상 상태 유동장 해석을 통해 비행체 표면으로의 열유속을 도출한다. 이 열유속을 비정상 전도 열전달 해석에 적용하여 시간에 따른 비행체 표면 온도를 도출한다. 그러나 이러한 방식은 전도 열전달 해석을 수행할 때 비행체 표면 온도가 증가함에 따라 감소하는 열유속이 반영되지 않아 실제보다 과도한 열유속이 유입되어 비행체 표면의 온도를 과대 예측할 수 있다. 따라서 본 연구에서는 연성 연계 기법과 비행체 표면으로의 열유속 변화를 반영할 수 있는 비정상 복합 열전달 해석을 결합한 준-비정상 기법(quasi-transient method)을 사용하였다(Bae et al., 2017). 연성 연계 기법과 달리 준-비정상 기법은 비행체 전도 열전달 해석을 수행할 때 비정상 복합 열전달 해석을 수행하여 시간에 따른 표면 온도와 열유속의 변화를 반영할 수 있다.
따라서 본 연구는 마하수 7까지 가속하는 가상의 극초음속 미사일의 비행 시나리오를 반영하기 위해 준-비정상 기법을 적용하여 수치 해석을 수행하였다. 또한 해당 비행 시나리오에 대해 준-비정상 기법과 비정상(full transient) 해석 결과를 비교하여 준-비정상 기법의 정확도와 해석 효율성을 입증하였다.
2. 본 론
본 장에서는 준-비정상 기법을 소개한 후 수치 해석을 수행하기 위한 레이돔 형상과 가상의 비행 시나리오를 반영한 해석 조건을 제시하였다.
2.1 준-비정상 기법
준-비정상 기법은 계산 용량의 한계로 인해 비행체의 복합 열전달(conjugate heat transfer) 문제에 대한 비정상 해석이 어려운 경우 이를 효율적으로 수행할 수 있는 기법이다. 준-비정상 기법은 비행 시나리오를 시간에 따라 임의의 조건에 의해 구간으로 나누어 정상 상태 유동장 해석과 비정상 복합 열전달 해석을 수행하는 방식이다. 비정상 점성 압축성 유동에 대한 RANS(Reynolds-averaged Navier-Stokes equation) 방정식의 적분 형태는 식 (1)과 같이 표현된다.
식 (1)에서 는 임의의 검사 체적(control volume) V의 제어 면을 나타내고, 은 제어 면에 수직인 단위 벡터(unit vector)를 의미한다. 보존 상태 변수 벡터 와 대류 플럭스 , 그리고 점성 플럭스 는 각각 식 (2)와 같이 정의된다.
식 (2)에서 첨자는 각각 축 방향과 반경 방향을 나타낸다. 는 유체 속도, 그리고 는 반변 속도(contravariant velocity)로 로 표현할 수 있다. 𝜌는 유체의 밀도, 는 압력, 는 총에너지, 는 전체 엔탈피, 𝜏는 점성 응력 텐서, 그리고 는 유동에서의 열 플럭스는 나타낸다. 비정상 고체 영역에서의 열전도를 계산하기 위한 열전도 지배 방정식은 식 (3)와 같다.
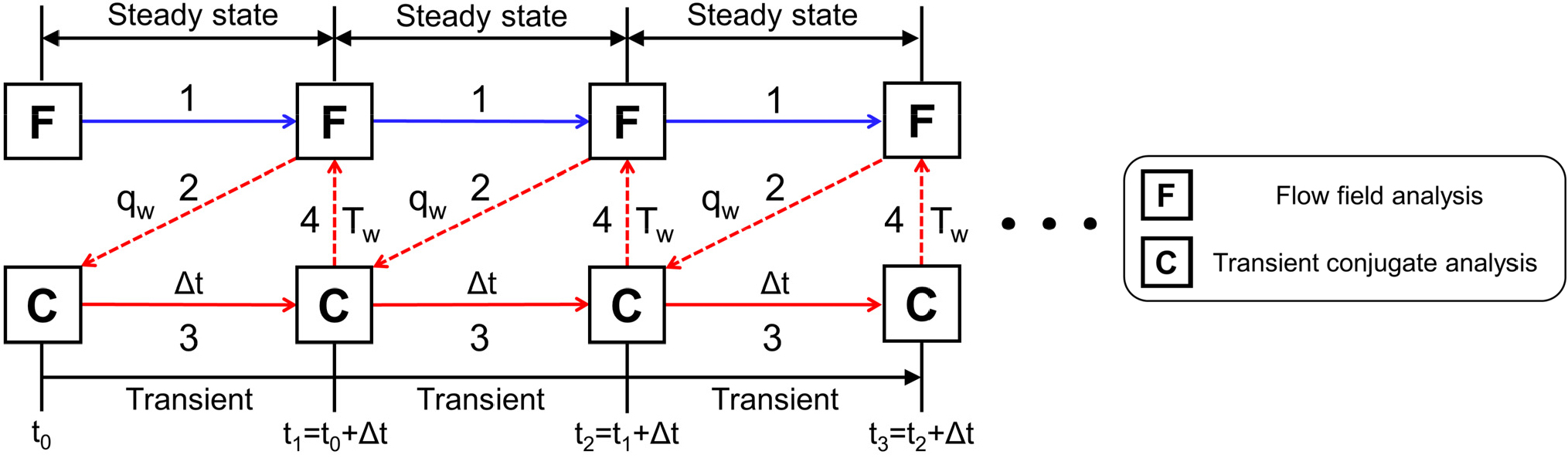
식 (2)에서 는 고체의 밀도, 는 고체의 비열, 는 고체의 비열, 는 고체의 열전도도, 그리고 는 외부 열원을 나타낸다. Fig. 2는 준-비정상 기법을 수행하기 위한 방법을 도식적으로 나타낸다. 시작 시간(tn)과 종료 시간(tn+1)을 가지는 비행 시나리오의 임의의 구간에 대해 준-비정상 기법을 수행하는 절차는 다음과 같다.
1) 초기 레이돔 벽의 온도로 해당 구간의 유동 조건에 대해 정상 상태 해석을 수행하여 정상 상태에 수렴시킨다.
2) 정상 상태 해석을 통해 도출된 레이돔 벽면으로의 열유속을 레이돔 벽면의 경계 조건으로 적용한다. 그리고 고체와 유체 간의 온도와 열유속의 연속성을 위해 식 (4)와 식 (5)와 같은 경계 조건을 레이돔 벽면에서 만족하도록 한다.
3) tn에서 tn+1까지 비정상 복합 열전달 해석을 수행한다.
4) 비정상 복합 열전달 해석을 통해 얻어진 레이돔 벽면의 온도를 디리클레 경계 조건(Dirichlet boundary condition)으로 활용한다.
5) 레이돔 벽면의 온도를 기준으로 다음 시간 구간의 정상 상태 해석을 수행한다.
식 (4)와 식 (5)에서 와 는 각각 유체와 고체의 열전도도 그리고 와 는 유체와 고체 경계면에서의 온도 구배를 나타낸다. 상기 과정은 각 구간에 대해 반복된다. tn에서 tn+1까지 비정상 복합 열전달 해석 과정에서 레이돔 벽면에 가해지는 열유속에 의해 레이돔의 온도가 상승하고 이에 따른 열유속 변화가 반영된다.
2.2 형상 및 수치 해석 조건
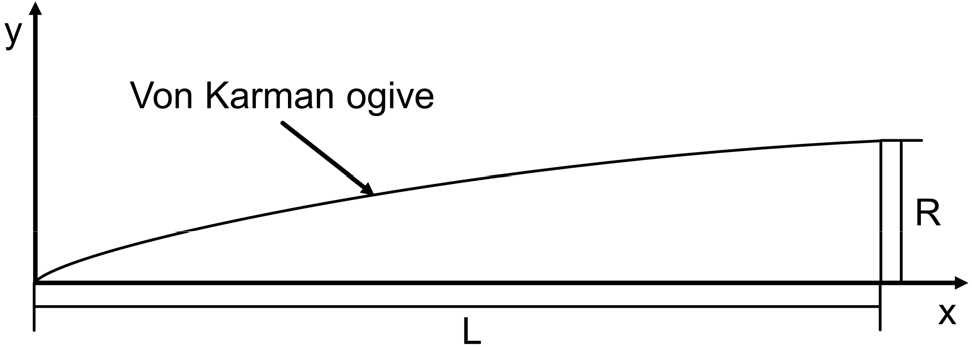
본 연구에서는 수치 해석을 위해 ANSYS Fluent 2022 R2를 사용하였으며 압축성 유동 해석에 유리한 density-based solver를 적용하였다. 각 변수의 차분화에는 2nd order upwind 기법을 적용하였다. 수치 해석에 사용된 컴퓨터의 프로세서는 Intel(R) Xeon(R) CPU E5-2690 v4이다. 본 연구 레이돔의 형상은 우수한 공기역학적 특성을 가지는 Von Karman ogive 형상으로 선정하였다(Nielsen, 1960). Von Karman ogive 형상은 수학적으로 항력을 줄이기 위해 도출된 형상으로 식 (6)과 (7)에 의해 형상이 정해진다. 식 (7)에서 C 값이 0일 때를 Von Karman ogive 형상이라 칭한다.
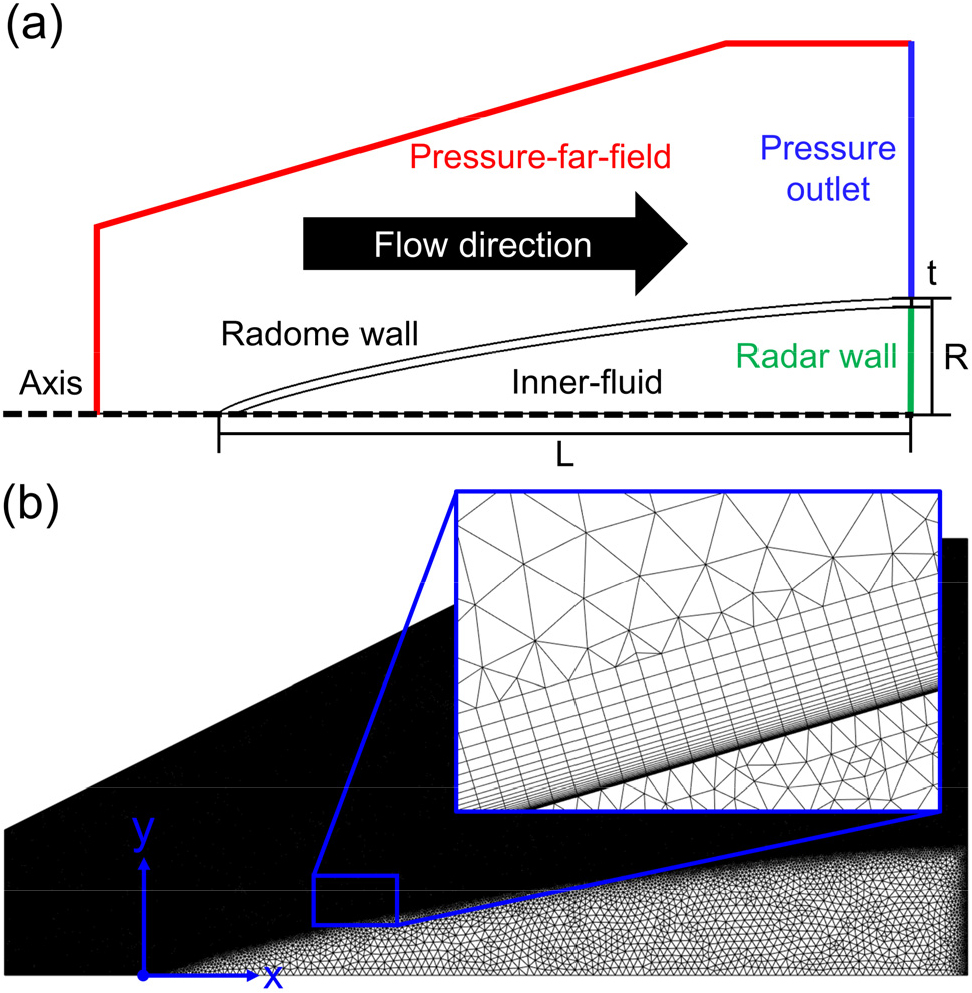
식 (6)과 식(7)에서 은 Fig. 3에서 보이듯이 레이돔의 길이이고 은 레이돔의 반지름을 의미한다. 레이돔의 형상을 단순화하기 위해 미사일 동체와의 접합부는 수치 해석에 고려하지 않았다. 레이돔의 길이는 560mm이고 반지름은 93.0mm이다. 수치 해석에 사용된 축 대칭 이차원 도메인은 Fig. 4(a)와 같다. 유동의 입구 조건은 pressure-far-field 조건, 유동의 출구 조건은 pressure outlet 조건을 사용하였다. 레이돔 내부의 Radar wall은 레이더의 작동 온도를 고려하여 343.15K의 등온 조건을 부여하였다.
식 (8)에서 는 레이돔 벽의 두께, 은 정수, λ는 레이더 주파수의 파장 길이, 그리고 ε은 소재의 유전 상수를 나타낸다. 레이돔 벽의 소재는 레이돔 제작에 일반적으로 사용되는 Pyroceram 9606이 사용되었으며, Pyroceram 9606의 물성치는 Table 1과 같다. Pyroceram 9606은 유리-세라믹 계열에 속하는소재로 가열되는 소재가 녹는 대신 연화되는 특성을 가진다. 소재의 연화점에서 소재의 물성치가 급격하게 변하기 때문에 레이돔의 기능을 유지할 수 없다(Stookey, 1958). 따라서 본 연구에서는 Pyroceram 9606의 연화점인 1623.15K을 재료의 최대 허용 온도로 선정하였다. 레이돔 벽은 레이더 전파의 투과를 위해 반파장 구조를 가진다고 가정하였고 반파장 벽은 식 (8)과 같이 소재의 유전 상수와 레이더 주파수의 파장 길이에 의해 결정된다(Sunil et al., 2001). 미사일 레이더의 주파수는 X-band 레이더 주파수 중 하나인 10GHz로 가정하였다. 식 (8)에 의해 도출된 반파장 벽 구조의 레이돔 벽 두께는 6.3mm이다.
Table 1.
Properties of the radome material; Pyroceram 9606 (Salmon et al., 2010)
| Density | 2,610kg/m3 |
| Specific heat capacity | 821J/kgK |
| Thermal conductivity | 4.08W/mK |
| Softening temperature | 1623.15K |
| Dielectric constant | 5.58 |
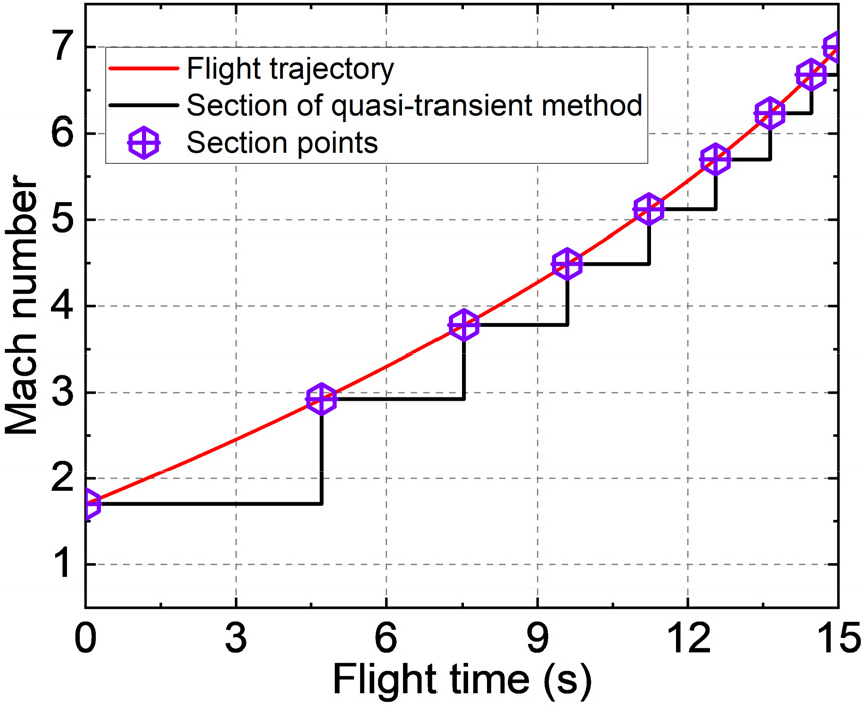
준-비정상 기법을 적용하여 비행 시나리오를 반영한 레이돔의 열전달 특성을 분석하기 위해 본 연구에서 가상의 비행 시나리오를 선정하였다. 가상의 미사일은 극한 조건을 도출하기 위해 극초음속 미사일(hypersonic missile)로 가정하였다. 극초음속 미사일은 발사 후 가속되어 극초음속에 다다르게 된다(Kramer et al., 2023). 본 연구에서 고려된 가상의 비행 시나리오는 미사일이 고도 10,000m에서 마하수 1.7로 비행하는 전투기에서 발사되어 15초 동안 마하수 7로 가속한다고 가정하고 미사일이 가속되는 구간만을 고려하였다. 미사일의 고도는 10,000m에서 11,600m까지 상승한다. 미사일의 속도가 가속되면서 전온도가 상승하기 때문에 본 연구에서는 시간에 따른 유동의 전온도를 기준으로 해석 구석을 구분하였다. 시간에 따른 미사일의 속도와 고도를 고려한 이상 기체의 전온도는 식 (9)와 같이 나타낼 수 있다. 전온도의 차이가 250K일 때를 기준으로 해석 구석을 선정하였다.
식 (9)에서 와 는 각각 전온도와 정온도, 은 마하수, 그리고 γ는 비열비를 나타낸다. 미사일의 비행 궤적과 준-비정상 기법 적용을 위한 구간은 Fig. 5에 표시되어 있다. 총 9개의 구간으로 구분되었으며 각 구간에 대한 마하수와 고도는 Table 2에 기술되어 있다. 각 구간 고도의 대기압과 정온도와 같은 대기 조건은 ‘U.S. standard atmosphere, 1976’을 근거하여 반영하였다(U.S. Government Printing Office, 1976).
Table 2.
Flow conditions of flight scenario by sections for quasi-transient method
준-비정상 기법의 정확도와 해석 효율성을 평가하기 위해 동일한 비행 시나리오에 대해 비정상 해석을 수행하였다. 비정상 해석을 위해 변화하는 속도와 고도는 User Define Function(UDF)을 이용하여 ANSYS Fluent에 반영하였다. 초음속 난류 유동의 시간 스케일을 고려하여 5 × 10-4초의 시간 간격으로 비정상 해석을 수행하였다.
2.3 격자 독립성과 난류 모델 검증
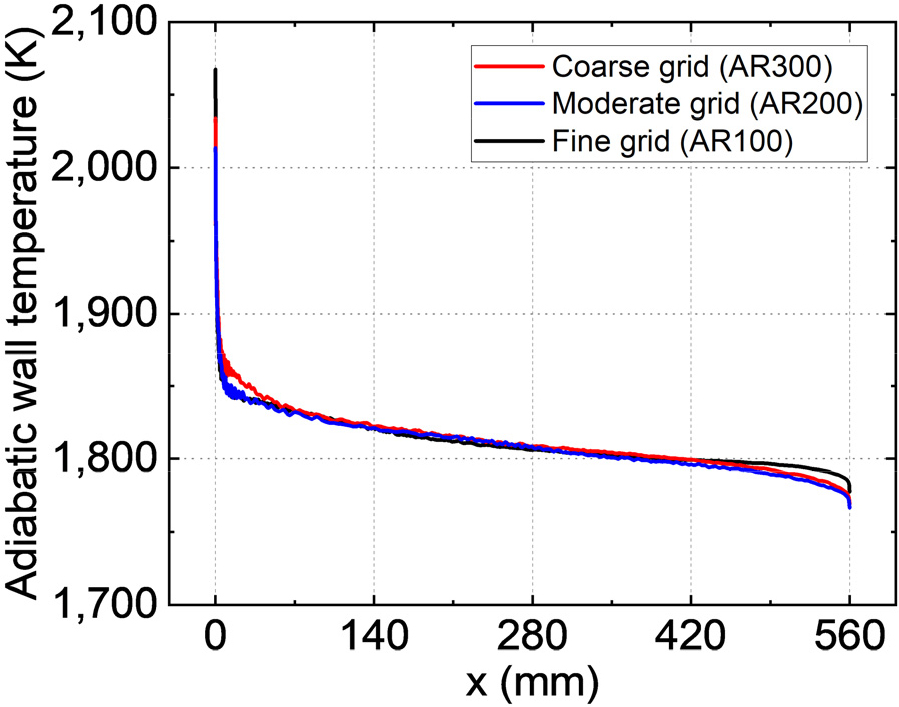
본 연구의 레이돔 형상에 대한 격자는 Fig. 4(b)와 같다. 비정렬 격자를 적용하였으며 레이돔 벽면에서의 y+ 값은 1 미만이 되도록 격자를 생성하였다. 격자 독립성을 검증하기 위해 동일한 10,000m 고도에서 마하수 7인 유동에 대해 레이돔 벽면에서의 격자 종횡비를 다르게 하여 레이돔 단열벽의 온도를 비교하였다. 격자 독립성 결과는 Fig. 6과 같고 종횡비가 100일 때 단열벽의 온도가 비교적 수렴하는 것을 볼 수 있다. 따라서 약 46만 개의 비정렬 격자를 사용하여 수치 해석을 진행하였다.
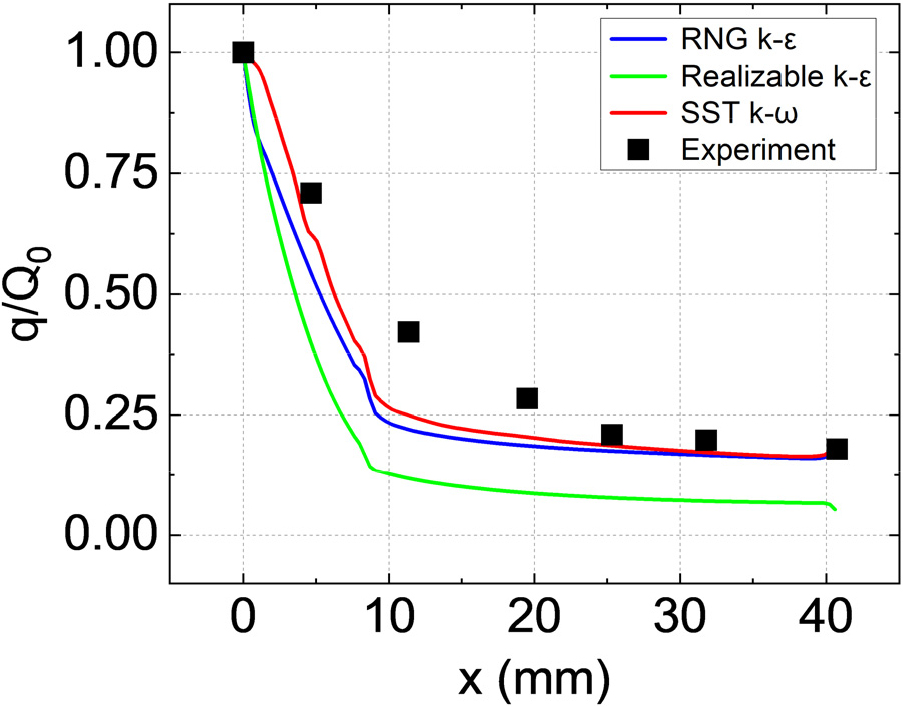
초음속 유동 내의 열전달을 예측하기 위한 난류 모델을 선택하기 위해 무딘 레이돔(blunted radome) 형상에 대해서 난류 모델을 검증하였다. Saravanan 등(2009)은 길이가 40.6mm이고 반지름이 30.5mm인 무딘 레이돔 형상에 대해서 주류의 마하수 7.96, 주류의 정압 205Pa, 그리고 주류의 정온도가 143K 때의 유동 조건에서 레이돔 벽의 온도가 300K으로 일정할 때의 레이돔 벽의 열유속을 측정하였다. Fig. 7은 실험값과 여러 난류 모델을 적용하여 수치 해석으로 도출한 레이돔 벽의 열유속을 비교한 결과를 나타낸다. 레이돔 벽에서의 열유속 분포 해석 결과의 경향은 실험값과 비슷한 경향을 보였지만 SST k-ω 모델이 다른 난류 모델과 비교할 때 오차 10% 이내로 비교적 정확하게 레이돔 벽의 열유속을 예측하였다. 따라서 본 연구에서는 SST k-ω 모델을 사용하여 수치 해석을 수행하였다.
3. 해석 결과 및 분석
3.1 준-비정상 기법 해석 결과 및 분석
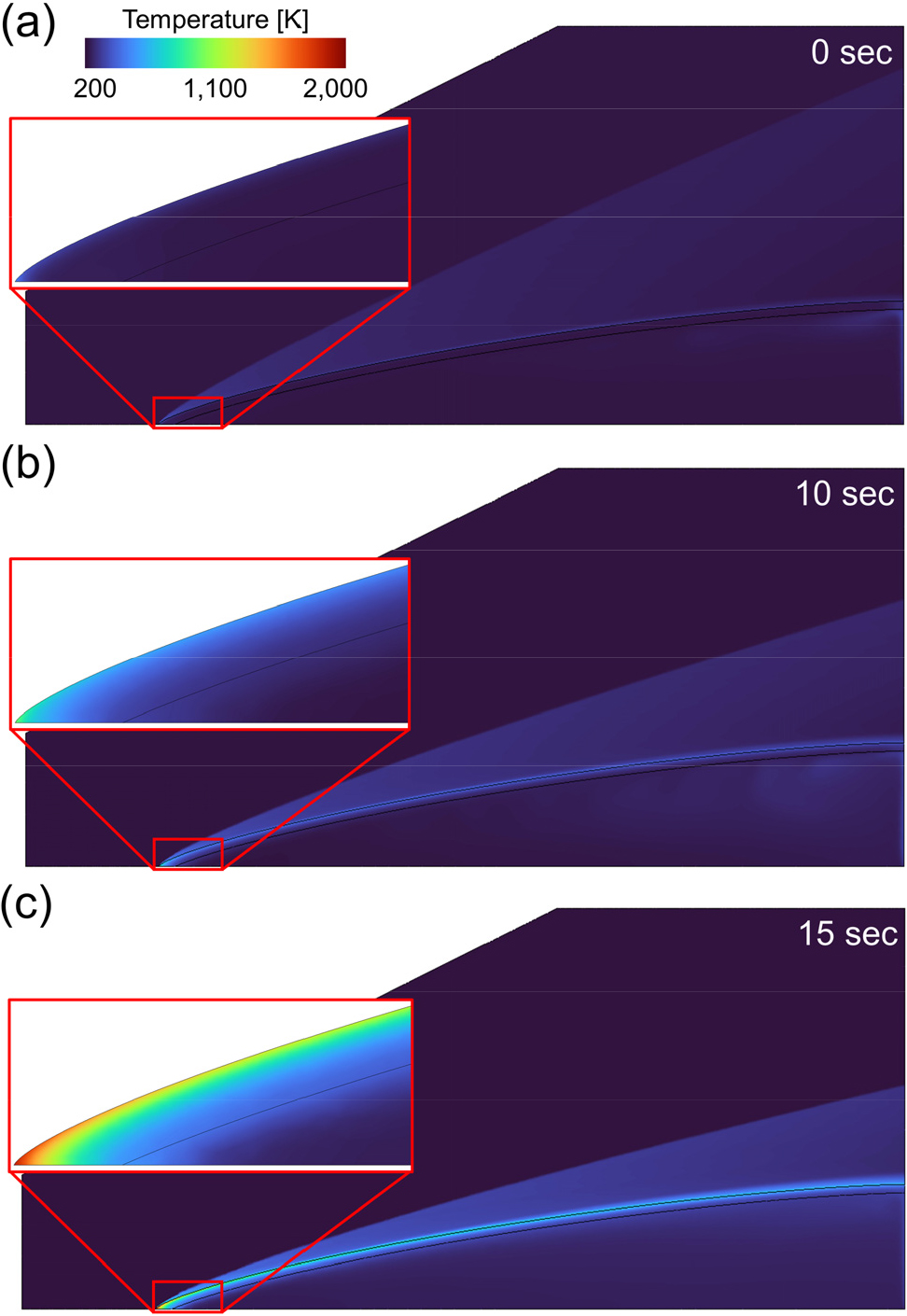
Fig. 8은 준-비정상 해석 결과에서 5초, 10초, 그리고 15초 후의 유체 영역과 레이돔 벽의 온도 단면을 나타낸다. 초음속 유동은 레이돔과 만나 경사 충격파가 발생하고 충격파를 지나면서 유동은 온도와 압력이 회복된다. 시간 구간에 따라 주류의 마하수가 증가하기 때문에 충격파의 각도가 줄어드는 것을 온도 단면을 통해 확인할 수 있다. 또한 시간이 지남에 따라 레이돔 벽의 온도는 외부 유동장에 의한 공력 가열에 의해 상승하는 것을 확인할 수 있다. 준-비정상 기법을 적용했을 때 시간 구간에 따라 유동 조건이 각 구간마다 일정하게 유지되므로 유동 영역은 구간에 따라 불연속적으로 변화를 보인다. 하지만 고체 영역은 비정상 복합 열전달 해석이 수행되었기 때문에 연속적으로 시간에 따라 온도가 변화한다.
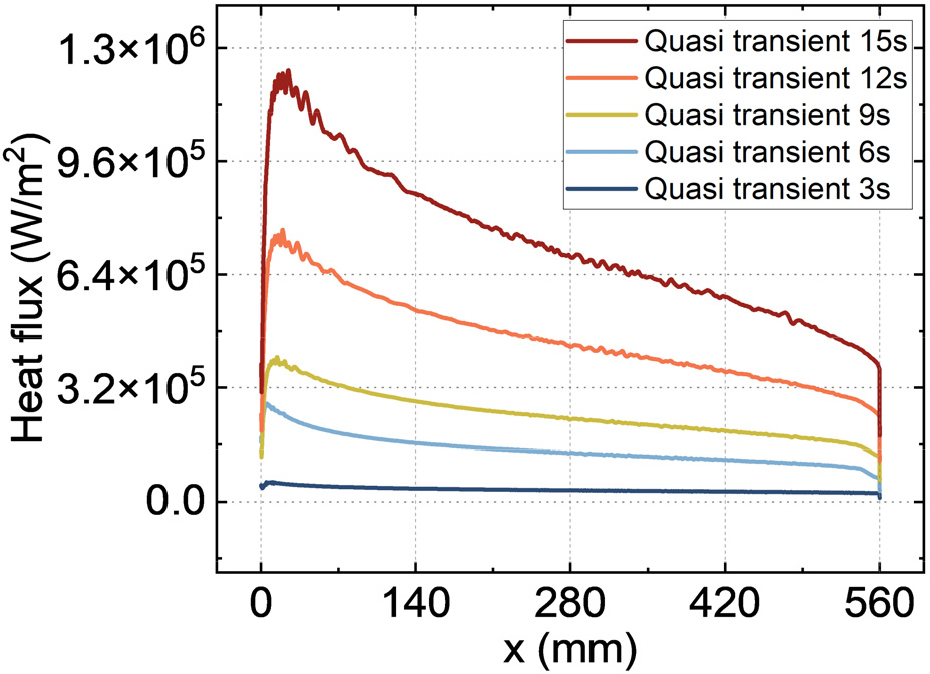
Fig. 9는 0초에서 15초까지 시간에 따른 레이돔 외벽의 열유속 분포를 나타낸다. 비행 시나리오에 의해 시간에 따라 미사일의 속도가 증가하므로 레이돔 외벽에 가해지는 열유속이 증가하는 것을 알 수 있다. 이는 레이돔 외벽의 온도도 시간에 따라 상승할 것임을 나타낸다. 레이돔 외벽의 최고 열유속은 레이돔의 정체점(x = 0mm)에서 x 방향으로 40mm 떨어진 곳에서 나타난다. 이는 준-비정상 해석 수행 시 각 시간 단계별로 비정상 복합 열전달 해석을 수행할 때 일정 속도의 유동장 내에서 레이돔 정체점에서의 온도가 빠르게 수렴하기 때문이다. 따라서 각 시간 단계별로 비정상 복합 열전달 해석이 시작될 때는 레이돔 정체점이 가장 열유속이 높지만 정체점의 온도가 수렴되면서 레이돔 외벽의 최고 열유속의 위치가 이동하게 된다. 다음 시간 단계의 비정상 복합 열전달 해석이 수행될 때는 유동장의 속도가 상승하기 때문에 해당 현상은 반복되게 된다. 레이돔 외벽 열유속의 차이는 시간이 지나면서 마하수가 증가하기 때문에 더욱 커진다.
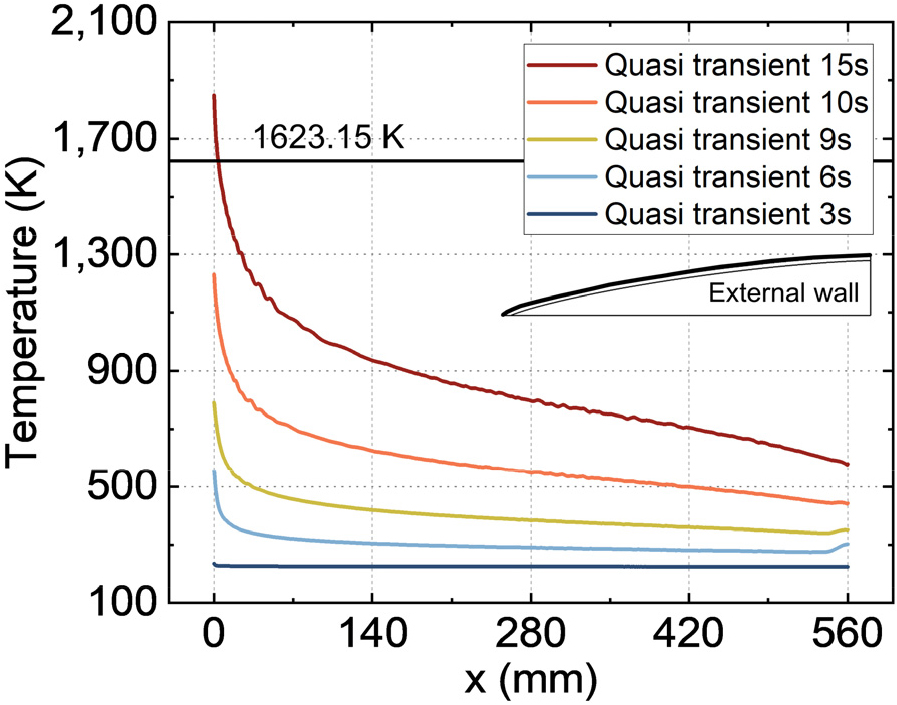
Fig. 10은 0초에서 15초까지 시간에 따른 레이돔 외벽의 온도 분포를 나타낸다. 시간에 따른 열유속 분포를 통해 알 수 있듯이 레이돔 벽의 온도는 미사일이 가속됨에 따라 시간이 지나면서 상승한다. 레이돔 외벽의 온도는 정체점에서 가장 높고 벽의 x 방향을 따라 점차 감소한다. 정체점에서 주류의 유속이 0이 되어 전온도에 가깝게 온도가 회복되기 때문이다. 이후 유동의 경계층이 발달하면서 회복 계수가 감소하여 레이돔의 외벽 온도가 감소한다. 특히 15초 일 때 레이돔 정체점을 포함한 레이돔 외벽의 일부가 Pyroceram 9606의 최대 허용 온도인 1623.15K을 초과하여 가열되는 것을 볼 수 있다. 이는 레이돔이 본 연구의 극초음속 미사일의 비행 시나리오에 대해 레이돔에서 열적으로 문제가 생기는 것을 의미한다.
3.2 준-비정상 기법과 비정상 해석 결과 비교
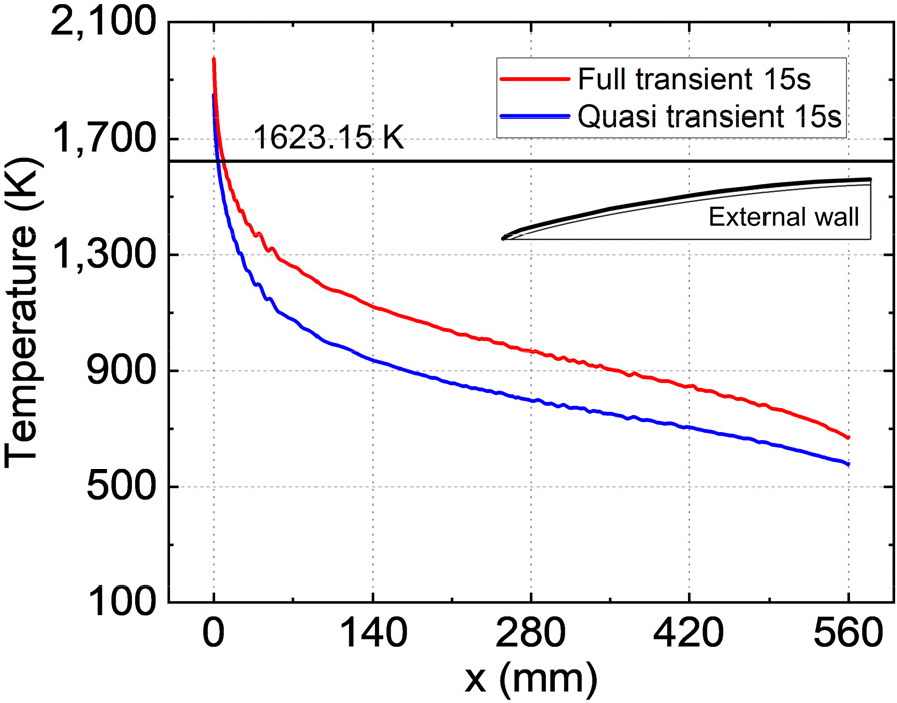
Fig. 11은 준-비정상 기법을 적용한 결과와 비정상 해석 결과를 15초에서의 레이돔 외벽의 온도 분포를 통해 비교한 결과이다. 레이돔 외벽 온도 분포의 경향성은 일치하지만 준-비정상 기법을 적용했을 때 레이돔 외벽의 온도가 과소 예측되는 것을 확인할 수 있다. 레이돔 외벽 온도의 차이는 최소 90K에서 최대 190K 정도 발생하고 레이돔 외벽의 끝단에서 가장 작고 정체점에서 x 방향으로 약 50mm 이후에는 온도 차이가 비교적 일정하게 차이가 나는 것을 볼 수 있다. 이러한 레이돔 외벽 온도에 대한 과소 예측은 비정상 해석이 준-비정상 기법에 비해 5 × 10-4초의 짧은 시간 구간의 유동 변화가 고려되었기 때문이다. 준-비정상 기법에서는 약 0.5초에서 4.7초의 시간 간격에 대해 각 구간의 대표 마하수가 유동장의 조건으로 적용되었기 때문에 비정상 해석에 비해 마하수 증가의 반영이 되지 않아 과소 예측되었다. 또한 본 연구에서 가정된 비행 시나리오는 미사일의 가속 구간만을 고려하여 가속 이후로 일정한 속도로 순항하는 구간이 없고 마하수 1.7에서 마하수 7까지 큰 폭으로 가속하기 때문에 레이돔 외벽의 온도 차이가 다소 크게 발생하였다.
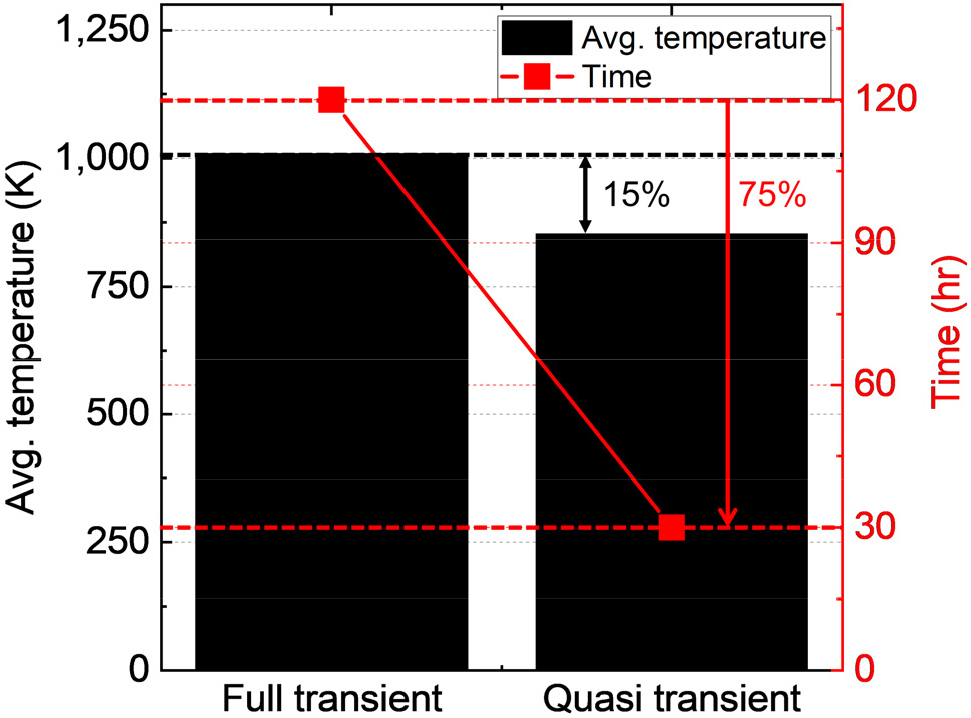
Fig. 12는 준-비정상 기법 결과와 비정상 해석 결과를 15초에서의 레이돔 평균 온도와 해석 소요 시간 측면에서 비교한 그래프이다. 외벽 온도의 경우 전체 비정상 해석의 경우 1010K이고 준-비정상 해석의 경우 854K으로 약 15% 이내의 정확도를 가지고 예측하는 것을 볼 수 있다. 또한 비정상 해석은 120시간이 소요되었고 그에 반해 준-비정상 기법을 적용하였을 때는 30시간이 소요되었음으로 해석 소요 시간 측면에서 75%가 감소한 것을 알 수 있다. 따라서 준-비정상 기법을 적용하여 비행 시나리오를 반영하여 레이돔의 열전달 특성을 분석하는 경우 비정상 기법과 비교하여 소요 시간을 유의미하게 단축시켜 효율적이다.
4. 결 론
본 연구에서는 준-비정상 기법을 적용하여 극초음속 미사일의 가상 비행 시나리오를 고려한 레이돔의 열전달 특성을 분석하였다. 또한 비정상 해석 결과와 준-비정상 해석 결과를 비교하여 준-비정상 기법의 정확성과 효율성을 입증하였다.
준-비정상 기법을 적용하여 수치 해석을 수행하였을 때 시간에 따라 변화하는 속도와 고도가 반영되고 있음을 온도 단면을 통해 확인할 수 있었다. 시간에 따른 레이돔 외벽의 열유속과 온도 분포는 본 연구의 비행 시나리오에서 미사일이 가속되면서 지속적으로 레이돔이 가열되고 있음을 나타낸다. 특히 15초 이후에 레이돔 외벽의 일부분이 레이돔의 소재인 Pyroceram 9606의 최대 허용 온도 이상으로 상승하여 열적인 문제가 발생 할 것을 예상할 수 있다. 준-비정상 기법을 적용한 해석 결과와 비정상 해석 결과의 비교를 통해 준-비정상 기법이 레이돔 벽의 평균 온도는 15% 이내로 비교적 정확하게 예측이 가능하고 해석 소요 시간은 75%가 감소해 계산 용량 측면에서 효율적임을 알 수 있다.
본 연구 결과는 레이돔 설계 시 비행 시나리오에 따라 변화하는 속도와 고도를 고려해야 함을 시사하며 준-비정상 기법이 비행 시나리오를 효율적으로 반영할 수 있음을 보여준다. 후속 연구로 준-비정상 기법의 정확도를 높이기 위해 비행 시나리오 상의 시간 단계 선정 기준과 시간 단계 별 유동 조건 선정 기준에 대한 연구가 필요하다.