1. 서 론
세계 곳곳에서 지진재해가 최근 다수 발생하고 있다. 이러한 지진재해 중 일부가 구조물을 위한 설계지진 예측치보다 크게 일어나는 경우가 종종 발생함에 따라 지진 안전에 대하여 우려가 제기되고 있다. 특히나, 2011년 동일본 대지진을 비롯한 2016년 경주 지진 및 2017년 포항 지진과 같이 설계기준을 초과하는 큰 지진이 원자력발전소(원전) 인근에서 발생함에 따라 원자력시설에 대한 안전성이 큰 관심 대상이 되고 있다(Kwag et al., 2020c). 현재, 원자력시설 지진 안전성 평가는 지진 및 구조물의 다양한 불확실성을 반영하여 전체 시스템의 리스크를 평가해야 하기 때문에 지진 확률론적 안전성 평가(Seismic Probabilistic Risk Assessment: SPRA) 기법을 통하여 수행하고 있다. SPRA는 부지 내 지진재해 발생 확률(지진재해도), 주요 기기의 확률론적 내진 안전성(지진취약도), 및 노심손상 등의 사고 시나리오 분석을 통하여 원자력시설 전체 지진 리스크를 평가한다. 원전 지진 리스크 평가를 위한 구체적인 이론, 절차 및 상세한 예제는 EPRI(Electric Power Research Institute) 보고서(EPRI, 2003; 2018)에 자세히 기술되어 있다.
원자력시설 SPRA에서 정량적인 사고 시나리오 분석을 위하여 고장 수목(Fault Tree: FT) 및 사건 수목(Event Tree: ET)의 시스템 분석 기법을 이용하여 다양한 사고 시나리오를 작성하고, 수목을 이루는 기본 사건의 파괴확률은 주요 기기의 지진취약도를 통하여 고려한다. 여기서, FT 및 ET를 통한 시스템 분석 시, 수목을 이루는 기기 사이의 관계를 기본적이면서 독립으로 가정하기 때문에 Boolean 대수 방법을 통하여 사고 확률을 정량화할 수 있다. 이에 따라, 현재 원자력시설 SPRA 지진 리스크 정량화는 대부분 Boolean 대수 방법을 통하여 수행하고 있고, 이러한 정량화를 위한 전산코드/소프트웨어는 SEISMIC, SECOM2-Boolean, PRASEE, 등이 있다(EPRI, 2002; Kim et al., 2011; Kwag et al., 2017; Oh and Kwag, 2018). 개발된 전산코드 특징은 Boolean 대수 방법을 통하여 지진 리스크를 정량화하기 때문에 기기(기본 사건) 사이 독립 혹은 완전 종속 가정에만 정확한 사고 지진 리스크를 산정할 수 있다(Ellingwood, 1990; Kwag and Gupta, 2017; Kwag et al., 2018).
기기 간 부분종속 관계는 지진 리스크에 적지 않는 영향을 미치는 것으로 알려져 있고, 최근 이러한 관계를 고려하는 연구가 진행되고 있다(Kim et al., 2020; Eem et al., 2021). 이러한 배경 아래, 기기 사이 모든 논리 조건에서 부분종속 관계를 정확하게 고려할 수 있는 샘플링기반 SPRA 방법이 제안되었다(Kwag et al., 2020a). 이 방법은 지진세기마다 각각의 기기에서 지진 응답과 내력으로 분리하여 각각 샘플링하고, 각 추출된 샘플마다 서로 값을 비교하여 안전(“0”)과 파괴(“1”)로 분류한다. 여기서, 분류된 샘플들을 기반으로 기기로 이루어진 시스템(상위 사건)의 안전 및 파괴 여부는 “AND”, “OR”, 등의 논리 게이트를 통하여 평가하게 된다. 최종적인 각 기기 및 시스템 파괴확률은 총 추출 샘플수와 파괴 샘플수의 비로 계산된다. 이러한 접근방법은 사건 사이 부분종속 관계를 샘플 추출 단계에서 고려할 수 있어 정확한 지진 리스크 평가를 가능하게 한다. 그러나 이는 샘플링 기반 방법이므로 정확한 지진 리스크 산정을 위하여 모든 지진세기마다 충분한 샘플을 추출하는 것이 필수적이다(Kwag et al., 2019; 2020b).
이에 따라 본 연구에서는 기존 방법에 소요되는 계산 비용을 줄이기 위하여 효과적인 방법을 고안한다. 이를 위하여 본 연구에서는 기존 방법의 샘플링 추출 기법인 몬테카를로 샘플링(Monte Carlo Sampling: MCS) 방식을 라틴하이퍼큐브 샘플링(Latin Hypercube Sampling: LHS) 방식으로 변경하는 것을 제안하여 적은 샘플수 추출 구간에서도 지진 리스크 값의 정확도를 개선한다. 또한, 기존 지진세기 세분화 정도를 최종 지진 리스크 결과와 연계하여 이를 최적의 값으로 결정하는 방법을 제안한다. 이러한 제안은 궁극적으로 기존 방법의 계산 효율성 증대에 일정부분 기여할 것으로 판단된다.
2. 연구 동기
지진재해 및 기기의 무작위성 및 불확실성을 고려하여 지진재해의 세기에 따른 기기의 조건부 파괴확률을 구하는 과정을 지진취약도 분석이라 한다. 원자력 산업계에서 활용하는 지진취약도 분석의 방법 중 하나로는 이른바 응답계수법(Ebisawa et al., 1994)이 있다. 응답계수법은 대상 기기에 대하여 모든 지진재해 세기에서 응답 R과 내력 C로 구분하여 취약도 분포를 기술하는 것이 특징이다. 응답계수법에 의한 기기의 대한 지진취약도는 아래와 같은 함수로 표현할 수 있다.
여기서, Rm 및 Cm은 응답 및 내력에 관련한 중앙값을 의미한다. βR은 응답 R과 관련한 무작위성 및 불확실성에 관련한 로그표준편차를 의미하고, βC는 내력 C와 관련한 무작위성 및 불확실성에 관련한 로그표준편차를 나타낸다.
최근 Kwag 등(2020a)은 이러한 응답계수법을 활용하여 샘플링기반 SPRA 평가 방법을 제안한 바 있다. 또한, 이 연구에서는 현재 가장 많이 활용하는 EPRI 지진취약도 방법인 변수분리법의 변수를 응답계수법의 변수로 변환하는 방법에 대하여 자세히 기술하였다. 기본적으로 이 방법은 아래와 같은 수식으로 표현될 수 있고, 개념적인 계산 절차 및 관련 계산 순서도는 해당 논문에 잘 기술되어 있다.
여기서, LN(α,β)은 중앙값 α 및 로그표준편차 β를 따르는 로그정규분포를 나타낸다. R(a)는 중앙값 Rm(a) 및 로그표준편차 βR를 따르는 로그정규분포를 의미하고, C(a)는 중앙값 Cm(a) 및 로그표준편차 βC를 따르는 로그정규분포를 나타낸다. 이 방법은 지진재해 세기 “a” 마다 각각의 기기에 대하여 정의된 응답 분포 및 내력 분포에 대하여 각각 샘플을 추출하여, 각 추출된 샘플에서 R과 C값을 서로 비교하고 각각의 해당 기기의 상태를 safe(“0”) 혹은 fail(“1”)의 binary state 형태로 표현하게 된다. 또한, FT(“OR” gate & “AND” gate) 및 기기 binary 상태를 기반으로 sub-system 및 top system의 상태를 평가하기 때문에 이들의 상태 또한 binary 상태로 나타낼 수 있게 된다. 최종적으로는 각각의 지진재해 세기마다, 각각의 기기, sub-system 및 top system에서 총 추출 샘플 수와 failure state (“1”)를 가진 샘플 수의 비로 파괴확률을 산정한다. 이 방법의 장점은 샘플링 단계에서 기기 간의 상관성을 고려하여 샘플 추출이 가능하기 때문에 직관적으로 기기 상관성을 고려할 수 있다는 것이다. 또한, 충분한 샘플 수를 확보하면 정확한 해에 가까워지기 때문에 해의 근사로 인한 결과의 보수성/비보수성을 배제할 수 있다. 그러나 개발된 방법의 특성 상, 지진재해 세기마다 R 및 C의 각각의 확률변수에 대하여 다량의 샘플을 추출해야 하기 때문에 계산 시간이 많이 소요된다는 단점이 있다. 또한, 지진재해 세기를 어느 정도로 세분화하느냐가 지진취약도와 최종 지진 리스크 값의 정확도에 영향을 미치게 된다.
3. 제안 방법
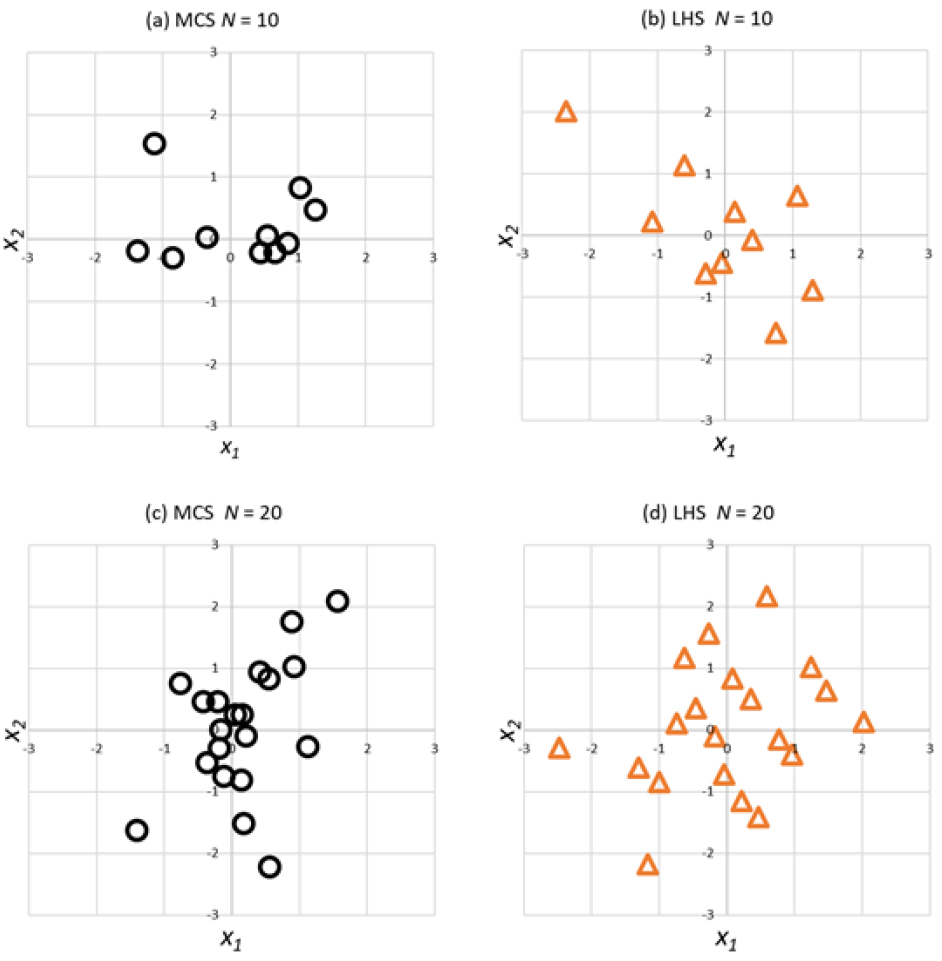
현재의 샘플링기반 SPRA 평가 방법은 샘플 추출방법으로 MCS 방법을 활용한다. MCS 방법은 각각의 확률변수에 대해 N 개의 샘플을 독립적으로 무작위 방법을 통하여 추출한다. 이에 따라, 이 방법은 다차원 확률변수 공간 영역에서 일부공간에는 추출된 샘플이 없거나, 혹은 다른 일부공간에서는 추출된 샘플이 밀집될 수 있다는 단점이 있다. 반면에, LHS 방법은 가능한 모든 값에 걸쳐 샘플을 보다 균일하게 분산시키는 것을 목표로 한다. 각 확률변수 분포를 동일한 확률의 일정 간격으로 분할하고, 각 간격에서 하나의 샘플을 선택한다. 이러한 LHS 접근 방식은 MCS 방법과 비교하여 다차원 확률변수 공간에서 균일한 샘플 추출을 가능하게 하여 상대적으로 샘플링 오류를 줄일 수 있다. Fig. 1은 x1및 x2의 확률변수 공간에서 MCS 및 LHS 방법으로 추출된 샘플 N = 10 및 N = 20 일 경우에 대하여 서로 비교하여 보여주고 있다. Fig. 1에서 확인할 수 있는 바와 같이 MCS 추출 샘플은 밀집된 영역들이 존재하는 반면에 LHS 추출 샘플은 확률변수 공간에서 비교적 균일하게 분포함을 확인할 수 있다. 이에 따라 본 연구에서는 LHS 방법을 샘플링기반 SPRA에 적용하여 기존의 MCS 방법을 적용한 결과와 비교하였다.
한편, SPRA에서 원자력시설의 지진 리스크 산출은 지진재해도 곡선과 지진취약도 곡선을 콘볼루젼하여 이루어진다. 아래 식은 이러한 콘볼루젼 과정을 보여주고 있다.
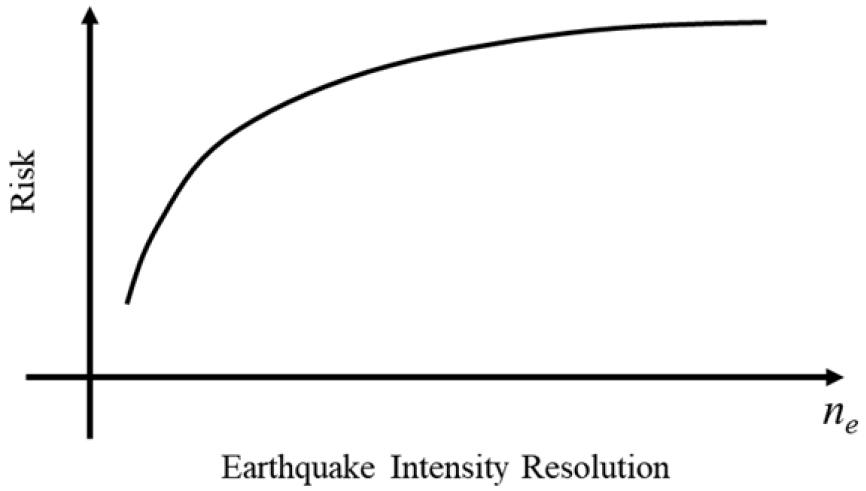
식 (5)에서 볼 수 있듯이 지진 리스크 값 산출은 지진세기(a) 영역에서 지진취약도(Pf(a)) 값과 지진재해도(H(a)) 미분 값의 곱한 값을 적분하여 산출할 수 있다. 그러나 이를 수치적으로 수행할 시 적분 형태는 이산화 형태로 이루지기 때문에 지진세기 영역을 어느 정도로 세분화시키는 지가 지진 리스크 값의 정확도에 적지 않는 영향을 미치게 된다. 즉, 지진세기 ai 의 개수 ne을 증가시켜가면, 지진 리스크 값은 정확한 값으로 수렴하게 된다. 이에 따라 본 연구에서는 지진세기의 세분화 정도를 지진 리스크 값의 수렴정도에 따라 최적으로 결정하는 방법을 고안하였다. Fig. 2는 지진세기 세분화 정도에 따른 지진 리스크 수렴과정을 개념적으로 보여주고 있다. Fig. 2에서 확인할 수 있듯이 지진 리스크 값은 ne가 일정 값 이상이 되면 크게 변동이 없는 것을 확인할 수 있다. 그러므로 최적의 ne 를 정의하면, 지진취약도 계산을 위한 기기의 파괴확률 도출에 소요되는 총 샘플 추출수를 감소시킬 수 있게 된다.
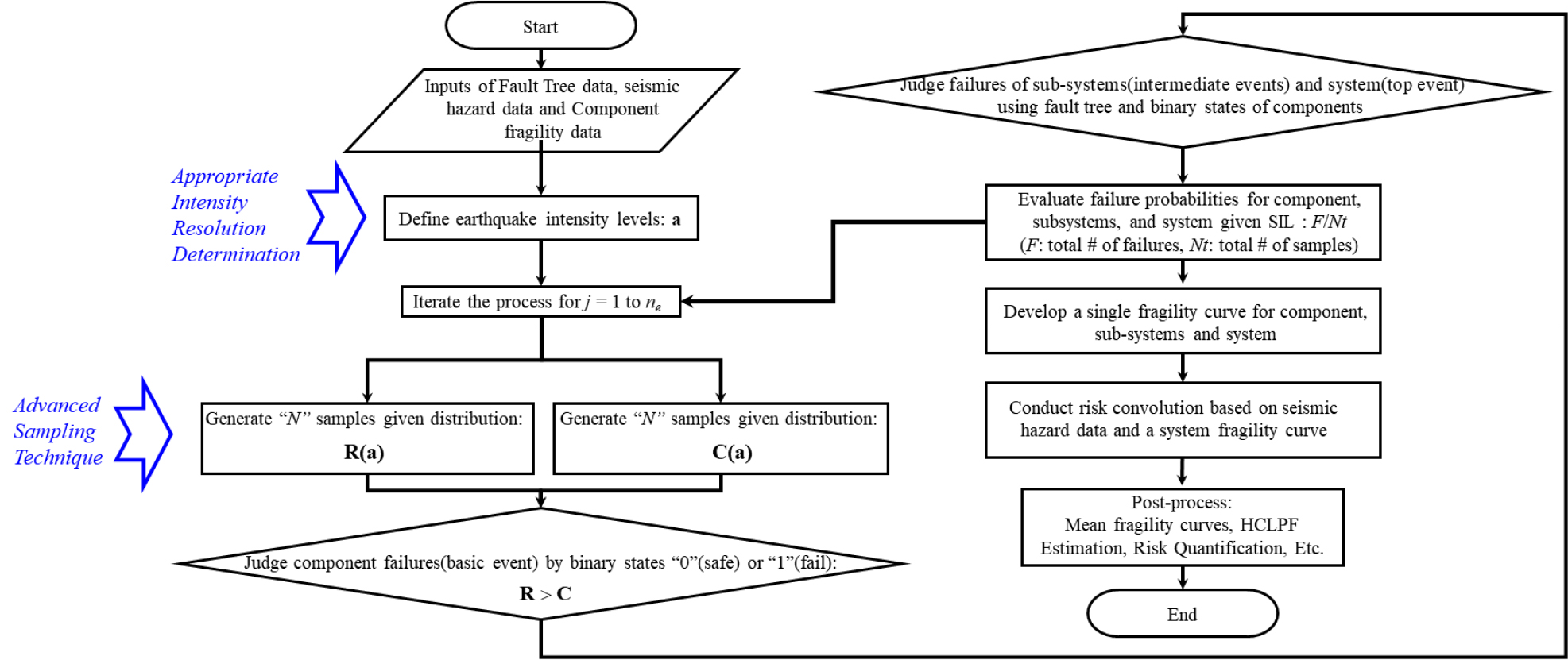
결과적으로, Fig. 3은 본 연구의 제안과 결합된 개선된 샘플링기반 SPRA 정량화 과정을 순서도 형식으로 보여주고 있다. Fig. 3에서 기존의 정량화 과정에 본 연구의 제안이 추가된 부분은 화살표 형태 나타내었다. Fig. 3에서 확인할 수 있듯이, 기존의 절차를 개선한 부분은 크게 2가지이다. 첫번째는 샘플 추출 방식을 MCS 방법에서 LHS 방법으로 변경한 것이다. 나머지 하나는 지진세기 세분화 정도를 최종 지진 리스크 값의 수렴성을 기반으로 최적의 값을 도출하는 것이다. 이러한 본 연구의 두가지 제안은 기존 방법의 계산 성능을 향상시킬 수 있을 것으로 판단된다.
4. 수치 검증
이 번 장에서는 본 연구의 제안이 결합된 샘플링기반 SPRA 접근법을 실제 LGS(Limerick Generating Station) 원자력발전소(원전) 문제(Ellingwood, 1990)에 적용하여, 그 결과를 기존 방법의 결과와 비교하여 제안된 방법의 효율성을 검증하였다. LGS 원전 지역의 지진재해도 결과, 기기 지진취약도 및 랜덤 고장 확률은 Ellingwood(1990) 및 Kwag 등(2020b) 참고문헌에 자세히 기술되어 있다. LGS 원전의 사고 시나리오별 지진취약도 분석을 위한 시스템 모델 식은 아래와 같다.
여기서, Si는 기기 지진취약도를 의미하고, 는 1-Si을 의미한다. CM은 노심손상(Core Meltdown: CM) 사고를 나타내고, 식 (7) ,(8), (9), (10), (11), (12)의 6가지 사고 시나리오의 조합으로서 식 (13)과 같이 간략하게 표현할 수 있다.
위의 시스템 모델 식에서 확인할 수 있듯이, 실제 원전 CM 사고는 기기 파괴 사이의 교집합과 합집합의 다양한 조합으로 평가된다. 여기서, 각각의 기기 파괴 확률은 기기 지진취약도 정보와 랜덤 고장확률이 사용된다. 기기 지진취약도 정보는 식 (1) 및 식 (2)로 계산된 파괴확률 값으로 지진세기마다 그 값이 달라진다. 최종 CM 리스크는 식 (5)에서 살펴본 바와 같이 CM 시나리오부터 계산된 시스템 지지진취약도와 LGS 지역의 지진재해도 곡선의 콜볼루젼을 통하여 산출된다. 본 연구에서는 지진세기 분포를 PGA(Peak Ground Acceleration) 기준으로 0.05g부터 2.0g까지 0.01g 간격으로 총 196개로 세분화하였다.
본 연구에서는 위에서 정의된 시스템 모델 식을 기반으로 여러가지 방법을 총 2가지 사례에 적용하여 그 결과를 살펴보았다. 구체적으로 2가지 사례는 (1) 모든 기기 간 독립조건; (2) 원자로건물 내 기기 S11, S12, S13, S14 완전종속조건, DG건물 내 기기 S15, S16 완전종속조건, 및 이외 다른 모든 기기는 독립조건일 경우로 구성된다. 고려된 2가지 사례 연구를 통하여 다음과 같은 비교 분석을 수행하였다. (a) 독립 조건과 완전종속조건은 Boolean 대수 방법을 통하여 정확한 해를 산출할 수 있기 때문에, 기존 방법 및 본 연구 제안 방법을 통해 얻어진 결과를 Boolean 대수 방법의 결과와 비교하여 검증하였다. (b) 샘플링 방법 사이 효율성 비교는 결과를 산출하는데 필요한 총 추출된 샘플 개수 비교를 통하여 수행하였다. (c) MCS 및 LHS 방법 적용에 따른 결과는 각각의 지진세기에서 샘플링 개수(Nt)를 증가시키며 시스템 지진취약도의 정확도를 산출하여 서로 비교하였다.
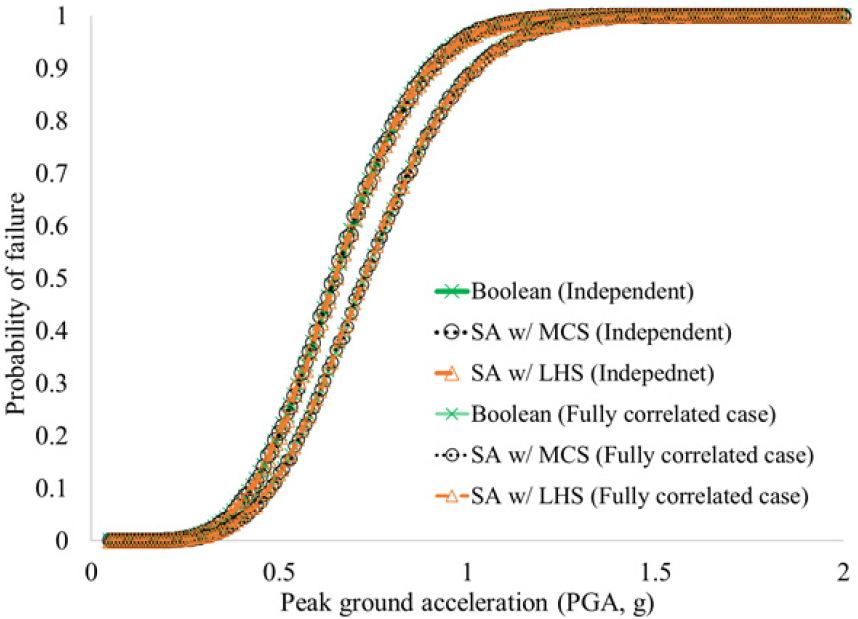
구체적으로 본 연구에서 제안된 방법(Sampling Approach(SA) with LHS), 기존의 방법(SA with MCS), 및 Boolean 대수 방법을 적용하여 LGS 시스템 지진취약도 해석을 수행하였다. Fig. 4는 이러한 방법들을 적용하여 얻은 CM 시나리오 평균 시스템 지진취약도 결과를 독립조건 및 완전종속조건에 대하여 보여주고 있다. Fig. 4에서 확인할 수 있듯이, 고려하는 두가지 사례와 관련하여 본 연구의 제안 방법 및 기존 방법 모두 Boolean 대수 방법 결과와 거의 일치함을 육안으로 확인할 수 있다. 이 결과는 지진세기 분할 ne = 196이고, 각각의 지진세기 마다의 샘플 수 Nt = 1E4일 경우이다.
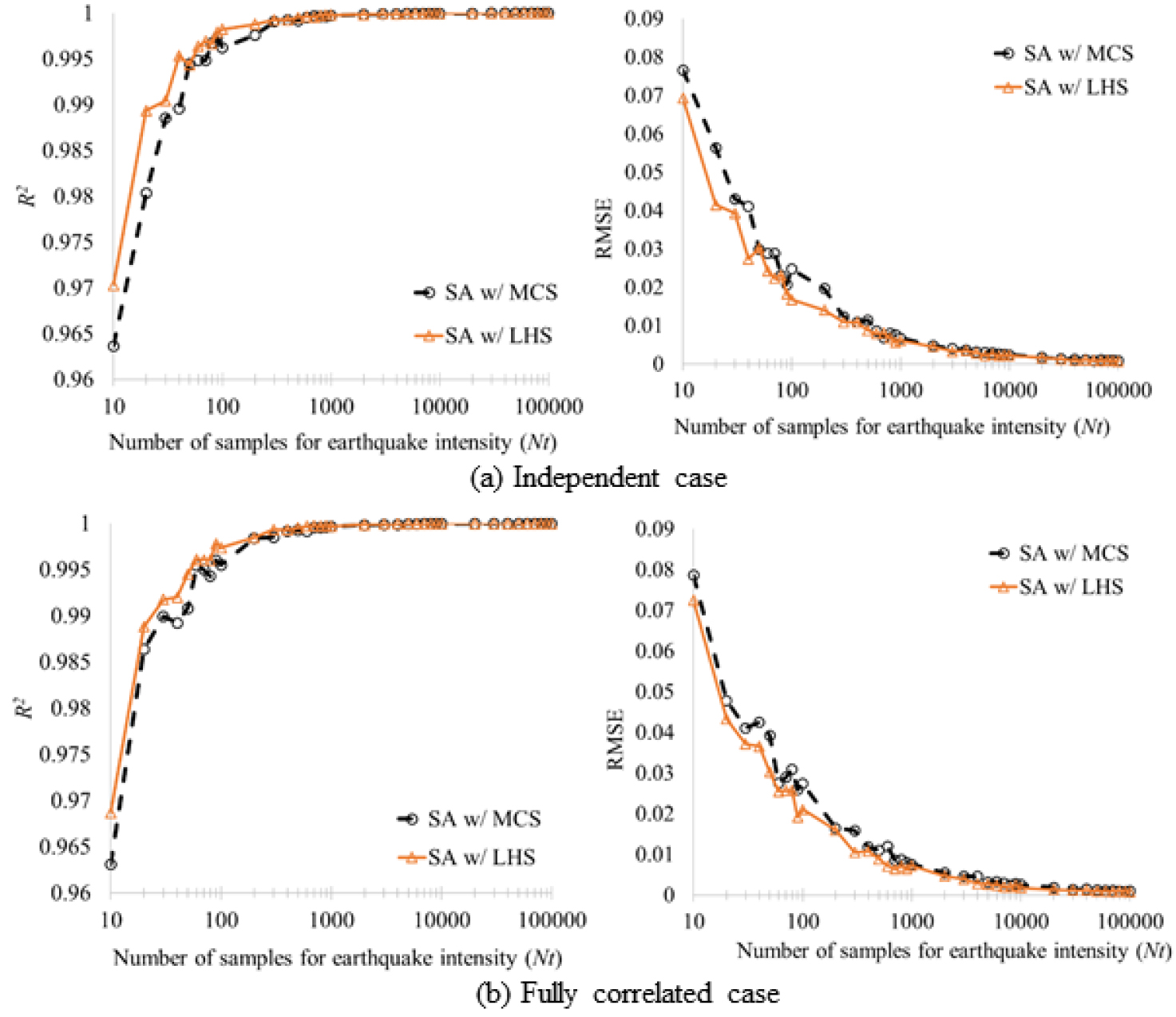
CM 시스템 지진취약도의 정량적 결과 비교를 위하여 R2 및 RMSE(Root Mean Squared Error) 지표를 활용하였다. R2는 결정계수(Coefficient of Determination)를 의미하며 0에서 1사이 값을 가지고, 예측 값(샘플링 기반 방법)과 정해(Boolean 대수 방법)의 상관관계가 높을수록 1에 가까워진다. RMSE는 예측 값과 정해의 차이를 제곱하고 합산한 후 제곱근 한 값으로서 0에 가까울수록 두 데이터 셋의 상관관계가 높아진다. 구체적으로, 샘플링 개수 Nt에 따른 두 샘플링 방법의 해 수렴성을 확인해 보았다. Fig. 5은 CM 시나리오 독립조건 및 완전종속조건에 관련하여 Nt가 증가함에 따라 두 샘플링 방법의 R2 및 RMSE 값을 나타낸 그래프이다. Fig. 5에서 확인할 수 있듯이, 두 방법이 두 사례에서 대략 Nt = 1E4개 샘플 이상일 경우, 두 방법을 통한 결과의 정확도가 거의 정해에 가까워 지는 것으로 확인할 수 있다. 여기서 주목할 점은 Nt = 1E3개 샘플 이하 일 때는 기존 방법이 본 연구의 제안 방법에 비하여 해의 정확도가 떨어짐을 볼 수 있다. 그러므로 샘플링기반 SPRA 방법이 LHS 방법과 통합되는 경우가 MCS 방법과 결합되는 경우보다는 적은 샘플 수 영역(Nt<= 1E3)에서 해의 정확도를 높일 수 있을 것으로 보인다.
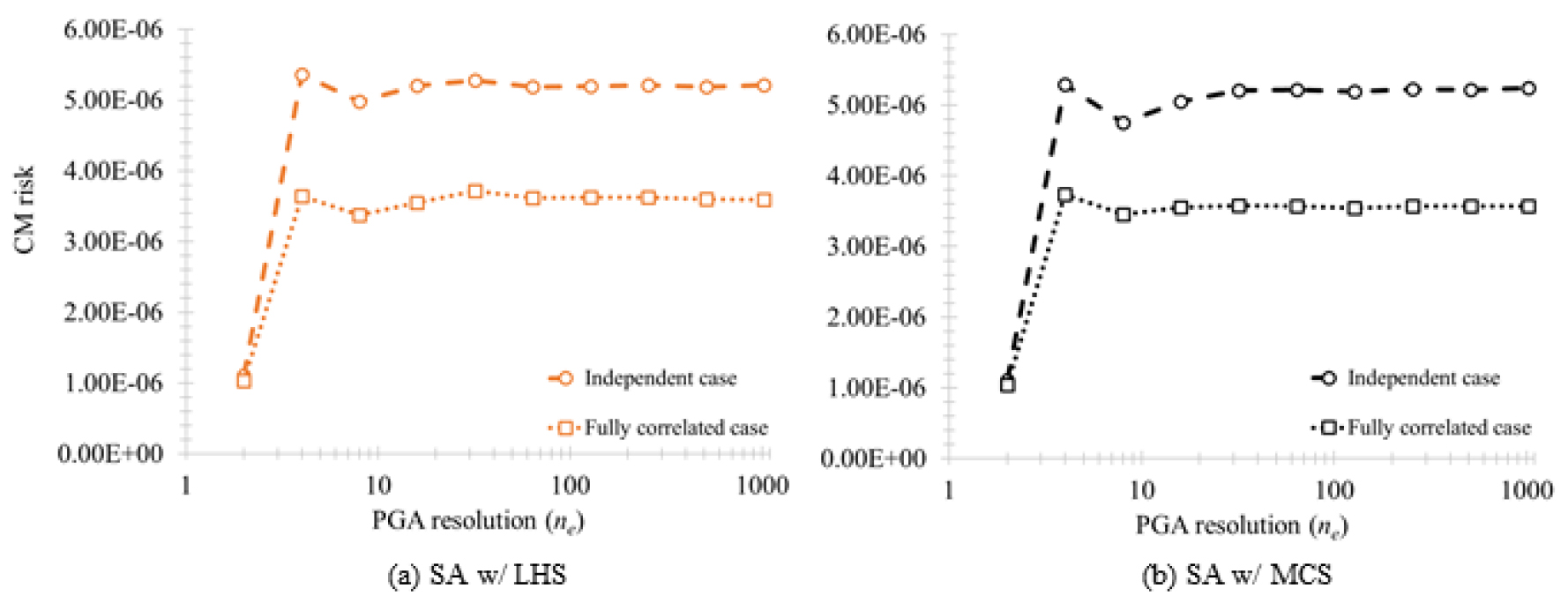
Fig. 6은 지진세기 분할 수에 따라, CM 리스크 값의 변화를 보여주고 있다. Fig. 6에서 확인할 수 있는 바와 같이, ne가 증가함에 따라 리스크 값이 하나의 값으로 수렴하고, 그 값의 변화가 거의 없음을 확인할 수 있다. 특히나, 약 ne = 50 개 이상이면 리스크 값의 변화가 크게 나타나지 않음을 확인할 수 있었다. 이에 따라 본 연구의 제안이 결합된 샘플링기반 SPRA는 ne = 100 개의 지진세기 분할을 이용하여 최종 시스템 지진취약도 및 리스크 결과를 도출하였다. 결과적으로 주어진 LGS 원전 SPRA 문제에 있어서 정해와 비슷한 최종 리스크 결과값 산정을 위하여 기존의 방법은 총 “196×2×1E4”개의 샘플수 추출을 필요로 하였다. 반면에 본 연구의 제안이 결합된 방법은 비슷한 정확도의 리스크 결과 값 산출을 위하여 총 “100×2×1E4”개의 샘플수 추출이 소요되었다. 이는 제안된 방법이 기존 방법에 비하여 총 추출샘플 수 기준으로 약 2배의 효율성을 확보할 수 있었다는 의미를 가지게 된다.
LGS 원전 시나리오별 리스크의 정량적인 비교 결과는 모든 사고 시나리오에 대하여 HCLPF(High-Confidence-Low-Probability -of-Failure) 및 리스크를 활용하여 Tables 1, 2에 정리하였다. 기본적으로 기존 연구, Boolean 대수 방법, 기존 방법 및 본 연구 제안 방법의 리스크 결과 및 소요된 총 추출 샘플수를 비교하여 나타내었다. Table 1에는 추가적으로 타 연구에서 LGS 원전 독립조건에서 수행된 SPRA 결과(Ellingwood, 1990; Kim et al., 2011; Kwag et al., 2020b)인 리스크 및 HCLPF 값을 같이 나타내었다. HCLPF는 고신뢰도저파손확률을 의미하는 값으로 보통 지진취약도 곡선의 대표 내진성능값을 의미한다. 이는 원자력 기기, 구조, 및 시스템 내진성능에 주로 활용하는 값으로서 통계적으로는 95%-신뢰도 지진취약도 곡선에서 5%-파괴확률 혹은 평균 지진취약도 곡선에서 1%-파괴확률에 해당하는 지진세기 값으로 산출된다. 리스크 값은 앞서 소개한 식 (5)의 방법 대로 산출할 수 있다. 기존 방법의 리스크 결과는 CM 시스템 지진취약도 결과와 마찬가지로 지진세기 분할 ne = 196이고, 각각의 지진세기 마다의 샘플 수는 Nt = 1E4일 경우이다. 반면에, 본 연구의 제안이 결합된 방법(Table 1 및 Table 2의 마지막 두 개의 열)은 지진세기 분할 수의 경우 ne = 100을 사용하였다.
Table 1.
Comparison of HCLPF and mean risk for LGS NPP accident scenarios according to other studies and each method(Independent case)
| Seq. | Ellingwood (1990) | Kim et al.(2011) | Boolean Algebra (Kwag et al., 2020b) | Sampling approach w/ MCS | Sampling Approach w/ LHS & Optimal PGA resolution | |||
| Risk(/yr) | HCLPF(g) | HCLPF(g) | Risk(/yr) | HCLPF(g) | Risk(/yr) | HCLPF(g) | Risk(/yr) | |
| TEUX | 3.40E-06 | 0.295 | 0.295 | 3.84E-06 | 0.304 | 3.53E-06 | 0.305 | 3.51E-06 |
| TRb | 1.10E-06 | 0.416 | 0.416 | 1.14E-06 | 0.407 | 1.14E-06 | 0.423 | 1.13E-06 |
| TRpv | 4.70E-07 | 0.546 | 0.546 | 4.67E-07 | 0.543 | 4.69E-07 | 0.552 | 4.65E-07 |
| TECC | 1.50E-06 | 0.421 | 0.421 | 1.47E-06 | 0.418 | 1.46E-06 | 0.427 | 1.45E-06 |
| TRC | 6.00E-07 | 0.516 | 0.516 | 6.40E-07 | 0.511 | 6.44E-07 | 0.508 | 6.40E-07 |
| TEW | 1.20E-07 | - | - | 1.24E-07 | - | 1.20E-07 | - | 1.98E-07 |
| CM | 5.00E-06 | 0.281 | 0.281 | 5.44E-06 | 0.284 | 5.14E-06 | 0.285 | 5.17E-06 |
| # of samples | - | - | - | - | 196×1E4×2 | 100×1E4×2 | ||
Table 2.
Comparison of mean risk for LGS NPP accident scenarios according to each method(Fully correlated case)
| Seq. | Boolean Algebra(Kwag et al., 2020b) | Sampling approach w/ MCS | Sampling Approach w/ LHS & Optimal PGA resolution | |||
| HCLPF(g) | Risk(/yr) | HCLPF(g) | Risk(/yr) | HCLPF(g) | Risk(/yr) | |
| TEUX | 0.351 | 1.76E-06 | 0.363 | 1.48E-06 | 0.361 | 1.46E-06 |
| TRb | 0.416 | 1.14E-06 | 0.420 | 1.14E-06 | 0.417 | 1.12E-06 |
| TRpv | 0.546 | 4.67E-07 | 0.554 | 4.68E-07 | 0.552 | 4.61E-07 |
| TECC | 0.473 | 8.27E-07 | 0.472 | 8.11E-07 | 0.472 | 8.20E-07 |
| TRC | 0.516 | 6.40E-07 | 0.508 | 6.40E-07 | 0.515 | 6.40E-07 |
| TEW | - | 1.27E-07 | - | 2.27E-07 | - | 3.00E-07 |
| CM | 0.308 | 3.84E-06 | 0.311 | 3.65E-06 | 0.312 | 3.67E-06 |
| # of samples | - | - | 196×1E4×2 | 100×1E4×2 | ||
Tables 1, 2로부터 확인할 수 있듯이, 고려한 두 사례와 관련하여 기존의 방법 및 본 연구의 제안 방법 모두 거의 정확한 해와 가까운 값을 도출함을 확인할 수 있다. 이는 타연구의 독립조건의 결과와도 거의 유사한 것으로서 두 샘플링 방법 결과의 신뢰성을 확인할 수 있다. 또한, 제안된 방법의 결과와 기존 방법의 결과를 서로 비교했을 때, 제안된 방법이 비교적 적은 샘플 수로도 정해와 거의 일치하는 값을 도출함을 볼 수 있었다. 구체적으로 제안된 방법은 결과 산출에 필요한 총 추출 샘플 개수를 약 1/2배로 낮추었다. 결과적으로 앞 선 논의에서도 확인할 수 있었듯이 이러한 결과는 기존 방법 대비 제안된 방법의 계산 효율성을 입증한다고 할 수 있겠다. 또한, 적은 샘플링 추출 영역에서는 본 연구의 제안 방법이 LHS 방법을 활용하기 때문에 기존의 MCS 방법을 이용하는 것보다 정확도를 높일 수 있어 추가적인 효율성을 확보할 수 있을 것으로 판단된다.
5. 정리 및 결론
본 연구에서는 샘플링기반 SPRA 방법의 계산 성능을 개선하기 위한 효과적인 방법을 제안하였다. 본 연구에서 제안한 방법의 주요한 특징은 다음과 같다. 기존의 샘플링기반 SPRA 방법의 샘플링 추출 기법인 MCS 방식을 LHS 방식으로 변경하여 적은 샘플수 추출 구간에서도 지진 리스크 값의 정확도를 개선한다. 또한, 기존 방법의 지진세기 세분화 정도를 최종 지진리스크 결과 수렴성과 연계하여 최적의 지진세기 세분화 값을 도출함으로써, 계산에 필요한 총 샘플 추출 횟수를 최소화한다.
제안된 방법의 유효성을 검증하기 위하여, 본 연구의 제안이 결합된 SPRA 방법을 실제 원전 예제에 적용하였다. 결과적으로, 본 연구의 제안 방법이 기존의 방법과 비교하여 최적의 지진세기 세분화 정도 값을 활용함으로써 유사한 결과 정확도 내에서 약 2배 갸량의 효율성을 확보할 수 있었다. 마지막으로, 샘플링기반 SPRA방법이 LHS 기법과 통합되는 경우, 기존의 MCS 기법과의 결합보다는 적은 샘플 수 영역(Nt <= 1E3)에서 해의 정확도를 높일 수 있는 것으로 확인되었다. 이러한 결과는 본 연구 제안 방법이 기존 방법에 비하여 추가적인 효율성을 확보할 수 있다는 의미를 내포한다. 그러므로 본 연구의 제안은 샘플링기반 SPRA방법의 계산 효율성 증대에 일정 부분 기여할 수 있을 것으로 판단된다.