1. 서 론
2. 연구 대상
2.1 예제 모델
2.2 시공단계해석
3. 축소량 해석 결과
3.1 메가구조모델 축소량
3.2 아웃리거 구조모델 축소량
4. 장기거동에 따른 영향
4.1 비구조요소에 대한 영향
4.2 구조요소에 대한 영향
5. 결 론
1. 서 론
초고층 건물에서는 횡력저항시스템을 통한 수평변위 제어와 더불어 건물의 높이 증가에 따른 압축력의 증가로 발생할 수 있는 구조적 안전성과 사용성 문제를 구조설계단계에서 필수적으로 검토해야 한다. 최근 초고층 건물에서 주로 사용되고 있는 콘크리트 재료의 수직 부재에서는 응력 차이와 시간의존적 재료성질의 차이로 인해 부등축소현상이 발생한다. 수직부재에서 재하되는 하중에 의해 탄성 축소가 발생하며 콘크리트의 시간의존적 재료성질에 의해 발생하는 크리프와 건조수축과 같은 비탄성 축소가 장기간에 걸쳐 발생한다(Kim et al., 2003; Li et al., 2016; Samarakkody et al., 2017; Song and Kim, 2018). 이러한 기둥축소현상은 수직부재별로 상이하게 발생하며, 구조물에서의 부등축소는 보, 슬래브와 같은 구조요소에 추가적인 하중을 유발하며 칸막이벽, 커튼월 등과 같은 비구조요소의 파손 등 문제점을 발생시킨다(Kim and Shin, 2011). 이러한 이유로 초고층 건물의 설계 및 시공단계에서 콘크리트의 장기적 거동으로 인한 수직축소량에 대해서 중요하게 고려하고 적절한 분석을 통해 예측 및 검토해야 한다.
국내외에서는 기둥축소현상에 대해 부등축소량의 예측과 예측 결과를 이용한 시공단계에서의 보정방법 등에 대한 연구가 활발히 진행되었다. 부등축소량 예측을 위하여 Moon과 Choi(2018)는 기둥축소량 발생 요인에 대해 분석하였으며 축소량 기준에 대해 비교하였고, Lu 등(2013)은 AEMM(Age-adjusted Effective Modulus Method)을 통한 크리프 축소량 계산법을 제시하였고 수직부재의 축소량을 예측하였다. 또한, 시공단계의 보정방법을 위하여 Park 등(2010)은 이동평균법과 누적 오차를 고려하여 건물의 수직부재의 상호간 부등축소량 보정기법을 제시하였다. 특히, Kim과 Kim(2022)은 60층 규모 건물을 대상으로 횡력저항시스템에 따른 부등축소 영향을 분석하였으며, 수직부재의 단면설계 지배하중에 따라 기둥축소량이 다르게 나타남을 확인하였다. 해당 연구에서는 60층 규모의 초고층 모델에 대해서 설계 지배하중 조합에 따른 수직부재 장기거동의 변화를 확인하였지만, 중력하중에 의한 탄성축소 및 크리프의 영향이 크게 나타날 것으로 예측되는 큰 규모의 건물에 대해서는 경향이 다를 수 있다.
따라서 이 연구에서는 기존연구(Kim and Kim, 2022)에서 분석한 건물에 비하여 기둥축소의 영향이 클 것으로 예측되는 120층 규모의 해석 모델을 계획하여 시공단계해석을 수행한 후 콘크리트의 장기거동 영향을 분석하고자 한다.
2. 연구 대상
2.1 예제 모델
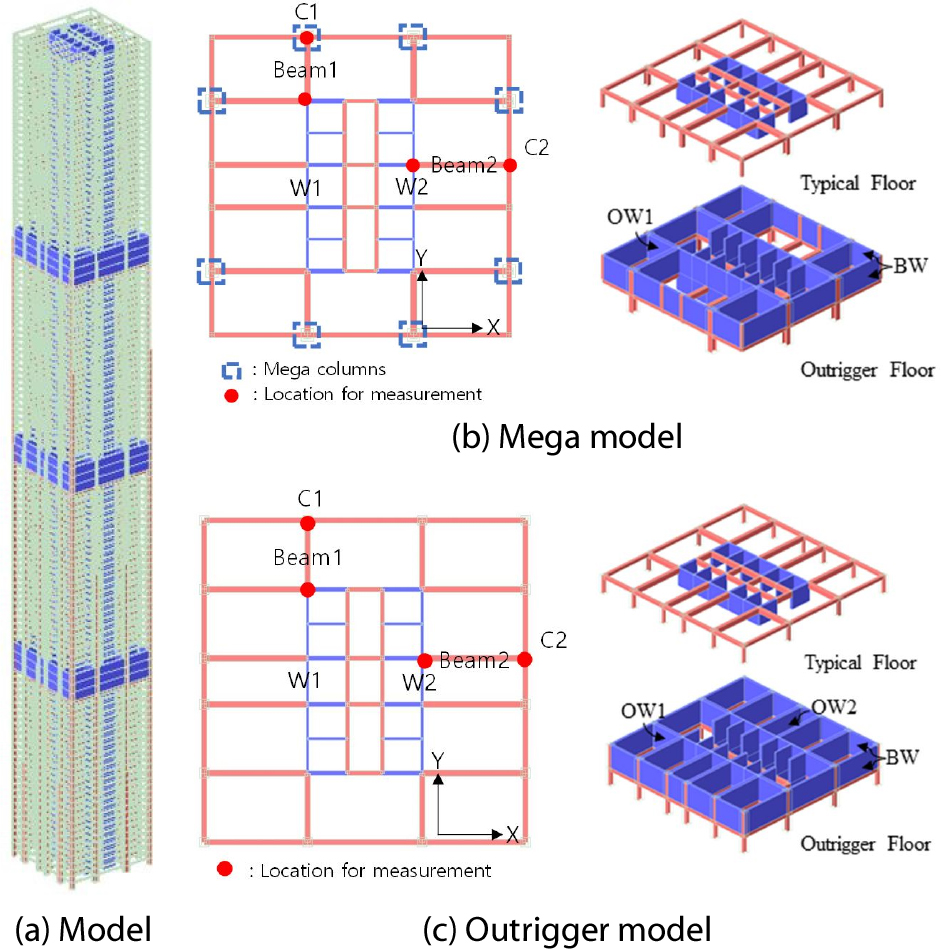
이 연구의 예제 모델은 높이 515.7m(기준층 층고 4.2m, 아웃리거층 층고 5.5m), 세장비는 ‘9.37’인 120층의 초고층 건물로서, 사용한 횡력저항시스템은 메가구조 시스템(메가구조모델)과 아웃리거 시스템(아웃리거 구조모델)이다(Fig. 1). 메가구조 시스템(Fig. 1(b))에서 샛기둥(C2)은 중력하중에만 저항하며, 아웃리거층에서 축력이 메가기둥(C1)으로 전이된다. 이에 반해 아웃리거 시스템(Fig. 1(c))에서 모든 기둥(C1, C2)이 횡력에 저항하도록 설계되었다.
평면은 한 변의 길이가 55m인 정방형이며, 중앙에 RC 코어 벽체가 존재하며 외부 테두리에 RC 및 SRC 기둥이 배치되어 있다. 또한, 아웃리거 벽체와 벨트월을 3개소에 설치하였으며, 29~31층, 59~61층, 89~91층에 배치되었다. 특히, 아웃리거 벽체와 연결된 기둥은 SRC 기둥으로 계획하였다. 단면설계를 위한 중력하중 조건과 횡하중 적용 조건은 Kim과 Kim(2022)에서 제시한 조건(KDS 41 00 00, 2019)을 동일하게 적용하였고 이를 각각 Tables 1과 2에 정리하였다.
Table 1
Vertical load condition
Table 2
Lateral load condition
| Wind Load | Earthquake | ||
| Basic speed | 26m/s | EPA | 0.176g |
| Exposure category | B | Site class | S3 |
| Importance factor | 1.05 | Importance factor | 1.2 |
국내 건축구조기준(KDS 41 00 00, 2019)에 따라 단면 설계를 진행하였으며, 기둥과 벽체는 매 15개 층마다 구분하여 RC 부재의 콘크리트 설계기준 압축강도는 35~80MPa로 적용하였고 SRC 부재의 콘크리트 설계기준 압축강도는 35~70MPa이다. 또한, SRC 부재의 강재는 매 30개 층씩 구분하여 SM 275TMC~SM 460TMC를 적용하였다. 부재의 단면설계는 해석 모델의 콘크리트 설계압축강도, 강종, 기둥의 단면치수, SRC 내 H형강의 치수, 전단벽의 두께와 수직 부재의 기하형상치수(Notational member size, h)를 모델에 따라 Tables 3과 4에 정리하였다. 특히, SRC 의 경우, 기존의 RC 기둥 해석방법을 사용하여 축소량을 예측하면 실제보다 과다하게 나타난다고 알려져 있어 이를 보완한 방법(Kim et al., 2005)과 같이 H형강으로 건물 분할된 단면에 대한 기하형상치수를 각각 계산하고 전체 면적에 대한 분할된 단면의 면적비를 고려하여 기하형상치수에 가중평균하여 SRC 기둥의 기하형상치수를 산정하였다.
Table 3
Details of columns in each model
Table 4
Details of walls in each model
2.2 시공단계해석
이 연구에서는 선행연구(Kim and Kim, 2022)와 개별 부재의 초기 재하일, 상대습도, 시공 일정 및 하중재하 방식 등의 조건을 동일하게 설정하였다. 개별 부재 초기 재하일은 3일로 설정하였으며 1개층 당 공기는 5일로, 아웃리거층은 15일로 설정하였다. 시공단계해석 및 분석의 단순화를 위하여 코어와 골조는 동시에 시공되는 것으로 가정하였으며, 슬래브 자중(Slab self weight)과 시공활하중(Construction Live Load)은 코어와 골조가 시공될 때 재하하였다. 마감하중(Superimposed Dead Load) 재하는 시공활하중보다 4개 층 후행하며 마감하중 재하시 시공활하중을 제거한다. 하중재하가 완료되고 70일 후에 활하중(Live Load)을 전 층에 재하하였다. 착공부터 활하중 재하까지 총 780일이 소요되며, 총 135단계의 시공단계로 구성되었다. 시공단계해석은 범용구조해석프로그램인 MIDAS Gen으로 진행하였으며, 콘크리트 재령에 따른 강도 및 강성 변화, 시간 경과에 따른 크리프 및 건조수축 등의 콘크리트 재료 모델은 국내 콘크리트구조설계기준(KDS 14 20 00, 2021) 모델을 적용하였다.
3. 축소량 해석 결과
3.1 메가구조모델 축소량
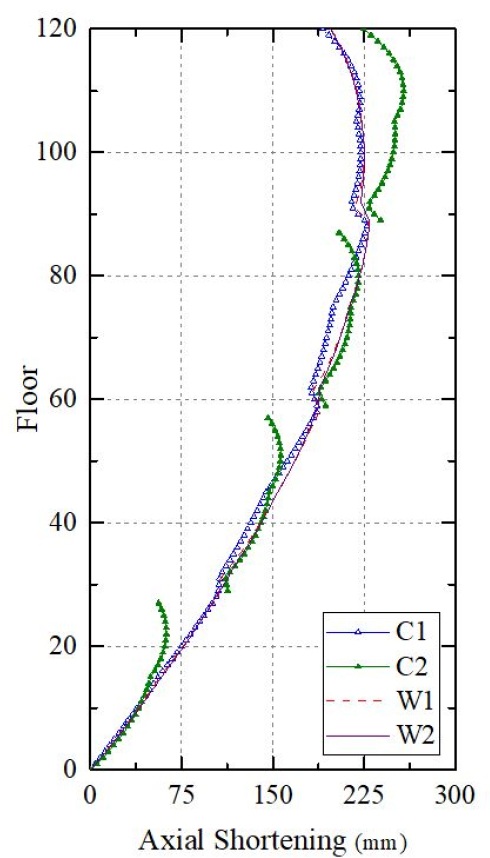
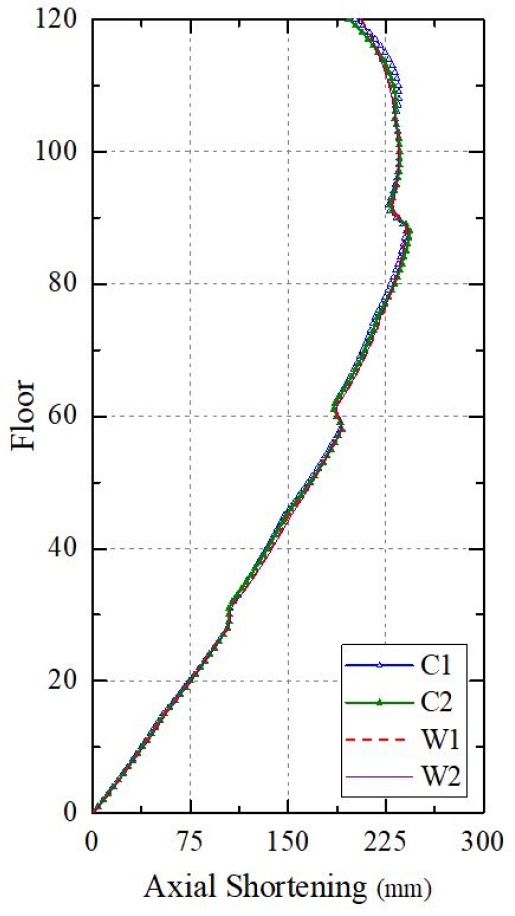
입주완료 후 최대 절대축소량이 발생하는 Stage 135(11,730일, 입주 후 30년이 경과한 단계)의 각 수직부재에서 인접 슬래브 타설 후에 발생하는 절대축소(sub to)에 의해 발생한 수직부재의 수직변위를 층에 따라 Fig. 2에 나타냈다. SRC 메가기둥인 C1에서 발생한 최대 절대축소량은 227.3mm(88층)이고, 인접 벽체 위치 W1에서는 229.8mm(88층)이다. 축력이 전이되는 RC 샛기둥인 C2에서는 257.7mm(110층)이고, 인접한 벽체 위치 W2에서는 229.6mm(89층)이다. Fig. 2에서 아웃리거층 하부 C2 위치는 중력하중전이로 기둥이 지지되지 않아 절대축소량은 불연속하게 나타났으며, 29층, 59층, 89층에서 C2의 갑작스러운 절대축소량 증가현상이 발생하였다.
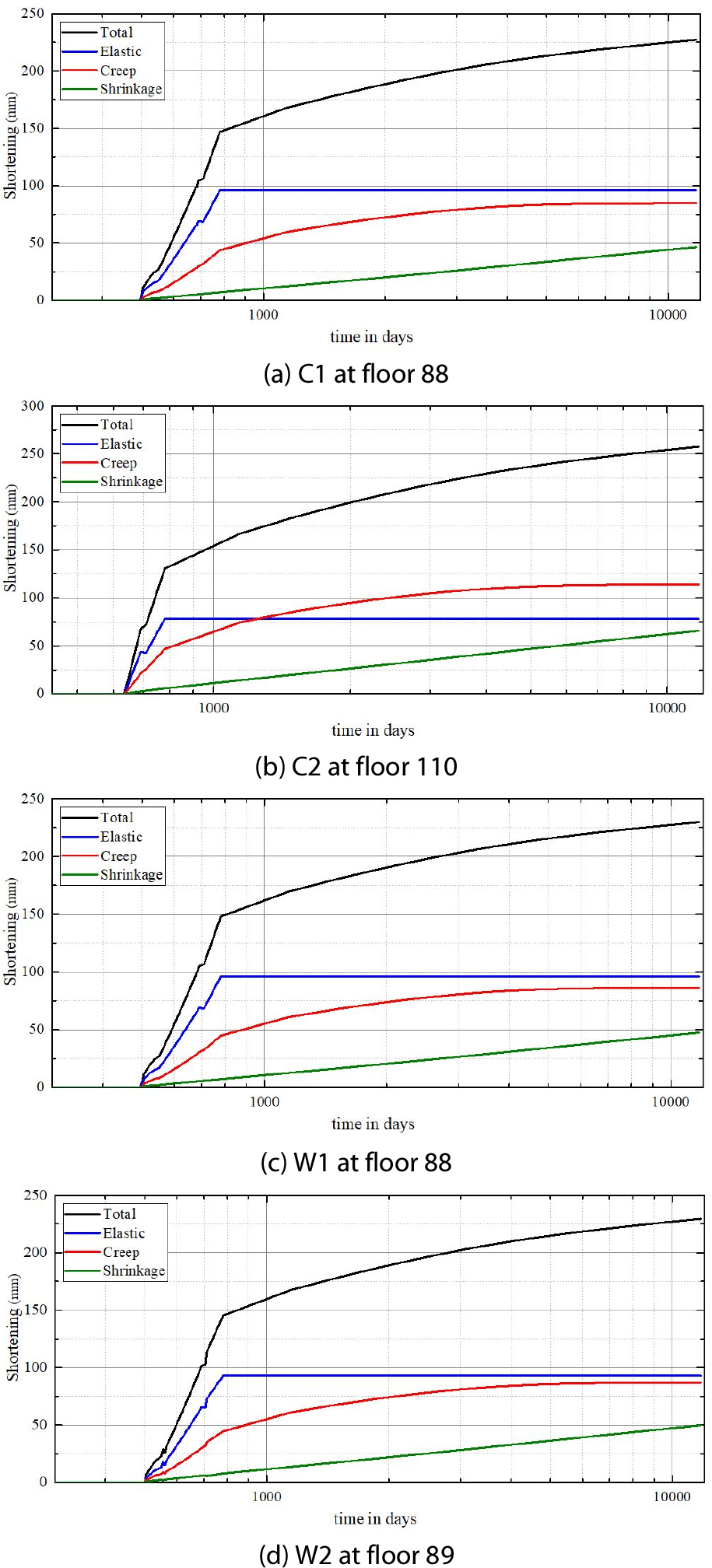
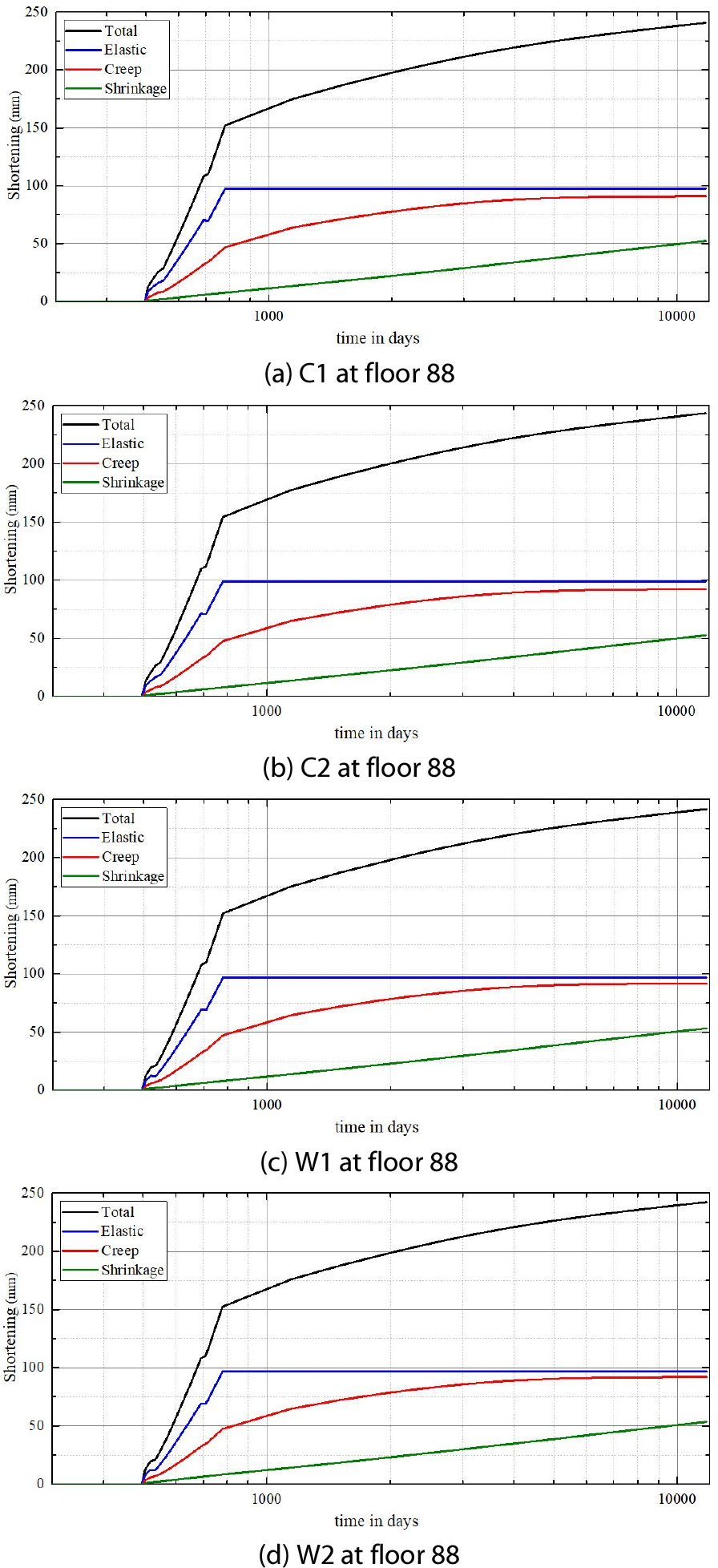
각 수직부재별로 최대 절대축소량이 발생한 층에서 골조시공단계부터 입주완료(780일) 후 30년(11,730일)까지 영향요인별 축소량의 변화를 Fig. 3에 나타냈다. 메가기둥 C1의 경우 골조시공(Stage 88, 500일)부터 축소량이 발생하였으며 입주완료 시점(Stage 129, 780일) 이후 하중에 변화가 없으므로 탄성축소량의 변화는 나타나지 않았다. 또한, 비탄성 거동의 경우 입주완료 시점부터 5년(2,605일) 간 크리프가 건조수축보다 빠르게 발현되었다. 그러나 5년 이후 크리프와 건조수축의 발현속도가 역전하여 나타났고 입주완료부터 17년(6,985일) 이후 추가적으로 발생하는 크리프축소량은 거의 없었으며, 총 축소량의 증가는 건조수축의 영향을 주로 받는 것으로 나타났다(Fig. 3(a)). 또한, 샛기둥인 C2의 경우도 골조시공(Stage 110, 640일) 이후 유사한 축소 경향이 발생하였다(Fig. 3(b)). 인접벽체(W1, W2)의 절대축소량에서도 기둥과 유사한 변화가 확인되었다(Figs. 3(c) and 3(d)).
최대 절대축소량이 발생한 단계인 Stage 135에서 영향요인별 축소량을 통해 절대축소량에 대한 지배적 요인에 대해 분석하였고 이를 절대축소량에서의 비중(%)과 함께 Table 5에 정리하였다. Stage 135에서 C2를 제외하고 메가기둥(C1)과 인접벽체(W1, W2)는 유사한 결과를 확인할 수 있다. 탄성축소량이 약 40% 이상 수준으로 나타나 절대축소량에 대해 가장 큰 비중을 차지하였으며 비탄성 거동 중 크리프축소량이 약 37% 이상, 건조수축축소량이 약 20% 이상 수준으로 나타났다. C2의 경우에는 절대축소량에 대해 탄성축소량이 약 30.4% 수준으로 발생하였으며 크리프축소량이 44.2%로 가장 큰 비중을 차지하였다.
Table 5
Axial shortening in mega model at stage 135
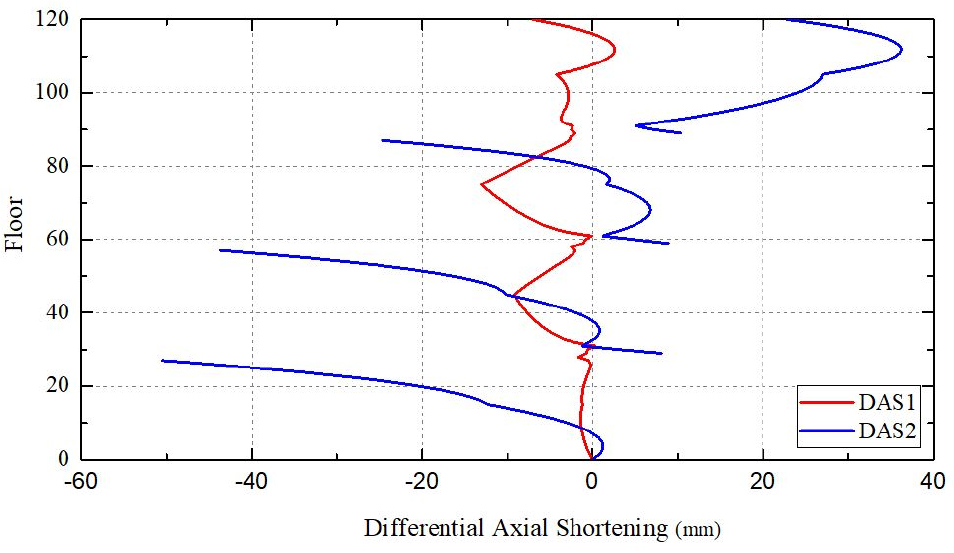
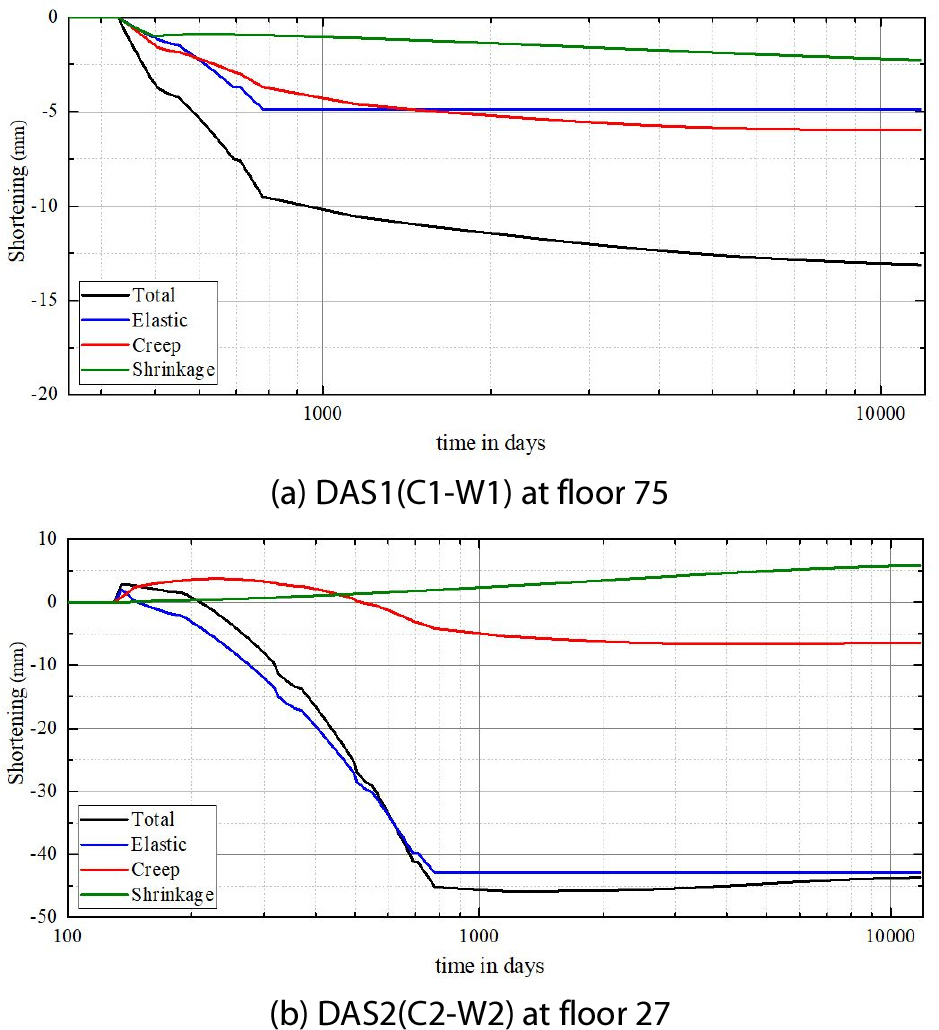
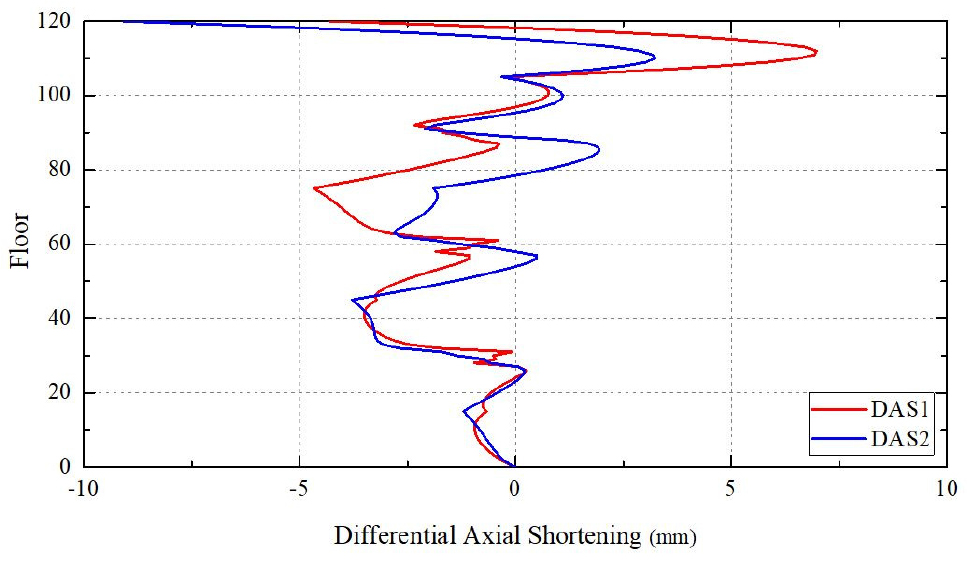
Stage 135에서 수직부재의 절대축소량 차이로 발생한 부등축소량을 Fig. 4에 나타냈다. 이때, 부등축소량은 “기둥의 절대축소량 – 벽체의 절대축소량”으로 정의하였다. SRC 메가기둥 C1과 RC 벽체 W1 간 부등축소량(DAS1)의 최댓값은 –13.1mm(75층)이며, RC 샛기둥 C2와 RC 벽체 W2 간 부등축소량(DAS2)의 최댓값은 –43.7mm(27층)이다. DAS1은 아웃리거층에서 기둥의 축소를 구속하면서 아웃리거층과 인접층에서 감소하여 나타났으며, 아웃리거 벽체를 통해 기둥의 축력이 인접벽체로 하중이 전이되어 대부분의 층에서 음수값으로 발생한 것으로 판단된다. 기존연구(Kang et al., 2010)에 따르면 아웃리거 벽체를 통해 하중이 전이되어 재분배되는 과정에서 아웃리거층 하부에서 전단벽의 축력이 증가하는 것으로 나타났다. DAS2의 경우 하부층에서 상부의 아웃리거층에 가까워질수록 C2에서 부담하는 축력이 감소하고 W2에서 상부구조물의 하중을 부담하면서 W2의 축소량이 C2의 축소량보다 크게 나타나 음수값으로 발생하였다(Fig. 4).
최대 부등축소 발생층의 부등축소 추이를 확인하기 위해 골조시공부터 Stage 135까지의 영향요인별 부등축소량을 분석하여 Fig. 5에 정리하였다. DAS1의 경우 모든 영향요인에서 음수값으로 산출되면서 전 단계에서 음수값으로 산출되었다(Fig. 5(a)). 아웃리거층을 통해 하중이 재분배되면서 탄성 부등축소량과 크리프 부등축소량이 음수값으로 산출된 것으로 판단된다. 또한, 기둥(C1)과 벽체(W1)의 기하형상치수는 각각 1,941mm, 297mm로 W1의 건조수축축소량이 C1보다 크게 발생하여 건조수축 부등축소량도 음수값으로 산출된 것으로 판단된다. DAS2의 경우 골조시공시점에는 양수값으로 산출되었으나 서서히 감소하여 음수값으로 변화하였으며, 입주완료 후 1년이 경과한 시점에서 최댓값 –45.8mm이 발생하고 이후 Stage 135까지 음수값으로 유지되었다(Fig. 5(b)). 골조시공 초기에는 중력하중의 영향을 적게 받는 W2의 축소량이 C2의 축소량 보다 작게 발생하였기 때문에 DAS2가 양수값이었으나, C2가 아웃리거층에 근접할수록 부담하는 축력이 0이 되고 아웃리거층에서 하중이 재분배되면서 W2의 축력이 증가하여 DAS2가 음수값으로 변화하였다.
최대 부등축소량이 발생한 단계에서 부등축소량에 대한 지배적인 요인을 분석하기 위해 최대 부등축소량에 대한 영향요인별 부등축소량을 Table 6에 정리하였다. 최대 DAS1의 경우 모든 영향요인에 대해 C1이 W1보다 작게 축소하여 DAS1이 음수값으로 산출되었다. Stage 135에서 부등축소량에 대해 크리프와 탄성축소가 부등축소량에 대해 지배적으로 나타났다. DAS2의 경우 Stage 135에서 탄성축소가 부등축소량에 대해 지배적인 요인으로 나타났으며, 탄성축소와 크리프가 증가요인으로 작용하였고 건조수축이 감소요인으로 작용하였다.
Table 6
DAS in mega model at stage 135
| Location | Floor | DAS | |||
| Elastic | Creep | Shrinkage | Total | ||
| C1-W1 | 75 | -4.9mm | -6.0mm | -2.2mm | -13.1mm |
| C2-W2 | 27 | -43.0mm | -6.5mm | 5.8mm | -43.7mm |
선행연구(Kim and Kim, 2022)의 60층 모델과 비교했을 때 탄성축소의 영향이 큰 비중을 차지하는 것으로 나타났다. 이는 건물의 규모가 커지면서 수직부재에서 부담하는 중력하중의 영향이 증가하였기 때문이다.
3.2 아웃리거 구조모델 축소량
시공단계해석 결과로부터 아웃리거 구조모델의 Stage 135에서 수직부재의 절대축소에 의한 수직변위를 층에 따라 Fig. 6에 나타냈다. 아웃리거 벽체(OW1)와 연결된 SRC 기둥인 C1에서 최대 절대축소량은 240.7mm(85층)이고, 인접 벽체 W1에서는 241.7mm(82층)이다. 아웃리거 벽체(OW2)와 연결된 SRC 기둥인 C2에서 최대 절대축소량은 243.5mm(83층)이고, 인접 벽체인 W2에서는 242.4mm(83층)이다(Fig. 6). 아웃리거 구조모델의 기둥과 벽체는 매우 유사한 축소량을 나타냈다. 특히, 아웃리거층에서 하중이 재분배되는 과정을 여러 번 거치면서 하부층으로 갈수록 기둥과 벽체의 축소량이 보다 유사해지는 것으로 나타났다.
각 수직부재별로 최대 절대축소량이 발생한 층에서 골조시공단계부터 Stage 135까지 영향요인별 축소량을 Fig. 7에 나타냈다. 기둥(C1, C2)과 인접벽체(W1, W2)는 입주완료 후 5년 간 크리프가 건조수축보다 빠르게 발현되었으나 5년 후부터 크리프의 발현속도가 서서히 감소하여 크리프와 건조수축의 발현속도가 역전되었다. 또한, 입주완료 후 17년이 경과한 시점부터 크리프축소량의 증가는 거의 없고 비탄성축소량은 주로 건조수축에 의해 발생하였다(Fig. 7).
최대 절대축소량이 발생한 Stage 135에서 영향요인별 축소량을 통해 절대축소량에 대한 지배적 요인에 대해 분석하여 절대축소량에서의 비중(%)과 함께 Table 7에 정리하였다. 아웃리거 구조모델의 기둥(C1, C2)은 인접 벽체(W1, W2)와 대단히 유사한 축소 경향을 나타냈다. Stage 135에서 절대축소량 중 탄성축소가 가장 큰 비중을 차지하였으며 약 40.6% 미만 수준으로 나타났고, 그 다음으로 크리프(38.0% 미만), 건조수축(22.1% 미만) 수준으로 나타났다.
Table 7
Axial shortening in outrigger model at stage 135
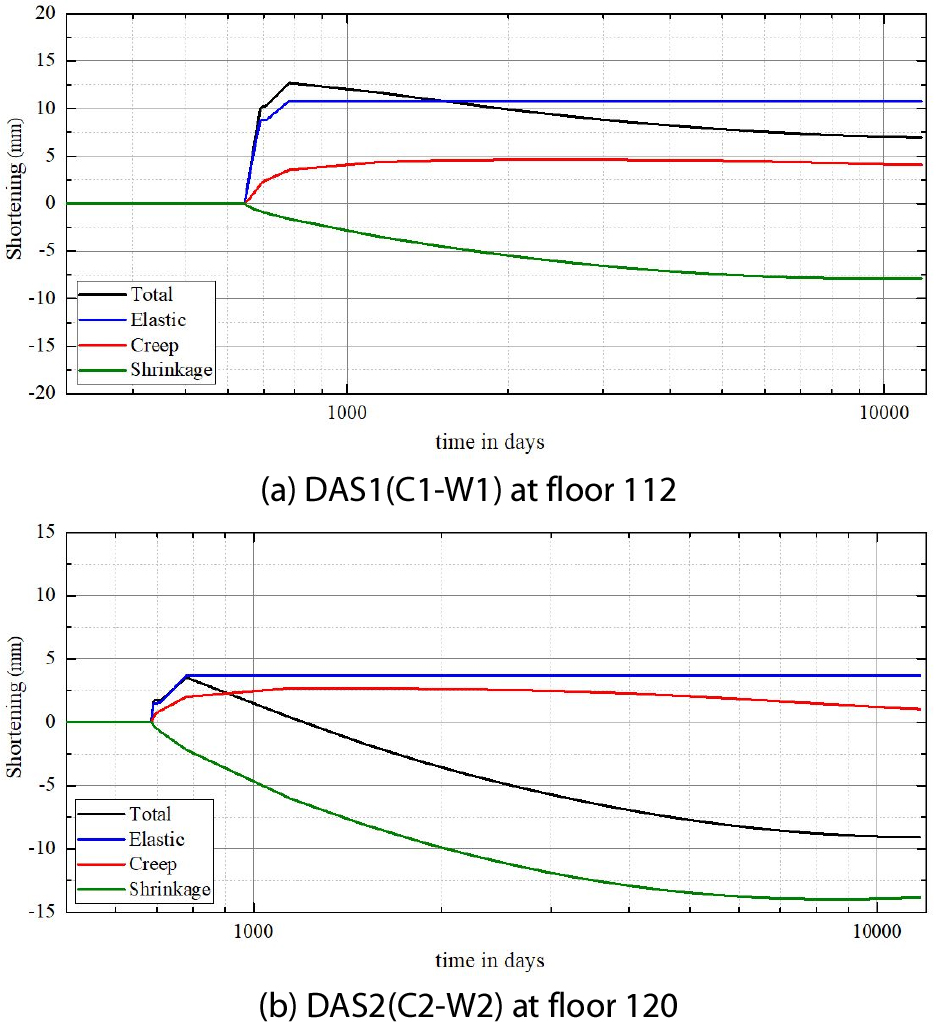
Stage 135에서 발생한 절대축소량 차이에 따른 부등축소량을 Fig. 8에 제시하였다. SRC기둥 C1과 인접 벽체 W1의 부등축소량(DAS1)의 최댓값은 7.0mm(112층)이고 SRC기둥 C2와 인접 벽체 W2의 부등축소량(DAS2)의 최댓값은 –9.1mm(120층)이다. 아웃리거 벽체가 기둥(C1, C2)을 구속하여 아웃리거층에서 인접층에 비해 DA S1과 DAS2가 감소하여 나타났다. 또한, 아웃리거층에서 아웃리거 벽체를 통해 하중이 재분배되면서 아웃리거층 하부에서 벽체의 축소량 증가로 부등축소량이 음의 방향으로 증가하였다.
최대 부등축소 발생층의 부등축소 추이를 확인하기 위해 최대 부등축소 발생층의 시공시점부터 Stage 135까지 시간에 따른 축소량을 Fig. 9에 나타냈다. 입주완료(Stage 129) 후 DAS1과 DAS2는 꾸준히 감소하는 것으로 나타났다(Fig. 9). DAS1의 경우 Stage 129에서 12.7mm로 최댓값이 발생하였고 이후 서서히 감소하였다. 비탄성 거동 중 크리프 부등축소량은 증가요인으로 작용하였으나 건조수축 부등축소량은 감소요인으로 작용하였다. 크리프 부등축소량의 경우 입주완료 후 1년부터 증가속도가 서서히 감소하였고, 5년 경과시점부터 오히려 감소하는 것으로 나타났다. 따라서, 감소요인으로 작용하는 건조수축이 지배적인 요소로 작용하여 총 부등축소량은 점차 감소하였다(Fig. 9(a)). DAS2의 경우 최대 부등축소량 발생층(Stage 135)이 120층이므로 축력의 영향이 대단히 작게 나타나 탄성과 크리프 부등축소량이 대단히 작게 발생하였다. 골조 시공 후 크기가 지속적으로 증가하다가 입주완료 후 21년 경과한 시점부터 축소량이 감소하였다. 그러나 건조수축축소량이 탄성 및 크리프축소량보다 월등히 크기 때문에 총 부등축소량은 건조수축 부등축소량과 유사한 경향을 나타내고 있다(Fig. 9(b)).
시간이 경과함에 따라 최대 부등축소 발생층에서 부등축소량에 대한 지배적인 요인을 확인하기 위해 영향요인별 축소량(Stage 135)을 분석하여 Table 8에 정리하였다. DAS1의 경우 부등축소에 대해 탄성축소와 크리프가 증가요인으로 건조수축이 감소요인으로 작용하였다. DAS2의 경우 탄성축소와 크리프가 감소요인으로 건조수축이 증가요인으로 작용하였다.
4. 장기거동에 따른 영향
4.1 비구조요소에 대한 영향
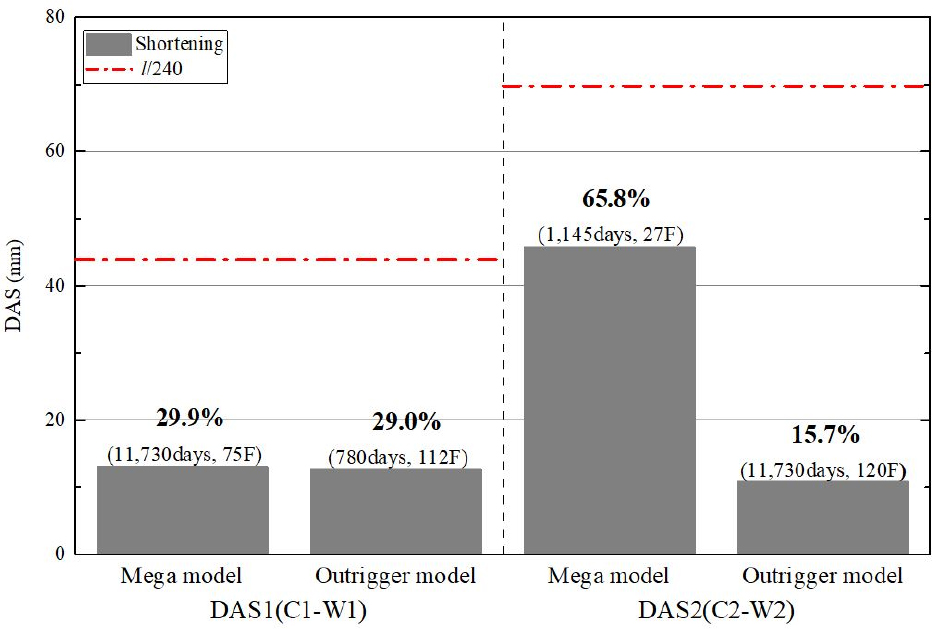
부등축소량에 대한 최대 허용한계치는 경간길이의 1/240 (Kim and Kim, 2022)이며 각 모델의 최대 부등축소량에 대해 검토하였다. 또한,이를 최대 허용한계치에 대한 비율로 시공일정 및 발생층과 함께 Fig. 10에 나타냈다. 두 모델의 최대 DA S1과 DAS2는 모두 최대 허용한계치를 만족하였다. 메가구조모델의 DAS2는 최대 허용한계치의 65.8% 수준으로 발생하였고 그 외의 경우 30% 미만 수준으로 발생하였다. 특히, 선행연구(Kim and Kim, 2022)와 비교하였을 때, 60층 모델에 비해 메가구조모델에서 DAS1은 31.2%p, DAS2는 21.1%p 감소하였고 아웃리거 구조모델에서 DAS1은 56.4%p, 32.5%p 감소하여 120층 모델이 최대 허용한계치에 대한 여유도가 증가하였다.
메가구조모델과 아웃리거 구조모델에서 수직부재의 설계지배하중조합을 Table 9에 정리하였다. 메가구조모델의 샛기둥인 C2는 전 층에서 중력하중조합에 의해 설계되어 인접벽체 W2와의 부등축소가 크게 발생하여 최대 허용한계치의 65.8%로 발생하였다. 그 외의 기둥들에서는 전 층에서 횡하중에 의해 설계되어 인접벽체와 절대축소량에서 큰 차이를 보이지 않았으며 최대 허용한계치의 30% 미만 수준으로 발생하였다. 이와 같이 선행연구의 60층 모델과 유사하게 120층 모델에서도 인접부재들의 지배하중조합 조건에 따라 축소량에서 차이가 발생하는 것을 확인하였다. 특히, 샛기둥을 제외한 모든 수직부재들이 횡하중이 포함된 하중조합에 의해 설계된 120층 모델의 부등축소량은 60층 모델의 부등축소량보다 작은 것으로 확인되었다.
Table 9
Governing load combination for section
| model | ID | Floor | Load combination |
|
Mega model | C1 | 1-30 | 1.2DL±1.3W+1.0LL |
| 61-120 | 1.2DL-1.0E+1.0LL | ||
| C2 | 1-120 | 1.2DL+1.6LL | |
| W1 | 1-105 | 1.2DL±1.3W+1.0LL | |
| W2 | 106-120 | 0.9DL±1.3W | |
| Outrigger model | C1 | 1-75 | 1.2DL±1.3W+1.0LL |
| C2 | 76-120 | 1.2DL-1.0E+1.0LL | |
| W1 | 1-90 | 1.2DL±1.3W+1.0LL | |
| W2 | 91-120 | 0.9DL±1.3W |
4.2 구조요소에 대한 영향
4.2.1 수평부재의 휨모멘트
수평부재의 부재력은 공칭 휨모멘트(Mn)에 대한 시공단계 총 휨모멘트(Mconst : MDL+LL+Mcreep+Mshrinkage)의 비율이 가장 높은 부재를 대상으로 분석하였으며, 이때 단부 휨모멘트를 설계단계 휨모멘트(Mdesign), 시공단계 탄성 휨모멘트(MDL+LL), 비탄성 거동으로 인한 크리프와 건조수축 휨모멘트(Mcreep & Mshrinkage) 및 시공단계 총 휨모멘트(Mconst)로 구분하여 공칭 휨모멘트에 대한 비율(%)과 함께 Table 10에 정리하였다.
Table 10
Bending moment of horizontal elements in each structure model(unit : kN·m)
메가구조모델에서 Beam1의 최대 시공단계 총 휨모멘트(Mconst)는 입주완료 후 30년이 경과한 시점(Stage 135, 11,730일)의 74층 기둥 측 단부에서 발생하였다. 시공단계 탄성 휨모멘트(MDL+LL)는 시공단계해석으로 탄성 축소량(up to)이 보정되면서 설계단계 휨모멘트(Mdesign)보다 1.9%p 작게 발생하였다. 74층 메가기둥은 벽체에 비해 대단히 크게 설계되면서 기둥과 벽체 간 강성차이가 증가하여 벽체 측에서 정(+) 방향의 설계단계 휨모멘트 발생하였고 기둥 측에서 상대적으로 큰 부(-) 방향의 설계단계 휨모멘트가 발생하였는데, 시공단계 탄성 휨모멘트에서도 동일한 현상이 관찰되었다. 또한, 시공단계 총 부재력에 대해서 비탄성 거동 중 크리프 휨모멘트(Mcreep)는 시공단계 탄성 휨모멘트와 반대 방향으로 작용하여 감소요인으로 작용하고 건조수축 휨모멘트(Mshrinkage)는 증가요인으로 작용하였다. 특히, 크리프의 영향이 건조수축보다 작게 나타나 비탄성 거동 부가하중(Mcreep+Mshrinkage) 은 –296.1kN⋅m로, 부(-) 방향 공칭 휨모멘트의 11.9% 수준으로 나타났다. 이로 인해 시공단계 총 휨모멘트는 시공단계 탄성 휨모멘트보다 12%p 증가하여 나타났다. 이 때, 시공단계 효과와 시간의존적 재료성질을 반영한 최대 휨모멘트가 공칭 휨모멘트의 75.6% 수준이나, 이는 비계수 하중조합에 의한 부재력이며, 강도저감계수를 반영한 설계강도까지 고려할 경우 안전성에 대한 여유도가 크게 감소하므로 부재의 단면 재설계에 대한 검토가 필요할 것으로 판단된다.
아웃리거 구조모델의 수평부재에서는 대체적으로 메가구조모델의 부재력 경향과 유사하게 나타났으나 비탄성 거동에서 차이를 보였다. Beam1의 경우, 최대 시공단계 총 휨모멘트는 입주완료 시점(Stage 129, 780일)의 112층 벽체 측에서 발생하였다. 또한, 크리프와 건조수축 휨모멘트가 시공단계 탄성 휨모멘트와 반대 방향으로 작용하였고, 비탄성 거동 부가하중이 정(+) 방향 공칭 휨모멘트의 28.1% 수준으로 발생하면서 시공단계 총 휨모멘트는 시공단계 탄성 휨모멘트보다 감소하여 나타났다. Beam2의 경우, 최대 시공단계 총 휨모멘트는 Stage 129의 28층 기둥 측에서 발생하였다. 비탄성 거동으로 인한 부가하중 중 크리프 휨모멘트는 감소요인으로 작용하였으나 건조수축 휨모멘트는 증가요인으로 작용하였으며, 크리프 휨모멘트의 영향이 건조수축보다 크게 나타났다. 또한, 정(+) 방향 공칭 휨모멘트의 1.1% 수준의 부가하중으로 인해 시공단계 총 휨모멘트는 시공단계 탄성 부재력보다 미소하게 감소하였다.
수평부재에서 비탄성 거동으로 인한 부가하중은 공칭 휨모멘트의 28.1% 이하 수준으로, 일부 부재에서 시간의 경과에 따라 휨모멘트가 감소하는 것으로 나타났다. 건물의 규모가 커짐에 따라 기둥이 상대적으로 크게 설계될 경우 기둥 강성이 증가하면서 기둥과 벽체 간 강성 차이가 커질 수 있으며, 벽체 측에서 미소한 부(-) 방향의 휨모멘트 혹은 정(+) 방향의 휨모멘트가 발생하고 기둥 측에서 대단히 큰 부 방향의 휨모멘트가 발생할 수 있다. 이로 인해 비탄성 거동 부가하중이 시공단계 총 휨모멘트에 대해 증가요인으로 작용하게 되며 계수하중과 설계강도까지 고려한다면 부재 안전성에 대한 검토가 필요할 수 있다.
4.2.2 아웃리거 벽체의 전단력
아웃리거 벽체의 부재력은 각 모델의 아웃리거층(29~31층, 59~61층, 89~91층)에서 부재의 공칭 전단력(Vn)에 대한 시공단계 총 전단력(Vconst : VDL+LL+Vcreep+Vshrinkage)의 비율이 가장 높은 부재를 대상으로 설계단계 전단력(Vdesign), 시공단계 탄성 전단력(VDL+LL), 크리프와 건조수축 전단력(Vcreep & Vshrinkage) 및 시공단계 총 전단력(Vconst)을 분석하였고, 이를 공칭 전단력에 대한 비율(%)로 Table 11에 정리하였다.
Table 11
Shear force of outrigger walls in each structure model(unit : kN)
메가구조모델의 경우, C1과 W1 간 아웃리거 벽체(OW1)는 입주완료 후 30년이 경과한 시점(Stage 135, 11,730일)의 89층에서 시공단계 총 전단력(Vconst) +22,284.7kN이 발생하였다. 또한, 시공단계 탄성 전단력(VDL+LL)은 시공단계해석 특성으로 설계단계 전단력(Vdesign)보다 3.6%p 작게 발생하였고, 선행연구(Kim and Kim, 2022)의 60층 모델에 비해 건물의 규모가 커지면서 7.2%p 가량 증가하였다. 비탄성 거동으로 발생한 크리프와 건조수축 전단력(Vcreep & Vshrinkage)은 시공단계 총 전단력에 대해서 증가요인으로 작용하여 시공단계 총 전단력이 시공단계 탄성 전단력보다 34.5%p 증가하였으며 건조수축 전단력의 영향이 대단히 크게 작용하였다.
아웃리거 구조모델의 경우, 메가구조모델의 전단력 경향과 동일하게 나타났으며, 60층 모델에 비해 시공단계 탄성 전단력은 2.1(OW2)~11.3(OW1)%p 증가하였다. C1과 W1을 연결한 아웃리거 벽체(OW1, 91층)에서 시공단계 총 전단력에 대해 증가요인으로 작용한 크리프와 건조수축 전단력은 공칭 전단력의 22.9% 수준으로 발생하였다. C2와 W2를 구속한 아웃리거 벽체(OW2, 91층)에서는 비탄성 거동으로 발생한 부가하중은 시공단계 총 전단력에 대해 증가요인으로 작용하였으며 공칭 전단력의 22.8% 수준으로 나타났다. 한편, 횡하중 포함 설계지배하중조합(1.2DL±1.3W+1.0LL)으로 설계된 두 모델의 아웃리거 벽체(OW1)는 중력하중에 의해 부재력이 크게 증가함으로써 강도저감계수를 반영한 설계강도로 고려할 경우 안전성에 대해 치명적인 문제가 발생할 것으로 판단된다. 메가구조모델의 OW1에서는 계수하중 소요 전단력이 +36,282.1kN이었으나 비탄성 거동으로 인한 부가하중까지 고려하면 +52,341.3kN이 발생하여 재설계가 필요한 것으로 나타났다. 마찬가지로, 아웃리거 구조모델의 경우 OW1에서는 소요 전단력이 +21,130.0kN이나 시공단계해석에 의한 부가하중을 고려하면 +28,013.5kN이 발생하므로 단면에 대해 재설계가 필요한 것으로 나타났다.
이와 같이 아웃리거 벽체는 건물의 규모가 커지면서 전단력에서의 중력하중의 비중이 선행연구(Kim and Kim, 2022)에 비해 증가하였다. 또한, 비탄성 부가하중은 아웃리거 벽체에 대단히 큰 영향을 미쳤으며, 이러한 영향을 고려하여 단면을 재설계해야 하는 경우가 발생할 것으로 판단된다.
5. 결 론
이 연구에서는 횡력저항시스템에 적용에 따른 120층 규모 초고층 건물의 장기거동 영향을 분석하였다. 각 수직부재의 절대축소량과 부등축소량을 비교 및 검토하였으며, 이에 따른 건물의 사용성과 안전성을 검토하였다.
1)수직부재의 절대축소량을 비교한 결과, 기둥의 절대축소량은 메가구조 시스템을 적용한 모델에서 중력하중의 영향을 크게 받는 샛기둥으로 인해 아웃리거 시스템을 적용한 모델보다 크게 발생했다.
2)수직부재의 부등축소량을 비교한 결과, 두 시스템 모두 아웃리거 벽체로 인해 아웃리거층에서 부등축소량이 감소하였다. 또한, 아웃리거 벽체를 통한 하중 재분배 과정을 거치면서, 하부층으로 갈수록 기둥과 벽체의 기둥축소 경향이 보다 유사하게 나타났다.
3)비구조요소에 대한 사용성을 검토한 결과, 두 시스템 모두 부등축소량에 대한 최대 허용한계치를 만족하였다. 그러나 중력하중조합으로 설계된 메가구조 시스템의 샛기둥은 인접 벽체와의 부등축소량에서 최대 허용한계치에 대해 상대적으로 여유도가 작게 나타났다.
4)수평부재에 대한 안전성을 검토한 결과, 건물이 높아짐에 따라 기둥과 벽체 간의 강성 차이 증가로 인해 최대 부재력이 증가한 상황에서 비탄성 거동으로 인한 부가하중이 부재력을 더욱 증가시킬 수 있다. 특히, 메가구조 시스템을 적용할 경우 이러한 현상은 뚜렷하게 나타나며 계수하중과 강도저감계수를 적용한 설계강도까지 고려할 경우 안전성에 대한 여유도가 크게 감소할 수 있는 것으로 나타났다.
5)아웃리거 벽체에 대한 안전성을 검토한 결과, 건물의 규모가 커지면서 중력하중의 비중이 높아졌다. 또한, 비탄성 거동으로 인한 부가하중이 증가요인으로 작용하여, 아웃리거 벽체의 재설계 필요성이 발생할 것으로 판단된다.
초고층 건물일수록 수직부재에서 축력의 비중이 증가하므로 축력의 영향이 커지며, 축력의 장기편심 및 이에 따른 2차 효과가 증가할 수 있다. 향후 이러한 다양한 요소들이 초고층 건물의 장기거동에 미치는 영향에 대한 추가적인 연구가 요구된다.