1. 서 론
2. 충돌 시나리오
2.1 항공기 충돌 관련 설계기준
2.2 충돌 시나리오 설정
3. 대상 교량 및 수치해석 모델 작성
3.1 대상 교량
3.2 수치해석 모델 작성
3.3 재료 특성
3.4 정적 및 동적 거동 검토
4. 충돌해석 기법
4.1 직접법과 간접법
4.2 Implicit-Explicit switching 기법
4.3 충돌해석 조건 및 케이스
5. 충돌해석 결과
6. 결 론
1. 서 론
국내외 사장교의 설계, 재료, 시공 및 유지관리 분야는 지속적인 관심, 연구 및 실험을 통하여 관련 지식과 해석 기술이 발전함에 따라 고도화되어 왔다. 이와는 다르게 사장교에 대한 안전성 평가 분야는 사회적으로나 공학적으로나 과거에는 크게 필요성을 느끼지 못하였다. 하지만, 2001년에 발생한 미국 9.11 테러는 사장교와 같은 중요 사회기반시설의 안전성에 대한 사회적 경각심을 불러일으켰고, 이와 동시에 사회기반시설의 재난에 대한 대비가 크게 이슈화되면서 사장교의 안전성에 대한 공학적 검토의 필요성을 인식하게 되었다. 현재 여러 국가에서는 재난에 대한 대비를 위하여 유지관리 등 관련 분야에서 지속적인 예산이 투입되고 있으며, 특히 사장교와 같은 경간이 긴 교량의 경우 공공성이 매우 높은 사회기반시설물 중 하나이기 때문에 재난으로 인한 사고 발생 시 막대한 인명피해와 경제적 손실을 초래할 수 있다. 재난은 지진, 태풍 및 홍수 등과 같은 자연재난과 화재, 충돌 및 폭발과 같이 사고 및 테러 등으로 발생하는 사회재난으로 분류할 수 있다. 이 중 자연재난인 지진과 사회재난인 화재에 대한 교량의 안전성 및 구조성능 평가 분야는 과거부터 지속적인 연구와 실험을 바탕으로 설계기준이나 지침이 규정되어 있다. 충돌에 대한 교량의 안전성 및 구조성능 평가 분야는 대부분 차량과 교각의 충돌(Cao et al., 2019; Chung et al., 2014; Kim et al., 2010, 2014; Omar and Mohamed, 2017; Zhou et al., 2017), 차량과 방호울타리의 충돌(Park et al., 2014; Woo et al., 2004)에 대한 연구가 수행되어 왔으며, 설계기준 및 지침도 규정되어 있는 상황이다. 또한, 최근 국내에서는 ‘도로교설계기준(한계상태설계법)-케이블교량편(MOLIT, 2016)’에 케이블교량의 선박충돌에 대한 설계기준이 규정되었으며, 국내, 외 관련 연구(Fan et al., 2020; Gholipour et al., 2018, 2020; Guo et al., 2020; Lee, 2020a, 2020b)가 활발히 진행 중이다. 하지만, 이와는 다르게 사회재난 중 하나인 항공기 충돌에 대한 구조성능 평가 분야는 대부분 원자력 발전소 구조물을 중심으로 기술개발이 진행되어 왔으며, 교량에 대한 평가 기술개발은 찾아보기 어려운 상황이다.
Fig. 1에 실제 교량에서 발생한 항공기 충돌사고를 나타내었다. 2015년 대만의 난양대교에서 항공기의 날개가 일반도로교량의 상부구조에 충돌하여 교량에 손상을 준 사고가 있었으며, 2016년 중국 상하이에서 수륙양용 비행기인 Cessna 208b 경비행기가 후항대교에 충돌하여 교량에 큰 피해를 준 사고 사례가 있었다. 이처럼 항공기 충돌사고는 그 사례가 많지는 않지만 발생할 경우 교량에 큰 피해를 발생시킬 수 있다. 하지만, 앞서 언급하였듯이 이를 사전에 평가할 수 있는 기준 또는 방법이 확실하게 정립되어 있지 않은 실정이다. 일반적으로 사장교의 구조성능을 평가하기 위하여 구조해석(유한요소해석)이 많이 수행되지만, 충돌하중에 대한 구조해석은 일반적인 설계목적의 구조해석과 달리 사장교의 복잡한 거동 메커니즘과 하중 및 재료의 동적 특성을 고려할 수 있는 특수해석 기술을 필요로 한다.
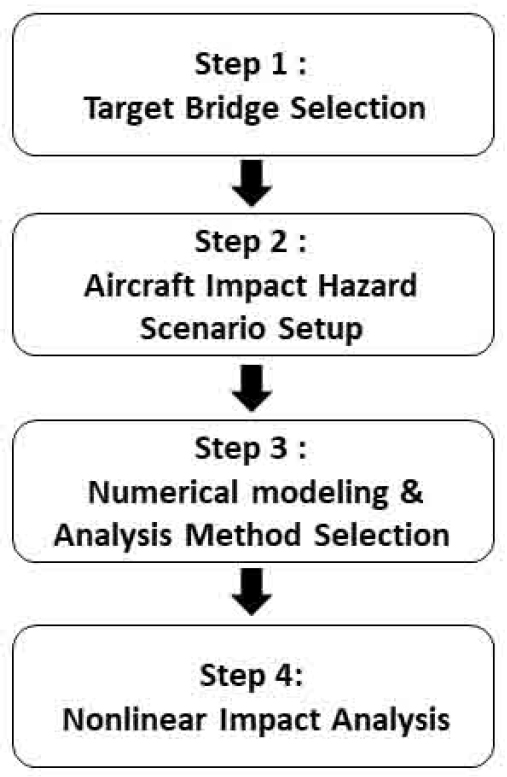
따라서, 본 연구에서는 Fig. 2와 같은 해석 절차를 통해 사장교에 항공기가 충돌하는 상황을 수치해석적으로 모사하였으며, 항공기 충돌에 대한 사장교의 구조거동 평가를 수행하기 위한 충돌 시나리오 설정 방법 및 해석 기법을 다루었다. 또한, 충돌해석 수행 후 교량에 발생하는 주요 응답을 분석하여 본 연구에서 설정한 항공기 충돌 시나리오가 사장교에 미치는 영향을 검토하였다. 대상교량은 서해안 고속도로 상의 서해대교 사장교로 하였으며, 대상교량에 대한 설명은 3.1절에 수록하였다.
2. 충돌 시나리오
다양한 항공기 충돌 시나리오에서 적절한 시나리오를 설정하여 충돌하중의 크기를 설정하는 것은 대상 교량의 항공기 충돌에 대한 구조성능 평가 및 위험도 분석을 수행하기 위해 필수적인 작업이다. 다음 절에 항공기 충돌 시나리오를 설정하기 위한 관련 설계기준 및 과정을 나타내었다.
2.1 항공기 충돌 관련 설계기준
일반적으로 교량에서 발생하는 충돌사고는 예측할 수 없으며, 교량을 손상 및 붕괴시키는 충돌사고의 유형은 차량이 교량 하부구조인 교각에 충돌하여 피해를 일으키는 경우가 대부분이다. 또한, 해상교량에 한해서는 주탑 하단부의 선박 충돌사고와 드물지만, 항공기 추락에 의한 충돌사고가 있다. 사장교의 경우 대부분이 해상에 위치한 교량이기 때문에 차량이 교량 하부로 통행하면서 주탑이나 교각에 충돌하여 피해를 일으킬 수 있는 상황이 아니며, 사장교와 같은 케이블교량에 대한 선박 충돌과 관련해서는 이미 ‘도로교설계기준(한계상태설계법)-케이블교량편(MOLIT, 2016)‘과 같은 설계기준으로 규정되어 있으므로, 본 연구에서는 앞서 설명하였듯이 비교적 연구가 진행되지 않은 교량의 항공기 충돌에 대한 시나리오만을 고려하였다. 현재 국내외에는 항공기 충돌에 대한 교량의 구조성능 평가와 관련된 설계기준 및 기타 자료는 없는 상황이며, 대부분 항공기 충돌과 관련된 자료는 원자력 발전소를 대상으로 하고 있다. 따라서, 항공기 충돌 시나리오를 설정하기 위하여 국내외의 항공기 충돌과 관련된 설계기준(USNRC, 1997; EDF, 1998; USNRC, 2009; KINS, 2016)을 참고하여 대상 교량에 발생할 수 있는 충돌 시나리오를 검토하였다.
미국의 연방법 10CRF100.10 및 100.20(USNRC, 1997)은 원자력 발전소 부지 선정 기준을 명시하고 있다. 미국 연방법과 안전심사지침에서는 부지 선정 기준을 만족할 경우 원자력 발전소 설계 시 항공기 충돌을 고려하지 않도록 하고 있다. 또한, 10CRF50.150(USNRC, 2009)에 인위적인 항공기 충돌평가와 관련된 사항 및 충돌하중에 대해서 제시되어 있다. 이때, 대상 항공기는 미국의 장거리 운항용 대형 민항기이며, 항공기의 연료 주입량, 충돌 속도 및 충돌 각도를 고려하도록 규정하고 있다.
독일에서는 1960년대에 경비행기의 충돌을 설계에 반영하였고, 1970년대에는 확률론적 안전성 평가 결과 군용기의 추락 확률이 기준 확률인 10-7/년을 초과하는 10-6/년으로 나타나 군용기 충돌을 원전 설계 시 반영하였다. 그러나 1980년대에 군용기 추락 확률이 10-6/년에서 10-7/년으로 하향 조정된 바 있다. 독일의 BASF社에서는 원자력 발전소 위치를 중심으로 반경 1km 이내에 30년 동안 항공기 종류별 추락할 확률을 조사하여 정리하였으며, 이를 Table 1에 나타내었다. 대형 항공기의 추락 확률을 기준 확률 이하로 매우 낮게 평가하였으나, 군용기와 경비행기는 충돌을 고려해야 하는 확률 범주에 속하는 것을 확인할 수 있다.
Table 1.
Probability of an aircraft crash
| Aircraft type | Probability of crash |
| Light aircraft | 2×10-5 |
| Military aircraft | 2×10-6 |
| Large aircraft | 5×10-11 |
프랑스의 원자력 발전소 설계기준인 RCC-G(EDF, 1998)에서는 규정된 입지 조건을 만족할 경우 상업용 민항기의 추락 확률을 10-8/년, 군용기의 추락 확률을 10-7/년으로 보고 있으므로, 상업용 민항기와 군용기에 대한 충돌사고는 고려하지 않고 있다. 하지만, Lear Jet 23 및 Cessna 210과 같은 경비행기에 대한 충돌사고 시나리오는 고려하도록 명시되어 있다.
국내에서는 경수로형 원자력 발전소 안전심사지침(KINS, 2016)에 항공기 충돌에 대한 지침이 규정되어 있다. 안전심사지침에는 항공기 재해 사고의 확률이 10-7/년 이하일 경우 원자력 발전소 설계 시 항공기 충돌에 대하여 고려할 필요가 없다고 명시되어 있으며, 다음의 경우가 이에 해당한다. 첫 번째, 발전소와 공항 간의 거리(D)가 8∼16km의 법정 거리 이내에 있고 계획된 연간 항공기 운항 횟수가 195D2 미만이거나, 원자력 발전소와 공항 간의 거리 D가 16km의 법정 거리 이상이고 계획된 연간 운항 횟수가 386D2 미만일 때, 두 번째, 연간 1,000대 이상 운항하는 훈련 항로는 제외하고, 원자력 발전소가 지상 훈련 항로를 포함하여 군사훈련 항로의 외곽 단으로부터 또는 비정상적인 긴장 상태를 유발시킬 수 있는 폭격 훈련과 같은 활동이 있는 장소로부터 최소 8km의 법정 거리 밖에 위치할 때, 세 번째, 원자력 발전소가 국영 항로, 대기 경로 또는 접근 경로상의 가장 가까운 외곽지로부터 최소 3km의 법정 거리 이상 떨어져 있을 때이다. 이렇게 제시된 조건에 만족하지 않는 경우는 항공기 재해에 대한 상세한 검토가 수행되어야 한다. 하지만, 국내의 모든 원자력 발전소는 부지 선정 기준에 적합한 부지에 건설되었기 때문에 설계 시 항공기 충돌을 고려하지 않은 것으로 확인된다. 다만, 울진 1, 2호기는 설계사인 프랑스의 설계기준에 따라 경비행기의 충돌이 고려되었다.
국내외 설계기준들에서는 항공기 재해 발생 확률을 이용하여 항공기 충돌의 반영 여부를 결정하고 있으며, 주로 경비행기를 대상으로 설계에 반영하도록 명시되어 있는 것을 확인할 수 있다. 또한, 위와 같이 언급한 국가들 외에도 영국, 스웨덴, 스위스 등에서도 원자력 발전소 설계 시 경비행기의 충돌사고 시나리오를 반영하고 있다. 다음 Table 2에는 국내외 원자력 발전소 설계기준에서 제시하고 있는 항공기별 주요 특징들을 나타내었다.
Table 2.
Characteristics of each aircraft considered in the impact scenario(KINS, 2009)
| Aircraft type | Impact area(m2) | mass(ton) | Impact velocity(m/s) |
| Sporting plane | - | 10 | 83 |
| Starfighter | - | 10 | 179 |
| Phantom | 7 | 20 | 215 |
| Lear Jet 23 | 12 | 5.7 | 100 |
| Cessna 210 | 4 | 1.5 | 100 |
2.2 충돌 시나리오 설정
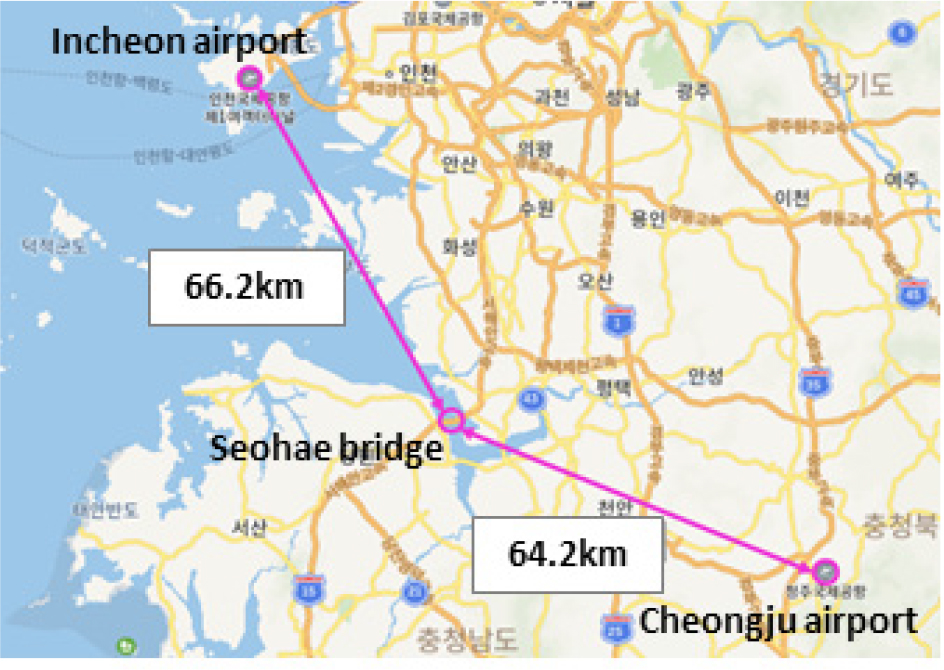
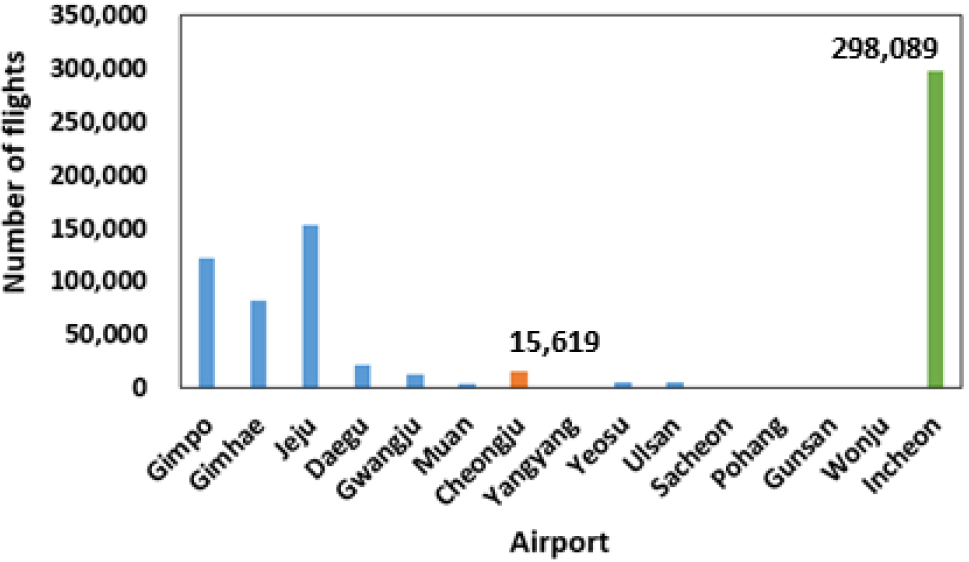
항공기 충돌 시나리오를 설정하기 위하여 앞 절에서 항공기 충돌과 관련된 원자력 발전소 설계기준을 살펴보았다. 우선 대상 교량의 위치를 기준으로 국내 경수로형 원자력 발전소 안전심사지침의 규정에 따라 항공기 충돌의 가능성을 다음과 같이 검토하였다. 대상 교량이 위치한 충청남도 당진시 신평면 매산리에서 가까운 거리에 위치한 공항과의 거리는 Fig. 3에 나타난 바와 같이 인천공항과의 거리 66.2km, 청주공항과의 거리 64.2km이다. 각각의 공항에 대하여 항공기 운항 현황 자료(KAC, 2020)를 검토하였을 때, Fig. 4와 같이 최근 1년 동안(2019.07~2020.06) 인천공항에서 운항된 항공기의 수는 약 300,000대이며, 청주공항에서 운항된 항공기의 수는 약 16,000대이다. 따라서, 경수로형 원자력 발전소 안전심사지침에서 제시하고 있는 기준에 따라 계산하면 항공기 충돌영향을 고려하여야 하는 기준 운항횟수의 값은 1,590,953(386×64.22=1,590,953)∼1,691,622(386×66.22=1,691,622)대의 수준을 보인다. 산정된 기준에 비해 두 공항 모두 충분히 낮은 운항 빈도를 보이기 때문에 대상 교량이 위치한 지점에서는 항공기 추락 확률이 10-7/년 이하인 것으로 나타난다. 또한, 대형 항공기의 비행고도를 분석해 보면 국내선 구간을 운항하는 B737기는 1,524m∼3,048m, 중거리 운항용인 B757 및 B767기는 4,267m∼8,534m, 장거리용인 B747기는 8,534m∼11,582m의 고도에서 비행하므로 대상 교량에 충돌할 가능성은 없다고 판단된다. 하지만, 앞 절에서 살펴본 국가별 설계기준에 따르면 항공기 재해 사고는 대형 항공기보다는 경비행기가 확률적으로 높은 것으로 나타나며, 경비행기의 경우 150m∼5,000m 높이까지 비행할 수 있고 경비행기의 충돌사고는 대부분 약 150m∼200m 고도에서 발생한다(대상 교량인 서해대교의 주탑 높이는 약 180m). 또한, 국외에서는 우리나라와는 다르게 경비행기를 민간에서 많이 이용하고 있으며, 이에 따른 사고가 종종 발생하고 있다. 경비행기의 종류가 육상기 뿐만 아닌 수상기, 수륙양용기 등 물 위에서 이·착륙하는 종류의 경비행기도 있는 것을 고려한다면 일반적으로 해상에 위치한 사장교에는 경비행기 충돌 가능성이 비교적 클 것으로 판단되며, 앞서 소개된 Fig. 1과 같이 중국 상하이에서 Cessna 208b 경비행기가 교량에 충돌한 사례가 있었다. 따라서, 국내외 설계기준, 경비행기의 비행고도와 실제 사고사례를 바탕으로 본 연구에서는 Cessna 210 경비행기가 교량의 주탑에 충돌하는 시나리오를 설정하였다. 이 연구에서는 케이블에 충돌하는 시나리오는 설정하지 않았지만, 향후 케이블에 충돌하는 시나리오도 고려하여 다양한 변수해석이 뒷받침된다면, 항공기 충돌에 대한 사장교의 구조성능 평가 분야를 보다 고도화할 수 있을 것으로 판단된다.
3. 대상 교량 및 수치해석 모델 작성
3.1 대상 교량
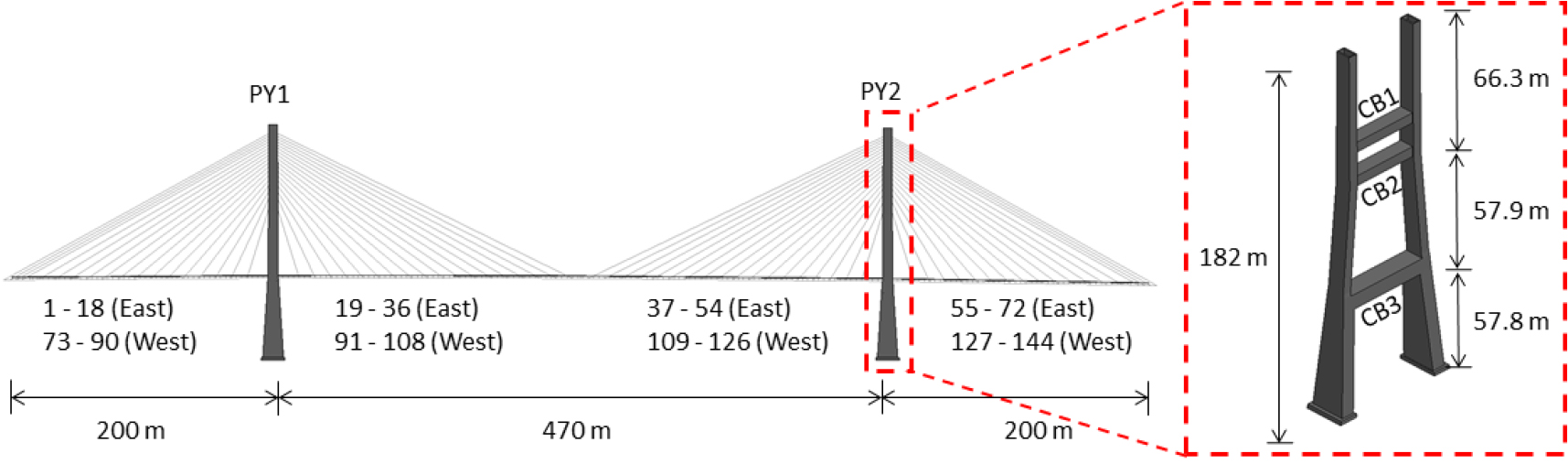
항공기 충돌하중을 받는 사장교의 구조성능을 평가하기 위하여 선정한 대상 교량은 Fig. 5에 나타난 바와 같이 서해대교의 사장교 구간으로, 대한민국 평택-당진을 연결하는 해상교량이다. 대상 교량은 주 경간 길이 470m, 측경간 길이 200m로 3개의 경간을 갖는다. 또한, H 형태의 RC 주탑 2개와 폭이 약 34m인 바닥판 양측에 서로 다른 면적 및 길이를 갖는 144개의 케이블이 2면으로 배치되는 형식이며, 바닥판은 강재 거더와 RC 프리캐스트 슬래브로 구성되어 있는 강합성 형식이다.
3.2 수치해석 모델 작성
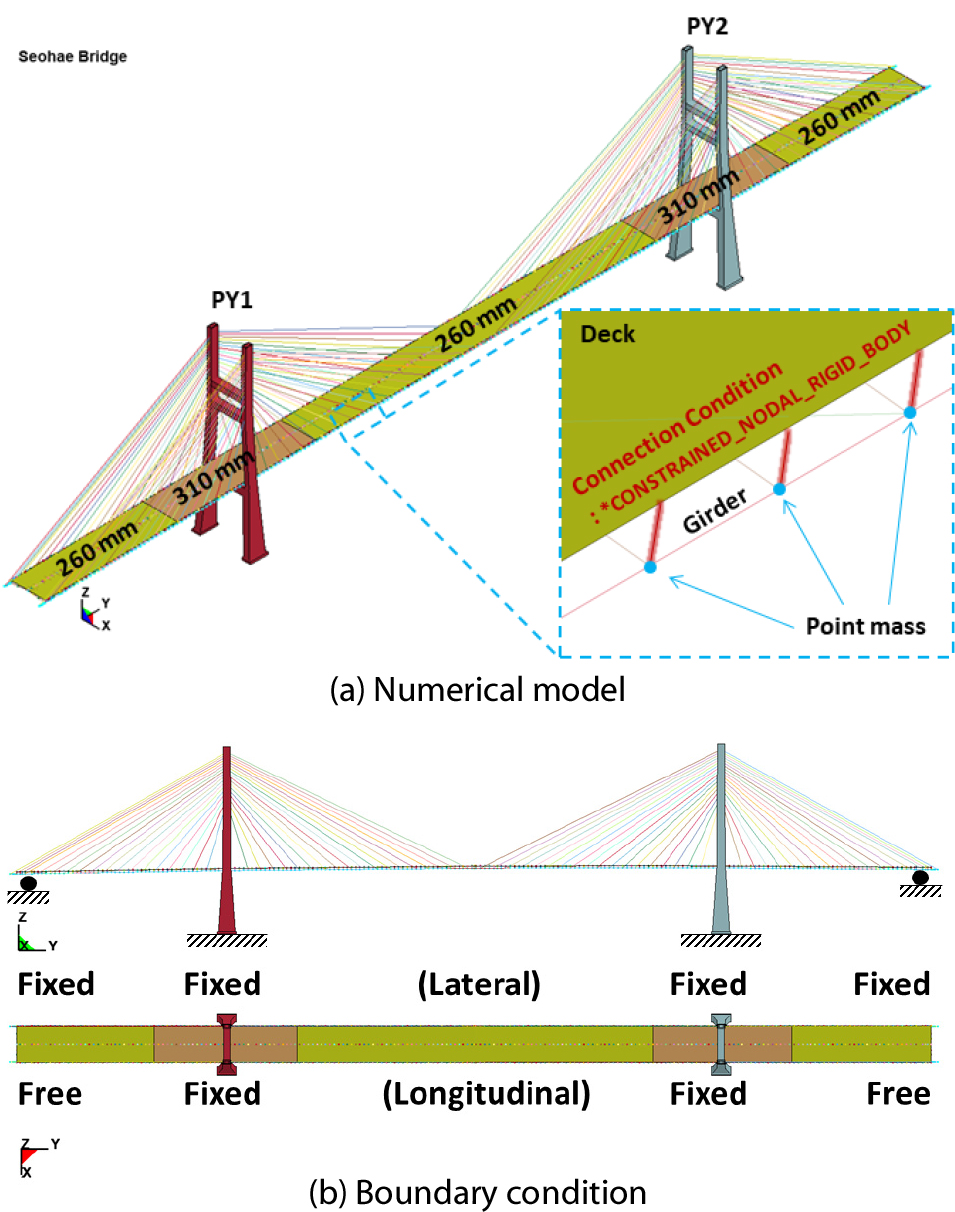
대상 교량의 수치해석 모델은 Fig. 6에 나타난 바와 같이 LS-DYNA(LSTC, 2020)를 사용하여 모델링하였다. 주탑은 8절점 Solid 요소를 사용하여 약 500mm~2,000mm, 충돌부는 100mm~200mm의 크기로 요소망을 구성하였다. PY2 주탑은 PY1 주탑보다 기초부가 2.37m 더 길다. 바닥판은 4절점 Shell 요소를 사용하여 약 2,000mm의 크기로 요소망을 구성하였다. 또한, 주탑부 바닥판의 두께는 310mm, 그 외 구간은 260mm로 모델링하였다. 철근, 거더 및 케이블은 2절점 Beam 요소 및 Truss 요소를 사용하여 단일 요소로 모델링하였다. 모델링에 소요된 총 절점 및 요소 수는 각각 51,596개 및 32,418개이다.
주탑의 콘크리트부와 철근의 합성조건은 LS-DYNA에서 제공하는 *CONSTRAINED_LAGRANGE_IN_SOLID 명령어를 사용하여 구현하였으며, 케이블 요소에는 정적 거동 검토 결과에서 도출된 케이블 장력을 도입하였다. 또한, 방호울타리, 중앙분리대, 케이블 정착부 및 점검차 레일 등의 질량은 해당위치의 절점에 point mass 요소를 사용하여 적용하였다.
작성된 수치해석 모델의 연결조건과 경계조건은 다음과 같은 방법으로 설정하였다. 바닥판, 거더 및 케이블을 Fig. 6(a)에 빨간색으로 표기한 부분과 같이 LS-DYNA에서 제공하는 *CONSTRAINED_NODAL_RIGID_BODY 명령어를 사용하여 강결하였으며, 바닥판과 주탑 하단 가로보 사이도 같은 방법으로 강결하였다. 경계조건으로는 Fig. 6(b)와 같이 주탑 하단부는 모든 자유도를 구속하였으며, 교각 지점부는 교축직각방향(x-dir) 및 연직방향(z-dir) 자유도만을 구속하였다. 이때 *BOUNDARY_SPC_SET 명령어를 사용하여 경계조건을 적용하였다.
3.3 재료 특성
충돌해석을 위한 재료모델을 선정할 때는 재료의 여러 가지 주요 특성들을 고려해야 한다. 특히, 변형률 속도(strain rate)에 따른 강도 증가 효과를 고려하여 재료모델을 구성해야 한다. 따라서 본 연구에서는 LS-DYNA에서 제공하는 다음과 같은 재료모델을 선정하여 적용하였다.
콘크리트 재료모델은 LS-DYNA에서 콘크리트의 비선형 재료거동 및 변형률 속도 효과 등을 재료모델 내에 포함하고 있는 *MAT_WINFRITH_CONCRETE 모델을 적용하였다. Winfrith concrete 모델은 충격하중을 받는 철근콘크리트 구조물을 해석하기 위한 목적으로 개발되었으며, 많은 연구자들에 의해 사용되고 있다. 주탑과 바닥판의 콘크리트 압축강도(fck)를 40MPa로 적용하였으며, 인장강도(fct)는 2.62MPa로 적용하였다.
철근, 거더 및 케이블은 *MAT_PLASTIC_KINEMATIC 재료모델을 적용하였다. 이 재료모델은 변형률 속도 효과, 재료의 등방성 및 kinematic hardening을 고려하며, 재료의 비선형을 bi-linear 형태로 가정한다. 이때, 변형률 속도 효과를 반영하기 위해 사용되는 Cowper-Symonds 모델의 재료상수 C와 p는 다음의 식 (1)을 사용하여 산정하였다(Lee and Kim, 2007).
where, : yield stress(MPa)
Table 3에 각 재료모델에 사용된 주요한 입력값을 정리하여 수록하였다.
Table 3.
Material model input parameters
3.4 정적 및 동적 거동 검토
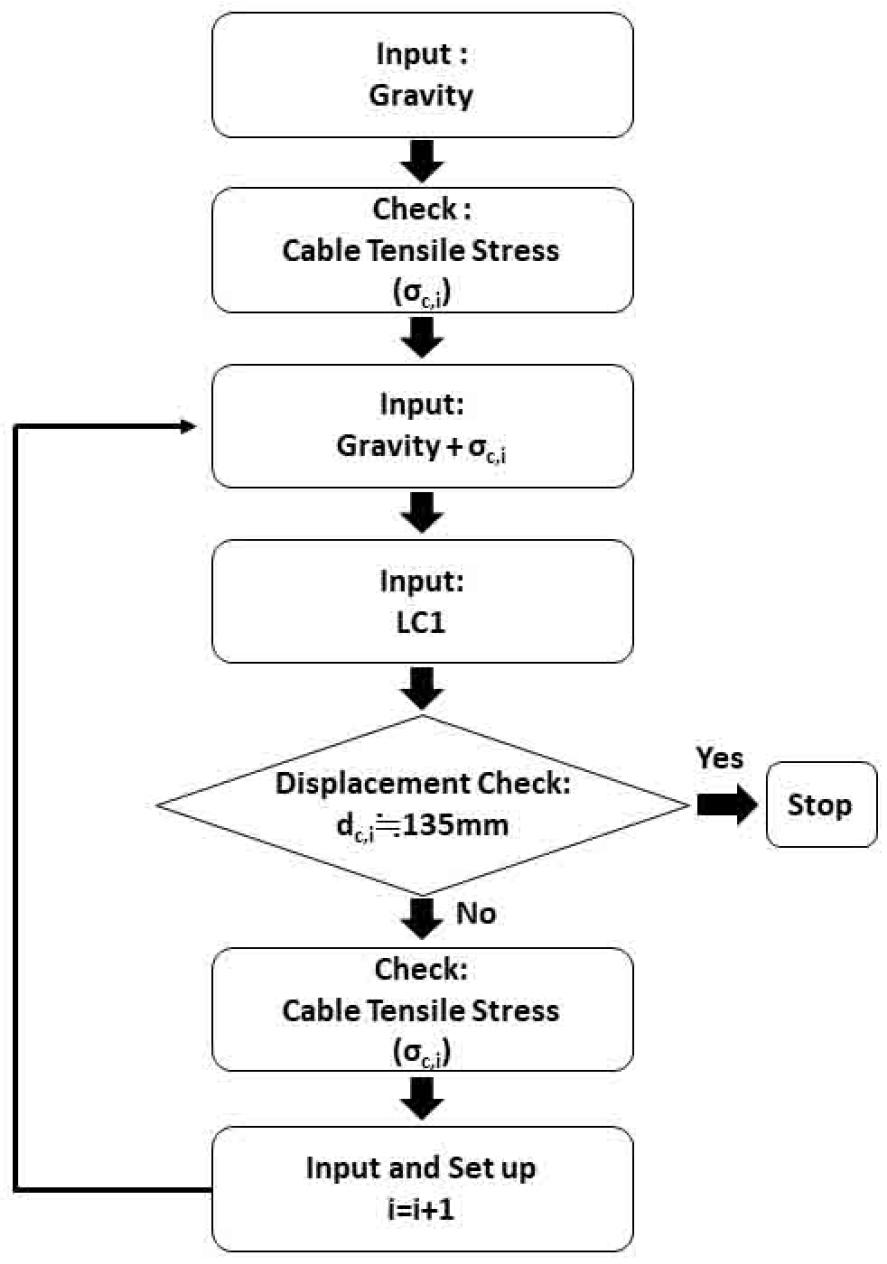
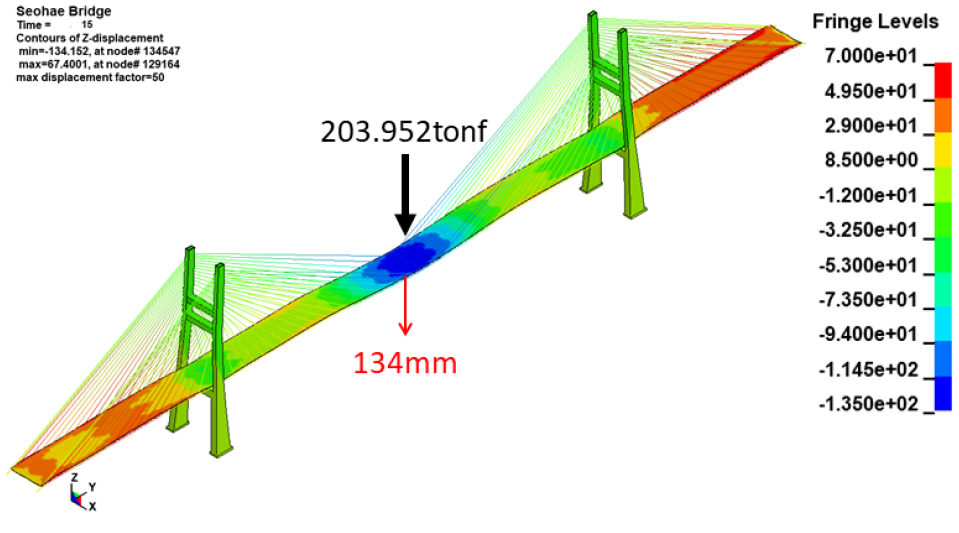
작성된 수치해석 모델의 정적 및 동적 거동을 검토하기 위하여 정적하중에 대한 해석 및 고유치 해석을 수행하였다. 수치해석 모델의 적절성은 참고문헌(Yoon, 2002; Park et al., 2015)과 비교하여 확인하였다. 정적 거동 검토는 Fig. 7에 나타난 알고리즘과 자중 적용 후 Fig. 8과 같이 사장교 구간 중앙경간에 하중 203.952tonf을 재하하여 케이블의 초기장력 및 초기형상을 결정하였다. 초기형상 결정 해석 알고리즘은 다음과 같은 방법으로 진행되었다. 첫 번째로, 수치해석 모델에 자중을 도입하여 케이블에 도입된 장력을 검토한다. 두 번재로, 자중, 케이블 장력을 재하한 뒤, 수준측량 시 재하한 하중 203.952tonf을 도입하여 사장교 구간 중앙경간의 처짐을 검토한다. 마지막으로 중앙경간의 처짐 값이 측정치인 약 135mm에 도달할 때까지 케이블의 장력을 계속 조정하여 초기형상을 결정하였다.
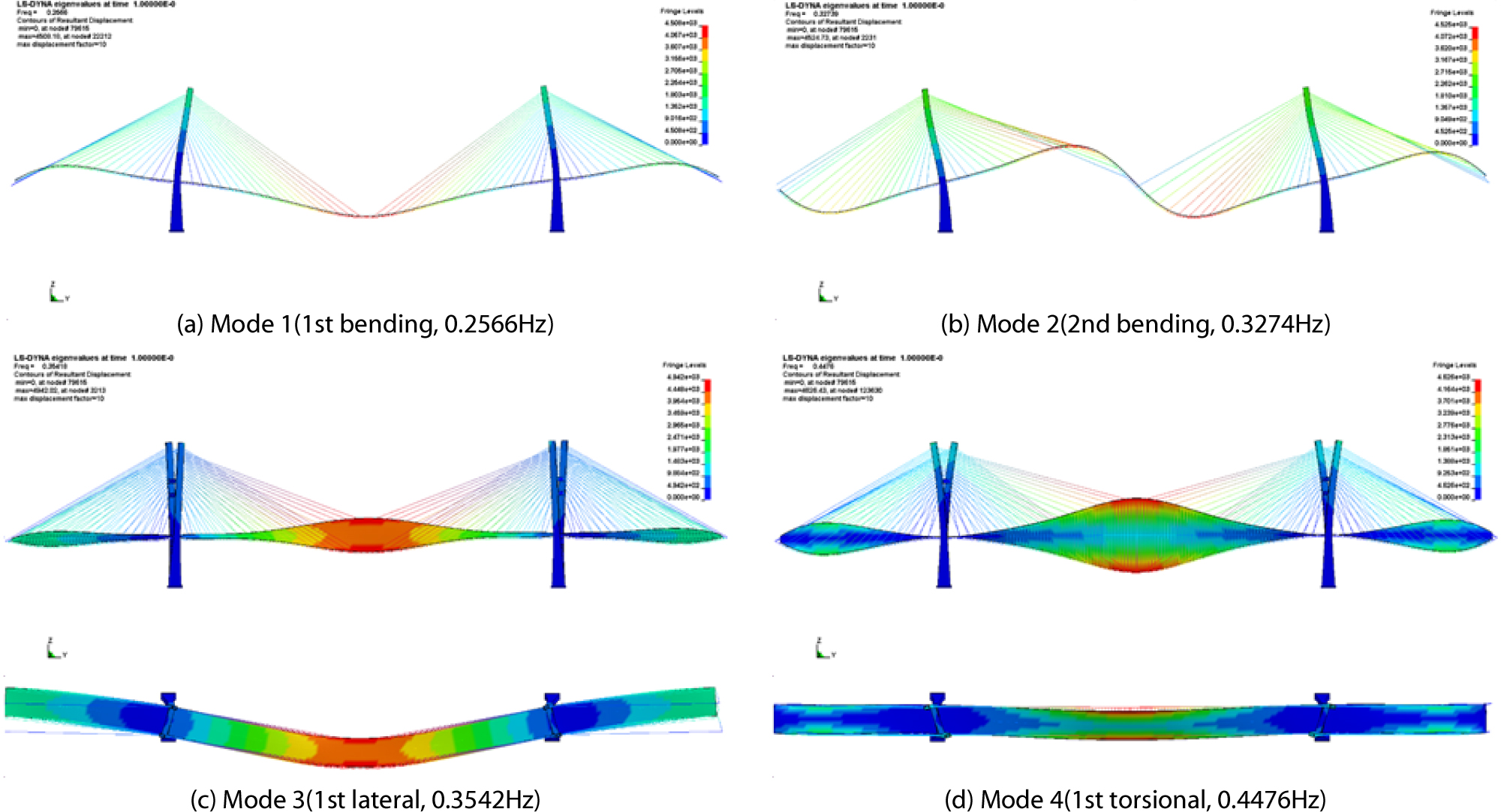
동적 거동 검토는 고유치 해석을 수행하여 총 20개의 모드를 추출하였으며, Fig. 9에 대표 모드 4개를 나타내었다. Table 4에는 선행연구결과에 기술되어 있는 고유진동수와 해석 결과의 고유진동수 및 고유모드를 요약하여 나타내었다. 검토 결과, 수평 1차 모드의 고유진동수가 비교적 큰-4.91%의 오차율을 보이지만, 나머지 3개의 대표 모드에서 고유진동수가 2% 이내의 오차율을 보이는 것을 확인하였다. 따라서, 정적 및 동적 거동 검토를 통하여 수치해석 모델이 적절하게 작성되었음을 확인하였다.
4. 충돌해석 기법
4.1 직접법과 간접법
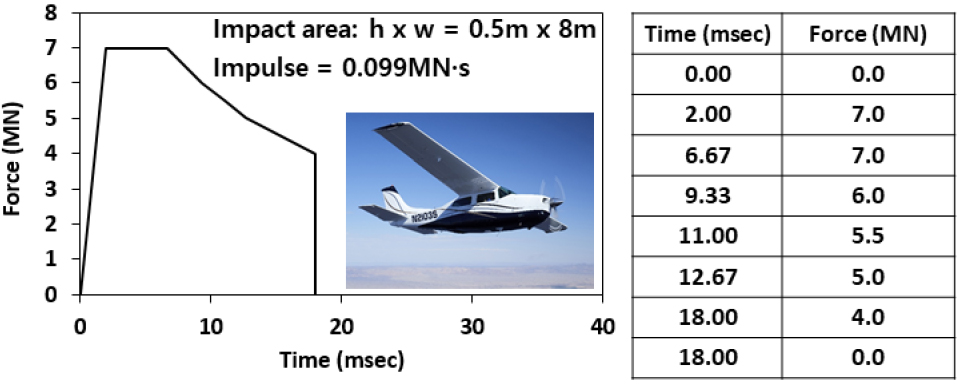
충돌해석 기법은 충돌해석 시 충돌하중을 고려하는 방식에 따라 간접법과 직접법으로 구분된다. 이중 충돌하중-시간함수를 이용한 방법이 간접법에 해당되며, 항공기의 수치해석 모델을 이용한 미사일-타겟 상호작용 해석법이 직접법에 해당된다. 직접법은 충돌체 모델을 대상 피충돌체(구조물)에 직접 충돌시키는 방법으로 충돌체(항공기)의 복잡한 형상 때문에 해석시간이 오래걸리나 충돌 직후의 복합적인 연쇄거동을 분석하기 위해 주로 사용된다. 간접법의 경우 충돌체를 직접 충돌시키지 않고 하중-시간함수를 사용하기 때문에 해석시간 단축에 유리하나 충돌 직후의 복합적인 연쇄거동을 파악하기 힘든 단점이 있다. 앞서 설정된 시나리오를 바탕으로 주탑에 충돌하중을 적용하기에는 직접법보다는 간접법을 사용하는 것이 해석에 효율적일 것으로 판단되므로 간접법을 이용한 해석을 수행하였다. 해석에 사용된 충돌하중-시간함수는 다음 Fig. 10과 같이 국내외 원자력 발전소 설계기준에서 제시하고 있는 Cessna 210의 충돌하중-시간함수를 사용하였으며, 최대하중 7MN, 충격량 0.099MN·s, 충돌 면적 4m2(가로 8m, 세로 0.5m) 등의 특징을 갖고 있다. 충돌하중은 *LOAD_SEGMENT_SET 및 *SET_SEGMENT 명령어를 사용하여 하중 면적에 등분포하중이 적용되도록 하였다.
4.2 Implicit-Explicit switching 기법
수치해석 분석을 위한 해석기법으로는 Implicit 기법과 Explicit 기법이 있으며, 각 기법의 효율성을 고려하여 해석기법을 선정하여 사용한다. Implicit 기법은 반복 계산을 통해 해를 찾는 기법이며 정확도가 높은 특징을 갖는다. 하지만, 비선형성이 크면 해의 수렴이 어렵고, 정확도가 떨어지는 단점이 있다. 따라서, Implicit 기법은 일반적으로 비선형성이 크지 않은 자중 해석과 같은 정적 및 준정적 해석을 수행할 때 사용된다. Explicit 기법은 반복 계산을 하지 않기 때문에 수렴성 문제가 근본적으로 발생되지 않는다는 장점이 있으나, 해의 정확도가 낮다는 단점을 가지고 있다. 따라서, 비선형성이 큰 짧은 순간에 대변형이 발생하거나 큰 하중이 작용하는 충돌해석과 같은 종류의 해석에서 주로 사용된다.
위와 같이 Implicit 기법과 Explicit 기법은 장단점과 특징이 다르다. 따라서, 본 연구에서는 각 해석기법의 장점만을 고려하여 해석을 수행할 수 있는 Implicit-Explicit switching 기법을 사용하여 항공기 충돌에 대한 사장교의 구조거동 평가를 수행하였다. 해석은 초기형상해석과 충돌해석으로 나누어 수행하였으며, 초기형상해석은 Static-Implicit 기법, 충돌해석은 Dynamic-Explicit 기법으로 해석으로 수행하였다. switching 기법은 *CONTROL_ IMPLICIT_GENERAL 명령어를 사용하여 수행하였다.
4.3 충돌해석 조건 및 케이스
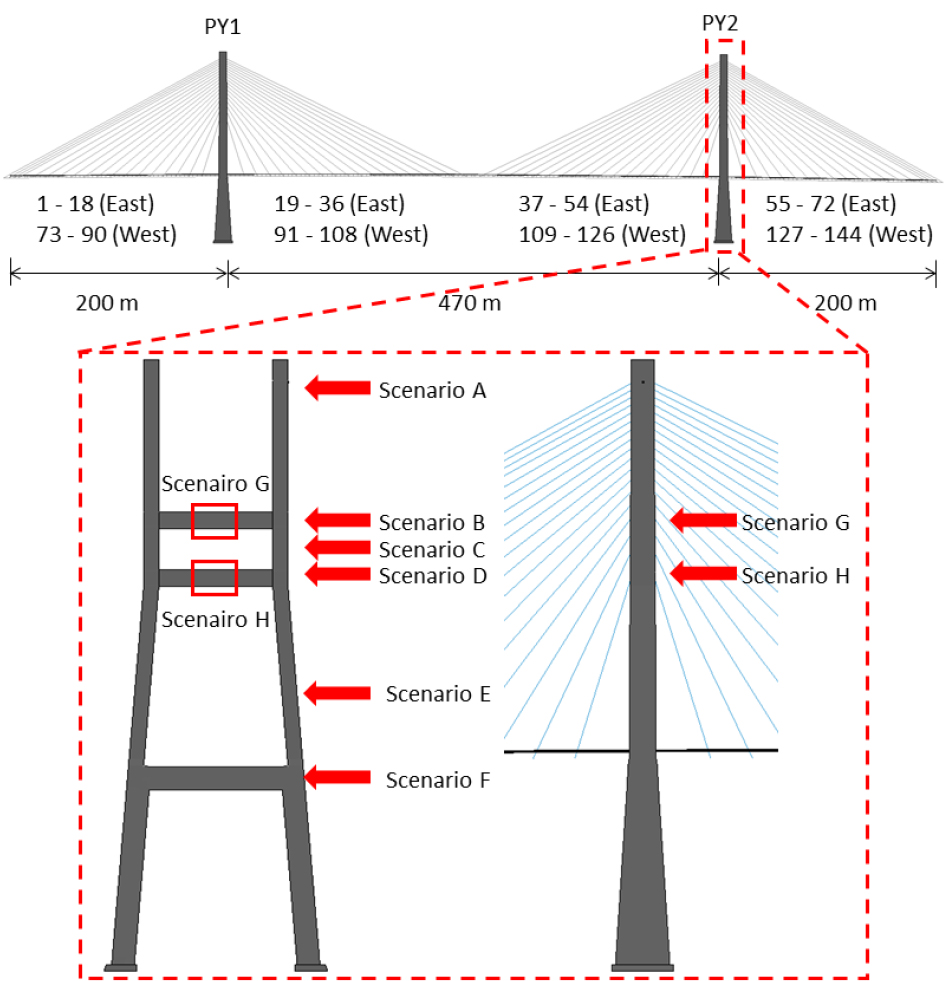
본 연구에서 설정한 충돌해석 케이스는 앞서 설정된 시나리오를 바탕으로 주탑에 충돌하중을 적용하는 케이스를 설정하였으며, 충돌하중이 적용될 주탑은 기초부가 비교적 더 긴 PY2 주탑을 선정하였다. 충돌 각도의 경우, 실제 사고에 의한 항공기 추락 시 가장 빈번한 추락 각도는 수평면에서 0~15도이며, 본 연구에서는 가장 큰 충돌 효과를 발생시키는 직각 충돌(수평면에서 0도)을 가정하였다. 이와 같이 충돌 대상과 각도를 설정한 후에 충돌하중-시간함수가 적용 가능한 면적, 충돌 방향 및 주탑의 높이를 고려하여 총 8개의 케이스를 설정하였다. Fig. 11에 설정된 충돌해석 케이스를 나타내었으며, Table 5에 충돌 위치 및 방향으로 간략히 정리하여 나타내었다.
5. 충돌해석 결과
항공기 충돌에 대한 사장교의 구조거동을 평가하기 위해 주요 응답인 바닥판의 수직 변위 및 케이블의 장력 변화에 대한 결과를 분석하였다.
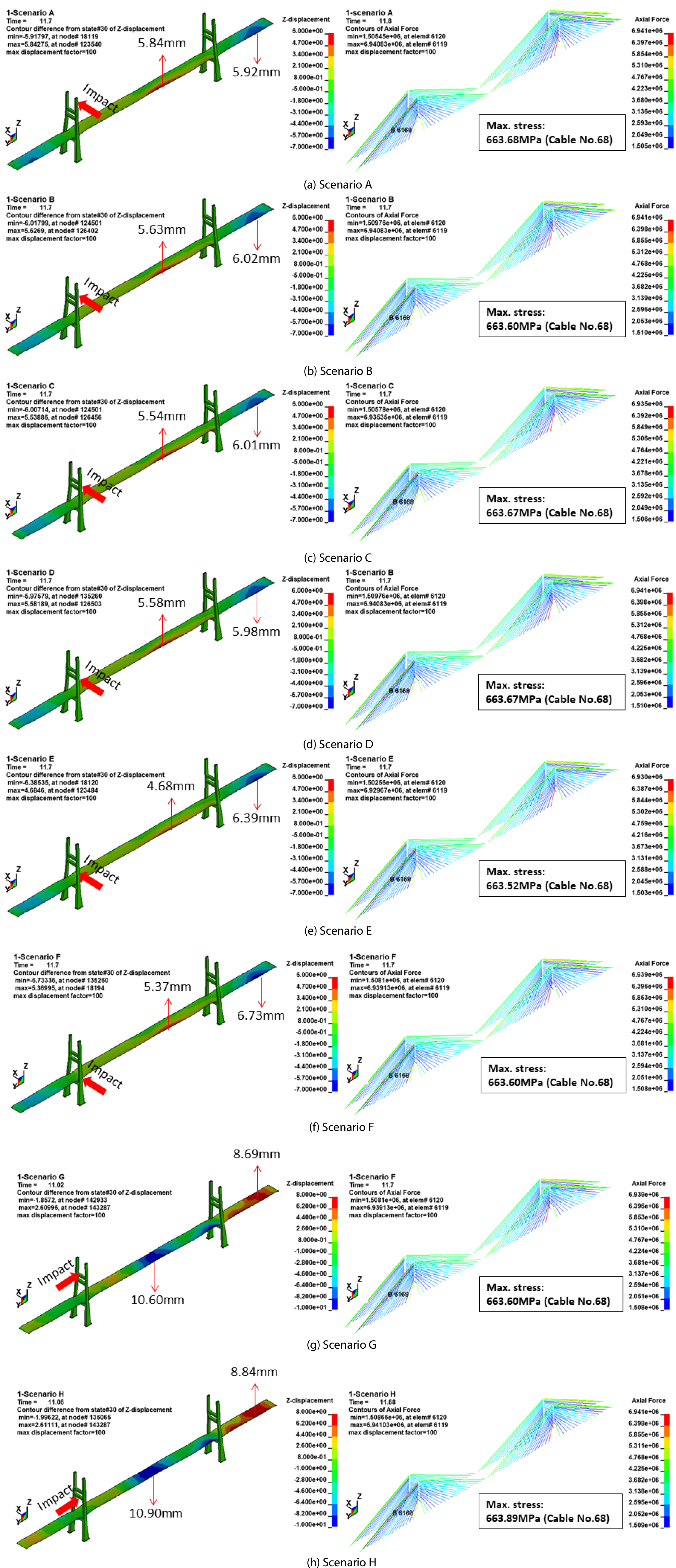
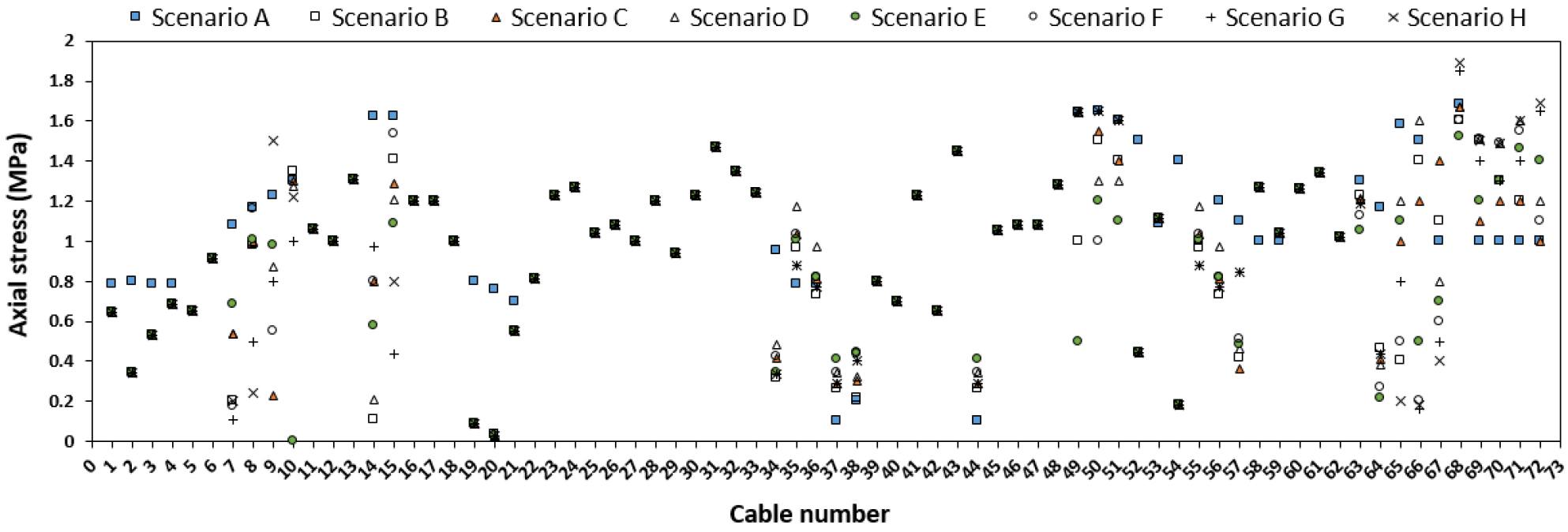
Table 6 및 7에 항공기 충돌 시나리오별 해석 결과를 나타내었으며, 본 연구에서 설정한 항공기 충돌 시나리오에서는 사장교에 큰 영향을 미치지 못하는 것으로 나타났다. 항공기 충돌로 인한 바닥판의 최대 수직 처짐 및 솟음을 검토한 결과, 교축직각방향(x-dir)으로 충돌하는 시나리오 A~F는 바닥판의 최대 수직 처짐이 5.92mm~6.73mm 수준으로 측경간에서 발생하며, 최대 솟음은 4.68mm~5.84mm로 중앙견간에서 발생하게 된다. 이때, 최대 처짐 및 솟음은 케이블 1번~72번이 배치된 면 즉, 충돌하는 면에 배치된 케이블 위치에서 발생한다. 이와는 반대로 교축방향(y-dir)으로 충돌하는 시나리오 G 및 H는 바닥판의 최대 처짐이 중앙경간에서 각각 10.60mm 및 10.90mm가 발생하며, 최대 솟음은 충돌하중을 받는 PY2 주탑이 아닌 PY1 주탑 위치의 측경간에서 각각 8.69mm 및 8.84mm가 발생한다. 응답의 크기를 비교하면 교축방향(y-dir) 충돌 시나리오가 교축직각방향(x-dir) 충돌 시나리오보다는 영향이 비교적 크지만, 대상 교량의 경간 길이(주경간 470m, 측경간 200m)를 고려한다면, 매우 작은 크기의 수직 처짐 및 솟음이 발생하는 것을 알 수 있다. 항공기 충돌로 인해 케이블에 발생하는 최대 응력은 모든 시나리오에서 68번 케이블에 최대 약 664MPa 크기의 최대 응력이 발생하는 것을 확인하였다. 하지만, 68번 케이블의 초기 설계응력 크기가 662MPa인 것을 고려한다면, 시나리오별 케이블의 최대 응력 변화량은 1.60MPa~ 1.89MPa 수준이다. 모든 케이블의 최대 응력 변화량을 검토하면 0~2MPa 수준으로 나타난다. 또한, PTI(2007)에서 규정하고 있는 케이블의 최대 허용응력(0.5fu=882.5MPa)을 고려한다면 모든 케이블은 최대 허용응력 범위내에 있다는 것을 확인할 수 있다. 따라서, 본 연구에서 설정한 항공기 충돌 시나리오는 대상 교량에는 큰 영향을 미치지 못하는 것으로 판단된다.
Table 6.
Maximum deflection and camber results with locations
Table 7.
Maximum and variation stress of cable results
Fig. 12는 시나리오별 충돌해석 결과인 변위 분포 및 케이블 응력 분포를 나타내었으며, 결과 출력 시점은 최대 변위 및 응력이 발생하는 시점이다. 변위 분포의 표시 범위는 각 시나리오 A~F는 –7mm~6mm로, 시나리오 G 및 H는 –10mm~ 8mm로 설정하였다. 또한, scale factor를 100배로 적용하여 과장되게 표현하였다. Fig. 13은 시나리오별 케이블의 최대 응력 변화량을 나타내었다. 다만, 2면 배치되어 있는 케이블 모두를 나타내지는 않았으며, 바닥판의 최대 수직 처짐 및 솟음이 발생하는 면에 위치한 케이블들인 1번~72번 케이블의 변화량을 나타내었다.
6. 결 론
본 연구에서는 사장교에 항공기가 충돌하는 상황을 수치해석적으로 모사하기 위한 시나리오 설정 및 평가 절차를 제시하였으며, 이를 바탕으로 수치해석을 통한 구조거동을 평가하였다. 이로부터 얻은 주요 결론은 다음과 같다.
1) 항공기 충돌에 대한 사장교의 구조거동 평가를 위한 적절한 충돌 시나리오를 설정하기 위하여 국내외 원자력 발전소 설계기준을 분석하고, 실제 사고사례, 비행고도, 대상 교량의 주탑 높이 등을 고려하여 Cessna 210 경비행기에 대한 충돌 시나리오로 설정하는 절차를 제시하였다.
2) 사장교의 복잡한 거동 메커니즘을 현실적으로 모사할 수 있는 모델링 기법과 충돌해석을 수행하기 위한 해석기법을 제시하였다.
3) 바닥판의 최대 수직 처짐 및 솟음을 검토하였으며, 검토 결과 교축직각방향(x-dir)으로 충돌하는 시나리오 A~F에서는 바닥판의 최대 수직 처짐이 측경간에서 4.68mm~ 5.84mm가 발생하며, 최대 수직 솟음은 중앙경간에서 5.92mm~6.73mm가 발생한다. 이와는 다르게 교축방향(y-dir)으로 충돌하는 시나리오 G 및 H에서는 최대 수직 처짐이 각각 중앙경간에서 10.60mm 및 10.90mm가 발생하며, 최대 수직 솟음은 각각 8.69mm 및 8.84mm가 발생한다. 교축방향(y-dir) 충돌 시나리오가 교축직각방향(x-dir) 충돌 시나리오보다 비교적 응답의 크기가 크게 나타나지만, 대상 교량 경간의 길이를 고려한다면 매우 작은 값인 것을 확인할 수 있다.
4) 케이블의 최대 응력 및 변화량을 검토하였으며, 검토 결과 케이블의 최대 응력은 모든 시나리오에서 68번 케이블에 약 664MPa이 발생한다. 68번 케이블의 초기 설계응력 크기가 662MPa인 것을 고려한다면 변화량은 1.6MPa~ 1.89MPa 수준으로 확인된다. 68번 케이블을 제외하고도 나머지 케이블에서도 모두 0~2MPa의 최대 응력 변화량을 보인다. 또한, PTI(2007)에서 규정하고 있는 케이블의 최대 허용응력(0.5fu=882.5MPa)을 고려한다면 모든 케이블은 최대 허용응력 범위내에 있다는 것을 확인할 수 있다. 따라서, 본 연구에서 설정한 충돌 시나리오는 대상 교량에 큰 영향을 미치지 못할 것으로 판단된다.
이러한 결과로부터 본 연구에서 제시한 충돌해석 절차가 사장교의 구조거동을 평가할 수 있는 기법으로 활용될 수 있을 것으로 기대되며, 향후 다양한 충돌 시나리오를 통한 구조거동 평가가 이루어진다면 운용 중 사장교의 구조성능에 대한 정밀한 검토가 가능할 것으로 판단된다.