Feasibility Analysis of Applying Particle Filtering for Data-based Updating of Existing Seismic Fragility

Jinhyuk Lee; Jeong-Rae Cho; Hyejin Yoon

doi:10.7734/COSEIK.2025.38.1.43

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 28 February 2025. 43-55
https://doi.org/10.7734/COSEIK.2025.38.1.43

Feasibility Analysis of Applying Particle Filtering for Data-based Updating of Existing Seismic Fragility

데이터 기반 기존 지진취약도 업데이트를 위한 파티클 필터링 적용 타당성 분석

Jinhyuk Lee¹^*

Jeong-Rae Cho²

Hyejin Yoon³

이 진혁¹^*

조 정래²

윤 혜진³

¹Postdoctoral Researcher, Department of Structural Engineering, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

²Senior Research Fellow, Department of Structural Engineering, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

³Research Fellow, Department of Structural Engineering, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

¹한국건설기술연구원 구조연구본부 박사후연구원

²한국건설기술연구원 구조연구본부 선임연구위원

³한국건설기술연구원 구조연구본부 연구위원

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

This study analyzes the applicability of Particle Filtering (PF) to update existing seismic fragility curves using shake table test data. PF is particularly well-suited for addressing nonlinear and non-Gaussian problems, offering higher accuracy and stability compared to traditional Bayesian updating methods, such as Unscented Transformation (UT) and Markov Chain Monte Carlo (MCMC). The results demonstrate that PF yields more conservative seismic fragility curves in HAZUS, HRC, and strain-based damage states than the existing methods, while maintaining stability even under conditions of high uncertainty. In particular, the resampling process in PF effectively reduces uncertainty, thereby leading to more reliable seismic fragility evaluations. These findings suggest that PF represents a valuable tool for enhancing the accuracy and stability of seismic fragility assessments in earthquake engineering.

Keywords

shake table test

seismic fragility curves

particle filtering

Bayesian updating

resampling

본 논문에서는 진동대 실험 데이터를 활용하여 기존 지진취약도 곡선을 업데이트하기 위해 파티클 필터링(Particle Filtering, PF)의 적용 타당성을 분석하였다. PF는 비선형적이며, 비가우시안적인 문제를 다루는 데 적합하며, 기존 베이지안 업데이트 기법인 분산점 변환(Unscented Transformation, UT)과 마르코프 연쇄 몬테카를로(Markov Chain Monte Carlo, MCMC)에 비해 지진취약도 곡선 업데이트 과정에서 더 높은 정확성과 안정성을 제공하였다. 연구 결과, PF는 HAZUS, HRC, 변형률 기반(Strain-based) 손상 상태에서 기존 기법보다 더 보수적인 지진취약도 곡선을 도출하였으며, 불확실성이 큰 상황에서도 안정적인 결과를 제공하였다. 특히, PF는 재추출(Resampling) 과정을 통해 불확실성을 효과적으로 감소시켜 더 신뢰할 수 있는 지진취약도 평가 결과를 제공하였다. 본 연구는 PF가 지진공학 분야에서 지진취약도의 정확성과 안정성을 높이는 데 유용한 도구임을 시사한다.

키워드

진동대 실험

지진취약도 곡선

파티클 필터링

베이지안 업데이트

재추출

MAIN

1. 서 론
2. 기존 연구 분석
2.1 대상 실험체: 2층 철근콘크리트 골조
2.2 수치 모델링 및 지진취약도 곡선 생성
2.3 진동대 실험
2.4 해석적 지진취약도의 베이지안 업데이트
3. 지진취약도 업데이트를 위한 베이지안 기법
3.1 분산점 변환(Unscented Transformation)
3.2 마르코프 연쇄 몬테카를로(Markov Chain Monte Carlo)
3.3 파티클 필터링: Particle Filtering
4. 파티클 필터링 적용 타당성 분석
4.1 HAZUS 손상 상태
4.2 HRC 손상 상태
4.3 Strain-based 손상 상태
5. 결 론

1. 서 론

지진취약도는 구조물이 지진과 같은 외부하중으로 인해 손상될 확률을 계산할 수 있는 유용한 함수로 정의되며, 지진취약도 곡선은 도출 방식에 따라 경험적, 해석적, 판단적, 혼합형으로 분류된다. 경험적 곡선(Rossetto et al., 2015)은 지진 발생 이후 데이터 수집을 기반으로 한 통계적 방법에 의존하고, 해석적 곡선(D’Ayala et al., 2015; Lallemant et al., 2015)은 구조물의 수치 해석을 통해 도출된다. 정보가 부족할 경우, 전문가 의견에 따른 판단적 곡선(Jaiswal et al., 2012)도 지진취약도 곡선을 도출하는 데 채택될 수 있다. 혼합형 곡선은 구조물 수치 해석을 통한 해석적 곡선과 경험적, 판단적 곡선을 결합하여 도출할 수 있다(Kappos, 2016).

혼합형 지진취약도 곡선의 대표적인 예로, 실험 데이터를 활용하여 기존에 해석적으로 도출된 지진취약도 곡선을 업데이트하는 방식이 있다. 베이지안 방법론은 소규모 샘플 크기의 데이터를 모델링할 때 적합하지만, 추정값은 사전 분포에 민감할 수 있다. 특히 지진공학에서 취약도 곡선을 업데이트하는 방법은 수십 년 동안 실무에서 널리 사용되어 왔다. Singhal과 Kiremidjian(1998)은 노스리지 지진 중 수집된 건물 손상 데이터를 바탕으로 구축된 우도(Likelihood)를 사용하여 철근 콘크리트 건물에 대한 베이지안 업데이트 기법을 제시했다. 이때 관측된 데이터를 바탕으로 취약도 곡선의 중간값에 대한 신뢰구간을 구성하여 불확실성을 표현했다. 이러한 업데이트 과정은 관측된 데이터에 기반하므로, 연구 대상 구조물이 손상 통계가 수집된 구조물의 특성과 일치하지 않을 때, 적절하지 않을 수 있다.

취약도 곡선을 갱신하는 또 다른 접근 방식은 실험 결과를 사용하는 것이다. 예를 들어, Jaiswal 등(2012)은 세계 여러 지역의 건물 유형에 대해 전문가 의견을 바탕으로 도출한 취약도 곡선을 도출하였으며, 이러한 전문가 의견 기반의 취약도 곡선이 추가적인 실험 데이터나 현장 데이터를 통해 신뢰성 있는 취약도 곡선으로 업데이트될 가능성을 제시하였다. 또한, 베이지안 업데이트(Box and Tiao, 1992; Gelman et al., 2013) 기법은 Porter 등(2006)에 의해 광범위하게 조사되었으며, Unscented Transformation(UT)의 원리에 기반한 단순화된 방법(Julier and Uhlmann, 2000)을 제시했고, 이는 ATC-58 프레임워크에 의해 채택되었다. 이 접근법에서 사전 취약도 함수는 일반적으로 다섯 개 정도의 이산 점과 그에 대응하는 가중치로 구성된 결합 확률 함수로 표현된다. 실험 데이터를 기반으로 우도를 구축하여 이산 점에 할당된 가중치는 최종적으로 업데이트된다. 이 방법은 간단하고 효율적이지만, 이산적인 데이터 표현 방식이기 때문에 업데이트 결과에 편향이 발생할 가능성이 있다. 베이지안 업데이트를 위한 확률적 프레임워크는 지난 10년간 활발히 탐구되었다. 예를 들어, Koutsourelakis(2010)는 베이지안 추론의 맥락에서 Markov Chain Monte Carlo(MCMC) 방법을 사용해 취약도 곡선을 갱신했다. Li 등(2013)은 캘리포니아의 Meloland 도로교에 대한 취약도 곡선을 갱신할 때 유사한 접근 방식을 사용했다. Tekeste(2021), Tekeste 등(2022)의 연구에서는 실험 데이터를 기반으로 철근 콘크리트(Reinforced Concrete, RC) 구조물의 해석적으로 도출된 지진취약도 곡선을 베이지안 기법을 통해 업데이트하는 절차를 제안하였다. 이때, 진동대 실험에서 도출된 데이터를 사용하여 기존 해석적 취약도 곡선을 업데이트하며, 이 과정에서 UT와 MCMC기법을 적용하여 결과를 비교 분석하였다. 특히, HAZUS와 같은 다양한 손상 상태 모델에 따른 취약도 곡선을 업데이트하고, 실험 데이터가 신뢰도가 낮은 사전 분포에 미치는 영향을 강조하였다.

본 논문에서는 Tekeste(2021), Tekeste 등(2022)에서 기존에 수행한 진동대 실험 데이터를 활용하여 파티클 필터링(Particle Filtering, PF) 적용 타당성을 분석하였다. 또한, UT, MCMC 기반 분석 결과와 PF 분석 결과를 비교하여 지진취약도 업데이트를 위한 PF 적용 타당성을 분석하였다. 본 논문 2장에서는 Tekeste(2021), Tekeste 등(2022)에서 제시한 바와 같이, 지진취약도 곡선을 UT 및 MCMC 기반 베이지안 기법에 따라 업데이트한 연구를 간략히 소개한다. 3장에서는 UT, MCMC 및 PF의 개념, 특징, 적용 절차를 설명한다. 4장에서는 PF 적용 결과와 UT, MCMC기법 적용 결과를 비교 분석한다. 5장 결론에서는 수행된 결과들의 비교 분석을 통해 PF의 실질적인 적용 가능성과 한계점을 파악하고, 실험 데이터를 활용한 지진취약도 업데이트의 타당성을 검토한다.

2. 기존 연구 분석

서론에서 언급한 Tekeste(2021), Tekeste 등(2022)은 철근 콘크리트(RC) 구조물의 지진 취약도 곡선을 베이지안 기법으로 업데이트하는 방법을 제안했다. 이 연구의 목표는 실험 데이터를 활용하여 기존의 해석적 방법으로 도출된 지진취약도 곡선을 업데이트하는 것을 목표로 하며, 특히 진동대 실험(Shake table test)을 통해 얻은 데이터를 사용하여 베이지안 원리에 따라 지진취약도 곡선을 갱신하는 절차를 소개하고 있다. 이러한 접근법은 성능 기반 지진공학(Performance-based earthquake engineering)의 일환으로 구조물의 내진성능을 보다 정확하게 평가하기 위해 사용되었다. 진동대 실험은 지진 입력 강도를 단계적으로 증가시키며 구조물의 손상 상태를 평가하는 방법으로, RC 구조물의 내진성능을 실험적으로 검증하는 데 유용한 특징을 가지고 있다.

기존 연구에서 제안된 베이지안 업데이트는 해석적 지진취약도 곡선을 새로운 실험 데이터를 통해 수정하는 방식으로, 사전 정보(Prior)와 우도(Likelihood)를 결합하여 사후 분포(Posterior)를 얻는 절차를 따른다. 이 과정에서 베이지안 방법론의 핵심은 불확실한 데이터를 점진적으로 더 신뢰할 수 있는 데이터로 보완하는 것이다. 특히, UT와 MCMC 기법을 통해 베이지안 업데이트의 효율성과 정확성을 평가하며, 두 기법이 가지는 차이점을 비교･분석하였다.

2.1 대상 실험체: 2층 철근콘크리트 골조

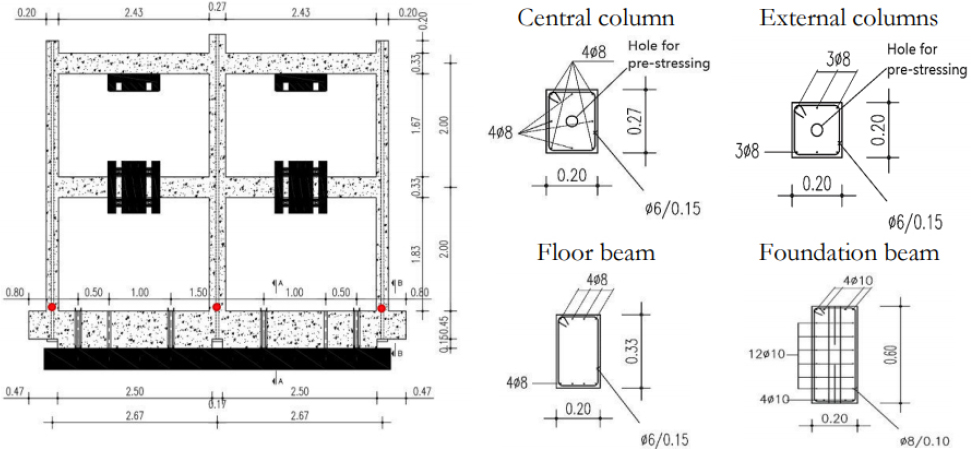
Tekeste(2021), Tekeste 등(2022)에서 채택한 대상 실험체는 2층 철근콘크리트 골조로, 이는 비내진 설계된 구조물을 기반으로 하여 포르투갈 리스본의 National Laboratory for Civil Engineering(LNEC) 건물의 3D 진동대에서 실험되었다. 이 실험체는 지진 강도(Intensity Measure, IM)를 단계적으로 증가시키면서 구조물의 반응을 평가하는 것이 목적이다. 실험체는 1:1.5 스케일로 축소된 구조물로, 일반적인 저층 철근콘크리트 건물의 구조적 특성을 반영하며, Fig. 1과 같다. 실험 목적은 비내진 설계된 철근콘크리트 구조물의 지진응답을 평가하여, 지진 하중에 대한 내진성능을 보다 정확하게 이해하는 데 있다. 특히, 진동대 실험에서 얻은 데이터를 통해 UT 및 MCMC 기반의 베이지안 업데이트 기법을 사용하여 수치해석을 통해 예측한 기존 해석적 지진취약도 곡선을 보완 및 갱신하고, 비내진 구조물의 취약성을 평가하는 데 중점을 두었다. 이를 통해 진동대 실험을 통해 점진적으로 증가하는 지진 강도 하에서 구조물의 거동과 손상 상태를 보다 정확히 파악할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-01/N0040380106/images/Figure_jcoseik_38_01_06_F1.jpg

Fig. 1.

2D RC frame (Tekeste, 2021)

2.2 수치 모델링 및 지진취약도 곡선 생성

Tekeste(2021), Tekeste 등(2022)의 연구에서는 Seismostruct 소프트웨어를 이용하여 2D 철근 콘크리트 골조를 수치 모델링하였다. 구조 요소는 비선형 해석이 가능하도록 힘 기반 요소(Force-based elements)로 모델링되었으며, 기초 보는 탄성 요소로 정의되었다. 기둥에 삽입된 프리스트레스트 강봉 역시 탄성적으로 모델링되어 기둥에 지속적인 축 하중을 가하여 프레임의 변형을 억제하는 역할을 했다. 철근은 Menegotto-Pinto 강재 모델을 사용해 비선형 거동을 반영하였으며, 콘크리트는 Mander 등(1989)이 제시한 모델을 통해 압축 및 인장 거동을 구현하였다(Mander et al., 1989; Menegotto and Pinto, 1973). 이러한 수치 모델을 통해 비선형 지진응답을 평가하기 위한 증분 동적 해석(Incremental Dynamic Analysis, IDA)이 30개의 지진기록을 사용하여 수행되었으며, 각 지진 기록은 규모 6.0~6.5에서 선택되었다(Tekeste, 2021, Appendix-6).

HAZUS와 Homogenized Reinforced Concrete(HRC) 손상 상태는 최대 층간 변위(Maximum inter-story drift, ISD_max)를 고려하여 지진취약도 곡선을 도출하는 데 사용되었다(Rossetto and Elnashai, 2003). 또한, Fig. 1의 실험체 하단 적색 점으로 표시된 바와 같이 육안으로 관찰할 수 있는 콘크리트 변형률에 대해서 모니터링하였다. 콘크리트 커버의 변형율이 +0.01%를 초과하면 균열이 발생(Cracking)하는 것을 의미하고, -0.2%를 초과하는 압축 변형률은 콘크리트 커버의 탈락(Spalling)을 의미한다. 또한, 콘크리트 중심부의 압축강도는 0.6% 이상의 변형률로 규정되며, 이는 콘크리트의 파쇄(Crushing)로 정의된다. 육안 관찰에 따른 콘크리트 균열, 탈락, 파쇄에 대한 손상 상태와 실험체 1층에서 기록된 최대 층간 변위에 따른 변형률을 고려하여 지진취약도 곡선을 도출하였다. 이러한 지진취약도 곡선 산출 결과는 4장에서 자세히 다루고 있다.

2.3 진동대 실험

Fig. 1에서 언급한 실험체는 National Laboratory for Civil Engineering(LNEC)의 3D 진동대에서 실험하였으며, 1:1.5 스케일로 축소된 2층 철근 콘크리트 골조가 사용되었다. 실험체의 기둥과 보는 HRC 기준에 따라 설계되었으며, 기초는 진동대에 강체로 연결되었다. 실험체의 각 층에는 각각 1.18톤과 1.13톤의 질량 블록이 배치되었으며, 이를 통해 지진 하중을 모사하였다. 진동대 실험은 지진 강도를 점진적으로 증가시키며 구조물의 응답을 평가하는 방식으로 진행되었다. 입력된 지진 하중은 0.1g에서 시작해 단계별로 증가하였으며, 각 단계에서 층간 변위 및 구조물의 손상상태가 기록되었다. 실험 데이터는 이후 수치 해석과 결합하여 베이지안 업데이트를 위한 자료로 활용되었다. 진동대 실험을 통해 실시간으로 구조물의 동적 응답을 모니터링하였으며, 실험 데이터는 해석적 취약도 곡선의 개선에 필요한 중요한 정보를 제공하였다.

2.4 해석적 지진취약도의 베이지안 업데이트

베이지안 업데이트는 기존의 해석적 지진취약도 곡선을 실험 데이터를 바탕으로 개선하는 방법론으로, 사전 정보(Prior)와 실험 데이터에 의한 우도(Likelihood)를 결합하여 사후 확률(Posterior)을 계산하는 방식으로 이루어진다(Ang and Tang, 2007). 철근 콘크리트 골조의 지진취약도에 대한 베이지안 업데이트 과정에서 크게 두 가지 손상 상태가 고려되었다. 첫 번째는 최대 층간 변위에 기반한 손상 상태로 HAZUS와 HRC 손상 상태를 따르고, 두 번째는 콘크리트 변형률 기반 손상 상태이다. 앞서 언급한 바와 같이, 변형률 기반(Strain-based) 손상 상태는 진동대 실험 중 육안으로 관측된 손상 데이터를 의미한다. 한편, 진동대 실험 중 1층에서 기록된 최대 층간 변위는 초과확률 매개변수 𝜀을 결정하는데 사용되었으며, 이에 대한 내용은 3.1절에서 다룬다.

HAZUS와 HRC 손상상태 기준을 바탕으로, 최대 층간 변위와 변형률 기반 손상상태의 차이를 고려한 베이지안 업데이트를 수행하였다. 이를 통해, 기존 해석적 모델과 실험 데이터를 결합하여 각 손상상태에 대한 지진취약도 곡선을 새롭게 갱신하였다. 베이지안 업데이트 과정에서 발생하는 불확실성을 고려하여, 실험 데이터를 통한 모델의 신뢰성을 향상시키기 위한 방법론을 강조하였으며, 기존의 해석적 지진취약도 곡선에 비해 통계적으로 유의미한 개선을 이루었다는 결론을 도출하였다.

3. 지진취약도 업데이트를 위한 베이지안 기법

본 3장에서는 베이지안 기법을 사용하여 기존 해석적 지진취약도를 업데이트하는 다양한 알고리즘을 설명한다. 우선 분산점 변환(Unscented Transformation, UT)과 마르코프 연쇄 몬테카를로(Markov Chain Monte Carlo, MCMC) 기반의 베이지안 업데이트 절차를 다루고, 추가적으로 본 논문에서 새롭게 접목시킨 파티클 필터링(Particle Filtering, PF) 기반의 베이지안 업데이트 기법을 소개한다.

지진취약도는 특정 구조물(또는 실험체)이 지진 강도(Intensity Measure, IM)에 따라 일정한 손상 상태에 도달할 조건부 확률(Conditional probability)을 나타낸다. 이는 지진 하중의 크기에 따른 손상의 가능성을 정량적으로 평가하는 도구로 사용된다. 일반적으로 지진취약도 함수는 식 (1)과 같이 누적분포함수(Cumulative Distribution Function, CDF) 형태로 표현된다(Baker et al., 2021; Lee et al., 2014; Park et al., 2023; Shinozuka et al., 2000).

(1)

P [D S | I M = X] = ϕ (\frac{\ln (\frac{X}{θ})}{σ})

여기서, DS는 특정 손상 상태(Damage State)를 나타내며, IM은 지진 강도를 의미하는 입력 변수로, 본 연구에서는 첫 번째 고유 진동수에서의 스펙트럼 가속도(S_a(T₁))와 최대 층간 변위(ISD_max)를 사용하였다(Tekeste, 2021, 6.5.3 Experimental test). $ϕ (\cdot)$ 는 표준 정규분포의 누적 확률 함수이며, 𝜃는 중앙값(Median), 𝜎는 대수표준편차(Lognormal standard deviation)를 나타내는데, 이는 지진취약도의 평가 결과로 도출되는 매개변수이면서, 동시에 베이지안 업데이트를 위한 입력 변수로 사용된다.

3.1 분산점 변환(Unscented Transformation)

분산점 변환(Unscented Transformation, UT)은 비선형 시스템에서 상태 추정을 수행하기 위해 개발된 기법으로, 베이지안 업데이트에서 사전 분포를 변환하는데 사용된다. UT는 칼만 필터(Kalman Filter)의 한계인 선형 근사의 문제를 극복하기 위해 도입된 방법으로, 상태 변수를 나타내기 위한 시그마 점(Sigma points)을 사용하여 비선형성을 더 정확하게 근사할 수 있다(Julier and Uhlmann, 2000). UT는 전체 분포 공간을 포괄하기 위해 2n+1개의 시그마 점을 도출하며, 사전 분포의 중앙값과 대수표준편차 파라미터인 $μ'$ , $β'$ 이 비선형 확률 함수를 통해 변환되고, 사후 확률 파라미터인 $μ''$ , $β''$ 이 계산된다. 이 접근법의 첫 번째 단계는 시그마 점의 좌표를 정의하는 것이다. 이후 취약도 곡선은 시그마 점에서 두 개의 확률 변수인 $μ'$ , $β'$ 의 분포로 정의되며, n = 2일 때, 5개의 시그마 점이 사용된다. 5개의 시그마 점은 Table 1과 같이 정의할 수 있다.

Table 1

Coordinates of sigma points in UT (Tekeste, 2021)

General formula	Median	Dispersion
For i = 0, $s_{i} = μ_{x}$	$s_{0, μ} = μ'$	$s_{0, β} = β'$
For i = 1 to n, $s_{i} = μ_{x} + γ \sqrt{P_{x, i}}$	$s_{1, μ} = μ' + γ \sqrt{P_{μ', 1}}$ $s_{2, μ} = μ'$	$s_{1, β} = β'$ $s_{2, β} = β' + γ \sqrt{P_{β', 2}}$
For i = n + 1 to 2n, $s_{i} = μ_{x} - γ \sqrt{P_{x, i}}$	$s_{3, μ} = μ' - γ \sqrt{P_{μ', 1}}$ $s_{4, μ} = μ'$	$s_{1, β} = β'$ $s_{2, β} = β' - γ \sqrt{P_{β', 2}}$

Table 1에서 𝛾는 스케일링 매개변수이고, $P_{x, i}$ 는 공분산 행렬의 요소이다. 𝛾와 공분산 행렬 P는 각각 식 (2), (3)과 같이 정의된다.

(2)

γ = \sqrt{n + 1}

(3)

P_{μ^{'}} = [\begin{matrix} σ_{μ^{'}}^{2} \\ 0 \end{matrix}]; P_{β^{'}} = [\begin{matrix} 0 \\ σ_{β^{'}}^{2} \end{matrix}]

또한, 시그마 점의 가중치는 식 (4)와 같이 정의된다.

(4)

w_{i}^{'} = \{\begin{cases} \frac{1}{γ^{2}}, if i = 0 \\ \frac{1}{2 γ^{2}}, if i \in [1, 2 n] \end{cases}

앞서 언급한 바와 같이, 진동대 실험은 입력 강도를 점진적으로 증가시키는 방식으로 실행된다. 주어진 손상 상태를 고려할 때, 진동대 실험 중 손상 상태의 초과 여부를 나타내는 이진수 백터, 𝜀를 계산할 수 있다. 따라서, 손상 기준 초과 식별자 𝜀를 사용하여 5개의 시그마 점 각각에 대한 해당 손상 상태의 우도 함수를 식 (5)와 같이 구성할 수 있다.

(5)

\begin{aligned} L (s_{i, μ} s_{i, β}) = & Π_{j = 1}^{N} {\{1 - Φ (\frac{\ln (i m_{j}) - s_{i, μ}}{s_{i, β}})\}}^{1 - ε_{j}} \times {\{Φ (\frac{\ln (i m_{j}) - s_{i, μ}}{s_{i, β}})\}}^{ε_{j}} \end{aligned}

여기서, $i m_{j}$ 는 진동대 실험의 j번째 단계에서 지진의 강도(IM)를 뜻하고, 𝜀의 크기는 N과 같다. 이를 토대로 사전 분포 가중치 $w_{i}'$ 를 다음의 식 (6), (7)을 통해 업데이트할 수 있다.

(6)

P_{t} (D a t a) = \sum_{i = 0}^{2 n} w'_{i} \times L (s_{i, μ}, s_{i, β})

(7)

w_{i}'' = \frac{w_{i}' \times L (s_{i, μ}, s_{i, β})}{P_{t} (d a t a)}

여기서, 정규화 상수, $P_{t} (d a t a)$ 를 계산하고, 5개의 시그마 점에서 업데이트된 가중치, $w_{i}''$ 를 사용하여 중앙값( $μ''$ )과 대수표준편차( $β''$ )의 사후 추정치를 식 (8), (9)를 통해 계산한다.

(8)

μ'' = \sum_{i = 0}^{2 n} w_{i}'' \times s_{i, μ}

(9)

β'' = \sqrt{\sum_{i = 0}^{2 n} w_{i}'' \times s_{i, β}}

3.2 마르코프 연쇄 몬테카를로(Markov Chain Monte Carlo)

마르코프 연쇄 몬테카를로(Markov Chain Monte Carlo, MCMC)는 베이지안 추론에서 매우 강력한 기법으로, 복잡한 확률 분포에서 사후 분포(Posterior distribution)를 직접적으로 샘플링할 수 있는 방법이다. MCMC는 복잡한 비선형 문제나 고차원 문제에서도 유연하게 적용될 수 있어, 베이지안 업데이트를 수행하는 데 있어 매우 유용하다(Brooks et al., 2011).

지진취약도 함수는 일반적으로 두 가지 매개변수로, 각각 대수정규분포의 중앙값( $θ_{1}$ )과 대수표준편차( $θ_{2}$ )로 지정된다. 이때, 중앙값( $θ_{1}$ )은 대수정규분포를 따르고, 대수표준편차( $θ_{2}$ )는 감마분포를 따르며, 각각 식 (10), (11)과 같이 표현된다.

(10)

θ_{1} ~ L N (μ_{θ_{1}}, σ_{θ_{1}}^{2})

(11)

θ_{2} ~ Gamma (c, λ); c = \frac{μ_{θ_{2}}^{2}}{σ_{θ_{2}}^{2}}, λ = \frac{μ_{θ_{2}}}{σ_{θ_{2}}^{2}}

Porter 등(2006)에 따르면, 중앙값( $θ_{1}$ )의 표준편차( $σ_{θ_{1}}$ )는 $θ_{2} / \sqrt{2}$ 와 같이 표현되고, 감마분포를 따르는 표준편차( $θ_{2}$ )의 평균( $μ_{θ_{2}}$ )과 표준편차( $σ_{θ_{2}}$ )는 각각 식 (12), (13)과 같이 표현된다.

(12)

μ_{θ_{2}} = θ_{2}

(13)

σ_{θ_{2}} = C O V_{θ_{2}} \times θ_{2}

또한, Porter 등(2007)에 따르면, 대수표준편차( $θ_{2}$ )의 변동계수(Coefficient of variation, COV), $C O V_{θ_{2}}$ 를 0.21로 가정하였으며, 본 논문에서도 이러한 값들을 적용하여 사전 분포를 도출하였다. 취약도 곡선의 사전 분포는 식 (14)와 같이 결합 확률 분포로 구성할 수 있다.

(14)

f' (θ_{1,} θ_{2}) = P (θ_{1} | μ_{θ_{1}}, σ_{θ_{1}}^{2}) \times P (θ_{2} | c, λ)

우도 함수의 경우, 식 (5)와 동일하지만, 연속 밀도 함수로 사용되며, 식 (15)와 같이 정의된다.

(15)

f'' (θ_{1,} θ_{2}) \propto L (d a t a | θ_{1}, θ_{2}) \times f' (θ_{1}, θ_{2})

한편, MCMC 기법의 기본 개념은 확률적 전이 과정을 통해 사후 분포에서 샘플을 반복적으로 추출하는 것이다. 이때 마르코프 연쇄(Markov Chain)의 특성을 사용하여 각 단계에서 현재 상태를 기반으로 다음 상태를 결정하며, 일정한 수의 반복 후에는 목표로 하는 사후 분포에서 샘플링된 결과를 얻을 수 있다. 이때, 샘플링을 위한 대표적인 MCMC 알고리즘으로 알려진 Metropolis-Hastings(M-H) 알고리즘을 적용하였다. M-H에 관한 더 상세한 정보는 참고문헌을 참조하길 바란다(Tekeste, 2021, 6.3.2.2.3 Metropolis-Hasting algorithm).

3.3 파티클 필터링: Particle Filtering

파티클 필터링(Particle Filtering, PF)은 비선형(Nonlinear) 및 비가우시안(Non-Gaussian) 시스템에서 상태 추정을 수행하기 위한 기법 중 하나로, 베이지안 업데이트 과정에서 불확실한 상태를 다수의 파티클로 나타내어 추정하는 방식으로 알려져 있다(Simon, 2006).

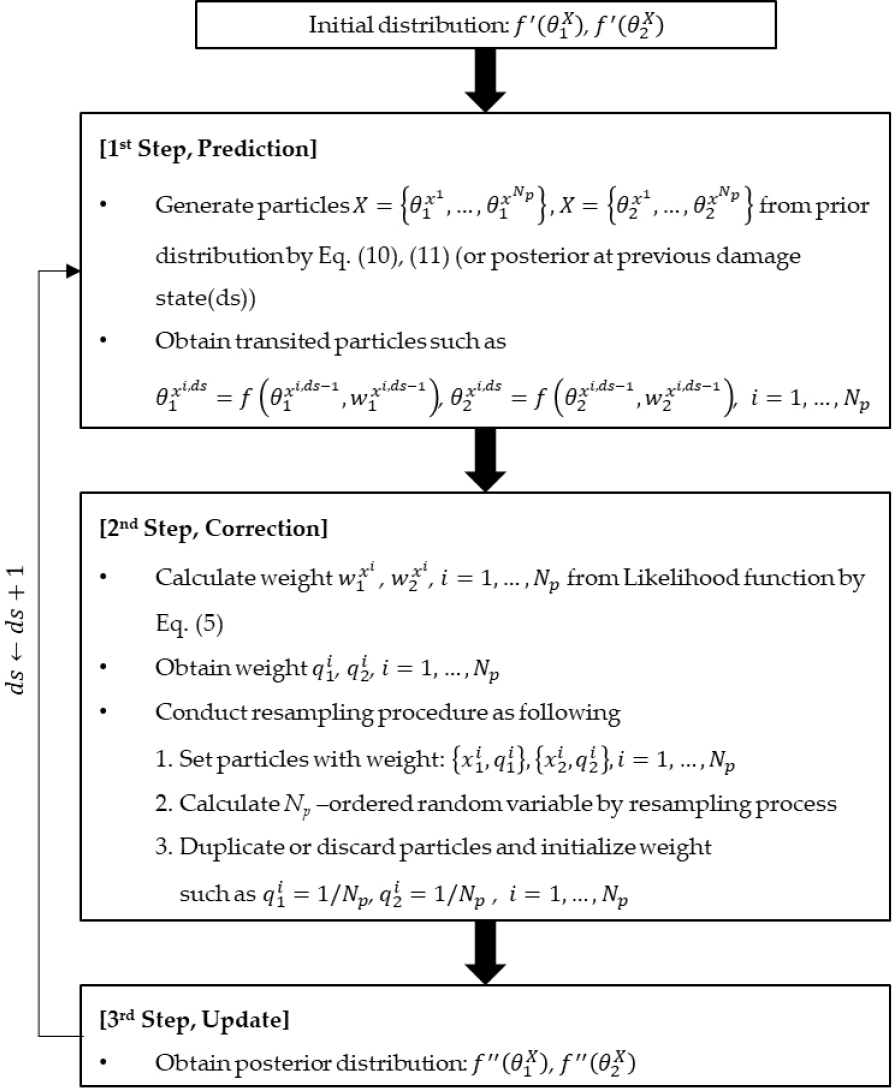
파티클 필터링은 크게 예측(Prediction), 보정(Correction), 갱신(Update)의 세 가지 주요 단계로 나뉜다(Fig. 2). 첫 번째 단계에서는 식 (10), (11)에서 밝힌 바와 같이 초기 상태 분포에서 무작위로 파티클을 샘플링한다. 각 파티클은 시스템(또는 확률분포)의 현재 상태를 나타내며, 이러한 샘플링 된 파티클은 시스템의 상태 공간을 대표한다. Jung 등(2024), Lee(2022) 등이 제시한 파티클 필터링 수행 시 유의미한 파티클 개수는 15,000개로, 본 연구에서도 15,000개의 파티클을 사용하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-01/N0040380106/images/Figure_jcoseik_38_01_06_F2.jpg

Fig. 2.

Schematic algorithm of Particle Filtering (PF)

두 번째 단계에서는 관측 데이터인 우도 함수(식 (5))를 사용하여 파티클들의 상태를 업데이트한다. 이 과정에서 각 파티클에 가중치(Weight, w)가 부여되며, 가중치는 파티클의 상태가 관측 데이터와 얼마나 일치하는지에 따라 결정된다. 즉, 중요한 상태를 나타내는 파티클일수록 높은 가중치를 부여받는다.

세 번째 단계는 갱신(Update)이다. 이때, 재추출(Resampling) 과정에서 가중치가 낮은 파티클은 제거되며, 높은 가중치를 가진 파티클은 복제된다. 이 과정에서 파티클의 개수는 유지되고, 이 과정을 통해 파티클의 불확실성을 감소시키고, 상태 추정의 정확성을 높이는 데 기여한다. 재추출은 가중치가 높은 파티클을 집중적으로 재조정하여, 보다 신뢰성있는 상태 추정을 가능하게 한다. 이 과정은 파티클의 분포를 사후 분포로 변환하는 과정으로 이어진다. PF에 관한 더 상세한 정보는 참고문헌을 참조하길 바란다(Jung et al., 2024; Lee et al., 2022; Lee et al., 2024).

PF와 UT, MCMC의 차이점은 추정 방식과 계산 효율성에서 두드러진다. UT는 평균과 공분산을 사용해 선형 근사를 수행하는 반면, PF는 선형 근사없이 복잡한 비선형 시스템에도 적용 가능하다. MCMC는 매우 정밀하지만 단순 샘플링에 따른 많은 계산 자원을 소모하는 반면, PF는 재추출 효과를 반영하여 계산 효율성이 뛰어나다.

4. 파티클 필터링 적용 타당성 분석

본 4장에서는 베이지안 기법을 적용한 파티클 필터링(PF) 기법의 실질적인 적용 타당성을 분석한다. 이를 위해 기존 연구인 Tekeste(2021)에서 제시한 UT, MCMC 기법을 사용한 3가지 손상 상태(HAZUS, HRC, Strain-based)에 대한 지진취약도 결과와 본 논문에서 제안하는 파티클 필터링 기반 지진취약도 결과를 비교･분석하였다.

4.1 HAZUS 손상 상태

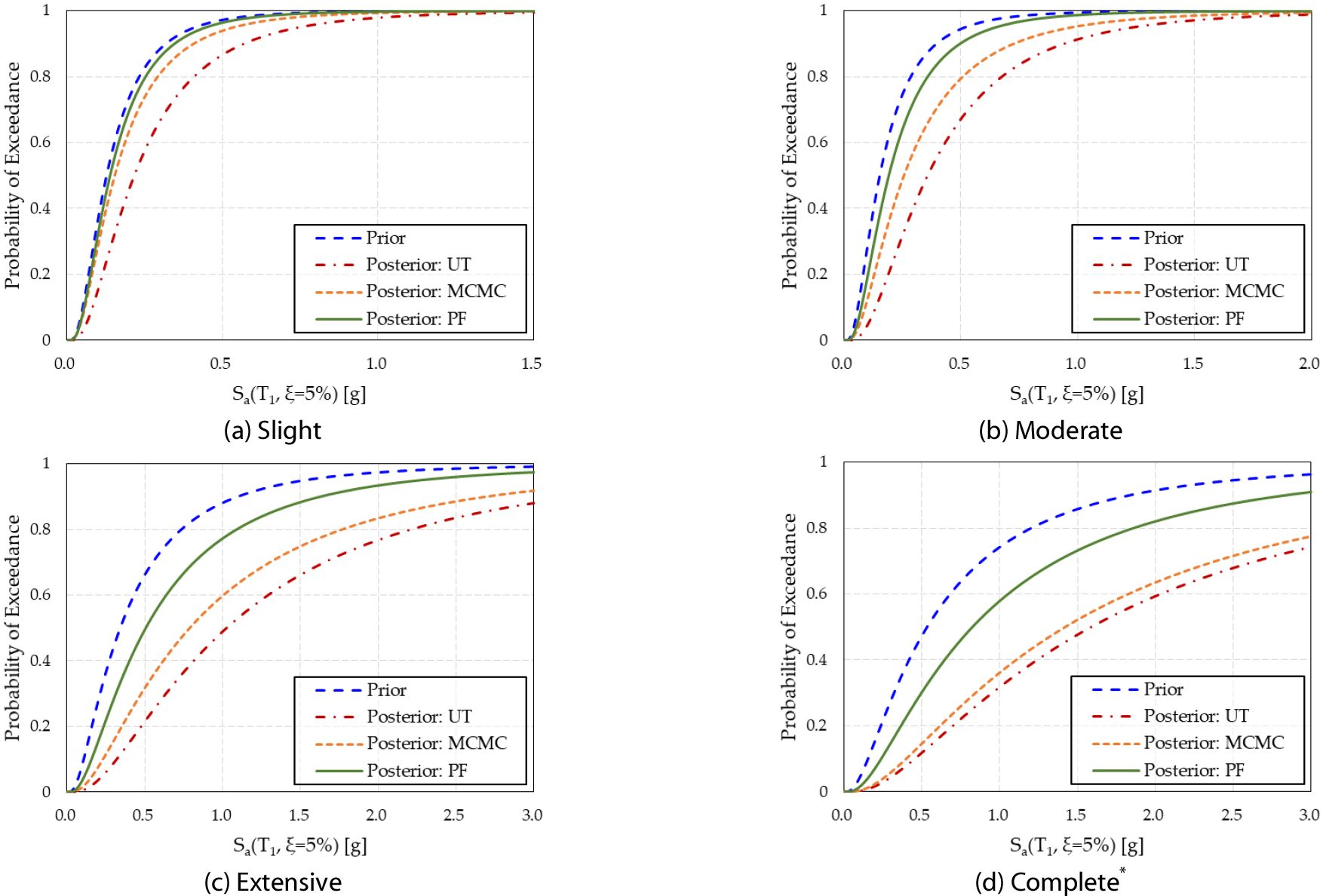
HAZUS 지침에서는 철근 콘크리트(RC) 골조 실험체의 평균 층간 변위에 기반하여 경미한(Slight), 보통의(Moderate), 광범위한(Extensive), 완전한(Complete) 총 4가지 손상 상태를 제공한다(Park et al., 2023). 해석적 지진취약도 곡선은 IDA를 통해 도출되었으며, 완전한(Complete) 손상 상태에서는 실험체의 최대 강도가 20% 감소한 손상 상태(이하, ‘Complete^*’)를 적용하였다. 사전 정보에 해당하는 해석적 지진취약도 곡선을 3가지 베이지안 업데이트 기법(UT, MCMC, PF)을 통해 갱신하였다. 베이지안 업데이트는 RC 골조에서 실시한 5단계의 진동대 실험 결과를 사용하여 수행되었다. 이때, 진동대 실험 중 최대 수평 가속도 측면에서 최대 지반 가속도는 0.72g로 기록되었으며, 실험체의 최종 손상 수준은 광범위한(Extensive) 손상 상태와 완전한(Complete) 손상 상태 사이로 측정되었다. 진동대 실험의 경우, 하나의 실험체에 대해 실험을 수행하면서, 5단계의 입력 지진 강도를 순차적으로 가하여 누적된 손상을 평가하는 방식으로 수행되었다(Tekeste, 2021, 6.4.2 Optimization of Bayesian updating using shaking table test). 베이지안 업데이트 과정에서 우도 함수는 Table 2에 제시된 초과 기준과 같이 구성되었으며, 진동대 실험 각 단계에서 기록된 최대 층간 변위를 HAZUS 손상 상태 변위 기준과 비교하여 구성하였다.

Table 2

Exceedance parameter, 𝜀, for the HAZUS damage states (Tekeste, 2021, Table 6-5)

Stages	PGA (g)	S_a(T₁) (g)	ISD_max (mm)	Inter-story drift(ISD) for HAZUS damage states
				Slight	Moderate	Extensive	Complete^*
				11.5 (mm)	18.4 (mm)	46 (mm)	118 (mm)
1	0.10	0.29	7.89	0	0	0	0
2	0.20	0.58	15.46	1	0	0	0
3	0.32	0.93	27.32	1	1	0	0
4	0.52	1.51	42.45	1	1	0	0
5	0.72	2.10	48.32	1	1	1	0

Table 3와 Fig. 3를 통해 UT, MCMC, PF 기법에 따른 HAZUS 손상 상태 취약성에 대한 비교 결과를 제시하였다. 먼저, Table 3과 같이 3가지 베이지안 기법에 대한 사후 확률 파라미터를 확인할 수 있는데, 3가지 방법 간 일관성 있는 비교를 위해 사전 확률 파라미터( $θ_{1}'$ , $θ_{2}'$ )는 모두 동일하게 설정하였다. 3가지 베이지안 업데이트 기법을 통해 갱신된 대수표준편차( $θ_{2}''$ )의 값이 사전 분포의 대수표준편차( $θ_{2}'$ ) 값과 유사한 값을 갖는데, 이는 우도 함수 식 (5)를 통해 계산된 우도 함수 분포 폭이 사전 분포 폭보다 크다는 것을 의미한다. 즉, 진동대 실험을 통해 계산된 우도 함수의 불확실성이 큰 경우, 사후 분포는 데이터(우도)보다 사전 분포를 더 많이 반영하도록 업데이트된다. 3가지 베이지안 업데이트는 모두 수치 해석을 통해 도출된 사전 분포의 중앙값이 증가된 것을 확인할 수 있는데, 이는 실제 진동대 실험 결과 반영에 따라 HAZUS 손상 상태에 도달하는 데 필요한 IM의 증가로 인한 것으로 분석되었다. 또한, Fig. 3와 같이 HAZUS 4가지 손상 상태에 대해서 3가지 베이지안 업데이트에 따른 중앙값( $θ_{1}''$ ) 추정치는 PF, MCMC, UT 순으로 대상 구조물의 성능을 보수적으로 평가하는 것으로 분석되었다. 이때, PF와 MCMC의 중앙값( $θ_{1}''$ )의 불확실성 지표인 표준편차( $σ_{1}''$ )를 비교해보면 모든 경우에 대해서 PF의 표준편차( $σ_{1}''$ )가 작게 나타난 것을 확인하였다(Table 3). 이를 통해, PF의 재추출 효과로 인해, UT, MCMC 대비 사전 분포의 특성을 보다 잘 반영하도록 업데이트된 것을 확인할 수 있다.

Table 3

Posterior point estimates of HAZUS damage states: UT vs MCMC vs PF

Bayesian probability model			HAZUS damage states
Bayesian probability model			Slight	Moderate	Extensive	Complete^*
Prior parameters		$θ_{1}'$ (g)	0.128	0.153	0.342	0.535
Prior parameters		$θ_{2}'$	0.711	0.742	0.909	0.962
Posterior parameters	UT	$θ_{1}''$ (g)	0.217	0.358	1.025	1.588
	UT	$θ_{2}''$	0.752	0.755	0.912	0.974
	MCMC	$θ_{1}''$ (g)	0.155	0.256	0.788	1.421
		$σ_{θ_{1}''}$	0.085	0.136	0.473	0.926
		$θ_{2}''$	0.758	0.812	0.959	0.988
		$σ_{θ_{2}''}$	0.154	0.165	0.202	0.212
	PF	$θ_{1}''$ (g)	0.140	0.192	0.506	0.826
		$σ_{θ_{1}''}$	0.056	0.079	0.249	0.418
		$θ_{2}''$	0.710	0.743	0.912	0.963
		$σ_{θ_{2}''}$	0.148	0.156	0.192	0.201

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-01/N0040380106/images/Figure_jcoseik_38_01_06_F3.jpg

Fig. 3.

Seismic fragility curve for HAZUS damage states

4.2 HRC 손상 상태

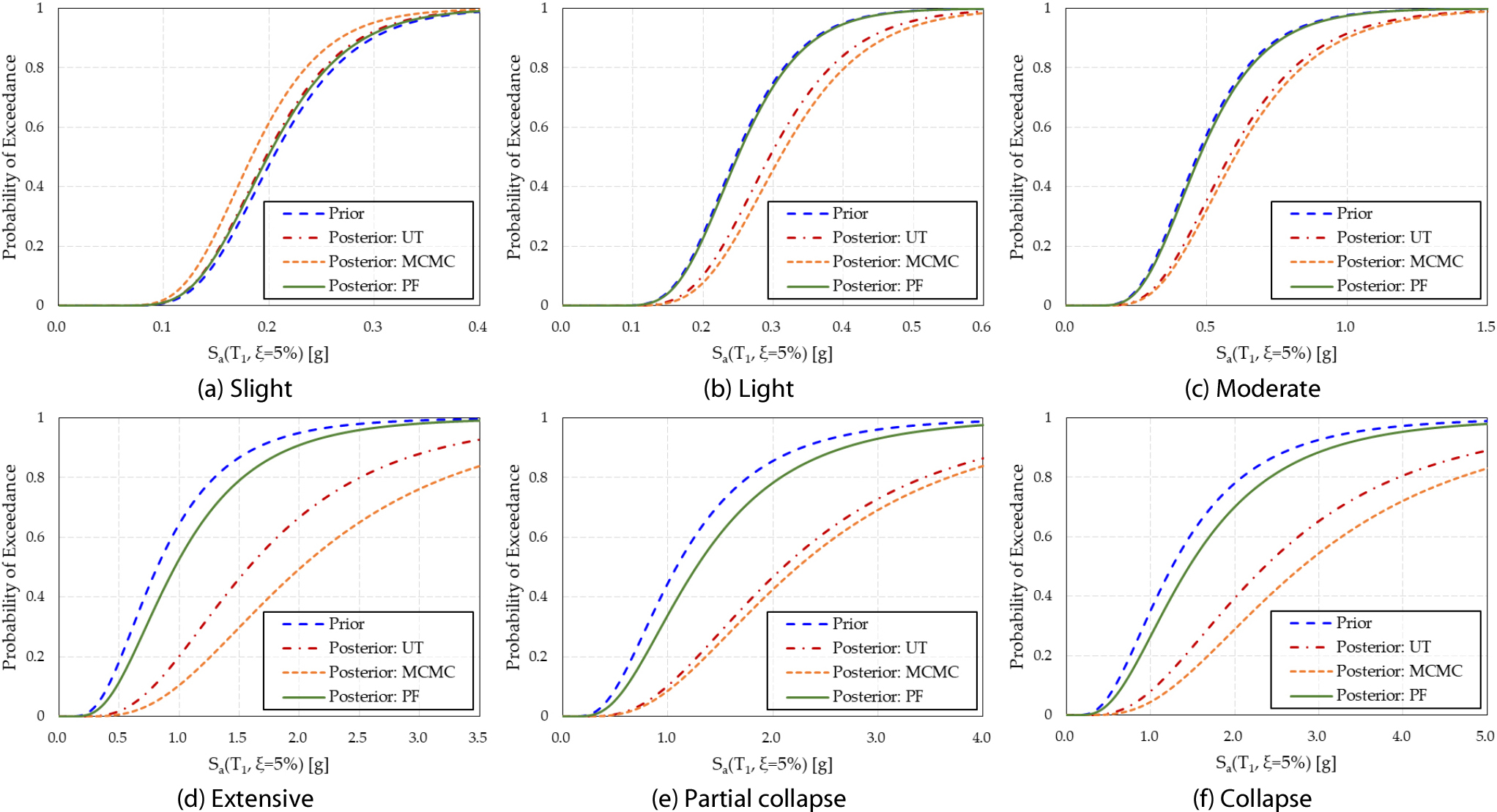
Homogenized Reinforced Concrete(HRC) 손상 상태는, 미세한(Slight), 경미한(Light), 보통의(Moderate), 광범위한(Extensive), 부분 붕괴(Partial collapse), 완전 붕괴(Collapse), 6가지 손상 상태를 고려하여 철근 콘크리트(RC) 골조 실험체의 평균 층간 변위율을 제공한다(Rossetto and Elnashai, 2003). 본 4.2절에서는 사전 정보에 해당하는 해석적 지진취약도 곡선을 3가지 베이지안 업데이트 기법(UT, MCMC, PF)을 통해 갱신하였다. 베이지안 업데이트 과정에서 우도 함수는 Table 4에 제시된 초과 기준과 같이 구성되었으며, 진동대 실험 각 단계에서 기록된 최대 층간 변위를 HRC 손상 상태 변위 기준과 비교하여 구성되었다.

Table 4

Exceedance parameter, 𝜀, for the HRC damage states (Tekeste, 2021, Table A-3)

Stages	PGA (g)	S_a(T₁) (g)	ISD_max (mm)	Inter-story drift(ISD) for HRC damage states
				Slight	Light	Moderate	Extensive	Partial collapse	Collapse
				7.4 (mm)	9.9 (mm)	23.5 (mm)	55.4 (mm)	98.2 (mm)	130.6 (mm)
1	0.10	0.29	7.89	1	0	0	0	0	0
2	0.20	0.58	15.46	1	1	0	0	0	0
3	0.32	0.93	27.32	1	1	1	0	0	0
4	0.52	1.51	42.45	1	1	1	0	0	0
5	0.72	2.10	48.32	1	1	1	0	0	0

Table 5와 Fig. 4를 통해 UT, MCMC, PF 기법에 따른 HRC 손상 상태 취약성에 대한 비교 결과를 제시하였다. 앞서 HAZUS 손상 상태에서 언급한 바와 달리, 미세한(Slight) 손상을 제외한 경미한(Light), 보통의(Moderate), 광범위한(Extensive), 부분 붕괴(Partial collapse), 완전 붕괴(Collapse), 5가지 손상에 대해서 MCMC는 UT에 비해 덜 보수적인 지진취약도 곡선을 산출하였다. PF의 경우, UT, MCMC 대비 사전 분포와 유사하고, 미세한(Slight) 손상을 제외한 나머지 손상에 대해서 보수적인 지진취약도 곡선을 산출하였다(Fig. 4). Fig. 4(a)와 같이, 미세한(Slight) 손상에서는 수치 해석을 통해 도출된 해석적 지진취약도 곡선이 3가지 베이지안 업데이트에 따른 지진취약도 곡선 대비 가장 보수적인 것으로 확인되는데, 이는 실제 진동대 실험 결과 반영에 따라 HRC의 미세한(Slight) 손상 상태에 도달하는 데 필요한 사전 해석적 지진취약도로 예측한 IM의 감소로 인한 것으로 분석되었다. 미세한(Slight) 손상을 제외한 5가지 손상 상태에 대해서 3가지 베이지안 업데이트에 따른 중앙값( $θ_{1}''$ ) 추정치는 PF, UT, MCMC 순으로 대상 구조물의 성능을 보수적으로 평가하는 것으로 분석되었다. 이는 HAZUS 손상 상태에서 밝힌 결과와는 달리, MCMC에 따른 지진취약도 곡선이 가장 보수적인 것으로 도출된 결과인데, HRC의 경우도, 우도 함수 분포의 불확실성이 사전 분포의 불확실성보다 더 큰 값을 가짐에도 불구하고, MCMC의 단순한 반복적 샘플링에 대한 위험성으로 인해 나타난 결과로 분석할 수 있다. 이에 반해, PF의 경우 가중치 개선에 따른 재추출 효과로 인해, 우도 함수 분포 대비 낮은 불확실성을 갖는 사전 분포의 특성을 보다 잘 반영하도록 업데이트된 결과로 확인할 수 있다. PF와 MCMC의 중앙값( $θ_{1}''$ )의 불확실성 지표인 표준편차( $σ_{θ_{1}''}$ )를 비교해 보면 모든 경우에 대해 PF의 표준편차( $σ_{θ_{1}''}$ )가 작게 나타난 것을 확인할 수 있다(Table 5).

Table 5

Posterior point estimates of HRC damage states: UT vs MCMC vs PF

Bayesian probability model			HRC damage states
Bayesian probability model			Slight	Light	Moderate	Extensive	Partial collapse	Collapse
Prior parameters		$θ_{1}'$ (g)	0.204	0.246	0.465	0.818	1.083	1.258
Prior parameters		$θ_{2}'$	0.297	0.294	0.382	0.544	0.578	0.601
Posterior parameters	UT	$θ_{1}''$ (g)	0.197	0.295	0.580	1.581	2.099	2.360
	UT	$θ_{2}''$	0.295	0.306	0.396	0.546	0.585	0.612
	MCMC	$θ_{1}''$ (g)	0.183	0.310	0.600	2.017	2.235	2.805
		$σ_{θ_{1}''}$	0.041	0.065	0.152	0.725	0.870	1.197
		$θ_{2}''$	0.294	0.308	0.397	0.558	0.588	0.606
		$σ_{θ_{2}''}$	0.063	0.066	0.084	0.118	0.125	0.129
	PF	$θ_{1}''$ (g)	0.199	0.249	0.474	0.965	1.272	1.459
		$σ_{θ_{1}''}$	0.037	0.046	0.111	0.305	0.431	0.519
		$θ_{2}''$	0.298	0.293	0.381	0.547	0.580	0.602
		$σ_{θ_{2}''}$	0.062	0.062	0.080	0.112	0.122	0.126

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-01/N0040380106/images/Figure_jcoseik_38_01_06_F4.jpg

Fig. 4.

Seismic fragility curve for HRC damage states

4.3 Strain-based 손상 상태

본 절에서는 HAZUS 및 HRC 손상 상태와 더불어 육안으로 관찰할 수 있는 균열(Cracking), 박리(Spalling), 압축파괴(Crushing), 3가지 손상 상태에 대한 지진취약도 곡선을 업데이트한 결과를 수록한다. 먼저, Table 6와 같이 변형률 기반(Strain-based) 손상 상태의 초과 기준은 진동대 실험 중 손상을 육안으로 검사하여 최종적으로 결정하였다. 이는, HAZUS나 HRC처럼 손상 상태에 따른 지진 강도를 평가하는 방식이 아닌, 층간 변위에 따른 누적 변형율을 기준으로 지진취약도를 평가한 방식이다.

Table 6

Exceedance parameter, 𝜀, for Strain-based damage states (Tekeste, 2021, Table 6-7)

Test stages	PGA (g)	S_a(T₁) (g)	ISD_max (mm)	Visual inspection for Strain-based damage states
				Cracking	Spalling	Crushing
				Strain in the concrete cover exceeding +0.01%	Compressive (negative) strains larger than -0.2%	Strain in the concrete core above 0.6%
1	0.10	0.29	7.89	0	0	0
2	0.20	0.58	15.46	1	0	0
3	0.32	0.93	27.32	1	0	0
4	0.52	1.51	42.45	1	1	0
5	0.72	2.10	48.32	1	1	1

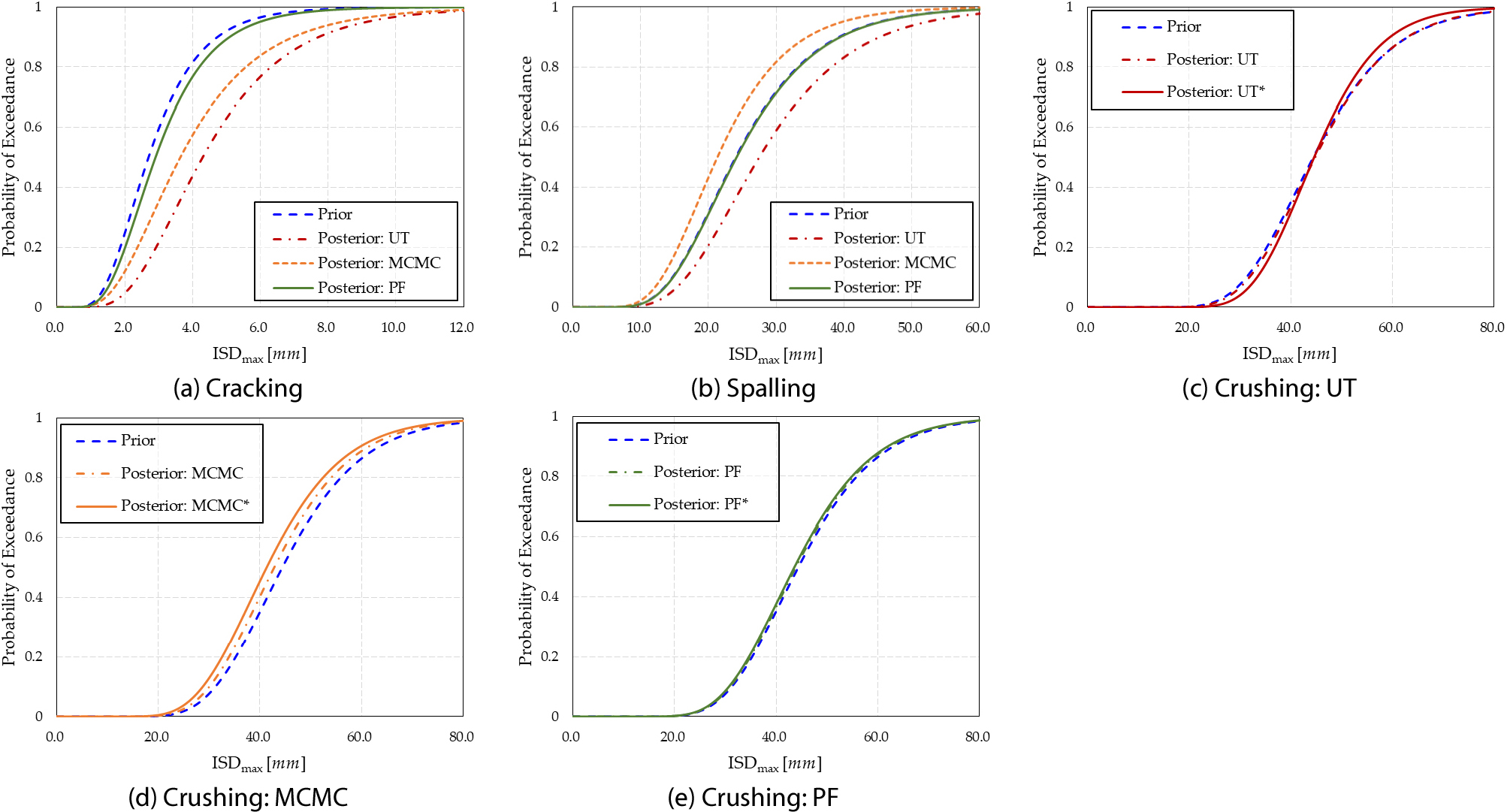
Table 7과 Fig. 5를 통해 UT, MCMC, PF 기법에 따른 Strain-based 손상 상태의 지진취약도를 비교하였다. Fig. 5(a)에서는 IDA로 계산된 해석적 지진취약도 곡선보다, 3가지 베이지안 업데이트 기법을 사용한 지진취약도 곡선이 보수적으로 산정된 것을 확인할 수 있다. 이는 진동대 실험을 통해 균열(Cracking)이 발생한 층간 변위 값이 증가했으며, 이를 우도 함수로 반영한 결과로 분석된다. 반면, 콘크리트 박리(Spalling)의 경우, MCMC를 적용한 결과 층간 변위 값이 감소하는 경향을 보였는데(Fig. 5(b)), PF와 MCMC의 중앙값( $θ_{1}''$ )의 표준편차( $σ_{θ_{1}''}$ )를 비교했을 때, 각각 5.171, 5.144로 유사한 값을 보였다. 이는 박리(Spalling) 손상에 대한 지진취약도 곡선이 향후 신뢰성 있는 추가 실험 데이터를 바탕으로 추가 분석될 필요가 있음을 시사한다. 한편, 압축파괴(Crushing) 손상의 경우, IDA에 따른 해석적 지진취약도 신뢰성이 상대적으로 떨어진다. 이는 심각한 손상 상태에 도달할 때까지 충분한 지진 가속도 데이터를 확보하기 어려운 등 다양한 원인에 기인한다.

Table 7

Posterior point estimates of Strain-based damage states: UT vs MCMC vs PF

Bayesian probability model			Strain-based damage states
Bayesian probability model			Cracking	Spalling	Crushing	Crushing^*
Prior parameters		$θ_{1}'$ (mm)	2.700	24.040	44.400	44.400
Prior parameters		$θ_{2}'$	0.439	0.383	0.274	0.274
Posterior parameters	UT	$θ_{1}''$ (mm)	4.300	27.520	44.770	44.570
	UT	$θ_{2}''$	0.458	0.389	0.266	0.226
	MCMC	$θ_{1}''$ (mm)	3.640	21.340	42.810	41.320
		$σ_{θ_{1}''}$	1.199	5.171	9.225	13.015
		$θ_{2}''$	0.508	0.377	0.276	0.282
		$σ_{θ_{2}''}$	0.097	0.080	0.058	0.120
	PF	$θ_{1}''$ (mm)	2.907	24.174	43.902	43.618
		$σ_{θ_{1}''}$	0.788	5.144	7.564	9.417
		$θ_{2}''$	0.438	0.383	0.273	0.274
		$σ_{θ_{2}''}$	0.092	0.079	0.057	0.113

^*Bayesian updating considering a diffuse prior

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-01/N0040380106/images/Figure_jcoseik_38_01_06_F5.jpg

Fig. 5.

Seismic fragility curve for Strain-based damage states

따라서, 압축파괴(Crushing) 손상 상태에 대한 불확실성을 넓게 반영하기 위해 사전 분포 중앙값( $θ_{1}'$ )의 표준편차( $σ_{θ_{1}'}$ )를 $θ_{2}'$ 로 설정하고, 사전 표준편차( $σ_{θ_{1}'}$ )의 변동 계수(COV)는 2배로 늘린 0.42를 적용하여 보다 넓은 분포를 고려하였다. 분석 결과, MCMC와 PF는 사전 분포를 기반으로 손상 상태를 업데이트하므로, 사전 분포에 부여된 가중치에 의해 압축파괴(Crushing)가 더 빠르게 발생한다고 예측하는 경향을 보였다(Fig. 5(d), (e)). 이는 사전 해석적 지진취약도 곡선에 비해 MCMC와 PF를 통해 도출된 결과가 보수적으로 산정되었음을 의미하며, 이는 심각한 손상 상태에서 불확실성이 큰 지진이 발생한 상황에서도 MCMC와 PF가 효과적인 업데이트 도구로 활용될 수 있음을 시사한다. 반면, UT 기법의 경우, Fig. 5(c)와 같이 중앙값을 기준으로 손상 발생 확률이 비대칭적으로 나타나며, 이는 손상 발생 예측이 복잡하고 신뢰성이 떨어질 수 있음을 의미한다. 특히, 중앙값( $θ_{1}''$ )을 기준으로 확률 분포가 상이하게 변화하는 경향을 보이며, 이는 손상 발생 예측의 불확실성을 증가시키는 요인으로 작용할 수 있다.

본 연구에서는 압축파괴(Crushing) 손상 상태의 불확실성을 고려해 넓은 분포를 가진 사전 정보를 활용한 PF와 MCMC를 적용한 결과, PF는 MCMC 대비 사전분포의 불확실성이 증가한 경우에도 일관된 결과를 도출하는 것을 확인할 수 있었다. 이는 재추출 과정을 통해 사전 정보의 특성을 보다 정확하게 반영했기 때문으로 분석된다.

5. 결 론

본 연구에서는 진동대 실험 데이터를 기반으로 기존 지진취약도 곡선을 업데이트하기 위한 파티클 필터링(Particle Filtering, PF)의 적용 타당성을 평가하였다. PF는 UT와 MCMC와 비교하여 계산 효율성과 지진 취약성 평가의 정확성 측면에서 우수한 결과를 보였다. 특히, PF는 해석적, 현장, 실험 데이터 등을 모두 반영하여 다양한 데이터 기반의 취약도 곡선 신뢰성을 높일 수 있는 유연성을 제공한다. 이를 통해 PF의 적용 가능성이 넓어지며, 다양한 상황과 데이터 환경에서 지진위험 평가의 중요한 도구로 활용될 수 있을 것으로 기대한다. 본 연구의 주요 결과는 다음 4가지로 요약할 수 있다.

1) PF는 HAZUS 손상 상태에서 기존 연구(Tekeste, 2021)에서 제시된 베이지안 업데이트 기법(UT, MCMC) 보다 더 보수적인 결과를 도출하였다. 예를 들어, 경미한(Slight) 손상 상태에서 PF의 사후 확률 중앙값( $θ_{1}''$ =0.140g)이 MCMC( $θ_{1}''$ =0.155g)와 UT( $θ_{1}''$ =0.217g)에 비해 보수적이었다. 또한 PF는 HAZUS 손상 전반에서 중앙값의 표준편차( $σ_{θ_{1}''}$ )가 MCMC 보다 낮아 불확실성이 감소되었으며, 사전 해석적 지진취약도 곡선에 더 잘 일치하는 지진취약도 곡선을 확인할 수 있었다. 이는 우도 함수 분포보다 더 좁은 분포 폭을 가진 사전 분포가 PF에 의해 더 많이 반영되도록 업데이트된 결과로 분석된다.

2) PF는 HRC 손상 상태에서도 기존 연구(Tekeste, 2021)에서 제시된 베이지안 업데이트 기법(UT, MCMC)보다 더 보수적인 결과를 도출하였다. HRC 손상 상태는 미세한(Slight), 경미한(Light), 보통의(Moderate), 광범위한(Extensive), 부분 붕괴(Partial Collapse), 완전 붕괴(Collapse) 등 6가지로 나뉘며, 실험 데이터를 바탕으로 PF는 미세한(Slight) 이상의 손상 상태에서 더 보수적인 지진취약도 곡선을 산출하였다. 부분 붕괴(Partial Collapse) 손상 상태를 예로 들면, PF의 사후 확률 중앙값( $θ_{1}''$ =1.272g)은 UT( $θ_{1}''$ =2.099g), MCMC( $θ_{1}''$ =2.235g)에 비해 더 낮고 보수적이었으며, 표준편차( $σ_{θ_{1}''}$ )가 0.431로, MCMC ( $σ_{θ_{1}''}$ =0.870)에 비해 불확실성이 적었다. 즉, PF는 사전 분포와 실험데이터 특성에 맞는 재추출 과정을 통해 불확실성을 줄이며 다양한 조건을 반영한 취약도 곡선을 도출할 수 있는 가능성을 확인하였다.

3) PF는 변형률 기반(Strain-based) 손상 상태에서도 불확실성이 증가한 상황에서 안정적이고 일관된 결과를 도출하였다. PF는 MCMC에 비해 사전 분포의 불확실성이 증가한 경우에도 사전 해석적 지진취약도 곡선과 유사한 결과를 도출하였으며, 특히, 압축파괴(Crushing) 손상에 대해서 안정적인 지진취약도 곡선을 도출하였다. PF와 MCMC 모두 넓은 사전 분포에 따른 손상 상태에서 보수적인 결과를 도출했으나, PF는 재추출 과정을 통해 불확실성이 증가한 상황에서도 일관된 결과를 유지하는 경향을 보였다. 반면, UT는 중앙값을 기준으로 한 손상 발생 확률의 비대칭성이 넓은 사전 분포로 갈수록 커지는 경향을 보이므로 불확실성을 더욱 크게 반영하는 경향이 있었다.

4) PF는 다양한 손상 상태에서 기존 기법보다 보수적이고 안정적인 결과를 도출하였다. 지진취약도 곡선의 참값은 엄밀히 말해 존재하지 않으나, 본 연구에서는 PF를 활용하여 좁은 폭의 사후 분포를 도출하며 실험 데이터를 통해 불확실성을 감소시키고 사전 분포를 효율적으로 반영하는 결과를 제시하였다. 이는 PF가 UT 및 MCMC 대비 계산 효율성과 데이터 활용 측면에서 강점을 가지는 기법임을 확인한 것으로, 다양한 데이터와 조건에서의 적용 가능성을 입증한다.

본 연구에서 제안한 PF 기반 베이지안 업데이트 기법은 향후 지진공학 분야에서 실험 데이터를 효과적으로 활용하여 구조물의 내진 성능을 보다 정확하게 평가하는 데 기여할 수 있을 것으로 기대한다. 다만, 제한된 실험 데이터를 보완하기 위해 추가적인 연구가 필요하다. 특히, 다양한 구조물에 대한 적용 가능성을 검토하기 위해 신뢰성 있는 해석, 현장, 실험 데이터 등의 확보와 활용이 중요할 것으로 판단된다. 실험 데이터를 활용한 PF를 통해 기존 해석적 지진취약도 곡선을 갱신하는 방법론의 효용성을 입증하였다. 단일 실험 데이터의 결정론적 한계를 확률론적 모델링으로 보완하고, 실험체의 불완전한 대표성을 인지한 채 불확실성을 반영함으로써, 신뢰성 높은 지진취약도 평가를 가능하게 하였다. 또한, 해석적 지진취약도와 실험 손상 상태 간의 구체적인 차이에 대한 추가 분석이 이루어진다면, 지진취약도 평가의 신뢰도를 더욱 높일 수 있을 것으로 기대한다.

Acknowledgements

본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호 RS-2021-KA163162).

References

Ang, A., Tang, W. (2007) Probability Concepts in Engineering: Emphasis on Applications in Civil and Environmental Engineering, 2^nd ed.; Wiley: Hoboken, NJ, USA, pp.346~365.

Baker J.W., Bradley, B.A., Stafford, P.J. (2021) Seismic Hazard and Risk Analysis, Cambridge University Press, p.578.

10.1017/9781108425056

Box, G., Tiao, G. (1992) Bayesian Inference in Statistical Analysis, John Wiley & Sons, New York.

Brooks, S., Gelman, A., Jones, G., Meng X.-L. (2011) Handbook of Markov Chain Monte Carlo, Chapman and Hall/CRC Taylor and Francis Group, New York.

10.1201/b10905

D'Ayala, D., Meslem, A., Vamvatsikos, D., Porter, K., Rossetto, T., Silva, V. (2015) Guidelines for Analytical Vulnerability Assessment of Low/Mid-Rise Buildings, GEM Technical Report, 2014-12 v1.0.0.

Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A., Rubin, D.B. (2013) Bayesian Data Analysis, 3rd edn. Taylor and Francis Group (ed.). CRC Press, New York.

10.1201/b16018

Jaiswal, K.S., Aspinall, W., Perkins, D., Wald, D.J., Porter, K.A. (2012) Use of Expert Judgment Elicitation to Estimate Seismic Vulnerability of Selected Building Types, In: 15th World Conference on Earthquake Engineering, Lisbon, Portugal.

Julier, S., Uhlmann, J. (2000) A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators, IEEE Trans Autom Control, 45(3), pp.477~482.

10.1109/9.847726

Jung, D., Lee, J., Baek, C., An, D., Yang, S. (2024) Predicting Concrete Pavement Condition for Sustainable Management: Unveiling the Development of Distresses through Machine Learning, Sustain., 16(2), p.573.

10.3390/su16020573

Kappos, A.J. (2016) An Overview of the Development of the Hybrid Method for Seismic Vulnerability Assessment of Buildings, Struct. Infrastruct. Eng., 12(12), pp.1573~1584.

10.1080/15732479.2016.1151448

Koutsourelakis, P.S. (2010) Assessing Structural Vulnerability Against Earthquakes using Multi-Dimensional Fragility Surfaces: A Bayesian Framework, Probab. Eng. Mech., 25(1), pp.49~60.

10.1016/j.probengmech.2009.05.005

Lallemant, D., Kiremidjian, A., Burton, H. (2015) Statistical Procedures for Developing Earthquake Damage Fragility Curves, Earthq. Eng. Struct. Dynam., 44(9), pp.1373~1389.

10.1002/eqe.2522

Lee, J.-H., Jung, D.-H., Lee, M.-S., Jeon, S.-I. (2022) A Feasibility Study for the Prediction of Concrete Pavement Condition Index (CPCI) Based on Machine Learning, Appl. Sci., 12, p.8731.

10.3390/app12178731

Lee, S., Yi, W., Kim, H. (2014) Seismic Fragility Functions for Steel Moment Resisting Frames using Incremental Dynamic Analyses, J. Comput. Struct. Eng. Inst. Korea, 27(6), pp.149~ 158.

10.7734/COSEIK.2014.27.6.509

Lee, S.-H., Kim, M., Yi, S.-R. (2024) Comparison of the Applicability of Bayesian Filters for System Identification of Sudden Structural Damage, J. Comput. Struct. Eng. Inst. Korea, 27(6), pp.149~158.

Li, J., Spencer, B.F., Elnashai, A.S. (2013) Bayesian Updating of Fragility Functions using Hybrid Simulation, J. Struct. Eng., 139(7), pp.1160~1171.

10.1061/(ASCE)ST.1943-541X.0000685

Mander, J.B., Prestley, J.N., Park, R. (1989) Theoretical Stress- Srain Model for Confined Concrete, J. Struct. Eng., 114(8), pp.1804~1826.

10.1061/(ASCE)0733-9445(1988)114:8(1804)

Menegotto, M., Pinto, P. (1973) Method of Analysis of Cyclically Loaded RC Plane Frames Including Changes in Geometry and Nonelastic behavior of Elements under Normal Force and Bending, Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, Int. Assoc. Bridge & Struct. Eng., Zurich, Switzerland.

Park, S., Cho, J.-R., Cho, C.-B., Kim, D.-C., Lee, J. (2023) Seismic Fragility Analysis of Single-Degree-of-Freedom Model Based on Input Earthquake Ground Motions in Strong and Low-to-Moderate Seismic Regions, J. Comput. Struct. Eng. Inst. Korea, 36(6), pp.371~380.

10.7734/COSEIK.2023.36.6.371

Porter, K., Kennedy, R., Bachman, R. (2006) Developing Fragility Functions for Building Components for ATC-58, Applied Technology Council, Redwood City, California, USA.

Porter, K., Kennedy, R., Bachman, R. (2007) Creating Fragility Functions for Performance-based Earthquake Engineering, Earthq. Spectra, 23(2), pp.471~489.

10.1193/1.2720892

Rossetto, T., Elnashai, A. (2003) Derivation of Vulnerability Functions for European-type RC Structures based on Observational Data, Eng. Struct. 25(10), pp.1241~1263.

10.1016/S0141-0296(03)00060-9

Rossetto, T., Ioannou, I., Grant, D.N. (2015) Existing Empirical Fragility and Vulnerability Relationships: Compendium and Guide for Selection, Vulnerability Global Component Project. GEM Technical Report, 2015-01 v1.0.0.

Shinozuka, M., Feng, M.Q., Lee, J., Naganuma, T. (2000) Statistical Analysis of Fragility Curves, J. Eng. Mech., 126(12), pp.24~31.

10.1061/(ASCE)0733-9399(2000)126:12(1224)

Simon, D. (2006) Optimal State Estimation: Kalman, H-Infinity, and Nonlinear Approaches, John Willey & Sons: Hoboken, NJ, USA, pp.461~483.

10.1002/0470045345

Singhal, A., Kiremidjian, A. (1998) Bayesian Updating of Fragilities with Application to RC Frames, J. Struct. Eng., 124(8), pp.922~929.

10.1061/(ASCE)0733-9445(1998)124:8(922)

Tekeste, G.G. (2021) Real-Time Hybrid Simulation including a Shaking Table - Development and Application to Soil-Structure Interaction, Ph.D. thesis, University of Aveiro (UA), Portugal.

Tekeste, G.G., Correia, A.A, Costa, A.G. (2022) Bayesian Updating of Seismic Fragility Curves through Experimental Tests, Bull. Earthq. Eng., 2023(21), pp.1943~1976.

10.1007/s10518-022-01589-4

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Feasibility Analysis of Applying Particle Filtering for Data-based Updating of Existing Seismic Fragility

ABSTRACT

MAIN

Fig. 1.

2D RC frame (Tekeste, 2021)

(1)

Table 1

Coordinates of sigma points in UT (Tekeste, 2021)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

Fig. 2.

Schematic algorithm of Particle Filtering (PF)

Table 2

Exceedance parameter, 𝜀, for the HAZUS damage states (Tekeste, 2021, Table 6-5)

Table 3

Posterior point estimates of HAZUS damage states: UT vs MCMC vs PF

Fig. 3.

Seismic fragility curve for HAZUS damage states

Table 4

Exceedance parameter, 𝜀, for the HRC damage states (Tekeste, 2021, Table A-3)

Table 5

Posterior point estimates of HRC damage states: UT vs MCMC vs PF

Fig. 4.

Seismic fragility curve for HRC damage states

Table 6

Exceedance parameter, 𝜀, for Strain-based damage states (Tekeste, 2021, Table 6-7)

Table 7

Posterior point estimates of Strain-based damage states: UT vs MCMC vs PF

Fig. 5.

Seismic fragility curve for Strain-based damage states

Acknowledgements

References