Improvement of the Phase Section Method for Multi-material Topology Optimization

Min-sung Kang; Cheolwoong Kim; Jeonghoon Yoo

doi:10.7734/COSEIK.2022.35.2.65

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 April 2022. 65-71
https://doi.org/10.7734/COSEIK.2022.35.2.65

Improvement of the Phase Section Method for Multi-material Topology Optimization

다중 물질 위상최적설계를 위한 페이즈섹션 설계법 개선

Min-sung Kang¹

Cheolwoong Kim²

Jeonghoon Yoo³^*

강 민성¹

김 철웅²

유 정훈³^*

¹Graduate Student, Graduate School of Mechanical Engineering, Yonsei University, Seoul, 03722, Korea

²Graduate Student, Graduate School of Mechanical Engineering, Yonsei University, Seoul, 03722, Korea

³Professor, Department of Mechanical Engineering, Yonsei University, Seoul, 03722, Korea

¹연세대학교 대학원 기계공학과 석사과정

²연세대학교 대학원 기계공학과 박사과정

³연세대학교 기계공학부 교수

^{*Corresponding Author}

ABSTRACT

Recently, multi-material structural topology optimization is more critical because it provides reasonable solution to weight reduction challenges and can as well provide effective conceptual design. For conventional multi-material topology optimization (MMTO), the number of design variable increases when the number of candidate materials increases, and accordingly, a significant increase in computational time occurs. Therefore, MMTO with a single design variable, such as the phase section method (PSM) was proposed . This research is focused on improving the PSM, considering three major limitations: the composition ratio does not represent the area or volume ratio, design variables are not sufficiently concentrated to target values, and certain materials are created less than they are required. To address such limitations, the redefined composition ratio and adjusted parameters for better convergence are proposed. The validation of proposed modifications is verified via two- and three-dimensional numerical examples.

Keywords

topology optimization

multi-material

phase section method

single variable

composition ratio

최근에는 경량화 문제에 대한 합리적인 솔루션을 제공하고 유용한 개념설계를 제공할 수 있는 다중 재료 구조 위상최적화가 더욱 중요해지고 있다. 기존의 MMTO(Multi-Material Topology Optimization)의 경우 후보 물질의 수가 증가할수록 설계변수의 수도 증가하고, 결과적으로 계산 시간이 크게 증가한다. 따라서 PSM(Phase Section Method)과 같은 단일 설계변수를 갖는 MMTO가 제안되었다. 본 연구는 조성비가 면적이나 부피비를 나타내지 못하고, 설계변수가 목표치에 충분히 집중되지 않고, 특정 재료가 요구량보다 적게 생성되는 PSM의 세 가지 주요 제한점을 고려하여 이를 개선하는데 중점을 둔다. 이러한 한계를 극복하기 위해 재정의된 조성비와 더 나은 수렴을 위한 조정된 매개변수를 제안한다. 제안된 수정 사항의 유효성을 2차원 및 3차원 수치 예제를 통해 검증한다.

키워드

위상최적설계

다중 물질

페이즈 섹션 방법

단일변수

조성비

MAIN

1. 서 론
2. 페이즈섹션 설계법
2.1 설계변수의 정의
2.2 정식화
2.3 물성치 정의
2.4 설계변수 최신화
3. 기존 PSM의 한계점 및 개선사항
3.1 기존 방법의 한계점
3.2 개선사항
4. 수치예제 결과
4.1 2차원 수치예제 결과
4.2 3차원 수치예제 결과
5. 결 론

1. 서 론

구조물에서의 위상최적설계는 설계영역 내에 물질을 적절히 배치하여 목적함수를 최소화하고 제한조건을 만족하는 설계방법으로써 구체적인 초기 설계가 필요하지 않고 구조 내부에 새로운 공간의 생성이 가능하여 설계 자유도가 높다. 위상최적화의 방법으로는 균질화 설계법(homogenization design method), SIMP(Solid isotropic material with penalization) 기반의 밀도법, 레벨셋 방법(level set method), 페이즈필드 설계법(phase field design method) 등이 사용되고 있다.

균질화 설계법은 복합재로 구성된 물질의 대표 물성치를 계산하는 방법을 위상최적설계에 적용한 것이다(Bendsøe and Kikuchi, 1988). 균질화 설계법은 다중 스케일의 구조를 설계할 수 있으나, 상당한 계산량을 요구하여 확장성에 한계가 있다. 이에 따라, SIMP 기반의 밀도법이 제시되었다(Sigmund, 2001). 이는 요소의 밀도에 따라 영률(Young’s modulus)과 같은 물성치를 보간하는 방법으로 균질화법에 비해 간단하여 적용이 용이하다. 레벨셋 설계법은 해밀턴-자코비(Hamilton-Jacobi) 방정식에 의해 물질 간 영역을 분리하는 경계를 형성하나, 물질 영역 내부에서의 위상변화는 불가능하다. 이를 보완하기 위해 확산-반응 방정식 기반의 페이즈필드 설계법이 제시되었다(Choi et al., 2011; Go et al., 2018). 이 방법에서는 물질을 구분하기 위해 영역의 개념을 사용하며 double well potential (DWP)을 적용하여 형상의 변화를 구조물의 경계에 한정시킬 수 있다(Takezawa et al., 2010).

최근에는 이러한 위상최적화 방법에 기반하여 다중물질 위상최적설계(multi-material topology optimization, MMTO)를 위한 연구가 구조물의 경량화 등을 목적으로 활발히 진행되고 있다. 일반적인 MMTO는 N개의 후보 물질로 설계하기 위해 N-1개의 설계변수가 필요하다(Bendsøe and Sigmund, 1999). 그러나 후보 물질 개수에 따라 설계변수의 개수가 증가하여 계산 시간이 지대하게 증가한다는 문제가 있으며 수렴성도 나빠진다.

설계변수 개수 증가에 따른 계산 시간 문제를 개선하기 위해 단일변수를 기반으로 하는 MMTO 방법들이 제시되고 있다. 먼저, SIMP 기반 보간법을 활용한 단일변수 MMTO 설계법은 연속적이고 단조 증가하는 다수의 보간 함수들로 하나의 설계변수를 표현하여 MMTO를 구현한다(Zuo and Saitou, 2017). 하지만 각 보간 함수가 연결되는 지점에서 기울기가 불연속으로 민감도 계산에 어려움이 있다.

이를 극복하기 위해 페이즈필드 설계법을 기반으로 하는 페이즈섹션 설계법(phase section method, PSM)이 제시되었다(Seong et al., 2019). 이 방법은 단조 증가이며 기울기가 연속적인 값을 갖는 SIMP 기반의 보간법을 사용한다. 이를 위하여 설계변수가 대상이 되는 물질을 나타내는 기준값에 수렴하도록 두 개의 추가적인 함수를 사용한다. 그러나 기존의 PSM은 중간물질 영역이 많이 생성되고, 특정 물질의 영역이 설계의 요구 조건에 비하여 적게 생성되는 현상이 있다.

본 연구에서는 이러한 현상을 분석하고 개선하여 더욱 신뢰도 높은 결과를 도출하였다. 물질의 조성비 함수 재정의와 시간 독립적인 함수를 사용 및 파라미터 수정을 수행했으며, 제시한 방법을 검증하기 위해 2차원 및 3차원 half-MBB beam의 컴플라이언스(compliance) 최소화 수치예제를 수행하였다. 본 연구에서는 상용패키지인 COMSOL® 5.5와 MATLAB®을 사용하여 모델 해석과 최적화를 수행하였다.

2. 페이즈섹션 설계법

2.1 설계변수의 정의

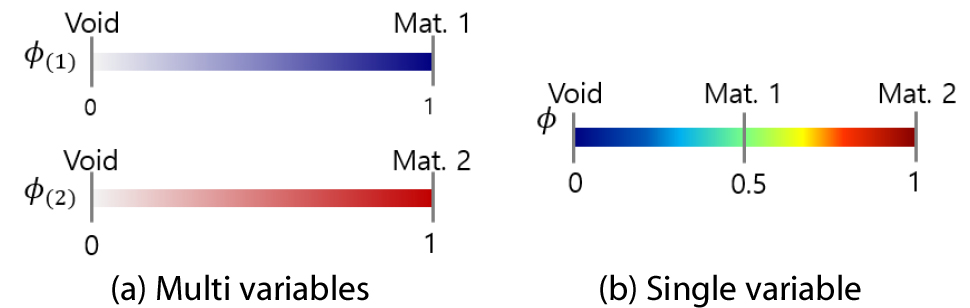
일반적인 MMTO의 경우, 후보 물질 개수에 상응하는 설계변수 개수가 필요하다. Fig. 1(a)에서 0과 1사이의 연속적인 값을 갖는 설계변수 $ϕ_{(1)}$ 과 $ϕ_{(2)}$ 는, 1인 경우 각각 물질 1과 물질 2를 나타내며, 둘 다 0인 경우 공간(void)을 나타내어 세 개의 물질의 상(phase)을 표현한다. 설계변수 개수가 증가하면 계산 시간이 증가하므로, PSM에서는 Fig. 1(b)와 같이 단일변수 $ϕ$ 로 다중 물질 설계를 구현하였다. 설계변수 값이 0인 경우 공간, 0.5인 경우 물질 1, 그리고 1인 경우 물질 2를 나타낸다.

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F1.jpg

Fig. 1.

Two types of design variable definition of MMTO for three-phase materials

2.2 정식화

단일변수 다중물질 위상최적설계를 위한 정식화는 다음과 같이 표현된다.

(1)

\min_{ϕ} F (ϕ, u (ϕ)) = \int_{Ω_{D}} p \cdot u d Ω + \int_{Γ_{N}} t \cdot u d s s . t . a (u, v) = l (v) for u \in U, \forall v \in U G (ϕ) = V - V_{r e q} \leq 0 H (ϕ) = C_{m} (ϕ) - C_{r e q_{m}} (ϕ) = 0 where V = \int_{Ω_{D}} ϕ dx / |Ω_{D}| C_{m} = \frac{\int_{Ω_{D}} {\tilde{c}}_{m} d x}{|Ω_{D}|}, {\tilde{c}}_{m} = \exp (- \frac{(ϕ - ϕ_{m})^{2}}{2 σ^{2}}) 0 < ϕ_{\min} \leq ϕ \leq 1, m = 1, 2, . . ., N

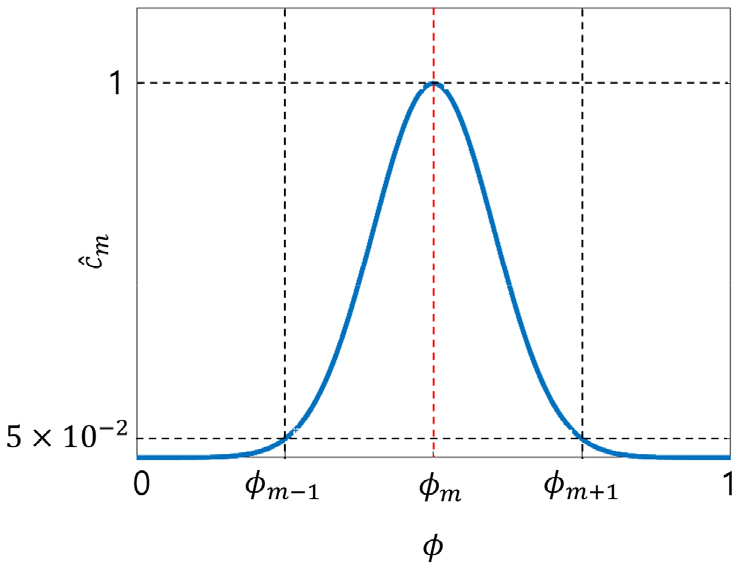
목적함수 $F$ 는 구조물의 컴플라이언스를 의미하며, $ϕ$ 와 $u$ 는 각각 설계변수와 물리해석의 상태변수를 의미한다. 제한조건 $G$ 는 생성된 물질의 총량을 제한한다. 생성된 모든 물질이 설계영역에서 차지하는 비율인 부피 비율(volume ratio) $V$ 와 부피 비율 요구조건 $V_{r e q}$ 로 표현된다. 제한조건 $H$ 는 각 물질이 생성된 정도를 나타내며 그 양을 제한하게 된다. $m$ 번째 물질이 설계영역에서 차지하는 비율인 조성비(composition ratio) $C_{m}$ 과 조성비 요구조건 $C_{r e q_{m}}$ 으로 표현된다. 조성비는 ${\tilde{c}}_{m}$ 를 설계영역에 걸쳐 적분하고 설계영역의 면적으로 나누어 계산한다. Fig. 2에 나타낸 ${\tilde{c}}_{m}$ 함수는 정규분포 함수로, $ϕ_{m}$ 에 위치한 설계변수는 1로, $ϕ_{m}$ 에서 멀어질수록 적은 값으로 평가한다. 조성비는 2차원 설계에선 면적 비율을, 3차원 설계에선 체적 비율을 의미한다. $ϕ_{m}$ 은 $m$ 번째 물질을 나타내는 설계변수 기준값으로 설계변수가 $ϕ_{m}$ 에 수렴하면 해당 물질을 나타낸다. 예를 들면 Fig. 1(b)에서 $ϕ_{m}$ 은 0, 0.5, 1이 된다. $ϕ_{m i n}$ 은 10^-5로 정의되며 구조해석 과정에서 특이점 문제를 방지하기 위한 상수이다. $n$ 은 설계하려는 후보 물질의 개수를 나타낸다(Seong et al., 2019).

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F2.jpg

Fig. 2.

${\tilde{c}}_{m}$ is a normal distribution function used to calculate the composition ratio

2.3 물성치 정의

PSM의 물성치 보간함수는 다음과 같이 정의된다.

(2)

E (ϕ) = ϕ^{p} E_{N} E_{m} = ϕ_{m}^{p} E_{N}

벌칙 계수 $p$ 는 중간영역을 억제하는 역할을 하고 일반적으로 3으로 설정한다(Sigmund, 2001). $E_{N}$ 은 후보 물질 중 가장 영률이 높은 물질의 영률이며 설계변수가 1인 경우에 해당한다. 그 이하의 경우는 설계변수 $ϕ$ 에 따라 보간된 영률을 가진다. 추가로 $E_{n}$ 은 각 후보 물질의 영률을 나타내므로 보간 함수에 따라 해당 영률을 갖는 $ϕ$ 를 각 물질을 나타내는 기준값 $ϕ_{m}$ 으로 설정한다.

2.4 설계변수 최신화

설계변수의 업데이트는 다음의 확산-반응 방정식을 기반으로 이루어진다(Seong et al., 2019).

(3)

\frac{\partial ϕ (x, t)}{\partial t} = κ \nabla^{2} ϕ - \{q_{1} χ (ϕ) + q_{2} [ψ (ϕ) + 1] \frac{\partial \bar{F}}{\partial ϕ}\} \in Ω_{D} \frac{\partial ϕ (x, t)}{\partial t} = 0 \in \partial Ω_{D} 0 < t < T

여기서, 우변 첫 번째 라플라시안(Laplacian) 항은 헬름홀츠 필터로 작용하며, $κ$ 는 확산계수로 필터의 강도를 조절한다. $χ (ϕ)$ 와 $ψ (ϕ)$ 함수는 설계변수가 각 물질로 수렴할 수 있도록 돕는 역할을 하며 다음과 같이 정의된다.

(4)

χ (ϕ) = - \sin ((N - 1) (2 π ϕ - \frac{π}{N - 1}))

(5)

ψ (ϕ) = \cos ((N - 1) (2 π ϕ - \frac{π}{N - 1})) + 1

$χ (ϕ)$ 의 경우, 각 물질을 나타내는 기준값 $ϕ_{m}$ 은 0으로 평가한다. $ϕ_{m}$ 를 초과한 경우 양수 값, 미만인 경우 음수 값을 가지며 설계변수 업데이트 시 해당 값을 $ϕ_{m}$ 으로 수렴하게 돕는다. $q_{1}$ 은 설계 파라미터로 $χ (ϕ)$ 과 결합하여 해당 기능의 강도를 결정하며 제한조건이 수렴할수록 증가하여 영향력이 증대된다. $ψ (ϕ)$ 의 경우, 각 물질을 나타내는 기준값 $ϕ_{m}$ 에서 최소값을 가지므로 해당 지점에서의 민감도를 감소시켜 설계변수가 $ϕ_{m}$ 에 수렴하도록 돕는다. $ψ (ϕ)$ 는 식 (3)에서 $ψ (ϕ)$ +1로 사용되므로 $ϕ_{m}$ 에서의 민감도는 0이 아니다. $q_{2}$ 는 설계 파라미터로 $ψ (ϕ)$ 와 결합하여 해당 기능의 강도를 결정하는데, 클수록 영향력이 증대되며 0.5로 고정된 값을 사용하였다. $\bar{F}$ 는 Augmented Lagragian 함수로 다음과 같이 나타낸다.

(6)

\bar{F} = F (ϕ, u (ϕ)) + [λ_{0} \hat{G} (ϕ) + \frac{r_{0}}{2} {\{\hat{G} (ϕ\}}^{2}] + \sum_{m = 1}^{N - 1} [λ_{m} {\hat{C}}_{m} (ϕ) + \frac{r_{m}}{2} {\{{\hat{C}}_{m} (ϕ)\}}^{2}] \hat{G} (ϕ) = \max (G (ϕ), - \frac{λ_{0}}{r_{0}}) {\hat{C}}_{m} (ϕ) = \min [0.5, \max \{- 0.5, (C_{m} - C_{r e q_{m}}) / C_{r e q_{m}}\}]

해당 항의 도함수는 식 (3)과 같은 확산-반응 방정식 기반의 설계변수 업데이트 식에서 민감도 역할을 한다. $r_{0}$ 와 $r_{ㅡ}$ 은 제한조건 $G$ 와 $H$ 에 대한 벌칙인자, $λ_{0}$ 와 $λ_{m}$ 은 Lagrange 승수이다. $C_{m}$ 은 설계변수 초기값에 따라 큰 값을 가지며 -0.5와 0.5 사이의 값을 갖도록 제한하였다.

3. 기존 PSM의 한계점 및 개선사항

3.1 기존 방법의 한계점

조성비는 각 물질의 전체 설계영역에서 차지하는 비율을 나타내며 면적 및 체적 비율로 사용될 수 있다. 따라서 모든 조성비를 합한 값이 1이 되어야 유클리드 차원 크기에 맞는 물리적 의미가 있다. 기존 PSM의 경우 조성비의 총합이 1을 크게 초과하여 면적 및 체적 비율을 온전히 나타내지 못한다. 또한, 식 (1)의 𝜎 값을 변경하면 조성비의 총합이 달라지므로 총합이 1이 되게 하도록 모델별로 적절한 𝜎값을 찾아야 하는 한계점이 있으며, 조성비 제한조건을 만족했음에도 물질이 적게 생성되는 문제도 발생한다. $C_{m}$ 번째 물질의 조성비 $C_{m}$ 계산에서는 $m$ 번째 물질만을 포함해야 하나 기존 PSM은 $m \pm 1$ 번째 물질을 Fig. 2과 같이 상대적으로 큰 5×10^-2로 평가한다. 따라서, $C_{m}$ 계산 시 $m \pm 1$ 번째 재료를 많이 포함하므로, 실제로 $m$ 번째 물질은 적게 생성되었음에도 제한조건을 만족하게 된다.

컴플라이언스 최소화 문제는 물질의 총량이 많을수록 컴플라이언스가 감소한다. 따라서 무게 비율 $V$ 가 상한값에 도달하여 제한조건이 활성화되는 것이 일반적이나 기존의 방법은 이를 만족하지 못하는 경우가 발생한다.

설계변수 𝜙는 기준값 $ϕ_{m}$ 에 수렴해야 각 물질을 잘 나타내게 된다. 기준값 $ϕ_{m}$ 에 수렴하지 못한 설계변수들은 중간물질을 나타내며, 식 (2)에 의해 후보 물질의 물성치와 다른 값을 가지는 가상의 물질이라 할 수 있으며 실제 제작에 어려움이 있다. 따라서 중간물질이 많은 경우 설계 결과를 신뢰하기 어려우며 이를 제작하기 위해서는 별도의 후처리 가공이 필요하다는 단점이 있다.

3.2 개선사항

기존의 조성비를 다음의 식 (7)과 같이 조성비의 총합으로 나누고 합계를 1.01로 유지하였다. 이를 통해 어떠한 𝜎값을 사용하더라도 조성비의 총합이 일정하게 유지되어 조성비를 면적 및 체적 비율로 사용할 수 있다. 조성비는 등가 제한조건으로 사용되므로 약간의 완화를 위해 1%의 오프셋을 설정하여 합계를 1.01로 설정하였다. 이는 제한조건 H가 등가의 조건이므로 수렴성의 확보를 위함이다.

(7)

C_{m} (ϕ) = 1.01 \frac{\int_{Ω_{D}} \exp (- \frac{(ϕ - ϕ_{m})^{2}}{2 σ^{2}}) d x}{| Ω_{D} | \sum_{m = 1}^{N - 1} C_{m}}

또한, 𝜎값은 $σ_{o r i g}$ 보다 1.5배 작은 값을 사용했다. $σ_{o r i g}$ 를 사용하면 Fig. 2와 같이 주변의 $m \pm 1$ 번째 물질을 5×10^-2로 평가한다. 반면에, $σ_{o r i g}$ /1.5을 사용하면 1.2×10^-3으로 평가하므로 m번째 물질을 더 포함하여 중간물질의 생성을 억제하게 되므로 $σ_{o r i g}$ /1.5로 조성비를 계산한다.

식 (3)에서 시간 $t$ 에 대해 차분법을 적용하고 정리하면 다음과 같이 표현된다.

(8)

\frac{ϕ' - ϕ}{∆ t} = κ \nabla^{2} ϕ - \{q_{1} χ (ϕ) + q_{2} [ψ (ϕ) + 1] \frac{\partial \bar{F}}{\partial ϕ}\}

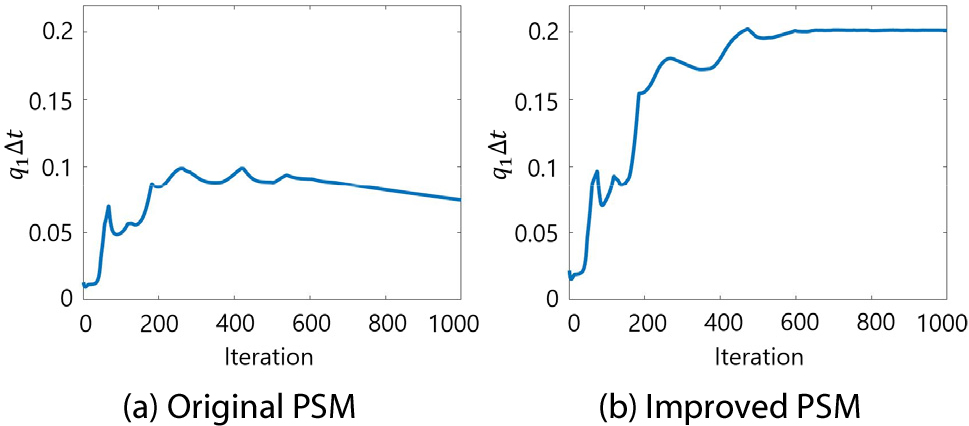
$q_{1}$ 은 조성비 제한조건이 수렴함에 따라 증가하여 $χ (ϕ)$ 의 영향력을 증대시킨다. 그러나 기존 PSM은 $∆ t$ 가 점차 감소하므로 $χ (ϕ)$ 의 영향력은 Fig. 3(a)와 같이 감소한다. 따라서 다음과 같이 $q_{1}$ 을 재정의하여 $∆ t$ 의 감소에도 $χ (ϕ)$ 의 영향력을 Fig. 3(b)와 같이 유지하도록 하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F3.jpg

Fig. 3.

$q_{1} Δ t$ change as iteration increases

(9)

q_{1}' = q_{1} \frac{Δ t_{0}}{Δ t}

4. 수치예제 결과

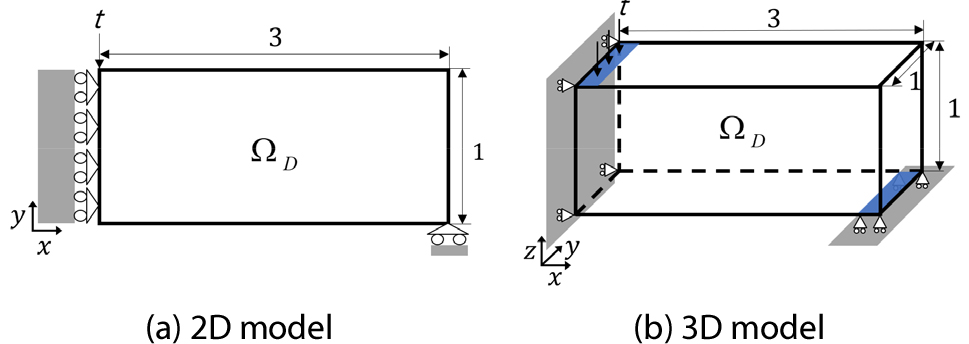
본 연구에서는 Fig. 4에 나타낸 2차원 및 3차원 half-MBB beam을 대상으로 컴플라이언스 최소화 예제를 수행하여 제안된 방법의 유용성을 검증하였다. Half-MBB beam은 좌측면에 대칭 조건이 적용되어 있으며 좌측 상단에 하중을 가하게 된다. 2차원 모델의 경우 180×60개의 정사각형 요소로 3차원 모델은 60×20×15개의 정육면체 요소로 구성된다.

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F4.jpg

Fig. 4.

Schematic design of MBB beam model

4.1 2차원 수치예제 결과

Fig. 4(a)의 2차원 half-MBB beam 컴플라이언스 최소화를 위하여 기존 PSM에서는 ${\tilde{c}}_{m}$ 함수의 𝜎는 2.043×10^-1, 확산계수 𝜘는 5.000×10^-4, 무게 비율 제한조건의 벌칙인자 $r_{0}$ 는 4.320×10^-4, 조성비 제한조건의 벌칙인자 $r_{m}$ 은 2.880×10^-4을 사용했다. 개선된 PSM에서 𝜎는 기존의 값보다 1.5배 작은 1.362×10^-1을 사용했으며 그 외의 파라미터는 같은 값을 사용하였다.

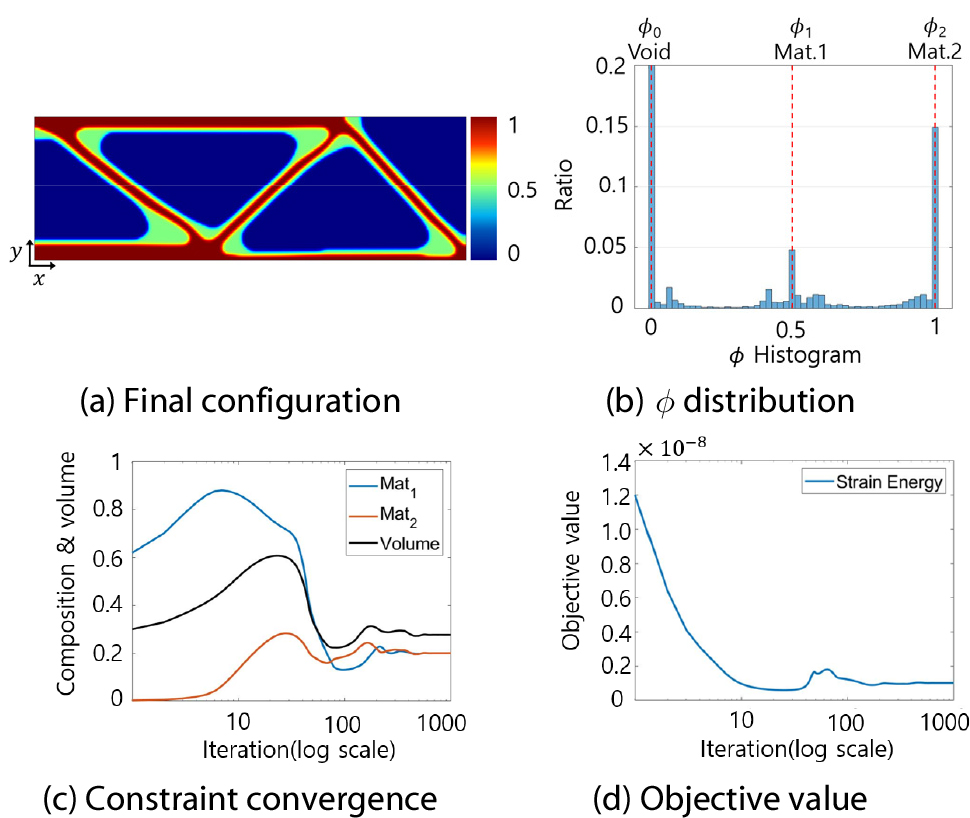
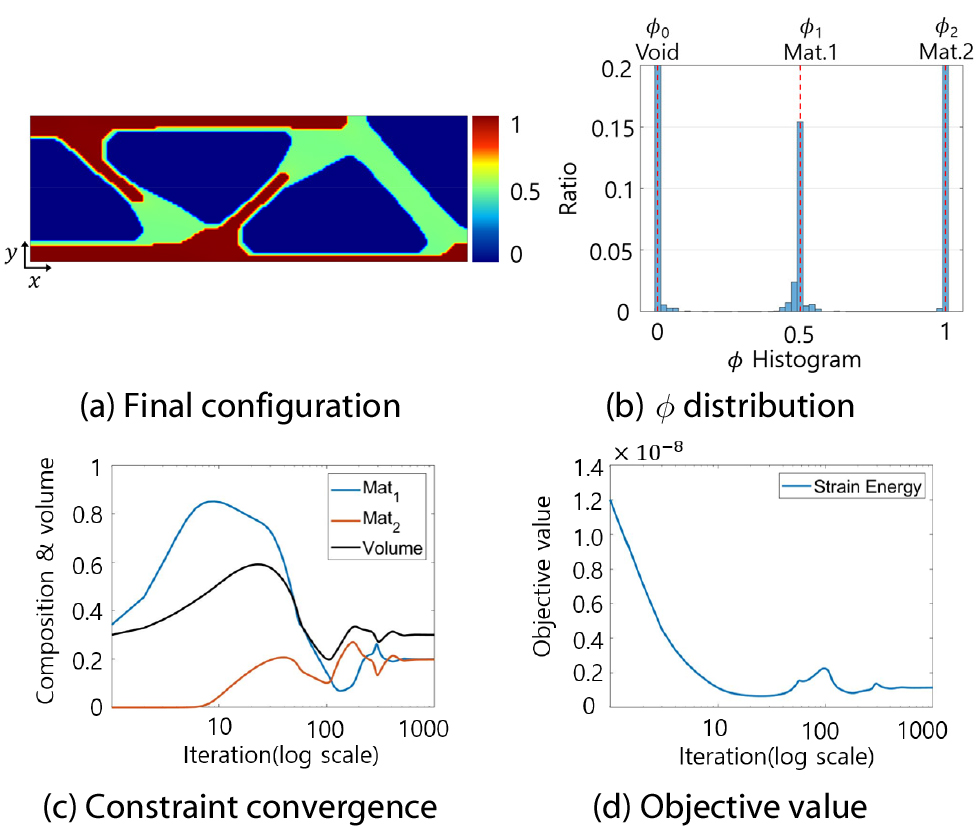
Fig. 5와 6은 기존 PSM과 개선된 PSM의 2차원 설계결과를 나타낸다. Fig. 5와 6(a)에서 파랑색은 공간, 연두색은 물질 1 그리고 붉은색은 물질 2를 나타낸다. Fig. 5(c)와 6(c)에서와 같이 두 설계법 모두 제한조건이 수렴함을 확인할 수 있으며 Fig. 5(d)와 6(d)에서 목적함수 값 또한 모두 안정적으로 수렴함을 알 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F5.jpg

Fig. 5.

2D results of the original PSM

Table 1과 2에서 표시한 바와 같이 두 설계법 모두 물질 1의 조성비 요구조건은 0.2로, 설계영역의 20%를 차지하도록 설정했으며 해당 제한조건은 수렴하였다. Table 3은 PSM 방법의 개선 전후의 비교를 보여주고 있다. 기존 PSM 경우 물질 1의 실제 면적 비율은 15.52%인 반면, 개선된 PSM은 19.76%로 요구조건인 20%에 근접하였다. 이는 Table 3에서 개선된 PSM은 물질 1의 조성비 $C_{1}$ 이 물질 1이 71.22%만 포함된 반면에 개선된 PSM은 96.61% 포함하여 더욱 정확하게 물질 1이 생성된 양을 평가하기 때문으로 판단된다. 또한, Table 1에서 기존 PSM의 조성비 합계는 1.047이고 무게 제한조건이 비활성화되지만, Table 2에서 나타낸 바와 같이 개선된 PSM은 조성비의 합계가 1.010으로 1에 근접하며 무게 제한조건이 활성화된다.

Table 1

2D result summary of the original PSM

Result
Stop iteration	512
Objective value	1.015×10^-9
Volume	$V_{r e q}$ =0.3	0.276
Composition ratio	$C_{0}$	0.647
	$C_{r e q_{1}}$ 0.2	0.200
	$C_{r e q_{2}}$ =0.2	0.200
	Sum	1.047

Table 2

2D result summary of the improved PSM

Result
Stop iteration	620
Objective value	1.138×10^-9
Volume	$V_{r e q}$ =0.3	0.300
Composition ratio	$C_{0}$	0.612
	$C_{r e q_{1}}$ =0.2	0.200
	$C_{r e q_{2}}$ =0.2	0.198
	Sum	1.010

Table 3

Comparison of 2D original and improved PSM results

Case	Actual area ratio	Material1 in $C_{1}$	Mean error	Sum of variance
Original	15.52%	71.22%	4.10%	1.09×10^-2
Improved	19.76%	96.61%	0.76%	5.13×10^-4

Fig. 5(b)와 6(b)는 각각 기존 PSM과 개선된 PSM의 설계변수 𝜙의 분포를 나타낸다. Fig. 5(b)는 기존 PSM이 기준값 $ϕ_{m}$ 에 수렴하지 못한 중간물질이 많은 것을 보여주지만, Fig. 6(b)는 개선된 PSM이 기준값 $ϕ_{m}$ 에 잘 수렴한 것을 보여주고 있다. 이를 수치적으로 비교하기 위해 각 기준값 $ϕ_{m}$ 기준으로 설계변수의 평균 및 분산을 계산했으며 Table 3에서 평균 오차는 4.10%에서 0.76%로, 분산은 1.09×10^-2에서 5.13×10^-4으로 감소하여 중간물질 생성이 많이 감소함을 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F6.jpg

Fig. 6.

2D results of the improved PSM

4.2 3차원 수치예제 결과

본 개선안의 확장성을 확인하기 위해 세 개의 물질로 Fig. 4(b)의 3차원 half-MBB beam 모델에 대해 컴플라이언스 최소화 설계를 수행하였다. 기존 PSM의 경우 2차원 수치예제와 동일한 파라미터를 사용했으며, 개선된 PSM에서는 중간물질 감소와 수렴 안정성을 위해 수정된 확산계수와 벌칙인자를 사용하였다.

식 (3)의 확산계수는 값이 적을수록 물질 간 간격이 좁혀져 중간물질이 감소한다. 그러나 동시에 형상이 복잡해져 물질 간 경계가 많아지고 중간물질이 증가하게 된다. 2차원 설계에서는 경계선으로 물질을 구분하므로 적은 확산계수 값을 사용하나, 3차원 설계의 경우 경계면으로 물질을 구분하므로 확산계수의 값을 증가시킨다. 따라서 3차원 설계에서 2차원 설계와 같이 적은 확산계수를 사용하는 것은 오히려 중간물질을 증가시킬 수 있으므로 기존의 확산계수보다 10배 큰 확산계수인 5.0×10^-3을 사용하였다.

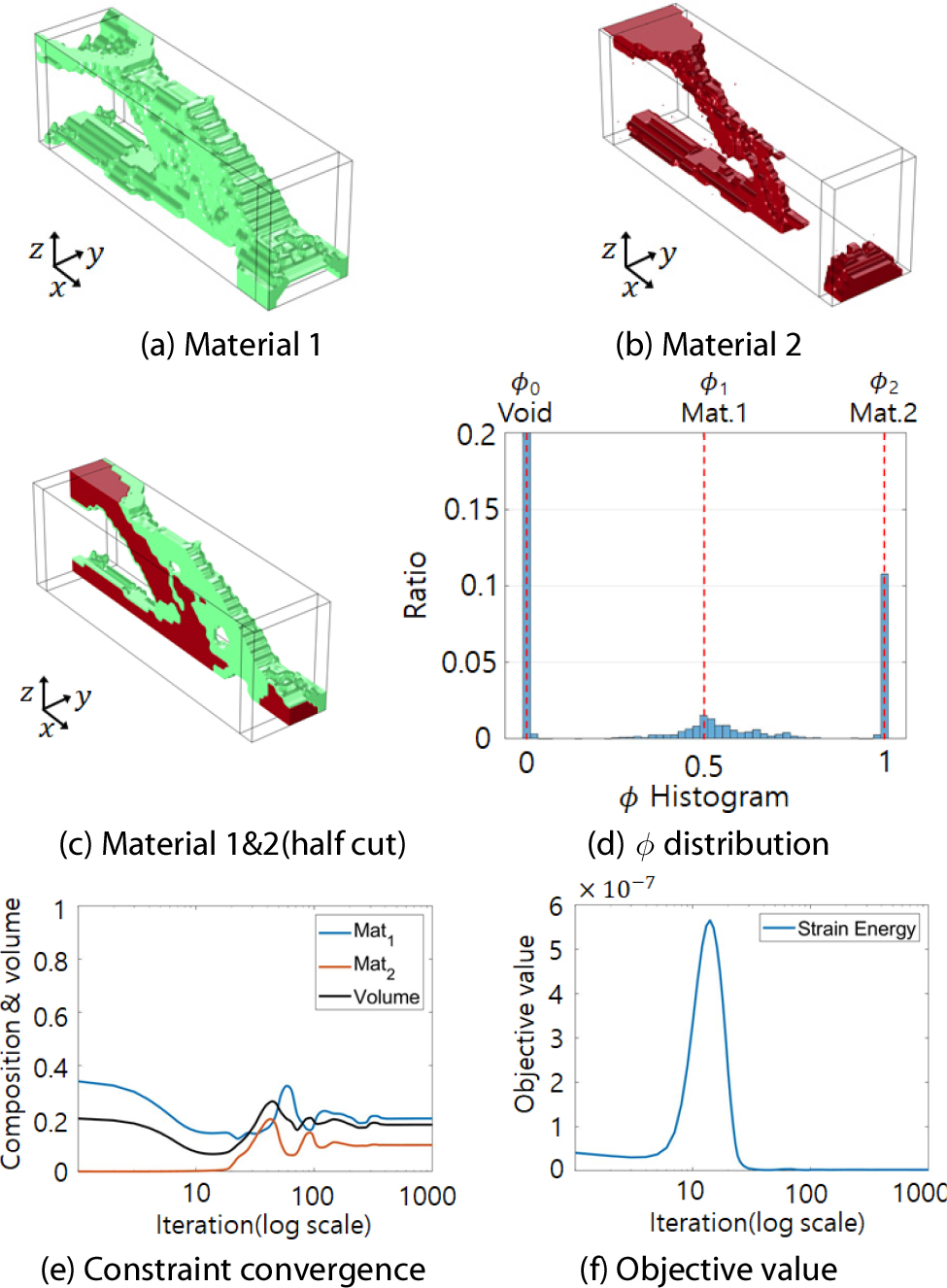
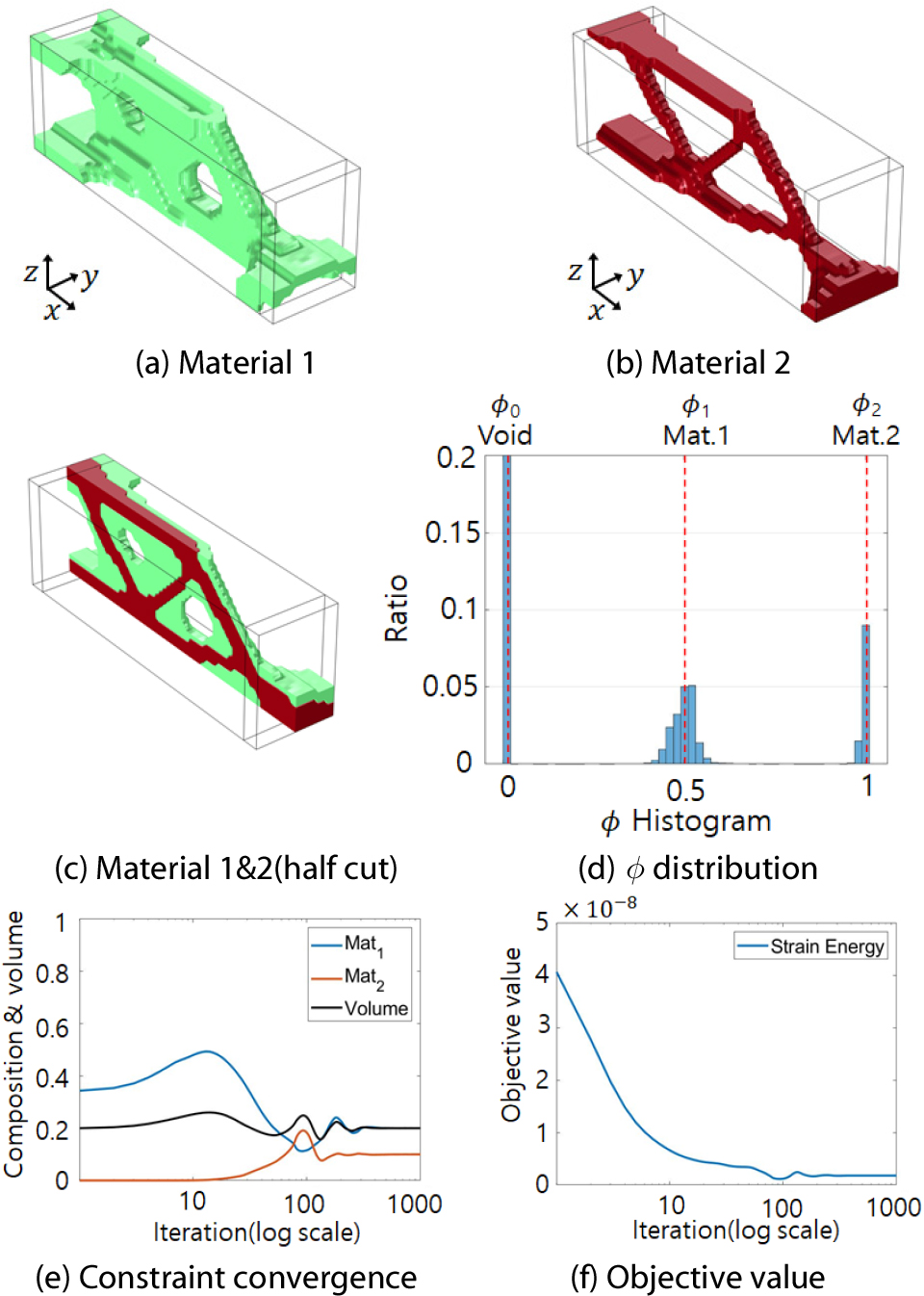
제한조건의 벌칙인자는 그 값이 클수록 빠르게 제한조건에 수렴하나, 너무 큰 경우 목적함수의 민감도 영향을 상쇄하여 설계 초기 단계에서 목적함수 값이 매우 크게 증가하여 수렴성에 어려움을 발생시킬 수 있다. 따라서 무게 비율 제한조건의 벌칙인자 $r_{0}$ 는 기존의 값보다 5배 작은 값인 8.640×10^-5, 조성비 제한조건의 벌칙인자 $r_{m}$ 은 기존의 값보다 10배 작은 값인 2.880×10^-5을 사용하였다. Fig. 7과 8은 기존 PSM과 개선된 PSM의 3차원 설계결과를 나타낸다. Fig. 7과 8(e)와 8(f)는 두 설계법 모두 제한조건이 잘 수렴하고 목적함수 값 또한 둘 다 안정적으로 수렴하는 것을 보여주고 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F7.jpg

Fig. 7.

3D results of the original PSM

https://static.apub.kr/journalsite/sites/jcoseik/2022-035-02/N0040350201/images/Figure_jcoseik_35_02_01_F8.jpg

Fig. 8.

3D results of the improved PSM

Table 4와 5에서 두 설계법 모두 물질 1의 조성비 요구조건은 0.2로 설계영역의 20%를 차지하도록 설정했으며 해당 제한조건은 둘 다 수렴하고 있다. 그러나 Table 6에서 기존 PSM은 물질 1의 실제 면적 비율이 9.88%인 반면에 개선된 PSM은 18.44%로 요구조건인 20%에 근접한다. 이는 Table 6에서 개선된 PSM은 물질 1 조성비 $C_{1}$ 이 물질 1을 49.41%만 포함하지만, 개선된 PSM은 92.28% 포함하여 보다 정확하게 물질 1이 생성된 양을 평가했기 때문이다. 또한 Table 4에 나타낸 바와 같이 기존 PSM의 조성비 합계는 1.050이고 무게 제한조건이 비활성화된 반면에, Table 5에서 표시된 개선된 PSM은 조성비의 합계가 1.010으로 1에 근접하였으며 무게 제한조건이 활성화되고 있다.

Table 4

3D result summary of the original PSM

Result
Stop iteration	424
Objective value	2.380×10^-9
Volume	$V_{r e q}$ =0.2	0.177
Composition ratio	$C_{0}$	0.750
	$C_{r e q_{1}}$ =0.2	0.200
	$C_{r e q_{2}}$ =0.1	0.100
	Sum	1.050

Table 5

3D result of improved PSM

Result
Stop iteration	467
Objective value	1.792×10^-9
Volume	$V_{r e q}$ =0.2	0.200
Composition ratio	$C_{0}$	0.710
	$C_{r e q_{1}}$ =0.2	0.200
	$C_{r e q_{2}}$ =0.1	0.100
	Sum	1.010

Table 6

Comparison of 3D original and improved PSM results

Case	Actual volume ratio	Material1 in $C_{1}$	Mean error	Sum of variance
Original	9.88%	49.41%	3.87%	1.17×10^-2
Improved	18.44%	92.28%	0.16%	7.62×10^-4

Fig. 7과 8의 (d)는 각각 기존 PSM과 개선된 PSM의 설계변수 𝜙 분포를 나타낸다. Fig. 7(d)에서 기존 PSM은 기준값 $ϕ_{m}$ 에 수렴하지 못한 중간물질이 많은 반면에 Fig. 8(d)에서 개선된 PSM은 기준값 $ϕ_{m}$ 에 수렴한 설계변수 분포를 나타낸다. Table 6에서 나타낸 바와 같이 평균 오차는 3.87%에서 0.16%, 분산은 1.17×10^-2에서 7.62×10^-4으로 감소하여 중간물질이 많이 감소함을 확인할 수 있다.

5. 결 론

기존의 페이즈섹션 설계법은 다중물질 위상최적설계를 단일변수화하여 계산 시간을 감소시킴과 동시에, 단조증가이며 기울기가 연속적인 SIMP 기반의 물성치 보간함수를 사용하여 최적설계 과정에서의 수렴성을 확보하였다. 그러나 새롭게 도입한 조성비가 면적이나 부피비를 정확히 나타내지 못하고 중간물질 많이 생성되며, 특정 물질이 요구조건이 비해 실제로는 적게 생성되는 현상이 발생한다. 본 연구에서는 앞서 언급한 현상을 개선하기 위해 조성비를 재정의하고 낮은 𝜎값을 사용하며, $χ (ϕ)$ 함수를 $∆ t$ 감소의 영향을 받지 않게 하였다. 그 결과 2차원 수치예제에서 실제 면적비는 27.3% 증가하고 중간물질 생성 척도인 평균 오차는 81.5%, 분산은 95.3% 감소하였다. 3차원 구조설계에서는 추가적으로 증가된 확산계수와 감소된 벌칙인자를 사용하였으며, 그 결과로 3차원 수치예제에서 실제 체적비는 86.6% 증가하고 중간물질 생성 척도인 평균 오차는 95.9%, 분산은 93.5% 감소하였다. 이러한 결과를 통하여 개선된 페이즈섹션 설계법이 앞서 언급한 현상들을 개선하고 우수한 결과를 나타냄을 확인할 수 있다. 향후의 연구에서는 후보 물질의 개수를 늘리고 다양한 벤치마크 수치예제를 수행하여 본 개선안의 강건성과 확장성을 확인하는 연구가 요구된다.

Acknowledgements

본 논문은 2019년도 한국연구재단의 지원(NRF-2019R1A2 B5B01069788)과 2020년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원(No.20204030200010)을 받아 수행한 연구입니다.

References

Bendsøe, M.P., Kikuchi, N. (1988) Generating Optimal Topologies in Structural Design using a Homogenization Method, Comput. Methods Appl. Mech. Eng., 71(2), pp.197~224. 10.1016/0045-7825(88)90086-2

Bendsøe, M.P., Sigmund, O. (1999) Material Interpolation Schemes in Topology Optimization, Arch, Appl. Mech., 69(9), pp.635~654. 10.1007/s004190050248

Choi, J.S., Yamada, T., Izui, K., Nishiwaki, S., Yoo, J. (2011) Topology Optimization using a Reaction-Diffusion Equation, Comput. Methods Appl. Mech. Eng., 200(29-32), pp.2407~2420. 10.1016/j.cma.2011.04.013

Go, J., Seong, H.K., Kim, H., Park, J., Yoo, J. (2018) RF Collimator Design Having Multi-Dielectric Structure Using the Phase Field Design Method, J. Comput Struct. Eng. Inst. Korea, 31(1), pp.47~52. 10.7734/COSEIK.2018.31.1.47

Seong, H.K., Kim, C.W., Yoo, J., Lee, J. (2019) Multiphase Topology Optimization with a Single Variable Using the Phase‐Field Design Method, Int. J. Numer. Methods Eng., 119(5), pp.334~360. 10.1002/nme.6052

Sigmund, O. (2001) A 99 Line Topology Optimization Code Written in Matlab, Struct. Multidisc. Optim., 21(2), pp.120~127. 10.1007/s001580050176

Takezawa, A., Nishiwaki, S., Kitamura, M. (2010) Shape and Topology Optimization based on the Phase Field Method and Sensitivity Analysis, J. Comput. Phys., 229(7), pp.2697~2718. 10.1016/j.jcp.2009.12.017

Zuo, W., Saitou, K. (2017) Multi-Material Topology Optimization using Ordered SIMP Interpolation, Struct. Multidisc. Optim., 55(2), pp.477~491.

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Improvement of the Phase Section Method for Multi-material Topology Optimization

ABSTRACT

MAIN

Fig. 1.

Two types of design variable definition of MMTO for three-phase materials

(1)

Fig. 2.

c~m is a normal distribution function used to calculate the composition ratio

(2)

(3)

(4)

(5)

(6)

(7)

(8)

Fig. 3.

q1Δt change as iteration increases

(9)

Fig. 4.

Schematic design of MBB beam model

Fig. 5.

2D results of the original PSM

Table 1

2D result summary of the original PSM

Table 2

2D result summary of the improved PSM

Table 3

Comparison of 2D original and improved PSM results

Fig. 6.

2D results of the improved PSM

Fig. 7.

3D results of the original PSM

Fig. 8.

3D results of the improved PSM

Table 4

3D result summary of the original PSM

Table 5

3D result of improved PSM

Table 6

Comparison of 3D original and improved PSM results

Acknowledgements

References

${\tilde{c}}_{m}$ is a normal distribution function used to calculate the composition ratio

$q_{1} Δ t$ change as iteration increases