1. 서 론
2. ISRS 스케일링 근사 방법: 여러 가지 접근
3. 대상 원전 건물 및 입력 지진동
4. ISRS 스케일링 근사 방법 검증
5. ISRS 스케일링 근사 방법이 지진 응답 및 성능에 미치는 영향
6. 요약 및 결론
1. 서 론
구조물내 응답스펙트럼(In-Structure Response Spectrum: ISRS) 및 층응답스펙트럼(Floor Response Spectrum: FRS)은 원자력발전소(원전)의 시스템, 구조물 및 기기(Structures, Systems, and Components, SSC)에 대한 내진설계 및 내진성능 평가의 입력으로 일반적으로 사용된다. 이에 따라 ISRS의 효율적이고 정확한 산정은 원전 SSC 내진 설계 및 지진 확률론적안정성평가(Probabilistic Safety Assessment, PSA)에서 매우 중요하다. ASCE/SEI 4-16(2017)은 ISRS를 Fig. 1과 같이 시간이력해석(Time History Analysis, THA) 또는 직접 스펙트럼-대-스펙트럼 방법(Direct Spectrum to Spectrum Method: DSS method)(Calvi and Sullivan, 2014; Jiang et al., 2015; Li et al., 2015; Lucchini et al., 2017a; 2017b; Sharma and Singh, 1983; Singh, 1975; 1980; Sullivan et al., 2013)에 의하여 생성할 수 있다고 기술하고 있다. 그러나 이러한 절차는 정교한 ISRS를 산출할 수 있지만, 이는 번거로울 뿐만 아니라 계산 비용도 많이 소요된다는 한계점이 존재한다.
기존 원전의 지진 PSA 및 수명 연장 프로젝트 수행 시, 일반적으로 설계기준지진(Design Basis Earthquake, DBE)의 설계지반응답스펙트럼(Design Ground Response Spectrum, DGRS)에 대한 ISRS를 활용할 수 있다. 그러나 설계 당시와는 다르게 부지의 고유한 DGRS(혹은 등재해도스펙트럼 Uniform Hazard Spectrum, UHS) 또는 지진 PSA 평가용지진(Review Level Earthquake, RLE) 스펙트럼을 고려하는 것이 필수적으로 요구될 경우 새로운 ISRS 도출이 필요하게 된다. 또한, 원전 지진 PSA 및 수명 평가 등의 프로젝트 범위와 예산은 원전 건물 구조물에 대한 완전한 지진응답 재해석을 수행할 수 없는 상황을 종종 발생시킨다. 더욱이 지진응답 재해석을 위한 구조물 모델에 대한 제한된 정보만이 있는 경우가 존재할 수도 있다. 이에 따라 실제 엔지니어링 업무에서 기존 ISRS를 스케일링하는 방법은 비용이 상당한 지진응답 재해석 수행없이 새로운 ISRS를 얻기 위한 효율적이고 경제적인 접근 방식일 수 있다.
ISRS 스케일링 방법은 정교한 방법과 근사 방법이 있다. 우선 정교한 방법은 구조모델의 동적특성인 고유주파수(Natural frequencies), 참여계수(Participation factors), 모드형상(Mode shape matrix 혹은 Eigen-vector) 등의 상세한 정보가 모두 제공되는 경우 THA 및 DSS 절차를 활용하여 기존 ISRS로부터 새로운 ISRS를 정밀하게 도출한다(Crandall and Mark, 1963; EPRI, 2002; 2018; Jiang et al., 2017). 다음으로 근사 방법은 구조물의 동적특성과 관련하여 정보가 전혀 존재하지 않거나, 혹은 주요 모드 고유주파수 정보는 있으나 참여계수 및 모드형상 정보는 부분적으로만 존재하는 경우에 사용할 수 있다. 이 방법은 이와 같이 제한된 정보만 제공되는 경우에 기존 ISRS로부터 보다 단순한 절차로 간략하게 새로운 ISRS를 생성하게 된다(EPRI, 2002; 2018). 그러나 현재 이러한 방법에 대한 구체적인 접근과 절차는 상세히 제시되지 않아 적용에 대한 한계가 존재한다. 따라서 적용 절차에 대한 여러 가지 접근법 개발이 필요한 상황이다.
이러한 배경아래 이번 연구는 ISRS 스케일링 근사 방법에 대한 여러 가지 접근법을 개발하고 제공하고자 한다. 또한, 이러한 스케일링 근사 방법으로 도출된 ISRS가 THA 방법을 이용한 정확한 ISRS와 정확도에서 어느 정도의 차이가 발생하는지 분석한다. 마지막으로 ISRS 정확도 차이로 인하여 원전 1차 구조물인 격납건물에 지지된 2차 시스템인 배관계통의 지진응답 및 내진성능에 어느 정도 영향이 있는지 분석하였다.
2. ISRS 스케일링 근사 방법: 여러 가지 접근
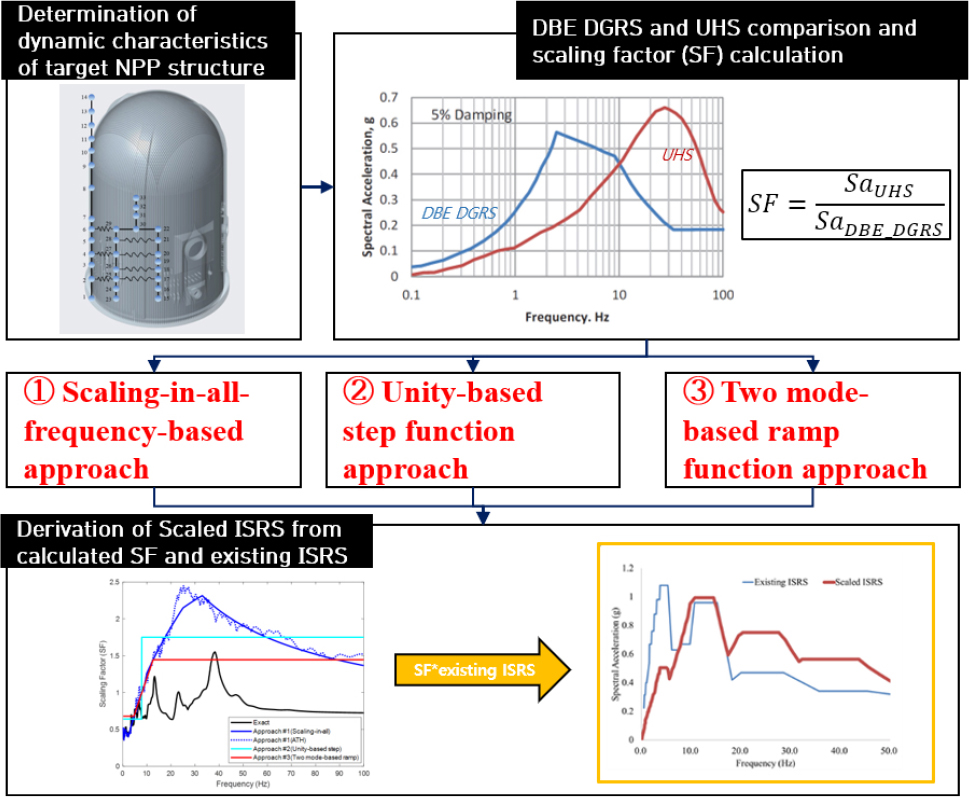
기존의 DBE DGRS 로부터 도출된 ISRS 가 존재하는 경우 새로운 부지 고유 DGRS(혹은, UHS)에 대하여 원전 구조물 모델의 내진 재해석없이 기존의 ISRS로부터 스케일링된 ISRS를 생성하는 근사 방법에 대한 여러 가지 접근법을 소개한다. 이러한 접근법은 Fig. 2와 같은 그림의 절차로 구성된다.
ISRS 스케일링 근사 방법에 대한 여러 가지 접근법을 구체적으로 설명하면 다음과 같다. Fig. 3은 전체 ISRS 스케일링 근사 방법의 절차를 개념적으로 보여준다. Fig. 3 내 파란색 점선 박스는 이미 존재하는 결과를 표현한다. 빨강색 실선 박스는 새롭게 정의된 대상 부지의 UHS를 대상으로 내진 재해석없이 스케일링된 ISRS를 구하는 절차를 나타낸다. 이러한 스케일링된 ISRS를 도출하기 위해서는 기존 지반에서 DBE DGRS 및 부지 UHS로부터 스케일링지수(Scaling Factor, SF)를 도출하고, 이를 기존 ISRS와 곱하여 새로운 스케일링된 ISRS를 생성한다. 본 연구에서는 SF를 구하는 방법을 크게 3가지 접근으로 구분하였다.
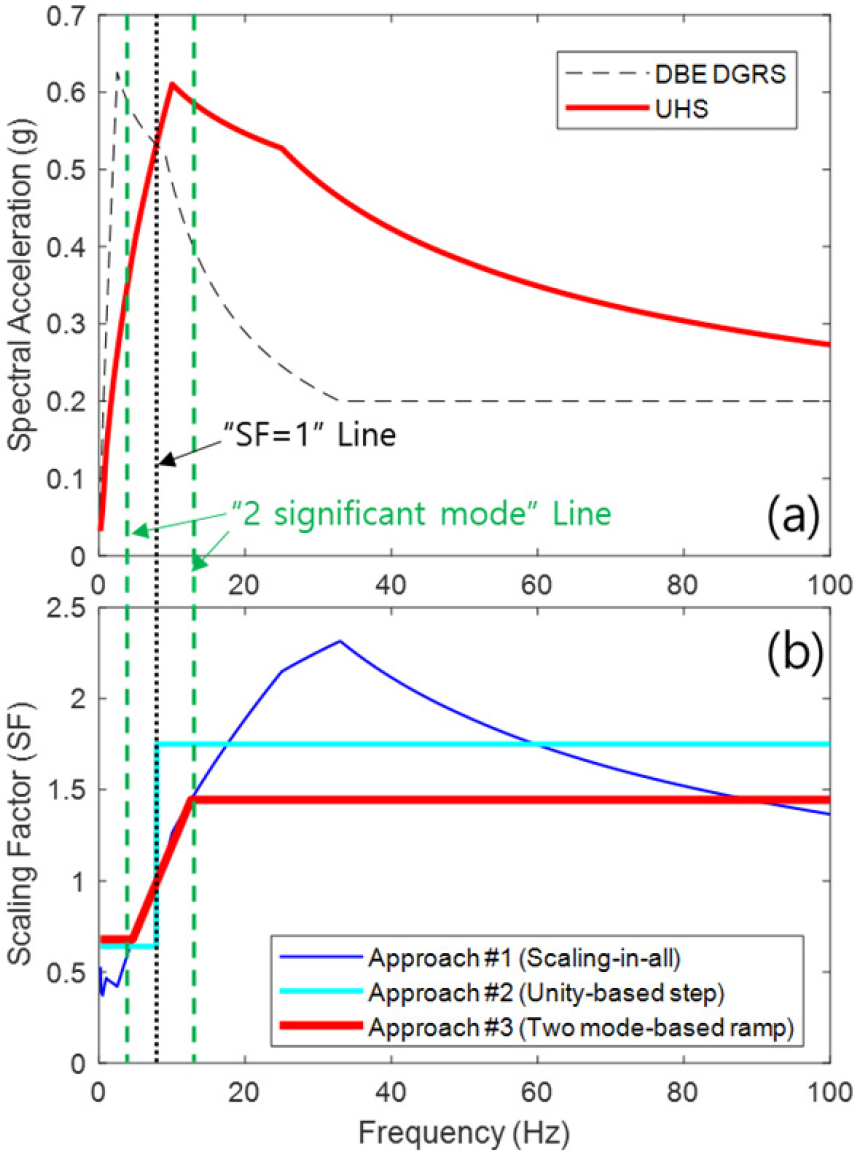
Fig. 4는 SF 도출에 대한 접근법 3가지를 개념적으로 보여주고 있다. 첫 번째와 두 번째는 대상 원전 구조물 해석 모델의 동적 특성을 전혀 모른다고 가정했을 때 사용할 수 있는 방법이다. 첫 번째인 Scaling-in-all-frequency-based approach는 DBE DGRS 및 UHS의 스펙트럼가속도(Spectral Acceleration, Sa) 값을 모든 주파수 영역에서 비교하여, 모든 주파수 마다 SF를 산출한다. Fig. 4(b)의 파랑색 실선 그래프는 주어진 DBE DGRS 및 UHS로부터 첫 번째 접근방법(Scaling-in-all-frequency-based approach)을 통하여 구한 SF 결과를 보여준다. 두 번째로 Unity-based step function approach는 DBE DGRS 및 UHS의 Sa 크기가 역전이 일어나는 점(즉, SF = 1)을 중심으로 SF가 1보다 작은 영역과 SF가 1보다 큰 영역을 각각 분리하여 각각의 두 주파수 영역의 SF값의 평균을 취하여 SF를 Step function으로 도출한다. Fig. 4(b)의 하늘색 실선 그래프는 두 번째 방법(Unity-based step function approach)으로부터 구한 SF 결과를 보여준다. 세 번째는 대상 원전 구조물 해석 모델의 동적 특성을 고유주파수 및 참여계수(혹은 질량참여율)의 제한된 정보만 제공된 경우에 사용할 수 있는 방법이다. 이는 Two mode-based ramp function approach로서 대상 모델의 주요모드 2가지를 식별하고 그 모드의 해당하는 SF값을 기반으로 램프 함수 형식으로 SF를 도출한다. Fig. 4(b)의 빨강색 실선 그래프는 세 번째 방법(Two mode-based ramp function approach)으로부터 구한 SF 결과를 보여주고 있다.
3. 대상 원전 건물 및 입력 지진동
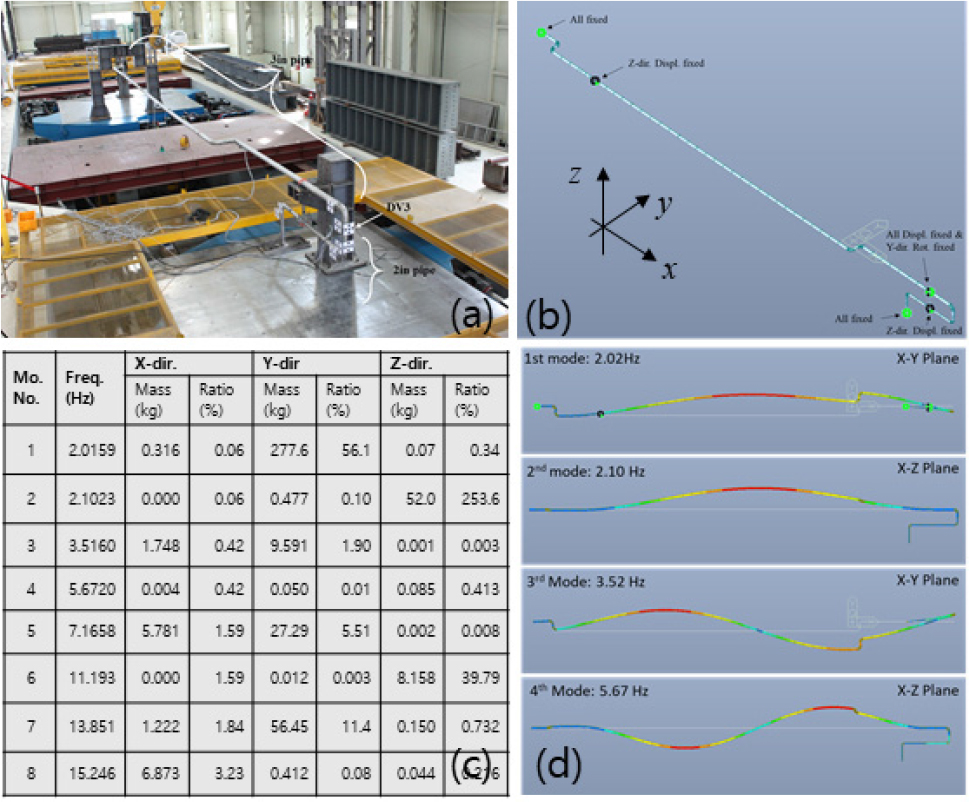
방법 검증을 위한 원전 구조물은 Fig. 5(a)의 한국표준형원전(OPR-1000)의 격납건물 수치모델을 대상으로 하였다. 대상모델은 Fig. 5(b)와 같이 각층의 질량중심과 강성중심을 고려하여 집중질량모델로 구성하였다. 격납건물의 전체질량, 사용한 재료 특성값, 부재의 특성값, 집중질량모델 등에 대한 구체적 정보는 격납건물 지진해석보고서를 포함한 이전 연구들을 참조하였다(KEPCO E&C, 1992; Kwag et al., 2022).
이 연구에서 활용한 대상 집중질량모델은 MIDAS 해석프로그램을 사용하여 수립하였고, 고유치해석을 수행한 결과 1차모드 고유진동수는 약 4.56Hz로 산정되었고, 연직방향 고유진동수는 약 12.17Hz로 나타났다. Fig. 6은 구체적인 수치모델 형상과 관련 주요모드 형상을 보여주고 있다. 이러한 결과는 격납건물 지진해석 보고서, 이전 연구 등(KEPCO E&C, 1992; Kim et al., 2013; Kwag et al., 2022)에 나타난 고유진동수 결과와 유사한 것으로 나타나 해당 모델의 신뢰도가 확보된 것을 확인할 수 있었다(Table 1 참조).
Table 1.
Comparison of mode analysis results (unit: Hz)
| 3D model | Lumped-mass stick model | |||
| Kim et al., 2013 | KEPCO, 1992 | Kim et al., 2013 | This Study | |
| 1st Mode (Horizontal) | 4.48 | 4.56 | 4.56 | 4.56 |
| 4th Mode (Vertical) | 12.65 | 12.17 | 12.18 | 12.17 |
입력 지진동으로 이 연구는 크게 2가지를 사용하였다. 하나는 USNRC Regulatory Guide(RG)1.60(USNRC RG 1.60, 2014) DGRS이고, 다른 하나는 고려하는 격납건물 구조물의 해당 부지 UHS이다. Fig. 7은 USNRC RG1.60 DGRS와 UHS 형상을 비교하여 보여주고 있다. 그림으로부터 확인할 수 있듯이 국내 부지 특성을 반영한 UHS가 USNRC RG1.60 DGRS에 비하여 고주파수 영역에서 입력지진동 에너지가 크게 발생함을 볼 수 있다. 이는 국내 지진 특성을 반영한 결과로서 UHS가 USNRC RG1.60 DGRS에 비하여 해당 부지에서 현실적으로 발생 가능한 지진이다. 구체적으로 USNRC RG1.60 DGRS는 SSE(Safe Shutdown Earthquake) 0.2g에 앵커된 설계스펙트럼이다. UHS는 해당 부지에서 지진재해도 분석을 통하여 도출된 스펙트럼이다. UHS의 영주기가속도(Zero Period Acceleration: ZPA) 값은 0.273g이다. 결과적으로 2개의 목표스펙트럼에 해당되는 인공지진파(Artificial Time Histories: ATH)을 생성하였고, 이러한 인공지진파가 목표 스펙트럼을 잘 부합하는지 검증하였다. 구체적으로 인공지진파는 임의의 주기함수 합과 포락함수의 곱으로 가정하였고, 계산된 스펙트럼이 목표 스펙트럼을 만족할 때까지 반복적인 절차를 수행하여 도출하였다(USNRC, 2007). Fig. 7은 이러한 인공지진파로부터 계산된 5%-감쇠비 응답스펙트럼 결과로서 해당 인공지진파로부터 계산된 응답스펙트럼이 목표 스펙트럼을 전반적으로 잘 모사함을 확인할 수 있다.
4. ISRS 스케일링 근사 방법 검증
ISRS 스케일링 근사 방법의 정확도를 검증하기 위하여 우선 USNRC RG1.60 DGRS 및 UHS에 기반하여 THA 방법(즉, ISRS를 정확하게 계산할 수 있는 방법)을 통하여 주요 위치에서 각각의 정확한 ISRS를 산정하였다. 지진응답해석 시 구조물의 감쇠는 5%로 고려하였고(USNRC RG 1.61, 2007), 감쇠행렬은 레일라이 감쇠접근법을 이용하여 도출하였다. 이러한 정확한 USNRC-ISRS, UHS-ISRS 및 관련 SF는 ISRS 스케일링 근사 방법을 통하여 도출된 SF 및 스케일링된 ISRS 결과의 유효성을 검증하는데 사용한다. ISRS의 산출 주요 위치는 Polar Crane이 위치하고 있는 절점 12(즉, N12), 및 주요 배관시스템이 설치되어 있는 절점 4(즉, N4)를 대상으로 하였다. 각 노드에서의 ISRS 산출 시, 설치된 구조물의 특성에 따라 감쇠비는 N12에서 5%를, N4에서 4%를 고려하였다. 이러한 감쇠비는 USNRC RG 1.61(2007)의 요건을 기반으로 해당 기기 및 시스템에 부합하는 감쇠비 값으로 선정하였다.
결과로서 Fig. 8 및 Fig. 9는 각각 THA 방법을 이용하여 도출한 N12 및 N4에서 정확한 USNRC-ISRS 및 UHS-ISRS를 비교하여 나타내고 있다. 입력지진파의 특성상 UHS-ISRS 가 USNRC-ISRS에 비하여 10Hz 이상의 고주파 영역에서 상대적으로 증폭이 많이 발생함을 확인할 수 있다. 이러한 THA 방법 기반으로 산출된 USNRC-ISRS 및 UHS-ISRS로부터 정확한 SF를 도출하였고, 이는 다음의 간단한 ISRS 스케일링 방법의 SF 값을 검증하는데 활용하였다.
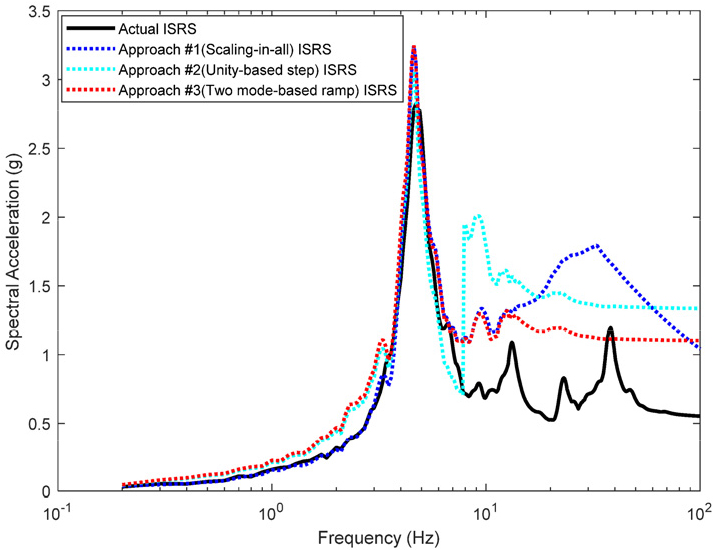
다음으로 위에서 계산한 정확한 USNRC-ISRS를 기반으로 ISRS 스케일링 근사 방법을 적용하여 관련 SF를 계산하고, 스케일링된 UHS-ISRS를 도출하였다. 2장에서 소개하였듯이 SF 계산은 서로 다른 3가지 접근법을 활용하였다. Fig. 10 및 Fig. 11은 각각 서로 다른 3가지 접근법에 기반한 N12에서 도출한 SF 값과 스케일링된 UHS-ISRS를 정확한 결과와 같이 나타내었다. 그림으로부터, ISRS 스케일링 근사 방법은 10Hz 미만 저주파에서 유사한 값을 산출하지만, 10Hz 이상 고주파에서 부정확한 값을 산정함을 확인할 수 있다. Fig. 12 및 Fig. 13은 각각 N4에서 도출한 SF 값과 스케일링된 UHS-ISRS을 정확한 결과와 같이 나타내었다. 그림으로부터 ISRS 스케일링 근사 방법이 20Hz 미만 저주파에서 비슷한 값을 주지만, 20Hz이상 고주파에서 부정확한 값을 줌을 확인할 수 있다.
결과적으로 ISRS 스케일링 근사 방법은 저주파에서 비교적 유사하게 ISRS를 도출하지만, 고주파에서는 그 정확도가 감소함을 볼 수 있었다. 이러한 결과는 유사한 연구인 EPRI의 “Benchmark studies to verify an approximate method for spectra scaling”(EPRI, 2018)의 주요 결과와 비슷한 경향을 보이고 있다. 따라서, 원전 구조물에 지지되는 기기 구조물의 고유주파수가 저주파인 경우에 있어서 이러한 ISRS 스케일링 근사 방법은 유효하게 사용될 수 있을 것으로 보인다. 3가지의 서로 다른 SF 계산 방식을 통하여 도출한 ISRS의 형상은 서로 유사하였고, 정확도 면에서 큰 차이를 보이지는 않았다. 다만, 한 가지 주목할 점은 구조물에 대한 동적해석 결과 정보를 전혀 사용하지 않는 2가지 방법(Scaling-in-all-frequency-based approach 및 Unity-based step function approach)은 구조물 동적해석 결과를 포함시키는 나머지 방법과 비교하여 정확도가 크게 훼손되지 않는다는 것이다.
5. ISRS 스케일링 근사 방법이 지진 응답 및 성능에 미치는 영향
이번 장에서는 ISRS 스케일링 근사 방법을 통한 ISRS가 정확한 ISRS와 비교하여 대상 기기의 지진응답 및 내진성능에 어떠한 영향을 미치는지 살펴보았다. 기본적으로 입력 스펙트럼 형상의 변화가 관련 결과에 미치는 영향을 검토하는 것이 주요 목적이므로 지진해석 방법 중 응답스펙트럼해석(Response Spectrum Analysis, RSA)을 이용하여 대상 시스템의 지진응답을 산정하였다. RSA 적용 시 모드별 최대응답 조합은 인접모드 간의 상관관계를 비교적 정확하게 고려할 수 있는 CQC(Complete Quadratic Combination) 접근법을 이용하였다.
대상 기기로 N4에 위치한 주요 배관시스템인 격납건물 CVCS charging line을 고려하였다(Cheung et al., 2013). 언급된 배관계통을 바탕으로 진동대실험이 수행된 바 있고, 이를 기반으로 유한요소해석 모델이 수립되고 검증되었다(Kwag et al., 2020). Fig. 14는 실험 배관계통 형상, 해석 모델, 모드해석 결과, 모드형상 등을 보여준다. 이 연구에서는 지진입력을 해석모델의 Y방향만을 고려하였다. 이는 이 방향의 배관시스템이 지진입력에 대하여 취약하기 때문이다. Fig. 15는 N4위치의 4%-감쇠비 입력 UHS-ISRS결과와 배관모델의 주요 4가지 모드를 겹쳐서 나타내었다.
결과적으로 지진 RSA 주요 결과인 최대 수직응력은 Table 2에 정리하여 나타내었다. 접근법 1인 Scaling-in-all-frequency-based approach는 정확한 ISRS와 비교하여 결과의 차이가 상당히 적었다. 그러나 접근법 2 및 3인 Unity-based step function approach 및 Two-mode-based ramp function approach는 정확한 ISRS와 비교하여 결과의 차이가 접근법 1에 비하여 크게 발생하였다. 이러한 오차 결과의 이유는 Fig. 15를 통하여 설명할 수 있다. 접근법 1의 ISRS는 정확한 ISRS와 비교하여 4개의 주요모드 위치에서의 Sa 값이 거의 유사했다. 그러나 접근법 2 및 접근법 3의 ISRS는 정확한 ISRS에 비하여 4개의 주요모드 위치에서의 Sa 값이 상이했고, 특히나 1차 모드의 Sa 값이 정확한 ISRS의 값에 비하여 비교적 큼을 확인할 수 있다. 이에 따라, 두 접근법에 의한 결과가 정확한 ISRS의 결과보다 보수적으로 도출됨을 유추할 수 있게 된다.
Table 2.
The results of seismic analyses of RSA of target piping model results: Maximum combined normal stresses
마지막으로 EPRI 변수분리에 의한 지진취약도 평가 방법(EPRI, 2018)을 이용하여 배관계통의 내진성능을 평가하였다. 배관계통의 내진성능 평가 시, 현재의 해석모델 상태를 배관의 중앙값 성능으로 가정하였고, 이와 관련한 다양한 무작위성 및 불확실성은 기존의 연구결과를 활용하여 정의하였다. 관련 로그표준편차는 EPRI 원전 배관의 내진성능의 변동성 지침(EPRI, 2013)에 따라 무작위성 및 불확실성에 관한 로그표준편차는 각각 0.30 및 0.50 값을 사용하였다.
구체적으로 지진입력에 대한 지진취약도 평가 시, 배관 한계 성능상태로 가장 취약한 배관 요소에서의 발생 응력 값을 기준으로 하였다. 배관 지진취약도 평가를 위한 정량적 한계 기준은 ASME 설계 기준의 허용응력 수준으로 정의하였다. 이 연구에서 사용된 배관(ASME CLASS 1 SA-312 GRADE TP 316)은 Section III, Division I, Subsection NB(ASME, 2007)의 적용이 가능하며, 이를 응력 기준을 활용하였다. 여기서, 지진 하중에 의해서 배관에 작용하는 주응력은 3*Sm 수준(Level D)으로 제한된다. 이 연구에서는 Sm 값은 ASME 스테인레스강(16Cr-12Ni- 2Mo)의 설계응력강도(Design stress intensity, -30~40도 금속 온도) 값인 138MPa를 이용하였다.
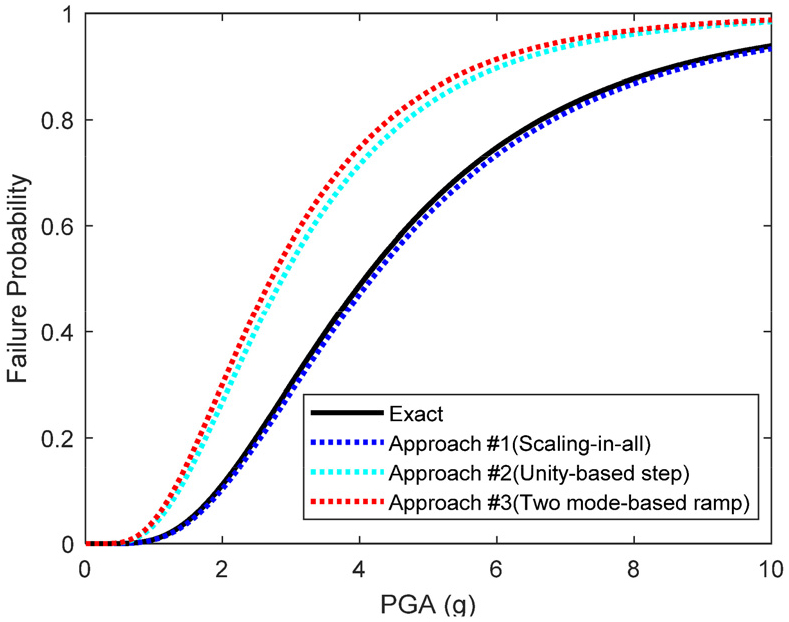
Fig. 16은 각각의 접근법을 통한 대상 배관시스템의 평균 지진취약도 곡선을 비교하여 보여주고 있다. Table 3는 배관 지진취약도 곡선의 고신뢰도저파손확률(High-Confidential-Low-Probability-of-Failure: HCLPF) 값을 비교하여 보여주고 있다. HCLPF는 확률분포 형태의 취약도 곡선 결과를 하나의 값 형태로 제시할 수 있기 때문에 원전 구조물, 기기 및 시스템의 대표 내진성능을 나타내는데 사용된다. 그림 및 표로 확인할 수 있듯이, 접근법 2 및 3의 결과는 지진응답해석의 보수적 결과로 인하여 정확한 ISRS의 기반한 결과와 비교하여 내진성능 값이 감소함을 확인할 수 있다. 그러나 이러한 접근법 2 및 3의 ISRS 결과와 정확한 ISRS 결과의 HCLPF 내진성능 차이는 지진 RSA와 관련한 결과보다는 그 오차가 작게 평가되었다.
6. 요약 및 결론
이 연구는 ISRS 스케일링 근사 방법에 대한 여러 가지 접근법을 개발하였고 이를 제공하였다. 또한, 이러한 스케일링 근사 방법으로 도출한 ISRS가 THA 방법을 이용한 정확한 ISRS와 비교하여 정확도에서 어느 정도의 차이가 발생하는지 분석하였다. 마지막으로 산출된 ISRS의 정확도 차이로 인하여 원전 구조물에 지지된 배관시스템의 지진응답 및 내진성능에 어느 정도 영향이 있는지 살펴보았다.
그 결과 본 연구에서 제시된 ISRS 스케일링 근사 방법의 3가지 접근법은 저주파에서 비교적 유사하게 ISRS를 도출하지만 고주파에서는 그 정확도가 감소함을 볼 수 있었다. 따라서, 제시된 방법은 대상 시스템의 동적 거동을 10-20Hz 저주파 영역의 소수의 모드로 결정할 수 있는 구조물에 대하여 사용하는 것이 바람직할 것으로 보인다.
그리고 하나의 예로서 고려한 대상 배관시스템의 지진응답 및 내진성능과 관련하여 접근법 1인 Scaling-in-all-frequency-based approach의 결과는 정확한 ISRS의 결과와 비교하여 그 차이가 상당히 적었다. 그러나 접근법 2 및 3인 Unity-based step function approach 및 Two-mode-based ramp function approach는 이러한 결과 차이가 접근법 1에 비하여 크게 발생하였다. 그러나 이는 하나의 예제 결과로서 이를 ISRS 스케일링 근사 방법의 지진응답 및 내진성능 정확도로 일반화시킬 수는 없다. 궁극적으로 ISRS 스케일링 근사 방법의 결과와 정확한 ISRS의 결과 차이 정도는 고려하는 시스템의 주요 모드의 Sa 결과에서 얼마나 서로 유사한 지에 따라서 결정될 것으로 판단된다. 마지막으로 제안하는 방법은 고진동수 영역에서 기본적으로 그 정확성이 낮기 때문에 활용성이 제한적이라는 한계가 존재하므로 이러한 한계를 극복하기 위한 개선된 방법론 등에 관한 연구가 향후에 추가적으로 이루어져야 할 것으로 보인다.