1. 서 론

최근 건설공사 중 콘크리트를 타설하는 과정에서 거푸집 및 동바리와 관련된 사고가 빈번하게 발생하고 있으며, 광주 아파트 상부층 붕괴(2022), 인천 서구 아파트 지하 주차장 붕괴(2023) 등 다층지지 RC 구조 시스템에서 시공 중 붕괴 사고가 연이어 발생하였다. 시공 중 발생하는 붕괴 사고는 콘크리트 강도의 미발현으로 인한 강도 부족, 거푸집 및 동바리 설치상태 불량, 재료의 불량 등 다양한 원인이 있지만, 일반적으로 철근 콘크리트 건물에서는 타설된 슬래브 콘크리트가 완전히 경화할 때까지 강도와 강성이 충분히 발현되지 못하여 슬래브 재령 초기에는 슬래브가 지지할 수 있는 범위를 넘어서는 과하중이 작용할 수 있으므로 붕괴 사고의 위험성이 존재하고 있다.

시공 중 강도 및 강성이 완전히 발현되지 않은 슬래브들은 자중을 동바리로 연결된 하부층들과 나누어 부담하게 되며(ACI Committee 347, 2005), 하부층들로 전달되는 하중은 균등하게 분배되지 않고 콘크리트의 강성비에 따라 분배된다. 이러한 다층지지 RC 구조의 특성에 따라 시공 중 콘크리트의 강성과 시공 하중을 충분히 검토하여 구조설계 및 시공계획에 반영하여 시공 중 구조적 안전성을 확보할 필요가 있다. 슬래브 콘크리트의 강성은 층당 시공 주기, 동바리 지지층 수 등의 시공 조건, 슬래브 두께 변화 등의 설계 조건과 같은 다양한 변수에 따라 달라질 수 있으며, 이에 따라 동바리로 연결된 다층지지 구조 시스템에 포함된 각 슬래브에 분포되는 시공 하중의 크기가 변화한다.

슬래브 시공 하중을 예측하는 이전 연구에서는 동바리 강성 효과 및 균열에 따른 유효 단면 강성 효과를 고려하여 새로운 시공 하중 산정 방법을 개발(Hwang et al., 2010)하거나 유한 요소 모델을 통한 다층지지 RC 구조 건물 시공 중 슬래브와 동바리의 하중 변화에 대한 분석(Alvarado et al., 2010), 동바리 제거에 따른 슬래브 과하중 분석(Azkune et al., 2010), 현장계측을 통해 RC 벽식 아파트의 시공 중 하중 및 거동 분석(Kang et al., 2009) 등과 같이 슬래브 두께가 일정한 상황에서의 연구가 주로 이루어졌다.

반면 특정 층의 슬래브 두께가 증가하는 경우 슬래브 시공 하중의 분포가 변화하며 슬래브의 안전성에 미치는 영향이 달라진다는 것이 확인되었으나(Han and Kim, 2024), 시공 조건과 설계 조건이 모두 동일한 경우에 대해서만 분석이 이루어졌으므로 슬래브 콘크리트 강성에 영향을 줄 수 있는 조건들을 고려한 연구가 필요하다.

따라서, 이 연구에서는 RC 슬래브들로 구성된 다층지지 구조 시스템에서 슬래브 두께가 증가하는 PIT층이 존재하거나, 층별 용도가 달라 슬래브 두께가 일정하지 않은 비기준층이 존재하는 경우 시공 주기, 동바리 지지층 수의 시공 조건과 증가하는 슬래브 두께, 슬래브 두께 증가층 수의 설계 조건 변화가 시공 하중에 미치는 영향을 분석하였다.

2. 시공 하중의 산정

시공 하중을 산정하기 위해서는 시공 단계를 고려한 산정법이 사용되어야 한다. 이 연구에서는 시공 하중을 산정할 때 간단한 수계산을 통해 시공 하중을 산정하는 방법인 간편법(Grundy and Kabaila, 1963)을 사용하여 시공 하중을 산정하였다. 간편법에서는 동바리와 기초의 강성을 무한 강성으로 가정하고, 각 층 슬래브의 재료 강성인 콘크리트 재령에 따른 탄성계수의 비율만 고려하여 시공 하중을 산정한다. 간편법에 의해 산정된 시공 하중과 계측 결과의 비교에 따르면(Puente et al., 2007), 비교적 양호한 정확성을 보이면서 해석 과정의 간편성으로 인해 실무에 적합한 것으로 검증되었다.

기존 간편법의 경우 시공 하중 산정 과정에서 동바리로 지지 된 슬래브 콘크리트의 하중을 전체 강성의 합에 대한 해당 층 강성의 비율인 슬래브 강성비에 따라 시공 하중을 분배하고 있다. 그러나 모든 슬래브 두께가 일정하지 않은 경우 슬래브 두께 변화에 의해 슬래브 콘크리트 단면 강성이 변화하므로 슬래브들의 강성 비율이 달라져 시공 하중의 분배가 변화한다. 따라서 슬래브 두께가 변화하는 다층지지 RC구조 시스템에서 간편법을 사용해 시공 하중을 산정할 때는 슬래브 콘크리트 재료 강성과 함께 슬래브 단면 강성을 포함하여 슬래브 시공 하중을 산정하여야 한다(Han and Kim, 2024).

시공과정에서 일부 슬래브의 콘크리트는 경화되고 있는 과정이므로, 콘크리트의 강성과 강도가 지속적으로 변화하며, 단순히 슬래브에 작용하는 시공 하중의 크기만으로 슬래브 손상이나 안전성 등에 대한 영향을 평가할 수 없다. 슬래브 콘크리트 재령이 클수록 슬래브를 구성하는 콘크리트의 강도와 탄성계수가 커지므로 동일한 시공 하중이 작용하더라도 균열 및 처짐이 감소한다(Choi et al., 2012). 따라서 시공 하중의 영향을 검토할 때에는 슬래브에 작용하는 시공 하중의 크기와 함께, 슬래브 콘크리트의 재령에 따른 역학적 성능의 변화를 고려하여야 한다. 이 연구에서는 시공 하중과 콘크리트 재령에 따른 강도에 대한 지배조건을 결정하기 위해 시공 손상 변수 K를 다음과 같이 정의하였다(Kim, 2009).

여기서, wt: 콘크리트 재령 t일에서 슬래브 시공 하중의 크기, wD: 해당 슬래브 1개 층의 자중, fc,t: 재령 t일에서의 콘크리트 압축 강도이다. 구조기준에서 제시하는 콘크리트의 인장 균열 강도와 균열 모멘트는 콘크리트 압축 강도의 제곱근에 비례하므로, 콘크리트 압축 강도의 제곱근에 대한 슬래브 시공 하중의 비를 슬래브의 시공 손상 변수로 정의하였다. 슬래브 콘크리트의 재령이 28일 이상으로 설계강도를 충분히 발휘하며(fc,t=fc,28), 해당 슬래브를 지지하는 하부 동바리가 제거되어 자체 자중만을 지지하는(wt=wD) 경우 시공 손상 변수 K=1로 정의한다.

3. 슬래브 콘크리트 재령별 시공 하중과 시공 손상 변수

슬래브 두께가 변화하는 비기준층을 포함하는 다층지지 RC구조에서의 시공 하중 분포와 슬래브 손상을 분석하기 위하여, 슬래브 단면 강성을 포함한 간편법을 적용하여 슬래브 시공 하중과 시공 손상 변수를 산정한다.

1개 층 공사 기간을 4일, 동바리 지지층 수를 3개 층으로 하고, 시공 활하중 0.5D가 작용하며 N층에서 슬래브 두께가 1.5배 증가하는 비기준층이 발생하는 것을 기본 모델(Typical Model)로 설정하였다. 여기서, D는 기준층 슬래브의 1개 층 자중을 의미한다. Fig. 1은 간편법에 따라 산정된 기본 모델의 시공 하중, 시공 손상 변수의 변화를 나타낸 그래프이다.

Fig. 1.

Analytical Results of Typical Model

시공 변수로는 시공 주기를 3일/5일, 동바리 지지층 수 4개 층/5개 층, 설계 변수로는 슬래브 두께 증가량 2.0h 및 두께 증가 층 개수가 2개 층이 되는 것으로 설정하여 각 조건의 변화가 시공 하중 및 시공 손상 변수에 미치는 영향을 분석하였다. 여기서, h는 기준층 슬래브의 두께를 의미한다.

3.1 시공 주기의 영향

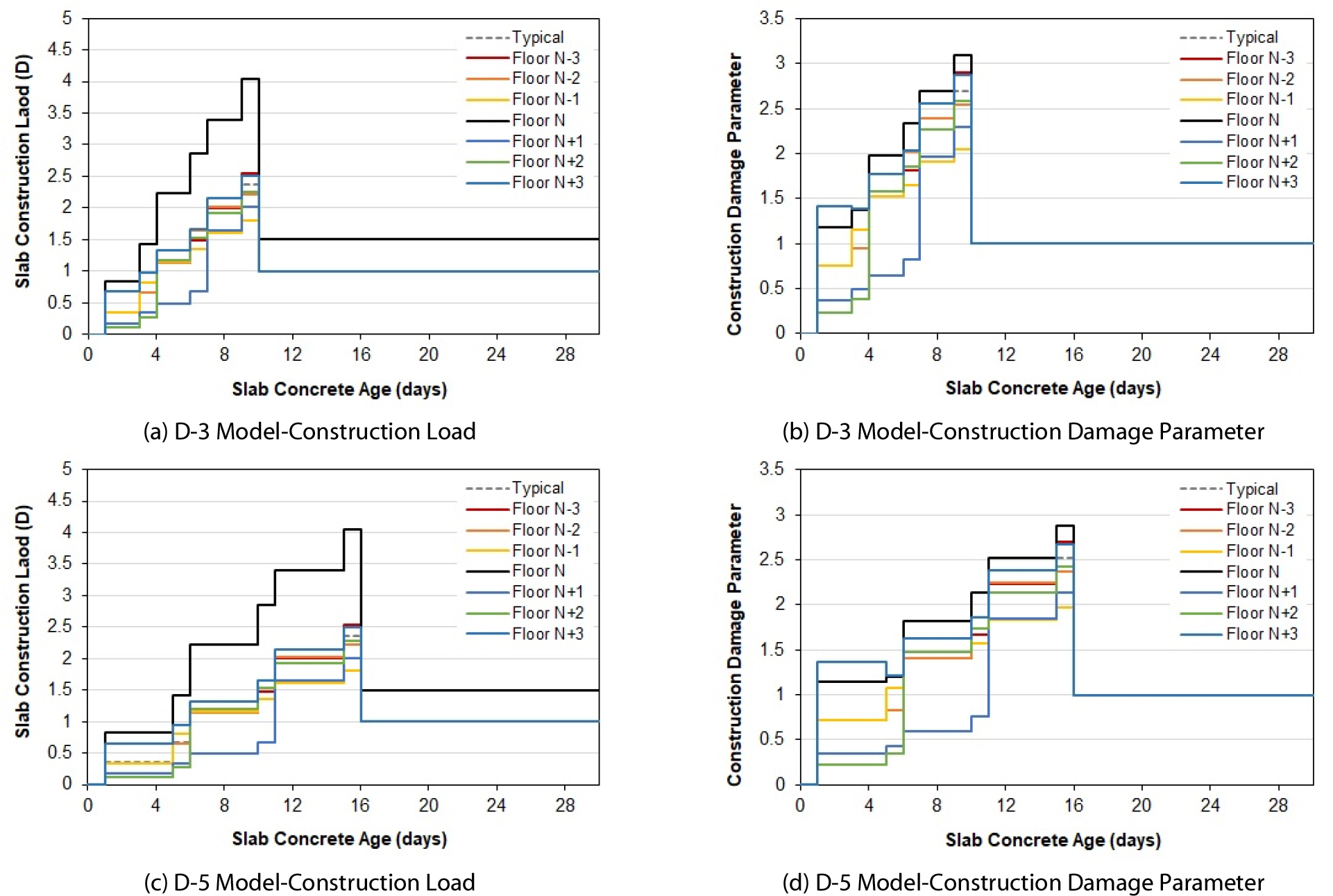
Fig. 2는 시공 주기가 3일(D-3 Model), 5일(D-5 Model)로 변화하는 경우 시공 하중과 시공 손상 변수의 변화를 나타내는 그래프이며, 시공 하중은 기준층 슬래브 1개층 자중 D에 대한 비율로 나타내었다. 그림에서 동바리 제거 이후 자신만의 자중을 지지하는 슬래브의 경우, 콘크리트 재령이 28일 미만일 때의 시공 손상 변수는 최대 1.06~1.13인 상태가 발생하나 실제 슬래브의 안전성에 미치는 영향은 적을 것으로 판단하여 1.0으로 단순화하여 표현하였다. Fig. 1의 기본 모델과 비교할 때, 시공 주기가 3일로 줄어드는 경우와 5일로 늘어나는 경우 모두 각 층이 부담하는 시공 하중 크기는 변화가 없거나 아주 적은 변화만 있었다. 다만, 간편법의 시공 하중 분배 시점이 시공 주기에 따라 변화하여 각 시공 하중이 작용하는 시점의 변화만 나타났다. 시공 손상 변수는 작용하는 시점의 변화뿐만 아니라 시공 주기가 3일로 줄어드는 경우 시공 손상 변수가 증가하고, 시공 주기가 5일로 길어지는 경우에는 시공 손상 변수가 감소하였다. 시공 하중의 크기는 각 층 시공 하중 분배 시점에 거의 동일하게 작용하나, 콘크리트의 재령에 따른 강도 발현이 시공 주기가 길어질수록 커지기 때문에 시공 손상 변수가 변화하는 모습이 나타났다.

Fig. 2.

Analytical Results with Different Construction Periods

3.2 동바리 지지층 수의 영향

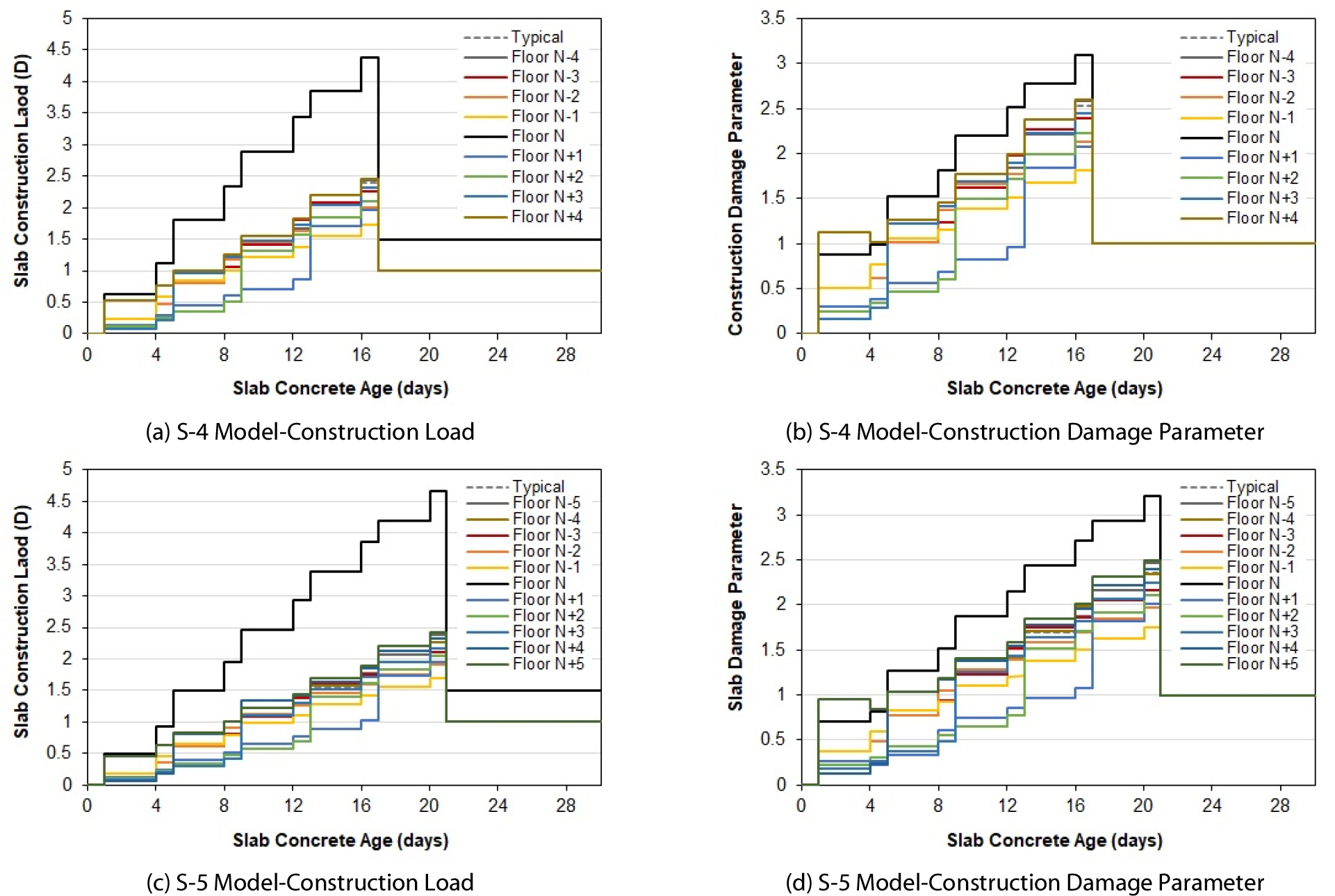
Fig. 3은 동바리 지지층 수가 4개 층(S-4 Model), 5개 층(S-5 Model)으로 변화하는 경우 시공 하중과 시공 손상 변수의 변화를 나타내는 그래프이다. Fig. 1의 기본 모델과 비교할 때, 동바리 지지층 수가 늘어나면 분배되는 총 하중의 크기가 증가하고, 상대적으로 강성비가 큰 두께가 증가하는 N층에서의 시공 하중은 증가한다. 이와 반대로 상대적으로 강성비가 작은 N층 인접층에서는 시공 하중이 감소한다. 또한 초기 재령의 N+3층의 경우 동바리 지지층 수가 3개일 경우에는 N+3층 콘크리트 타설과 함께 연결되어 있던 두께가 증가하는 N층의 동바리가 제거되어 타 층에 비하여 N층 두께 증가의 영향을 비교적 덜 받았으나, 동바리 지지층 수가 늘어나며 N+3층 타설 시점에 N층의 동바리가 제거되지 않아 두께 증가의 영향을 기존보다 많이 받게 되어 시공 하중이 크게 감소하는 모습을 나타냈다. 시공 손상 변수의 경우 N층에서는 시공 하중의 증가로 인하여 증가하였고, N층 이외의 층에서는 시공 하중이 감소하여 시공 손상 변수 또한 감소하는 모습을 나타냈다.

Fig. 3.

Analytical Results with Different Number of Shores

3.3 슬래브 두께 증가량 및 두께 증가층 수의 영향

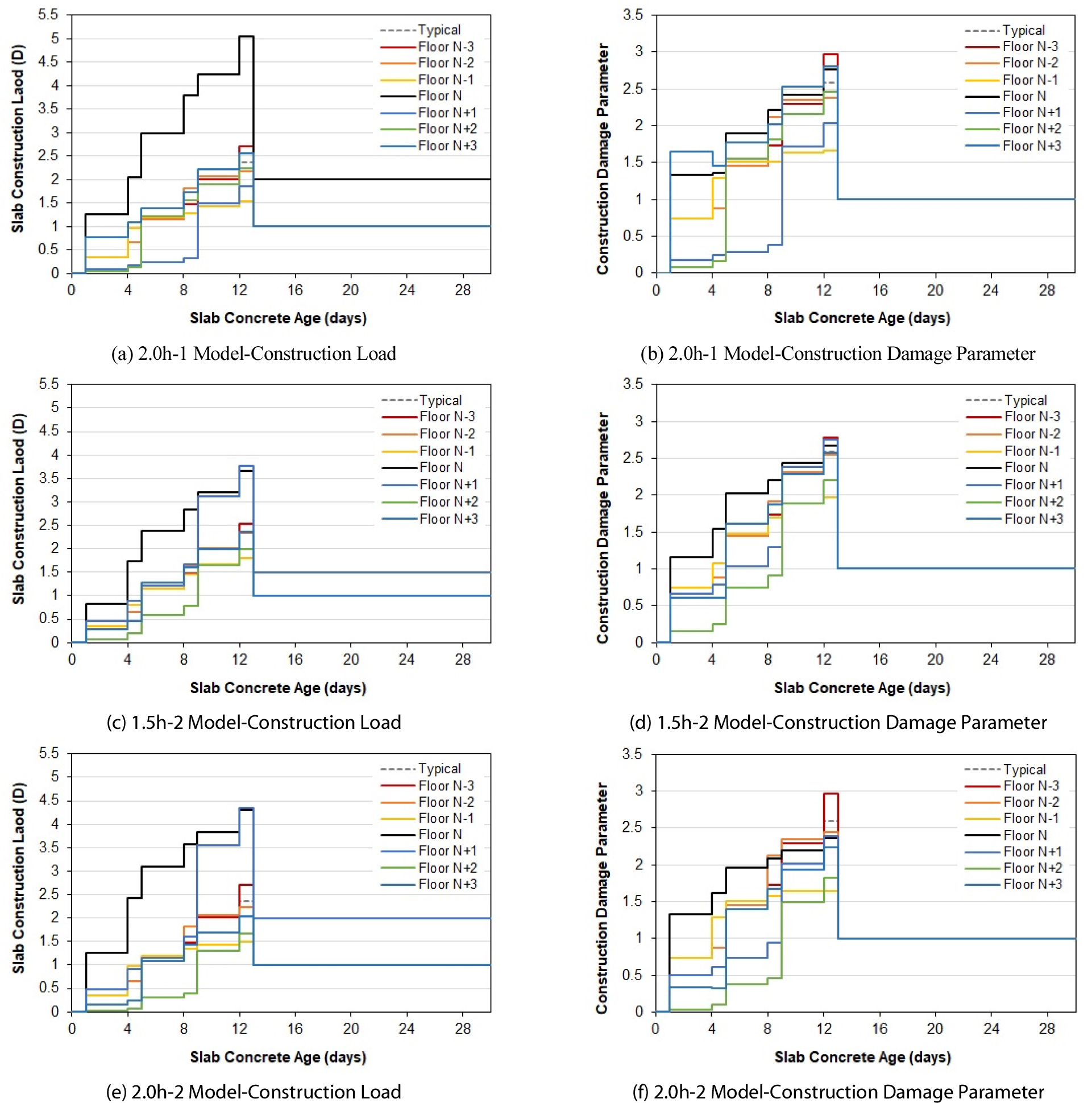
Fig. 4는 두께 증가량이 2.0h(2.0h-1 Model)로 변화하는 경우와 두께 증가 층수가 2개 층(1.5h-2 Model)으로 변화하는 경우, 두께 증가 층수와 두께 증가량이 함께 증가하는 경우(2.0h-2 Model) 시공 하중과 시공 손상 변수의 변화를 나타내는 그래프이다. 두께 증가량만 증가하는 경우(Fig. 4(a), (b)) 두께가 증가하는 N층에서의 강성비가 크게 증가하게 되고 이에 따라 N층에서 부담하는 시공 하중이 증가하게 된다. N-3층은 N층의 두께 증가로 인한 총 하중의 크기가 커져 N층 타설 시점에 N-3층에 분배되는 시공 하중이 증가하게 되고, 이에 따라 재령에 따른 시공 하중이 소폭 증가하는 모습을 나타냈다. N+3층의 경우 두께가 증가한 N층의 동바리가 제거되는 시점에 N층이 지지하고 있던 큰 시공 하중이 동일한 강성비를 가진 슬래브들에 재분배되며 소폭 증가하는 모습이 나타났다. 시공 손상 변수의 경우 N층의 시공 하중이 크게 증가하였으나, 시공 하중 증가의 영향보다 자중 증가의 영향을 크게 받아 결과적으로 감소하였고, 시공 하중이 증가한 N-3층과 N+3층을 제외한 층들에서는 시공 손상 변수가 감소하는 모습을 나타냈다.

Fig. 4.

Analytical Results with Different Amount of Slab Thickness Increase/Number of Increase Slabs

두께 증가 층수만 늘어나는 경우(Fig. 4(c), (d)) N-2층과 N-1층에서의 시공 하중은 N+1층 두께 증가의 영향을 받는 재령 12일, 8일~12일에서 각각 소폭 증가하는 경향을 나타냈다. N층의 경우 N+1층 타설 시점에는 늘어나는 총 하중으로 인해 시공 하중이 잠시 증가하나, N+1층 슬래브의 재령에 따른 강성비가 증가함에 따라 N+1층에서 지지하는 시공 하중이 증가하여 N층의 시공 하중은 감소하였다. N+2층의 경우 N+1층 하중 증가의 영향으로 시공 하중이 감소하였고, N+3층의 경우 N층 슬래브의 두께만 증가하는 경우 N+3층 타설 시점에 N층의 동바리가 제거되어 슬래브 두께 증가의 영향을 비교적 덜 받았으나, 두께 증가 층수가 늘어나는 경우 N+1층 슬래브 두께의 증가 영향을 받아 시공 하중이 감소하는 결과가 나타났다. 시공 손상 변수의 경우 N+1층에서 시공 하중이 크게 증가하였으나 자중 증가의 효과를 받아 시공 손상 변수는 시공 하중의 증가량과 비교하여 적게 증가하였고, N-3층의 경우 N+1층이 타설되기 전에 동바리가 제거되기 때문에 두께 증가 층수 변화의 영향을 받지 않아 변화가 나타나지 않았다. 그 외 층에서는 시공 하중의 변화와 동일한 경향이 나타났다.

두께 증가량과 두께 증가 층수가 함께 증가하는 경우(Fig. 4(e), (f)) N-3층과 N-2층에서는 N층 두께 증가량이 늘어남에 따라 분배되는 총 하중이 증가하여 시공 하중이 증가하고, N-1층에서는 N+1층의 두께 증가의 영향을 받아 N+1층의 강성이 발현되는 시점부터 시공 하중이 감소하였다. N층의 경우 N+1층의 두께가 함께 증가하였기 때문에 시공 하중이 감소해야 하지만 두께 증가 층들의 두께가 늘어나 총 하중이 크게 증가하여 분배되는 시공 하중이 증가하는 모습을 나타냈다. N+1층 상부층(N+2층~N+3층)은 N+1층 두께 증가의 영향으로 시공 하중이 감소하였다. 시공 손상 변수의 경우 N-3층과 N-2층에서는 시공 하중이 증가의 영향으로 증가하였고, N층의 경우 시공 하중은 증가하였으나 자중 증가의 영향을 크게 받아 시공 손상 변수가 감소하였다. 두께가 증가하는 N+1층 또한 시공 하중은 크게 증가하였으나, N층과 마찬가지로 자중 증가의 효과로 인해 시공 손상 변수는 소폭 증가하는 모습을 나타냈다. N+1층 상부층(N+2층~N+3층)은 시공 하중이 감소하여 시공 손상 변수 또한 감소하였다.

4. 시공 및 설계 변수에 따른 해석 결과 분석

“3. 슬래브 콘크리트 재령별 시공 하중과 시공 손상 변수”에서는 각 시공 조건과 설계 조건이 변화할 때 층별 시공 하중과 시공 손상 변수의 변화에 대해 분석하였다. 구조물의 안전성을 판단하기 위해서는 최대로 작용하는 시공 하중과 시공 손상 변수, 동바리 축력을 산정하여 검토하여야 하며, 기본 모델(Typical Model)에 대한 상대 비율을 백분율(%)로 표기하여 분석하였다.

4.1 최대 시공 하중

Table 1은 기본 모델과 각 변수에 따른 모델의 최대 시공 하중을 정리한 표이다. 최대 시공 하중은 시공 주기의 변화의 영향은 거의 받지 않으며, 동바리 지지층 수가 증가할 때는 총 하중의 증가와 강성비의 영향으로 N층에서 최대 시공 하중이 8.4%(S-4 Model), 15.3%(S-5 Model) 증가하였다. 또한, N층을 제외한 동바리 연결 층(N-3층~N-1층, N+1층~N+3층)에서는 최대 시공 하중이 기본 모델 대비 약 2.5%~17.3% 감소하며, 두께 증가층과 멀어질수록 감소하는 비율이 증가하였다. 두께 증가량이 증가하는 경우 N층의 슬래브 두께가 약 66.7% 증가하였으나, 최대 시공 하중이 작용하는 시점의 강성비에 따라 N층의 최대 시공 하중은 약 25% 증가하였다. 두께 증가층 수가 많아지는 경우 기존의 두께가 증가했던 N층에서는 상대적으로 강성비가 낮아져 최대 시공 하중이 동일한 두께의 두께 증가층 수가 적은 경우와 비교하여 9.9%(1.5h-2 Model), 18.3%(2.0h-2 Model) 감소하였다. 또한, 1.5h-2 Model, 2.0h-2 Model에서 새롭게 두께가 증가한 N+1층은 기본 모델, 2.0h-1 Model의 N충과 두께가 동일함에도 강성비의 영향으로 기본 모델, 2.0h-1 Model의 N층과 비교하여 6.9%(1.5h-2 Model), 13.7%(2.0h-2 Model) 감소하는 모습이 나타났다. 최대 시공 하중은 2.0h-1 Model의 N층에서 124.7%, 2.0h-2 Model의 N+2층에서 73.1% 로 가장 크게 증가 및 감소가 이루어졌으며, 변수 중 두께 증가량과 두께 증가층 수가 최대 시공 하중에 가장 큰 영향을 미쳤다.

4.2 최대 시공 손상 변수

Table 2는 기본 모델과 각 변수에 따른 모델의 최대 시공 손상 변수를 정리한 표이다. 시공 주기가 변화하는 경우 최대 시공 하중의 변화는 거의 나타나지 않았으나, 재령에 따른 강도발현의 영향으로 시공 주기가 줄어드는 D-3 Model의 전 층에서 약 4% 증가하였고, 시공 주기가 늘어나는 D-5 Model에서 약 3% 감소하였다. 동바리 지지층 수가 증가하는 경우 두께가 증가하는 N층의 최대 시공 하중이 증가함에 따라 N층의 최대 시공 손상 변수는 4.7%(S-4 Model), 8.5%(S-5 Model) 증가하였으나, 시공 하중 증가 비율에 비해서는 적은 증가율이다. 또한, N층을 제외한 동바리 연결 층에서 기본 모델 대비 5.4%~21.9% 감소하고 최대 시공 하중과 마찬가지로 두께 증가층과 멀어질수록 감소하는 비율이 증가하였다. 두께 증가량이 증가하는 경우 최대 시공 하중은 약 25% 증가하였으나, 자중 증가의 영향으로 최대 시공 손상 변수는 6.4% 감소하였다. 두께 증가층 수가 많아지는 경우 N층의 강성비가 상대적으로 낮아짐에 따라 동일한 두께의 두께 증가층 수가 적은 경우와 비교하여 N층의 최대 시공 손상 변수가 9.8%(1.5h-2 Model), 13.9%(2.0h-2 Model) 감소하였다. 또한, 1.5h-2 Model, 2.0h-2 Model에서 새롭게 두께가 증가한 N+1층은 기본 모델, 2.0h-1 Model의 N충과 두께가 동일하지만 기본 모델, 2.0h-1 Model의 N층과 비교하여 최대 시공 손상 변수가 각각 7.1%(1.5h-2 Model), 13.7%(2.0h-2 Model) 감소하는 모습이 나타났다. 최대 시공 손상 변수는 기본 모델과 비교하여 S-5 Model의 N층에서 108.5%, 2.0h-2 Model의 N+2층에서 73.1%로 가장 크게 증가 및 감소가 이루어졌다. 두께 증가층의 최대 시공 손상 변수는 시공 주기가 짧을수록, 동바리 지지층 수가 증가할수록 증가하는 것으로 나타났으나, 두께 증가량 및 두께 증가층 수가 증가하면 오히려 감소하는 것으로 나타났다.

4.3 최대 동바리 축력

각 층의 동바리 축력은 상부에서 전달되는 하중과 해당 층 슬래브 콘크리트 자중의 합으로부터 해당 층 슬래브 콘크리트가 지지하는 하중을 제외하고 하부로 전달되는 하중으로 산정하였다. Table 3은 기본 모델과 각 변수에 따른 모델의 최대 동바리 축력을 정리한 표이다. 강성비가 크게 낮아지는 S-5 Model을 제외한 N층의 최대 동바리 축력은 N층 타설 시점에 발생하며,N층 하부층(N-2층~N-1층)의 최대 동바리 축력도 N층 타설 시점에 발생한다. N층 상부층(N+1층~N+3층)의 경우 N층과 연결된 동바리가 제거되기 직전에 가장 큰 최대 동바리 축력이 작용한다. 시공 주기가 변화할 때 최대 시공 하중의 분포 변화가 없어 최대 동바리 축력은 동일하였다. 동바리 지지층 수가 증가할 때는 총 하중이 증가하고, 시공 하중이 분포되는 층 수가 증가하므로 상부층이 부담하는 시공 하중이 감소하고 하부 슬래브로 전달되는 하중이 증가하여 동바리 축력은 N층을 제외한 동바리 연결층(N-3층~N-1층, N+1층~N+3층)에서 10.5%~87.7% 증가하였다. 두께 증가량이 커질 경우 총 하중의 증가로 기본 모델 대비 최대 동바리 축력은 N—1층에서 15.5%, N층에서 25% 증가하였고, N층 강성 변화의 영향을 적게 받는 N+3층을 제외한 N층 상부층(N+1층~N+2층)에서는 N층 강성 증가의 영향으로 최대 동바리 축력이 6.3%~19.6% 증가하였다. 두께 증가층 수가 늘어나는 경우 N+1층에서 부담하는 시공 하중이 증가하여 N+2층과 N+3층의 최대 동바리 축력이 3.6%~32.5%(1.5h-2 Model), 28.3%~46.1%(2.0h-2 Model) 증가하였고, 1.5h-2 Model, 2.0h-2 Model에서 새롭게 두께가 증가한 N+1층은 기본 모델, 2.0h-1 Model의 N충과 두께가 동일하지만 총 하중의 증가로 기본 모델, 2.0h-1 Model의 N층과 비교하여 최대 동바리 축력이 각각 7.5%(1.5h-2 Model), 12.4%(2.0h-2 Model) 증가하는 모습이 나타났다. 동바리 축력은 기본 모델과 비교하여 S-5 Model의 N+3층에서 187.7%, 1.5h-2 Model의 N+1층에서 84.3%로 가장 크게 증가 및 감소가 이루어졌으며, 동바리 지지층 수와 두께 증가층 수가 동바리 축력에 가장 크게 영향을 미쳤다.

5. 결 론

다층지지 RC 구조 시스템의 일부 층에서 슬래브 두께가 증가하는 비기준층이 발생하는 경우, 시공 조건과 설계 조건의 변화에 따른 시공 하중, 시공 손상 변수, 동바리 축력의 변화에 대해 분석하였으며, 분석 결과를 요약하면 다음과 같다.

1) 다층지지 RC 구조 시스템에서 슬래브 두께가 변화하는 비기준층 발생시 시공 조건 및 설계 조건에 따라 시공 하중, 시공 손상 변수, 동바리 축력이 변화한다.

2) 시공 하중은 시공 주기 변화의 영향은 거의 받지 않으며, 두께 증가 층수와 증가량이 가장 큰 영향을 미치고 두께 증가 층수와 증가량이 증가할수록 시공 하중이 증가한다.

3) 시공 손상 변수는 동바리 지지 층수가 증가할 때 두께 증가 층에서 증가하나, 기준층에서는 크게 감소한다.

4) 슬래브 두께 증가 층수와 증가량이 증가하면, 일부 층의 시공 손상 변수가 크게 증가한다.

5) 동바리 축력은 시공 주기 변화의 영향은 거의 받지 않으며, 동바리 지지 층수 증가에 의해 가장 크게 증가한다.

따라서 일부 층의 슬래브 두께가 증가하는 다층지지 RC 구조 시스템의 시공 조건과 설계 조건이 변화할 때 각 조건의 변화가 시공 하중, 시공 손상 변수, 동바리 축력에 미치는 영향을 고려하여야 하며, 시공 하중과 시공 손상 변수는 두께 증가량과 두께 증가층 수의 영향이 가장 크고, 동바리 축력은 동바리 지지 층수와 두께 증가층 수가 가장 큰 영향을 미침을 알 수 있다. 이 연구의 결과가 건축물의 다양한 조건에 모두 적용할 수 있는 일반화된 내용은 아니며, 시공 조건과 설계 조건뿐 아니라 양생 온도와 기간 등 환경적인 요인에 의하여 콘크리트의 강도 발현이 달라져 시공 하중이 변화할 수 있으므로 이에 대한 추가적인 분석이 필요하다.