Stress Concentration Analysis of Printed Circuit Heat Exchanger Channels Using a Submodeling Technique

Seunghun Lee; Jin-Seong Park; Jong-Rae Cho; Moonhong Kim

doi:10.7734/COSEIK.2025.38.2.91

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 April 2025. 91-101
https://doi.org/10.7734/COSEIK.2025.38.2.91

Stress Concentration Analysis of Printed Circuit Heat Exchanger Channels Using a Submodeling Technique

부모델링 기법을 이용한 인쇄 회로 열교환기 채널의 응력 집중 분석

Seunghun Lee¹

Jin-Seong Park²

Jong-Rae Cho³

Moonhong Kim⁴^*

이 승훈¹

박 진성²

조 종래³

김 문홍⁴^*

¹MS student, Department of Refrigeration and Air Conditioning Engineering, Korea Maritime & Ocean Univ, Busan, 49112, Korea

²Technical Researcher, DongHwa Entec, Busan, 46753, Korea

³Emeritus Professor, Division of Mechanical Engineering, Korea Maritime & Ocean University, Busan, 49112, Korea

⁴Associate Professor, Division of Mechanical Engineering, Korea Maritime & Ocean University, Busan, 49112, Korea

¹한국해양대학교 냉동공조공학과 석사과정

²동화엔텍 기술연구원

³한국해양대학교 기계공학부 명예교수

⁴한국해양대학교 기계공학부 부교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In this study, stress concentration analyses of Printed Circuit Heat Exchanger (PCHE) channels are performed. To accurately determine the stresses at the channel tips, where stress is concentrated, a submodeling technique based on the analysis results of the entire system is employed. In the submodel, elastic and plastic analyses are performed considering the detailed geometric features of the channel tip and irreversible plastic deformation. By analyzing the stresses obtained from both elastic and plastic analyses, the influence of the fine geometric features at the channel tip on the overall stress distribution of the PCHE is examined. Additionally, the maximum von Mises stress values obtained from the elastic and plastic analyses of the submodel are compared to identify stress concentration tendencies and plastic deformation at the channel tip.

Keywords

printed circuit heat exchanger

thermo-mechanical analysis

stress concentration

submodeling technique

finite element method

본 연구에서는 인쇄 회로 열교환기 채널에서의 응력 집중 해석을 수행하였다. 응력 집중이 발생하는 응력 집중부의 응력을 도출하기 위해 전체 시스템의 해석 결과를 활용하는 부모델링 기법을 사용하였다. 미세한 기하학적 형상과 비가역적 소성 변형을 고려한 부모델의 탄성 및 소성 해석을 수행하였다. 탄성 및 소성 해석에서 얻은 응력을 통해 미세한 기하학적 형상이 PCHE의 응력 분포에 미치는 영향을 파악하였다. 탄성 해석과 소성 해석에서의 최대 폰 미제스 응력을 비교하여 응력 집중부의 응력 집중 경향과 소성 변형을 확인하였다.

키워드

인쇄 회로 열교환기

열-구조 해석

응력 집중

부모델링 기법

유한요소법

MAIN

1. 서 론
2. PCHE 열-구조 해석을 위한 모델과 경계 조건 및 수송 물성치
2.1 PCHE 모델
2.2 작동 유체와 전열판의 물성치
2.3 PCHE 해석을 위한 지배방정식, 경계 조건, 그리고 수송 물성치
3. 응력 집중 분석을 위한 PCHE의 열-구조 해석
3.1 전체 PCHE 모델에 대한 열-구조 해석 결과
3.2 부모델링 기법을 사용한 PCHE 모델에 대한 열-구조 해석 결과
4. 결 론

1. 서 론

인쇄 회로 열교환기(Printed Circuit Heat Exchanger, PCHE)는 기존 열교환기에 비해 높은 열전달 성능과 압력 저항 능력, 그리고 단순한 구조를 가진다(Ayub, 2003; Jayakumar et al., 2008; Neeraas et al., 2004; Southall and Dewson, 2010). 이러한 장점은 PCHE의 독특한 제작 과정에서 기인한다. 작동 유체가 흐르는 채널은 화학적 에칭 공정을 통해 전열판 내부에 형성되며(Bowdery, 2006), 채널이 형성된 전열판들은 층층이 쌓여 확산 접합 공정을 거친다(Huang et al., 2019). 이 두 공정은 추가적인 브레이징 합금(braze alloy) 없이 전열판을 구성하는 단일 합금만을 사용하여 수행된다. 따라서 PCHE는 전열판을 구성하는 해당 단일 합금의 물성치에 기반하여 고온 및 고압 환경에서도 안정적인 성능을 발휘한다(Mylavarapu et al., 2012). PCHE의 이러한 구조적 특성으로 인해 고성능 열교환을 요구하는 수소 에너지(Brown, 2002), 차세대 원자력 발전(Kim et al., 2008), 태양열 발전(Utamura and Tamaura, 2006)과 같은 분야에서 그 수요가 점차 증가하고 있다.

열교환기의 주된 기능은 열전달을 효율적으로 수행하는 것이지만, 높은 온도 차이로 인한 열적 하중과 압력에 의한 기계적 하중을 견뎌내는 구조적 강건성 또한 설계 과정에서 반드시 고려되어야 한다(Bennett et al., 2020). PCHE의 내부 채널은 화학적 에칭과 확산 접합 공정을 통해 날카로운 형상을 가진 응력 집중부(channel tip)를 형성한다. 응력 집중부에서 발생하는 응력 집중은 PCHE의 수명에 결정적인 영향을 미칠 수 있는 소성 변형을 유발한다. 응력 집중부의 응력은 PCHE 설계 단계에서 중요한 검토 대상이며, 이를 정확히 파악하기 위해서는 응력 계산이 필수적이다. 이를 위해 주로 수치 해석적 접근 방식을 사용하여 응력을 계산한다(Lee et al., 2016). 만약 곡률반경이 0이라면, 수치 해석적 접근 방식은 날카로운 응력 집중부에서 이론적으로 무한대의 응력을 도출하기에 수렴된 해를 구할 수 없다. 따라서, 응력 집중부에 미세한 기하학적 형상인 곡률반경을 부여하여 수치적으로 수렴된 해를 구하는 것이 일반적이다(Bennett et al., 2020; Lee and Lee, 2014). 그러나 전체 시스템에 비해 매우 작은 응력 집중부에 미세한 기하학적 형상과 비가역적 소성 변형을 추가로 반영할 경우, 높은 계산 비용이 요구된다.

본 연구의 목적은 PCHE 채널의 응력 집중부에서 발생하는 응력을 정확히 도출하고, 이를 통해 응력 집중을 분석하는 것이다. 이 과정에서 응력 집중부의 미세한 기하학적 형상과 비가역적 소성 변형으로 인해 발생하는 과도한 계산 비용 문제를 해결하는 것이 필수적이다. 이를 위해 본 연구는 PCHE 전체 시스템의 해석 결과를 활용하는 부모델링 기법을 채택한다. 부모델링 기법은 세밀한 격자망을 가진 부모델에 전체 모델의 해석 결과인 온도와 변위 정보를 경계 조건으로 적용한다. PCHE 구조상 응력 집중부는 전체 시스템에 비해 매우 작은 비중을 차지하고, 이를 제외한 대부분의 영역에서는 탄성 변형만을 경험한다. 따라서, 본 연구는 주변 탄성 영역의 해석 결과를 경계 조건으로 사용하여, 채널 끝단의 기하학적 형상이 온전히 표현된 부모델 해석을 수행한다.

PCHE의 구조적 강건성 평가는 ASME Boiler and Pressure Vessel Code Section VIII Divison 2(BPVC VIII-2)를 따른다(Boiler, 2010). ASME BPVC VIII-2는 응력 집중부에서 발생하는 피크 응력(peak stress)을 포함한 최대 폰 미제스 응력(von Mises stress) 값을 구조적 강건성 평가 지표로 사용한다. 응력 집중부는 다각형 구멍에서의 곡률반경에 따른 응력 집중 경향과 유사한 경향을 보임과 동시에 소성 변형이 발생할 가능성이 높다(Chauhan and Sharma, 2016; Sharma, 2012). 이에 따라, 본 연구는 PCHE 전체 시스템의 해석 결과를 경계 조건으로 사용하는 부모델의 탄성 해석과 소성 해석을 각각 수행한다. 부모델에 적용한 경계 조건에 대한 비교를 통해 응력 집중부의 미세한 기하학적 형상이 PCHE의 전체 응력 분포에 미치는 영향을 파악한다. 또한, 부모델의 탄성 해석과 소성 해석을 통해 도출된 최대 폰 미제스 응력 값을 비교하여 응력 집중부의 응력 집중 경향과 소성 변형을 확인한다.

2. PCHE 열-구조 해석을 위한 모델과 경계 조건 및 수송 물성치

이 장에서는 유한 요소 열-구조 해석에 사용된 PCHE 모델의 치수와 두 작동 유체 및 전열판의 물성치에 대하여 설명한다. 유한 요소 열-구조 해석에 사용된 PCHE 모델은 실제 산업에서 사용되는 PCHE에 비해 작은 크기를 가지는 프로토타입(prototype) 모델을 사용하였으며, PCHE 내부의 두 작동 유체는 서로 평행류 흐름을 보이도록 설정하였다.

2.1 PCHE 모델

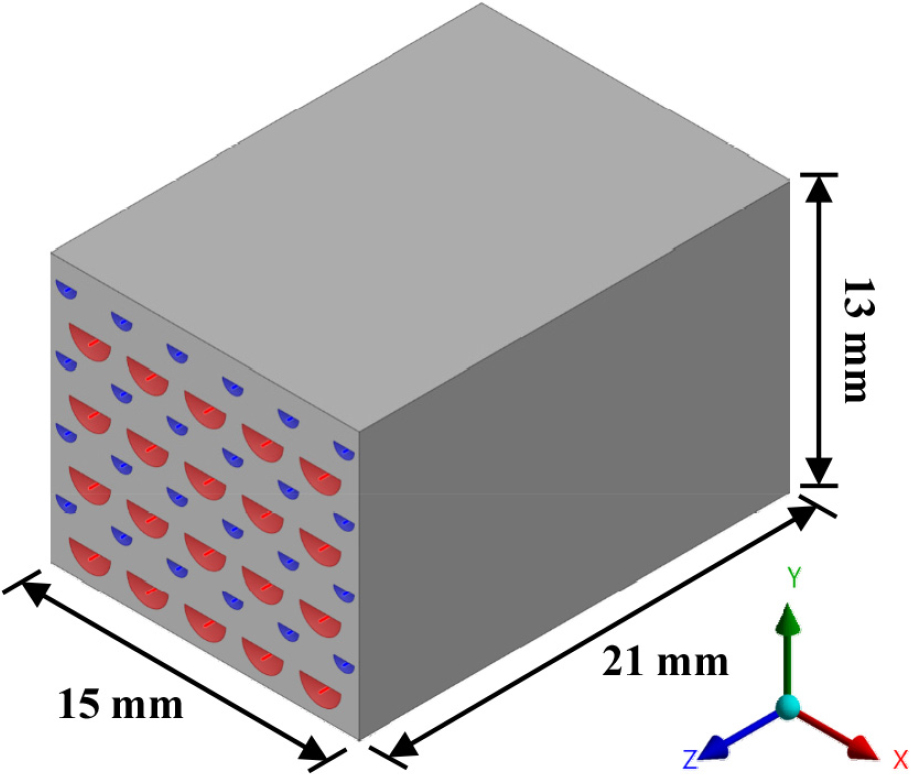
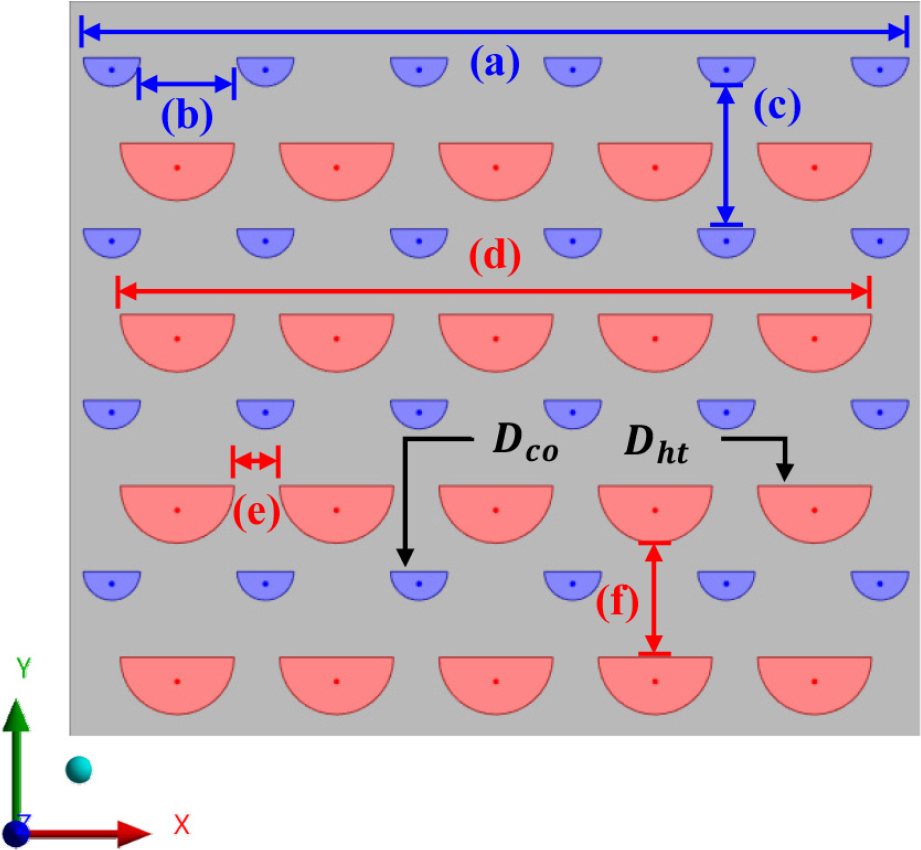
Fig. 1은 PCHE 시스템에서 대칭을 고려한 일부 형상을 나타내고 있다. PCHE는 육면체 형상이며 길이, 폭, 높이는 각각 21mm, 15mm, 그리고 13mm이다. 저온의 유체가 흐르는 채널은 푸른색, 고온의 유체가 흐르는 채널은 붉은색으로 표현하였다. 두 작동 유체가 흐르는 채널은 8개의 층을 가지며, 채널 단면 형상은 Fig. 2와 같다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F1.jpg

Fig. 1.

PCHE model

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F2.jpg

Fig. 2.

Channel cross sectional shape of PCHE model

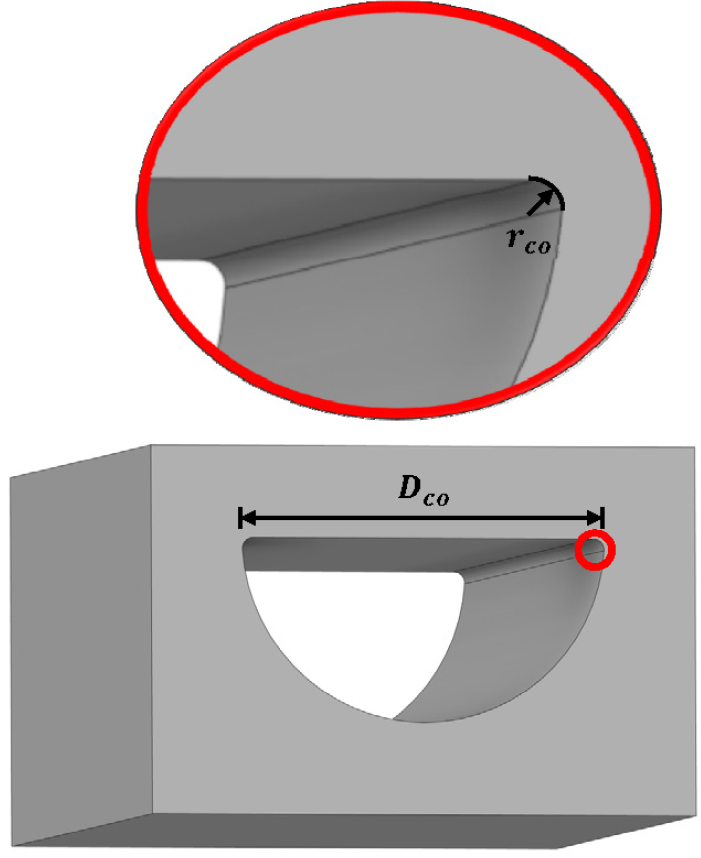
PCHE는 화학적 에칭 공정을 통해 채널이 형성된 전열판을 쌓은 후, 확산 접합 공정을 거쳐 만들어진다. PCHE 공정 특성 상 응력 집중이 발생하는 응력 집중부가 형성되며, 응력 집중부의 형상은 마음대로 조절할 수 없다. 특정 목적에 맞는 PCHE를 개발하기 위해 개발의 초기 단계에서 프로토타입 모델을 만들고 이를 기반으로 설계 방법론을 검증하는 것은 일반적이다. Fig. 3은 1.6mm와 3mm의 채널 직경을 가지는 PCHE를 개발하기 위해 사용한 프로토타입들의 모습이다. 두 PCHE의 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )는 각각 0.1⁄1.6(=0.0625), 0.2⁄3(=0.0667)으로 0.06-0.07 사이의 값을 보인다. 이를 통해 실제 PCHE가 가지는 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )는 채널 직경의 크기와 상관없이 평균적으로 0.06-0.07 사이의 값을 보인다고 가정하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F3.jpg

Fig. 3.

Actual photo of the two fabricated PCHEs: (a) Overall view of PCHE, (b) Channel cross section of PCHE 1, (c) Channel tip microstructure of PCHE 1, (d) Channel cross section of PCHE 2, and (e) Channel tip microstructure of PCHE 2

본 연구의 목적은 응력 집중부의 미세한 기하학적 형상으로 인한 PCHE 채널의 응력 집중을 분석하는 것이다. PCHE 제작 과정에서 채널 직경과 응력 집중부의 형상은 변경될 수 있기에, 다양한 경우를 고려하고자 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )를 0.03에서 0.1 범위에서 0.01씩 차이를 둔 8개의 PCHE 모델을 생성하였다. 이때, 작동 유체의 높은 압력과 큰 온도 변화로 인해 큰 응력이 발생하는 저온 유체 채널의 비 $(r_{c o} / D_{c o})$ 만을 변경하였으며 이는 Fig. 4와 같다. 상대적으로 작은 응력이 발생하는 고온 유체 채널의 비 $(r_{h t} / D_{h t})$ 는 모든 PCHE 모델에서 0.03으로 고정하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F4.jpg

Fig. 4.

Channel diameter ( $D_{c o}$ ) and radius of curvature ( $r_{c o}$ ) at cold fluid channel tip

2.2 작동 유체와 전열판의 물성치

본 연구에서 사용된 저온의 유체는 액화 질소, 고온의 유체는 glycol water이다. 두 작동 유체의 물성치는 모두 온도와 압력의 함수로 표현된다. 본 연구에서는 액화 질소와 glycol water의 압력을 각각 30MPa, 0.3MPa로 일정하다고 가정하였다. 따라서, 액화 질소와 glycol water의 물성치는 모두 온도의 함수로 표현할 수 있다. 액화 질소와 glycol water의 물성치는 상용 프로그램인 REFPROP을 통해 도출하였으며 각각 Table 1, Table 2와 같다.

Table 1.

Material properties of liquid nitrogen ( $L N_{2}$ )

Temp [K]	Density [kg/m³]	Viscosity [Pa･s]	Specific heat [J/kg･K]	Thermal Cond [W/m･K]
103	785.2	0.0001207	1823	0.1373
123	721.4	0.000085	1801.4	0.1133
143	654.1	0.0000636	1795.5	0.0924
162	586.6	0.00005	1785.4	0.076
182	522.2	0.0000409	1749.3	0.0646
202	463.6	0.0000349	1681.8	0.0568

Table 2.

Material properties of glycol water

Temp [K]	Density [kg/m³]	Viscosity [Pa･s]	Specific heat [J/kg･K]	Thermal Cond [W/m･K]
298	1068.7	0.00317	3350.4	0.3802
323	1055.9	0.00169	3442.1	0.3942

PCHE의 전열판을 구성하는 재료는 A240-304이다. A240-304의 물성치는 ASME BPVC, Sec II, Part D를 통해 도출하였으며, Table 3과 같다.

Table 3.

Material properties of A240-304

Temp [K]	Density [kg/m³]	Specific heat [J/kg･K]	Thermal Cond [W/m･K]
298	8030	500	16.3
Thermal expansion coefficient [K^-1]		Elastic Modulus [MPa]	Poisson’s Ratio
0.0000153		195	0.31

2.3 PCHE 해석을 위한 지배방정식, 경계 조건, 그리고 수송 물성치

열교환이 일어나는 동안 PCHE의 운전 조건은 거의 일정하다. 따라서 본 연구에서는 작동 중인 PCHE를 정상상태의 장치라고 가정한다. PCHE 속 작동 유체의 에너지 보존은 다음과 같이 표현된다.

(1)

C_{p} Δ T = h (T_{m} - T_{s})

여기서, $C_{p}$ , $Δ T$ , $h$ , $T_{m}$ , 그리고 $T_{s}$ 는 각각 정압비열, 온도 차, 대류 열전달계수, 작동 유체의 입구와 출구의 평균 온도, 그리고 표면 온도를 나타낸다.

PCHE의 힘 평형은 다음과 같이 표현된다.

(2)

\nabla ∙ σ = 0

여기서, ▽, 그리고 𝜎는 각각 델 연산자(del operator), 그리고 Cauchy 응력 텐서(Cauchy stress tensor)를 나타낸다.

이때, 응력이 변형률과 온도 구배와 선형적인 관계라고 가정한다면, 그 관계를 다음과 같은 구성 방정식으로 표현할 수 있다.

(3)

σ = C : ϵ - C : β Δ T

여기서, $C$ , 𝜖, 그리고 𝛽는 각각 탄성 텐서(elasticity tensor), 변형률 텐서(strain tensor), 그리고 열팽창계수 텐서(thermal expansion coefficient tensor)를 나타낸다.

PCHE 내부의 열전달은 다음과 같이 표현되는 푸리에의 열전도 법칙을 따른다고 가정한다.

(4)

q = - k ∙ \nabla T

여기서, $q$ 그리고 $k$ 는 각각 열 유속 벡터(heat flux vector)와 열전도도 텐서(thermal conductivity tensor)를 나타낸다.

식 (1)을 통해 유동장을 단순화하였으며, 식 (2), (3), (4)는 유한요소법(FEM)을 사용하여 풀었다. 열 해석은 ANSYS steady-state thermal을 사용하여 수행하였으며, 열-구조 해석은 ANSYS mechanical을 사용하여 수행하였다. 유한 요소 열-구조 해석에 필요한 정보는 작동 유체의 질량유량과 작동 유체의 입구 온도, 그리고 두 작동 유체 채널의 대류 열전달계수이다. 본 연구에서 사용된 액화 질소와 glycol water의 전체 질량유량은 각각 10kg/hr, 100kg/hr이며, 입구 온도는 각각 103.15K, 313.15K이고, 출구 온도는 각각 183.15K, 307.15K이다.

유동장을 단순화하는 식 (1)을 사용하기 위해선 두 작동 유체의 대류 열전달계수에 대한 계산이 필요하다. 두 작동 유체의 대류 열전달계수는 다음과 같이 표현된다.

(5)

h = \frac{N u k_{f}}{D_{h}}

여기서, $N u$ , $k_{f}$ , 그리고 $D_{h}$ 는 각각 작동 유체의 Nusselt 수(Nusselt number), 작동 유체의 열전도도, 그리고 직경 $D$ 를 가지는 채널의 수력 직경을 나타낸다. 채널의 수력 직경은 다음과 같이 표현된다.

(6)

D_{h} = \frac{π D}{2 (π / 2 + 1)}

식 (5)를 풀기 위해선 두 작동 유체의 Nusselt 수에 대한 계산이 필요하다. 본 연구에서는 계산의 정확성을 위해 작동 유체의 입구와 출구의 평균 온도에서의 물성치를 사용하여 두 작동 유체의 Nusselt 수를 계산하였다. Nusselt 상관식은 Reynolds 수( $R e$ )와 Prandtl 수( $P r$ )의 함수로 표현된다. 액화 질소와 glycol water의 Reynolds 수와 Prandtl 수는 각각 아래의 두 수식을 통해 계산하였다.

(7)

R e = \frac{\bar{ρ} u D_{h}}{\bar{μ}}

(8)

P r = \frac{{\bar{C}}_{p} \bar{μ}}{\bar{k}}

여기서, $ρ$ , $u$ , $\bar{μ}$ , ${\bar{C}}_{p}$ , 그리고 $\bar{k}$ 는 각각 입구와 출구의 평균 온도에서의 밀도, 작동 유체의 입구 속도, 입구와 출구의 평균 온도에서의 점성계수, 입구와 출구의 평균 온도에서의 열전도도를 나타낸다.

식 (7)을 통해 계산한 액화 질소와 glycol water의 Reynolds 수는 각각 2,836과 10이다. 난류 흐름을 보이는 액화 질소의 Nusselt 수는 Choi(1991)가 제안한 천이 및 난류 영역(2,500<Re<20,000)에서의 Nusselt 상관식을 통해 계산하였다.

(9)

N u = \frac{3.82}{10^{6}} R e^{1.96} P r^{1 / 3}

층류 흐름을 보이는 glycol water의 Nusselt 수는 Erdoğan 등(2006)이 제안한 반원형 단면 채널에서의 Nusselt 수를 사용하였다.

(10)

N u = 4.088

유한 요소 열-구조 해석에 필요한 정보인 작동 유체의 질량유량과 작동 유체의 입구 온도는 주어진 값과 동일한 값을 사용하였으며, 액화 질소와 glycol water 채널의 대류 열전달계수는 각각 식 (5)를 통해 계산된 값인 3,623W/m²﹡K, 870W/m²﹡K을 사용하였다.

3. 응력 집중 분석을 위한 PCHE의 열-구조 해석

본 장에서는 응력 집중 분석을 위해 수행한 PCHE의 유한 요소 열-구조 해석 과정에 대해 설명한다. 본 연구에서는 PCHE 내부에 흐르는 두 작동 유체 사이의 열교환과, 변경되는 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )로 인한 채널의 응력 집중 경향만을 분석하고자 한다. 이러한 이유로 유한 요소 열 해석에서 PCHE는 주위 환경과 단열 상태라고 가정하였다. 유한 요소 열-구조 해석은 유한 요소 열 해석에서 도출한 열 하중과 두 작동 유체의 압력을 적용하여 수행하였으며, 강체 운동을 방지하기 위해 변위 제약 조건을 적용하였다.

3.1 전체 PCHE 모델에 대한 열-구조 해석 결과

PCHE의 구조상 응력 집중부는 전체 PCHE 시스템에 비해 매우 작은 비중을 차지하며, 이를 제외한 대부분의 영역에서는 탄성 변형을 경험한다. 이러한 이유로 PCHE의 열-구조 해석은 탄성 해석을 기반으로 수행하는 것이 일반적이다. 다만, 응력 집중이 발생하는 응력 집중부의 곡률반경이 0일 경우, 유한 요소 탄성 해석 수행 시 이론적으로 무한대의 응력이 도출되기에 수렴된 해를 구할 수 없다. 따라서, 응력 집중부에 유한한 곡률반경을 적용한 후 유한 요소 탄성 해석을 수행하여 수렴된 해를 구하는 것이 일반적이다.

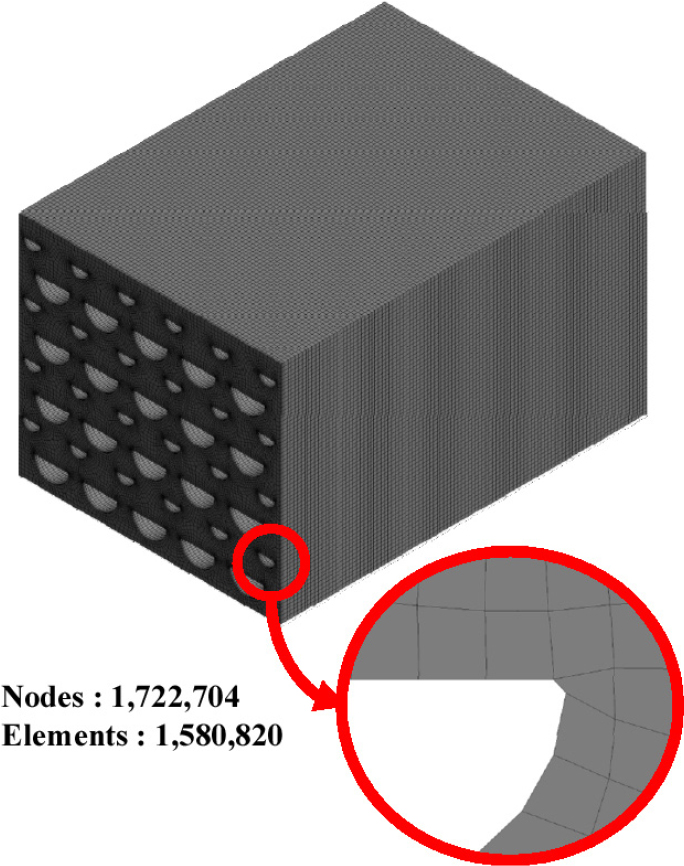
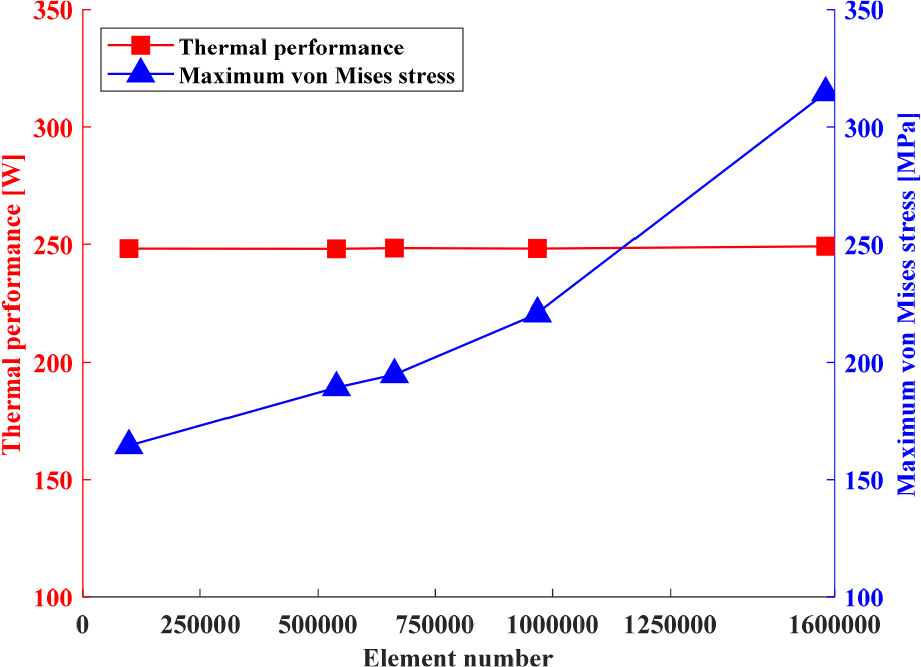
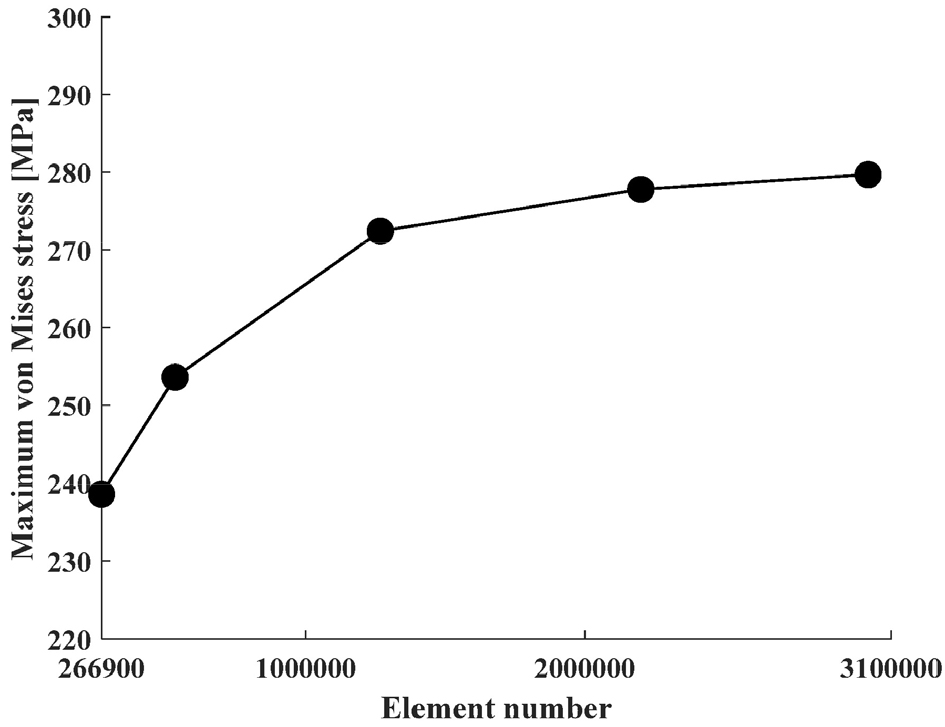
응력 집중부의 미세한 기하학적 형상인 곡률반경은 전체 PCHE 시스템에 비해 크기가 매우 작아 수렴된 해를 구하기 위해선 다수의 자유도(degrees of freedom)를 고려해야 한다. 이는 Fig. 5와 같이 다수의 격자망을 사용하더라도 미세한 기하학적 형상인 곡률반경을 온전히 표현하기 어렵다는 점을 의미한다. 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 0.03인 전체 PCHE 모델에 대한 격자망 수렴도 분석 결과는 Fig. 6과 같다. PCHE의 열 성능은 격자망의 개수가 250,000개 이상이 되면 그 값이 수렴하지만, 최대 폰 미제스 응력의 경우 1,580,820개의 격자망을 사용하더라도 그 값이 수렴하지 않았다. 이는 최대 폰 미제스 응력이 발생하는 응력 집중부의 미세한 기하학적 형상을 격자망이 온전히 표현하지 못했기 때문이다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F5.jpg

Fig. 5.

PCHE model and channel tip elements ( $r / D$ =0.03)

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F6.jpg

Fig. 6.

Mesh convergence analysis for PCHE model ( $r / D$ =0.03)

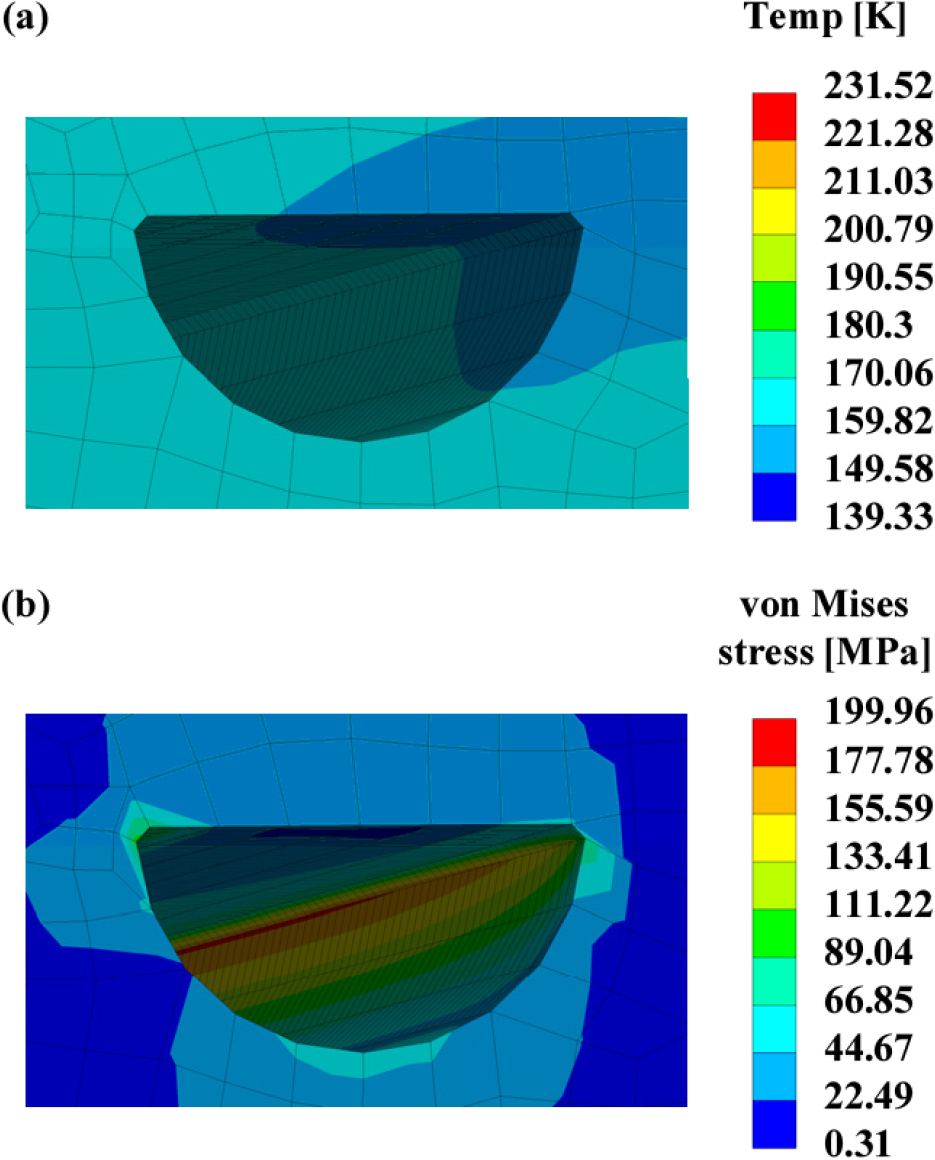
채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 0.03인 전체 PCHE 모델 속 응력 집중부의 온도 분포와 응력 분포는 Fig. 7과 같다. 응력 집중부의 응력이 특정 값으로 수렴하기 위해선 Fig. 7에 표현된 격자망보다 많은 수의 격자망을 사용하여 응력 집중부의 미세한 기하학적 형상을 온전히 표현해야 한다. 유한 요소 해석에서 증가하는 계산 비용 문제를 해결하기 위해 일반적으로 사용하는 방식은 부모델링 기법이다. 본 연구에서도 응력 집중부의 미세한 기하학적 형상을 온전히 표현함과 동시에 계산 비용을 줄이기 위해 부모델링 기법을 추가로 사용하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F7.jpg

Fig. 7.

Finite element thermo-mechanical analysis for PCHE model ( $r / D$ =0.03) : (a) Temperature distribution, and (b) Stress distribution

3.2 부모델링 기법을 사용한 PCHE 모델에 대한 열-구조 해석 결과

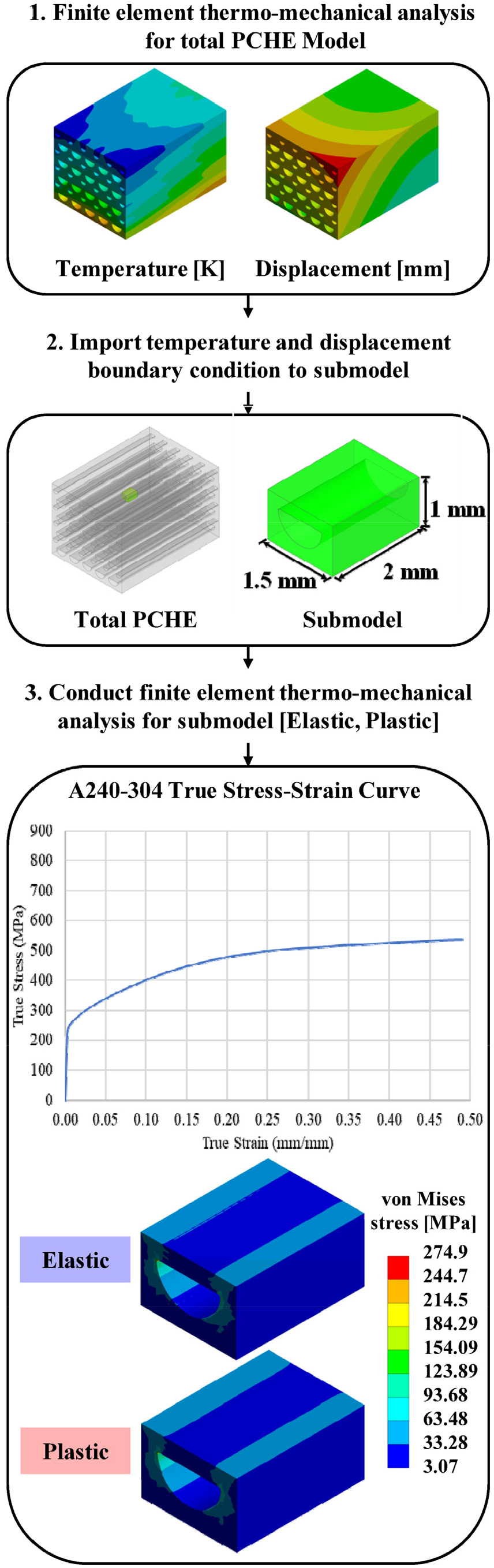
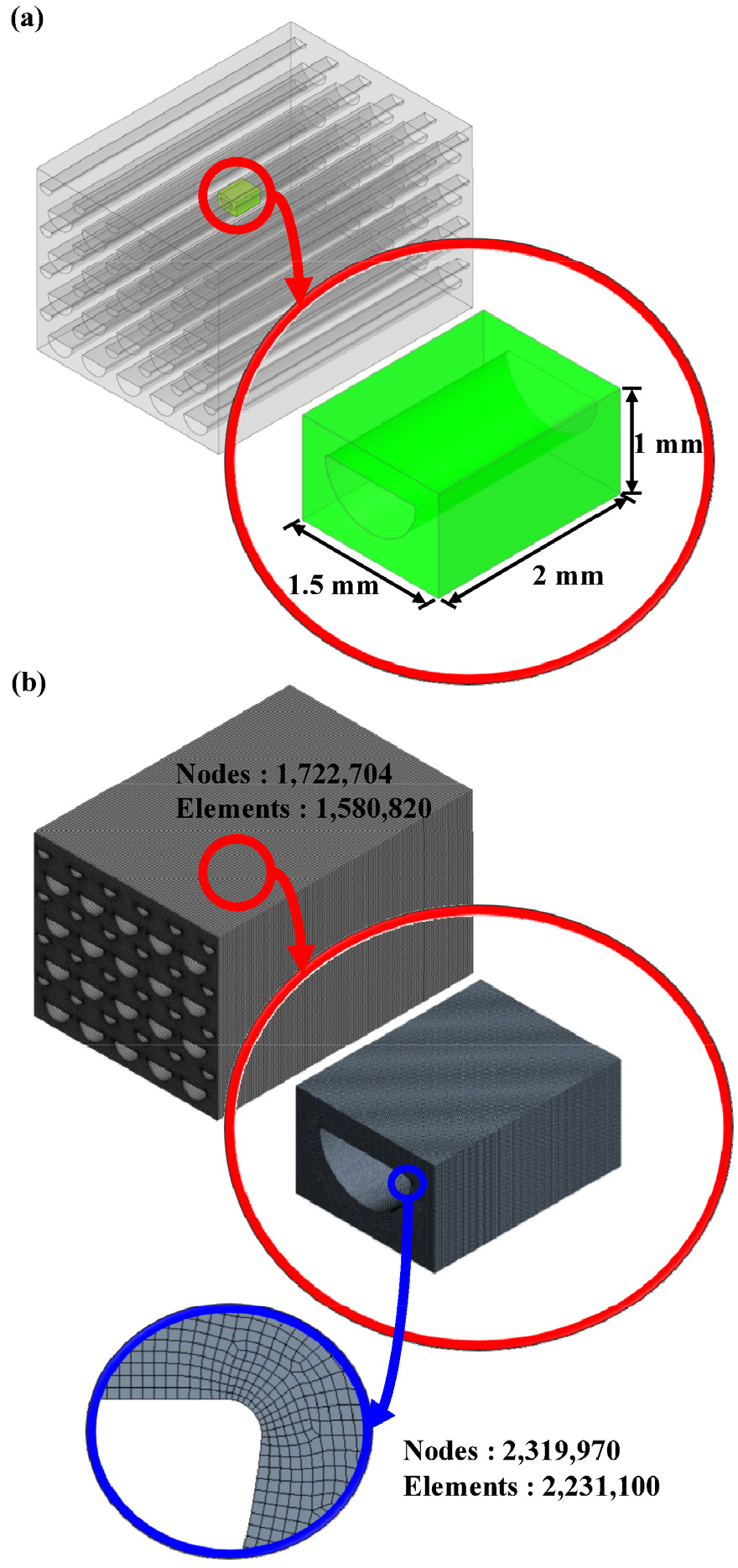
3.1장에서 수행한 성긴 격자망을 가지는 전체 모델의 열-구조 해석을 통해 전체 모델의 온도와 변위 정보를 도출할 수 있다. 전체 모델의 온도와 변위 정보 중, 부모델 영역에 해당하는 온도와 변위만을 새로운 부모델에 부여한다. 부모델에 부여되는 온도와 변위는 전체 모델과 부모델의 격자망 조밀도에 따라 내삽(interpolate)된다. 부모델링 기법의 전체 흐름도와, 부모델링 기법을 적용한 영역 및 부모델의 격자망은 각각 Fig. 8, Fig. 9와 같다. 부모델을 사용하면 응력 집중부의 미세한 기하학적 형상을 온전히 표현할 수 있기에 응력 집중부의 정확한 응력 분포를 도출할 수 있다. 부모델링을 진행한 응력 집중부의 응력 수렴도 분석 결과는 Fig. 10과 같다. 부모델에 2,319,970개 이상의 격자망을 사용할 경우, 응력 집중부의 응력이 수렴하는 것을 확인하였다. 이는 전체 모델에 대한 열-구조 해석에서 미세한 기하학적 형상을 가지는 응력 집중부의 응력을 수렴시키기 위해서는 2,319,970개의 격자망보다 100배 이상 많은 격자망이 필요함을 의미한다. 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 서로 다른 8개의 부모델에 대한 열-구조 해석은 모두 2,300,000개 이상의 격자망을 사용하여 수행하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F8.jpg

Fig. 8.

Flow chart of submodel analysis

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F9.jpg

Fig. 9.

Details of submodel ( $r / D$ =0.03): (a) Location, and (b) Elements

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F10.jpg

Fig. 10.

Mesh convergence analysis for submodel ( $r / D$ =0.03)

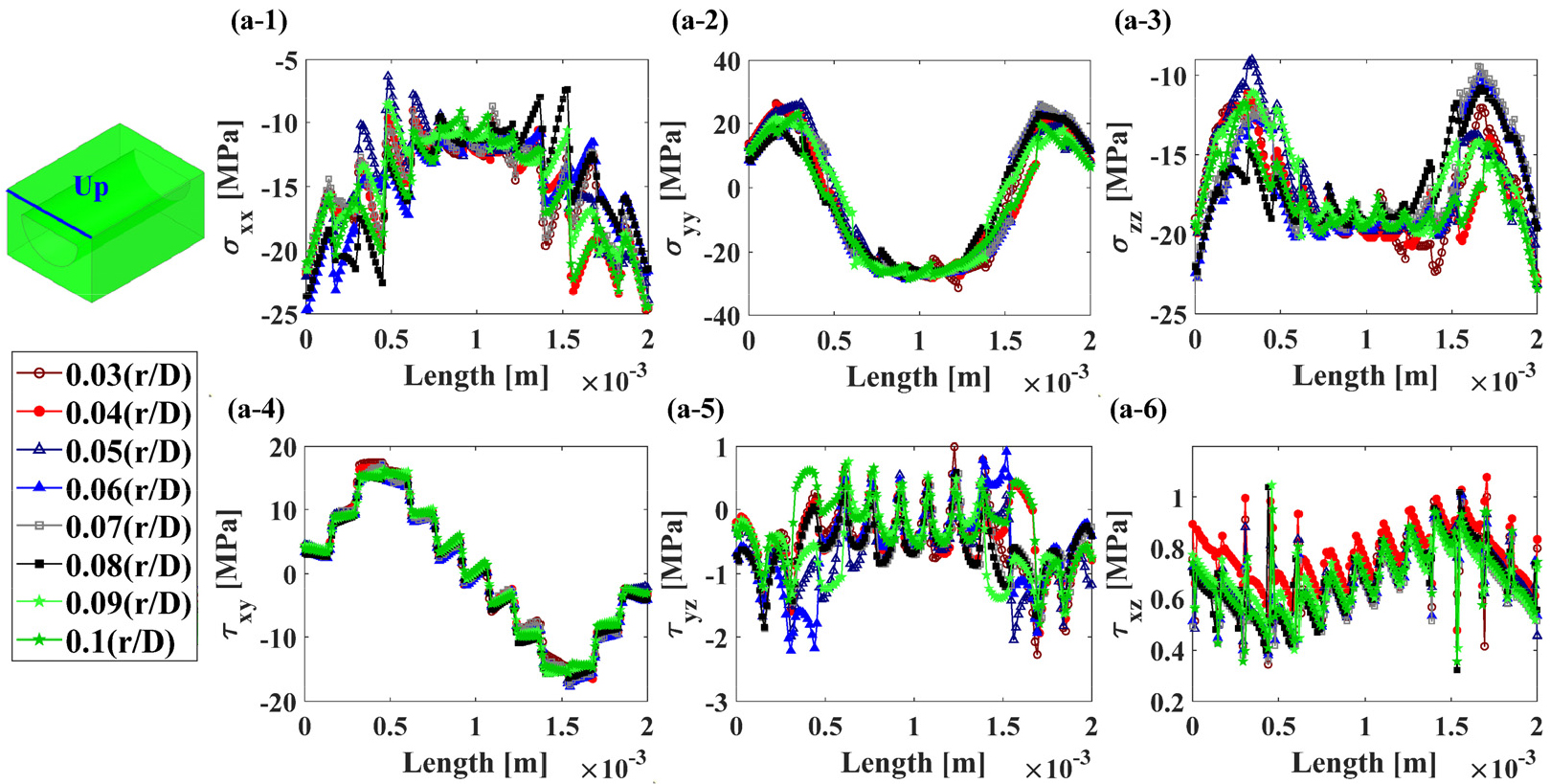
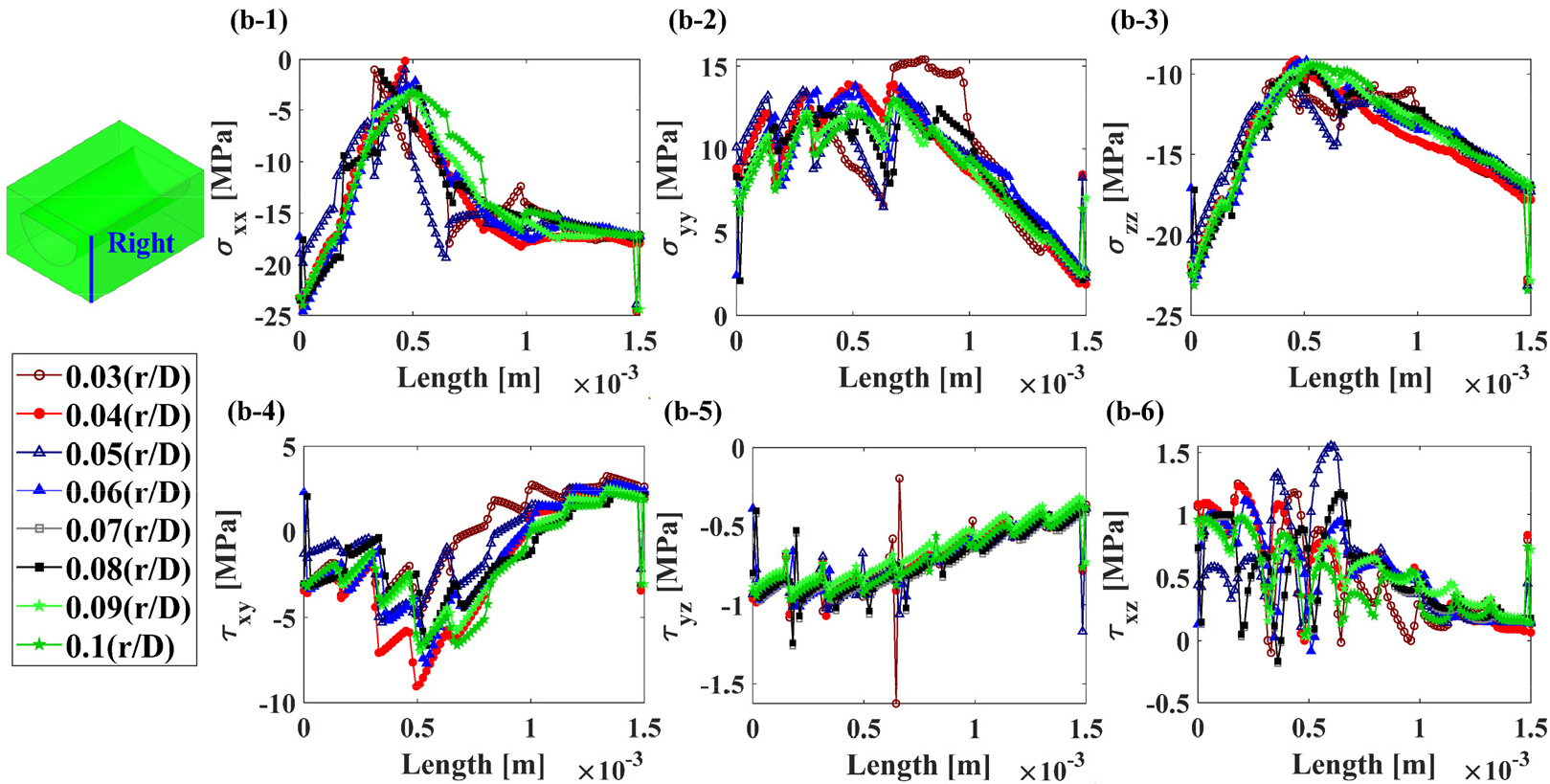
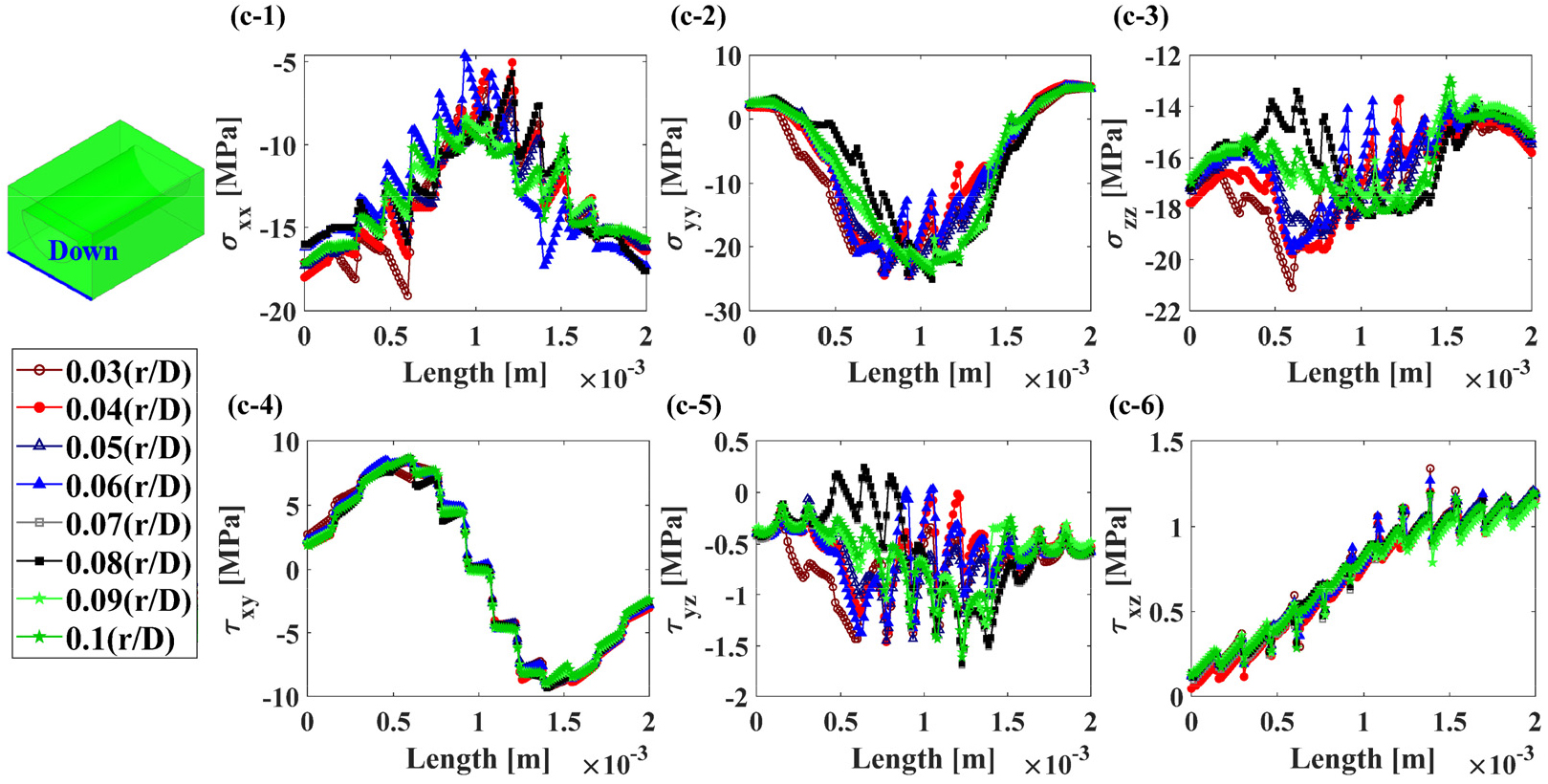
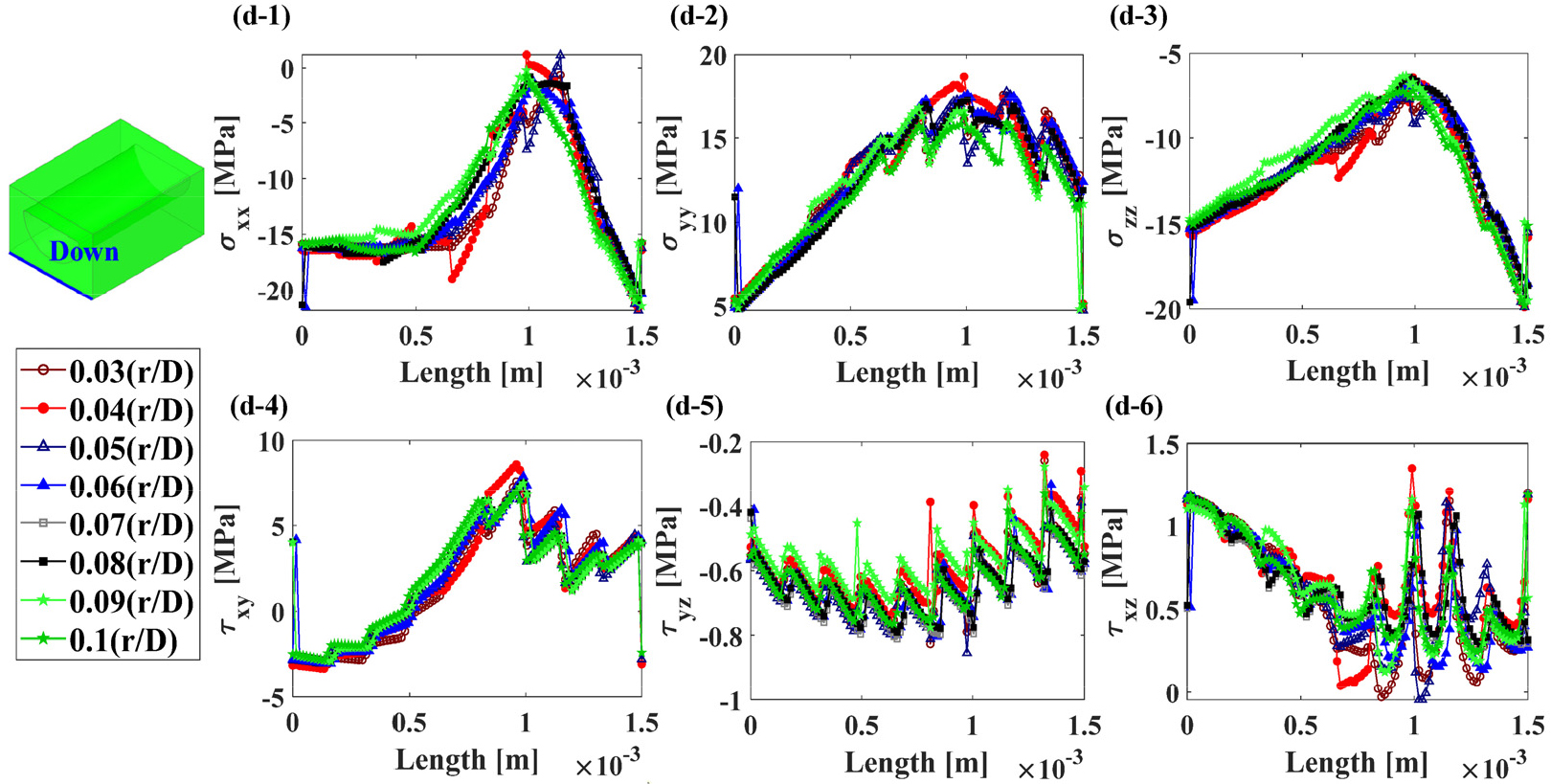
응력 집중부를 제외한 PCHE의 대부분의 영역은 탄성 변형을 경험한다. 따라서, 부모델에 경계 조건으로 부여하는 온도와 변위 정보는 전체 모델의 탄성 해석을 통해 도출된 값을 사용하였다. 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 서로 다른 8개의 전체 PCHE 모델의 온도와 변위로 인한 부모델의 응력 성분 차이는 Fig. 11, Fig. 12, Fig. 13, 그리고 Fig. 14와 같다. 이를 통해 응력 집중부의 미세한 기하학적 형상의 변화는 탄 변형을 경험하는 영역의 응력 분포에 큰 영향을 주지 않는다는 것을 확인하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F11.jpg

Fig. 11.

Stress components at submodel up location: $σ_{x x}$ (a-1), $σ_{y y}$ (a-2), $σ_{z z}$ (a-3), $τ_{x y}$ (a-4), $τ_{y z}$ (a-5), and $τ_{x z}$ (a-6)

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F12.jpg

Fig. 12.

Stress components at submodel right location: $σ_{x x}$ (b-1), $σ_{y y}$ (b-2), $σ_{z z}$ (b-3), $τ_{x y}$ (b-4), $τ_{y z}$ (b-5), and $τ_{x z}$ (b-6)

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F13.jpg

Fig. 13.

Stress components at submodel down location: $σ_{x x}$ (c-1), $σ_{y y}$ (c-2), $σ_{z z}$ (c-3), $τ_{x y}$ (c-4), $τ_{y z}$ (c-5), and $τ_{x z}$ (c-6)

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F14.jpg

Fig. 14.

Stress components at submodel left location: $σ_{x x}$ (d-1), $σ_{y y}$ (d-2), $σ_{z z}$ (d-3), $τ_{x y}$ (d-4), $τ_{y z}$ (d-5), and $τ_{x z}$ (d-6)

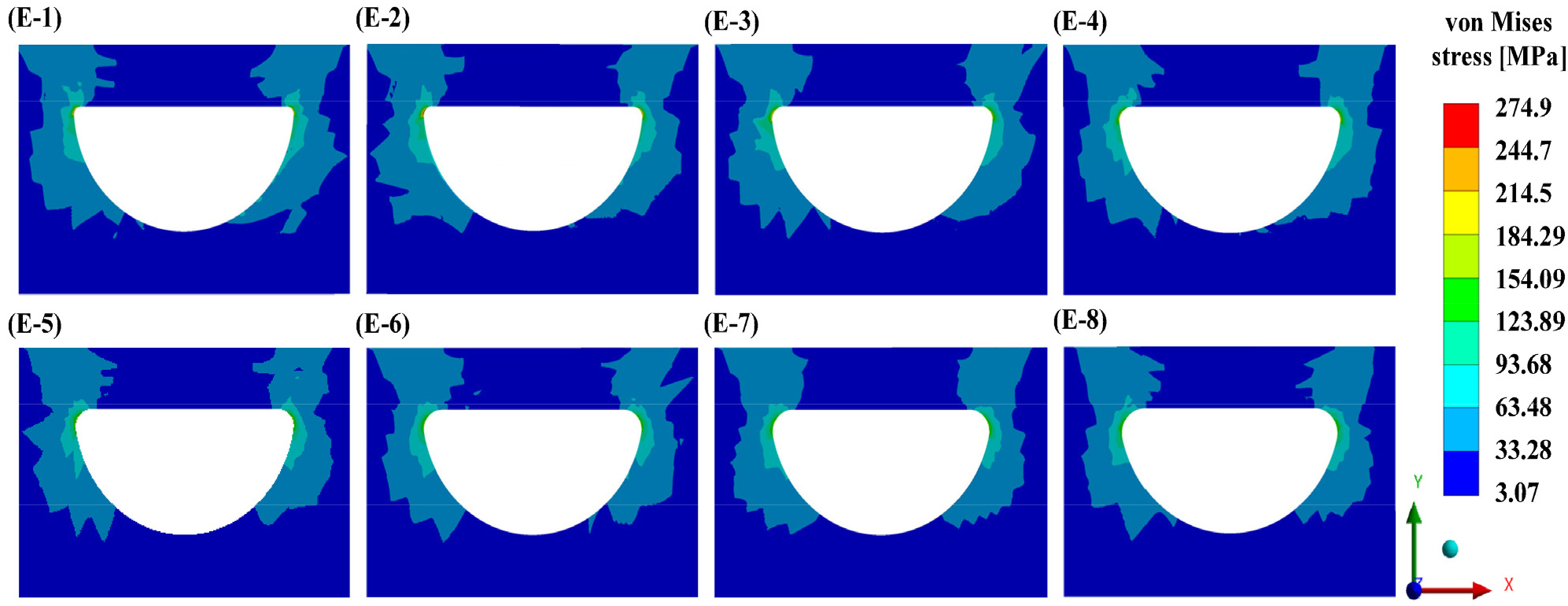
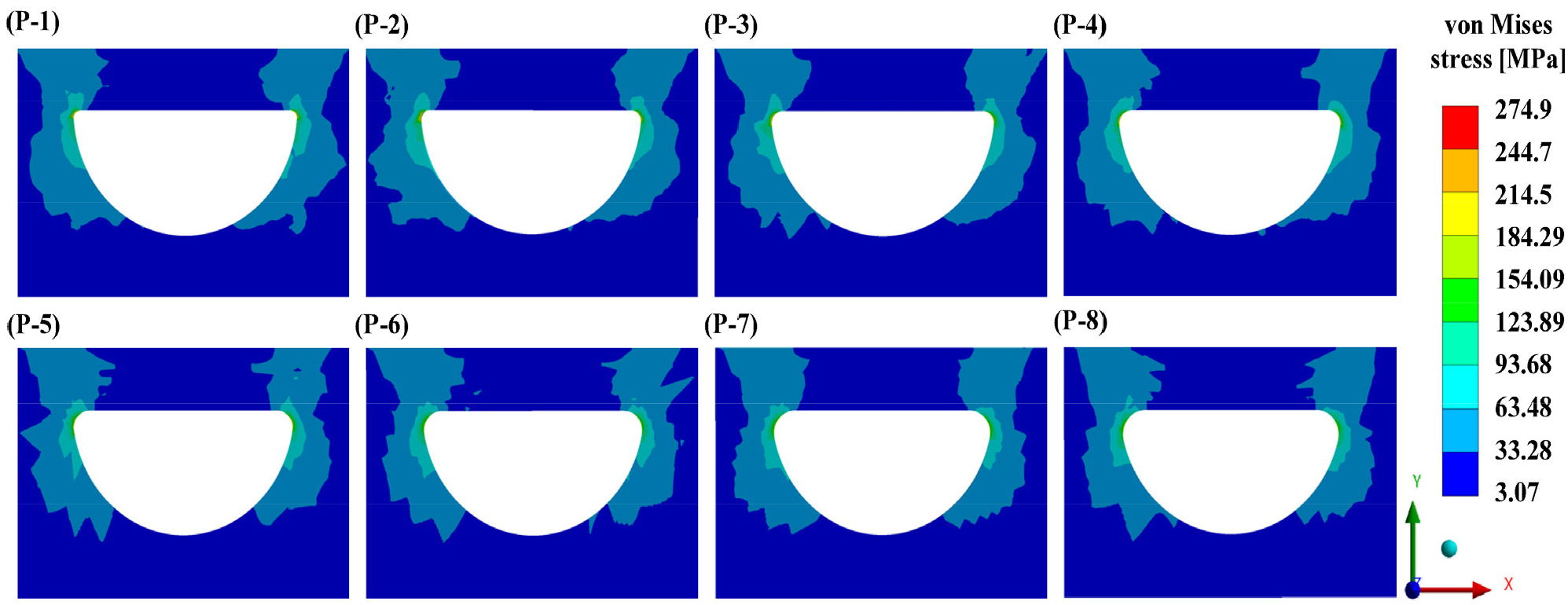
탄성 변형을 경험하는 영역의 온도와 변위 정보를 경계 조건을 부여한 부모델에 대한 탄성 해석과 소성 해석에서의 응력 분포는 각각 Fig. 15, Fig. 16과 같다. 단면의 응력 분포는 탄성 해석과 소성 해석 사이에 큰 차이를 보이지 않는다. 이는 소성 영역이 상대적으로 작기 때문이다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F15.jpg

Fig. 15.

Stress distribution around the channel tip in elastic analysis: (E-1) $r / D$ =0.03, (E-2) $r / D$ =0.04, (E-3) $r / D$ =0.05, (E-4) $r / D$ =0.06, (E-5) $r / D$ =0.07, (E-6) $r / D$ =0.08, (E-7) $r / D$ =0.09, and (E-8) $r / D$ =0.1

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F16.jpg

Fig. 16.

Stress distribution around the channel tip in plastic analysis: (P-1) $r / D$ =0.03, (P-2) $r / D$ =0.04, (P-3) $r / D$ =0.05, (P-4) $r / D$ =0.06, (P-5) $r / D$ =0.07, (P-6) $r / D$ =0.08, (P-7) $r / D$ =0.09, and (P-8) $r / D$ =0.1

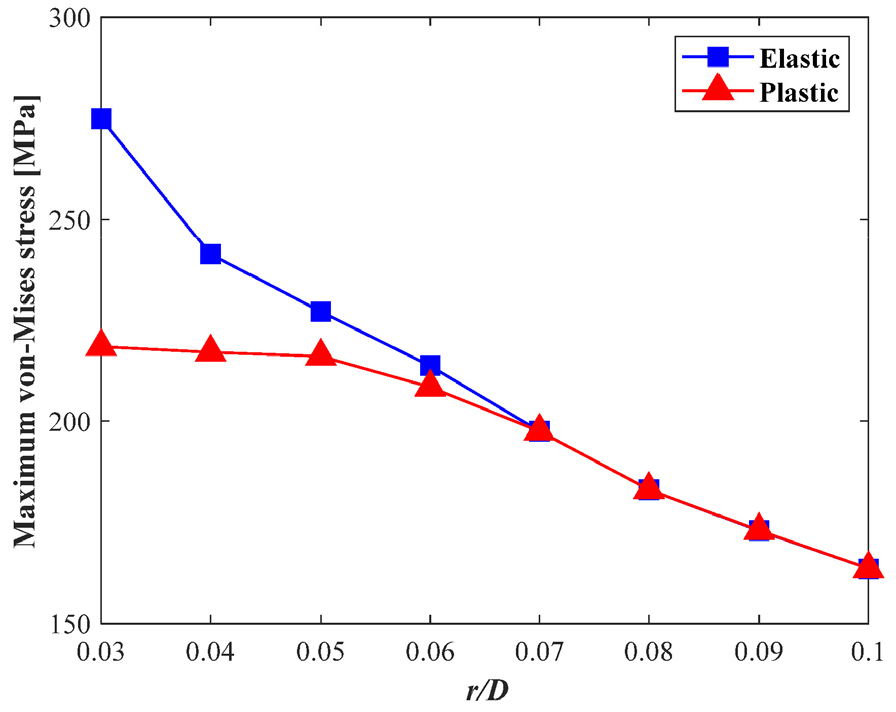
응력 집중부에서 도출되는 최대 폰 미제스 응력만을 비교한 결과는 Fig. 17과 같다. 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 0.06보다 클 경우, 탄성 해석과 소성 해석에서의 폰 미제스 응력이 유사함을 확인하였다. 그러나 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 0.06보다 작다면 응력에 대한 과대평가로 인해 폰 미제스 응력의 오차가 최대 56.5MPa 정도 발생함을 확인하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380203/images/Figure_jcoseik_38_02_03_F17.jpg

Fig. 17.

Comparison of maximum von Mises stress

5. 결 론

본 연구에서는 PCHE 채널의 응력 집중 분석을 수행하였다. 화학적 에칭과 확산 접합 공정을 거치며 형성되는 날카로운 형상의 응력 집중부는 소성 변형을 유발할 수 있으며, 이는 PCHE 채널의 응력 집중부에서 발생하는 응력에 결정적인 영향을 미칠 수 있다. PCHE 설계 단계에서 응력 집중부의 정확한 응력 계산은 필수적이며, 이를 위해 계산 비용을 줄이면서도 응력 집중부의 미세한 기하학적 형상을 온전히 표현할 수 있는 부모델링 기법을 사용하였다.

부모델에 경계 조건으로 부여한 온도와 변위로 인한 응력 성분을 비교한 결과, 응력 집중부의 미세한 기하학적 형상인 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )는 탄성 변형을 경험하는 영역의 응력 분포에 큰 영향을 주지 않는다는 것을 확인하였다. 부모델에 대한 탄성 해석과 소성 해석 결과, 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 작을수록 응력 집중이 발생하는 경향이 있으며, 이는 다각형 구멍에서의 곡률반경에 따른 응력 집중 경향과 유사함을 확인하였다. 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 0.06보다 클 경우, 응력에 대한 과대평가가 발생하지 않아 탄성 해석만으로도 PCHE 채널의 응력 집중을 온전히 고려할 수 있다. 그러나 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )가 0.06보다 작다면 응력에 대한 과대평가로 인해 PCHE 채널의 응력에 최대 56.5 MPa 정도의 오차가 발생한다. PCHE 채널의 응력 집중부 응력을 정확히 도출하기 위해선 채널 직경( $D$ )에 대한 곡률반경( $r$ ) 비( $r / D$ )에 따라 적합한 해석 방식을 선정해야 한다.

Acknowledgements

이 논문은 2024년도 정부(산업통상자원부)의 재원으로 한국산업기술기획평가원 소재부품장비기술개발사업의 지원을 받아 수행된 연구임(과제번호 : 20022454).

References

Ayub, Z.H. (2003) Plate Heat Exchanger Literature Survey and New Heat Transfer and Pressure Drop Correlations for Refrigerant Evaporators, Heat Trans. Eng., 24(5), pp.3~16.

10.1080/01457630304056

Bennett, K., Chen, Y.T. (2020) One-Way Coupled Three-Dimensional Fluid-Structure Interaction Analysis of Zigzag-Channel Supercritical CO₂ Printed Circuit Heat Exchangers, Nucl. Eng. & Des., 358, p.110434.

10.1016/j.nucengdes.2019.110434

Boiler, A.S.M.E. (2010) Pressure Vessel Code AN International Code VIII Division 2 Alternative Rules 'Rules for Construction of Pressure Vessels.

Bowdery, T. (2006) LNG Applications of Diffusion Bonded Heat Exchangers, AIChE Spring Meeting, In: 6th Topical conference on natural gas utilization, Orlando, April 23-27.

Brown, L.C. (2002) High Efficiency Generation of Hydrogen Fuels using Nuclear Power Annual Report August, General Atomics, San Diego, CA (United States).

10.2172/804347

Chauhan, M.M., Sharma, D.S. (2016) Stress Concentration at the Corners of Polygonal Hole in Finite Plate, Aerosp. Sci. & Technol., 58, pp.197~206.

10.1016/j.ast.2016.08.014

Choi, S.B. (1991) Fluid Flow and Heat Transfer in Microtubes, Micromechanical Sensors, Actuators, and Systems, ASME, pp.123~134.

Erdoğan, M.E., Imrak, C.E. (2006) The Effects of Duct Shape on the Nusselt Number, Math. & Comput. Appl., 11(3), p.235.

10.3390/mca11020235

Huang, C., Cai, W., Wang, Y., Liu, Y., Li, Q., Li, B. (2019) Review on the Characteristics of Flow and Heat Transfer in Printed Circuit Heat Exchangers, Appl. Therm. Eng., 153, pp.190~205.

10.1016/j.applthermaleng.2019.02.131

Jayakumar, J.S., Mahajani, S.M., Mandal, J.C., Vijayan, P.K., Bhoi, R. (2008) Experimental and CFD Estimation of Heat Transfer in Helically Coiled Heat Exchangers, Chem. Eng. Res. & Des., 86(3), pp.221~232.

10.1016/j.cherd.2007.10.021

Kim, D.E., Kim, M.H., Cha, J.E., Kim, S.O. (2008) Numerical Investigation on Thermal-Hydraulic Performance of New Printed Circuit Heat Exchanger Model, Nucl. Eng. & Des., 238(12), pp.3269~3276.

10.1016/j.nucengdes.2008.08.002

Lee, S.G., Gong, D.H., Sim, J.S., Shin, S.J. (2016) Verification and Suggestion of Optimization Method for Rivet Arrangement with Regard to Stress Concentration between Hole-Edge and Hole-Hole on a 2-D Plate, J. Comp. Struct. Eng. Inst. Korea, 29(6), pp.491~498.

10.7734/COSEIK.2016.29.6.491

Lee, Y., Lee, J.I. (2014) Structural Assessment of Intermediate Printed Circuit Heat Exchanger for Sodium-Cooled Fast Reactor with Supercritical CO₂ Cycle, Ann. Nucl. Energy, 73, pp.84~95.

10.1016/j.anucene.2014.06.022

Mylavarapu, S.K., Sun, X., Christensen, R.N., Unocic, R.R., Glosup, R.E., Patterson, M.W. (2012) Fabrication and Design Aspects of High-Temperature Compact Diffusion Bonded Heat Exchangers, Nucl. Eng. & Des., 249, pp.49~56.

10.1016/j.nucengdes.2011.08.043

Neeraas, B.O., Fredheim, A.O., Aunan, B. (2004) Experimental Data and Model for Heat Transfer, in Liquid Falling Film Flow on Shell-Side, for Spiral-Wound LNG Heat Exchanger, Int. J. Heat & Mass Trans., 47(14~16), pp.3565~3572.

10.1016/j.ijheatmasstransfer.2004.01.009

Sharma, D.S. (2012) Stress Distribution Around Polygonal Holes, Int. J. Mech. Sci., 65(1), pp.115~124.

10.1016/j.ijmecsci.2012.09.009

Southal, D., Dewson, S.J. (2010) Innovative Compact Heat Exchangers, Int. Congr. Adv. Nucl. Power Plants 2010, ICAPP 2010, 1, pp.218~226.

Utamura, M., Tamaura, Y. (2006) A Solar Gas Turbine Cycle with Super-Critical Carbon Dioxide as a Working Fluid, In Turbo Expo: Power for Land, Sea, and Air, 42398, pp.329~335.

10.1115/GT2006-90864

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Stress Concentration Analysis of Printed Circuit Heat Exchanger Channels Using a Submodeling Technique

ABSTRACT

MAIN

Fig. 1.

PCHE model

Fig. 2.

Channel cross sectional shape of PCHE model

Fig. 3.

Actual photo of the two fabricated PCHEs: (a) Overall view of PCHE, (b) Channel cross section of PCHE 1, (c) Channel tip microstructure of PCHE 1, (d) Channel cross section of PCHE 2, and (e) Channel tip microstructure of PCHE 2

Fig. 4.

Channel diameter (Dco) and radius of curvature (rco) at cold fluid channel tip

Table 1.

Material properties of liquid nitrogen (LN2)

Table 2.

Material properties of glycol water

Table 3.

Material properties of A240-304

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Fig. 5.

PCHE model and channel tip elements (r/D=0.03)

Fig. 6.

Mesh convergence analysis for PCHE model (r/D=0.03)

Fig. 7.

Finite element thermo-mechanical analysis for PCHE model (r/D=0.03) : (a) Temperature distribution, and (b) Stress distribution

Fig. 8.

Flow chart of submodel analysis

Fig. 9.

Details of submodel (r/D=0.03): (a) Location, and (b) Elements

Fig. 10.

Mesh convergence analysis for submodel (r/D=0.03)

Fig. 11.

Stress components at submodel up location: σxx(a-1), σyy(a-2), σzz(a-3), τxy(a-4), τyz(a-5), and τxz(a-6)

Fig. 12.

Stress components at submodel right location: σxx(b-1), σyy(b-2), σzz(b-3), τxy(b-4), τyz(b-5), and τxz(b-6)

Fig. 13.

Stress components at submodel down location: σxx(c-1), σyy(c-2), σzz(c-3), τxy(c-4), τyz(c-5), and τxz(c-6)

Fig. 14.

Stress components at submodel left location: σxx(d-1), σyy(d-2), σzz(d-3), τxy(d-4), τyz(d-5), and τxz(d-6)

Fig. 15.

Stress distribution around the channel tip in elastic analysis: (E-1) r/D=0.03, (E-2) r/D=0.04, (E-3) r/D=0.05, (E-4) r/D=0.06, (E-5) r/D=0.07, (E-6) r/D=0.08, (E-7) r/D=0.09, and (E-8) r/D=0.1

Fig. 16.

Stress distribution around the channel tip in plastic analysis: (P-1) r/D=0.03, (P-2) r/D=0.04, (P-3) r/D=0.05, (P-4) r/D=0.06, (P-5) r/D=0.07, (P-6) r/D=0.08, (P-7) r/D=0.09, and (P-8) r/D=0.1

Fig. 17.

Comparison of maximum von Mises stress

Acknowledgements

References

Channel diameter ( $D_{c o}$ ) and radius of curvature ( $r_{c o}$ ) at cold fluid channel tip

Material properties of liquid nitrogen ( $L N_{2}$ )

PCHE model and channel tip elements ( $r / D$ =0.03)

Mesh convergence analysis for PCHE model ( $r / D$ =0.03)

Finite element thermo-mechanical analysis for PCHE model ( $r / D$ =0.03) : (a) Temperature distribution, and (b) Stress distribution

Details of submodel ( $r / D$ =0.03): (a) Location, and (b) Elements

Mesh convergence analysis for submodel ( $r / D$ =0.03)

Stress components at submodel up location: $σ_{x x}$ (a-1), $σ_{y y}$ (a-2), $σ_{z z}$ (a-3), $τ_{x y}$ (a-4), $τ_{y z}$ (a-5), and $τ_{x z}$ (a-6)

Stress components at submodel right location: $σ_{x x}$ (b-1), $σ_{y y}$ (b-2), $σ_{z z}$ (b-3), $τ_{x y}$ (b-4), $τ_{y z}$ (b-5), and $τ_{x z}$ (b-6)

Stress components at submodel down location: $σ_{x x}$ (c-1), $σ_{y y}$ (c-2), $σ_{z z}$ (c-3), $τ_{x y}$ (c-4), $τ_{y z}$ (c-5), and $τ_{x z}$ (c-6)

Stress components at submodel left location: $σ_{x x}$ (d-1), $σ_{y y}$ (d-2), $σ_{z z}$ (d-3), $τ_{x y}$ (d-4), $τ_{y z}$ (d-5), and $τ_{x z}$ (d-6)

Stress distribution around the channel tip in elastic analysis: (E-1) $r / D$ =0.03, (E-2) $r / D$ =0.04, (E-3) $r / D$ =0.05, (E-4) $r / D$ =0.06, (E-5) $r / D$ =0.07, (E-6) $r / D$ =0.08, (E-7) $r / D$ =0.09, and (E-8) $r / D$ =0.1

Stress distribution around the channel tip in plastic analysis: (P-1) $r / D$ =0.03, (P-2) $r / D$ =0.04, (P-3) $r / D$ =0.05, (P-4) $r / D$ =0.06, (P-5) $r / D$ =0.07, (P-6) $r / D$ =0.08, (P-7) $r / D$ =0.09, and (P-8) $r / D$ =0.1