1. 서 론

등기하해석법(IGA: IsoGeometric Analysis)은 NURBS(Non-Uniform Rational B-Splines)와 같은 CAD 데이터로부터 주어지는 기저함수를 이용하여 별도의 요소망 생성없이 해석하는 방법이다(Hughes et al., 2005). NURBS는 자유 형상 표면 등 어떠한 형태도 정확하게 표현할 수 있는 수학적 기저함수이다. CAD 데이터를 이산화 과정없이 바로 이용하기 때문에 수직 벡터나 곡률과 같이 높은 차수의 기하형상을 정확하게 계산할 수 있기 때문에 정확한 기하 형상을 요구하는 쉘 구조물의 해석에 매우 적합한 방법이다. 하지만, 텐서량으로 표현된 NURBS로 복잡한 기하형상을 표현하는 데는 한계가 있으며, 특히, 국부적으로 미세한 형상 표현을 하기 위해서는 좀 더 세밀한 조정점을 구성하여야 하는데, 이를 위해서 T-spline이나 PHT-spline 과 같은 특별한 함수를 사용하여야 한다(Hughes et al., 2005). 이를 해결하기 위해서는 조정점의 밀도가 다른 여러 개의 NURBS를 사용하는 다중패치모델(multipatch model)을 사용하여야 한다.

다중 패치 모델에서 패치 사이의 경계에서 연속성이 부족하기 때문에 이를 이용한 등기하해석에서는 경계면에서 변위(displacement)와 견인힘(traction)에 대한 연속 조건을 부과하여야 한다. Embar와 Dolbow(2010)는 spline 기반의 기저함수를 이용한 유한요소법에서 니셰(Nitsche) 방법을 이용하여 이러한 경계 조건을 부가하는 방법을 제안하였다. 니셰 방법은 변분식으로 표현된 지배방정식에 변위차와 끌림힘의 차의 곱으로 이루어진 포텐셜 함수(potential function)의 변분을 추가해 두 영역의 경계에서의 연속조건을 부가할 수 있는 방법이다. Nguyen 등(2014)와 Guo와 Ruess(2015)는 이러한 니셰 방법을 이용하여 등기하해석법에서 다중 패치로 이루어진 모델을 해석할 수 있는 방법을 제안하였다. Kim과 Koo(2017)는 밀도가 다른 조정점을 가지고 있는 다중 패치 문제어서 니셰 방법을 이용하면 변위장 뿐 아니라 응력장에서도 패치 사이의 연속성을 부가할 수 있음을 보였다. Kim 등(2023)는 이러한 니셰 방법을 1차 전단변형을 고려한 기하학적으로 엄밀한 쉘요소에 적용하여, 막(membrane), 굽힘(bending) 거동 뿐 아니라 전단 거동 합력에 대한 경계 조건을 유도하였다.

등기하해석에서는 NURBS 기저함수가 적분 요소사이에서 높은 연속성을 가지고 있다. 이러한 속성은 변위장과 회전장에서 같은 차수의 기저함수를 사용하는 1차 전단변형을 고려한 쉘의 해석에서 추가적인 제한조건으로 작용할 수 있다(Adam et al., 2014). 적분 요소 사이의 연속성을 낮추어 이러한 문제를 해결할 수 있는데, Kim 등(2022)의 논문에서는 베지어 추출법(Bézier extraction)을 사용하여 NURBS 기저함수의 연속성을 낮추었다. 이와 동시에 변위장과 회전장에서 같은 차수의 기저함수 사용으로 인해 발생하는 해석 장의 불일치(analysis field inconsistency)를 해결하기 위해 가정된 자연 변형률(ANS: Assumed Natural Strain)을 동시에 적용하였다.

니셰 방법으로부터 유도된 식의 양정 행렬(positive definite matrix)를 보장하기 위해서 안정화 매개변수(stability parameters)를 도입하였다. 이 매개변수는 일반화된 고유치해석(generalized eigenvalue analysis)을 얻을 수 있으며, 두 패치 사이의 조정점 망의 밀도차에 따라 다른 최적화된 안정화 계수를 구할 수 있다.

본 논문에서는 니셰 방법을 적용한 다중 패치 등기하해석법에 대해서 살펴보고 이 방법을 1차원 전단 변형을 고려한 기하학적으로 엄밀한 쉘의 해석에 적용하였다. 제시한 방법이 패치간 변위장과 응력장의 연속성을 보장함을 몇몇 수치 예제를 통해서 보여주도록 하겠다. 추가로 양정행렬을 보장하기 위한 최적의 안정화 계수를 구하는 방법을 살펴보고 조정점 밀도에 따른 다중 패치 등기하해석의 결과를 분석하고 최적의 안정화 매개변수 값를 제안하였다.

2. 본 론

이 장에서는 다중 패치 등기하해석을 위한 니셰 방법을 소개한 후, 이 방법을 1차 전단변형을 고려한 쉘의 해석에 적용한 방법을 보여주도록 하겠다. 또한, 최적의 안정하 매개변수를 구하기 위한 수식 전개 과정과 함께 최적의 안정화 매개변수 값을 수치적 예제를 통해서 제안하도록 하겠다.

2.1 니셰 방법(Nitsche’s method)

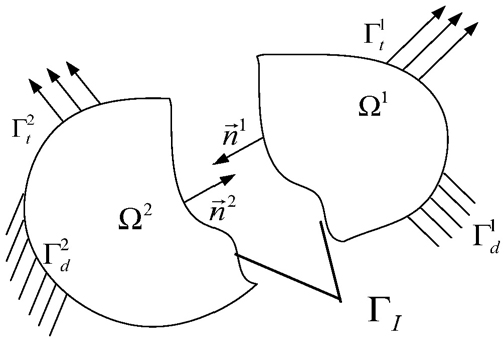
Fig. 1과 같이 2개의 영역 Ω1과 Ω2로 이루어진 영역에 대한 변분방정식은 다음과 같이 표현할 수 있다.

Fig. 1.

Multipatch problem

여기서, a(∙,∙)과 l(∙)은 각각 이중선형(bilinear) 에너지 항과 선형(linear) 하중항이며,Z¯k는 영역 Ωk의 경계Γ¯dk에서 변위경계조건을 만족시키는 함수공간을 의미한다. 두 영역 Ω1과 Ω2 사이의 패치 경계를 ΓI라 한다면, 패치 경계에서는 다음과 같이 변위 uk와 각 영역의 경계에 수직방향 n→k의 견인힘(traction) Sk(u)(k=1,2)의 연속조건은 다음과 같다.

여기서, Sk(u)은 영역 Ωk에서 표면에 작용하는 견인힘이며, 응력 요소 σijk(u)와 수직벡터요소 njk을 이용해 코시 법칙(Cauchy law)에 의해 Sik=σijk(u)njk 과 같다(k=1,2). 이러한 경계조건은 다음과 같이 주어진 포텐셜 함수(potential function)의 변분을 식 (1)에 더하여 부가할 수 있다.

여기서, 경계적분항 표현식은 각각 다음과 같다.

식 (3)의 우변 첫 번째 항은 패치 경계 ΓI에서 변위와 견인힘의 연속 조건을 부과하기 위한 항이며, 두 번째 항은 식 (3)의 이산화 방정식이 양정행렬이 되기 위한 안정화 항으로 𝜅은 안정화 매개변수이다. 식 (3)을 변위에 대한 변분을 취하여 식 (1)의 우변에 더하면 다음과 같은 최종 니셰 방정식을 얻을 수 있다.

2.2 1차 전단 변형을 고려한 기하학적으로 엄밀한 쉘

Roh와 Cho(2004)는 일반화된 곡선 좌표계(GCC: Generalized Curvilinear Coordinate)에서 1차 전단변형을 고려한 기하학적으로 엄밀한 쉘의 해석을 수행하였다. 1차 전단변형을 고려한 쉘의 변위 벡터 z는 다음과 같이 정의한다.

여기서, θ1, θ2, θ3은 곡선좌표계를 나타내며, Aα는 변형전 쉘의 면내 곡선 벡터(𝛼=1,2), A3은 쉘 면의 수직 단위 벡터를 나타내며 좌표계 θ1와 θ2에 따라 달라지는 기저벡터이다. uα와 ψα는 곡률 벡터 Aα에 대한 면내 변위와 회전 성분을 나타내며 w(θ1,θ2)는 수직방향의 처짐성분을 나타낸다. 식 (6)을 이용한 응력-변형률에 대한 구성방정식은 다음과 같다(Roh and Cho, 2004).

nαβ, mαβ 그리고 qα은 각각 막, 굽힘, 전단에 대한 응력성분을 나타내며 이에 대한 변형률 성분은 다음과 같다.

여기서, Bαβγμ은 일반화된 곡선 좌표계에서의 탄성계수이다. (∙)α||β는 공변 미분(covariant differentiation)을 나타내며, bβα은 혼합 곡률 텐서(mixed curvature tensor)를 나타낸다. 쉘의 경계에서 면내 합력 Nγ(𝛾=1,2), 면 끝단에 수직한 축 단위벡터 v=vαAα에 대한 굽힘 모멘트 -MB, 면 끝단에 접하는 축 단위벡터 t=tαAα에 대한 굽힘 모멘트 H, 그리고 전단력 Q는 식 (7)을 이용하여 다음과 같이 구할 수 있다.

상세한 유도 과정은 Roh와 Cho(2004)의 논문을 참고할 수 있다. 식 (9)는 쉘의 경계에서의 합력을 나타내며, 이는 멀티 패치 문제에서 패치 간 경계 ΓI에서 견인력 S(u)의 성분은 이러한 합력으로 표현된다.

2.3 다중 패치 등기하해석 이산화

일반화된 곡률 좌표계에서 면내 좌표계 θ1, θ2을 이용하여, A번째 조정점(control point)에 해당하는 NURBS 기저함수 RA(θ1,θ2)를 생성할 수 있다(Kim et al., 2022; 2023). 등기하해석법에서는 이러한 NURBS 기저함수를 이용하여 다음과 같은 변위장 u를 정의한다.

여기서, yA은 A번째 조정점에 해당하는 변위 계수(coeffcient)이며, R은 NURBS 기저함수 RA(θ1,θ2)로 구성된 기저함수 행렬이고, y은 변위 계수 yA로 구성된 변위 계수 벡터이다. 식 (10)을 이용해 식 (7)을 이산화한 방정식은 다음과 같다.

여기서, 밑첨자 m, b, s는 각각 막거동, 굽힘 그리고 전단 거동항을 나타내며, Cm, Cb, Cs와 Bm, Bb, Bs는 각각 막, 굽힘, 전단 거동에 대한 탄성계수와 변위-변형률 관계 행렬을 나타낸다. 식 (6)과 식 (9)로부터 쉘 구조물에 대한 변위벡터와 견인력 벡터는 다음식과 같이 나타낼 수 있다.

식 (9)와 식(10)을 이용하여 식 (12)의 견인력 벡터 S(u)는 다음과 같이 이산화할 수 있다(Kim et al., 2023).

여기서, vm,b,s는 막거동, 굽힘, 전단거동의 기하학적 연동을 표현하는 행렬로 상세한 표현식은 Kim 등(2023)을 참고할 수 있다. 식 (10), (11), (12), (13)을 식 (5)로 표현된 니셰방정식에 대입하면, 다음과 같은 형태의 최종 이산화 식을 얻을 수 있다.

여기서, K는 식 (1)의 좌변항으로부터 얻어진 강성행렬이고, KN은 식 (5) 좌변에서 두 번째 항으로부터 얻어진 다중 패치 경계에서의 강성행렬을 나타내며, Kstab은 식 (14)의 좌변 강성행렬들의 합이 양정행렬이 되도록 하는 안정화 강성행렬을 의미한다. KN과 Kstab은 경계 ΓI을 따라 적부하는 경계적분항으로 추가적인 계산비용은 크지 않다. 니셰 방법은 결합되는 영역의 강성행렬 K에 경계에서 계산된 강성행렬 KN과 Kstab을 더하기만 하면 되므로, 기존 등기하해석 코드를 그대로 사용할 수 있는 장점이 있을 뿐 아니라, 추가적인 자유도가 필요없어 행렬의 크기가 변하지 않고, 대칭성도 보장하기 때문에 기존에 사용하는 행렬 풀이 프로그램을 그대로 사용이 가능하다.

등기하해석에서는 NURBS 기저함수가 적분 요소사이에서 높은 연속성을 가지고 있다. 이러한 속성은 변위장과 회전장에서 같은 차수의 기저함수를 사용하는 1차 전단변형을 고려한 쉘의 해석에서 추가적인 제한조건으로 작용할 수 있다(Adam et al., 2014). 적분 요소 사이의 연속성을 낮추어 이러한 문제를 해결할 수 있는데, 본 논문에서는 Kim 등(2022)에서 제시한 방법을 따라 등기하해석에서 1차 전단변형 쉘요소의 잠김(locking)현상을 해결하기 위해 가정된 자연 변형률(ANS: Assumed Natural Strain)과 베지어 추출(Bézier extraction) 방법을 동시에 사용하였다.

2.4 안정화 계수

식 (13)이 양정행렬이 되도록 하기 위한 안정화 매개변수x는 일반화된 고유치 해석 방법을 통해 그 최적값을 구할 수 있다(Embar and Dolbow, 2010). 서로 다른 조정점의 밀도를 가지는 두 패치의 경계에서 수치적 안정성을 보장하기 위해서 다음 식을 만족시키는 요소망 의존 상수 C>0가 존재해야 한다.

여기서, L2-norm은 다음과 같이 정의한다.

식 (5)의 우변에서 변위 u와 그것의 변분 값 u¯ 대신에 z∈Z¯1∪Z¯2∪ΓI을 대입하여 정리하여 다음과 같은 이중 선형 방정식으로 표현할 수 있다.

Cauchy-Schwarz 부등식을 이용하면, 식 (17)의 우변항에서 변위와 견인힘의 경계 적분항은 다음과 같이 표현할 수 있다.

식 (18)을 식 (17)에 대입하고, 식 (15)를 이용하면, 다음과 같은 식을 얻을 수 있다.

식 (19)가 양정행렬이 되기 위해서는 κ≥C2가 되어야 하는 것을 알 수 있다. C2의 값은 식 (15)를 변분을 취하여 다음과 같은 고유치 문제를 풀어서 구할 수 있다.

여기서, s는 고유 벡터이며 Λ 고유치로 이 고유치의 최대값 Λmax을 상수 C2, 즉, C2=Λmax 으로 정한다. 식(19)로 부터 안정화 매개변수는 다음과 같이 정할 수 있다.

Embar와 Dolbow(2010)의 논문에서는 적합한 안정성 매개변수로 κ=2C2=2Λmax으로 제안하고 있다. 다음의 수치예제에서는 이렇게 제시된 수치의 적합성을 검증하고, 이보다 더 나아가 두 패치 사이의 조정점 망의 밀도차이에 따른 안정화 매개변수 값을 구해보고 보다 더 적합한 안정화 매개변수 값을 제시하도록 하겠다.

2.5 수치예제 결과 및 고찰

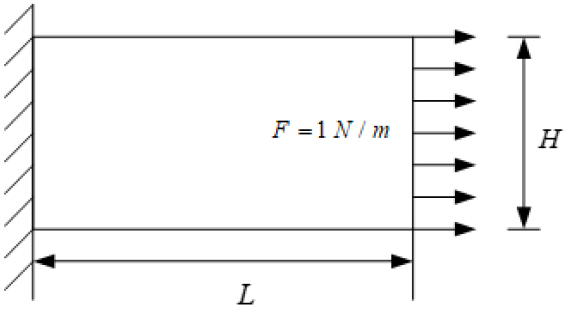
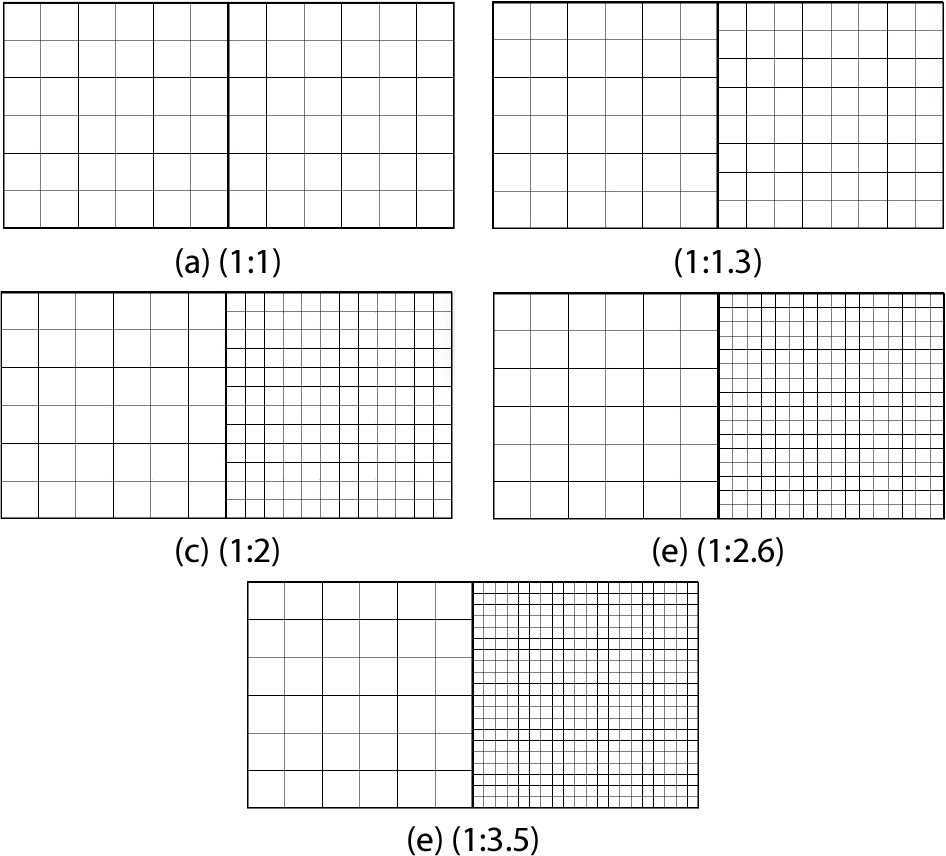
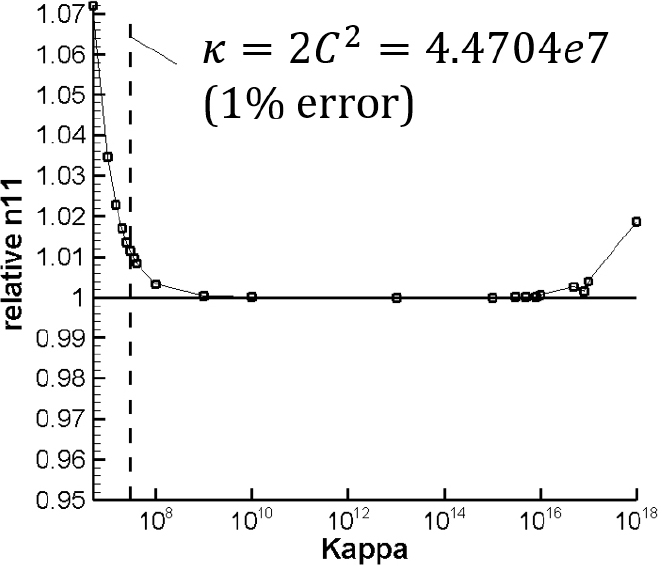
이 논문에서 제시한 니셰 방법을 이용한 다중 패치 등기하해석을 검증하기 위해 기하학적으로 엄밀한 쉘 구조물에 대한 수치해석을 수행하였다. 모든 예제의 기저함수의 차수는 p=3을 사용하였다. 첫 번째 예제에서는 2.3절에서 유도한 안정화 매개변수의 결과를 검증하고 연결된 두 패치 사이의 조정점 요소망 밀도에 따른 안정화 매개변수의 값과 응력해의 정확도를 비교･검토해 보았다. Fig. 2에서 단위길이당 균등하중 F=1N/m를 받는 2차원 평판의 응력 해석을 해 보았다. 이 평판의 폭(L)과 높이(H)의 비는 L=2H와 같으며, 폭의 중간을 나누어 2개의 NURBS패치가 연결된 다중 패치를 사용하였다. 사용한 패치의 조정점 밀도는 Fig. 3과 같다. 본 문제의 정해는 n11=σxx=1.0N/m2Fig. 3(b)의 (1:1.3)의 조정점 모델의 해의 결과는 Fig. 4와 같다. 이 모델에 대한 안정성 매개변수는 κ=2C2=4.4704e7이며, 이때 Fig. 4와 같이 응력은 약 1% 내의 오차를 보인다.

Fig. 2.

Multipatch problem

Fig. 3.

Test model for stability parameter (control point mesh density ratio)

Fig. 4.

Stress contour for n11

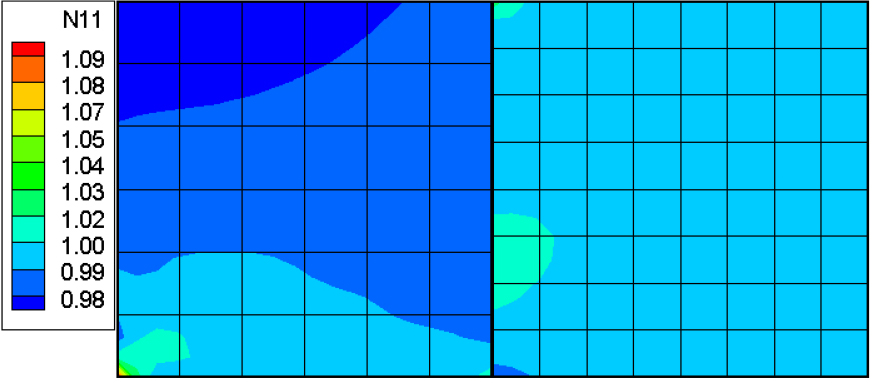
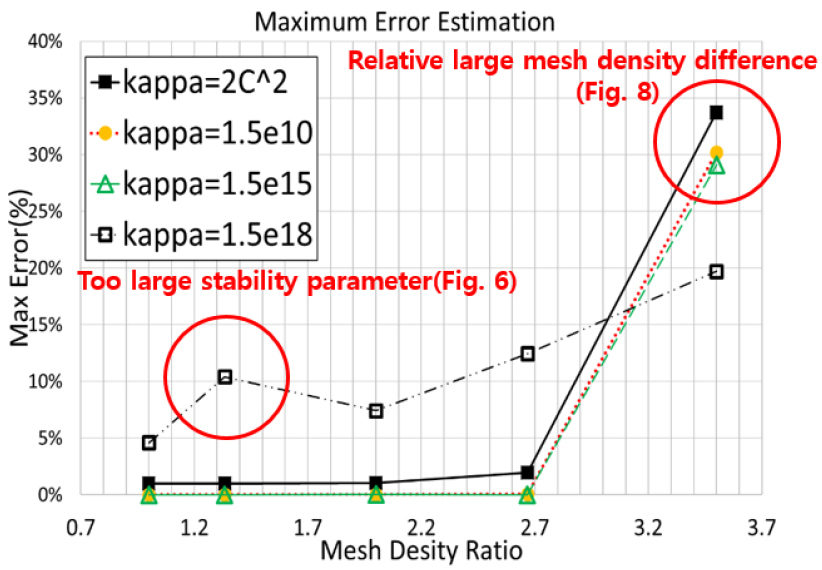
Fig. 4는 Fig. 3(b) 모델에 대해서 안정화 매개변수의 크기에 따른 평면내 응력 n11의 상대 오차 그래프이다. Fig. 5는 Fig. 3(b)에서 주어진 (1:1.3)의 요소망 밀도비를 가지는 모델에 대해서 𝜅 값에 대한 응력 n11의 상대 오차를 나타낸 그래프이다. κ=2C2일 경우 1%의 오차를 보이나 그보다 큰 안정화 매개변수를 가질 경우 오차가 거의 없어지는 것을 알 수 있다. 하지만 너무 큰 안정화 매개변수 값은 강성행렬의 condition number가 나빠져 Fig. 6처럼 수치적 문제를 일으킬 수 있다. Fig. 7은 두 연결된 패치의 요소망 비의 차이와 안정화 매개변수 𝜅의 값에 따른 두 패치 사에의 경계에서의 응력 오차를 나타낸 그래프이다.

Fig. 5.

Variation in the relative in-plane normal stress with the magnitude of the stability parameter

Fig. 6.

Numerical stability problem for too large stability number (κ=1.5e18) when (1:1.3) mesh density ratio

Fig. 7.

Maximum error (%) according to mesh density ration and stability parameter

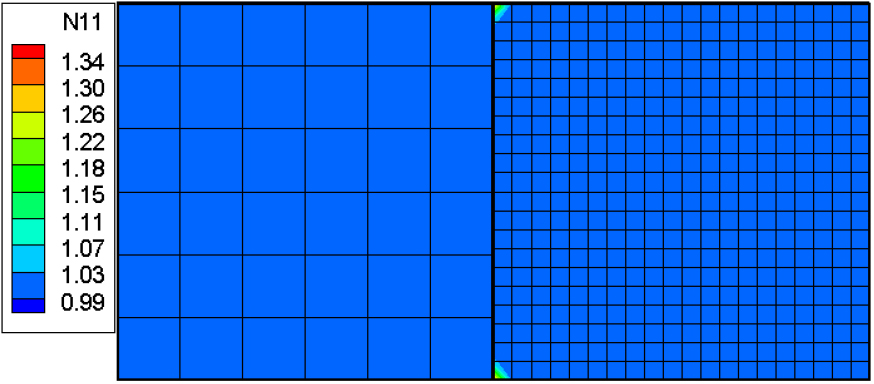
안정화 계수가 κ=1.5e10~1.5e15 사이일 경우 두 패치사이의 경계점에서의 응력 오차는 큰 차이를 보이지 않는다. 이는 Fig. 5의 결과와도 일치하다. 즉, 적정 안정화 매개변수는 κ=103C2~108C2의 범위를 갖는 것을 알 수 있다. 오히려, 두 패치 사이의 요소망 밀도가 클 경우 적정 안정화 매개변수를 갖는다 하더라도 경계에서 응력 오차가 커질 수 있다. Fig. 8은 Fig. 3(e)의 (1:3.5) 비율의 조정점 요소망 밀도비를 가질 때 경계에서의 응력 오차를 보여주고 있으며, 위면과 아랫면의 경계 끝에서 요소망의 크기 차이로 인한 강성차이로 인해 패치간 약 30%의 응력 오차를 보여주고 있다. Fig. 7의 결과 조정점 요소망 밀도 비가 대략 (1:2.7) 이하일 경우 오차가 거의 없는 것을 확인할 수 있다.

Fig. 8.

Numerical error for relative large mesh density difference (1:3.5) between two connected patches (κ=1.5e15)

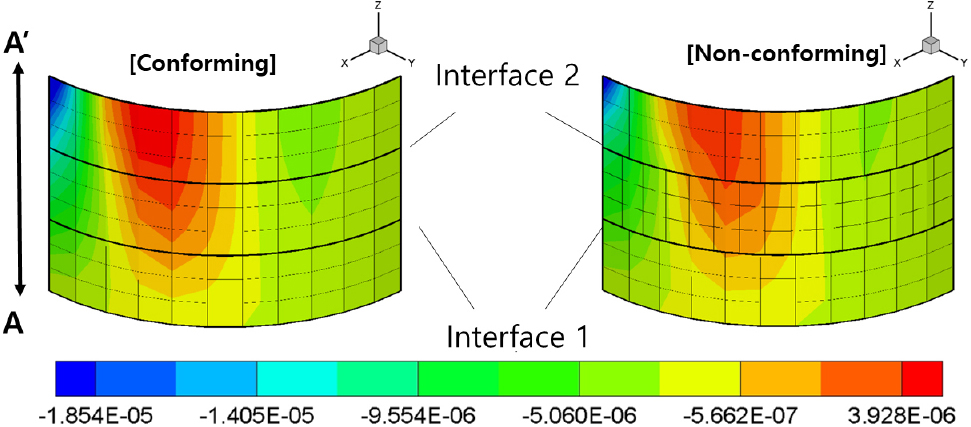
두 번째 예제는 기하학적으로 엄밀한 쉘 문제에 대해서 니셰 방법을 이용한 다중 패치 모델 해석에서 변위 연속성을 검토하는 예제이다. Fig. 9와 같이 주어진 Pinched cylinder 문제에 대해서 Fig. 10과 같이 다중 패치 모델을 구성해 변위장의 연속을 검토해 보았다. 안정화 매개변수는 κ=2C2이다.

Fig. 9.

Pinched cylinder problem with displacement contour (Roh and Cho, 2004)

Fig. 10.

Displacement for conforming and non-conforming meshes

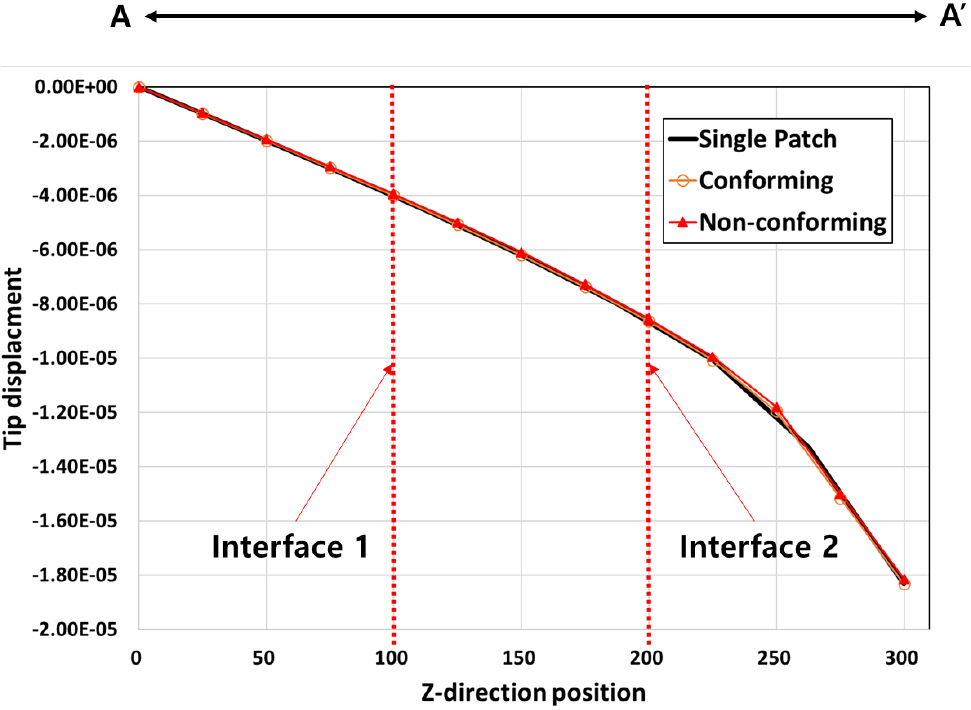
Fig. 10은 단위패치와 적합요소망(conforming mesh) , 비적합 요소망(non-confirming)을 사용하였을 경우 변위장을 나타낸 그림이다. 그림의 AA’ 선을 따라 Interface 1과 Interface 2에서 변위장을 Fig. 11에 도시하였고, 다중 패치 모델에서 패치간 요소망이 일치하는 경계 적합 요소망일 뿐 아니라 경계 비적합 요소망을 사용하였을 경우 모두 경계에서 변위 연속조건을 만족시킴을 알 수 있다.

Fig. 11.

Displacement continuity check for conforming and non-conforming meshes

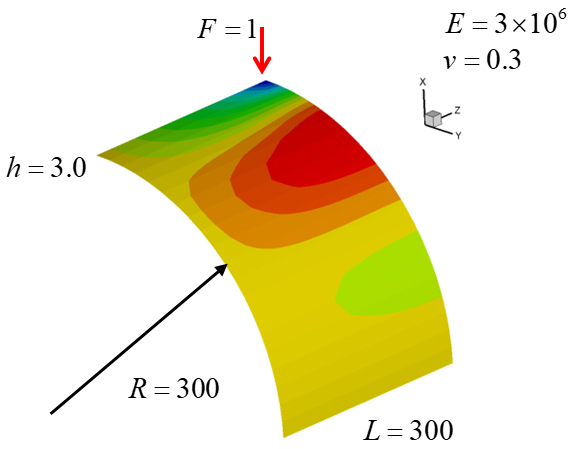
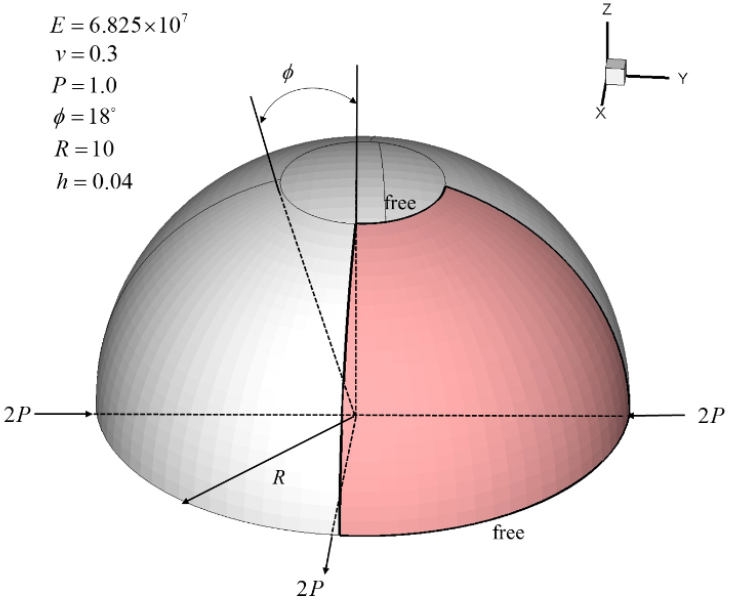
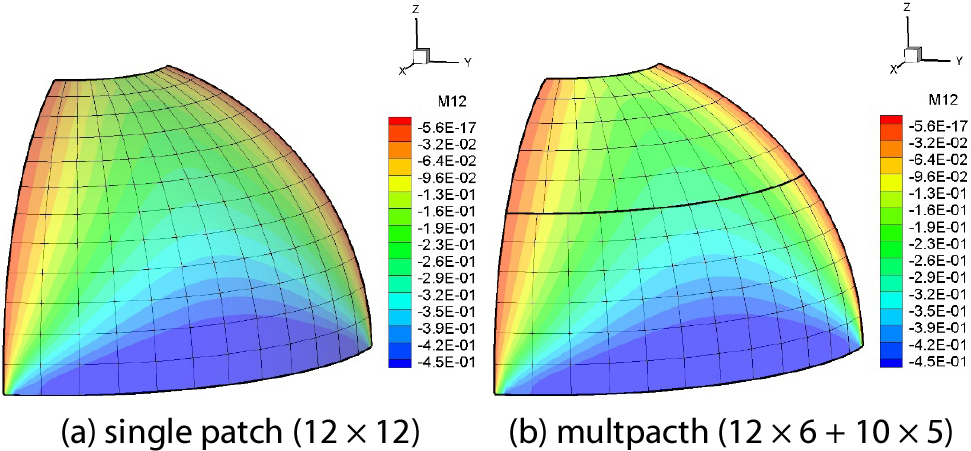
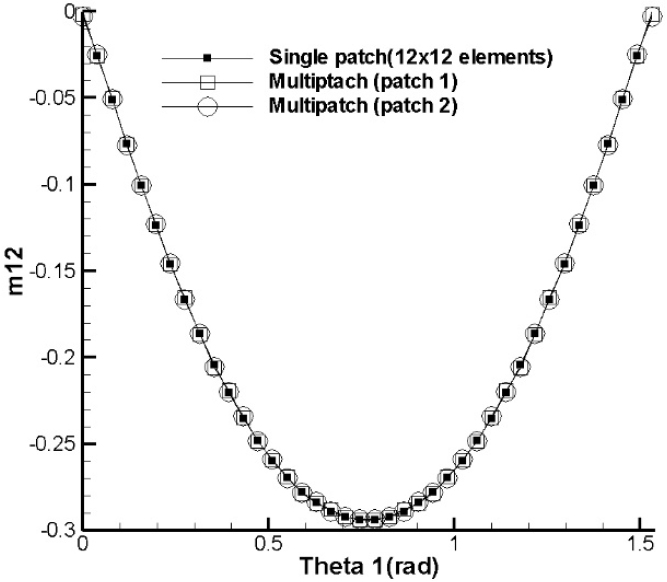
마지막 예제로 Fig. 12의 Pinched hemisphere 쉘 구조물에 대해서 면내 굽힘응력 m12의 연속성을 검토해 보았다. 사용한 모델은 Fig. 13와 같이 아랫면 12 × 6 윗면 10 × 5의 요소망을 다중 패치 모델이며, 사용한 안정화 매개변수는 κ=2C2이다. Fig. 13에서 알 수 있듯이 비슷한 요소망을 갖는 12 × 12 단일 패치 모델과 비교하였을 때 구조물 전체적으로 동일한 응력장을 보여주고, 패치간 응력 연속성도 Fig. 14과 같이 다중 패치모델의 상단 패치(patch 1)과 하단 패치(patch 2)의 패치 경계에서의 응력이 단일 패치의 같은 위치에서의 응력과 일치하며, 패치간 연속적임을 알 수 있다.

Fig. 12.

Pinched hemisphere shell

Fig. 13.

Stress continuity check

Fig. 14.

Stress continuity check for m12

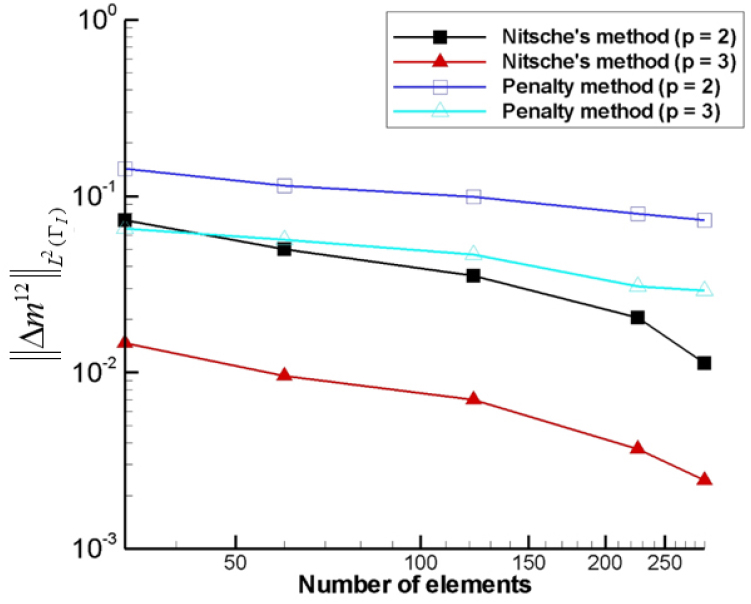
추가적으로 니셰 방법의 정확성을 패널티 방법(경계면에서의 변위 연속성을 패널티 매개변수로 부가하는 방법)과 비교하여 두 패치의 경계에서의 응력의 차이∥∆m12∥L2(ΓI)에 대한 수렴성을 검토하였다. Fig. 15에서 알 수 있듯이 NURBS 기저함수가 2차(p=2)일 경우와 3차(p=3)일 경우 모두 패널티 방법보다 니셰방법의 수렴성이 더 빠르다는 것을 알 수 있다.

Fig. 15.

Stress convergence test

3. 결 론

본 논문에서는 다중 패치 모델에 대해서 니셰 방법을 이용하여 등기하해석을 하는 방법을 제시하고 기하학적으로 엄밀한 쉘의 구조해석에 적용해 보았다. 니셰 방법은 패치 경계에서의 변위장과 견인힘의 연속성을 적분형태로 부가한다. 추가적인 강성행렬은 자유도를 증가시키지 않고, 경계에서의 적분으로 계산되기 때문에 계산비용의 증가가 크지 않는다. 수치적인 안정성을 위해 도입한 안정성 매개변수는 일반화된 고유치 해석을 통해서 구할 수 있다. 본 논문에서는 수치적인 예제를 통해 적합한 안정성 매개변수 값을 κ=103C2~108C2의 범위로 제안하였다. 실제로 수치적인 안정성을 결정하는 것은 두 패치 사이의 조정점 요소망의 밀도 차이임을 확인하였고, 조정점 요소망의 밀도가 1:2.7 이하일 때 니셰방법이 정확한 결과를 줄 수 있음을 확인하였다. 몇몇 수치예제를 통해 니셰 방법이 기하학적 거동이 복잡한 쉘 문제에서 변위장 뿐 아니라 응력장의 연속성을 보장함을 보였고, 기존의 패널티 방법보다 패치간 응력 차이의 수렴성이 빠르다는 것을 확인하였다.