Accuracy Verification Through Comparison of Interior Ballistic Simulations Using a Lumped Parameter Model and Experimental Results

Gyu-Seok Son; Gyu-Cheol Choi; Min-Seop Kwon; Hojun Lee; Hyeokwon Kim; Min-Seok Oh; Young-In Park; Soo-Ho Chang; Jeaho Jung

doi:10.7734/COSEIK.2025.38.2.109

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 April 2025. 109-115
https://doi.org/10.7734/COSEIK.2025.38.2.109

Accuracy Verification Through Comparison of Interior Ballistic Simulations Using a Lumped Parameter Model and Experimental Results

집중 매개변수 모델을 이용한 강내탄도 해석과 시험 비교를 통한 정확도 검증

Gyu-Seok Son¹

Gyu-Cheol Choi²

Min-Seop Kwon²

Hojun Lee²

Hyeokwon Kim³

Min-Seok Oh⁴

Young-In Park⁴

Soo-Ho Chang⁵

Jeaho Jung⁶^*

손 규석¹

최 규철²

권 민섭²

이 호준²

김 혁원³

오 민석⁴

박 용인⁴

장 수호⁵

정 재호⁶^*

¹Graduate Student, School of Mechanical Engineering, ChungBuk National University, Cheongju, 28644, Korea

²Undergraduate Student, School of Mechanical Engineering, ChungBuk National University, Cheongju, 28644, Korea

³Graduate Student, Department of Mechanical Engineering, Korea Advanced Institute of Science and Tecnology, Daejeon, 34141, Korea

⁴Senior Research Engineer, Poongsan Defense R&D Institute, Gyeongju, 780801, Korea

⁵Principal Research Engineer, Poongsan Defense R&D Institute, Gyeongju, 780801, Korea

⁶Professor, School of Mechanical Engineering, ChungBuk National University, Cheongju, 28644, Korea

¹충북대학교 기계공학부 석사과정

²충북대학교 기계공학부 학사과정

³한국과학기술원 기계공학과 석사과정

⁴풍산 방산기술연구원 선임연구원

⁵풍산 방산기술연구원 이사

⁶충북대학교 기계공학부 교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

This study analyzed the muzzle velocity and chamber pressure of a projectile, which was fired from a 40 mm L/70 barrel weapon system using the IBHVG2 (Interior Ballistics of High Velocity Guns, version 2) code, and compared the results with experimental data. The Chambrage model, based on the Lumped Parameter Model, was used to analyze the projectile velocity and chamber pressure, and a total of 10 firing tests were conducted. The reaction rate coefficient of the propellant, used as an input parameter for the analysis, was estimated through closed bomb tests. A comparison of the analysis and experimental results revealed approximate deviations of 6% in the muzzle velocity and 8% in the maximum chamber pressure. In conclusion, the study validated the effectiveness and predictive accuracy of the IBHVG2 model while identifying potential areas for improvement.

Keywords

IBHVG2

interior ballistic

chamber pressure

base pressure

closed boom test

본 연구는 강내탄도 해석 코드 IBHVG2(Interior Ballistics of High Velocity Guns, version 2)를 이용하여 40mm L/70 포신을 가진 무기체계에서 발사체의 출구 속도와 약실 압력을 해석하고, 시험 결과와 비교를 수행하였다. 집중 매개변수 모델(Lumped Parameter Model)을 기반으로 한 Chambrage 모델을 적용하여 탄환 속도와 약실 압력 해석을 수행하였고 시험은 총 10회를 수행하였다. 해석 인자로 들어간 추진제의 반응률 계수는 폐쇄 폭발 실험(Closed Bomb Test)를 통해 추정하였다. 해석과 시험을 비교한 결과 탄환의 출구 속도는 약 6% 정도 오차를, 약실 최대 압력은 8% 정도의 오차를 보였다. 결론적으로 IBHVG2 모델의 유효성과 예측 정확도를 확인하였으며, 개선의 여지가 있음을 확인하였다.

키워드

IBHVG2

강내 탄도학

약실 압력

기저 압력

폐쇄 폭발 실험

MAIN

1. 서 론
2. 이론적 배경
2.1 IBHVG2의 기본 가정
2.2 지배방정식
2.3 압력구배 계산 모델
2.4 탄환 이동
3. 강내 탄도 시험 및 해석 결과 비교
3.1 점화제 및 추진제 정보
3.2 탄환, 포신 정보
3.3 해석과 시험간 결과 비교
4. 결 론

1. 서 론

국방산업에서 탄도 예측은 무기체계의 공격력 증대와 방어 효율성 향상을 위한 핵심 기술로, 현대 군사 작전에서 필수 불가결한 요소이다. 정확한 타격과 효율적 방어는 탄도 궤적의 정밀한 예측을 통해 달성되며, 이는 다양한 무기체계의 설계 및 운영에서 성능 평가, 운영 계획 수립, 요격 시스템 개발 등 광범위한 응용 분야를 가지고 있다.

탄도 예측은 크게 강내탄도와 강외탄도로 구분된다. 강내탄도는 발사체가 화포의 포신 내부를 이동하는 동안의 거동을 다루며, 발사 압력, 추진제 연소, 발사체 가속 등 내부 역학적 요소가 주요 분석 대상이다. 반면, 강외탄도는 발사체가 포신을 벗어난 후부터 목표물에 도달할 때까지의 비행 궤적을 예측하는 것으로 공기 저항, 중력, 스핀 안정성 등 외부 환경적 요인이 고려된다.

이 중 강내탄도 해석은 무기체계 성능 최적화의 핵심으로 평가된다. 특히, 발사체의 초기 속도(발사 속도)는 목표물에 도달하는 사거리와 명중률에 직접적인 영향을 미치므로 포신 내부에서 발생하는 연소 압력, 마찰력, 가스 유동 등의 요인을 정밀하게 예측하는 것이 필수적이다. 가장 대중적으로 사용되는 코드는 1983년 Franz Lynn에 의해 개발된 IBHVG2(Interior Ballistics of High Velocity Guns, version 2)로 내부의 온도와 압력을 집중 매개변수 모델(lumped parameter model)로 가정하여 빠른 결과를 도출하는 특징을 가지고 있다. 그러나 이러한 모델은 공간적 분포를 상세히 반영하지 못하는 한계가 있다. 이후 집중 매개변수 모델의 한계를 극복하기 위해 1차원 이상 유동(1-D, two-phase flow)을 해석하는 XKTC 코드(Gough, 1990)가 개발되었으며, 다차원 다상 유동을 해석하기 위한 NGEN(Next-Generation)코드(Gough, 1993) 또한 개발되었다. 그리고 국내에서는 Jang 등(2012)이 1차원 강내탄도해석 코드와 장진성 개발한 바 있으며, Sung 등(2011)은 2차원 강내탄도 해석 코드를 개발을 하였고 이후 Jang 등(2015)이 3차원 강내탄도해석 코드를 개발하였다.

IBHVG2 이후 개발된 코드 들은 공간을 1차원 이상으로 차분화하여 해석을 수행하며 IBHVG2 결과와 비교하여 검증을 수행하였다. 하지만 IBHVG2 자체 결과의 정확도에 대한 검증을 수행한 연구 결과는 저자가 아는 한도내에서는 없었다. 따라서 본 연구에서는 IBHVG2에서 사용한 강내탄도 해석 모델을 기반으로 이론적 예측 결과와 시험 결과값을 비교함으로써 모델의 유효성과 예측 정확도를 검증하고 무기체계 개발에 있어 해석의 신뢰도를 평가해 보고자 한다.

2. 이론적 배경

이 장에서는 강내탄도 해석 코드(IBHVG2)의 기본 가정을 소개한 후, 해석에 사용되는 지배방정식을 소개한다. 이후 지배방정식의 계산에 사용되는 탄환 밑면 압력값을 구하기 위한 세 가지 모델을 소개하고자 한다.

2.1 IBHVG2의 기본 가정

IBHVG2(Anderson and Fickie, 1987)에서는 다음과 같은 가정들을 하고 있다. 첫째, 시스템의 에너지 균형의 경우 가스의 초기 에너지는 가스의 내부 에너지와 손실 에너지의 합으로 가정하며 손실 항에는 시스템에서의 일 및 열전달이 포함된다. 둘째, 추진제의 연소로 인해 생기는 가스의 경우 추가 반응을 하지 않는다고 가정한다. 셋째, 기체는 Nobel-Able의 혼합물로 가정되어 이상 기체 법칙을 따른다. 넷째, 챔버 모델링의 경우 Lumped Parameter Model로 모델링하여 챔버 내 가스 압력과 밀도는 균일하게 분포한다고 가정한다. 다섯째, 모든 추진제는 그레인(grain) 표면에 수직으로 연소되며, 연소된 층은 균일한 두께를 가진다고 가정한다. 여섯째, 발사체의 운동 및 회전 에너지 계산 시, 발사체의 밀도가 균일하다고 가정한다.

2.2 지배방정식

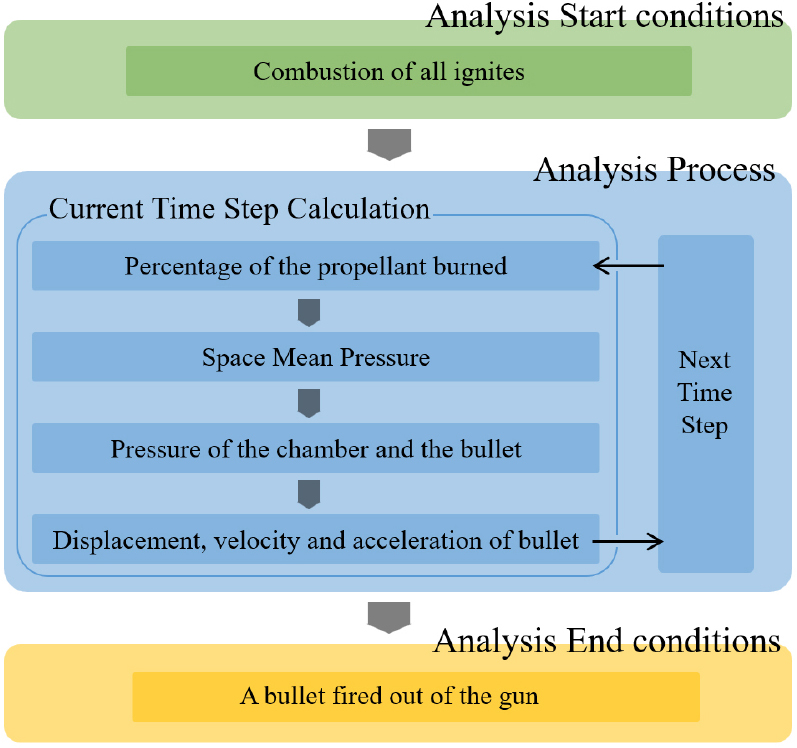
IBHVG2에서는 Fig. 1과 같이 포신과 추진제의 형상, 탄환의 무게 등 다양한 조건에서 탄환의 출구 속도를 계산하는 것이 목적이다. 이를 위해 다양한 설계 인자를 파일로 입력 받아 구동되며 전체적은 계산 과정은 다음과 같다. 먼저 챔버의 온도를 열역학 1법칙을 사용하여 계산하고 이로부터 챔버의 압력을 추정한다. 그리고 계산된 챔버 압력으로부터 구배를 고려하여 탄약 밑면의 압력을 계산하고 이를 통해 탄약에 가해지는 힘을 구한다. 가해진 힘을 통해 이동 속도를 결정하며 시간의 흐름에 따라 위치를 계산하고 출구에서의 속도를 계산한다(Anderson and Fickie, 1987).

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F1.jpg

Fig. 1.

Computational process performed by IBHVG2

챔버의 평균 온도는 열역학 1법칙을 통해 계산되며 다음 식 (1), (2)를 사용한다.

(1)

T_{mcan} = \frac{\sum_{k} \frac{F_{k} m_{k}}{γ_{k} - 1} + \frac{F_{p} m_{p}}{γ_{p} - 1} - L}{\sum_{k} \frac{F_{k} m_{k}}{(γ_{k} - 1) T_{f k}} + \frac{F_{p} m_{p}}{(γ_{p} - 1) T_{f p}}}

(2)

F = R T_{f}

여기서, $F$ 는 단위 질량당 추진에너지(impetus), $R$ 은 기체상수, $T_{f}$ 는 추진제 혹은 점화제가 발화시 낼 수 있는 온도, 𝛾는 비열비, $L$ 은 손실, $m$ 은 질량, 하첨자 $()_{k}$ 는 추진제 인덱스, 하첨자 $()_{p}$ 는 점화제, 하첨자 $()_{f}$ 는 화염온도를 의미한다. 이때, 추진제의 경우 여러 종류의 추진제가 들어갈 수 있어 그 종류에 따라서 인덱스 번호를 매긴다. 따라서 $F_{k}$ 는 추진제의 단위 질량당 추진에너지를 의미하고 $F_{p}$ 는 점화제의 단위질량당 추진에너지를 의미한다. 평균 온도는 covolume 고려한 이상기체 상태방정식에 대입하여 식 (3)으로 평균 압력을 구한다.

(3)

P_{mean} (t) = (T_{mean} (t) [\sum_{k} \int \frac{F_{k} {\dot{m}}_{k}}{T_{f k}} d t + \frac{F_{p} {\dot{m}}_{p}}{T_{f p}}]) / (V_{c} + A_{b} [x_{p} + x_{r}] - \sum_{i} n_{i} V_{i} - \sum_{k} \int η_{k} {\dot{m}}_{k} d t - η_{p} {\dot{m}}_{p})

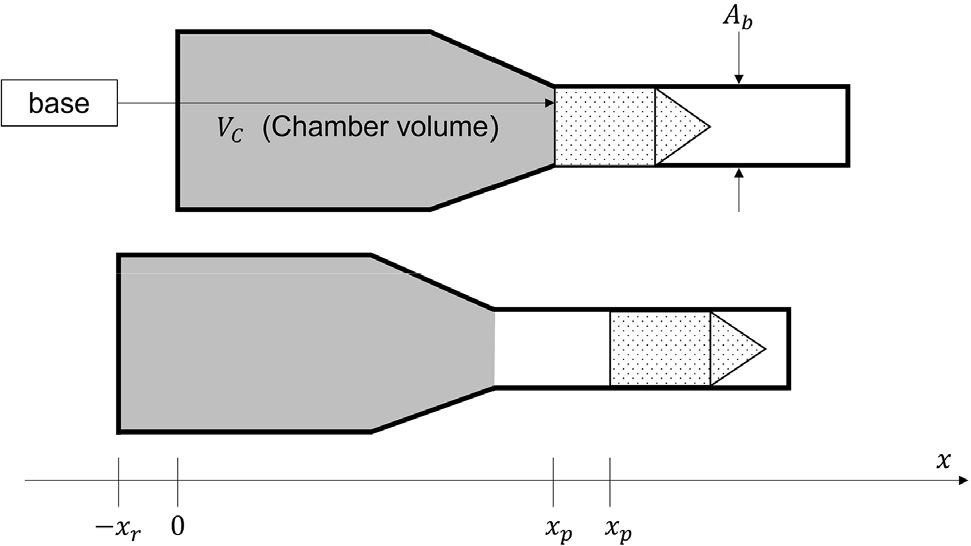
여기서, 𝜂는 covolume을 의미하며 Fig. 2와 같이 $V_{c}$ 는 챔버 체적, $A_{b}$ 는 총열의 단면적, $x_{p}$ 는 탄환 base의 x-좌표, $x_{r}$ 은 반동으로 밀려난 총기 바닥면의 x-좌표, $n$ 은 추진제의 타들어간 비율, $V$ 는 추진제 체적을 의미한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F2.jpg

Fig. 2.

Schematic Diagram of Interior Ballistics Analysis

$i$ 번째 추진제가 $j$ 번째 표면에서 가스로 바뀌는 비율은 다음 식 (4)와 같이 구할 수 있다.

(4)

{\dot{m}}_{i j} = n_{i} ρ_{i j} S_{i j} r_{i j}

여기서, $S_{i j}$ 는 추진제의 표면적을 의미하며 추진제의 형상에 따라서 달라질 수 있다. 그리고 이때의 연소 속도 $r_{i j}$ 는 다음 식 (5)와 같이 구할 수 있다.

(5)

r_{i j} = β_{i j} {[P_{mean}]}^{α_{i j}}

여기서, 𝛼, 𝛽는 반응률을 결정하는 계수로 폐쇄 폭발 실험(Closed Bomb Test; CBT)으로부터 결정한다.

2.3 압력구배 계산 모델

2.3.1 Lagrange 모델

Lagrange 모델은 압력 변화를 1차원의 연속 방정식과 운동량 보존 방정식으로부터 계산하고 약실 압력을 평균 압력으로 표현하여 탄환 밑면의 압력을 계산하는 모델이다. 이는 단순 평균 압력보다 실제 내부 유동을 반영한 밑면 압력을 사용하게 되므로 보다 정확한 탄속 예측을 할 수 있는 장점이 있다. 이 모델은 비점성 유체를 가정하여 다음 식 (6), (7)과 같은 연속방정식과 운동량 보존 방정식을 지배방정식으로 사용한다.

(6)

\frac{\partial ρ}{\partial t} + \frac{\partial (ρ u)}{\partial z} = 0

(7)

- \frac{1}{ρ} \frac{\partial P}{\partial z} = \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial z} = 0, 0 \leq z \leq z_{p}, z_{p} = x_{p} + x_{r}

여기서, $u$ 는 포신의 길이방향 속도, $z$ 는 포신 내부의 위치, 𝜌는 밀도를 나타낸다. 집중 모델의 가정에 따라 길이방향의 밀도 변화는 없으며 약실과 탄환 밑면의 경계조건을 적용하면 다음 식 (8)과 같은 압력 식이 도출된다.

(8)

P_{base} = \frac{3 P_{mean} + \frac{Σ C_{i}}{m_{p}} [P_{res} + P_{air}]}{3 + \frac{Σ C_{i}}{m_{p}}}

여기서, 하첨자 $()_{m a e n}$ 은 평균을 의미, $()_{b a s e}$ 는 탄환 밑면, $()_{r e s}$ 는 마찰 저항, $()_{a i r}$ 는 공기 저항, $i$ 는 추진제 인덱스를 의미한다. 그리고 $C$ 는 추진제 질량, $m_{p}$ 는 탄환 질량이다. 이와 같이 바닥면의 압력이 도출되면 식 (3)으로 부터 계산된 평균 압력만으로 탄환 바닥면의 압력 산출이 가능해진다.

2.3.2 Pidduck-Kent 모델

Pidduck-Kent 모델(Pidduck, 1937)은 강내탄도 현상을 단순화하여 구한 결과를 기반으로, 총알 무게에 대한 추진제 무게의 비를 무차원 변수로 사용해 평균 압력을 계산하고, 이를 바탕으로 탄환 바닥면의 압력을 보간하여 구할 수 있도록 구성된 모델이다. 이때 총알 무게 대비 추진제의 비(𝜃), 탄환 바닥면의 압력은 다음 식 (9), (10), (11), (12)와 같이 계산한다.

(9)

θ \equiv \frac{\sum C_{i}}{m_{p}}

(10)

P_{base} = \frac{P_{mean}}{1 + \frac{θ}{Δ}}

(11)

Δ (θ) = 3 + a θ + b θ^{2} + c θ^{3} + d θ^{4} + e θ^{5}

(12)

a = a_{1} + \frac{a_{2}}{γ}, b = b_{1} + \frac{b_{2}}{γ}, c = c_{1} + \frac{c_{2}}{γ}, d = d_{1} + \frac{d_{2}}{γ}, e = e_{1} + \frac{e_{2}}{γ}

여기서, 각 계수 $a$ , $b$ , $c$ , $d$ , $e$ 는 Vinti와 Kravitz(1949) 문헌을 참고한다.

2.3.3 Chambrage 모델

Lagrange 모델은 총의 장약실이 총신의 연장으로 보고 동일 직경의 원통 형태를 가정한다. 이 과정에서 장약실의 직경 대비 총신의 직경 비는 무시된다. 이로 인해 탄속의 결과에 차이가 발생할 수 있으며, 이를 보정한 모델이 Chambrage 모델이다. 이 모델은 다음 식 (13), (14), (15), (16), (17), (18), (19), (20)과 같이 탄환 밑면의 압력을 계산한다(Frederick, 1988).

(13)

P_{base} = \frac{P_{mean} + a_{3} J_{1} + h J_{2} - \frac{a_{3} J_{3} + h J_{4}}{V (z_{p})}}{1 - a_{4} J_{1} + \frac{J_{3} a_{4}}{V (z_{p})}}

(14)

a_{3} = \frac{C_{T} A}{V^{2} (z_{p})} [\frac{A v_{p}^{2}}{V (z_{p})} + \frac{A P_{r c s}}{m_{p}}]

(15)

a_{4} = \frac{- C_{T} A^{2}}{m_{p} V^{2} (z_{p})}

(16)

h = \frac{- C_{T} v_{p}^{2} A^{2}}{2 V^{3} (z_{p})}

(17)

J_{1} = \int_{0}^{z_{p}} \frac{V (z)}{A (z)} d z

(18)

J_{2} = \frac{V^{2} (z)}{A^{2} (z)}

(19)

J_{3} = \int_{0}^{z_{b}} A (z) J_{1} (z) d z

(20)

J_{4} = \int_{0}^{z_{p}} A (z) J_{2} (z) d z

여기서, $A$ 는 탄환 바닥면의 면적, $A (z)$ 는 약실 바닥면으로부터 $z$ 만큼 떨어진 위치에서의 단면적, $C_{T}$ 는 추진제 총 질량, $V (z)$ 는 약실 바닥면으로부터 $z$ 만큼 떨어진 위치까지의 체적, $v_{p}$ 는 탄환의 속도이다.

2.4 탄환 이동

탄환 밑면의 압력을 알고 탄환의 직경과 질량을 알면 탄환의 이동은 다음 식 (21)과 같이 뉴턴의 운동법칙으로 계산 가능하다.

(21)

\ddot{x_{p}} = \frac{[P_{base} - P_{r e s}] A}{m_{p}}

3. 강내 탄도 시험 및 해석 결과 비교

3.1 점화제 및 추진제 정보

시험에서 사용한 점화제는 다음 Table 1에 기술하였다. 점화제는 시작과 동시에 모두 연소된 것으로 가정하였다. 추진제는 정보는 다음 Table 2에 기술하였다. 여기서 식 (5)의 반응률 계수(𝛼, 𝛽 )는 CBT 실험을 통해 산출하였다.

Table 1.

Thermochemical properties of the Igniter

Flame Temperature	1924.1 (K)
Molecular Weight	57.939
Impetus	276.1 (J/g)
Specific Heat ratio	1.271
Density	1.7 (g/cc)
Covolume	0.537 (cc/g)

Table 2.

Thermochemical properties of the propellant

Flame Temperature	2881.5 (K)
Molecular Weight	23.8875
Impetus	1002.9 (J/g)
Specific Heat ratio	1.3826
Density	1.5 (g/cc)
Covolume	1.063 (cc/g)
Grain Shape	1 Perf Cylindrical

3.1.1 추진제 CBT 실험 결과

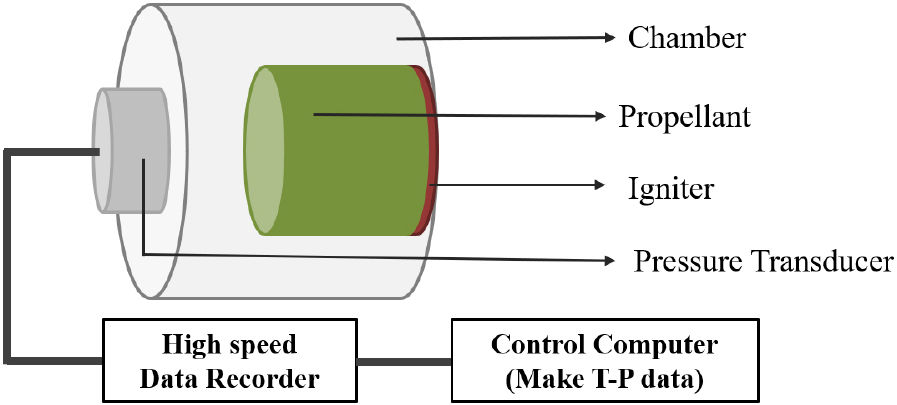
추진제의 CBT 실험은 Fig. 3과 같이 폐쇄된 공간에 추진제와 점화제를 투입한 후 내부를 연소시켜 시간에 따른 압력을 측정하는 실험이다. CBT 실험 결과를 통해 반응률 계수를 산출하기 위해서는 CBT 실험 분석 프로그램이 필요하며, 본 연구에서는 CBT 분석 프로그램으로 BRLCB 코드(Oberle and KooKer, 1993)를 사용한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F3.jpg

Fig. 3.

CBT Equipment overview

BRLCB는 고체 추진제의 고압 연소 연구와 관련된 모든 분석을 수행하기 위해 설계된 밀폐용기 데이터 분석 프로그램으로 다양한 환경에서 발생하는 CBT 실험 결과를 분석한다. Fig. 4와 같이 분석을 수행하며, 분석에 사용되는 지배방정식은 에너지 보존 법칙과 열역학 1 법칙으로 구성된다. 프로그램 결과로 시간에 따른 연소율 및 남은 추진제 비율, 현재 추진제의 표면적 등을 출력한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F4.jpg

Fig. 4.

Computational process performed by BRLCB

CBT 실험 분석 프로그램은 CBT 결과(Time - Pressure data)와 추진제의 정보를 활용하여 시간별로 추진제가 연소된 비율을 계산하며, 추진제의 연소비를 기반으로 추진제가 타들어가는 속도(연소율)를 계산한다. 추진제가 타들어가는 속도와 압력값의 25~75%구간을 log scale에서 선형 보간을 통해 반응률 계수(𝛼, 𝛽 )를 산출한다.

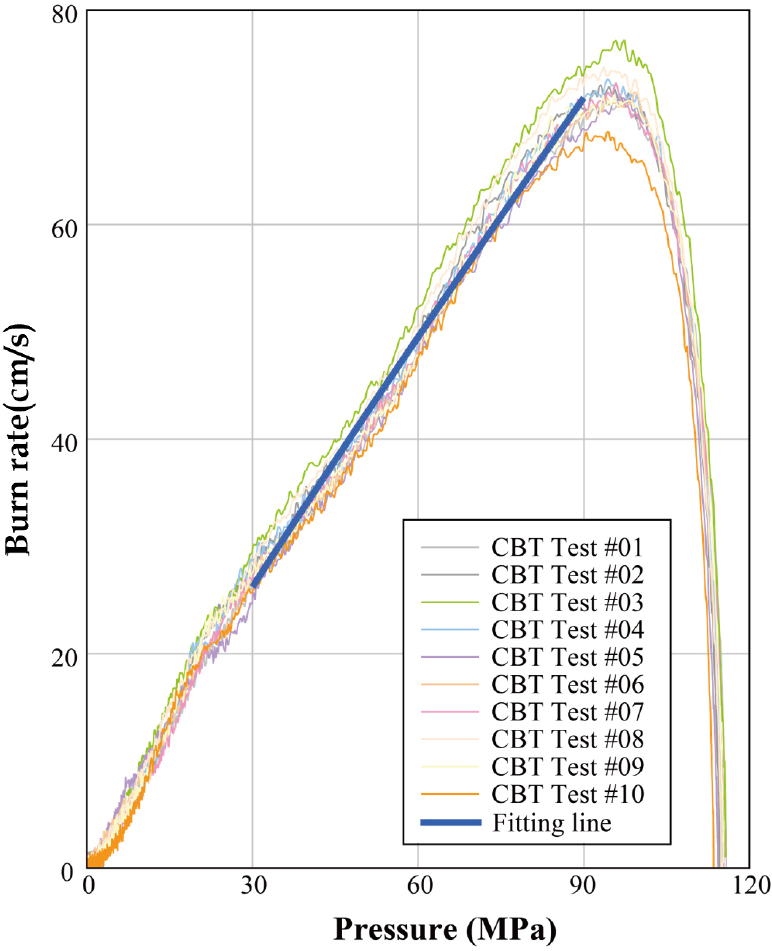
CBT 실험은 총 10회 진행되었으며, 본 연구에 사용된 반응률 계수는 Fig. 5 같이 모든 실험의 반응률 데이터의 평균값을 기반으로 산출하였고 반응률 결과는 Table 3에 나타냈다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F5.jpg

Fig. 5.

Data fitting curve through experimental data

Table 3.

Propellant reaction rate coefficient

Alpha (𝛼)	0.9173
Beta (𝛽)	0.011575 (m/s·MPa)

3.2 탄환, 포신 정보

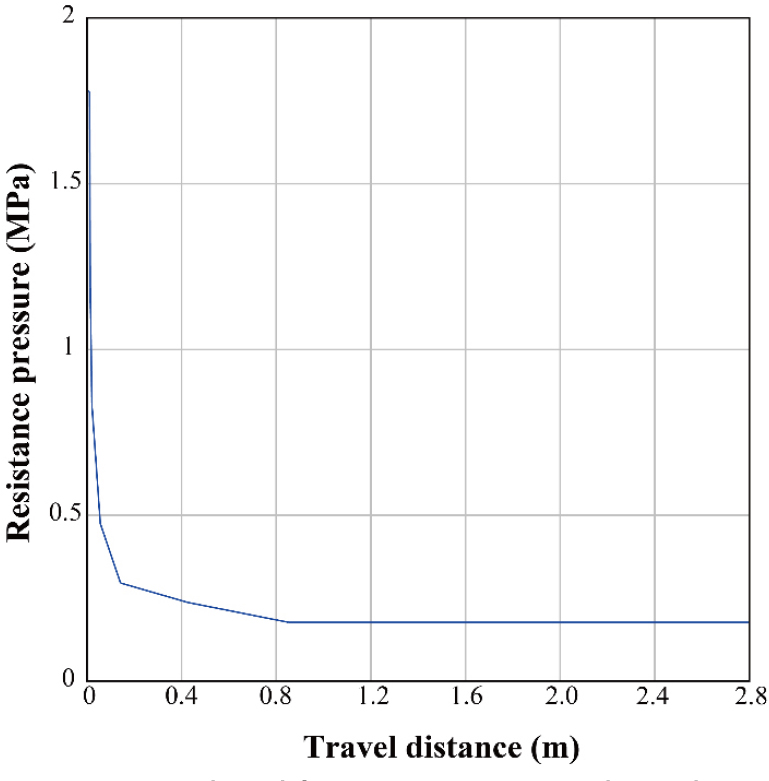
탄환과 포신의 정보는 Table 4와 같다. 시험과 해석은 40mm L/70 포신을 가진 무기체계에서 수행하였다. 탄환과 포신의 마찰력은 참고문헌(Siewert and Cytron, 2005)을 참고하여 산출하였으며 Fig. 6과 같다. 마찰력을 압력 단위로 산출하며 포신 입구에서는 마찰력이 높았다가 이동함에 따라 감소하여 특정값으로 수렴해 들어가는 형태를 띈다.

Table 4.

Specifications of the bullet and barrel

Chamber Volume	0.0175 (m³)
Groove Diameter	0.042 (m)
Bore Diameter	0.040 (m)
Arc Length Ratio of Groove to Bore (G/L)	2
Barrel Length	2.8 (m)
Rifling Pitch	35 (calibers/turn)
Chamber Diameter	0.057 (m)
Chamber Length	0.15 (m)
Barrel Taper Angle	16 (Degrees)
Projectile Weight	1.165 (kg)
Projectile Band Diameter	0.042 (m)
Projectile Band Length	0.014 (m)

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F6.jpg

Fig. 6.

Analyzed friction pressure results with projectile travel distance

3.3 해석과 시험간 결과 비교

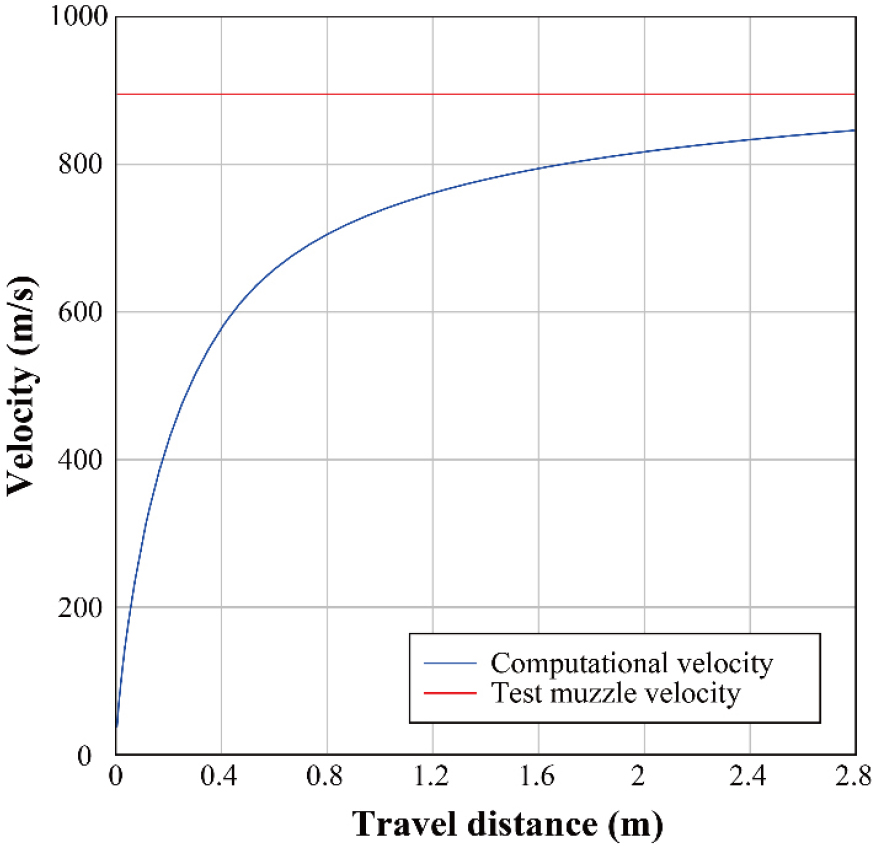
강내탄도 해석에서는 Table 1, 2, 3의 점화제, 추진제, 탄환, 포신의 정보를 기반으로 IBHVG2의 Chambrage 모델을 사용하였다. 시험은총 10회가 수행되었으며 출구에서의 탄속 측정과 약실에서의 최대 압력을 기록하였다. 이동 거리에 따른 해석 속도와 출구에서의 탄속 측정 결과를 비교하면 Fig. 7과 같다. 여기서 시험 결과는 10회의 평균 값을 사용하였으며 해석 결과에 비해 약 6% 빠른 속도를 보여주었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F7.jpg

Fig. 7.

Analysis results of projectile velocity according to travel distance and test muzzle velocity

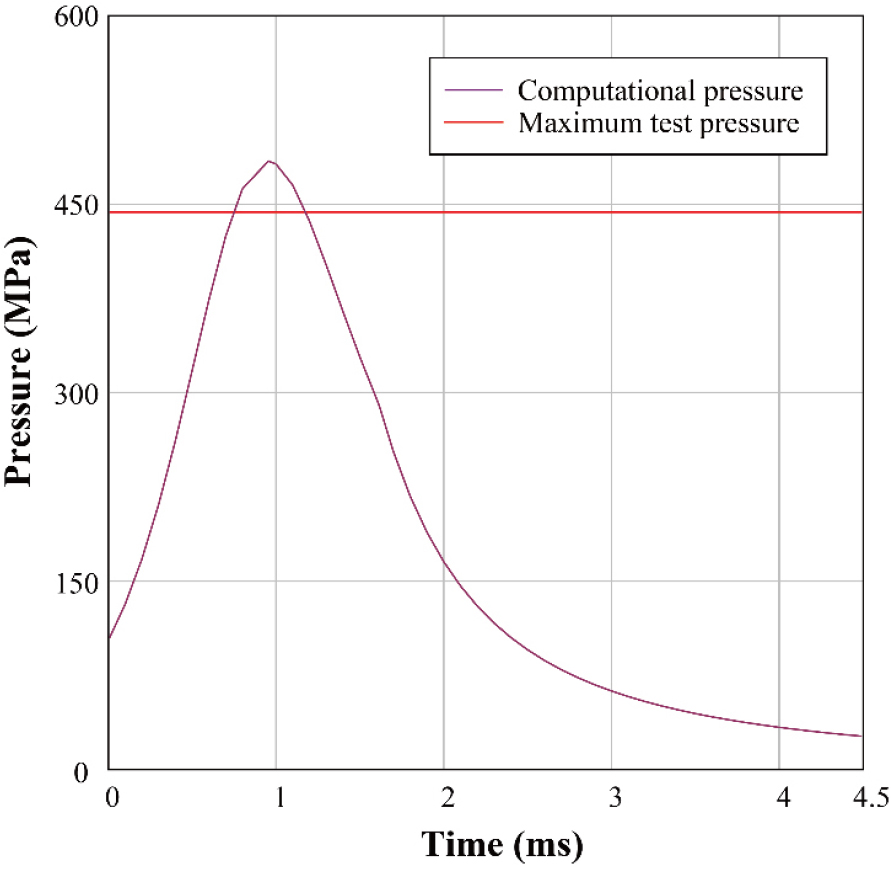
시험 최대 압력과 해석에서 나온 시간에 따른 압력 결과를 비교하면 다음 Fig. 8과 같다. 해석에서 예측한 출구까지 소요된 시간은 총 4.71ms였으며 약실 압력을 기준으로 최대 압력은 484.37MPa이었다. 시험에서 계측한 10회 평균 최대 압력은 443.75MPa로 해석에 비해 낮게 측정되었다. 이는 해석에서 초기에 점화제가 모두 연소된 것으로 가정하고 열손실을 무시하여 좁은 공간에 높은 에너지가 투여됨으로써 시험 결과에 비해 다소 높게 압력을 예측한 것으로 추정된다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2025-038-02/N0040380205/images/Figure_jcoseik_38_02_05_F8.jpg

Fig. 8.

Analysis results of chamber pressure over time and maximum test pressure

4. 결 론

본 연구에서는 강내탄도 해석 코드인 IBHVG2를 활용하여 40mm L/70 포신을 가진 무기체계에서의 발사체 거동을 이론적으로 예측하고, 이를 시험 결과와 비교함으로써 모델의 유효성과 예측 정확도를 검증하였다. 해석 과정에서는 IBHVG2의 집중 매개변수 모델(Lumped Parameter Model)을 사용하였으며, Chambrage 모델을 적용하여 발사체 거동을 추정하였다.

시험 결과와 해석 결과를 비교한 주요 항목은 출구 속도(Muzzle Velocity)와 최대 약실 압력(Maximum Chamber Pressure)이다. 출구 속도의 경우, 해석 결과는 시험 평균값에 비해 약 6% 낮은 값을 보였으며, 약실 최대 압력은 실험 측정 값이 해석 결과 대비 약 8% 낮게 측정되었다. 이는 이론 모델이 점화제의 연소 반응이 즉각적으로 진행된다고 가정한 결과로 추정된다.

본 연구에서는 IBHVG2 모델의 유효성을 검증하였고 IBHVG2의 압력 및 속도 예측 모델이 실험 데이터와 비교적 일치함을 확인하였다. 이 과정에서 폐쇄 폭발 시험(CBT) 결과를 바탕으로 추진제의 반응 계수를 도출하고, 이를 IBHVG2 모델에 반영함으로써 보다 현실적인 계산이 가능함을 확인하였다. 결론적으로, 해석과 시험 결과 간의 차이가 크지 않음을 보임으로써 무기체계의 발사 성능의 예측에 해석이 활용 가능함을 확인하였고 개선의 여지가 있음을 확인하였다. 향후 연구에서는 다차원 열유동 모델을 도입하고, 시험 환경을 보다 정밀하게 재현함으로써 더욱 정교한 강내탄도 해석을 수행하여 해석의 정확도를 증가시킬 예정이다.

Acknowledgements

본 연구는 KAIST 기계공학과 이필승 교수님과 풍산-KAIST 미래기술연구센터의 지원으로 수행되었습니다.

References

Anderson, R.D., Fickie, K. (1987) IBHVG2 (Interior Ballistics of High Velocity Guns, Version 2)-A User's Guide, Technical Report, BRL-TR-2829.

Frederick, W.R., Timothy, S.R. (1988) A Lumped -Parameter Interior Ballistic 0 Computer Code Using The TTCP Model, Memorandum Report, BRL-MR-3710.

Gough, P.S (1990) The XNOVAKTC Code, BRL-CR-627.

10.21236/ADA220153

Gough, P.S. (1993) Formulation of a Next-Generation Interior Ballistic Code, ARL-CR-68.

Jang, J.S., Oh, S.H., Rho, T.S. (2015) Three-Dimensional Computational Analysis of Interior Ballistics, Proc. Korean Soc. Propuls. Eng. Conf., pp.672~675.

Jang, J.S., Sung, H.G., Rho, T.S., Choi, D.H. (2012) Performance Analysis of Interior Ballistics using 1-D Numerical Method, J. Korean Mil. Sci. & Technol., 15(3), pp.241~249.

10.9766/KIMST.2012.15.3.241

Oberle, W.F., Kooker, D.E. (1993). BRLCB: A Closed- Chamber Data Analysis Program Part I-Theory and User's Manual, US Army Research Laboratory Technical Report, ARL-TR-36.

10.21236/ADA260493PMC281308

Pidduck, F.B. (1937) The Limiting Problem of Internal Ballistics, J. Appl. Phys., 8(2), p.144.

10.1063/1.1710269

Siewert, J., Cytron, S. (2005) Rifling Profile Push Tests: An Assessment of Bullet Engraving Forces in Various Rifling Designs, Contractor Report ARAET-CR-04002, Arrow Tech Associates & ARDEC, pp.708~712.

10.21236/ADA431357

Sung, H.G., Jang, J.S., Yoo, S.Y., Rho, T.S. (2011) Develop- ment of Numerical Code for Interior Ballistics and An- alysis of Two-phase Flow according to Drag Models, J. Korean Soc. Propuls. Eng., 15(6), pp.38~46.

Vinti, J.P., Kravitz, S. (1949) Tables for the Pidduck-Kent Special Solution for the Motion of the Powder Gas in a Gun, Technical Report, Defense Technical Information Center, ADA391151

10.21236/ADA394844

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Accuracy Verification Through Comparison of Interior Ballistic Simulations Using a Lumped Parameter Model and Experimental Results

ABSTRACT

MAIN

Fig. 1.

Computational process performed by IBHVG2

(1)

(2)

(3)

Fig. 2.

Schematic Diagram of Interior Ballistics Analysis

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

Table 1.

Thermochemical properties of the Igniter

Table 2.

Thermochemical properties of the propellant

Fig. 3.

CBT Equipment overview

Fig. 4.

Computational process performed by BRLCB

Fig. 5.

Data fitting curve through experimental data

Table 3.

Propellant reaction rate coefficient

Table 4.

Specifications of the bullet and barrel

Fig. 6.

Analyzed friction pressure results with projectile travel distance

Fig. 7.

Analysis results of projectile velocity according to travel distance and test muzzle velocity

Fig. 8.

Analysis results of chamber pressure over time and maximum test pressure

Acknowledgements

References