Design Optimization of Bracket for Wear Sensor of Automobile Brake Pads Based on Dynamic Kriging Surrogate Model

Jun-Yeong Jeong; Jung Joo Yoo; Kyung Seok Byun; Hyunkyoo Cho

doi:10.7734/COSEIK.2024.37.2.95

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 April 2024. 95-101
https://doi.org/10.7734/COSEIK.2024.37.2.95

Design Optimization of Bracket for Wear Sensor of Automobile Brake Pads Based on Dynamic Kriging Surrogate Model

자동차 브레이크 패드 마모량 측정센서 브라켓의 다이나믹크리깅 대리모델 기반 설계최적화

Jun-Yeong Jeong¹

Jung Joo Yoo¹

Kyung Seok Byun²

Hyunkyoo Cho²^*

정 준영¹

유 정주¹

변 경석²

조 현규²^*

¹Graduate Student, Mechanical Engineering, Mokpo National University, Muan,58554, Korea

²Professor, Mechanical Engineering, Mokpo National University, Muan,58554, Korea

¹국립목포대학교 기계공학과 박사과정

²국립목포대학교 기계공학과 교수

^{*Corresponding Author}

ABSTRACT

This paper introduces an optimized design for a sensor bracket used to measure the wear amount of an automobile brake pad, based on a dynamic kriging surrogate model. During testing, the temperature of the brake pad can increase beyond 600°C, which often causes sensor malfunction. Therefore, it is essential to optimize the shape of the sensor bracket to minimize heat transfer. To reduce the computational cost of the optimization, the heat-transfer simulation is replaced by a dynamic kriging surrogate model. Dynamic kriging utilizes the best combination of correlation and basis functions and constructs an accurate surrogate model. Following optimization, the temperature of the sensor position decreases by 7.57%. The results from the surrogate model under optimum conditions are verified by a heat-transfer simulation, and the design optimization using a surrogate model is found to be effective.

Keywords

surrogate model

dynamic kriging

design optimization

heat-transfer simulation

brake pad

본 논문에서는 다이나믹크리깅 대리모델 기반 자동차 브레이크 패드 마모량 측정센서 브라켓의 설계최적화를 소개한다. 브레이크 작동시 마찰재 바닥의 온도가 600°C 이상으로 상승하고, 이 열이 전달되어 센서의 기능을 상실시킨다. 따라서 열전달을 최소화하는 브라켓 형상의 설계최적화는 필수적이다. 최적화에 소요되는 계산비용을 절감하기 위해 다이나믹크리깅 대리모델로 열전달 시뮬레이션을 대체하였다. 다이나믹크리깅은 최적의 상관함수와 기저함수를 선정하였으며, 정확한 대리모델을 도출하였다. 최적화 결과 센서위치의 온도가 초기모델에 비해 7.57% 감소하였으며, 이를 열전달 시뮬레이션으로 다시 한번 확인하여 대리모델 기반 최적설계가 유의미함을 검증하였다.

키워드

대리모델

다이나믹크리깅

설계최적화

열전달 시뮬레이션

브레이크 패드

MAIN

1. 서 론
2. 브레이크 패드 마모량 측정센서와 브라켓
2.1 브레이크 패드 마모량 측정센서
2.2 브라켓 열전달 시뮬레이션
3. 설계변수 선정 및 샘플링
3.1 설계변수 선정
3.2 라틴하이퍼큐브 샘플링(Latin hypercube sampling)
4. 다이나믹크리깅 대리모델
4.1 크리깅(Kriging) 기법
4.2 다이나믹크리깅 기법
4.3 다이나믹크리깅 대리모델 구축
5. 최적설계 및 검증
5.1 최적설계 정식화
5.2 최적설계 결과
5.3 최적모델 열전달 시뮬레이션 결과검증
6. 결 론

1. 서 론

최근 자동차 성능의 급격한 발전에 발맞추어 차량 안전성 관련 기술개발이 큰 주목을 받고 있다. 차량의 성능이 향상되어 자동차의 출력이 높아지고 속도가 증가함에 따라 운전 안전성에 대한 소비자들의 요구도 높아지고 있어 관련 연구개발이 활발히 진행되고 있다. 차량의 안전성에 가장 중요한 영향을 미치는 것은 브레이크 시스템이다. 브레이크 시스템은 운전자의 안전한 주행에 필수적이며, 이의 오작동이나 고장은 심각한 교통사고로 이어질 수 있다. 자동차의 제동방식은 브레이크 패드 즉 마찰재가 차량의 운동에너지를 열에너지로 전환시킴으로써 차량을 감속시키는 것이다. 이때 과도한 마찰열과 압력 때문에 브레이크 패드가 마모되고, 이로 인해 브레이크 패드에 변형이 발생하면 브레이크가 제 기능을 다할 수 없게 된다. 이 때문에 올바른 교체시기에 브레이크 패드를 교체하여야 한다. 패드의 교체시기는 일반적으로 주행거리로 정하는데, 운전습관에 따라 브레이크 사용량이 다르고, 브레이크 제조사나 패드 재질별로 마모 특성이 달라 주행거리로 교체시기를 결정하는 것은 적절하지 않다. 시중에 가장 상용화 된 방식으로는 가청형 마모 센서가 있는데, 이는 브레이크 패드가 허용 두께 이하로 마모되면 센서가 디스크 브레이크 로터에 접촉되어 고음의 소리로 경고하는 방식이다. 그러나 이 방식도 운전 중에는 소음으로 인해 잘 듣지 못하는 경우가 많다.

이 문제를 해결하기 위해 최근 가변저항 센서를 활용한 브레이크 패드 마모량 측정 연구가 이루어졌다. Kim 등은 Fig. 1과 같이 샤프트와 가변저항을 케이스에 넣고, 이를 브레이크 패드에 고정하였다(Kim, 2021). 캘리퍼의 유압을 통해 마모량만큼 샤프트가 움직이면 움직인 거리를 가변저항이 측정하고 이 값을 마모량으로 환산하여 측정하는 방식이다. 하지만 Fig. 2와 같이 다이나모미터 시험 중에 브레이크 패드의 온도가 600°C 이상 상승하고 이로 인해 센서가 오작동함을 발견하였고, 브라켓을 추가하여 케이스와 패드를 분리하고 열의 전달을 줄이고자 하였다(Yoo, 2023). 그럼에도 불구하고 이때 생기는 마찰열이 측정센서를 지지하는 브라켓을 타고 센서로 전해지고, 이는 센서의 수명 외에도 측정값의 변동성이 확대되거나 부정확해질 수 있어 본 연구에서는 열전달을 최소화하는 최적의 브라켓 형상을 얻고자 한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370203/images/Figure_jcoseik_37_02_03_F1.jpg

Fig. 1.

Brake pad wear sensor principle

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370203/images/Figure_jcoseik_37_02_03_F2.jpg

Fig. 2.

Brake disc sensor dynamometer test result using variable resistance and thermocouple

브라켓 형상의 최적화에는 다수의 열전달 시뮬레이션 결과가 필요하다. 하지만 시뮬레이션을 여러 번 수행하기 위해서는 계산비용이 많이 소모된다. 이를 해결하기 위해서 본 연구에서는 다이나믹크리깅(Dynamic kriging) 기반 대리모델 기법을 적용하였다. 먼저 브라켓의 형상을 8개의 설계변수로 나타내고, 이의 설계범위 내에 라틴하이퍼큐브 샘플링(Latin hypercube sampling) 기법으로 총 200개의 샘플을 선정하였다. 200개의 샘플에 대한 열전달 시뮬레이션을 수행하고, 이를 바탕으로 다이나믹크리깅 대리모델을 구축하였다. 구축한 대리모델을 이용하여 열전달을 최소화하는 브라켓 형상의 최적설계를 수행하였으며, 최적설계점에서 시뮬레이션을 다시 한번 수행하여 최적설계 결과의 타당성을 검증하였다.

2. 브레이크 패드 마모량 측정센서와 브라켓

2.1 브레이크 패드 마모량 측정센서

브레이크 패드 마모량 측정센서를 활용한 측정원리는 다음과 같다. 먼저, 차량의 제동 시 발생하는 마찰에 의한 힘으로 브레이크 패드가 마모되고, 그 힘에 의해서 선형 가변저항 센서에 결합된 샤프트가 브레이크 패드와 디스크가 압축된 만큼 상승하게 된다. 이때 생긴 변화를 브레이크 패드 잔량으로 환산하여 차량 운전자에게 정보를 제공하는 구조이다. 하지만 브레이크 패드의 마찰열로 인해 센서가 잦은 고장을 일으켰고, 이를 개선하고자 Fig. 3과 같이 센서와 패드를 분리하는 브라켓을 설치하였다(Yoo, 2023).

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370203/images/Figure_jcoseik_37_02_03_F3.jpg

Fig. 3.

Wear measurement sensor with bracket

2.2 브라켓 열전달 시뮬레이션

자동차 브레이크 패드 마모량 측정센서 브라켓의 설계 최적화를 위해서 초기 브라켓 모델의 열전달 시뮬레이션을 수행하였다. 시뮬레이션에는 ANSYS Workbench 2202 R2 프로그램의 Steady-State Thermal 기능이 사용되었다. Fig. 4에 나타낸 해석모델의 노드와 요소는 각각 157,717개 109,960개가 사용되었고, 센서부의 형상이 원형이고(Fig. 4 참조), 센서위치의 온도 데이터가 중요하기 때문에 곡률 형상을 정확히 표현하기 위해 Tetrahedron 요소로 모델링하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370203/images/Figure_jcoseik_37_02_03_F4.jpg

Fig. 4.

Thermal analysis result

열전달 시뮬레이션의 경계조건은 다음과 같다. 주변 대류는 160°C로 설정하였으며 브레이크 패드의 마찰재 바닥(Pad bottom)은 600°C로 입력하였다. 이는 모두 Yoo 등이 수행한 다이나모미터 시험의 환경을 측정한 조건과 동일하다(Yoo, 2023). 해당 조건에서 센서가 부착되는 센서위치(Fig. 4 참고)의 온도를 열전달 시뮬레이션을 통해 확인하였다. 초기 브라켓 설계의 경우 센서위치의 온도는 174.887°C로 확인되었다.

3 설계변수 선정 및 샘플링

3.1 설계변수 선정

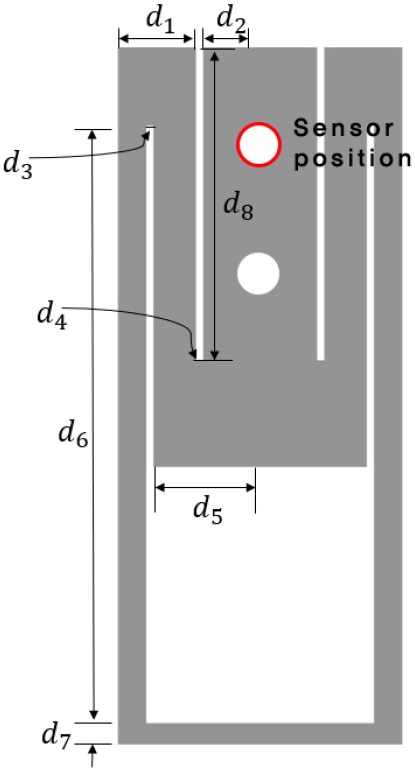
마모량 측정센서 브라켓의 설계최적화를 위해서 설계변수 $d_{i} (i = 1, 2, . . ., 8)$ 를 선정하였다. 설계변수는 Fig. 5에서 나타내었듯이 브라켓의 폭과 높이, 길이 등 총 8개로 구성되어 있다. 초기설계와, 설계변수의 하한 및 상한값은 Table 1과 같다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370203/images/Figure_jcoseik_37_02_03_F5.jpg

Fig. 5.

Design variables

Table 1.

Initial design variable

Design variable	Lower bound ( $d_{l b}$ )	Initial design (mm)	Upper bound ( $d_{u b}$ )
$d_{1}$	3.84	5.49	7.14
$d_{2}$	2.80	4.01	5.21
$d_{3}$	0.35	0.5	0.65
$d_{4}$	0.35	0.5	0.65
$d_{5}$	5.25	7.5	9.75
$d_{6}$	29.4	42	54.6
$d_{7}$	1.05	1.5	1.95
$d_{8}$	15.4	22	28.6

3.2 라틴하이퍼큐브 샘플링(Latin hypercube sampling)

열전달 시뮬레이션의 대리모델을 생성하기 위해서는 대리모델 구축에 필요한 훈련 데이터와 생성된 대리모델의 정확도를 판단하기 위한 테스트 데이터가 필요하다. 8개의 설계변수가 사용되므로 대리모델은 8차원이 되는데, 이러한 고차원 대리모델에 사용할 데이터에 상관관계가 발생하면 대리모델의 정확도에 부정적인 영향을 끼치는 경우가 발생한다. 따라서, 본 연구에서는 주어진 영역에서 고른 샘플을 추출하는 라틴하이퍼큐브 샘플링 기법(Olsson et al., 2003)을 활용하여 데이터를 샘플링하였다. 훈련 데이터 150개, 테스트 데이터 50개의 총 200개의 샘플을 도출하였다.

4. 다이나믹크리깅 대리모델

열전달 시뮬레이션을 대신하여 대리모델을 구축하는 기법으로 본 논문에서는 다이나믹크리깅을 사용하였다. 다이나믹크리깅은 비선형성이 큰 시뮬레이션 결과를 정확하게 묘사할 수 있는 것으로 알려져 있다(Song et al., 2013). 이 절에서는 크리깅과 다이나믹크리깅 기법에 대해 요약하고, 마모량 측정센서 브라켓의 열전달 시뮬레이션의 대리모델에 대해 설명한다.

4.1 크리깅(Kriging) 기법

크리깅 대리모델을 생성하기 위해서는 훈련 데이터인 $X = [x_{1}, x_{2}, \dots, x_{n}]^{T}, x_{i} \in R^{m}$ 와 훈련 데이터에 대한 결과값인 $y (x_{i}) \in R^{1}$ 가 필요하다. 크리깅 모델의 수학적 형태는 다음 식 (1)과 같다(Cressie, 1988).

(1)

y (x_{i}) = \sum_{j = 1}^{k} β_{j} f_{j} (x_{i}) + e (x_{i})

여기서, $k$ 는 기저함수(Basis function) 항의 수, $f_{j}$ 는 $j$ 번째 기저함수의 항, 그리고 $β_{j}$ 는 $j$ 번째 기저함수 항의 계수이다. 기저함수의 계수는 최소제곱법(Least square method)을 통해서 얻는다. $e = {[e (x_{1}), e (x_{2}), \dots, e (x_{n})]}^{T}$ 는 평균이 0이고 분산이 $σ^{2}$ 인 0이 아닌 공분산을 나타낸다. 공분산의 구조는 다음 식 (2)와 같다(Jeong, 2022).

(2)

E [e (x_{i}) ` e (x_{j})] = σ^{2} R (θ, ` x_{i}, ` x_{j})

여기서, $θ = [θ_{1}, θ_{2}, \dots, θ_{m}]^{T}$ 는 확률과정의 알려지지 않은 상관매개변수 벡터이고, $R (θ, x_{i}, x_{j})$ 은 상관행렬이다. 예시로 상관행렬의 상관함수가 가우시안 상관함수의 경우 형태는 다음 식 (3)과 같다(Zhao et al., 2011).

(3)

R (θ, x_{i}, x_{j}) = \prod_{l = 1}^{m} \exp (- θ_{l} {(x_{i, l} - x_{j, l})}^{2})

공분산 행렬을 구하려면 공분산 행렬에 사용되는 상관매개변수 𝜃 값을 얻어야 한다. 상관매개변수 값의 변화가 크리깅 모델의 정확도에 영향을 끼치기 때문에 최적의 상관매개변수 $θ_{o p t}$ 를 얻어야 한다. 최적의 상관매개변수를 얻을 때는 최대우도 추정법(Maximum likelihood estimation)이 가장 많이 사용되는데, 일반적으로 로그를 취하여 다음과 같은 로그우도함수를 최대화하는 $θ_{o p t}$ 를 구한다(Martin and Simpson, 2005).

(4)

\begin{aligned} ψ (θ) = & - \frac{n}{2} \ln [2 π σ^{2}] - \frac{1}{2} \ln [R] \\ - \frac{1}{2 σ^{2}} (y - F β)^{T} R^{- 1} (y - F β) \end{aligned}

여기서, $n$ 은 훈련 데이터의 개수이고, $| R |$ 은 R의 행렬식이다.

$σ^{2} = \frac{1}{n} (y - F β)^{T} R^{- 1} (y - F β)$ 는 앞에서 말했듯 공정분산, $β = {(F^{T} R^{- 1} F)}^{- 1} F^{T} R^{- 1} y$ 는 기저함수의 계수이다. 최적의 상관매개변수를 얻고 나면 크리깅 모델을 생성하여 예측하고자 하는 결과값을 얻어낼 수 있다. 예측값을 얻어내는 식은 아래 식 (5)와 같이 표현할 수 있다.

(5)

\hat{y} (x) = f^{T} β + r^{T} R^{- 1} (y - F β)

여기서, $r = [R (θ, x_{1}, α), \dots R (θ, x_{n}, α)]$ 은 모델을 생성하기 위한 훈련 데이터 $x_{i}$ 와 예측을 하고자 하는 지점 𝛼의 상관행렬이다.

4.2 다이나믹크리깅 기법

앞서 설명한 크리깅 기법은 모델을 생성할 때 선정하는 상관함수와 기저함수에 그 정확도가 큰 영향을 받는다. 따라서 모든 상관함수와 기저함수 조합의 크리깅모델을 생성하여 추가적인 테스트 데이터로 정확도 평가를 하지 않으면 어떠한 상관함수와 기저함수가 가장 높은 정확도를 갖는지 알 수 없다. 따라서, 본 연구에서는 훈련 데이터만 사용하여 최대(로그)우도 추정법과 교차검증(Cross validation) 결과를 기반으로 최적의 상관함수와 기저함수를 선정하는 다이나믹크리깅 기법을 적용하였다.

본 연구에서 사용된 다이나믹크리깅은 총 6개의 상관함수와 3가지 기저함수의 형태를 가지고 있다. 6개의 상관함수는 Table 2와 같으며 기저함수는 상수항, 일차다항식, 이차다항식의 3가지 형태이다.

Table 2.

Correlation functions (Song et al., 2013)

Correlation function	$R_{j} (θ_{j}, x_{1}, x_{2})$
Exponential	$\exp (- θ_{j} \| x_{2} - x_{1} \|)$
Gaussian	$\exp (- θ_{j} \| x_{2} - x_{1} \|^{2})$
Linear	$max {0, 1 - θ_{j} \| x_{2} - x_{1} \|}$
Spherical	$1 - 1.5 ξ_{j} + 0.5 ξ_{j}^{3}, ξ_{j} = min {1, θ_{j} \| x_{2} - x_{1} \|}$
Cubic	$1 - 3 ξ_{j}^{2} + 2 ϵ_{j}^{3}, ξ_{j} = min {1, θ_{j} \| x_{2} - x_{1} \|}$
Spline	$\begin{aligned} \{\begin{cases} \begin{array}{ll} 1 - 15 ξ_{j}^{2} + 30 ξ_{j}^{3}, & for 0 \leq ξ_{j} \leq 0.2 \\ 1.25 {(1 - ξ_{j})}^{3}, & for 0 < ξ_{j} < 1 \end{array} \\ \begin{array}{ll} 0, & for ξ_{j} \geq 1, \end{array} \end{cases} \\ where ξ_{j} = θ_{j} \| x_{2} - x_{1} \| \end{aligned}$

다이나믹크리깅 모델을 생성하는 순서는 다음과 같다. 훈련 데이터, 상관매개변수의 초기값과 상관매개변수의 상한 및 하한값의 범위를 제시하는 것을 시작으로 한다. 상수항 형태의 기저함수를 기반으로 6개의 상관함수 각각의 상관매개변수를 최적화한다. 이때 최적화에는 Hooke jeeves 기법이 사용된다. 최적화된 상관매개변수가 얻어지면 식 (4)를 통해 로그우도 값을 도출한다. 이때 6개의 상관함수별 로그우도 값을 비교하여 값이 가장 높은 상관함수를 선택한다. 다음으로 기저함수를 선택한다. 선정된 상관함수를 기반으로 3종의 기저함수 모델을 생성한다. 그 다음 훈련 데이터를 이용하여 생성된 모델의 교차검증을 진행한다. 가장 낮은 교차검증 값을 가지는 다항식의 형태를 기저함수의 형태로 지정한다. 선정된 상관함수와 기저함수 형식을 적용하여 크리깅 대리모델을 구축하면 다이나믹크리깅이 완료된다.

4.3 다이나믹크리깅 대리모델 구축

150개의 훈련 데이터를 기반으로 브레이크 패드 마모량 측정센서 열전달 시뮬레이션의 다이나믹크리깅 대리모델을 구축하였다. 다이나믹크리깅은 먼저 기저함수를 상수로 고정하고, 6개 상관함수 각각의 상관매개변수의 최적화를 진행하고 그 값을 입력한 로그우도 값을 Table 3과 같이 얻어내었다. 상관함수별 로그우도 값을 비교하여 가장 높은 값을 가지는 Exponential 상관함수를 선정하였다.

Table 3.

Maximum log-likelihood for correlation functions

Correlation function	Log likelihood
Gaussian	-0.9914
Cubic	-0.9920
Exponential	-0.8985
Linear	-0.9931
Spline	-0.9916
Spherical	-0.9844

다음으로 다이나믹크리깅은 기저함수를 선정한다. 앞에서 선정한 Exponential 상관함수를 고정하고, 기저함수를 상수, 일차, 이차다항식으로 바꿔가며 교차검증을 수행한다. 훈련 데이터 150개의 교차검증 값은 Table 4와 같다. 상수항은 190.4716, 일차다항식은 그보다 높은 254.9374, 이차다항식은 가장 낮은 교차검증 17.118값이 확인되어 가장 낮은 값을 보이는 이차다항식을 기저함수로 선정하였다. 일반적으로 다항식의 항이 높을수록 기저함수의 자유도가 높아져 교차검증 에러값이 낮아질 것이라 생각되지만, 본 연구의 경우 일차다항식이 상수항보다 높은 에러값을 보였다. 따라서, 다이나믹크리깅을 통해 어떤 기저함수를 사용할지도 검토하는 것이 필요한 과정임을 확인할 수 있다.

Table 4.

Cross validation data

Correlation function	Constant	Linear polynomials	Quadratic polynomials
Exponential	190.4716	254.9374	17.118

다음으로 다이나믹크리깅이 선정한 Exponential 상관함수와 이차다항식 기저함수가 올바른 선정이었는지 추가적인 50개의 테스트 데이터를 이용하여 확인하였다. 4.3절에서 다이나믹크리깅은 훈련 데이터 150개만으로 상관함수와 기저함수를 선정하였으며, 이 절에서 50개 테스트 데이터를 활용하여 정확도 검증을 하는 것은 부가적인 절차임을 밝힌다. 먼저 앞에서 사용한 150개의 훈련 데이터로, 3개 기저함수와 6개 상관함수를 조합한 총 18개의 대리모델을 생성하였다. 생성된 모델은 50개의 테스트 데이터를 통해 NRMSE(Normalized root mean square error)로 정확도를 판단하였다. NRMSE의 식은 다음 식 (6)과 같다.

(6)

N R M S E (%) = \frac{\sqrt{\frac{\sum_{i = 1}^{n_{t eot}} {({\hat{y}}_{i} - y_{i})}^{2}}{n_{test}}}}{y_{\max} - y_{\min}}

여기서, ${\hat{y}}_{i}$ 는 대리모델을 통해 얻은 열전달 시뮬레이션 결과이고, $y_{i}$ 는 테스트 데이터의 결과값이며, $n_{t e s t}$ 는 테스트 데이터의 수로 여기서는 50이다. 18개의 대리모델의 NRMSE 결과는 Table 5와 같다.

Table 5.

Accuracy of temperature surrogate models

Correlation function	Constant	Linear polynomials	Quadratic polynomials
Gaussian	18.14%	12.57%	3.25%
Cubic	18.14%	12.57%	3.25%
Exponential	10.84%	12.54%	3.25%
Linear	18.14%	12.57%	3.25%
Spline	18.14%	12.57%	3.25%
Spherical	18.14%	12.57%	3.25%

18개의 대리모델을 비교한 결과 상수 기저함수와 Exponetial 상관함수가 3.25%로 가장 낮은 NRMSE를 보여 다이나믹크리깅이 기저함수와 상관함수를 정확히 선정했음을 확인하였다. 다이나믹크리깅의 순서를 따라가보면, 상수 기저함수의 경우 Exponential 상관함수가 가장 낮은 NRMSE값을 보인다. 또한 Exponential 상관함수를 고정하였을 때에도 이차다항식의 기저함수가 가장 낮은 NRMSE값을 보이므로, 다이나믹크리깅 과정에서도 문제가 없었음을 다시 한번 확인할 수 있었다. 일차다항식보다 상수 기저함수가 낮은 NRMSE를 보이는 경우는 Exponential 상관함수 뿐인데, 이 역시 Table 4에서 이미 확인하였듯 다이나믹크리깅이 잘 검증하였다. 다이나믹크리깅 모델의 NRMSE는 3.25% 이므로 최적설계를 수행하기 충분한 정확도라 생각된다.

5. 최적설계 및 검증

5.1 최적설계 정식화

본 논문에서는 열전달 시뮬레이션 대리모델을 기반으로 마모량 측정센서 브라켓 설계최적화를 진행하였다. 최적설계 정식은 다음과 같다.

(7)

Minimize T (d) subject to d_{l b} < d < d_{u b}

여기서, d는 설계변수의 열백터이고 $T (d)$ 는 다이나믹크리깅 대리모델로 얻은 열전달 시뮬레이션 결과데이터이다. 제약조건은 라틴하이퍼큐브샘플링에 사용된 상한값과 하한값으로 하며 그 값은 Table 1에 나타나있다. 대리모델의 특성상 대리모델이 생성될 때 사용된 훈련 데이터의 범위 밖의 데이터에 대한 결과는 그 정확도가 상대적으로 낮기 때문에 이러한 제약조건을 두었다. 목적함수는 센서가 부착되는 위치의 온도인 열전달 시뮬레이션 대리모델의 결과값으로 하여 센서에 전달되는 열이 최소화되도록 하였다.

5.2 최적설계 결과

열전달 시뮬레이션 대리모델을 기반으로 설계최적화를 진행하였다. 최적화는 Matlab 2022b에서 fmincon 함수를 사용하여 순차 2차식 계획법(Sequential quadratic programing)으로 수행되었다. 브레이크 패드 마모량 측정센서 브라켓의 형상 설계최적화 결과는 Table 6과 같다.

Table 6.

Optimum design variable and Change

Design variable	Initial design (mm)	Optimal design (mm)	Change
$d_{1}$	5.49	4.564	-20.29%
$d_{2}$	4.01	4.044	0.84%
$d_{3}$	0.5	0.497	-0.60%
$d_{4}$	0.5	0.562	11.03%
$d_{5}$	7.5	8.553	12.31%
$d_{6}$	42	42.999	2.32%
$d_{7}$	1.5	1.578	4.94%
$d_{8}$	22	19.581	-12.35%

최적화 결과 $d_{1}$ 의 값이 -20.29%의 가장 큰 변화를 보였는데, 브레이크 패드 마찰재 바닥에서 마찰열이 올라와 브라켓 양단 다리를 통해 센서로 열이 전달되기 때문에 이를 차단하기 위해 크게 감소한 것으로 해석된다. 같은 이유로 좌우단과 센서의 거리를 최대한으로 하기 위해서 $d_{2}$ 와 $d_{4}$ 는 0.84%, 11.03% 증가하였다. 추가적으로 대류의 온도 조건도 존재하나 그 온도는 브라켓 다리를 통해서 전달되는 마찰열에 비해 그 규모가 작아 영향이 적은 것으로 판단된다.

실제 250°C의 온도를 기준으로 기존 모델의 경우 하부로부터 16.3mm 높이까지 열이 전달되는 것을 확인하였으나, 최적모델의 경우 7mm의 높이에서 250°C 온도 이하로 내려감을 확인하였다. Fig. 6을 통해 그 사실을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-02/N0040370203/images/Figure_jcoseik_37_02_03_F6.jpg

Fig. 6.

Initial model and optimal model

5.3 최적모델 열전달 시뮬레이션 결과검증

최적모델의 열전달 시뮬레이션 결과는 Table 7과 같다. 대리모델을 통해 얻은 결과는 162.581°C이며 이는 초기모델의 174.887°C 보다 12.306°C 낮아져 7.57% 감소함을 확인하였다. 4.3절에서 테스트 데이터를 이용하여 다이나믹크리깅 대리모델의 정확도를 검증하였으나, 최적설계점에서는 추가 열전달 시뮬레이션을 수행하여 정확성을 한 번 더 검증하였다. 시뮬레이션 결과는 162.541°C로 다이나믹크리깅 대리모델의 162.581°C와 차이가 0.04°C 밖에 나지 않아 최적설계가 정확한 대리모델을 기반으로 수행되었음을 검증할 수 있었다.

Table 7.

Comparison of results

Name	Temperature (°C)	Change
Initial model	174.887	0.00%
Surrogate model	162.581	-7.57%
Analysis	162.541	-7.60%

6. 결 론

본 연구에서는 자동차 브레이크 패드 마모량 측정센서 브라켓의 설계최적화를 수행하였다. 계산비용이 높은 열전달 시뮬레이션을 대신하여 대리모델을 사용함으로써 최적설계 전체의 계산비용을 낮출 수 있었다. 대리모델로는 기존의 크리깅 기법의 단점을 보완한 다이나믹크리깅 기법이 사용되었다. 대리모델의 구축과 정확도 평가에 사용할 데이터는 라틴하이퍼큐브 샘플링으로 영역에서 고르게 추출하였다.

라틴하이퍼큐브 샘플링 기법으로 추출한 200개의 샘플에 대한 열전달 시뮬레이션을 수행하였고, 그중 150개의 데이터로 다이나믹크리깅 대리모델을 생성하였다. 다이나믹크리깅은 Exponential 상관함수와 이차다항식 기저함수를 선정하였다. 다이나믹크리깅이 상관함수와 기저함수를 적절히 선정하였는지 확인하기 위해 6개 상관함수와 3개 기저함수의 모든 조합인 총 18개의 대리모델을 생성하였다. 18개의 대리모델에 나머지 50개 데이터를 입력하여 결과값을 도출한 후 NRMSE를 계산하여 정확도를 평가하였다. 비교 결과 본 연구에서 사용된 다이나믹크리깅이 선정한 Exponential 상관함수와 이차다항식 기저함수를 갖는 대리모델의 정확도가 가장 높음을 확인하였다.

다이나믹크리깅 대리모델을 활용하여 최적설계를 수행하였다. 최적설계점에서 센서위치의 온도는 162.581°C로 초기의 174.887°C와 비교하여 7.57% 감소하였으며, 이로부터 적절한 최적설계점이 도출되었음을 확인하였다. 최적설계점의 실제 열전달 시뮬레이션 수행 결과 센서위치의 온도는 162.541°C로, 다이나믹크리깅 대리모델의 결과와 0.04°C의 차이로 아주 근사함을 확인하였다. 따라서, 본 연구에서 구축한 다이나믹크리깅 모델의 정확성이 다시 한번 검증되었으며, 계산비용이 많이 소모되는 유한요소해석 등의 시뮬레이션을 대신하여 대리모델 기반 최적설계를 수행하는 것이 적절함을 확인하였다.

Acknowledgements

본 과제(결과물)는 2023년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과입니다(재단 과제관리번호: 광주전남플랫폼 2021RIS-002).

References

Cressie, N. (1988) Spatial Prediction and Ordinary Kriging, Math. Geol., 20(4), pp.405~421.

10.1007/BF00892986

Jeong, J. (2022) Design Optimization of Casing and Stay Vane of Reaction Hydro Turbine Using Dynamic Kriging Surrogate Model, Master's Course, Mokpo National University, p.96.

Kim, M. (2021) A Study on the Measurement of Real-Time Brake Pad Wear and Disk Temperature Using Variable Resistance and Thermocouple, Master's Course, Mokpo National University, p.68.

Martin, J.D., Simpson, T.W. (2005) Use of Kriging Models to Approximate Deterministic Computer Models, AIAA J., 43(4), pp.853~863.

10.2514/1.8650

Olsson, A., Sandberg, G., Dahlblom, O. (2003) On Latin Hypercube Sampling for Structural Reliability Analysis, Struct. Saf., 25(1), pp.47~68.

10.1016/S0167-4730(02)00039-5

Song, H., Choi, K.K., Lamb, D. (2013) A Study on Improving the Accuracy of Kriging Models by Using Correlation Model/Mean Structure Selection and Penalized Log-Likelihood Function, 10th World Conference on Structural and Multidisciplinary Optimization, pp.1~10.

Yoo, J. (2023) A Study on Brake Pad Wear and Disc Temperature Real-Time Monitoring Sensor Heat Resistance Characteristics, Master's Course, Mokpo National University, p.92.

Zhao, L., Choi, K.K., Lee, I. (2011) Metamodeling Method Using Dynamic Kriging for Design Optimization, AIAA J., 49(9), pp.2034~2046.

10.2514/1.J051017

Journal of the Computational Structural Engineering Institute of Korea 한국전산구조공학회 논문집 ISSN:1229-3059(Print) 2287-2302(Online)

Preview

Design Optimization of Bracket for Wear Sensor of Automobile Brake Pads Based on Dynamic Kriging Surrogate Model

ABSTRACT

MAIN

Fig. 1.

Brake pad wear sensor principle

Fig. 2.

Brake disc sensor dynamometer test result using variable resistance and thermocouple

Fig. 3.

Wear measurement sensor with bracket

Fig. 4.

Thermal analysis result

Fig. 5.

Design variables

Table 1.

Initial design variable

(1)

(2)

(3)

(4)

(5)

Table 2.

Correlation functions (Song et al., 2013)

Table 3.

Maximum log-likelihood for correlation functions

Table 4.

Cross validation data

(6)

Table 5.

Accuracy of temperature surrogate models

(7)

Table 6.

Optimum design variable and Change

Fig. 6.

Initial model and optimal model

Table 7.

Comparison of results

Acknowledgements

References