Seismic Retrofit Strategy Reducing Torsion-Induced Higher Mode Effects of Torsionally-Coupled Low-Rise Buildings

Yi-Seop Shin; Hyung-Joon Kim

doi:10.7734/COSEIK.2024.37.6.379

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 December 2024. 379-390
https://doi.org/10.7734/COSEIK.2024.37.6.379

Seismic Retrofit Strategy Reducing Torsion-Induced Higher Mode Effects of Torsionally-Coupled Low-Rise Buildings

횡-비틀림 거동하는 고차모드 지배 저층구조물의 내진보강 전략

Yi-Seop Shin¹

Hyung-Joon Kim²^*

신 이섭¹

김 형준²^*

¹Graduate Student (Ph.D Course), Department of Architectural Engineering, University of Seoul, Seoul, 02504, Korea

²Professor, Department of Architecture, University of Seoul, Seoul, 02504, Korea

¹서울시립대학교 건축공학과 박사과정

²서울시립대학교 건축학부 교수

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

The lateral-torsional behavior of low-rise buildings may amplify higher mode effects, requiring both nonlinear static and linear dynamic analyses for seismic performance evaluation according to relevant standards. The linear dynamic procedures involve significant safety factors, unintentionally leading to excessive seismic retrofitting designs. Engineers have employed trial-and-error methods to mitigate higher mode effects during seismic retrofit design. However, this approach requires substantial time and effort, and it is challenging to verify the optimality of the retrofit solutions. The current study establishes a mathematical model of low-rise buildings and conducts response spectrum analysis to independently assess the influence of torsion on higher mode effects. Based on these investigations, this study presents graphs and procedures that can be utilized for efficient seismic retrofit design. The proposed procedures demonstrate that the higher mode effects in low-rise buildings exhibiting lateral-torsional behavior can be reduced with minimal seismic retrofit.

Keywords

low-rise buildings

torsional effect

higher mode effect

seismic retrofit

response spectrum analysis

저층 건축물의 횡-비틀림 거동은 고차모드 효과를 증폭시킬 수 있으며, 내진성능평가 시 관련 기준은 고차모드 지배 구조물에 대해 비선형정적해석과 함께 선형동적해석을 추가로 수행하도록 규정하고 있다. 선형동적절차에는 상당한 안전계수가 적용되므로, 이는 과도한 내진보강설계로 이어질 수 있다. 이를 방지하기 위해 엔지니어들은 내진보강 시 고차모드 효과를 줄이기 위해 시행착오법을 사용해 왔다. 그러나 시행착오법에는 많은 시간과 노력이 소요되며, 결정된 보강안이 최적인지 확인하기 어렵다. 본 연구는 저층 건축물의 수학적 모델을 수립하고 응답스펙트럼해석을 통해 고차모드 효과에 비틀림이 독립적으로 미치는 영향을 파악하였다. 이를 바탕으로 효율적인 내진보강 설계를 위해 활용될 수 있는 도표와 절차를 제시하였다. 제시된 절차를 통해 최소한의 내진보강으로 횡-비틀림 거동하는 저층 건축물의 고차모드 효과를 효율적으로 감소시킬 수 있음을 확인하였다.

키워드

저층구조물

비틀림효과

고차모드효과

내진보강

응답스펙트럼해석

MAIN

1. 서 론
2. 건축구조물의 고차모드 효과
2.1 고차모드 효과에 의한 응답 증폭
2.2 고차모드 효과에 관련한 국내･외 기준
2.3 모드별 시스템 응답에 대한 기여도
3. 횡-비틀림 다층 시스템의 고차모드 효과
3.1 수학적 모델
3.2 횡-비틀림 시스템의 응답스펙트럼해석
3.3 고차모드 효과에 대한 비틀림의 영향
4. 고차 횡-비틀림 저층구조물의 내진보강 전략
4.1 보강 방향과 위치에 따른 비틀림 영향수준 변화
4.2 내진보강 절차 및 예시
5. 결 론

1. 서 론

지진 시 구조물의 동적응답에 대한 고차모드의 영향은 구조요소 및 비구조요소의 예상치 못한 손상으로 이어질 수 있다(Goltz, 1994; Hall, 1994; Maniatakis et al., 2013; Restrepo and Cowan, 2000; Villaverde, 1991). 고차모드 효과는 저층 구조물에 비해 상대적으로 긴 주기를 가지고 다수의 진동모드가 복합적으로 작용하는 고층 구조물에서 지배적인 것으로 알려져 있다. 이러한 이유로 고차모드의 영향에 대한 실험 및 해석 연구는 고층 구조물에 대해 집중적으로 수행되어 왔다(Guan et al., 2019; Hwang et al., 2000; Pennucci et al., 2012; Rafiei et al., 2019; Salimbahrami and Gholhaki, 2018). 그러나 저층 구조물에서도 횡-비틀림(Torsionally-coupled, TC)거동이 고차모드 효과를 증폭시킬 수 있으며(Hejal and Chopra, 1987), 대부분 저층인 학교 건축물과 관련한 현행 내진성능평가 관련 기준(Ministry of Education, 2021)에서도 고차모드의 지배 여부를 검토하도록 규정하고 있다.

국내･외의 내진설계 및 성능평가 관련 기준(ASCE/SEI 41-22, 2022; CEN, 2001; NZSEE, 2017; Ministry of Land, Infrastructure and Transport, 2021)에서는 구조물에 대한 고차모드 지배 여부를 검토하고, 고차모드 효과가 지배적으로 작용하는 구조물(이하 “고차구조물”이라 칭함)에 대해서는 비선형정적해석과 더불어 선형동적해석을 수행하도록 규정하고 있다. 선형동적해석은 구조물의 선형 가정에 따른 잠재적 문제를 보완하기 위해 상당한 안전계수를 요구하며, 이는 기존 저층 구조물에 대한 과도한 내진보강으로 이어질 수 있다. 이를 방지하기 위해 구조물의 내진보강 설계단계에서 고차모드 효과를 감소시켜 비선형정적해석만으로 성능평가를 수행할 수 있다. 엔지니어들은 이를 위해 시행착오법(Trial-and-error method)으로 보강의 방향, 위치와 보강량을 결정해 왔으나, 시행착오법은 많은 해석과 시간을 필요로 하며, 이를 통해 설계된 내진보강안이 최적인지에 대해서도 의문이 남는다.

본 연구는 횡-비틀림 저층 구조물의 비틀림이 고차모드 효과에 미치는 영향을 고찰하여, 이에 대한 직관적 이해를 바탕으로 내진보강 시 고차모드 효과를 감소시킬 수 있는 전략 제시를 목적으로 한다. 이를 위해 건축구조물의 고차모드 효과와 관련한 현행 내진설계 및 성능평가 기준과 선행연구를 분석하고자 하며, 저층 구조물에 대한 수학적 모델을 수립하고 응답스펙트럼해석을 수행하여 고차모드 효과에 대한 주요 영향인자를 파악하고자 한다. 분석을 바탕으로 저층 구조물의 내진보강 시 효율적으로 고차모드 효과를 줄일 수 있는 방법을 소개하고, 관련 절차를 예시를 통해 설명하고자 한다.

2. 건축구조물의 고차모드 효과

2.1 고차모드 효과에 의한 응답 증폭

과거 지진피해 사례에서 고차모드 효과에 의한 구조물 응답의 증폭은 구조물의 심각한 손상과 붕괴의 주요 원인으로 지적되었으며(Hall, 1994; Restrepo and Cowan, 2000; Villaverde, 1991), 지난 수십 년 동안 지진응답에 고차모드가 미치는 영향에 관한 연구들이 수행되었다(Blakeley et al., 1975; Panagiotou et al., 2011; Priestley et al., 1999). Blakeley 등(1975)은 고차모드 효과가 구조물의 지진응답을 증폭시킴을 처음으로 언급하였다. 이는 Panagiotou 등(2011)의 7층 캔틸레버 전단벽 구조물의 실대형 진동대 실험결과에 대한 분석에서 확인되었으며, 고차모드 효과가 각 층의 요구 전단력을 크게 증폭시킴이 확인되었다. Priestley 등(1999)는 5층 프리캐스트 콘크리트 건물의 실대형 유사동적실험을 통해 고차모드 효과가 층가속도를 증폭시킴을 확인하였다. 증폭이 가장 크게 발생한 최상층의 층가속도는 Uniform Building Code(ICBO, 1987)에 따른 횡하중을 크게 상회하였다.

2.2 고차모드 효과에 관련한 국내･외 기준

국내･외의 내진 성능평가 및 보강 관련 기준(ASCE/SEI 41-22, 2022; NZSEE, 2017; CEN, 2001; Ministry of Education, 2021; Ministry of Land, Infrastructure and Transport, 2021)에서는 구조물의 고차모드 지배 여부에 따라 해석 절차를 달리하도록 규정하고 있으며, 각각 고차모드 지배 여부의 검토를 위한 지표를 제시하고 있다. ASCE/SEI 41-22(2022)은 구조물의 고차모드 지배 여부 판단을 위해 서로 다른 두 해석모델에 대한 응답스펙트럼해석을 수행하도록 규정하고 있다. 첫 번째 해석모델은 모드별 참여질량의 합이 구조물 전체 질량의 90% 이상인 모델이고, 다른 하나는 기본모드(방향별로 질량참여율이 가장 큰 모드)만을 고려한 모델이다. 질량참여율의 합이 90% 이상인 모델과 다른 하나의 모델에 대한 응답스펙트럼해석을 통해 각각 계산된 j층의 층전단력, V_jT와 V_jF의 비를 H_j(=V_jT/V_jF)라 할 때, 어느 층에서라도 H_j > 1.3인 경우, 해당 구조물을 고차구조물로 간주한다. Ministry of Land, Infrastructure and Transport(2021)과 Ministry of Education(2021)의 관련 기준도 이와 동일하다.

NZSEE(2017)은 앞서 설명한 H_j에 대한 조건과 함께, 구조물의 고유주기에 대한 기준을 검토하도록 규정하고 있다. NZSEE(2017)에 따르면, H_j가 1.3보다 작게 해석되더라도 구조물의 고유주기가 1초 이상일 경우, 고차구조물로 간주한다. 반면, CEN(2001)는 별도의 응답스펙트럼해석 없이 구조물의 고유주기만으로 고차모드 지배 여부를 검토하도록 규정하고 있으며, 구조물의 두 축에 대한 고유주기가 2초 이하이고, 설계응답스펙트럼의 가속도일정구간 내 최대주기값인 T_c의 4배보다 작을 경우, 고차구조물이 아닌 것으로 간주한다. Table 1은 국내･외 기준의 고차모드 지배 여부 검토기준을 요약하여 보여준다.

Table 1.

Higher mode effect determination criteria in seismic design provisions

Seismic Design Provisions	Criteria
Seismic Design Provisions	Story Shear Force, V_j	Fundamental Period, T1
ASCE/SEI 41-22 (2022)	$\frac{V_{j, T}}{V_{j, F}} > 1.3$	-
Guidelines for Seismic Evaluation of Existing Buildings (2021)
Manual for Seismic Evaluation and Retrofit of School Buildings (2021)
NZSEE (2017)		$T_{1}$ <1 sec
CEN (2001)	-	$T_{1}$ <1 sec and $4 T_{c}$

2.3 모드별 시스템 응답에 대한 기여도

구조물의 고차모드 지배 여부를 결정하기 위한 응답스펙트럼해석에서 모드별 기여도(modal contribution)는 고차모드 효과가 구조물의 응답에 미치는 영향을 나타낼 수 있는 지표 중 하나이며, 기본모드를 제외한 모드의 기여도가 클수록 고차모드 효과가 큰 것으로 볼 수 있다. 시스템의 응답량 r에 대한 n차 모드의 기여도 최댓값 r_n은 다음 식 (1)과 같이 표현된다.

(1)

r_{n} = r_{n}^{s t} A_{n}

여기서, A_n은 n차 모드 주기 T_n에 대응되는 설계스펙트럼가속도, r_n^st는 응답 유형마다 달리 정의되는 모드정적응답(modal static response)이며, A_n과 r_n^st는 서로 독립적이다.

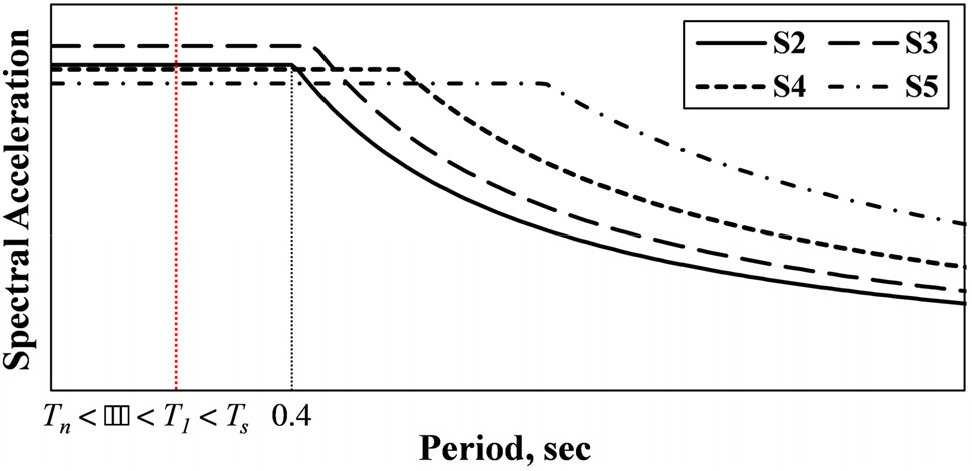
Fig. 1은 국내 내진설계기준(Ministry of Land, Infrastructure and Transport, 2021)을 참고하여 S₂~S₅ 지반 조건마다 작성한 설계응답스펙트럼을 보여준다. 구조물의 고유모드에 따른 주기는 모드의 차수가 높을수록 짧으므로, 1차모드의 주기가 T_c보다 긴 경우에는 1차모드와 비교하여 고차모드의 스펙트럼가속도가 큰 값을 가진다. 일부 기준(NZSEE, 2017; CEN, 2001)에서는 이를 고려하여 고차모드 지배 여부 판단을 위해 구조물의 주기를 검토하도록 규정하고 있다. 그러나 일반적으로 4층 이하의 저층 구조물은 그림에 나타낸 바와 같이 약 0.4초 이하의 가속도일정구간에 포함되는 고유주기를 가지며, 모드별 A_n의 차이에서 비롯된 고차모드 효과가 고층 구조물과 비교하여 매우 적을 것으로 생각된다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F1.jpg

Fig. 1.

Design acceleration response spectrum with fundamental periods of typical low-rise buildings

기본모드를 결정짓는 유효모드질량 M_n^*은 하중응답인 모드정적밑면전단력(modal static base shear force) V_bnst에 대응되는 모드정적응답이다. n차 유효모드질량 M_n^*을 전체 질량으로 나누어 질량참여율 M_n을 계산할 수 있으며, 모드별 질량참여율의 총합은 항상 1이므로, 기본모드 질량참여율 M_n이 작을수록 고차모드 기여도가 큰 것으로 볼 수 있다. Hejal과 Chopra(1987)는 1축 비대칭 평면을 가지는 횡-비틀림 단층 시스템의 횡방향 질량참여율이 횡-비틀림 진동수비 Ω와 정적편심율(static eccentricity ratio)에 따라 결정됨을 입증하였다. Ω는 횡-비틀림 단층 시스템의 횡강성에 대한 비틀림 강성의 상대적인 크기를 나타내는 변수로, 다음과 같이 계산할 수 있다.

(2)

Ω = ω_{r} / ω

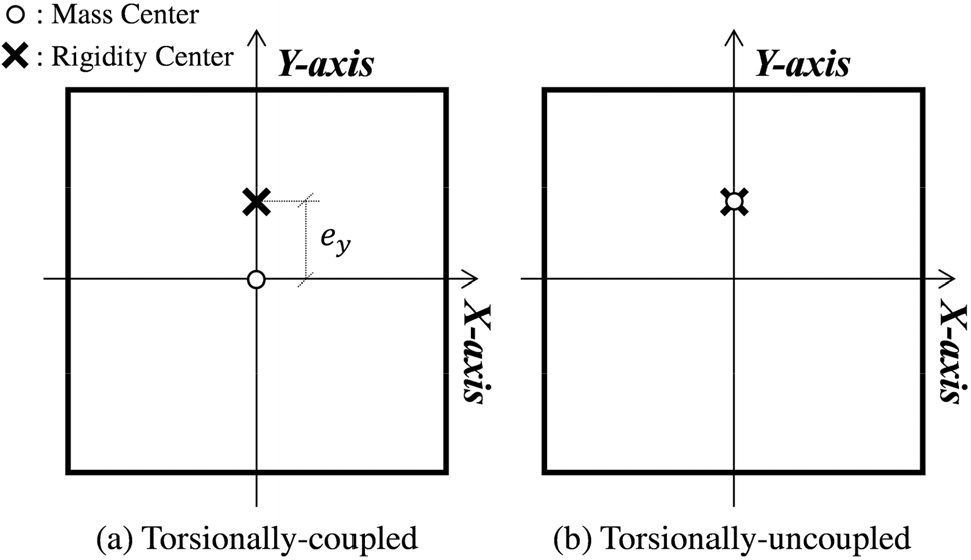
여기서, ω_r과 ω는 각각 비틀림과 횡방향에 대한 회전주파수로, Fig. 2(a)와 같은 비대칭 평면의 질량중심을 강성중심과 일치하도록 이동시켜 Fig. 2(b)와 같이 횡-비틀림 거동을 분리시킨 시스템(Torsionally-uncoupled system)으로부터 구할 수 있다. ω_r과 ω는 각각 다음과 같이 계산한다.

(3)

ω = \sqrt{K / m}

(4)

ω_{r} = \sqrt{K_{r C R} / I}

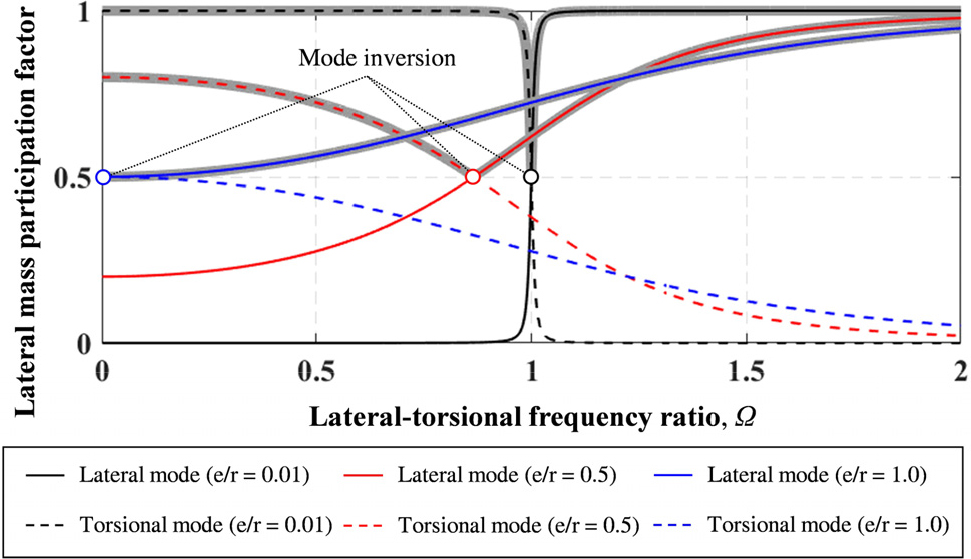
여기서, K_rCR은 강성중심에서의 비틀림강성이고, K는 단층 시스템의 횡강성 총합이며, m은 시스템의 질량이다. I는 관성모멘트로, 단면2차반경 r의 제곱과 m의 곱과 같다. Fig. 3은 Ω와 정적편심율 e/r에 따른 모드별 횡방향 질량참여율을 나타낸 것이며, 기본모드의 질량참여율 M_F를 회색 음영처리하였다. 횡-비틀림 거동과 관련한 두 모드의 횡방향 질량참여율은 Ω의 변화에 따라 1회 교차하며, 교점을 기준으로 기본모드가 변환되는 것을 알 수 있다. M_F가 기본모드 변환점에서 가장 낮은 것을 볼 수 있으며, e/r이 클수록 전반적으로 감소하는 것을 볼 수 있다. 또한, 기본모드 변환점의 Ω를 Ω_cr라 할 때, e/r이 0에 가까울수록 Ω_cr이 1에 근접하고, e/r이 증가할수록 Ω_cr이 0에 근접하는 것을 볼 수 있다. 이는 횡-비틀림 구조물의 Ω에 따라 구조물의 보강 위치 및 방향마다 고차모드 효과가 감소할 수도, 증가할 수도 있음을 뜻한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F2.jpg

Fig. 2.

Typical floor plan of torsionally-coupled and uncoupled building

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F3.jpg

Fig. 3.

Mass participation factors of TC single-story systems (after Hejal and Chopra, 1987)

3. 횡-비틀림 다층 시스템의 고차모드 효과

3.1 수학적 모델

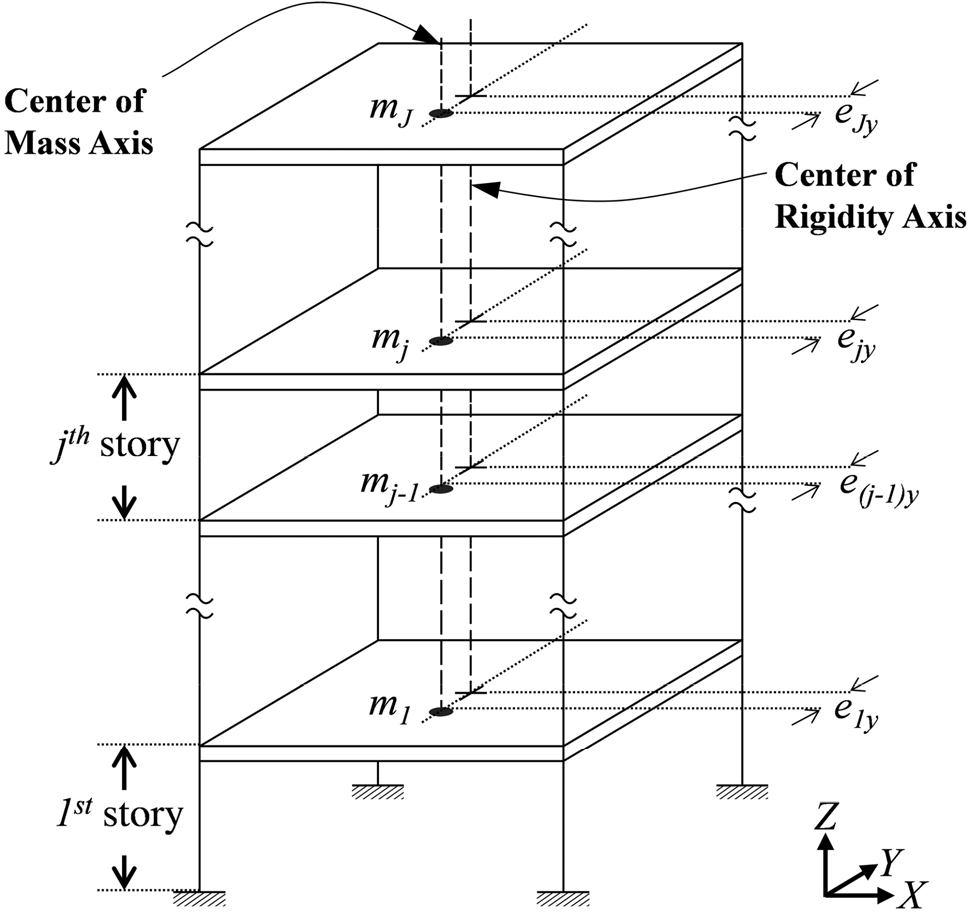
횡-비틀림 저층 구조물의 고차모드 효과를 분석하기에 앞서, 이에 대응되는 횡-비틀림 다자유도 시스템(MDOF_TC)에 대한 수학적 모델을 수립하였다. 본 연구에서 고려된 MDOF_TC는 Fig. 4에 나타난 바와 같이 X축에 대해서만 비대칭인 정규적 비대칭 시스템(Regularly Asymmetric System, RAS)이다. RAS는 모든 층의 질량중심이 평면에 수직한 한 축에 정렬되고, 각 층의 단면2차반경 r이 동일하며, 모든 층의 수직부재가 강한 격막에 구속되고 축방향 변위가 허용되지 않는 시스템이다(Hejal and Chopra, 1987). RAS는 각 층의 평면이 상이한 구조물의 모드특성을 반영할 수 없다는 한계를 가지고 있음에도 불구하고, 비틀림이 고차모드 효과에 미치는 영향을 직관적으로 파악하는 데 효과적일 것으로 판단된다. 해석의 편의성을 위해 모든 수직부재의 질량은 무시하였으며, 부재별 단면과 위치는 층마다 유지되는 것으로 가정하였다. J개 층마다 X, Y방향과 Z축에 대한 회전 자유도를 가지는 MDOF_TC의 질량중심에 대한 운동방정식은 다음 식 (5)와 같이 정리할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F4.jpg

Fig. 4.

Low-rise buildings considered in this study

(5)

[\begin{array}{lll} M \\ M \\ M r^{2} \end{array}] \{\begin{array}{l} \ddot{u_{x}} \\ \ddot{u_{y}} \\ \ddot{u_{r}} \end{array}\} + [\begin{array}{ccc} K_{x x} & K_{x r} \\ K_{y y} & K_{y r} \\ K_{x r}^{T} & K_{y r}^{T} & K_{r r} \end{array}] \{\begin{array}{l} u_{x} \\ u_{y} \\ u_{r} \end{array}\} = - M 1 {\ddot{u}}_{g}

여기서, ü_x, ü_y, ü_r은 각각 X, Y 방향과 회전에 대한 질량중심의 가속도벡터이며, u_x, u_y, u_r은 방향별 지반에 대한 상대변위벡터, ü_g는 지반가속도벡터이다. M은 $J \times J$ 크기의 질량행렬로, 행렬의 대각성분은 층별 질량과 같으며 이를 제외한 성분들은 0이다. M은 시스템의 전체 질량행렬 M_G에서 병진방향에 대한 부분행렬로, 회전에 대한 부분 질량행렬은 Mr²으로 나타낼 수 있다. 전체 강성행렬을 구성하는 부분 강성행렬 K_xx, K_yy, K_rr, K_xr, K_yr은 다음 식 (6), (7), (8), (9), (10)과 같이 정리할 수 있다.

(6)

K_{x x} = [\begin{array}{ccccc} (k_{1 . x} + k_{2 x}) & - k_{2 x} \\ - k_{2 x} & (k_{2 x} + k_{3 x}) & - k_{3 x} \\ - k_{3 x} & (k_{3 x} + k_{4 x x}) & ⋱ \\ ⋱ & ⋱ & - k_{J x} \\ - k_{J x} & k_{J x} \end{array}]

(7)

K_{y y} = [\begin{array}{ccccc} (k_{1 y} + k_{2 y}) & - k_{2 y} \\ - k_{2 y} & (k_{2 y} + k_{3 y}) & - k_{3 y} \\ - k_{3 y} & (k_{3 y} + k_{4 y}) & ⋱ \\ ⋱ & ⋱ & - k_{J y} \\ - k_{J y} & k_{J y} \end{array}]

(8)

K_{r r} = [\begin{array}{ccccc} (k_{1 r} + k_{2 r}) & - k_{2 r} \\ - k_{2 r} & (k_{2 r} + k_{3 r}) & - k_{3 r} \\ - k_{3 r} & (k_{3 r} + k_{4 r}) & ⋱ \\ ⋱ & ⋱ & - k_{J r} \\ - k_{J r} & k_{J r} \end{array}]

(9)

K_{x r} = - [\begin{array}{ccccc} (k_{1 x} e_{1 y} + k_{2 x} e_{2 y}) & - k_{2 x} e_{2 y} \\ - k_{2 x} e_{2 y} & (k_{2 x} e_{2 y} + k_{3 x} e_{3 y}) - k_{3 x} e_{3 y} \\ - k_{3 x} e_{3 y} & ⋱ & ⋱ \\ ⋱ & ⋱ & - k_{J x} e_{J y} \\ - k_{J x} e_{J y} & k_{J x} e_{J y} \end{array}]

(10)

K_{y r} = [\begin{array}{ccccc} (k_{1 y} e_{1 x} + k_{2 y} e_{2 x}) & - k_{2 y} e_{2 x} \\ - k_{2 y} e_{2 x} & (k_{2 y} e_{2 x} + k_{3 y} e_{3 x}) - k_{3 y} e_{3 x} \\ - k_{3 y} e_{3 x} & ⋱ & ⋱ \\ ⋱ & ⋱ & - k_{J y} e_{J x} \\ - k_{J y} e_{J x} & k_{J y} e_{J x} \end{array}]

여기서, k_jx, k_jy은 각각 j층 수직부재의 X와 Y 방향 횡강성의 총합이고, e_jx, e_jy는 각각 j층의 질량중심으로부터 강성중심까지 X, Y 방향으로 떨어진 거리이다. MDOF_TC는 Y축에 대칭이므로, 모든 층의 e_jx는 0이다. k_jr은 j층 질량중심에서의 비틀림강성으로, 다음 식 (11)과 같이 계산할 수 있다.

(11)

k_{j r} = k_{j r C R} + k_{j x} e_{j y}^{2} + k_{j y} e_{j x}^{2}

여기서, k_jrCR은 강성중심에서의 비틀림강성으로, j층의 각 수직부재 횡강성에 수직부재가 강성중심으로부터 떨어진 거리의 제곱을 곱하고 이를 모두 더하여 계산할 수 있다.

MDOF_TC는 Y축에 대칭이므로, K_yr = 0이며, 시스템의 Y 방향 거동은 다른 자유도로의 거동으로부터 독립적이다. 따라서, MDOF_TC는 부분 질량행렬 M과 부분 강성행렬 K_yy로 정의되는 2차원 다자유도 시스템(MDOF_y)과, X 방향과 Z축에 대한 회전 자유도를 가지는 X-비틀림 시스템(MDOF_x-r)로 분리할 수 있다. Y 방향과 독립된 MDOF_x-r의 고유치문제(eigen problem)는 다음 식 (12)와 같이 정리할 수 있다.

(12)

[\begin{array}{cc} K_{x x} - M ω_{k}^{2} & K_{x r} \\ K_{x r}^{T} & K_{r r} - M r^{2} ω_{k}^{2} \end{array}] Φ_{k} = 0

여기서, ω_k는 MDOF_x-r의 k차 모드 회전주파수이며, Φ_k는 k차 모드벡터이다. MDOF_x-r은 각 층마다 X 방향과 Z축에 대한 회전 자유도를 가지므로, 총 2J개의 고유치를 가진다.

MDOF_x-r의 모드벡터는 X-비틀림 단층시스템(SDOF_x-r)과 비틀림거동이 분리된 다층시스템(MDOF_x)의 모드벡터 조합으로 나타낼 수 있다(Hejal and Chopra, 1987). MDOF_x는 Fig. 2와 같이 모든 층의 질량중심을 강성중심과 일치시킨 것과 같다. MDOF_x에 대한 고유치문제는 다음 식 (13)과 같이 정의할 수 있다.

(13)

[K_{x x} - M ω_{m}^{2}] ϕ_{u c x, m} = 0

여기서, ω_m는 MDOF_x의 m차 모드 회전주파수이며, ϕ_ucx,m은 m차 모드벡터이다.

SDOF_x-r은 MDOF_x-r의 각 층과 동일한 편심율 e_jy/r( $e_{j y} = e_{y}$ )과, MDOF_x와 동일한 X-비틀림 진동수비 Ω_x를 가지는 시스템이다. SDOF_x-r에 대해 임의의 질량 m_s, X 방향 강성 k_sx, 강성중심에서의 비틀림강성 k_srCR을 설정하여 고유치문제를 다음과 같이 정의할 수 있다.

(14)

[[\begin{matrix} k_{s x} & - k_{s x} e_{y} \\ - k_{s x} e_{y} & (k_{s r C R} + k_{s x} e_{y}^{2}) \end{matrix}] - [\begin{matrix} m_{s} \\ m_{s} \end{matrix}] ω_{n}^{2}] \{\begin{array}{l} ϕ_{x, n} \\ ϕ_{r, n} \end{array}\} = 0

여기서, ω_n는 SDOF_x-r의 n차 모드 회전주파수이며, ϕ_x,n과 ϕ_r,n는 각각 n차 모드벡터의 X 방향과 회전 성분이다. 식 (2), (3), (4)에 따라 SDOF_x-r의 X 방향 회전주파수 ω_x는 $\sqrt{k_{s x} / m_{s}}$ 로, Ω_x는 $r \sqrt{k_{s r C R} / k_{s x}}$ 로 계산되므로, 식 (14)는 다음 식 (15)와 같이 정리할 수 있다.

(15)

[[\begin{array}{cc} 1 & - e_{y} / r \\ - e_{y} / r & {Ω_{x}^{2} + {(e_{y} / r)}^{2}} \end{array}] - [\begin{array}{cc} 1 \\ 1 \end{array}] {\overset{―}{ω_{n}}}^{2}] \{\begin{matrix} ϕ_{x, n} \\ r ϕ_{r, n} \end{matrix}\} = 0

여기서, ω_n는 SDOF_x-r의 n차 모드 회전주파수 ω_n를 ω_x로 정규화한 것이다.

각각 2개와 J개의 모드를 가지는 SDOF_x-r와 MDOF_x의 모드벡터를 조합하여 MDOF_x-r의 모드벡터 Φ_k와 회전주파수 ω_k는 다음 식 (16), (17)과 같이 나타낼 수 있다.

(16)

Φ_{k} = {\begin{cases} ϕ_{x, n} ϕ_{u c x, m} \\ ϕ_{r, n} ϕ_{u c x, m} \end{cases}}

(17)

ω_{k} = ω_{m} ω_{n} / ω_{x} = \bar{ω_{n}} ω_{m}

이를 다시 시스템의 전체 모드벡터로 정리하면, Φ에서 SDOF_x-r의 n차 모드와 MDOF_x의 m차 모드의 조합으로 표현되는 n-m차의 횡-비틀림 모드벡터와 Y 방향으로 독립적인 i차의 모드벡터는 각각 식 (18), (19)와 같다.

(18)

Φ_{n - m} = \{\begin{matrix} Φ_{x, n - m} \\ Φ_{y, n - m} \\ Φ_{r, n - m} \end{matrix}\} = {\begin{matrix} ϕ_{x, n} ϕ_{u c x, m} \\ 0 \\ ϕ_{r, n} ϕ_{u c x, m} \end{matrix}}

(19)

Φ_{i} = {\begin{cases} Φ_{x, i} \\ Φ_{y, i} \\ Φ_{r, i} \end{cases}} = \{\begin{matrix} 0 \\ ϕ_{y, i} \\ 0 \end{matrix}\}

여기서, Φ_x, Φ_y, Φ_r은 각각 Φ의 X, Y 방향과 비틀림에 대한 모드벡터이다.

3.2 횡-비틀림 시스템의 응답스펙트럼해석

일부 기준에서 구조물의 주기를 고차모드 지배여부 판정 지표로 제시하고 있으나, 본 연구는 비교적 짧은 주기를 가지는 저층 구조물을 대상으로 한다. 따라서 층전단력비 H_j를 고차모드 효과에 대한 지표로 사용하고, 이에 횡-비틀림 거동이 미치는 영향을 분석하기 위해 응답스펙트럼해석을 수행하였다. 응답스펙트럼해석에 사용된 설계응답스펙트럼은 시스템의 횡-비틀림 거동의 영향을 집중적으로 파악하고 해석을 단순화하기 위해 Fig. 1과 같이 0초와 가속도일정구간의 시작주기인 0.2T_c 사이의 스펙트럼가속도를 가속도일정구간과 동일한 값의 상수로 가정하였다. 또한, 시스템의 고유주기를 T_c보다 짧은 것으로 가정하여 응답스펙트럼의 형상이 고차모드 효과에 영향을 미치지 않도록 하였다. 두 병진방향에 대한 응답스펙트럼해석을 통해 각각 X와 Y 방향에 대한 층전단력비 H_jx, H_jy를 다음 순서에 따라 산정하였다.

1) 방향별 모드참여계수 P_x, P_y와 유효모드질량 M_x^*, M_y^* 계산

2) 모드밑면전단력 V_bx, V_by 계산

3) 수직분포계수 C_x,i, C_y,i 계산

4) 밑면전단력의 수직 분배를 통한 층별 모드횡하중 F_x, F_y 계산

5) j층 모드층전단력 V_jx,i, V_jy,i 계산

6) 모드층전단력의 조합으로 j층 전단력 V_jxT, V_jyT 계산

7) 방향별 j층 층전단력비 H_jy, H_jx 계산

MDOF_x-r의 X-비틀림 거동과 MDOF_y의 Y 방향 거동은 서로 독립적이므로, X와 Y 방향에 대한 모드참여계수 P_x, P_y는 각각 X 방향 n-m차 모드참여계수 P_x,n-m와 Y 방향 i차 모드참여계수 P_y,i와 같으며, 다음 식 (20), (21)과 같이 계산할 수 있다.

(20)

P_{x, n - m} = \frac{ϕ_{x, n} ϕ_{u c x, m}^{T} M 1}{Φ^{T} M_{G} Φ}

(21)

P_{y, i} = \frac{ϕ_{y, i}^{T} M 1}{Φ^{T} M_{G} Φ} = \frac{ϕ_{y, i}^{T} M 1}{ϕ_{y, i}^{T} M ϕ_{y, i}}

전체 시스템의 모드벡터 Φ에서 i차 모드에 대응되는 모드의 성분은 Y 방향 성분을 제외하고 모두 0이므로, 식 (21)에서 M_G와 Φ은 각각 M과 ϕ_y,i로 치환될 수 있다. 계산된 방항별 모드참여계수로부터 n-m차 모드의 X 방향과 i차 모드의 Y 방향 유효모드질량 M_x,n-m^*, M_y,i^*은 다음 식 (22), (23)과 같이 계산한다.

(22)

M_{x, n - m}^{*} = Φ^{T} M_{G} Φ P_{x, n - m}^{2} = \frac{{(ϕ_{x, n} ϕ_{u c x, m}^{T} M 1)}^{2}}{Φ^{T} M_{G} Φ}

(23)

M_{y, i}^{*} = ϕ_{y, i}^{T} M ϕ_{y, i} P_{y, i}^{2} = \frac{{(ϕ_{y, i}^{T} M 1)}^{2}}{ϕ_{y, i}^{T} M ϕ_{y, i}}

모드별 스펙트럼가속도 S_a는 시스템의 주기 및 응답스펙트럼의 형상과 상관없이 상수로 가정하였으므로, X 방향 n-m차와 Y 방향 i차 모드밑면전단력 V_bx,n-m와 V_by,i는 각각 유효모드질량에 동일한 S_a를 곱하여 계산할 수 있다. 모드밑면전단력은 이에 수직분포계수를 곱하여 층별 모드횡하중으로 분배시킬 수 있으며, X 방향 n-m차와 Y 방향 i차 모드의 수직분포계수 C_x,n-m과 C_y,i는 다음 식 (24), (25)와 같이 계산한다.

(24)

C_{x, n - m} = \frac{M Φ_{x, n - m}}{Φ_{x, n - m}^{T} M 1} = \frac{M ϕ_{u c x, m}}{ϕ_{u c x, m}^{T} M 1}

(25)

C_{y, i} = M ϕ_{y, i} / (ϕ_{y, i}^{T} M 1)

식 (18)에 나타난 바와 같이, $Φ_{x, n - m} = ϕ_{x, n} ϕ_{u c x, m}$ 이므로 식 (24)에서 비틀림과 관련된 스칼라 값 ϕ_x,n이 약분되며, MDOF_x-r의 수직분포계수가 비틀림에 독립적임을 알 수 있다. X 방향 n-m차와 Y 방향 i차 모드의 층별 모드횡하중 F_x,n-m, F_y,i은 방향별로 모드밑면전단력과 수직분포계수를 곱하여 다음 식 (26), (27)과 같이 계산할 수 있다.

(26)

F_{x, n - m} = M_{x, n - m}^{*} S_{n} C_{x, n - m} = [\frac{P_{u c x, m} S_{a}}{1 + {(r ϕ_{r, n} / ϕ_{x, n})}^{2}}] M ϕ_{u c x, m}

(27)

F_{y, i} = M_{y, i}^{*} S_{a} C_{y, i} = (P_{y, i} S_{a}) M ϕ_{y, i}

층전단력은 상부층의 횡하중을 전부 더한 것과 같으므로, X 방향 n-m차 모드층전단력 V_x,n-m은 다음 식 (28), (29)와 같이 계산한다.

(28)

V_{x, n - m} = A F_{x, n - m}

(29)

A = [\begin{array}{cccc} 1 & 1 & \dots & 1 \\ 0 & 1 & \dots & 1 \\ ⋮ & ⋱ & ⋱ & ⋮ \\ 0 & \dots & 0 & 1 \end{array}]

여기서, A는 행렬연산을 통해 층전단력을 계산하기 위해 사용된 행렬이며, Y 방향 i차 모드층전단력 V_y,i도 이와 동일하게 A와 F_y,i를 곱하여 계산할 수 있다. A에서 j번째 행벡터 A_j는 j층의 층전단력 산정을 위해 사용되는 벡터로, 방향별 i차와 n-m차 모드의 j층 모드층전단력 V_jx,n-m, V_jy,i는 다음 식 (30), (31)과 같이 정리할 수 있다.

(30)

V_{j x, n - m} = A_{j} F_{x, n - m} = [\frac{P_{u c x, m} S_{a}}{1 + {(r ϕ_{r, n} / ϕ_{x, n})}^{2}}] A_{j} M ϕ_{u c x, m}

(31)

V_{j y, i} = A_{j} F_{y, i} = (P_{y, i} S_{a}) A_{j} M ϕ_{y, i}

MDOF_TC의 모든 모드가 고려된 Y 방향 층전단력 V_jyT는 SRSS(Square root of sum of squares) 또는 CQC(Complete quadratic combination) 방법을 통해 J개 모드의 V_jy,i를 조합하여 계산할 수 있다. CQC 조합은 모드별 감쇠비와 진동수비를 통해 모드 사이의 확률적 상관관계를 고려하여 모드별 고유진동수의 차가 적은 경우에도 정확한 결과를 얻을 수 있다. CQC 조합 시 모드별 감쇠비를 0으로 고려하면 SRSS 조합과 동일한 결과를 나타내며, 본 연구에서는 계산의 편의성을 위해 SRSS 조합으로 다음 식 (32)와 같이 계산하였다.

(32)

V_{j y, i} = A_{j} F_{y, i} = (P_{y, i} S_{a}) A_{j} M ϕ_{y, i}

시스템의 Y 방향 층전단력비 H_jy는 V_jyT를 Y 방향 기본모드의 층전단력 V_jy1으로 나누어 다음 식 (33)과 같이 계산할 수 있다.

(33)

H_{j y} = \frac{V_{j y, T}}{V_{j y, 1}} = \sqrt{\sum_{i = 1}^{J} {(\frac{P_{y, i} A_{j} M ϕ_{y, i}}{P_{y, 1} A_{j} M ϕ_{y, 1}})}^{2}}

대상 시스템의 Y 방향 모드는 X 방향과 Z축에 대한 회전 자유도로부터 독립되므로, H_jy는 MDOF_y에 대한 응답스펙트럼해석으로 구해지는 층전단력비와 같음을 알 수 있다.

SDOF_x-r의 n차 모드와 MDOF_uc의 m차 모드가 모두 고려된 X 방향 층전단력 V_jxT는 다음 식 (34)와 같이 계산할 수 있으며,

(34)

V_{j x, T} = \sqrt{\sum_{n = 1}^{2} \sum_{m = 1}^{J} {([\frac{P_{u c x, m}}{1 + {(r ϕ_{r, n} / ϕ_{x, n})}^{2}}] A_{j} M ϕ_{u c x, m})}^{2}} \times S_{a}

이를 n차와 m차 모드에 대한 항으로 구분하여 다음과 같이 정리할 수 있다.

(35)

V_{j x, T} = \sqrt{\sum_{m = 1}^{J} {(P_{u c x, m} A_{j} M ϕ_{u c x, m})}^{2}} \times \sqrt{\sum_{n = 1}^{2} {\{1 + {(\frac{r ϕ_{r, n}}{ϕ_{x, n}})}^{2}\}}^{- 2}} \times S_{a}

시스템의 X 방향 층전단력비 H_jx는 식 (35)를 X 방향 기본모드의 모드층전단력 V_jx1으로 나누어 계산할 수 있다. ω_n-m는 n=1, m=1일 때 전체 시스템의 1차모드에 대응되므로, 층전단력비 H_jx는 다음 식 (36), (37), (38)과 같이 계산한다.

(36)

H_{j x} = \frac{V_{j x, T}}{V_{j x, 1}} = H_{j u c x} \times T_{r}

(37)

H_{j u c x} = \sqrt{\sum_{m = 1}^{J} {(\frac{P_{u c x, m} A_{j} M ϕ_{u c x, m}}{P_{u c x, 1} A_{j} M ϕ_{u c x, 1}})}^{2}}

(38)

T_{r} = \sqrt{1 + \{\frac{1 + {(r ϕ_{r, 1} / ϕ_{x, 1})}^{2}}{1 + {(r ϕ_{r, 2} / ϕ_{x, 2})}^{2}}\}}

여기서, H_jucx는 식 (33)과 같이 비틀림과 독립적으로 계산되며, MDOF_x의 j층 층전단력비와 같다. 또한, SDOF_x-r의 모드벡터로만 표현되는 T_r은 층전단력비 H_jx에 대한, 즉, X 방향 고차모드 효과에 대한 비틀림의 영향을 나타낸다.

3.3 고차모드 효과에 대한 비틀림의 영향

횡-비틀림 저층 구조물의 고차모드 효과 H_jx는 시스템의 질량 및 강성의 수직분포에 의한 영향과 비틀림에 의한 영향을 받으며, 각각 두 영향의 수준을 나타내는 H_jucx와 T_r은 서로 독립적임을 확인하였다. 따라서, 비틀림이 저층 구조물의 고차모드 효과에 미치는 영향은 횡-비틀림 다층 시스템으로부터 분리된 횡-비틀림 단층 시스템에 대한 고유치해석으로 T_r을 계산하여 파악할 수 있다. 횡-비틀림 단층 시스템에서 고차모드 효과를 나타내는 지표 중 하나인 질량참여율은 횡-비틀림 진동수비와 정적편심율에 따라 결정되며, SDOF_x-r의 T_r 또한 두 영향인자에 따라 나타낼 수 있다. 이때, SDOF_x-r의 X-비틀림 진동수비는 MDOF_x의 Ω_x와 같고, 정적편심율은 MDOF_TC의 층별로 동일한 e_y/r과 같다.

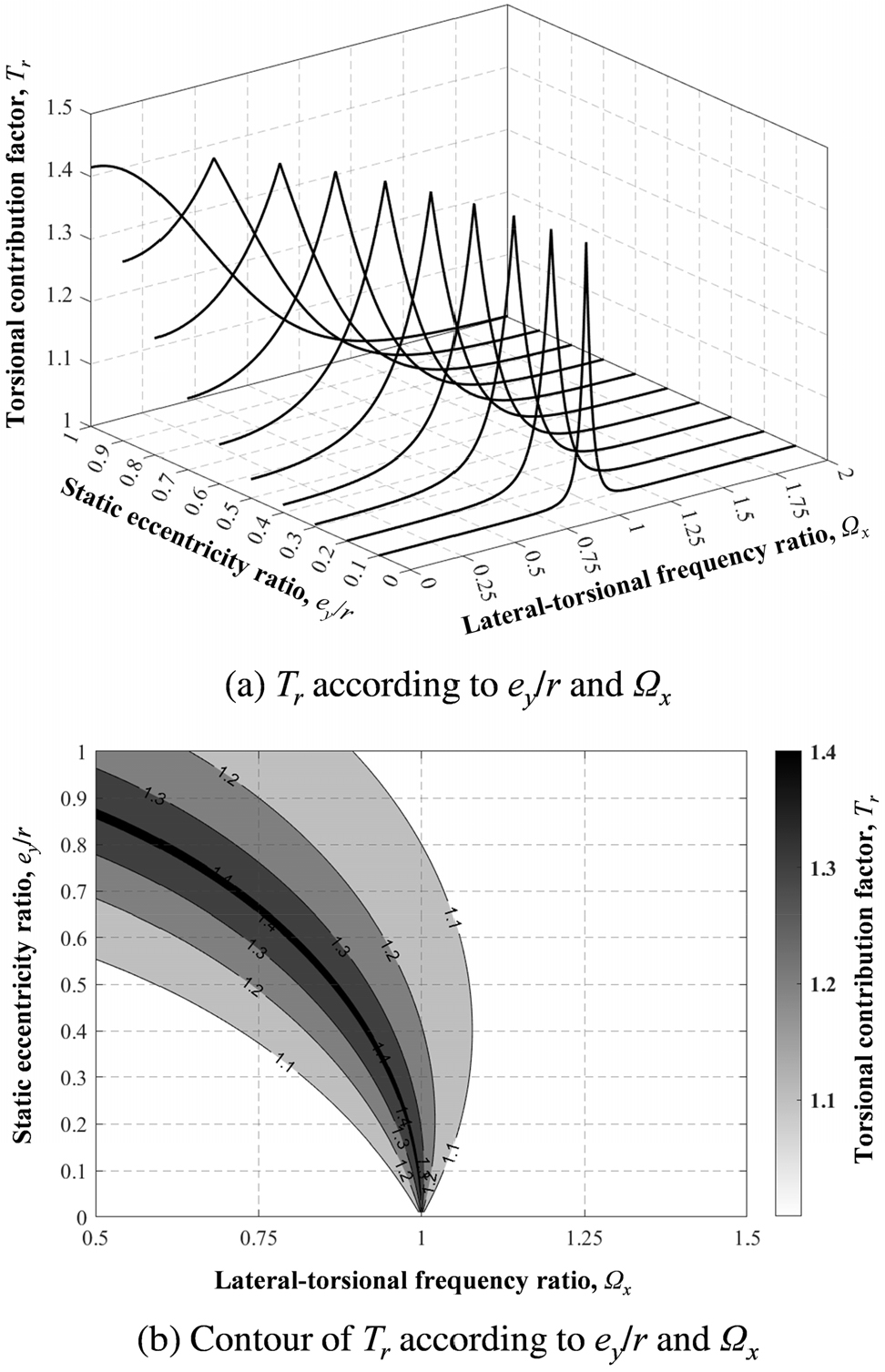
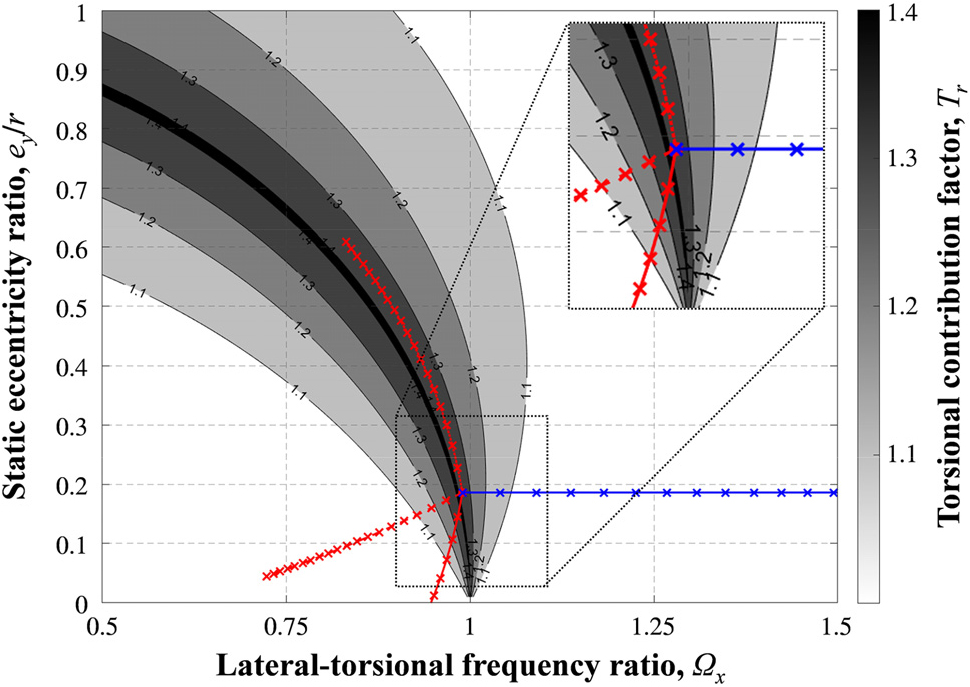
Fig. 5(a)와 (b)는 SDOF_x-r의 T_r을 e_y/r과 Ω_x에 따라 나타낸 것이다. Ω_x의 변화에 따라 T_r이 증가 또는 감소하는 것을 볼 수 있으며, 특정 Ω_x에서 T_r이 최댓값을 가지는 것을 알 수 있다. 이는 Fig. 2에 나타난 바와 같이, Ω_cr에서 기본모드의 변환과 동시에 M_F가 최소가 되기 때문이며, Ω_cr에서 T_r이 최댓값을 가진다. Fig. 2에서 e_y/r이 클수록 Ω_cr이 작아지는 특성도 그림에서 확인할 수 있다. 또한, e_y/r과 상관없이 T_r의 최댓값이 1.3보다 큰 것을 볼 수 있다. 이는 질량 및 강성의 수직분포에 따른 X 방향 고차모드 효과가 발생하지 않아 식 (36)에서 이의 영향을 나타내는 H_jucx가 1이라고 할지라도, 비틀림에 의한 영향만으로도 Ω_x에 따라 횡-비틀림 저층 구조물이 고차구조물로 분류될 수 있음을 뜻한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F5.jpg

Fig. 5.

Torsion-induced higher mode effects according to the influential parameters

Fig. 5(b)는 e_y/r과 Ω_x에 따른 T_r의 범위를 영역으로 나타내고 각 경계를 표시한 것으로, T_r의 값이 클수록 그래프 내에서 어둡게 나타냈다. e_y/r이 0일 경우에는 횡-비틀림 거동이 발생하지 않으므로 T_r이 1에 수렴하는 것을 알 수 있으며, e_y/r이 증가할수록 비틀림이 고차모드 효과에 미치는 영향이 증가하여 T_r이 크게 나타나는 영역이 확장되는 것을 볼 수 있다. 시스템의 Ω_x가 1보다 큰 경우는 X 방향 강성과 비교하여 비틀림 강성이 상대적으로 크므로, 고차모드 효과에 대한 비틀림의 영향이 전반적으로 크지 않음을 알 수 있다.

4. 고차 횡-비틀림 저층구조물의 내진보강 전략

4.1 보강 방향과 위치에 따른 비틀림 영향수준 변화

TC 저층 구조물로부터 분리된 TC 단층 시스템의 Ω와 e/r로부터 고차모드 효과에 대한 비틀림의 영향 수준이 결정됨을 확인하였다. TC 저층 구조물에 대한 보강의 방향과 위치에 따른 TC 단층 시스템의 Ω와 e/r의 변화를 파악하여 고차모드 효과에 대한 비틀림의 영향을 줄일 수 있는 내진보강 전략을 수립할 수 있다. 일반적으로 구조물의 두 주축과 평행한 방향으로 강성을 보강할 수 있으며, 선택된 보강 방향에 따라 내진보강 전략을 분류할 수 있다. Fig. 6(a)는 1축 비대칭 평면을 가지는 TC 단층 시스템에서 비틀림과 독립되지 않은 방향으로의 강성 보강을 나타내며, 이를 통해 기존의 편심을 줄일 수 있다. Fig. 6(b)는 비틀림과 독립된 방향으로의 보강을 나타내며, 강성의 대칭축과 정적편심율을 유지하고 비틀림강성을 증가시킬 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F6.jpg

Fig. 6.

Seismic retrofit strategy according to stiffening direction

Fig. 6(a)에서 D_yk와 D_ya는 각각 시스템의 강성중심과 보강위치가 X축으로부터 떨어진 거리이며, D_yk^*는 보강 후 강성중심과 X축 사이의 거리로, 다음 식 (39)와 같이 계산할 수 있다.

(39)

D_{y k}^{*} = \frac{k_{s x} D_{y k} + k_{a} D_{y a}}{k_{s r} + k_{g}} = D_{y k} + \frac{α}{1 + α} (D_{y a} - D_{y k})

여기서, k_sx는 식 (14)에서 설정한 SDOF_x-r의 X 방향 강성의 총합이고, k_a는 추가된 강성의 크기, α는 $k_{a} / k_{s x}$ 이다. 계산된 D_yk^*로부터 보강 후 정적편심율 $(e_{y} / r)^{*}$ 과 강성중심에서의 비틀림강성 $k_{r c R}^{*}$ 은 다음 식 (40), (41)과 같이 계산할 수 있으며,

(40)

(e_{y} / r)^{*} = (e_{y} / r) + \frac{α}{1 + α} (\frac{D_{y a} - D_{y k}}{r})

(41)

k_{r C R}^{*} = k_{r C R} + k_{s x} (D_{y k} - D_{y k}^{*})^{2} + k_{a} (D_{y a} - D_{y k}^{*})^{2}

보강 후의 횡-비틀림 진동수비 Ω_x^*는 다음과 같다.

(42)

Ω_{x}^{*} = \sqrt{\frac{k_{r C R}^{*}}{k_{s . x} r^{2}}} = \sqrt{\frac{Ω_{x}^{2}}{1 + α} + \frac{{(e_{y a} / r)}^{2} α}{(1 + α)^{2}}}

여기서, e_ya는 보강 전 강성중심으로부터 보강위치가 Y 방향으로 떨어진 거리를 나타낸다.

Fig. 6(b)에서 D_xk와 D_xa는 각각 보강 전 시스템의 강성중심과 보강위치가 Y축과 떨어진 거리를 나타낸다. 강성 및 질량 중심을 지나는 축을 기준으로 대칭인 두 위치에 강성 k_a를 절반씩 나누어 보강하여 X 방향 편심을 추가로 발생시키지 않을 수 있다. 보강 후 강성중심에서의 비틀림강성 $k_{r c R}^{*}$ 과 횡-비틀림 진동수비 Ω_x^*는 다음 식 (43), (44)와 같이 계산할 수 있다.

(43)

k_{r C R}^{*} = k_{r C R} + k_{a} (D_{x a} - D_{x k})^{2}

(44)

Ω_{x}^{*} = \sqrt{Ω_{x}^{2} + α (e_{x a} / r)^{2}}

여기서, e_xa는 보강 전 강성중심으로부터 보강위치가 X 방향으로 떨어진 거리를 나타낸다.

4.2 내진보강 절차 및 예시

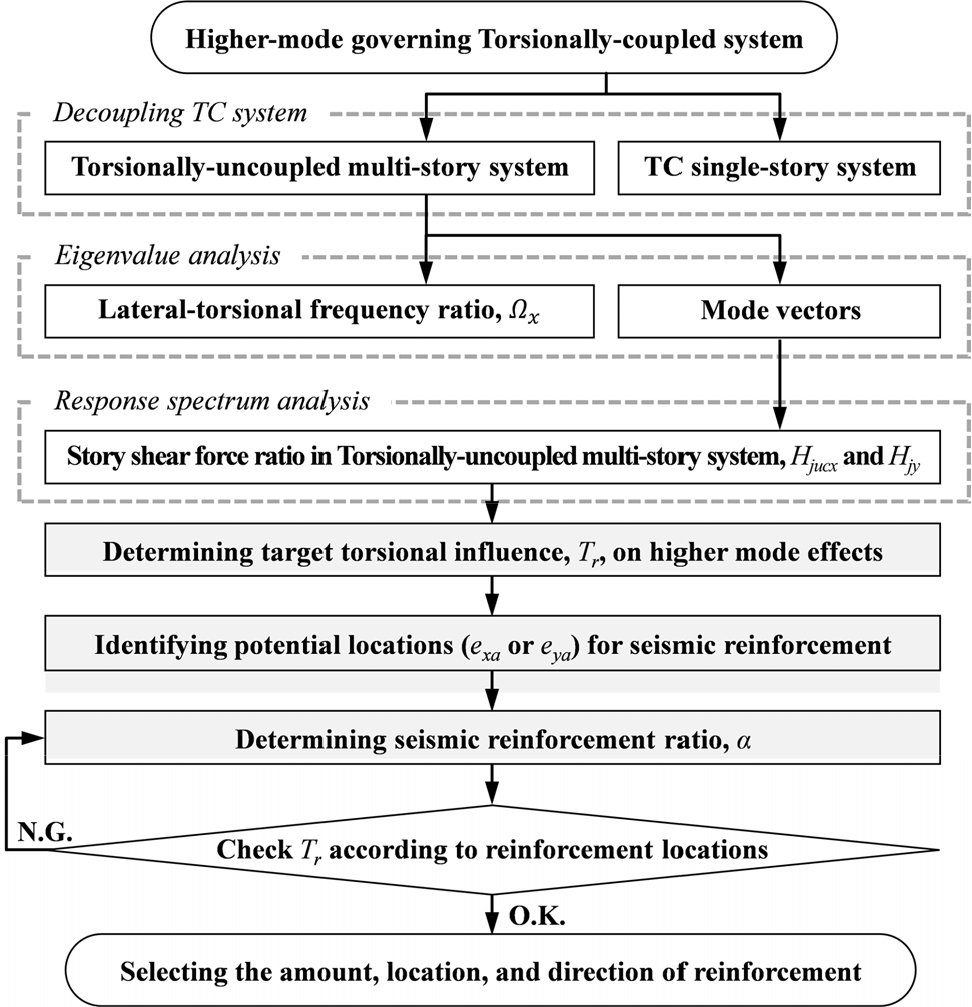
3장에서 분석하고 4.1에서 정리한 내용을 바탕으로 수립한 Fig. 7의 절차를 통해 고차 TC 저층 구조물의 내진보강 설계를 수행할 수 있다. TC 저층 구조물은 각 층의 질량중심을 강성중심과 일치시켜 횡-비틀림 거동이 분리된 TU(Torsionally-uncoupled) 다층 시스템으로 변환할 수 있으며, 이에 대한 고유치해석을 통해 얻어지는 횡-비틀림 진동수비 Ω와 기존의 정적편심율 e/r로 TC 단층 시스템을 정의할 수 있다. TU 다층 시스템의 고유치해석 결과로부터 응답스펙트럼해석을 수행하고 방향별 층전단력비를 계산할 수 있다. 식 (36)에 따라 Table 1의 고차모드 지배 판정 기준인 1.3을 TU 다층 시스템의 층전단력비로 나누어 고차모드 효과에 대한 비틀림 영향도 지표인 T_r의 한계값을 계산할 수 있다. 이후, TC 저층 구조물의 평면에서 보강의 대상이 되는 골조의 후보를 선택하고, 보강량을 나타내는 α를 결정한다. 보강을 통해 강성중심이 이동되었을 때의 정적편심율 $(e_{y} / r)^{*}$ 과 횡-비틀림 진동수비 Ω^*는 각각 식 (40)과 (42)를 통해 계산하고 Fig. 5(b)에서 T_r이 목표한 수준까지 감소되었는지를 확인할 수 있다. 강성중심을 유지하고 비틀림에 대해서만 보강되었을 때의 Ω^*는 식 (44)를 통해 계산할 수 있다. 최종적으로, 가장 적은 보강량을 통해 목표한 수준까지 T_r을 감소시킬 수 있는 골조를 선택하고 보강하여 고차모드 효과를 효율적으로 감소시킬 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F7.jpg

Fig. 7.

Seismic retrofit procedure reducing higher mode effects in low-rise buildings

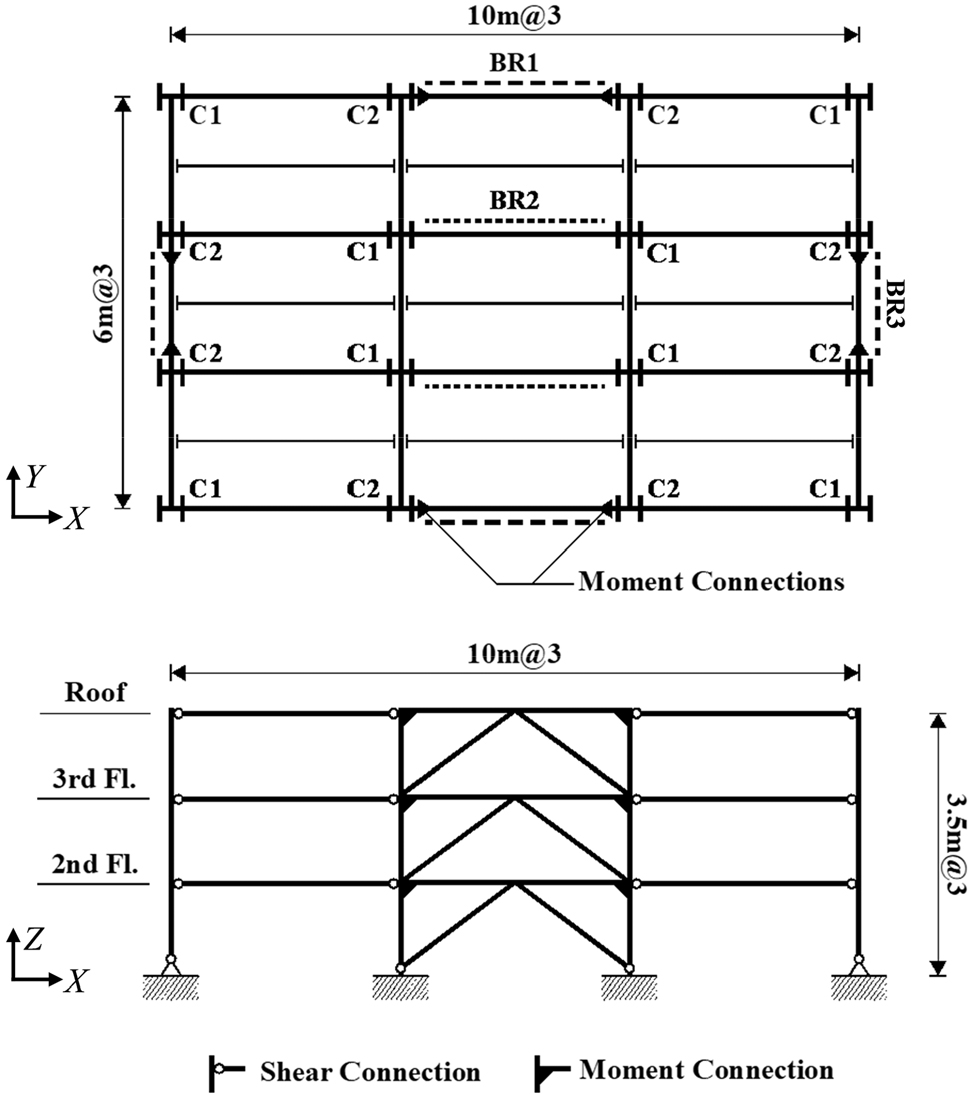
제시된 절차의 이해를 돕기 위해 Fig. 8의 평면과 입면을 가지는 예시 건물을 설정하였다. 예시 건물은 3.1절에서 설명한 RAS의 조건을 만족하며, 3.2절에서 설명한 바와 같이 주기가 가속도일정구간에 포함되는 것으로 가정할 수 있다. 예시 건물은 모든 층의 높이가 3.5m로 동일하고 각 층의 구조부재가 층마다 유지되는 3층 철골조로 구성되며, X와 Y 방향으로 각각 10m와 6m 길이의 3경간을 가진다. 모든 기둥(C1, C2)은 약축이 Y축과 일치하도록 배치하였으며, 보가 기둥에 모멘트접합되는 최외곽 골조의 가운데 경간을 제외한 모든 보-기둥 접합은 전단접합이다. 보-기둥 모멘트접합부를 가지는 골조는 역V형 가새를 추가로 가지며, 이를 그림에 BR1으로 나타냈다. BR2는 X 방향으로 저항하도록 배치된 역V형 가새들로, BR1과 다른 단면을 가지며, 이를 포함한 모든 구조부재의 단면을 Table 2에 요약하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F8.jpg

Fig. 8.

Three-story example building plan and elevation

Table 2.

Structural member sections of example building

Members	Shear connection frame	Moment connection frame
Columns	H-200 × 200 × 8/12 (C1)	H-350 × 350 × 12/9 (C2)
Girders	H-400 × 200 × 8/13	H-606 × 201 × 12/10
Beams	H-400 × 200 × 8/13	-
Braces	H-200 × 200 × 8/12 (BR1)	H-300 × 300 × 10/15 (BR2) H-200 × 204 × 12/12 (BR3)

예시 건물에 대한 보강설계에 앞서, 응답스펙트럼해석을 수행하고 고차모드 효과를 검토하기 위해 구조해석 프로그램 OpenSees(McKenna et al., 2012)를 활용하여 예시 건물을 모델링하였다. 1층 기둥의 지점은 모두 회전단으로 모델링하고, 강재의 탄성계수 E는 210 GPa로 설정하였다. 모든 보와 기둥 부재는 OpenSees에 내장된 함수인 elasticBeamColumn을 사용하여 모델링하였으며, 가새는 탄성의 truss로 모델링하였다. 예시 건물의 모든 수직 구조부재들이 X와 Y축에 대해 대칭임에 따라 각 층의 강성중심이 평면의 정중앙에 위치하므로, 편심에 의한 비틀림 효과를 고려하기 위해 385.5kN/g의 집중질량을 각 층의 강성중심으로부터 Y 방향으로 1.92m 떨어진 위치에 입력하였다. 또한, 관성모멘트를 고려하기 위해 10.37m로 가정한 각 층의 단면2차반경을 통해 회전질량을 계산하여 질량중심에 입력하였다. 각 층의 편심거리를 단면2차반경으로 나누어 계산되는 정적편심율 e_y/r은 0.186이며, 각 층의 강성과 입력된 질량을 Table 3에 요약하였다.

Table 3.

Floor mass and story stiffness of an example building

Story No.	Mass		Stiffness
	m_j, kN/g	m_jr_j², kN/g･m²	K_jx, kN/m	K_jy, kN/m	K_jr, kN･m
3rd	385.5	41,460	1.9 × 10⁶	5.6 × 10⁵	1.8 × 10⁸
2nd
1st

Table 4.

Story shear ratios of an example building

Story No.	X-direction			Y-direction
Story No.	V_jx,T, kN	V_jx,F, kN	H_jx	V_jy,T, kN	V_jy,F, kN	H_jy
3rd	551.7	393.2	1.40	717.8	698.8	1.03
2nd	970.4	708.9	1.37	1263.1	1260.3	1.00
1st	1212.7	884.8	1.37	1579.5	1574.1	1.00

Table 4에는 예시 건물의 응답스펙트럼해석 결과를 정리하였다. 예시 건물은 저층임에도 불구하고 X-비틀림 거동에 의해 모든 층의 층전단력비가 1.3 이상으로 나타났으며, 특히 최상층의 H_jx가 1.40으로 가장 크게 나타났다. 반면, 비틀림에 독립된 Y 방향으로의 층전단력비는 모든 층에서 1에 근접함을 볼 수 있다.

예시 건물의 Ω_x를 구하고 T_r의 목표 수준을 결정하기 위해 횡-비틀림 거동이 결합된 예시 건물의 집중질량점을 강성중심으로 이동시켜 TU 다층 시스템을 모델링하고 고유치해석을 수행하였다. Ω_x은 0.989로 해석되었으며, 횡강성이 층마다 유지되므로, 고유치해석 결과를 바탕으로 계산한 층전단력비는 최상층부터 최하층까지 1.03, 1.00, 1.00으로 Table 4의 H_jy와 같다. 따라서, 층전단력비가 최대로 나타나는 최상층을 기준으로 T_r의 목표 수준을 1.3/1.03≈1.2로 결정할 수 있다.

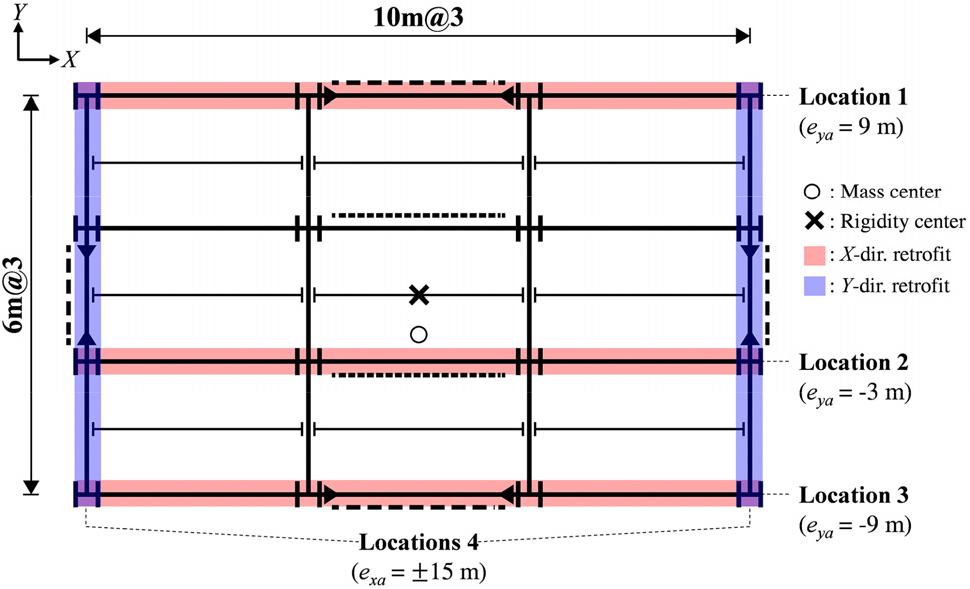
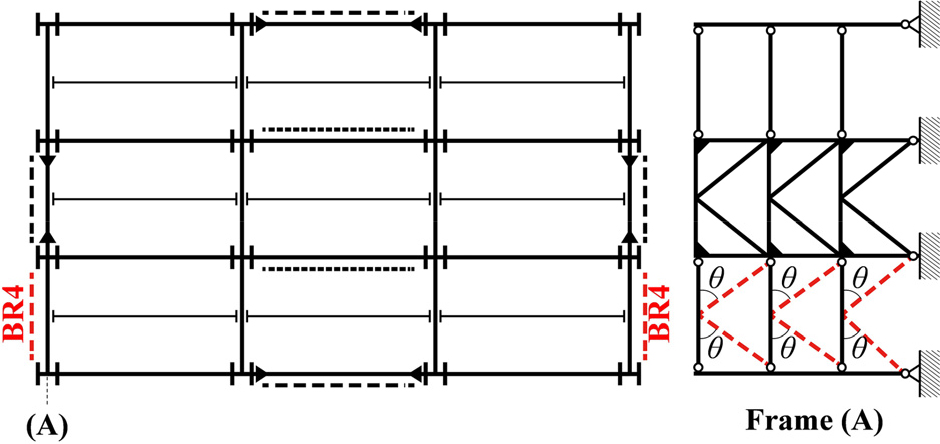
Fig. 9는 예시 건물의 잠재적 보강 위치를 표시한 것으로, 빨간색과 파란색 음영은 각각 X와 Y 방향 보강을 위한 골조를 나타낸다. X 방향 보강은 Fig. 6(a)와 같이 강성중심을 이동시키는 보강 방식에 해당되며, 일반적으로 편심을 줄이는 것이 비틀림 효과를 감소시키는데 유리하지만, 본 예제에서는 비교를 위해 편심을 증가시키는 보강 위치인 Location 1을 추가로 선택하였다. Y 방향 보강은 Fig. 6(b)와 같이 비틀림 강성을 증가시키는 방식에 해당되며, 최외곽에 위치한 두 골조를 가장 효율적인 보강 위치로 볼 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F9.jpg

Fig. 9.

Identified potential locations for seismic retrofit

Fig. 10은 선택한 골조에 대해 보강량 α를 0.05 간격으로 1까지 증가시키면서 식 (40), (42), (44)에 따라 계산한 $(e_{y} / r)^{*}$ 과 Ω^*를 나타낸 것이다. Location 1의 경우, 보강량 α가 증가함과 동시에 정적편심율이 함께 증가하여 T_r이 1.3보다 작아지지 않음을 볼 수 있다. 또한, Location 2에 보강할 경우에는 T_r이 1.2보다 작아지기 위해 약 0.1만큼의 α가 요구되지만, Location 3의 경우에는 이보다 큰 α가 요구되는 것을 볼 수 있다. 이는 저층 구조물의 고차모드 효과에 대한 비틀림 영향을 줄이는데 있어 정적편심율의 감소가 항상 최적의 선택이 되지는 않음을 보여준다. Locations 4에 보강하는 경우에는 약 0.05만큼의 α만으로도 T_r이 1.2보다 작아지는 것을 볼 수 있으며, 해당 위치가 본 예시 건물의 내진보강에 있어 최적임을 알 수 있다. 예시 건물의 평면은 강한 격막으로 구속된 것으로 가정하였으므로, 추가되는 강성의 크기가 동일하다면 Loactions 4에서 보강의 대상이 되는 경간의 위치 및 수는 해석결과에 영향을 미치지 않는다. 본 예시에서는 Fig. 11에 나타난 바와 같이 마지막 경간에 가새를 역V형으로 배치하여 0.05만큼의 α를 보강하고자 하였다. α는 보강 전 X 방향 횡강성에 대한 추가 강성 크기의 비이므로, 각 층별로 추가로 요구되는 횡강성은 α와 Table 3에 나타난 각 층의 X 방향 횡강성을 곱하여 0.05 × 1.9 × 10⁶kN/m = 95kN/mm로 계산할 수 있다. 두 골조에 각각 2개의 동일한 단면의 가새가 배치되므로, 가새부재마다 요구되는 축강성은 (95kN/mm)/4/ $\cos θ$ = 36.5kN/mm이다. 여기서, 𝜃는 Fig. 11에 나타난 바와 같이 가새와 보 사이의 각도를 나타낸다. 가새부재의 축강성은 가새부재의 단면적 A와 길이 L을 통해 EA/L로 계산할 수 있으므로, 최소 요구 단면적 A_min은 다음 식 (45)와 같이 계산할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F10.jpg

Fig. 10.

Influential parameters shifted in the graph with increasing retrofit amount at each location

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-06/N0040370603/images/Figure_jcoseik_37_06_03_F11.jpg

Fig. 11.

Seismic retrofit design of example building

(45)

A_{\min} \geq (36.5 k N / m m) \times 4.6 m / 210 G P a = 801 m m^{2}

따라서, 단면적이 813mm²인 등변앵글 L-70 × 70 × 6를 단면으로 가지는 가새부재(BR4)를 추가하여 보강계획을 수립할 수 있다. Table 5는 BR4를 추가한 모델에 대한 응답스펙트럼해석 결과와 T_r을 기존과 비교하여 보여준다. 기존 모델의 H_jucx는 앞서 언급한 바와 같이 최대 1.03으로 매우 낮으며, 이는 기존 모델의 고차모드 효과에 대한 횡강성 수직분포의 영향이 크지 않음을 나타낸다. 보강계획의 횡강성 분포는 보강 전과 같이 층별로 동일하므로 H_jucx가 유지되며, T_r이 1.37에서 목표한 값에 근접한 1.19까지 감소하였음을 볼 수 있다. 결과적으로, 고차모드 효과 수준의 지표인 H_jx의 최댓값이 1.40에서, 1.3보다 작은 1.22까지 감소하였다.

Table 5.

Influential factors of higher-mode governing and seismic retrofitted systems

Story No.	Higher-mode governing system			Seismic retrofitted system
Story No.	Hjucx	Tr	Hjx	Hjucx	Tr	Hjx
3rd	1.03	1.37	1.40	1.03	1.19	1.22
2nd	1.00		1.37	1.00		1.19
1st	1.00		1.37	1.00		1.19

5. 결 론

본 연구는 횡-비틀림 거동에 의해 고차모드 효과가 크게 나타나는 저층 구조물을 대상으로, 수학적 모델을 수립하고 응답스펙트럼해석을 수행하여 고차모드 효과에 대한 주요 영향인자를 파악하였다. 저층 구조물의 고차모드 효과에 비틀림이 독립적으로 미치는 영향을 식으로 정리하고 내진보강 설계 절차를 제시하였으며, 다음의 결론을 도출하였다.

1) 횡-비틀림 진동수비의 변화에 따라 단층 시스템의 기본모드가 변환되는 지점이 발생하며, 정적편심율이 커질수록 기본모드의 횡방향 질량참여율과 변환점에서의 횡-비틀림 진동수가 감소함을 확인하였다.

2) 횡-비틀림 다층 시스템의 고차모드 효과에 대해 시스템의 횡방향 거동과 비틀림이 미치는 영향을 서로 독립적으로 분리하여 식으로 정리하였다.

3) 본 연구에서 수립한 수학적 모델과 식을 바탕으로, 비틀림에 의한 고차모드 효과가 크게 발생하는 저층 구조물의 내진보강 계획 수립 시 활용될 수 있는 도표와 이를 활용한 절차를 제시하였다. 해당 절차는 보강의 방향, 위치, 그리고 보강량을 결정하는데 있어 기존의 시행착오법과 비교하여 고차모드 효과 감소를 위해 요구되는 반복해석의 수를 그래프에 대한 직관을 바탕으로 효율적으로 줄일 수 있음을 확인하였다.

4) 향후 다양한 지진 시나리오를 바탕으로 비틀림에 의한 고차모드 효과가 구조물의 내진성능에 미치는 영향 파악과, 제시한 절차의 적용에 따른 내진성능 향상 여부에 대한 검증이 필요할 것으로 생각된다.

Acknowledgements

이 논문은 2023년도 서울시립대학교 연구년교수 연구비에 의하여 연구되었음.

References

ASCE/SEI 41-22 (2017) Seismic Evaluation and Retrofit of Existing Buildings, American Society of Civil Engineers, Virginia, USA.

NZSEE (2017) The Assessment and Improvement of the Structural Performance of Earthquake Risk Buildings-Draft for General Release, New Zealand National Society for Earthquake Engineering, NZSEE.

Blakeley, R.W.G., Cooney, R.C., Megget, L.M. (1975) Seismic Shear Loading at Flexural Capacity in Cantilever Wall Structures, Bull. N.Z. Soc. Earthq. Eng., 8(4), pp.278~290.

10.5459/bnzsee.8.4.278-290

CEN (2001) Eurocode 8 - Design Provisions for Earthquake Resistance of Structures - Part 3, Brussels.

Goltz, J.D. (1994) The Northridge, California Earthquake of January 17, 1994: General Reconnaissance Report, In the Northridge, California Earthquake of January 17, 1994: General Reconnaissance Report.

Guan, M., Liu, W., Du, H., Cui, J., Wang, J. (2019) Combination Model for Conventional Pushover Analysis Considering Higher Mode Vibration Effects, Struct. Des. Tall & Spec. Build., 28(12), P.e1625.

10.1002/tal.1625

Hall, J.F. (1994) Northridge Earthquake January 17, 1994, Preliminary Reconnaissance Report.

Hejal, R., Chopra, A.K. (1987) Earthquake Response of Torsionally-Coupled Buildings, Doctoral Dissertation, University of California, Berkeley.

Hwang, J.H., Chun, Y.S., Lee, L.H. (2000) The Vertical Distribution of Lateral Seismic Forces to Account for the Contribution of the Higher Modes, J. Architect. Inst. Korea, 16(7), pp.3~8. (in Korean)

ICBO (1997) Uniform Building Code (UBC 1997), International Conference Building Officials, Whittier, California.

Maniatakis, C.A., Psycharis, I.N., Spyrakos, C.C. (2013) Effect of Higher Modes on the Seismic Response and Design of Moment-Resisting RC Frame Structures, Eng. Struct., 56, pp.417~430.

10.1016/j.engstruct.2013.05.021

McKenna, F., Fenves, G.L., Scott, M.H., Jeremic, B. (2012) Open System for Earthquake Engineering Simulation, Accessed April 7, 2012 (http://opensees.berkeley.edu)

Ministry of Education (2021) Manual for Seismic Evaluation and Retrofit of School Buildings, Ministry of Education. (in Korean)

Ministry of Land, Infrastructure and Transport (2021) Guidelines for Seismic Evaluation of Existing Buildings, Ministry of Land. (in Korean)

Panagiotou, M., Restrepo, J.I., Conte, J.P. (2011) Shake-Table Test of a Full-Scale 7-Story Building Slice, J. Struct. Eng., 137(6), pp.691~704.

10.1061/(ASCE)ST.1943-541X.0000332

Pennucci, D., Sullivan, T.J., Calvi, G.M. (2012) Prediction of Higher-Mode Response of Tall RC Wall Buildings, In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal.

Priestley, M.N., Sritharan, S., Cohley, J.R., Pampanin, S. (1999) Preliminary Results and Conclusions from the PRESS Five-Story Precast Concrete Test Building, PCI J., 44(6), pp.42~67.

10.15554/pcij.11011999.42.67

Rafiei, E., Danesh, F.A., Matou, F., Shamsaei, M. (2019) The Effects of Higher Modes on the Response Modification Factor of Tall RC Buildings, Int. J. Eng. & Technol., 11(1), p.45.

10.21817/ijet/2019/v11i1/191101203

Restrepo, J.I., Cowan, H.A. (2000) The Eje Cafetero Earthquake, Colombia of January 25 1999, Bull. N. Z. Soc. Earthq. Eng., 33(1), pp.1~29.

10.5459/bnzsee.33.1.1-29

Salimbahrami, S.R., Gholhaki, M. (2018) Analytical Study to Evaluate the Effect of Higher Modes of Reinforced Concrete Moment-Resisting Frames with thin Steel Shear Wall under Simple Pulse, Adv. Struct. Eng., 21(15), pp.2311~2325.

10.1177/1369433218773241

Villaverde, R. (1991) Explanation for the Numerous upper Floor Collapses during the 1985 Mexico City Earthquake, Earthq. Eng. & Struct. Dyn., 20(3), pp.223~241.

10.1002/eqe.4290200303

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Seismic Retrofit Strategy Reducing Torsion-Induced Higher Mode Effects of Torsionally-Coupled Low-Rise Buildings

ABSTRACT

MAIN

Table 1.

Higher mode effect determination criteria in seismic design provisions

(1)

Fig. 1.

Design acceleration response spectrum with fundamental periods of typical low-rise buildings

(2)

(3)

(4)

Fig. 2.

Typical floor plan of torsionally-coupled and uncoupled building

Fig. 3.

Mass participation factors of TC single-story systems (after Hejal and Chopra, 1987)

Fig. 4.

Low-rise buildings considered in this study

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

Fig. 5.

Torsion-induced higher mode effects according to the influential parameters

Fig. 6.

Seismic retrofit strategy according to stiffening direction

(39)

(40)

(41)

(42)

(43)

(44)

Fig. 7.

Seismic retrofit procedure reducing higher mode effects in low-rise buildings

Fig. 8.

Three-story example building plan and elevation

Table 2.

Structural member sections of example building

Table 3.

Floor mass and story stiffness of an example building

Table 4.

Story shear ratios of an example building

Fig. 9.

Identified potential locations for seismic retrofit

Fig. 10.

Influential parameters shifted in the graph with increasing retrofit amount at each location

Fig. 11.

Seismic retrofit design of example building

(45)