1. 서 론
1979년 미국 스리마일 섬 원전 사고, 1986년 소련 체르노빌 참사, 2011년 일본 후쿠시마 제1원전 사고 등에서 목격하였듯이 원전의 사고는 대형 인명 피해와 재산 피해, 반영구적인 방사선 오염이라는 참혹한 결과를 불러 일으킨다. 그러므로 원전 시설물은 다른 구조물보다 더욱 높은 안전성이 요구되고, 이는 지진에 대해서도 예외가 아니다.
원전 시설물의 지진안전성을 평가하기 위해서는 주구조물 뿐만이 아니라 구조물, 계통 및 기기(Structures, Systems, and Components, SSC) 또는 부계통의 지진해석도 수반되어야 한다(ASCE, 2017). 주구조물과 부계통의 동적 연계를 고려하기 위해 단순화된 부계통 모델을 주구조물 동적 모델에 포함하여 지진응답해석을 수행할 수 있다. 이 경우에도 부계통의 설계 및 검증을 위해서는 부계통에 대한 추가 비연계 동적해석을 수행하여 상세 응답을 얻을 필요가 있을 수 있고, 이를 위해 부계통 지지점에서의 입력운동을 생성해야 한다. 원전 시설물의 주구조물 모델에 포함되지 않은 경우에도 부계통의 지진해석을 위해서는 그 지지점에서의 입력운동을 작성해야 한다. 일반적으로 이 입력운동은 구조응답스펙트럼(in-structure response spectrum, ISRS)으로 정의되고, 응답이력방법(response history method, RHM) 또는 설계지반운동 응답스펙트럼으로부터 직접 작성할 수 있다(Jiang et al., 2015).
원전 시설물에 설치된 부계통의 확률론적 지진안전성평가는 설계기준지진(design basis earthquake)에 대한 ISRS를 활용하여 수행된다. 그러나 대상 부지의 지진재해도에 대한 이해가 향상됨에 따라 설계 당시와는 다른 등재해도 응답스펙트럼(uniform hazard response spectrum, UHRS) 또는 지반운동 응답스펙트럼(ground motion response spectrum, GMRS)이 작성될 수 있거나 평가용 지진(review level earthquake) 응답스펙트럼이 도출될 수 있다. 이 경우 설계에 사용된 ISRS와는 다른 새로운 ISRS를 도출하여 부계통의 확률론적 지진안전성을 평가해야 하지만, 이를 위해 원전 시설물에 대한 지진응답해석을 새로이 수행하는 것은 비용 측면에서 부담이 될 수 있다. 그러므로 지진응답 재해석을 수행하지 않고, 기존 ISRS로부터 신규 지반운동 응답스펙트럼에 부합하는 ISRS를 얻기 위해 다양한 ISRS 스케일링 기법이 개발되어 사용되고 있다.
ISRS 스케일링을 위해 크게 두 가지 방법이 사용되고 있다(EPRI, 2018). 첫 번째 방법은 고유진동수, 고유벡터, 참여계수를 알고 있을 때 무작위진동이론(random vibration theory, RVT)을 사용하여 스케일링을 수행하는 방법이다. 하지만, 이 방법은 대상 구조물의 고유진동수, 고유벡터, 참여계수 등 동적 특성을 정확히 알고 있을 때만 활용할 수 있는 방법이다.
두 번째 방법은 고유진동수와 참여계수만을 알고 있을 때 비례계수를 사용하는 단순화된 방법인데, 구조물 모델이 적절하게 작성되었고 신규 지반운동 응답스펙트럼이 기존 지반운동 응답스펙트럼과 유사할 때 암반 부지에 대해서 사용할 수 있다. 이 방법을 사용하여 스케일링을 수행할 때 각 진동수에서의 비례계수를 산정해야 하는데, 이를 위해서 세 가지 종류의 근사 방법을 사용할 수 있다(Kwag et al., 2024). 첫 번째 근사 방법 scaling-in-all-frequency-based approach는 기존 및 신규 지반운동 응답스펙트럼을 각 진동수에서 비교하여 비례계수(scaling factor)를 산출한다. 두 번째 방법 unity-based step function approach는 기존과 신규 지반운동 응답스펙트럼의 크기가 역전이 일어나는 진동수를 중심으로 각 영역의 응답스펙트럼 비의 평균을 취하여 비례계수를 계단 함수로 도출한다. 이 두 방법은 대상 구조물의 동적 특성을 전혀 모른다고 가정했을 때도 사용할 수 있는 방법이다. 마지막 방법 two mode-based ramp function approach는 대상 구조물의 고유진동수 및 참여계수에 대해 제한된 정보만 제공된 경우에 사용할 수 있는 방법으로, 대상 구조물의 주요 모드 두 개를 식별하고 그 모드 진동수에서의 지반운동 응답스펙트럼 비를 기반으로 램프(ramp) 함수 형식의 비례계수를 도출한다. 이 세 가지 ISRS 스케일링 근사 방법은 저진동수에서 비교적 유사하게 ISRS를 도출하지만, 고진동수에서는 그 정확도가 감소함이 관찰되었다(Kwag et al., 2024).
이 연구에서는 RVT를 사용하여 원전 시설물 부계통의 지진응답해석과 확률론적 지진안전성평가를 위한 ISRS 스케일링 기법을 새로이 제안하고자 한다. 새로운 방법은 고유진동수, 고유벡터, 참여계수 등 대상 구조물의 동적 특성에 대한 정보를 활용하지 않고, 구조응답과 지진지반운동의 PSD 함수의 비를 사용한다. 첨두값 계수를 사용하면 무작위 진동의 PSD 함수로부터 첨두값의 통계적 특성을 도출할 수 있기 때문에, PSD 함수가 주어지면 응답스펙트럼을 추정할 수 있다. 그러므로 지반운동 응답스펙트럼의 비를 사용하여 ISRS의 스케일링을 수행하는 것이 아니라, PSD 함수의 비를 활용하여 PSD 함수의 스케일링을 수행하고 이로부터 스케일링된 응답스펙트럼을 도출할 수 있을 것이다. 이를 위해 이 연구에서는 RVT에 기반하여 PSD 함수에 의해 정의되는 첨두값 계수와 이로부터 도출되는 응답스펙트럼을 간략히 살펴보고, 이를 활용하여 새로운 스케일링 기법을 제안하고자 한다. 그리고 제안된 RVT에 기반한 새로운 스케일링 기법에 의한 결과를 RHM 방법에 의한 참조해와 비교하여 그 정확성을 평가하고자 한다.
2. 무작위 진동에 의한 응답스펙트럼
무작위 진동의 가속도에 대한 파워스펙트럼밀도(power spectral density, PSD) 함수 가 주어지면 이 진동이 작용하는 단자유도 시스템의 유사가속도(pseudo-acceleration)에 대한 PSD 함수 는 다음과 같이 주어진다.
여기서, 과 𝜉는 각각 단자유도 시스템의 고유진동수와 감쇠비이다.
유사가속도의 첨두값은 해당 진동수 과 감쇠비 𝜉에 대한 스펙트럼 가속도 또는 응답스펙트럼의 세로 좌표를 제공한다. 무작위 진동의 첨두값의 통계적 특성은 대상 진동의 PSD 함수를 사용하여 추정할 수 있다. 즉, 식 (1)에 주어진 유사가속도에 대한 PSD 함수를 사용하여 첨두값 계수(peak factor)를 계산할 수 있고, 이로부터 응답스펙트럼의 통계적 특성을 추정할 수 있는 것이다. 다양한 종류의 첨두값 계수가 제안되었지만, 이 연구에서는 Der Kiureghian(1980)과 Igusa와 Der Kiureghian(1983)이 제안한 첨두값 계수를 사용할 것이다.
무작위 진동의 평균 과 표준편차 는 다음과 같이 표현된다.
여기서, 와 는 각각 평균과 표준편차에 대한 첨두값 계수이고, 은 고려하는 응답의 표준편차이다. 첨두값 계수 와 에 대하여 다음의 식이 제안되었다(Der Kiureghian, 1980; Igusa and Der Kiureghian, 1983).
여기서, 는 equivalent mean zero-crossing rate, 는 mean zero-crossing rate, 𝛿는 measure of dispersion, 은 PSD 함수 의 차 모멘트, 𝜏는 고려하는 응답의 등가 정상상태응답 지속시간(equivalent stationary response duration)인데, 이 연구에서는 ASCE(2017)의 정의에 따라 무작위 진동의 누적에너지가 총에너지의 5%에서 75%에 이르는 시간으로 정의한다.
식 (1)에 주어진 단자유도 시스템 유사가속도의 PSD 함수에 대응하는 첨두값 계수 , 와 표준편차 을 식 (3a), (3b), (3c), (3d), (3e), (3f) 및 (2c)로부터 얻을 수 있고, 식 (2a)와 (2b)를 사용하여 유사가속도의 첨두값 또는 응답스펙트럼을 얻을 수 있다. 응답스펙트럼은 평균 또는 평균+표준편차의 값으로 정의할 수 있는데, 이 연구에서는 평균의 값으로 정의하여 스케일링 기법을 제안할 것이다.
3. 무작위진동이론에 기반한 ISRS 스케일링 기법
2장의 첨두값 계수를 사용하여 무작위 진동의 PSD 함수로부터 응답스펙트럼을 추정할 수 있다. 이는 역으로 주어진 응답스펙트럼에 부합하도록 무작위 진동의 PSD 함수를 결정할 수 있음을 의미한다. 단, PSD 함수와 응답스펙트럼 간에는 일대일 대응이 성립하지 않으므로, 이 과정은 다수의 반복계산을 필요로 한다. 이와 같은 사실에 근거하여 RVT에 기반한 ISRS 스케일링 기법을 다음과 같이 새로이 제안하고자 한다.
1)(1-1단계) 주어진 기존 지반운동 응답스펙트럼에 부합하는 PSD 함수를 RVT를 사용하여 추정한다. 가정된 무작위 진동의 PSD 함수에 첨두값 계수를 적용하여 응답스펙트럼을 얻을 수 있는데, 이를 기존 지반운동 응답스펙트럼과 비교하여 그 비율의 제곱만큼 가정된 PSD 함수를 조정한다. 이와 같은 계산을 반복 수행하여 기존 지반운동 응답스펙트럼에 부합하는 PSD 함수를 얻을 수 있다.
2)(1-2단계) 기존 지반운동 응답스펙트럼에 부합하는 지진지반운동에 의한 원전시설물의 지진응답 및 ISRS를 RHM 등을 사용하여 산정하고, 이 ISRS에 부합하는 PSD 함수를 RVT를 사용하여 추정한다.
3)(1-3단계) (1-1단계)과 (1-2단계)에서 얻은 PSD 함수를 비교하여 이에 대응하는 비례계수를 산정한다.
4)(2-1단계) 신규 지반운동 응답스펙트럼에 부합하는 PSD 함수를 RVT를 사용하여 추정한다.
(2-2단계) (1-3단계)에서 얻은 비례계수를 (2-1단계)의 PSD 함수에 적용하여 부계통 응답의 PSD 함수를 산정한다.
(2-3단계) (2-2단계)에서 얻은 PSD 함수에 첨두값 계수를 적용하여 새로운 ISRS를 산정한다.
위와 같이 새로이 제안된 ISRS 스케일링 기법을 사용하여 신규 지반운동 응답스펙트럼에 대한 ISRS를 지진응답 재해석을 수행하지 않고 기존 ISRS로부터 얻을 수 있다.
4. 적용 예제
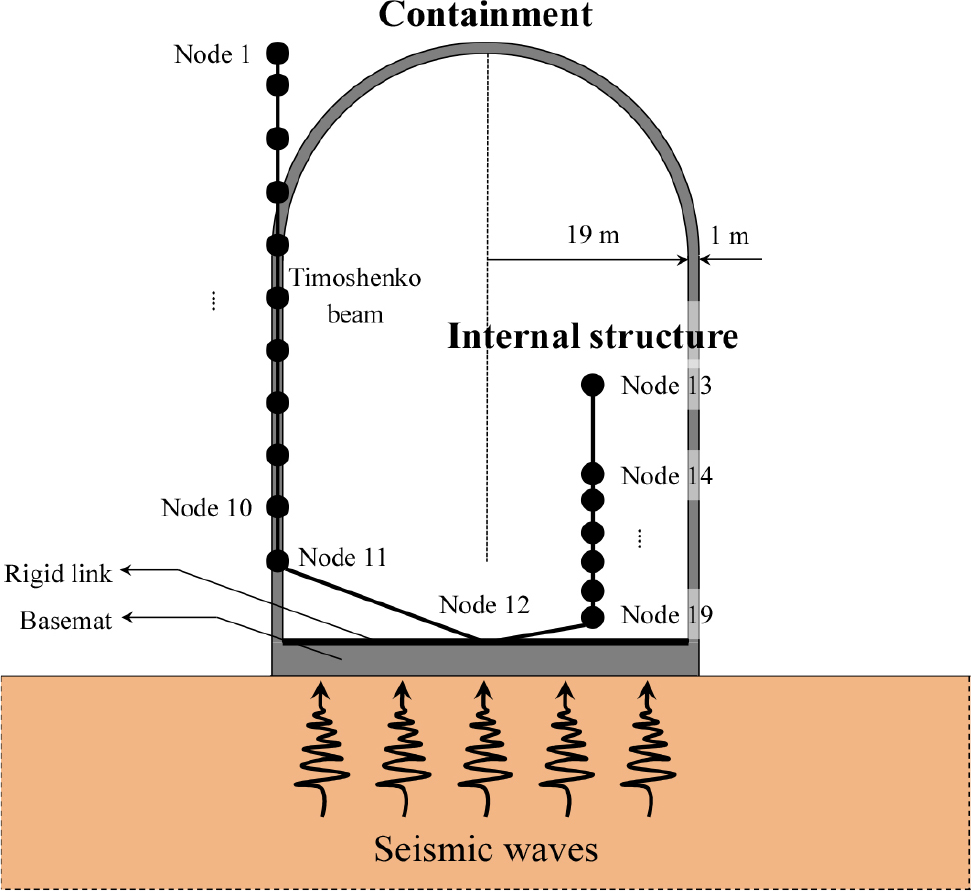
제안한 RVT에 기반한 ISRS 스케일링 기법을 적용하여 예제 원전구조물의 ISRS를 새로이 산정하고 이를 응답이력방법에 의한 ISRS와 비교하여 그 정확성을 검증한다. Fig. 1은 예제 원전 격납건물과 내부구조물을 보여주고 있다. 구조물 콘크리트의 탄성계수는 33.049GPa, 포아송비는 0.2778이다. 구조물은 전단 변형의 효과를 고려한 beam-stick 모델을 사용하여 모사하는데, 절점질량과 부재 정보는 Lee 등(2016)에 주어져 있다. 단, 구조물의 회전관성 효과는 무시한다. 구조물의 감쇠는 등가점성감쇠비 4%의 복소수 강성으로 모사한다(ASCE, 2017). 기초는 강체고 가정하고, 지반-구조물 상호작용 효과는 고려하지 않았다. 고정기초를 가진 구조물의 고유값 해석으로부터 얻어진 격납건물과 내부구조물의 기본진동수는 각각 5.26Hz와 11.95Hz이다.
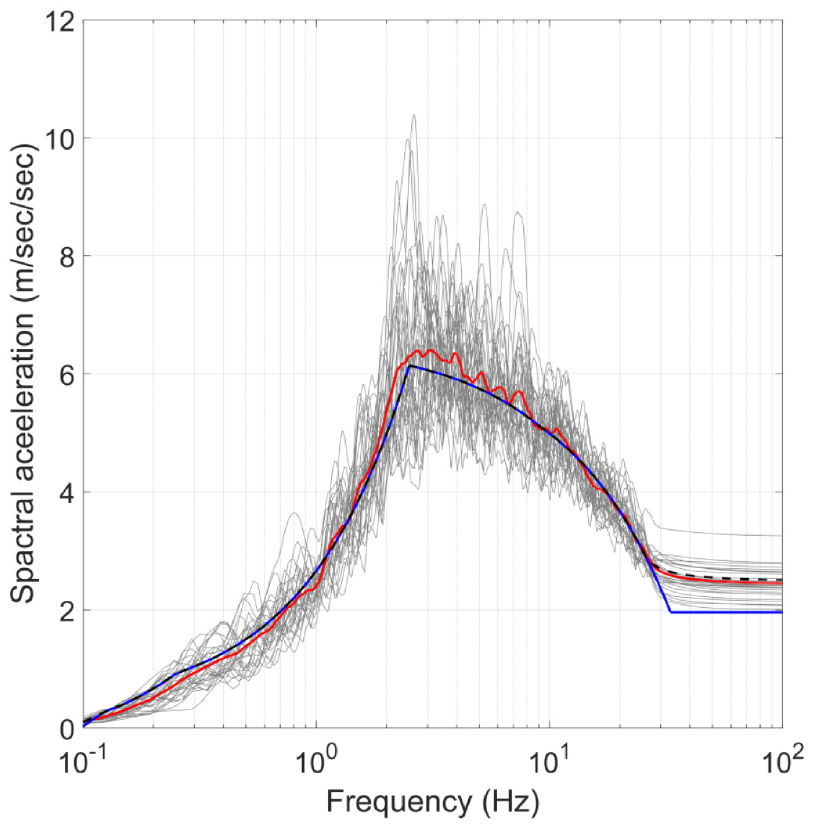
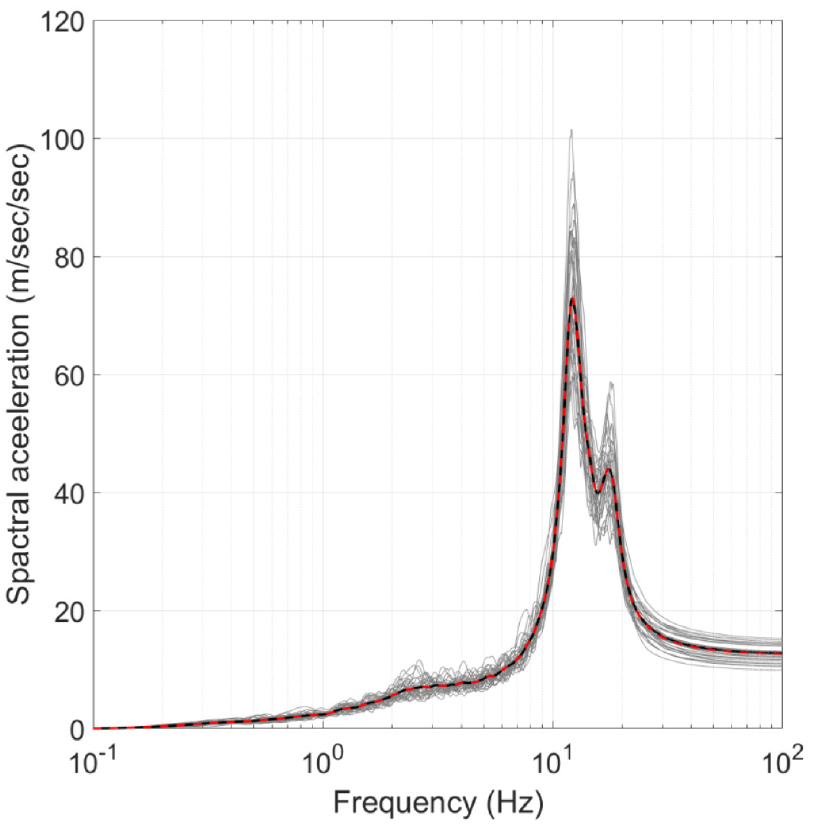
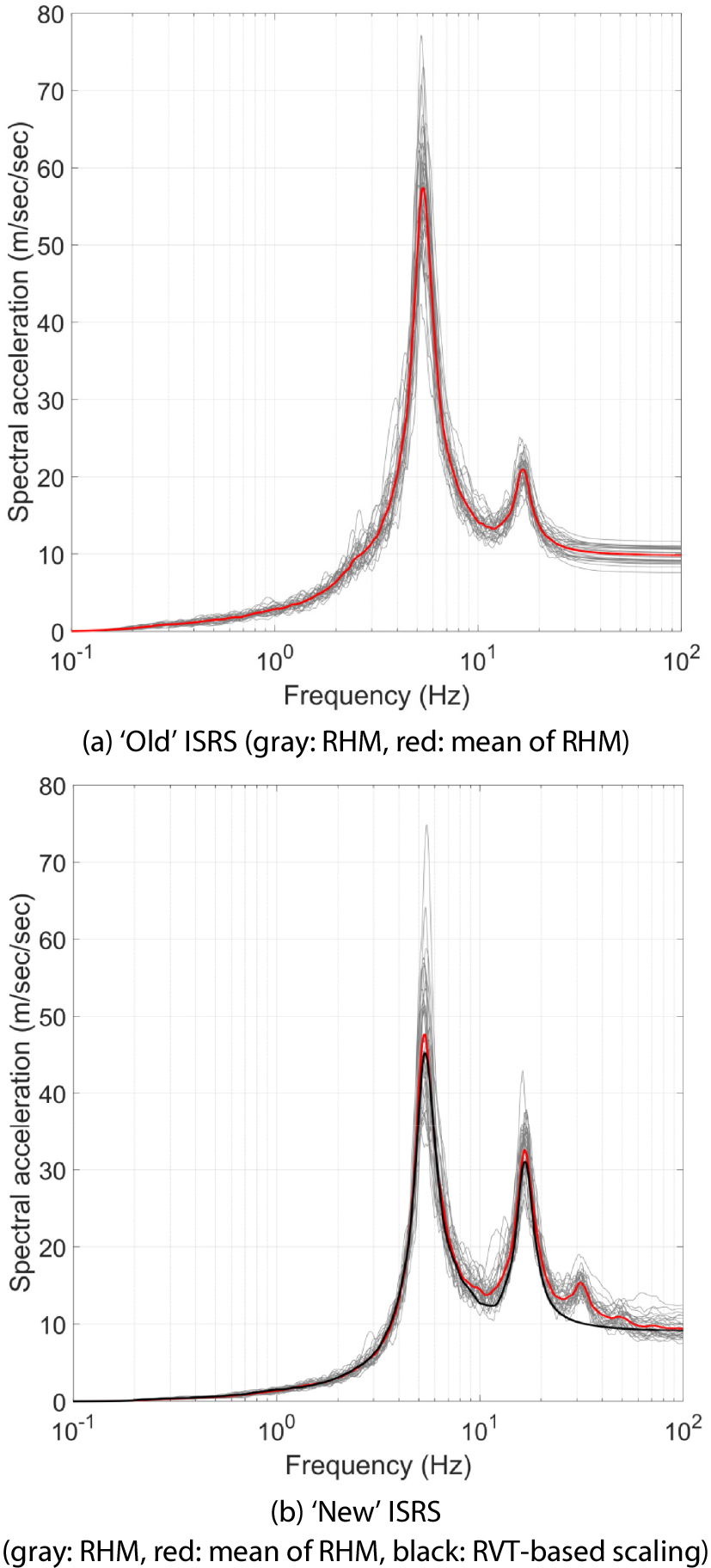
원전구조물의 내진설계를 위한 기존 입력지반운동 응답스펙트럼으로는 Fig. 2에 주어진 최고지반가속도 0.2g의 USNRC RegGuide 1.60(USNRC, 2014)의 지반운동 응답스펙트럼을 사용한다. 기존 입력지반운동 응답스펙트럼에 대한 원전구조물의 지진응답과 ISRS를 계산하기 위해 RHM을 사용한다. Fig. 2에 보인 바와 같이 기존 입력지반운동 응답스펙트럼에 부합하는 지진지반운동 30개를 생성한다(Vanmarcke and Gasparini, 1976). Fig. 2에서 회색은 생성된 30개 지진지반운동 각각의 단자유도계에 대한 응답스펙트럼이고, 적색은 이들의 평균을 보여주고 있다. 30개 지진지반운동을 사용하여 대상 구조물의 지진응답해석을 수행하여, 내부구조물 최상층의 ISRS 30개(gray)와 평균(red)을 Fig. 3과 같이 산정한다. Fig. 2에서 확인할 수 있는 바와 같이 생성된 지진지반운동은 30Hz 이하에서만 목표 응답스펙트럼과 잘 부합하는데, 지진지반운동을 합성할 때 고진동수 영역에서 이러한 차이를 보완하는 방법에 대해서는 추가적인 연구가 필요하다.
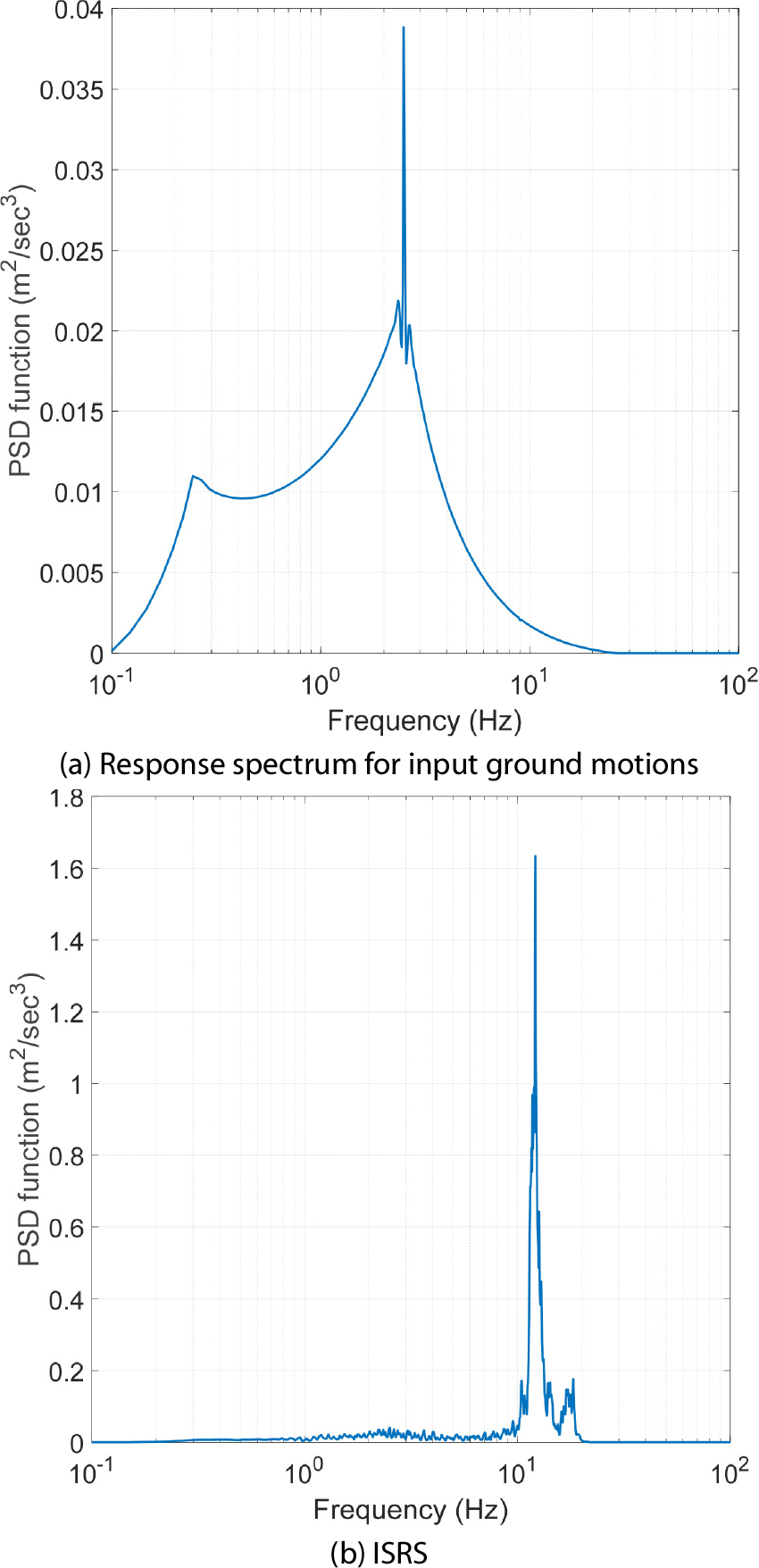
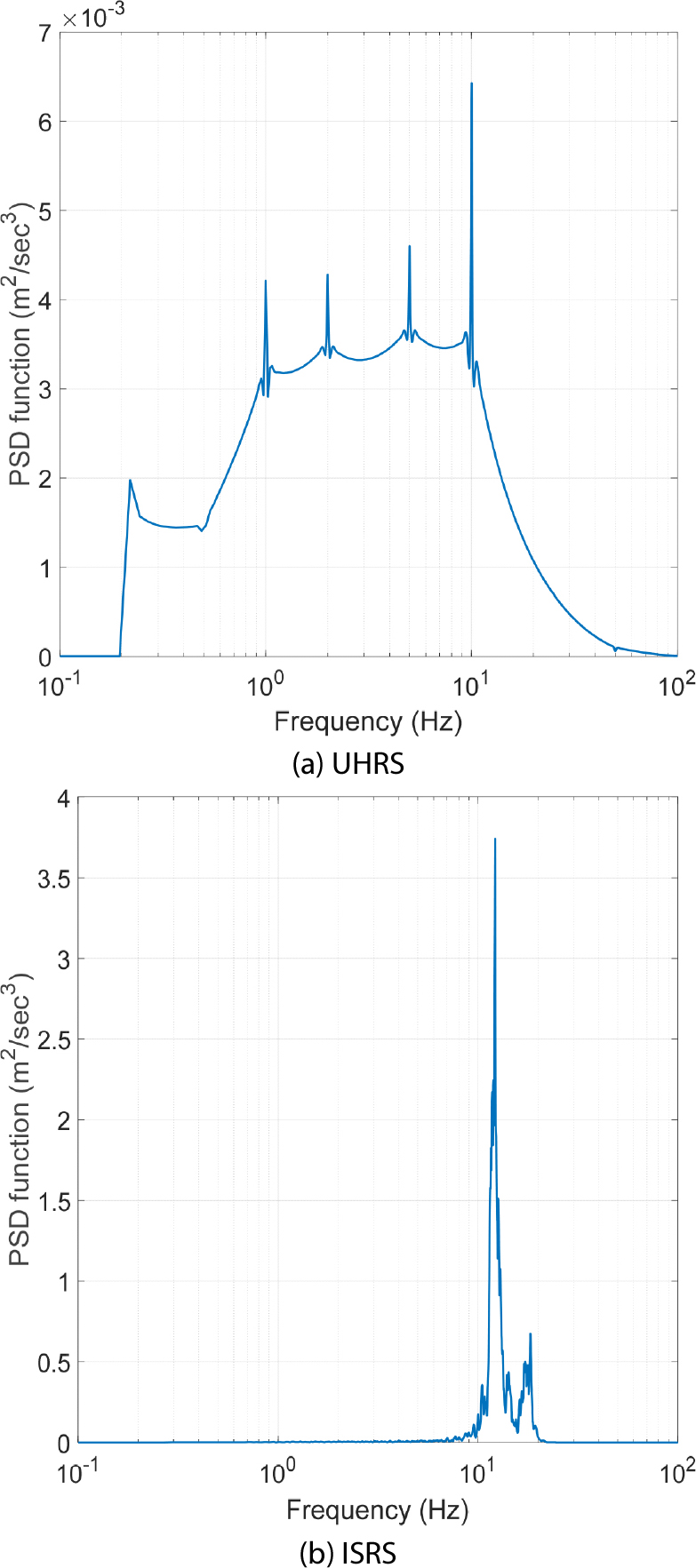
1)(1-1단계) 2장에서 서술한 RVT를 사용하여 Fig. 2의 입력지반운동 응답스펙트럼(blue)에 부합하는 PSD 함수를 Fig. 4(a)와 같이 산정한다. 산정된 PSD 함수는 2.49Hz에서 첨두값을 가지는데, 이는 Fig. 2의 목표 응답스펙트럼의 기울기가 2.5Hz에서 불연속이기 때문이다. Fig. 4(a)의 PSD 함수에 대응하는 응답스펙트럼(black)이 Fig. 2에 함께 도시되어 있는데, RVT를 적용하여 산정된 응답스펙트럼은 목표 응답스펙트럼(blue)과 잘 부합하는 것을 관찰할 수 있다. 하지만, 30Hz 이상의 고진동수 영역에서는 여전히 목표 응답스펙트럼과 잘 부합하지 않는다.
2)(1-2단계) RVT를 사용하여 Fig. 3의 ISRS(red)에 부합하는 PSD 함수를 Fig. 4(b)와 같이 산정한다. 이에 대응하는 응답스펙트럼(black)이 Fig. 3에 도시되어 있는데, 목표로 한 평균 ISRS(red)와 아주 잘 부합하는 것을 확인할 수 있다.
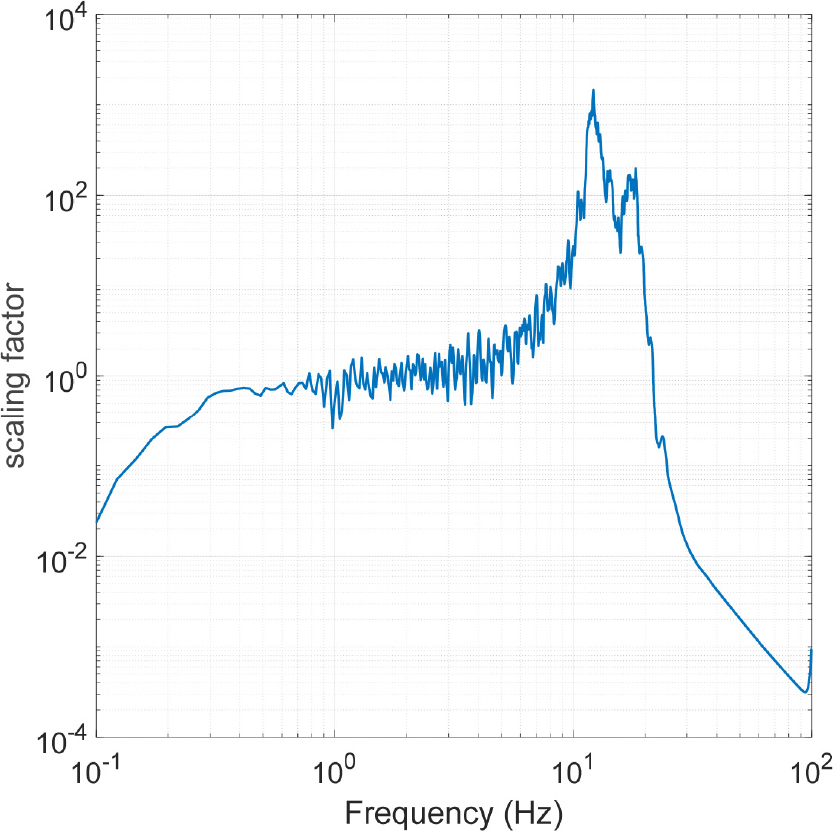
3)(1-3단계) Fig. 4의 PSD 함수로부터 ISRS와 입력지반운동 응답스펙트럼의 비율, 즉 비례계수를 Fig. 5와 같이 얻을 수 있다.
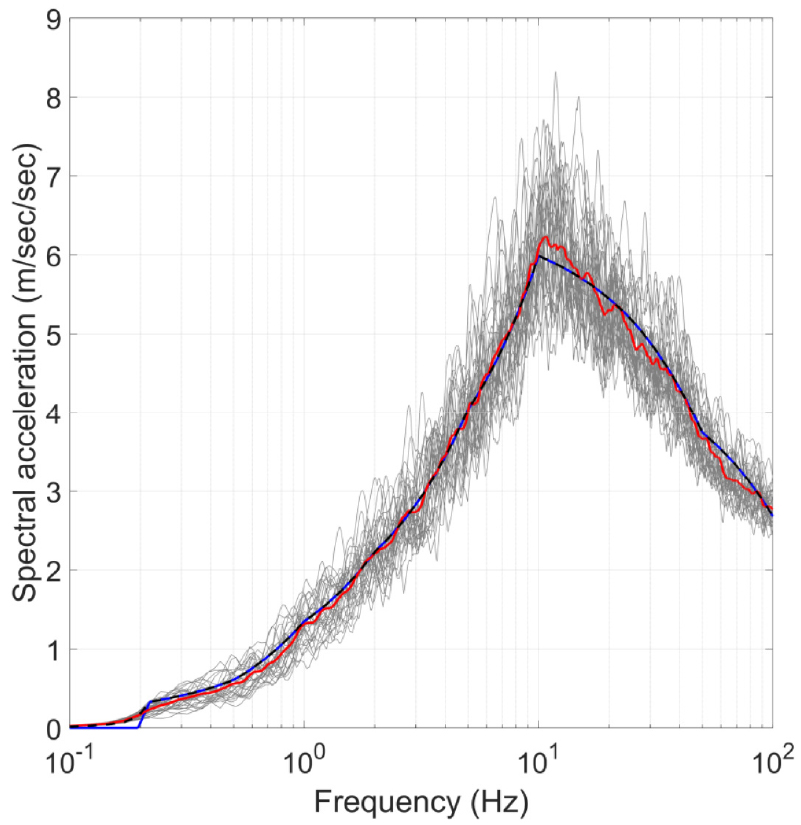
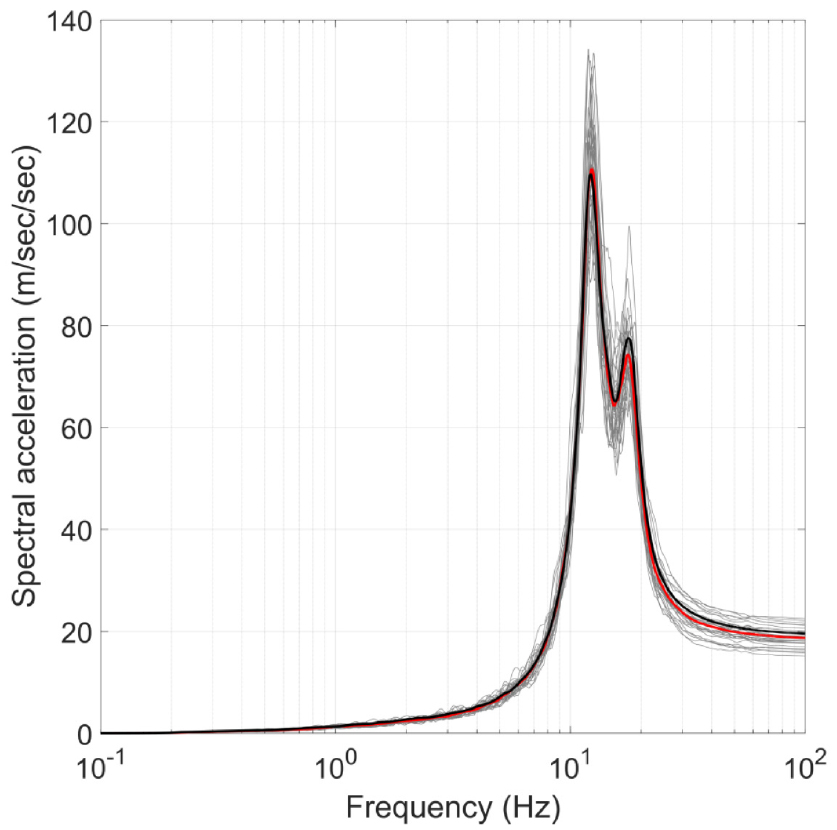
4)(2-1단계) 신규 지반운동 응답스펙트럼으로는 Fig. 6에 주어진 국내 원전부지의 UHRS(blue)를 사용하고자 한다. Fig. 2의 기존 입력지반운동 응답스펙트럼과 비교하였을 때, 10Hz의 고진동수 지반운동이 우세한 것을 관찰할 수 있다. 신규 입력지반운동 응답스펙트럼(blue)에 부합하는 PSD 함수를 RVT를 사용하여 Fig. 7(a)와 같이 산정한다. 신규 PSD 함수는 0.2, 0.5, 1, 2, 5, 10Hz 부근에서 국부 첨두값을 가지거나 기울기가 급격히 변하는데, 이는 신규 UHRS(blue)를 0.2, 0.5, 1, 2, 5, 10, 25, 50, 100Hz에서 조각적 선형(piecewise linear) 함수로 표현하였기 때문이다. Fig. 6에는 RVT를 사용하여 신규 PSD 함수로부터 도출된 응답스펙트럼(black)이 함께 도시되어 있는데, 목표로 하는 신규 UHRS(blue)와 잘 부합하는 것을 관찰할 수 있다.(2-2단계) Fig. 5의 비례계수를 Fig. 7(a)의 신규 PSD 함수에 적용하여 부계통 응답의 신규 PSD 함수를 Fig. 7(b)와 같이 산정한다. (2-3단계) RVT를 사용하여 Fig. 7(b)에 주어진 부계통 응답의 신규 PSD 함수로부터 대응하는 ISRS(black)를 Fig. 8과 같이 얻는다. 이상과 같이 RVT를 사용하여 신규 UHRS에 대한 예제 원전구조물의 ISRS를 추가적인 구조해석을 수행하지 않고 추정할 수 있다.
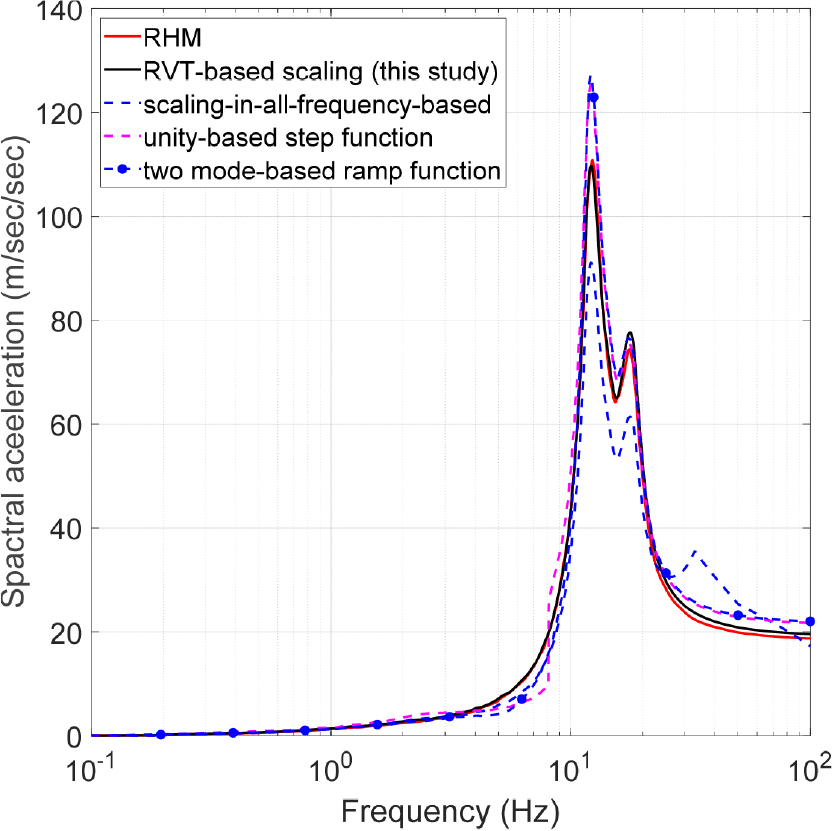
제안된 스케일링 기법의 정확성을 검증하기 위해 그 결과를 RHM에 의해 산정된 신규 ISRS와 비교하고자 한다. 신규 UHRS에 부합하도록 생성된 지진지반운동 30개(Vanmarcke and Gasparini, 1976)의 단자유도계 응답스펙트럼(gray)과 평균(red)이 Fig. 6에 도시되어 있고, 구조해석을 수행하여 이로부터 ISRS 30개(gray)와 평균(red)을 Fig. 8과 같이 산정할 수 있다. RVT에 기반한 스케일링 기법을 사용하여 산정한 ISRS(black)가 RHM을 사용하여 산정한 결과(red)와 잘 일치하는 것을 확인할 수 있다. 특히, 12.35Hz와 17.58Hz에서 발생하는 첨두들을 잘 표현할 수 있는 것을 관찰할 수 있다. 이상의 비교로부터 RVT에 기반하여 제안한 스케일링 기법이 신규 지반운동 응답스펙트럼에 대한 ISRS를 정확하게 예측할 수 있음을 확인할 수 있다.
2장에 언급한 바와 같이 Fig. 8의 결과는 응답스펙트럼을 첨두 응답의 평균으로 정의한 스케일링 기법에 의한 결과이다. 하지만, 응답스펙트럼을 평균+표준편차의 값으로 정의하여 스케일링을 수행할 수도 있는데, 이때의 결과도 여기에 보이지는 않았지만 Fig. 8의 결과와 거의 동일한 것을 확인할 수 있었다.
서론에서 언급하였듯이 비례계수를 산정하기 위해 세 가지 종류의 근사 방법이 사용되기도 한다(Kwag et al., 2024). 이 적용 예제에 대해서도 세 가지 종류의 근사 방법을 적용하여 ISRS 스케일링을 수행하고, 그 결과를 Fig. 9에 이 연구에서 제안한 RVT에 기반한 스케일링 기법의 결과와 비교한다. Fig. 9에서 확인할 수 있듯이, 세 가지 근사 방법에 의한 ISRS는 12.35Hz에서의 첫 번째 첨두를 잘 표현하지 못한다. 첫 번째 근사 방법 scaling-in-all-frequency-based approach는 12.35Hz에서의 첨두값을 과소평가하고, 다른 두 방법 unity-based step function approach와 two mode-based ramp function approach는 과대평가한다. 덧붙여 scaling-in-all-frequency-based approach는 17.58Hz의 국부 첨두를 잘 표현하지 못한다. 또한, 4~8Hz의 저진동수 영역에서의 ISRS는 과소평가되며, 20Hz 이상의 고진동수 영역에서의 ISRS는 과대평가되고 있는 것을 관찰할 수 있다. 이는 기존의 연구(Kwag et al., 2024)에서 관찰된 것과 유사한 결과이다.
Fig. 8의 ISRS는 내부구조물 최상단에서의 결과이다. 격납건물 최상단에서의 ISRS에 대해서도 RVT에 기반한 스케일링 기법을 동일하게 적용할 수 있을 것이고, 그 결과가 Fig. 10(b)에 제시되어 있다. 이 경우에도 5.35Hz와 16.60Hz의 첨두는 잘 표현할 수 있는 것을 관찰할 수 있다. 하지만, 31.30Hz에서의 세 번째 첨두 응답에 대해서는 그 증폭이 적절히 고려되지 않았다. 이는 Fig. 10(a)에 보인 기존 ISRS에서 세 번째 첨두가 관찰되지 않아, 스케일링 계수 산정 시 그 효과가 적절히 반영되지 않기 때문이다. 이를 고려하기 위해서는 기존 입력지반운동의 응답스펙트럼이 고진동수 영역에서 충분한 크기를 가져야 할 것이다.
이상에서 살펴본 바와 같이 RVT에 기반하여 이 연구에서 제안한 스케일링 기법은 신규 UHRS 또는 GMRS에 대한 ISRS를 정확하게 추정할 수 있고, 기존의 스케일링 기법과 비교하여 훨씬 더 우수한 결과를 도출할 수 있다.
5. 결 론
이 연구에서는 RVT에 기반하여 원전 시설물 부계통의 지진응답해석과 확률론적 지진안전성평가를 위한 ISRS 스케일링 기법을 새로이 제안하였다. 새로운 방법은 대상 구조물의 동적 특성에 대한 정보를 활용하지 않고, 구조응답과 지진지반운동의 PSD 함수의 비를 사용한다. 무작위 진동의 첨두값 계수를 사용하면 진동의 PSD 함수로부터 첨두값의 통계적 특성과 무작위 진동의 응답스펙트럼을 추정할 수 있다. 그러므로 이 연구에서는 무작위 진동의 PSD 함수의 비를 활용하여 PSD 함수의 스케일링을 수행하고 이로부터 스케일링된 응답스펙트럼을 도출하는 기법을 제안하였다. 제안된 RVT에 기반한 새로운 스케일링 기법을 예제 원전 구조물에 적용하고, RHM 방법에 의한 참조해와 비교하여 이 연구에서 제안한 새로운 스케일링 기법이 정확한 것을 확인하였다. 또한, 비례계수를 산정하기 위한 기존의 근사 방법들과 비교하여, 이 연구에서 제안한 기법은 ISRS의 첨두 등을 잘 표현할 수 있는 것을 관찰할 수 있었다. 그러므로, 새로운 스케일링 기법을 활용하면, 별도의 구조해석이나 구조물의 동특성 정보를 활용하지 않고도 새로운 지진재해도분석 결과가 반영된 신규 UHRS 또는 GMRS에 대한 원전 구조물의 신규 ISRS를 정확히 추정할 수 있을 것이다. 또한, 제안된 기법은 구조물의 동특성 정보가 필요하지 않으므로, 상시 진동이나 미소 지진 등에 대한 구조물의 동적 응답을 활용하여 실제 구조물의 ISRS 스케일링을 효율적이고 정확하게 수행할 수 있을 것이다.
향후 연구에서는 새로운 스케일링 기법을 좀 더 복잡한 원전 구조물 또는 지반-구조물 상호작용계에 적용하여 그 적용 가능성을 검토해야 할 것이고, 이를 토대로 부계통의 지진취약도평가, 지진위험도평가 등에 활용해야 할 것이다. 특히, 구조물의 동특성을 고려하지 않는 근사 스케일링 방법은 고진동수 영역에서 응답스펙트럼의 첨두값을 잘 모사하지 못하는 것으로 알려져 있으므로(EPRI, 2018), 구조응답스펙트럼의 고진동수 영역에서 다양한 첨두값을 가지는 구조물에 대해서 이 연구에서 제시한 방법의 적용 가능성에 대해 검토해야 할 것이다.