A Technique for Selecting Quadrature Points for Dimension Reduction Method to Improve Efficiency in Reliability-based Design Optimization

Ha-Yeong Kim; Hyunkyoo Cho

doi:10.7734/COSEIK.2024.37.3.217

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 June 2024. 217-224
https://doi.org/10.7734/COSEIK.2024.37.3.217

A Technique for Selecting Quadrature Points for Dimension Reduction Method to Improve Efficiency in Reliability-based Design Optimization

신뢰성 기반 최적설계의 효율성 향상을 위한 차원감소법의 적분직교점 선정 기법

Ha-Yeong Kim¹

Hyunkyoo Cho²^*

김 하영¹

조 현규²^*

¹Graduate Student, Department of Mechanical Engineering, Mokpo National University, Muan, 58554, Korea

²Associate Professor, Department of Mechanical Engineering, Mokpo National University, Muan, 58554, Korea

¹국립목포대학교 기계공학과 석사과정

²국립목포대학교 기계공학과 부교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/3.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

This paper proposes an efficient dimension reduction method (DRM) that considers the nonlinearity of the performance functions in reliability-based design optimization (RBDO). The dimension reduction method evaluates the reliability more accurately than the first-order reliability method (FORM) using integration quadrature points and weights. However, its efficiency is hindered as the number of quadrature points increases owing to the need for an additional evaluation of the performance function. In this study, we assessed the nonlinearity of the performance function in RBDO and proposed criteria for determining the number of quadrature points based on the degree of nonlinearity. This approach suggests adjusting the number of quadrature points during each iteration of the RBDO process while maintaining the accuracy of theDRM while improving the computational efficiency. The nonlinearity of the performance function was evaluated using the angle between the vectors used in the maximum probable target point (MPTP) search. Numerical tests were conducted to determine the appropriate number of quadrature points according to the degree of nonlinearity. Through a 2D numerical example, it is confirmed that the proposed method improves the efficiency while maintaining the accuracy of the dimension reduction method or Monte Carlo Simulation (MCS).

Keywords

Reliability-based Design Optimization (RBDO)

Dimension Reduction Method (DRM)

integration quadrature point

Most Probable Target Point (MPTP)

degree of nonlinearity

Performance Measure Approach (PMA)

본 논문에서는 신뢰성 기반 최적설계(RBDO)에서 성능함수의 비선형성을 고려한 효율적인 차원감소법(DRM)을 제안한다. 차원감소법은 적분직교점과 가중치를 사용하여 1차 신뢰도법(FORM) 보다 더 정확하게 신뢰도를 평가하는 반면 성능함수를 추가로 해석해야하기 때문에 적분직교점의 개수가 증가하면 효율성이 저해된다. 본 논문에서는 신뢰성 기반 최적설계에서 성능함수의 비선형도를 평가하고, 비선형도에 따라 적분직교점의 수를 결정하는 기준을 제안한다. 이를 통해 신뢰성 기반 최적설계가 진행될 때 반복마다 적분직교점의 수를 조절하여 차원감소법의 정확도는 유지하면서 계산의 효율성은 개선하는 방안을 제안한다. 성능함수의 비선형도 평가는 최대가능목표점(MPTP) 탐색에 사용한 벡터 사이의 각도를 통해 이루어지며, 수치 테스트를 통해 비선형도에 따른 적절한 적분직교점의 수를 도출하였다. 2차원 수치예제를 통해 개발된 방법이 차원감소법이나 몬테카를로 시뮬레이션(MCS)의 정확도는 유지하면서 효율성이 향상된다는 것을 확인하였다.

키워드

신뢰성 기반 최적설계

차원감소법

적분직교점

최대가능목표점

비선형도

목표성능치법

MAIN

1. 서 론
2. 신뢰성 기반 최적설계(RBDO)
2.1 신뢰성 기반 최적설계의 정식화
2.2 목표성능치 방법(PMA)
2.3 Enhanced Hybrid Mean Value(HMV+)
2.4 차원감소법을 이용한 신뢰성 기반 최적설계
3. 비선형도 평가와 적분직교점 선정
3.1 비선형도 평가법
3.2 차원감소법의 적분직교점 선정 테스트
4. 수치예제
5. 결 론

1. 서 론

기계시스템 설계에 있어 성능의 안정성을 저해하는 변동성은 불리한 요소이지만, 변동성이 없는 기계시스템은 현실적으로 찾아보기 어렵다. 따라서 치수, 물성치, 하중, 강도 등의 변동성을 고려하는 신뢰도분석을 시스템 설계에 적용하여 변동성을 정량화해야 한다. 현재는 시스템 설계최적화에 신뢰성분석을 접목하는 신뢰성 기반 최적설계(Reliability-Based Design Optimization, 이하 RBDO) 기법이 개발되어 변동성이 존재할 때 성능을 만족하는 최적설계점도 구할 수 있게 되었다.

Tu 등(1999)은 목표신뢰성을 만족하는 설계점 중 가장 위험한 설계점인 최대가능목표점(Most Probable Target Point, 이하 MPTP)을 찾아 RBDO를 수행하는 목표성능치법(Performance Measure Approach, 이하 PMA)을 제안하였다. PMA는 이전 RBDO의 확률제약조건을 개선하여 MPTP의 수렴성을 높였다. 하지만 본래의 PMA는 MPTP에서 성능함수를 선형 근사하는 1차 신뢰도법(First-order Reliability Method, 이하 FORM)을 사용하여 신뢰도를 평가하기 때문에 정확성이 떨어진다는 단점이 있다. 이를 개선하기 위한 2차 신뢰도법(Second-order Reliability Method, 이하 SORM)이 개발되었지만(Armen et al., 1987), 성능함수의 헷세행렬을 필요로하기 때문에 널리 사용되기 어려웠다.

차원감소법(Dimension Reduction Method, 이하 DRM)은 FORM을 활용한 신뢰도 평가의 정확성을 향상시키기 위해 개발되었다. Rahman과 Xu(2004)는 차원 감소를 위해 모멘트 기반 직교 규칙을 제안하였으며, Lee 등(2008)은 RBDO에 DRM을 적용하여 보다 정확한 RBDO 최적점을 찾을 수 있었다. DRM은 MPTP 주변에 적분직교점(Quadrature Point)을 배치하고, 그 점에서의 계산한 추가적인 성능함수값을 신뢰도 평가에 사용하여 정확성을 높인다. 다만, DRM의 정확성은 적분직교점을 많이 배치할수록 높아지지만, 그만큼 성능함수를 평가해야 하기 때문에 계산비용도 상승하게 된다. 따라서, 성능함수의 비선형도가 커서 신뢰도의 정확한 평가가 어려울 때에는 적분직교점을 많이 배치하고, 비선형도가 작을 경우에는 적게 배치할 필요가 있다.

따라서, 본 연구에서는 성능함수의 비선형도를 평가하고 이에 따라 적분직교점의 개수를 선정하는 기법을 제안한다. DRM을 이용한 신뢰도 평가에서 정확도를 높이기 위해 일반적으로 필요한 적분직교점의 개수는 3개 혹은 5개가 적당하다. 하지만, 성능함수가 선형에 가깝다면 적분직교점은 불필요하며, 반대로 비선형도가 크다면 5개보다 많은 적분직교점을 도입해야 할 수도 있다. 따라서 성능함수의 비선형도를 평가하여 적분직교점의 개수를 선정하는 것은 DRM을 사용한 신뢰성분석의 효율성을 개선하고 나아가 전체 RBDO의 효율성도 높일 수 있는 중요한 연구라 할 수 있다.

다음의 2절에서는 본 연구 수행에 기반이 되는 기존 연구를 간략히 정리한다. 3절에서는 성능함수의 비선형도를 평가하는 방법과 이를 통해 적분직교점의 수를 선정하는 과정에 대해 설명한다. 4절에서는 수치예제를 통해 개발된 방법을 검증하고, 5절에서 본 연구의 결론을 정리한다.

2. 신뢰성 기반 최적설계(RBDO)

이 절에서는 RBDO를 정식화하고, RBDO의 확률제약조건인 신뢰도를 평가하기 위한 PMA 및 HMV+(Enhanced Hybrid Mean Value) 기법에 대해 소개한다. 또한, 신뢰도의 정확성을 향상시키기 위한 DRM에 대해서도 소개한다.

2.1 신뢰성 기반 최적설계의 정식화

일반적으로 RBDO는 식 (1)과 같이 정식화 된다.

(1)

minimize cost (d) subject P (G_{i} (X) > 0) \leq P_{F}^{Tar}, i = 1, 2, . . ., m

여기서, cost는 목적함수로 설계 변수 d로 이루어져 있고, $G_{i} (X)$ 는 성능함수로 랜덤변수X로 이루어져 있다. $P_{F}^{Tar}$ 는 목표실패확률이다. 설계점에서 $G_{i} (X)$ > 0이면 위험한 설계로 간주하며, 식 (1)의 확률제약조건은 설계점에서의 실패확률이 목표치인 $P_{F}^{Tar}$ 보다 작아야 안전하다는 것을 의미한다. 목표실패확률의 계산은 다중적분을 포함하기 때문에 계산하기 어려운데, FORM에서는 성능함수를 선형으로 근사하고 정규누적분포함수 𝛷를 사용하여 식 (2)와 같이 간단하게 정의된다.

(2)

P_{F}^{Tar} = Φ (- β^{Tar})

여기서, $β^{Tar}$ 는 목표 신뢰도 지수로 신뢰도를 직접적으로 평가하는데 사용되며, 표준정규공간인 U-space에서 원점으로부터 MPTP까지의 거리로 계산될 수 있다. 이때, U-space에서 원점은 실제확률공간인 X-space에서 설계점이다.

2.2 목표성능치 방법(PMA)

PMA는 목표신뢰성지수 $β^{Tar}$ 를 이용하여 MPTP를 찾는다. 그렇기 때문에 MPTP의 위치가 성능함수의 한계표면상태에 존재하지 않으며, 비선형도가 큰 성능함수의 경우에도 안정적인 수렴성을 보인다(Tu et al., 1999). PMA의 확률제약조건은 식 (3)과 같이 정의된다.

(3)

minimize g (u) subject ∥ u ∥ = β^{Tar}

여기서, $g (u)$ 는 U-space에서 정의되는 성능함수이다. PMA의 확률제약조건은 U-space의 원점으로부터 $β^{Tar}$ 만큼 거리에 MPTP가 존재하며, $g (u)$ 값은 최소가 되어야 한다는 것을 의미한다.

2.3 Enhanced Hybrid Mean Value(HMV+)

HMV+ 방법(Youn et al., 2005)은 성능 함수 평가값의 비교로 아크보간방법을 사용하여 MPTP의 수렴 속도를 높이는 방법이다. HMV+ 방법은 HMV 방법을 통해 구한 MPTP, $u_{HMV}^{(k)}$ 를 U-space에서 성능함수를 평가한 값을 비교하여 HMV+방법 사용여부를 결정하고, 식 (4)를 이용하여 $u_{HMV +}^{(k)}$ 으로 업데이트 한다.

(4)

u_{H M V +}^{(k)} = u (t) = \frac{\sin [θ (1 - t)]}{\sin θ} u_{H M V}^{(k - 1)} + \frac{\sin (θ t)}{\sin θ} u_{H MV}^{(k)}

여기서, 𝜃는 $u_{H M V}^{(k)}$ 과 $u_{H M V}^{(k - 1)}$ 사이의 각도이며 식 (5)를 이용하여 계산될 수 있다.

(5)

θ = \arccos (\frac{u^{(k - 1)} \cdot u^{(k)}}{∥ u^{(k - 1)} ∥ ∥ u^{(k)} ∥})

또한, $t$ 는 $u_{HMV +}^{(k)}$ 을 계산하기 위해 필요한 상수로 수식 $h (t)$ 의 함숫값과 도함수를 이용하여 계산된다. $h (t)$ 와 $h (t)$ 에 포함된 상수 $a, b, c, d$ 는 식 (6)을 통해 정의된다.

(6)

\begin{aligned} h (t) = a + b t + c t^{2} + d t^{3}, 0 \leq t \leq 1 \\ a = h (0) \\ b = h^{'} (0) \\ c = - 3 h (0) + 3 h (1) - 2 h^{'} (0) - h^{'} (1) \\ d = 2 h (0) - 2 h (1) + h^{'} (0) + h^{'} (1) \end{aligned}

마지막으로 HMV+의 수렴 조건은 다음 식 (7)과 같다.

(7)

|\frac{n^{(k)} \cdot u^{(k)}}{∥ u^{(k)} ∥}| \leq ε_{0}

여기서, $ε_{0}$ 은 수렴파라미터이며, 수렴 조건이 $ε_{0}$ 보다 작으면 수렴했다고 보고 MPTP를 확정한다.

2.4 차원감소법을 이용한 신뢰성 기반 최적설계

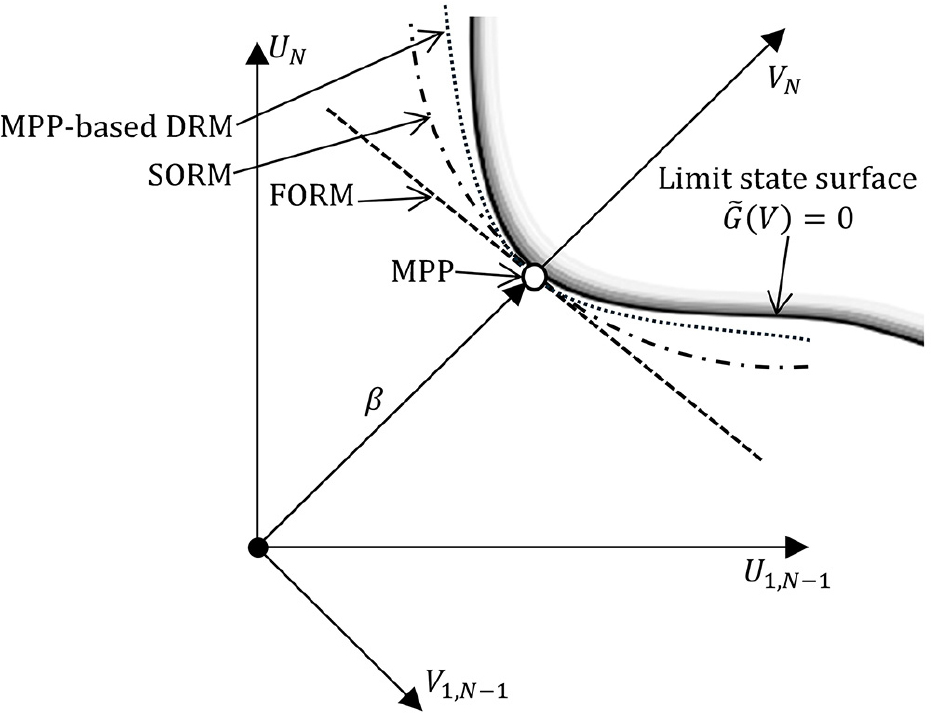
Rahman과 Xu(2004)과 Lee 등(2008)의 연구를 통해 Fig. 1에서와 같이 RBDO에 DRM을 적용하면서 신뢰도의 근사치 계산에 오차를 감소시켜 FORM, SORM보다 더 높은 정확성을 얻을 수 있게 되었다. 특히 Lee 등(2008)은 회전된 표준정규공간인 V-space의 개념을 도입하면서 신뢰도를 보정하고, MPTP를 업데이트 하였다. DRM을 이용한 보정된 신뢰도 $P_{F}^{DRM}$ 는 식 (8)과 같이 정의된다.

(8)

P_{F}^{D R M} = \frac{\prod_{i = 1}^{N - 1} \sum_{j = 1}^{n} w_{j} Φ (- β^{T a r} + \frac{\tilde{G_{i}^{s}} (v_{i}^{j})}{b_{1}})}{Φ {(- β^{T a r})}^{N - 2}}

여기서, $n$ 은 적분직교점 개수, $v_{i}^{j}$ 는 적분직교점의 위치, 그리고 $w_{j}$ 는 $v_{i}^{j}$ 에 해당하는 가중치이다. $\tilde{G} (v)$ 는 V-space에서 평가되는 성능함수이므로 $\tilde{G} (v) = g (u) = G (X)$ 으로 계산될 수 있으며, $\tilde{G^{s}} (v)$ 는 이동된 $\tilde{G} (v)$ 로 V-space의 MPTP인 $v *$ 에서 평가되는 성능함수와 $\tilde{G} (v)$ 의 차이를 이용하여 계산되며 식 (9)와 같이 표현될 수 있다.

(9)

\tilde{G^{s}} (v) = \tilde{G} (v) - \tilde{G} (v *)

또한, $b_{1}$ 은 v-spaec에서 v에 대한 $\tilde{G} (v)$ 의 민감도로 식 (10)과 같이 정의된다.

(10)

b_{1} = \frac{\partial \tilde{G} (v *)}{\partial v}

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370308/images/Figure_jcoseik_37_03_08_F1.jpg

Fig. 1.

U-space and rotated standard normal V-space

식 (8)은 식 (2)에 적분직교점과 가중치 개념을 도입하고, 결론적으로 목표실패확률을 보정하여 $P_{F}^{DRM}$ 을 산출하고, 식 (11), (12)와 같이 $β^{Tar}$ 및 MPTP를 업데이트 하는데 사용된다.

(11)

β^{(k + 1)} = β^{(k)} - (β^{DRM} - β^{Tar})

(12)

u_{D R M}^{(k + 1)} = \frac{β^{(k + 1)}}{β^{(k)}} u_{H M V +}^{(k)}

여기서, $β^{D R M}$ 은 식 (8)을 통해 구한 $P_{F}^{DRM}$ 의 신뢰도 지수로 식(2)를 이용하여 $β^{DRM} = - Φ^{- 1} (P_{F}^{DRM})$ 으로 계산되고 기존 신뢰도 지수 $β^{(k)}$ 와 업데이트된 신뢰도지수 $β^{(k + 1)}$ 의 비율을 이용하여 MPTP를 업데이트 한다. 이 때, $β^{(0)} = β^{Tar}$ 이다.

3. 비선형도 평가와 적분직교점 선정

일반적으로 RBDO에 DRM을 적용할 때, 계산비용의 상승을 억제하기 위해 3개의 적분직교점을 사용하여 신뢰성분석의 정확도를 높인다(Lee et al., 2008). 하지만, 성능함수의 비선형도가 높거나, RBDO 수행과정 중 비선형 정도가 설계점에 따라 바뀔 수 있다. 따라서, 일정 수의 적분직교점을 RBDO를 수행하는 동안 계속 사용하는 것은 계산 효율성이나 비용 측면에서 비효율적이다. 성능함수가 선형에 가까우면, FORM을 사용하여 계산비용을 줄이고 비선형도가 크면 5개 이상의 적분직교점을 사용하여 신뢰성 계산의 정확성을 높여야 한다. 따라서, 성능 함수의 비선형도에 따라 적분직교점 개수가 결정되어야 한다. 이 절에서는 본 연구에서 제안하는 비선형도 평가법과 이를 통해 적분직교점의 개수를 선정하는 연구에 대해 소개한다.

3.1 비선형도 평가법

성능함수의 비선형도를 평가하는 방법은 다양하나, 직관적으로는 성능함수의 2계 도함수인 헷세행렬을 생각할 수 있다. 하지만, 일반적으로 성능함수가 음함수기 때문에 헷세행렬을 구하기 어렵다. 또한, 성능함수의 스케일 문제가 있다. 예를 들어, $G (X) = X^{2}$ 와 $G (X) = 2 X^{2}$ 가 신뢰성 측면에서는 같은데 비해 2계 도함수는 후자가 2배이다. 즉, 성능함수의 스케일과 무관한 방법을 사용해야 한다. 또한, MPTP를 찾기 위해 계산한 성능함수 값을 사용하여 비선형도를 평가할 수 있다면, 추가 계산비용을 절약할 수 있기 때문에 더욱 효율적일 것이다.

본 연구에서는 식 (5)를 활용하여 비선형도를 평가한다. 식 (5)는 MPTP를 탐색하는데 사용하는 식으로 $(k - 1)$ 과 $k$ 번째 후보 MPTP 사이의 각도를 계산한다. 성능함수가 선형이면 MPTP는 반복 탐색 없이 1회에 찾을 수 있는 반면, 비선형도가 높으면 대체로 반복횟수가 높아지는데 착안하여, 비선형도 평가에서는 첫 번째 후보 MPTP와 탐색한 MPTP 사이의 각도를 활용하여 식 (13)과 같이 성능함수의 비선형도를 평가한다.

(13)

θ_{nonl} = \arccos (\frac{u^{(1)} \cdot u^{(last)}}{∥ u^{(1)} ∥ ∥ u^{(last)} ∥})

여기서, 계산되는 $θ_{n o n l}$ 값에 따라 비선형도가 평가되어 적분직교점의 개수가 결정될 것이며, 이는 첫 번째 MPTP 후보인 $u^{(1)}$ 과 탐색된 MPTP인 $u^{(last)}$ 사이각으로 정의된다.

3.2 차원감소법의 적분직교점 선정 테스트

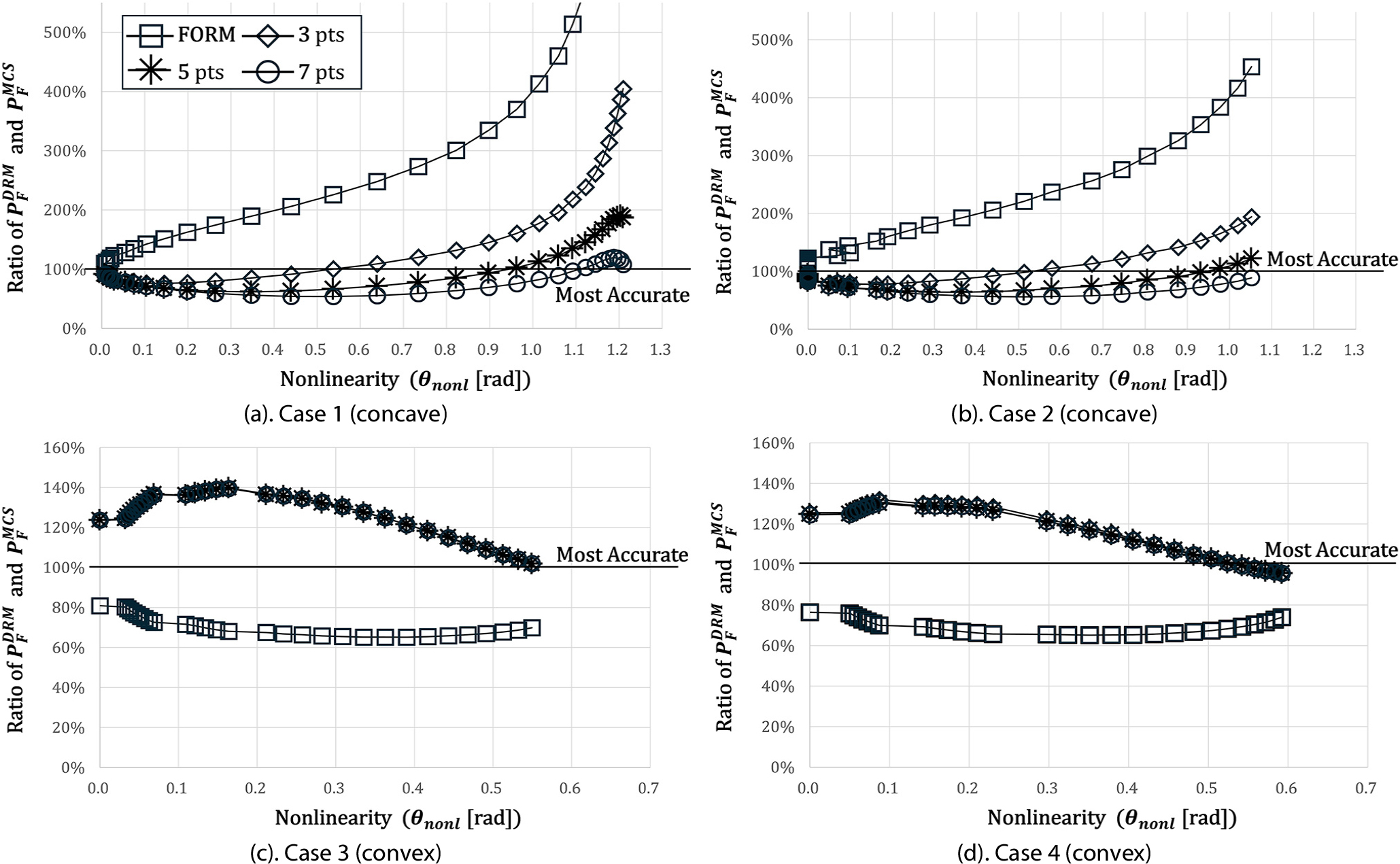
비선형도에 따라 $θ_{n o n l}$ 값의 경향성을 파악하고, 적분직교점의 수를 결정하기 위해 오목함수와 볼록함수 각각 두 개의 2차원 함수 예제로 테스트를 진행하였다. Table 1에 예제를 나타내었는데, 상수 $p$ 는 비선형도를 조절하는 상수로 $p$ 가 증가할수록 성능함수 $G (X)$ 의 비선형도가 커진다. Fig. 2에는 $p$ =15일 때 $G (X)$ 의 한계상태표면을 나타내었는데 함수의 전반적인 형상을 볼 수 있다. 함수의 형태는 설계점을 기준으로 식 (14)를 이용하여 확인할 수 있다(Youn et al., 2003).

(14)

ζ = (n^{(1)} - n^{(2)}) \cdot (n^{(2)} - n^{(last)})

여기서, $n^{(k)} = - \nabla g (u^{(k)}) / ∥ \nabla g (u^{(k)}) ∥$ 이다. 𝜁의 값에 따라 𝜁>0이면 볼록함수를, 𝜁≤0이면 오목함수를 의미한다.

Table 1

Nonlinearity evaluation examples

Case	Type	$G (X) (p = 1, 2, . . ., 30)$	𝜇	𝜎	$β^{Tar}$	Distribution
1	Concave	$0.05 \cdot 1 . 26^{p - 1} x_{1}^{2} - x_{2} + 6$	[0.5, 4.5]^T	[1.0, 1.0]^T	1.5	Normal
2	Concave	$1 - \frac{80}{0.2 \cdot {1.2}^{p - 1} {(x_{2} - 1)}^{2} + 8 (x_{1} - 1) + 104}$	[0.5, 0.5]^T	[1.0, 1.0]^T	1.5	Normal
3	Convex	$- 0.1 \cdot 1 . 05^{p - 1} x_{1}^{2} - x_{2} + 3$	[0.5, -30]^T	[1.0, 1.0]^T	1.5	Normal
4	Convex	$- 1 + \frac{80}{1 . 07^{p - 1} x_{2}^{2} - 8 x_{1} + 104}$	[9, 0.5]^T	[1.0, 1.0]^T	1.5	Normal

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370308/images/Figure_jcoseik_37_03_08_F2.jpg

Fig. 2.

Limit state of G(X) when $p$ =15

테스트에서는 $p$ 를 1씩 증가시켜 가며 비선형도를 증가시켰고, 설계점을 기준으로 MPTP를 찾았으며, 적분직교점의 수 $n$ 을 1, 3, 5, 7개로 증가시키며 DRM으로 실패확률 $P_{F}^{DRM}$ 을 계산한다. 여기서, 1개의 적분직교점을 사용하는 것은 FORM을 의미한다. 또한 같은 문제에 대해서 1억개의 샘플을 사용한 몬테카를로 시뮬레이션(Monte Calro Simulation, 이하 MCS)으로 실패확률 $P_{F}^{MCS}$ 을 구한다. 충분한 수의 샘플을 사용하였기 때문에 $P_{F}^{MCS}$ 는 매우 정확할 것이다. 마지막으로 $P_{F}^{DRM}$ 와 $P_{F}^{MCS}$ 를 비교하여 정확성을 확인한다.

테스트 결과를 Fig. 3에 그래프로 나타내었다. 수평축은 비선형도 $θ_{n o n l}$ 를 수직축은 정확도 $P_{F}^{DRM}$ / $P_{F}^{MCS}$ 를 나타낸다. 그래프상의 각 점은 $p$ 를 1씩 30까지 증가시키며 얻은 결과를 표시한 것인데, $p$ 가 증가하면 $θ_{n o n l}$ 도 증가하므로 3.1절에서 정의한 $θ_{n o n l}$ 가 성능함수의 비선형도를 잘 나타냄을 확인하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370308/images/Figure_jcoseik_37_03_08_F3.jpg

Fig. 3.

Nonlinearity evaluation results of concave performance function

Case 1~4에서 공통적으로 확인할 수 있는 것은 $θ_{n o n l}$ 값이 0에 가까울수록 적분직교점의 수와 관계없이 정확도가 비슷하다는 것이다. 이는 $G (X)$ 가 선형에 가까워 적분직교점을 늘려계산할 필요성이 없다는 것을 의미한다. 따라서, $n$ =1 즉, FORM을 사용하는 것이 바람직하다. $θ_{n o n l}$ 가 증가하면 FORM의 정확도는 떨어지는 반면 $n$ =3, 5, 7인 DRM의 정확도는 비교적 높고 안정적인 것으로부터 비선형도와 적분직교점의 수가 정확도에 미치는 영향을 분명히 확인할 수 있다.

Fig. 3(a), (b)는 $G (X)$ 가 오목함수인 경우 테스트 결과로, FORM은 $θ_{n o n l}$ 가 증가할수록 $P_{F}^{DRM}$ 를 과대평가하여 정확도가급격히 나빠지는 반면, $θ_{n o n l}$ =0.1~0.7일 때 $n$ =3을 사용하는 것이 가장 높은 정확도를 보이고, 비선형도가 커질수록 $θ_{n o n l}$ 값이 증가하면서 1.0까지는 $n$ =5를 사용하는 것이 바람직하며, $θ_{n o n l}$ 가 1.0보다 큰 경우, $n$ =7을 사용해야 함을 확인할 수 있다.

Fig. 3(c), (d)는 $G (X)$ 가 볼록함수인 경우 테스트 결과를 나타내었다. 볼록함수에서는 $n$ =3, 5, 7로 증가하더라도 DRM으로 평가한 $P_{F}^{DRM}$ 은 큰 차이가 없어 그래프가 서로 중첩되었다. 이는 $n$ =5, 7을 사용하는 것이 $n$ =3과 비교해 정확도가 향상되지 않는 다는 것을 의미하며, 따라서 5개나 7개의 적분직교점을 사용할 필요는 없을 것이다. FORM과 DRM으로 평가한 $P_{F}^{DRM}$ 은 오목함수의 경우보다 비교적 정확하였으며, FORM은 전반적으로 과소평가하나 DRM은 과대평가하였다. 테스트 결과에서 Case 3의 경우 $θ_{n o n l}$ 값이 0.26 미만, Case 4의 경우 0.16 미만일 때는 FORM을 사용하는 것이 적절함이 확인되었다. 그보다 큰 $θ_{n o n l}$ 경우 $n$ =3을 사용해야 한다.

검사테스트 결과를 종합하여 성능함수의 오목한 형태와 비선형도에 따라 적분직교점의 수를 선택하는 기준을 Table 2를 통해 제안한다. 본 연구를 통해 제안한 RBDO 기법은 확률제약조건으로 PMA, MPTP 탐색방법으로 HMV+, 탐색된 MPTP를 업데이트 하는 방법으로 DRM을 사용한다는 것은 기존 RBDO 기법과 동일하나, Fig. 4에 나타난 것처럼 DRM을 이용하여 MPTP를 업데이트 할 때 $G (X)$ 의 비선형도를 평가하고, 평가 결과에 따라 적절한 적분직교점의 개수를 선택한다는 점이 다르다.

Table 2

Range of quadrature points number selection

Quadrature points number (n)	Range of $θ_{n o n l}$ [rad]
Quadrature points number (n)	Concave	Convex
1	[0, 0.01)	[0, 0.15)
3	[0.01, 05)	[0.15
5	[0.5, 1.0)	-
7	[1.0	-

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370308/images/Figure_jcoseik_37_03_08_F4.jpg

Fig. 4.

Flow chart of developed method

4. 수치예제

이 절에서는 2차원 수치예제를 통해 제안된 비선형도 평가 기준과 이를 이용한 DRM의 적분직교점 개수 선정 기법에 대한 계산 효율성 및 정확성을 확인한다. 2차원 RBDO 예제는 식 (15)와 같이 정의된다(Zhou and Mourelatos, 2008).

(15)

minimize cost (d) = - \frac{(d_{1} + d_{2} - 10)^{2}}{30} - \frac{(d_{1} - d_{2} + 10)^{2}}{120} subject to P (G_{i} (X) > 0) \leq P_{F}^{Tar} = 5.00 %, i = 1, 2, 3 d^{L} < d < d^{U}, d \in R^{2} and X \in R^{2}

여기서, $X = [X_{1}, X_{2}]^{T}$ , $d = [d_{1}, d_{2}]^{T}$ , $d^{L} = [0, 0]^{T}$ , $d^{U} = [10, 10]^{T}$ 이며, 확률변수 X는 정규분포를 따른다고 가정한다. 또한 $β^{Tar} = - Φ^{- 1} (P_{F}^{Tar}) = 1.645$ , $μ = [5, 5]^{T}$ , $σ = [0.4, 0.4]^{T}$ 이며, 성능함수는 식 (16)과 같이 주어진다.

(16)

\begin{aligned} G_{1} (X) = & 1 - \frac{X_{1}^{2} X_{2}}{20} \\ G_{2} (X) = & - 1 + {(0.9063 X_{1} + 0.4226 X_{2} - 6)}^{2} \\ + {(0.9063 X_{1} + 0.4226 X_{2} - 6)}^{3} \\ - 0.6 {(0.9063 X_{1} + 0.4226 X_{2} - 6)}^{4} \\ - (- 0.4226 X_{1} + 0.9063 X_{2}) \\ G_{3} (X) = & 1 - \frac{80}{X_{1}^{2} + 8 X_{2} + 5} \end{aligned}

2D 수치예제의 RBDO 문제에 DRM을 활용하여 수행한 결과를 Table 3과 4에 정리하였으며, Fig. 5에는 예제의 비용함수의 등치선, 성능함수의 한계상태표면, 초기 설계점과 RBDO 최적점을 나타내었다. Table 3에는 RBDO 최적점에서 평가한 실패확률을 정리하였다. 모든 경우에 $P_{F}^{DRM}$ 은 4.9985%로 이는 PMA의 특성상 목표신뢰도지수 $β^{Tar}$ =1.645를 만족하도록 RBDO를 수행하기 때문이다. $G_{3} (X)$ 는 RBDO 최적점에서 떨어져있어 확률제약조건이 비활성이나 $P_{F}^{DRM}$ 이 4.9985%로 평가되는 것도 같은 이유에서이다. 정확도 비교를 위해 모든 경우에 대해 1억 개의 샘플과 MCS를 사용하여 $P_{F}^{MCS}$ 를 계산하였다. FORM의 경우 $G_{1} (X)$ , $G_{2} (X)$ 의 $P_{F}^{MCS}$ 는 각각 5.5726%, 2.7929%로 $P_{F}^{DRM}$ 의 4.9985%와 비교할 때 정확도가 매우 낮음을 확인할 수 있다. 반면 개발된 방법의 $G_{1} (X)$ , $G_{2} (X)$ 의 $P_{F}^{MCS}$ 는 각각 5.0042%, 4.7809%로 $P_{F}^{DRM}$ 의 4.9985%와 거의 일치한다. 따라서 개발된 방법의 정확도가 매우 높음을 확인할 수 있다.

Table 3

Probability of failure at RBDO optimum (%)

Method	$G_{1} (X)$			$G_{2} (X)$			$G_{3} (X)$
Method	$P_{F}^{DRM}$	$P_{F}^{MCS}$	Accuracy	$P_{F}^{DRM}$	$P_{F}^{MCS}$	Accuracy	$P_{F}^{DRM}$	$P_{F}^{MCS}$	Accuracy
FORM	4.9985	5.5726	89.70	4.9985	2.7929	178.97	4.9985	0	-
DRM 3 pts	4.9985	5.0011	99.95	4.9985	4.1258	121.15	4.9985	0	-
DRM 5 pts	4.9985	5.0010	99.95	4.9984	4.7869	104.42	4.9985	0	-
DRM 7 pts	4.9985	5.0016	99.94	4.9985	5.0163	99.72	4.9985	0	-
Developed	4.9985	5.0042	99.89	4.9984	4.7809	104.55	4.9985	0	-

Table 4

Results of 2D RBDO example

Method	Iteration of RBDO	Function Count				RBDO opt. $[d_{1}, d_{2}]^{T}$	Cost
Method	Iteration of RBDO	$G_{1} (X)$	$G_{2} (X)$	$G_{3} (X)$	Total	RBDO opt. $[d_{1}, d_{2}]^{T}$	Cost
FORM	9	79	98	61	238	[4.6434, 1.6460]^T	–1.8667
DRM 3 pts	9	132	150	115	397	[4.7200,1.6321]^T	–1.8710
DRM 5 pts	9	168	186	151	505	[4.7468,1.6197]^T	–1.8761
DRM 7 pts	9	203	222	187	612	[4.7555,1.6157]^T	–1.8777
Developed	9	98	166	61	325	[4.7467, 1.6197]^T	–1.8761

https://cdn.apub.kr/journalsite/sites/jcoseik/2024-037-03/N0040370308/images/Figure_jcoseik_37_03_08_F5.jpg

Fig. 5.

Cost function and limit state contours for 2D mathematical example

$G_{1} (X)$ 의 경우 3개 이상의 적분직교점을 사용한 DRM과 개발된 방법은 5.0011~5.0042%의 아주 근접한 $P_{F}^{MCS}$ 를 보이는데 이는 Fig. 3의 볼록함수 경우에서 이미 확인한 바 있다. $G_{2} (X)$ 의 경우 $n$ =7인 DRM이 5.0163%로 가장 정확하며 개발된 방법의 4.7809%는 $n$ \5인 DRM의 4.7869%와 매우 근접한 수준이다.

Table 4에는 RBDO를 수행하기 위해 식 (16)의 성능함수를 계산한 횟수가 나타나 있다. FORM은 추가적인 적분직교점을 사용하지 않기 때문에 계산횟수가 가장 적다. DRM을 사용할때 추가적분점의 수가 증가하면 계산횟수도 그에 상응하여 증가함을 볼 수 있다. 본 연구에서 개발된 방법을 보면 $G_{1} (X)$ 의 경우 98회 계산을 수행하는데, 이는 FORM의 79회와 $n$ =3인 DRM의 132회 사이에 있음을 알 수 있다. Fig. 4에서 볼 수 있듯이 $G_{1} (X)$ 는 볼록함수 이며, 이 경우 FORM 또는 $n$ =3인 DRM을 사용하도록 Table 2에서 추천하고 있으므로 이러한 결과가 도출된 것이다. 또한, 대체적으로 FORM을 사용하기 때문에 79회에 가까운 98회의 계산횟수가 도출되었다. $G_{2} (X)$ 의 설계점에 따라 함수의 형태가 볼록함수와 오목함수로 바뀌는데, RBDO 최적점에 가까워지면 오목함수가 된다. 이 경우에는 $n$ =7인 DRM까지 사용할 수 있는데, 개발된 방법의 계산횟수는 166으로 $n$ =3과 $n$ =5인 DRM의 150회와 186회 사이에 있다. $G_{3} (X)$ 의 경우는 완만한 볼록함수로 거의 선형에 가까워 개발된 방법에서는 FORM을 계속 사용하였다. 총 계산횟수를 보면 개발된 방법은 325회로 FORM의 238회보다는 많으나 $n$ =3인 DRM의 397회와 비교하면 82% 정도를 사용한 것이다. 따라서, $n$ =3인 DRM을 지속적으로 사용하는 것 보다 18% 정도 효율이 높음을 확인할 수 있다.

앞서 살펴본 Table 3, 4에서 확인할 수 있듯이 $G_{2} (X)$ 에서 개발된 방법은 $n$ =3인 DRM과 비슷한 수준의 계산횟수를 사용하지만 $n$ =5인 DRM의 정확성을 보이는 것으로 개발된 방법의 정확성과 효율성을 다시 한 번 확인할 수 있다. 앞에서 설명한 바와 같이 $G_{3} (X)$ 는 비활성 확률제약조건으로 $P_{F}^{MCS}$ 는 모두 0%이다.

5. 결 론

본 연구에서는 성능함수의 비선형도를 평가하고, 이에 따라 적절한 DRM의 적분직교점의 수를 제안하여 RBDO를 정확하고 효율적으로 수행하는 기법을 제안하였다. RBDO의 확률제약조건으로 목표신뢰도 값을 이용하여 신뢰도를 평가하는 PMA 방법을 사용하였고, HMV+를 사용하여 MPTP 탐색 효율을 높였다. 또한, DRM을 이용하여 MPTP를 업데이트 함으로써 신뢰도 평가의 정확도를 높였으며, MPTP벡터 사이각을 이용하여 비선형성을 평가하였다. 수치 테스트를 통해 비선형도에 따른 적분직교점의 수를 결정하는 기준을 제안하였고, 2차원 수치예제를 통해 개발된 방법이 DRM 및 MCS의 결과와 비교하여 정확하게 신뢰도를 평가하는 동시에 성능함수의 계산횟수를 감소시키는 것을 확인하여 계산 효율성과 정확성을 검증하였다.

본 논문의 3.2절에서 진행한 비선형도 평가는 $β^{Tar}$ =1.645으로 고정하여 진행되었다. $β^{Tar}$ 가 클수록 U-space에서 평가되는 성능함수의 비선형도는 높아질 수 있다. 따라서, 비선형도에 따른 적분직교점 선정 방법의 일반화를 위해 향후에는 더 넓은 $β^{Tar}$ 의 범위에 대한 비선형도 평가를 진행할 것이다.

References

Armen, D.K., Lin, H.Z., Hwang, S.J. (1987) Second‐Order Reliability Approximations, J. Eng. Mech., 113, pp.1208~1225.

10.1061/(ASCE)0733-9399(1987)113:8(1208)

Lee, I.J., Choi, K.K., Du, L., Gorsich, D. (2008) Inverse Analysis Method Using MPP-Based Dimension Reduction for Reliability-Based Design Optimization of Nonlinear and Multi-Dimensional Systems, Comput. Methods Appl. Mech. & Eng., 198, pp.14~27.

10.1016/j.cma.2008.03.004

Rahman, S., Xu, H. (2004) A Univariate Dimension-Reduction Method for Multi-Dimensional Integration in Stochastic Mechanics, Probab. Eng. Mech., 19, pp.393~408.

10.1016/j.probengmech.2004.04.003

Tu, J., Choi, K.K., Park, Y.H. (1999) A New Study on Reliability-Based Design Optimization, J. Mech. Des., 121, pp.557~564.

10.1115/1.2829499

Youn, B.D., Choi, K.K., Du, L. (2005) Adaptive Probability Analysis Using an Enhanced Hybrid Mean Value Method, Struct. & Multidiscip. Optim., 29 pp.134~148.

10.1007/s00158-004-0452-6

Youn, B.D., Choi, K.K., Park, Y.H. (2003) Hybrid Analysis Method for Reliability-Based Design Optimization, J. Mech. Des., 125, pp.221~232.

10.1115/1.1561042

Zhou, J., Mourelatos, Z.P. (2008) A Sequential Algorithm for Possibility-Based Design Optimization, J. Mech. Des., 130, p.011001

10.1115/1.2803250

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

A Technique for Selecting Quadrature Points for Dimension Reduction Method to Improve Efficiency in Reliability-based Design Optimization

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Fig. 1.

U-space and rotated standard normal V-space

(11)

(12)

(13)

(14)

Table 1

Nonlinearity evaluation examples

Fig. 2.

Limit state of G(X) when p=15

Fig. 3.

Nonlinearity evaluation results of concave performance function

Table 2

Range of quadrature points number selection

Fig. 4.

Flow chart of developed method

(15)

(16)

Table 3

Probability of failure at RBDO optimum (%)

Table 4

Results of 2D RBDO example

Fig. 5.

Cost function and limit state contours for 2D mathematical example

References

Limit state of G(X) when $p$ =15