1. 서 론

최근 국내외에서 중대형 지진이 자주 발생함에 따라 사회기반구조물의 내진성능 확보에 관한 관심이 높아지고 있다. 최근에는 국내 모든 교량 구조물에 대해 내진설계가 적용되는 등 토목구조물의 내진설계 기준이 강화되고 있으며, 내진설계가 되지 않은 국내 노후 사회기반구조물을 대상으로 부재 및 연결부의 내진 보강이 이루어지고 있다. 그러나 이러한 노력에도 불구하고 아직 적지 않은 수의 사회기반구조물이 충분한 내진성능을 확보하지 못한 상태이며, 이에 대한 내진성능 향상 조치를 계속할 필요가 있다(MOIS, 2023).

교량에는 받침이나 신축이음장치와 같이 외부 요인에 의한 변형을 흡수하는 활동관절시스템이 있다. 이 중 받침은 상부구조와 하부구조 사이에 위치하며 상부 하중을 교량 하부구조로 전달하는 역할을 한다. 우리나라는 교량의 지진 피해를 예방하기 위하여 내진성능이 우수한 받침을 사용하거나 면진받침, 댐퍼, 충격분산장치와 같은 별도의 내진장치를 연결해 보강하고 있다. 그러나 경주지진과 포항지진의 경우에 설계지진보다 규모가 작음에도 불구하고 교량받침 등의 연결부에 많은 손상이 발생하였다. 따라서 지진 시 교량의 구조적 안정성을 확보하기 위해서는 지진에 취약한 교량받침의 정확한 상태평가가 필요하다고 할 수 있다. 이를 토대로 받침의 내진성능을 정량적으로 분석해야 하며 교량의 중요성, 보강 비용, 보강 효율성 등을 고려해 적합한 내진성능 향상 기법을 적용해야 한다(Ahn et al., 2021; An and Lee, 2020; Nielson and DesRoches, 2007). 교량받침은 오존, 열, 빛, 반복하중과 같은 다양한 요인에 의해 점진적으로 열화가 발생하며, 받침의 노후화 및 결함으로 인해 장기적으로 교량 시스템의 성능에 문제가 발생할 수 있다(Matsuzaki, 2022). 또한 받침이 노후화되면 받침의 초기 성능이 저하되어 설계지진보다 작은 규모의 지진에 의해 피해를 입거나 상부 거더가 탈락할 수 있다(Kurino et al., 2021).

운용 중인 교량받침의 내진성능을 정량적으로 평가하기 위한 연구가 국내외에서 활발히 수행되었다(Kong et al., 2022; Zhong et al., 2022). 그런데 받침 자체의 내진성능 평가와는 달리 받침의 노후 상태를 고려한 교량 시스템의 내진성능에 관한 연구 사례는 많지 않다. 그동안 노후 교량의 내진성능 평가 시 재료의 역학적 성능 저하를 주로 고려했는데 이것만으로는 연결부를 중심으로 한 교량의 지진 취약성을 제대로 반영할 수 없다. 이를 위해서는 받침과 같은 교량 연결부의 수평강성 저하 효과를 고려해 노후 교량의 내진성능을 진단할 필요가 있다(Ghosh and Padgett, 2011). 따라서 이 연구는 노후 받침을 포함한 교량의 지진해석을 수행하고 받침의 상태에 따른 교량 시스템의 내진성능을 평가하였다.

이 논문은 도로교설계기준(한계상태설계법)(MOLIT, 2016)의 설계응답스펙트럼에 부합하는 인공지진파를 활용해 3경간 연속 콘크리트거더교의 지진응답을 평가한 결과를 제시한다. 교량의 포트받침을 고정단 및 가동단의 수평강성을 반영해 탄성 스프링으로 모델링하였고, 받침 강성의 변화에 따른 교량 상부 및 받침의 지진응답을 계산하여 지진 발생 시 받침의 노후화가 교량의 동적 거동에 미치는 영향을 분석하였다.

2. 연속 거더교의 유한요소모델링

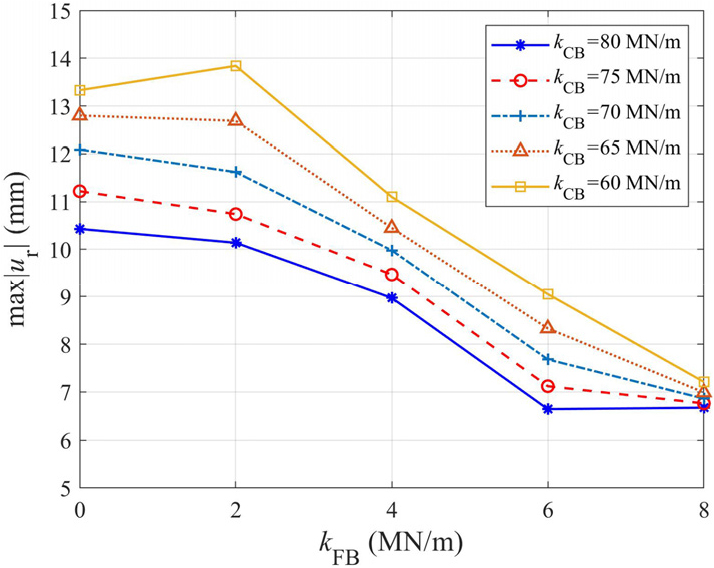
2.1 유한요소모델

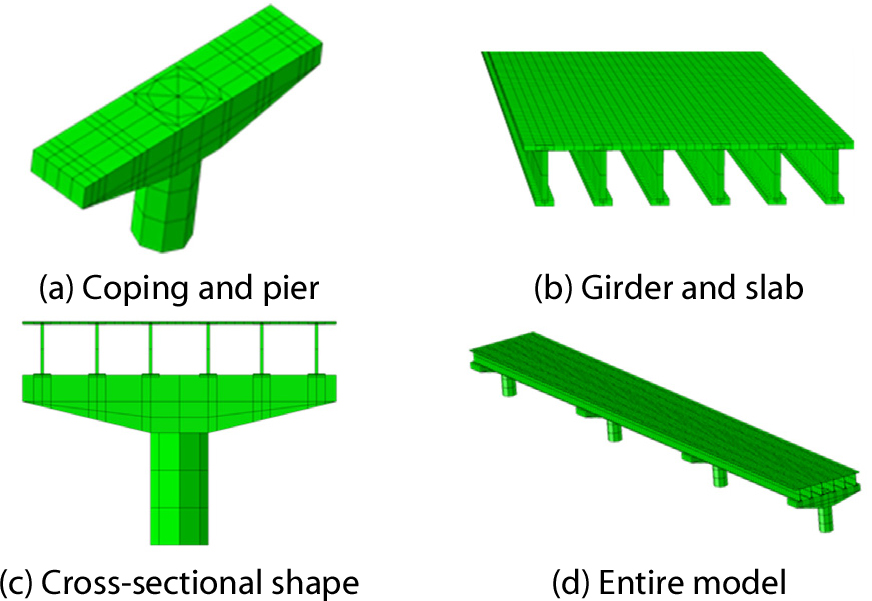
받침의 상태에 따른 교량의 내진성능 평가를 위하여 경상남도 합천군 소재 국도 24호선에 위치한 3경간 연속 프리스트레스트 콘크리트 거더교를 대상으로 유한요소해석 모델을 구성하였다. Fig. 1에 제시된 전체 교량 구간 중 P5, P6, P7, P8 교각을 포함한 3경간 구간을 대상으로 유한요소해석 프로그램인 ABAQUS(Dassault Systems, 2018)를 사용해 상부 및 하부구조를 모델링하였다. 교량의 전체 길이는 390m이고 해석 대상 3경간 구간의 길이는 90m이다. 실제 교량은 완만한 곡선교이나 구조해석의 편의를 위해 이를 직선교로 모델링하였다. Fig. 2는 이 교량의 주요 부분에 대한 유한요소모델을 나타낸다. 상부구조의 철근콘크리트 슬래브 및 거더는 4절점 쉘 요소(S4R)로 모델링하였고 철근콘크리트 교각은 6절점 솔리드 요소(C3D6)로 모델링하였다. 교각의 코핑부는 6절점 솔리드요소와 8절점 솔리드 요소(C3D8R)를 병용하여 모델링하였다.

Fig. 1.

Schematic of a girder bridge and a three-span continuous segment for investigation

Fig. 2.

Finite element model of a 3-span continuous girder bridge

2.2 고정단 및 가동단 포트받침

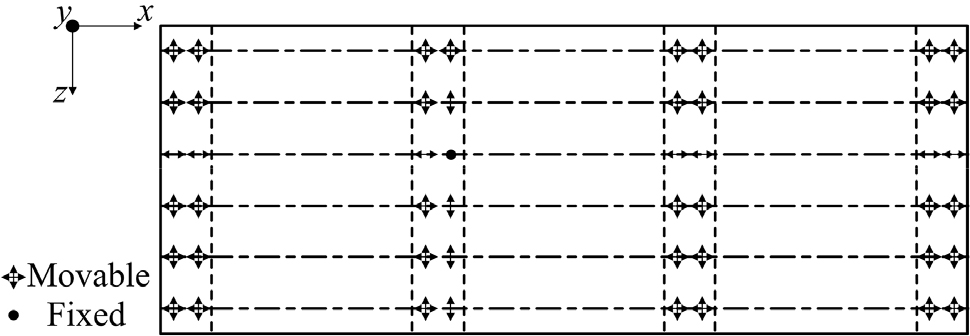
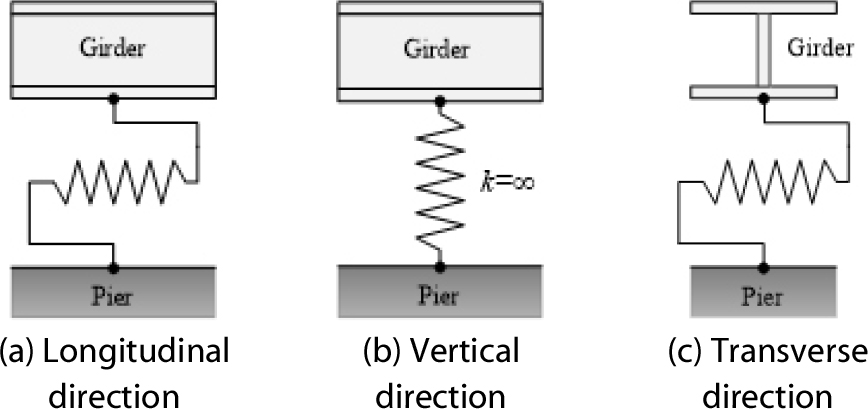
대상 교량의 받침이 포트받침임을 고려하여 상부구조와 하부구조의 연결부를 수평 및 수직 강성이 부여된 탄성 스프링으로 모델링하였다. 받침의 노후화가 없는 상태에서 고정단의 스프링 강성은 80MN/m로 설정하였고(Sofi and Steelman, 2017) 가동단의 스프링 강성은 0MN/m로 설정하였다. 연직 방향으로의 받침 강성은 구조해석의 오류가 발생하지 않는 범위에서 매우 큰 값으로 설정하였다(kv = 10⁹MN/m). Fig. 3은 대상 교량의 설계도에 제시된 받침 상세를 나타낸다. 코핑에 표시된 각 화살표는 받침 위치에서 상부구조의 이동 가능 방향을 나타낸다. 교축 방향과 교축 직각 방향 모두에 고정단과 가동단이 설치되어 있다. 특히 왼쪽에서 두 번째 교각의 코핑에는 6개의 교축 방향 고정단이 설치되어 있으며, 모든 교각에는 교축 직각 방향으로의 고정단이 두 개씩 존재한다. Fig. 4는 포트받침의 교축 방향, 교축 직각 방향, 연직 방향의 스프링 모델링을 나타내는 모식도이다.

Fig. 3.

Bearings of the 3-span continuous girder bridge

Fig. 4.

Schematics of the pot bearing spring model for the girder bridge

2.3 고유진동수 및 고유모드

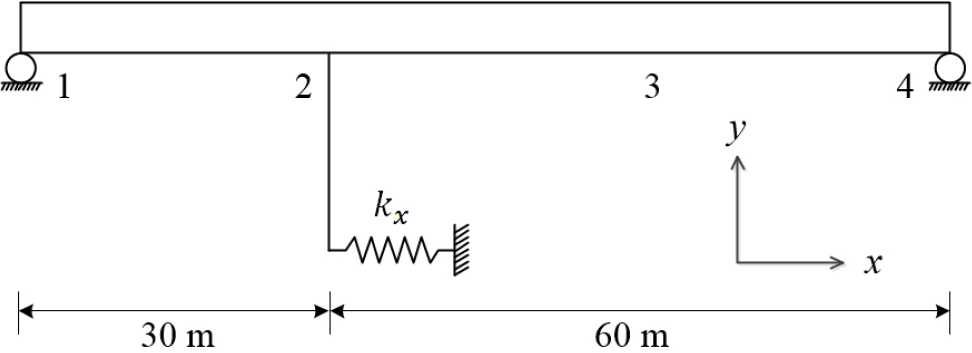
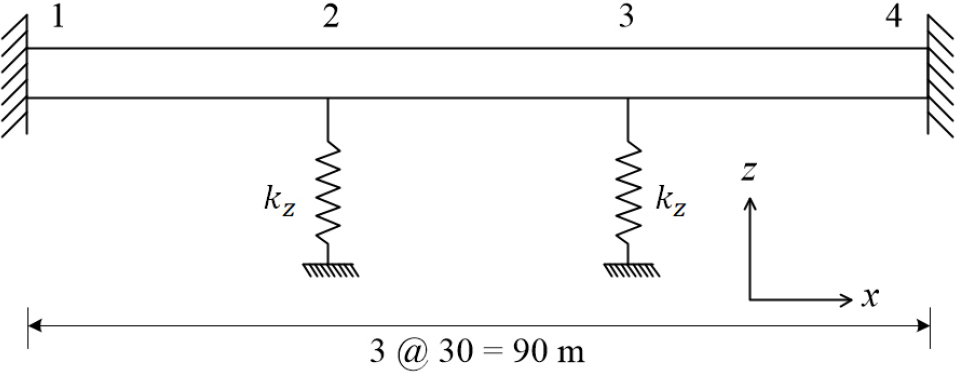
3경간 연속 거더교 모델의 타당성을 평가하기 위하여 유한요소해석을 통해 계산한 고유진동수를 설계도서에 제시된 고유진동수와 비교하였다. 설계도서는 고유진동수 계산을 위하여 전체 교량 구간 중 고정단 12번 교각의 교축방향 강성에 해당하는 스프링을 Fig. 5의 2번 위치에 배치하였다. 이 연구에서는 설계도서와 동일한 받침 조건을 설정하기 위하여 교각과 코핑을 없애고 Fig. 5와 같이 고정단 교각인 2번 위치에 kx = 19,752t/m의 종방향 스프링을 배치하였다. 이 강성은 12번 교각의 교축방향 강성으로서 고정단 교각 P5의 교축방향 강성과는 다르지만 설계도서와 동일한 조건으로 고유진동수를 계산하기 위해 그렇게 설정하였다. 슬래브 양단을 포함한 나머지 교각 위치에는 Fig. 3의 받침 조건을 고려하여 횡방향 및 연직방향 변위 자유도를 구속하였다. 횡방향 고유진동수를 계산하는 경우에는 Fig. 6와 같이 2번과 3번 받침 위치에 교각의 수평강성 스프링을 배치하였다. 이때 교축 직각방향으로의 스프링 강성 kz는 19.752t/m이며 슬래브 양단은 교축, 교축 직각, 연직방향으로 모두 구속하였다.

Fig. 5.

Longitudinal support conditions for calculating modal frequencies

Fig. 6.

Horizontal support conditions for calculating modal frequencies

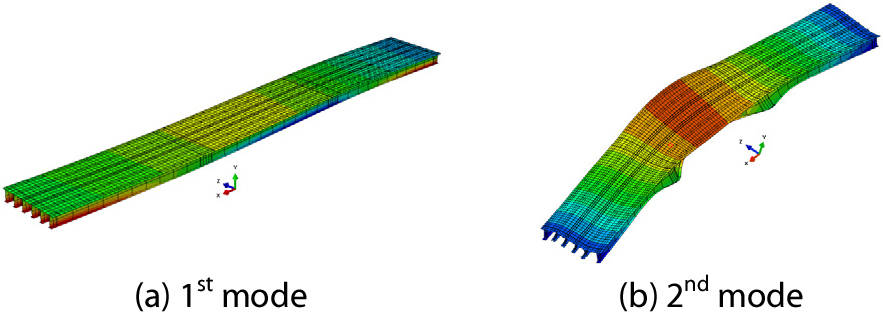
설계 고유진동수와 유한요소해석으로부터 구한 고유진동수를 Table 1에 제시하였다. 이 3경간 연속 거더교의 설계 고유진동수는 종방향으로 1.815Hz이고 횡방향으로 3.584Hz이다. 유한요소법으로 구한 고유진동수는 종방향으로 1.771Hz이고 횡방향으로 3.592Hz로서, 설계값과의 오차는 종방향과 횡방향이 각각 2.42%, 0.22%이다. 고유진동수 수치해의 설계값에 대한 오차가 양방향 모두 3% 미만으로서, 이로부터 3경간 연속 거더교의 유한요소모델이 적절히 구성되었음을 알 수 있다. Fig. 7은 대상 교량의 종방향 및 횡방향 모드형상을 나타내며, 1차 모드는 종방향 병진모드이고 2차 모드는 횡방향 하프사인 모드임을 알 수 있다.

Fig. 7.

Mode Shapes obtained using the support conditions in the design book

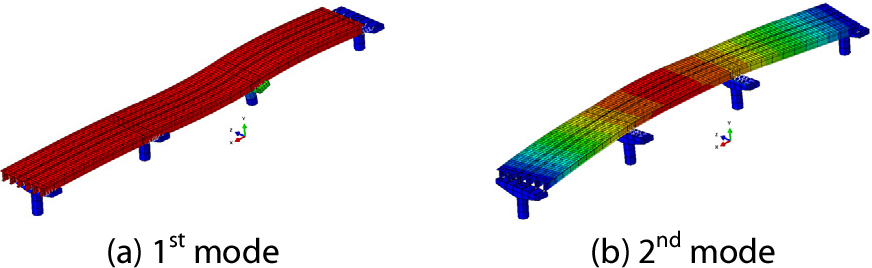
설계도서에서 교각의 수평강성 계산 시 고려한 교각 높이는 12번 교각의 높이로서 이 연구의 대상인 3경간 구간(P5~P8)의 교각 높이와는 다르다. 따라서 이 연구에서는 5번부터 8번 교각의 실제 높이를 고려해 고유진동수 해석을 추가로 수행하였다. Fig. 8은 교각의 실제 높이를 반영한 3경간 연속 거더교의 종방향 및 횡방향 모드형상을 나타낸다. 1차모드는 종방향 병진모드로서 고유진동수는 1.785Hz이며, 2차모드는 횡방향 하프사인 모드로서 고유진동수는 2.330Hz이다.

Fig. 8.

Mode shapes obtained by reflecting detailed modeling of piers and supports

3. 인공지진파에 대한 3경간 연속 거더교의 지진응답

3.1 인공지진파

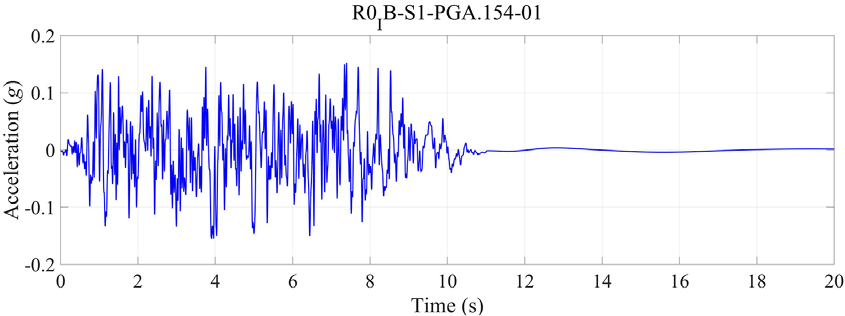
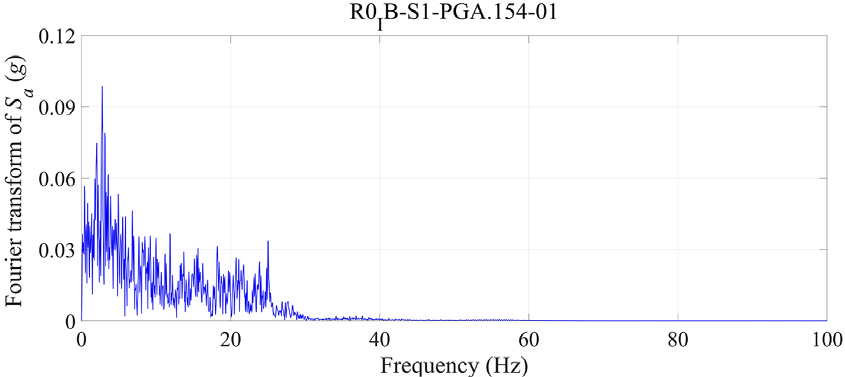
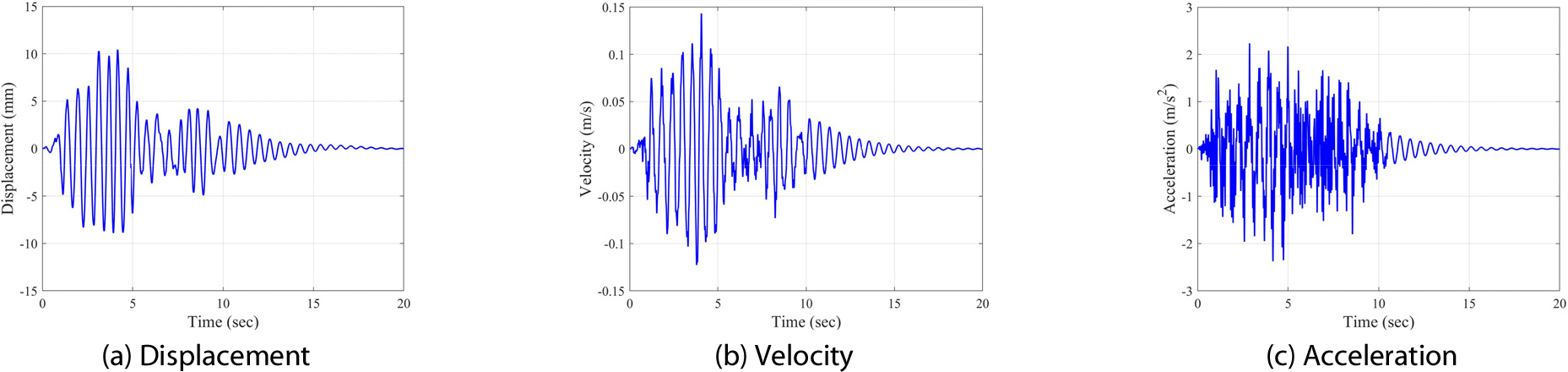
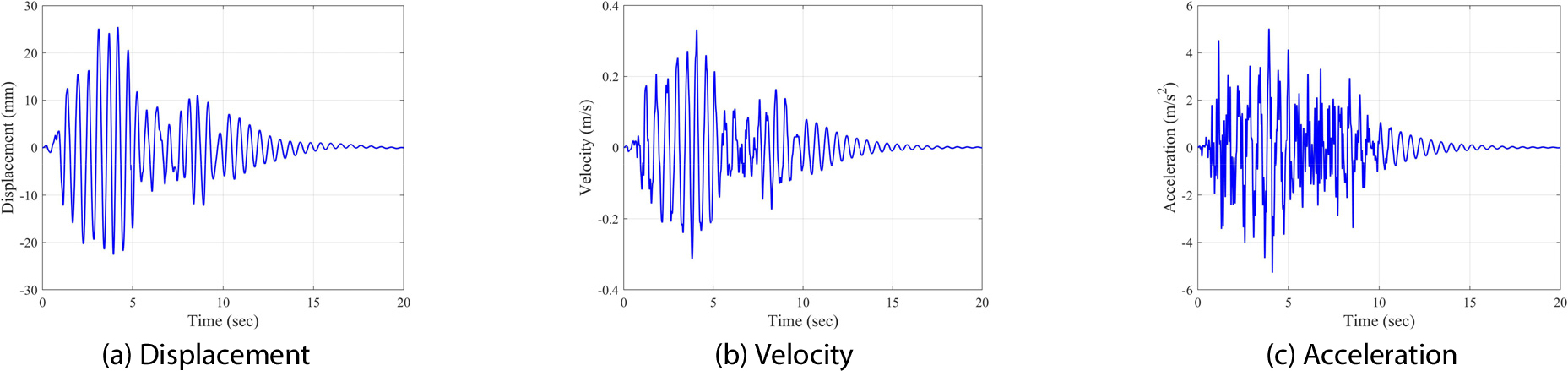
받침 상태에 따른 3경간 연속 거더교의 지진응답을 분석하기 위하여 도로교설계기준(한계상태설계법) 내진설계 규정의 설계응답스펙트럼에 부합하는 인공지진파를 이용하였다. 지속시간이 20초인 인공지진파 7개를 고려하였으며, 이 중 하나의 가속도 시간이력과 주파수 스펙트럼을 Fig. 9과 10에 나타내었다.

Fig. 9.

Acceleration time history of an artificial ground motion R01B-S1-PGA.154-01

Fig. 10.

Frequency spectrum of an artificial ground motion R01B-S1-PGA.154-01

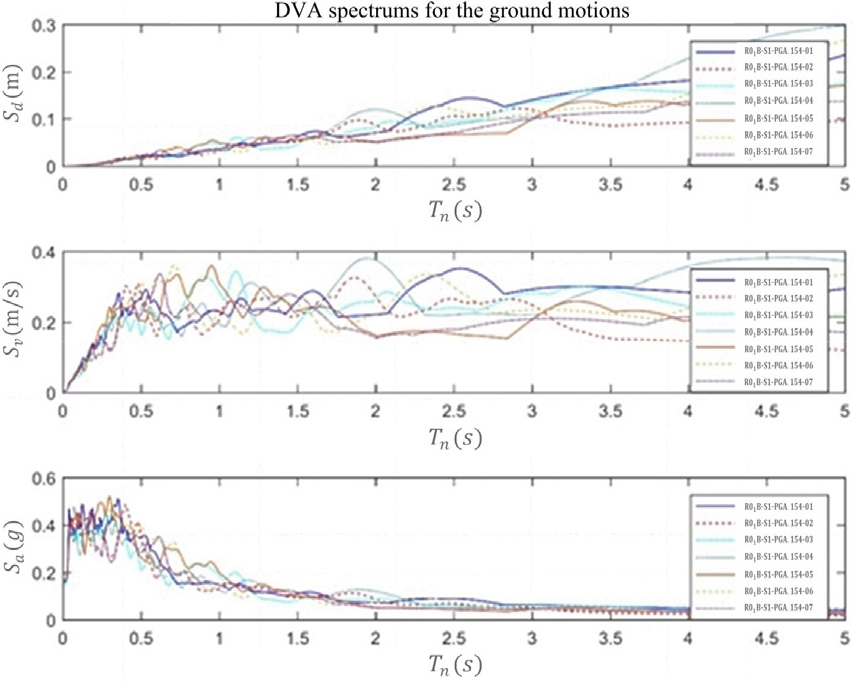
연구 대상 교량은 내진I등급 교량으로서 설계지진의 평균 재현주기가 1000년이다. 지반조건은 S1으로 가정하였다. 이 교량은 경남 합천군에 위치하므로 지진구역계수가 0.11이고 위험도계수가 1.4로서 가속도계수는 이들을 곱한 0.154g이다. 따라서 교량의 지진응답 계산 시 PGA가 0.154g인 인공지진파를 사용하였다. Fig. 11은 7개의 인공지진파 각각에 대한 변위, 속도, 가속도 응답스펙트럼을 나타낸다.

Fig. 11.

Displacement, velocity, and acceleration response spectra obtained using 7 artificial ground motions

3.2 3경간 연속 거더교의 지진응답

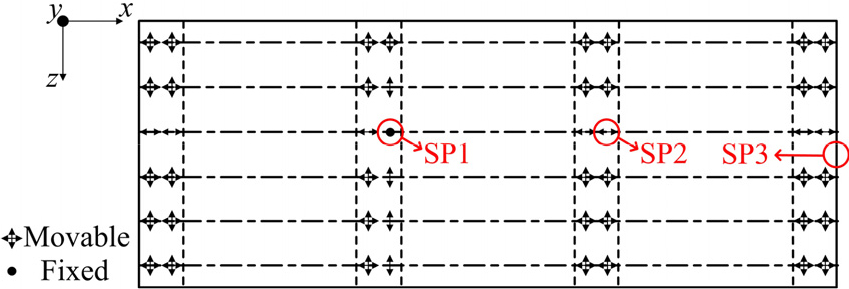
Fig. 9 및 10의 지진파에 대해 3경간 연속 거더교의 선형탄성 지진해석을 수행하였다. 받침의 노후화에 따라 고정단 및 가동단 받침과 상부 슬래브의 지진응답이 어떻게 변하는지 분석하기 위하여 우선 받침의 노후화를 고려하지 않은 경우의 변위, 속도, 가속도 응답을 제시한다. Fig. 12는 3경간 연속 거더교의 지진응답 sampling point인 고정단 SP1, 가동단 SP2, 슬래브 SP3의 위치를 나타낸다.

Fig. 12.

Response sampling points SP1, SP2, and SP3

인공지진파에 대한 고정단 SP1의 상대변위, 상대속도, 상대가속도 시간이력을 Fig. 13(a)~(c)에 나타내었다. 고정단에서 발생하는 절대최대 상대변위(max|ur|)는 0.0104m이며, 이때 고정단의 최대 수평력은 832kN(83.2tonf)으로 계산되었다. 지진가속도의 크기가 가장 큰 3~4초 구간에서 지진응답이 가장 크게 발생하였다. 인공지진파에 대한 가동단 SP2의 지진응답은 Fig. 14(a)~(c)와 같다. 노후되지 않은 가동단의 수평강성은 0이라고 가정하였으며, 이 경우 가동단의 상대변위, 상대속도, 상대가속도 응답은 고정단의 지진응답에 비해 약 2.5배 이상 크게 발생하였다.

Fig. 13.

Seismic responses at sampling point 1 (SP1) of a clamped bearing (Relative response are presented.)

Fig. 14.

Seismic responses at sampling point 2 (SP2) of a free bearing (Relative response are presented.)

지진 발생 시 인접 슬래브 간의 충돌, 신축이음부의 파괴, 낙교 등의 가능성을 평가하기 위하여 슬래브의 수평 변위 등의 조사가 필요하다. Fig. 15(a)~(c)는 슬래브 상단의 SP3에서 구한 변위, 속도, 가속도의 시간이력을 나타낸다.

Fig. 15.

Seismic responses at sampling point 3 (SP3) on the slab

4. 받침의 노후화를 고려한 교량의 지진해석

4.1 받침의 노후화를 고려한 강성 변화와 지진응답

고정단 받침의 수평강성 저하와 가동단 받침의 마찰저항 증가로 나누어 받침의 노후화에 따른 거더교의 지진응답 변화를 조사하였다. 유한요소모델의 고정단 수평강성 kCB와 가동단 수평강성 kFB를 변화시켜 지진해석을 수행하였다.

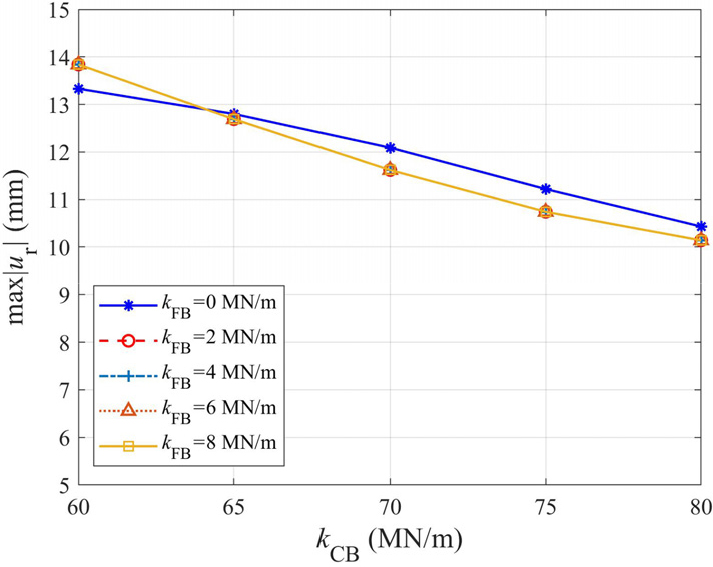
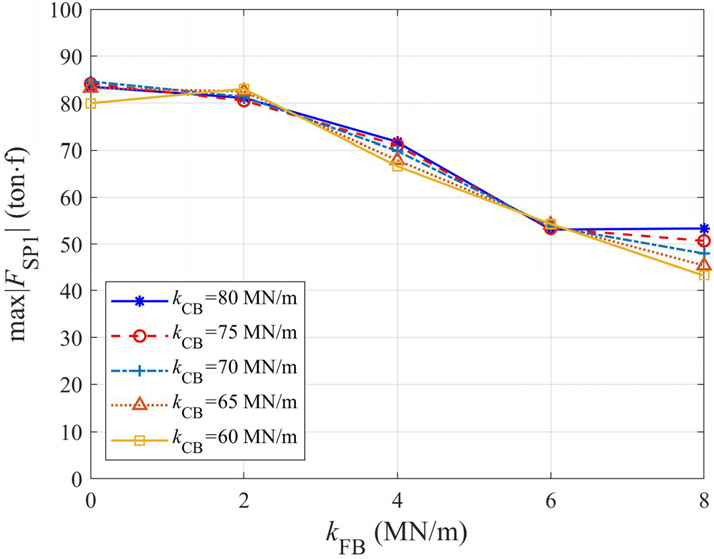
고정단 받침의 노후화를 반영하기 위하여 고정단 수평강성 kCB를 80MN/m에서 60MN/m까지 5MN/m씩 감소시켰다. Table 2는 kCB의 감소에 따른 교량의 종방향 및 횡방향 고유진동수와 인공지진파에 대한 고정단의 절대최대 상대변위 및 최대 수평력을 나타낸다. 고정단의 수평강성이 감소할수록 종방향과 횡방향의 고유진동수가 모두 감소하였다. 또한 절대최대 상대변위가 증가하였고 이는 고정단 받침이 노후화되면 교량 시스템이 초기 상태보다 유연해짐을 의미한다. 이때 고정단에 발생하는 최대 수평력에는 큰 변화가 없다.

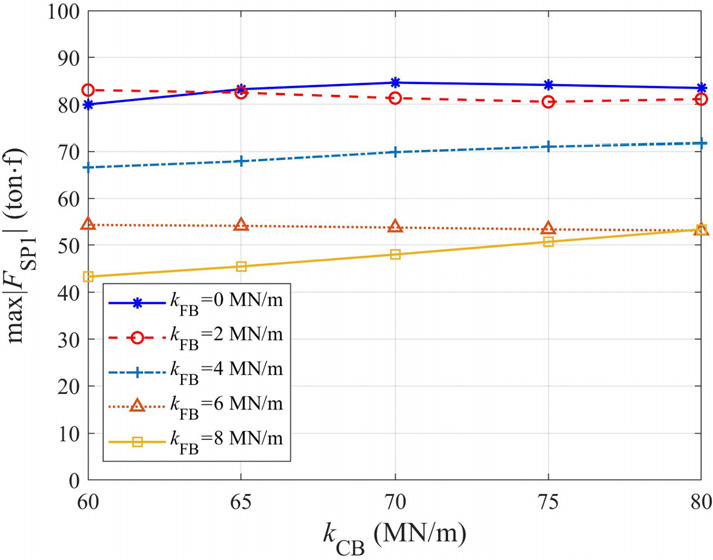
가동단 받침의 노후화로 인한 마찰저항의 증가를 나타내기 위해 가동단 수평강성 kFB를 0MN/m에서 8MN/m까지 2MN/m씩 증가시켰다. Table 3는 kFB의 증가에 따른 교량의 종방향 및 횡방향 고유진동수와 인공지진파에 대한 고정단 받침의 절대최대 수평력, 슬래브 상단의 절대최대 변위, 최대 휨인장응력을 나타낸다. 가동단 수평강성 kFB가 증가함에 따라 고정단에서의 수평력이 감소하였다. 이는 가동단 받침이 노후화되어 마찰저항이 증가하면 지진하중으로 인한 수평력을 가동단 받침이 일부 분담하고 고정단 받침의 수평력이 감소함을 의미한다. 또한 고유진동수가 증가하고 고유주기는 감소하여 이에 상응하는 변위 응답이 감소하였으며, 슬래브 상단의 절대최대 변위가 다소 감소하였다. 이러한 상황에서 가동단 SP2의 바로 위 거더 단면에 추가의 휨인장응력이 발생한다.

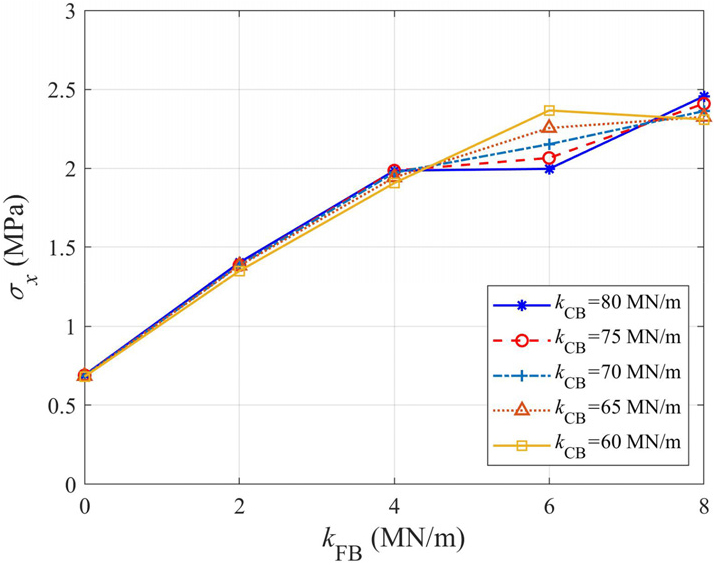
가동단 수평강성 kFB가 0이면 Fig. 9의 지진하중에 의해 가동단 위 거더 단면에는 0.691MPa의 추가 휨인장응력이 발생한다. 한편 kFB가 8MN/m로 증가하면 가동단 위 거더 단면에 2.456MPa의 추가 휨인장응력이 발생하였다. 받침의 노후화를 고려해 가동단 수평강성을 0MN/m에서 8MN/m까지 증가시키면 Fig. 9의 지진으로 인해 가동단 SP2의 상부 거더에 추가 휨인장응력이 350% 정도 증가함을 알 수 있다. 이는 가동단 받침이 지진 수평력을 분담하면서 상부 거더에 축구속 효과가 발생하고 이로 인해 가동단 위 거더 단면의 모멘트가 증가하기 때문인 것으로 평가된다. 그리고 이는 가동단 받침이 노후화되면 지진 발생 시 가동단 상부 거더에 휨인장응력이 무시할 수 없을 만큼 더해질 수 있음을 의미한다.

4.2 교량받침의 노후화 영향 분석

4.2.1 고정단 수평강성 kCB의 변화에 따른 지진응답

고정단 수평강성 kCB가 감소하면 고정단 받침의 절대최대 상대변위는 Fig. 16에서와 같이 증가하는 경향을 보인다. 이는 고정단 받침을 지지하는 모르타르의 균열과 앵커볼트의 부착력 감소 등 고정단의 노후화가 발생하면 지진 발생 시 고정단 받침의 수평강성 저하 효과로 인해 상대변위가 증가함을 의미한다. Fig. 17은 고정단 받침의 강성 변화에 따른 고정단의 수평 지진력을 나타낸다. kCB가 변하더라도 고정단 받침에 전달되는 수평 지진력에는 큰 변화가 없음을 알 수 있다. 그러나 고정단 받침의 수평 지진력이 비슷해도 kCB가 감소하면 해당 받침의 상대변위는 증가할 수 있다.

Fig. 16.

Absolute maximum relative displacement at the clamped bearing (SP1) to the change in kCB

Fig. 17.

Absolute maximum shear force at the clamped bearing (SP1) to the change in kCB

4.2.2 가동단 수평강성 kFB의 변화에 따른 지진응답

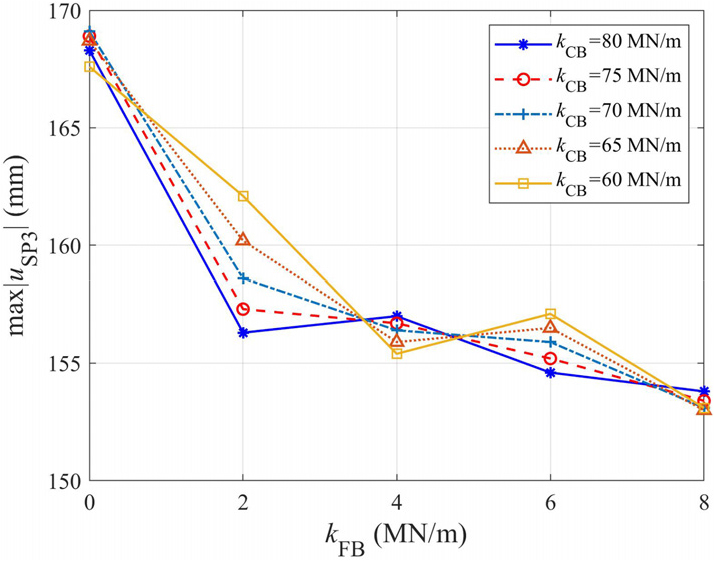
Fig. 18 및 19은 가동단 수평강성 kFB가 증가하면 고정단 받침의 절대최대 상대변위와 절대최대 수평력이 감소하는 경향이 있음을 보여준다. 이는 가동단의 노후화로 인해 마찰 강성이 증가할 경우, 지진 발생 시 가동단이 고정단 받침의 수평력을 일부 분담하게 되고 이에 따라 고정단 받침에 전달되는 수평 지진력이 다소 감소함을 의미한다. Fig. 20은 kFB의 증가에 따라 슬래브 상단 SP3의 절대최대 변위가 감소하는 경향이 있음을 보여준다. kCB = 80MN/m인 경우, SP3의 절대최대 변위는 가동단 수평강성 kFB가 0에서 80MN/m까지 증가할 때 약 8% 감소하였으며, 이는 가동단 수평강성 증가 시 고정단 받침의 상대변위가 감소하기 때문으로 평가된다. 그러나 가동단의 노후화로 인한 수평강성 증가는 거더의 휨인장응력 증가를 야기할 수 있다. Fig. 21은 kFB의 증가에 따라 가동단 위의 거더 단면에 추가되는 휨인장응력을 나타낸다. 가동단 수평강성 kFB가 증가함에 따라 가동단 바로 위 거더 단면에 추가로 발생하는 휨인장응력이 kFB = 0인 경우에 비해 3.5배 이상 증가할 수 있음을 알 수 있다.

Fig. 18.

Absolute maximum relative displacement at the clamped bearing (SP1) to the change in kFB

Fig. 19.

Absolute maximum shear force at the clamped bearing (SP1) to the change in kFB

Fig. 20.

Absolute maximum displacement at SP3 on the slab to the change in kFB

Fig. 21.

Tensile bending stress added due to the seismic load to the girder section immediately above the free bearing SP2 with respect to the change in kFB

5. 결 론

이 연구는 도로교설계기준(한계상태설계법)의 설계응답스펙트럼에 부합하는 인공지진파를 사용하여 받침의 노후화에 따른 3경간 프리스트레스트 콘크리트 거더교의 지진응답 변화를 분석하였다. 교량받침의 노후화는 고정단 받침의 앵커볼트 주변부 균열에 따른 수평강성 감소와 가동단 받침의 마찰저항 증가에 따른 가동단 수평강성 증가로 모델링하였다. 이에 따른 거더교의 지진응답 결과는 다음과 같다.

1) 받침의 노후화로 인해 고정단 받침의 수평강성이 감소할 경우, 지진으로 인한 고정단 받침의 절대최대 상대변위는 증가하는 경향을 보인다. 이는 받침을 지지하는 모르타르의 균열과 앵커 볼트의 탈락 가능성이 커짐을 의미한다.

2) 받침의 노후화로 인해 가동단 받침의 수평강성이 증가할 경우, 지진으로 인한 고정단 받침의 절대최대 상대변위와 절대최대 수평 지진력이 다소 감소한다. 이러한 결과는 가동단이 노후화되어 마찰저항이 증가하면 지진 시 가동단 받침이 고정단의 수평력을 일부 분담하고 이에 따라 고정단에 전달되는 수평 지진력이 다소 감소함을 의미한다.

3) 가동단 받침의 노후화에 따라 수평강성이 증가하는 경우, 지진 시 슬래브 상단의 절대최대 변위가 감소하였다. 이는 가동단의 수평강성이 증가함에 따라 고정단 받침의 상대변위가 감소하기 때문으로 평가된다.

4) 가동단 받침의 노후화로 인해 가동단의 마찰저항이 증가할 경우, 지진 발생 시 가동단 바로 위 거더 단면에 추가의 휨인장응력이 발생할 수 있다. 받침의 노후화로 인해 발생하는 이러한 구조계의 변화는 지진 시 교량에 예기치 못한 손상을 유발할 수 있다.