1. 서 론
2. 증기운 폭발을 받는 골조와 단일 부재의 해석 모델
2.1 골조와 단일 부재의 해석 모델
2.2 비선형 재료 모델
2.3 증기운 폭발하중
3. 증기운 폭발을 받는 골조와 단일부재의 동적 거동
3.1 모드해석
3.2 이격거리에 따른 골조와 단일 부재의 동적 거동
3.2 연성도에 따른 골조와 단일 부재의 거동
3.3 보-기둥 강성비에 따른 골조와 단일 부재의 거동
4. 결 론
1. 서 론
플랜트 시설물은 일반 건축물과 달리 유류, 가스 등의 유해 물질을 대량으로 포함하고 있어 화재, 폭발, 금전적 손실을 초래할 수 있다(Zerrouki and Smadi, 2017). 세계 위험 보고서 MARSH(2022)에 따르면 탄화수소 추출 및 가공을 수행하는 플랜트 시설물에서 경제적 손실을 유발하는 위험 요소 상위 100건 중 폭발 사고가 45건으로 가장 높은 비율을 차지한다. 플랜트 시설물에서 폭발 사고가 발생할 경우, 폭발에 노출된 구조물 뿐만 아니라 손상된 구조물의 파편으로 인하여 인접한 건물에 막대한 재산과 대량의 인명 피해를 초래할 수 있다(CCPS, 2012). 이에 따라 플랜트 시설물의 성격을 반영한 내폭설계 체계의 개발과 개선이 필요하다.
폭발의 영향성이 증가함에 따라 UFC 3-340-02(2008), ASCE(2010, 2011), Dusenberry(2010)의 문헌에서 플랜트 시설물의 내폭설계를 위한 가이드라인을 제시한다. 폭발하중을 받는 구조물은 단일 부재의 거동에 지배되기 때문에 전체 골조가 아닌 폭발하중을 받는 부재에 대해서만 해석을 수행하고 있는 형태이며, 단일 부재는 Biggs(1964)가 제안한 변환계수를 통해 단자유도 시스템(SDOF)으로 이상화하여 해석할 수 있다. 단자유도 시스템은 실용적인 용도에 적합한 근사치를 단기간에 얻기 위한 목적으로 활용된다.
보다 정확한 해석을 위한 연구로 Elvira 등(2006)은 유한요소해석 프로그램 DIANA, Jayasooriya 등(2011)은 LS-DYNA를 이용하여 철근 콘크리트 골조에 대한 폭발하중의 영향성을 분석하였다. Zhang 등(2017)은 등가 단자유도 해석법을 활용하여 CFST 기둥의 동적 거동을 분석하였으며, 이는 LS-DYNA의 해석 결과와 유사한 값을 나타내었다. Astarlioglu 등(2013)은 수정된 등가 단자유도 해석법을 통하여 철근 콘크리트 기둥의 거동을 분석하였으며 유한요소해석 프로그램인 ABAQUS의 결과와 1~17%의 차이를 보였다. 이와 같이 폭발하중을 받는 골조 및 단일 부재에 대하여 단자유도 방법과 유한요소 방법의 유사성에 관한 연구는 다수 진행되었다. 하지만 폭발하중을 받는 플랜트 시설물의 골조 모델과 단일 부재 모델과의 구조 거동에 대한 비교 연구는 이루어진 바가 거의 없다.
따라서 본 연구에서는 플랜트 시설물의 특성을 반영하여 폭발하중을 받는 골조와 단일 부재에 대하여 비선형 동적 해석을 수행하였다. 상용프로그램 MIDAS GEN을 활용하였으며 골조를 단일 부재로 단순화하여 해석할 수 있는 조건과 범위에 대하여 비교 및 분석하였다. 연구의 결과는 향후 내폭설계 가이드라인으로 활용될 수 있으며, 해석이 단순화됨에 따라 실무에서도 활용 가능할 것으로 판단된다.
2. 증기운 폭발을 받는 골조와 단일 부재의 해석 모델
2.1 골조와 단일 부재의 해석 모델
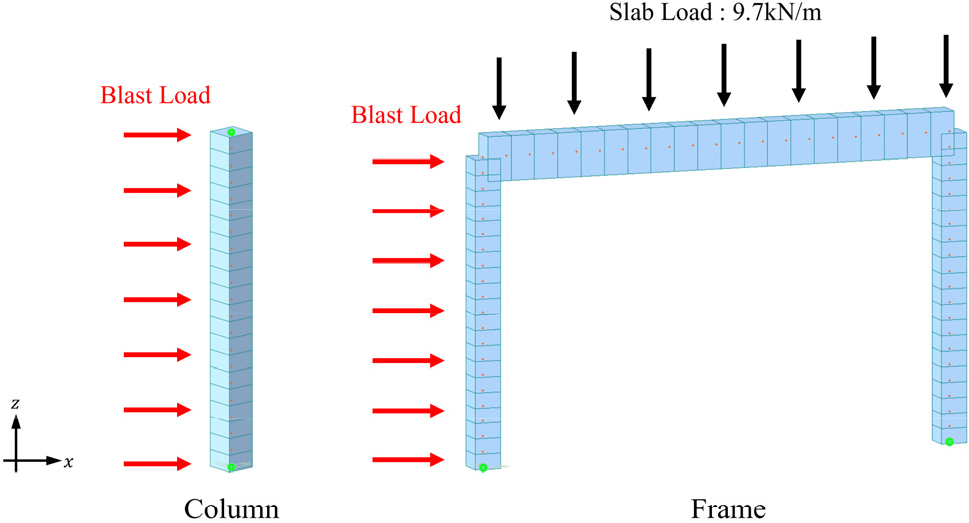
플랜트 시설물은 크게 거주자용 건물, 비거주자용 건물로 분류되며 공통적으로 배치되는 거주자용 건물은 제어실, 정비실, 관리실, 창고 등으로 구성된다. 이에 따라 골조 및 단일 부재 해석 모델을 구성하였으며 연성도, 경계조건, 보-기둥 강성비를 매개변수로 설정하여 비선형 동적 해석을 수행하였다.
본 연구의 기본 해석 모델은 거주자용 건물 중 관리실의 규모와 구조 부재의 평균 데이터를 사용하여 해석 모델을 구성하였다. 기둥의 단면은 0.3m × 0.3m, 높이는 3.5m이며, 보의 단면은 0.3m × 0.5m, 길이는 5.5m이다. 콘트리트와 철근의 재료적 특성은 석유화학 플랜트에서 일반적으로 사용되는 값으로, ASCE(2010)에서는 콘크리트 압축강도 27.6MPa, 철근 항복강도 414MPa을 제시하고 있다.
골조와 단일 부재의 경계조건, 골조의 횡변위를 고려하여 Table 1과 같이 7개의 해석 모델을 구성하였으며, 골조 모델은 슬래브의 자중을 고려한다. FEMA 273(1997)을 따라 기둥과 보의 유효 강성 또한 고려하였다. 플랜트 시설물은 일반적으로 단층 또는 저층으로 구성되므로 본 연구에서는 1층 골조에 대한 해석을 중점적으로 수행한다. 2-3층 골조의 동적 거동에 관해서는 추후 연구로 진행될 예정이다. Fixed - Free의 단부조건을 갖는 단일 부재는 중력하중과 폭발하중을 받는 기둥 부재의 구속조건으로 거의 사용되지 않으므로 본 연구에서는 제외하였다.
Table 1.
Analysis model of frame and single member
2.2 비선형 재료 모델
다양한 수치해석 방법 중 뉴마크 평균 가속도법을 적용하였다. 이 방법은 비선형 시스템 문제에 효과적으로 적용 가능하며, 안정적인 적분으로 대부분의 물리적 문제에 안정적으로 수렴한다.
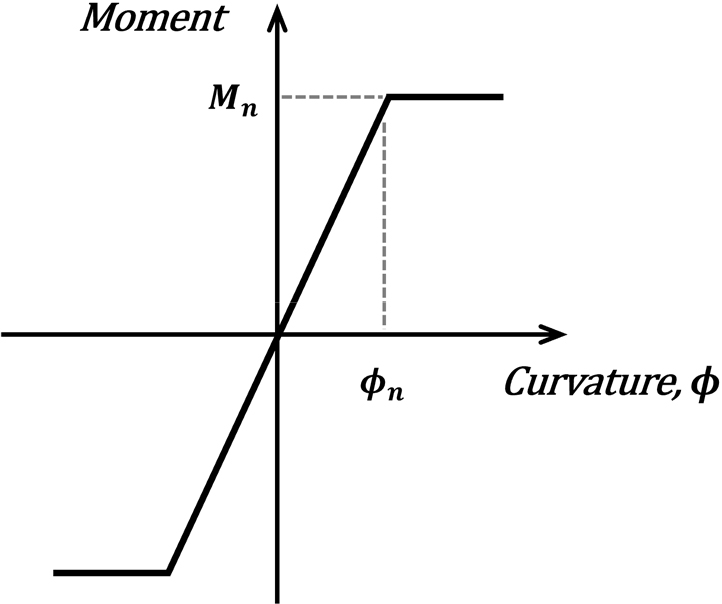
재료 비선형을 모델링하기 위하여 Beam-Column 유형의 집중형 소성 힌지를 적용하였다. 이는 부재의 양단부 및 중앙부에 위치한 회전 스프링에서 비탄성 거동이 집중되며 나머지 부분은 탄성 거동하는 형태이다. 비탄성 이력 거동은 경험적 이력 모델로서 정의되는 Skeleton Curve를 따르며, 부재의 양단부에는 모멘트-곡률 관계로 정의된 스프링이 배치되어 휨 성분에 대한 비탄성 거동을 모델링한다.
기둥과 보는 각 20개의 요소로 구성되어 있으며 기둥의 각 단부에 소성힌지를 적용하였다. 이는 분산형 힌지의 거동을 나타낼 수 있다. 이력 모델은 Fig. 1과 같은 탄성-완전소성으로 빔 요소의 탄성 거동과 소성 힌지의 소성 거동이 합쳐진 이력 모델이다.
2.3 증기운 폭발하중
CCPS(2012)에 따르면 플랜트 폭발의 대표적 유형은 증기운 폭발이며, 이는 많은 현장에서 주요 폭발 위험으로 간주되고 있다. 증기운 폭발은 유출된 가연성 물질이 공기와 혼합하여 증기운을 형성하고, 증기운이 점화원에 의해 발생하는 폭발로서 압력파 형태로 나타난다. 일반적으로 압력파는 내폭 설계의 단순화를 위해 Fig. 2와 같이 이상화된 압력파로 표현한다.
Lee 등(2024)은 해양플랜트 시설물의 탄화수소 누출 데이터를 통하여 재현주기별 증기운의 부피를 산정하였다. 본 연구에서는 최대 4,800년 재현주기 지진과 유사한 5,000년 재현주기 증기운 폭발(12,000m3)을 통하여 폭발하중을 산정한다.
증기운 폭발은 van den Berg(1985)가 제안한 멀티에너지법을 통하여 폭발하중으로 산정할 수 있다. 멀티에너지법은 가연성 구름 및 증기 구름에 존재하는 연소 에너지가 밀폐되거나 장애물의 영향으로 폭발에 기여할 것이라는 가정에 기초하며, 플랜트 가스 폭발과 가장 유사한 형태이다. 특성 곡선을 통하여 환산거리와 환산과압, 환산거리와 환산 지속시간의 관계를 산정할 수 있으며 폭발강도계수는 1부터 10까지 제시된다. Lee와 Kim(2021)에 따르면 폭발강도계수를 7 또는 8로 가정하면 플랜트 증기운 폭발의 폭압 모델을 비교적 정확하게 산정할 수 있다. 이에 따라 본 연구에서는 보다 보수적인 폭발하중의 산정을 위하여 폭발강도계수를 8로 가정한다.
폭발하중은 두 가지 유형으로 이격거리에 따른 폭발하중과 연성도에 따른 폭발하중으로 구분하여 산정하였다. 이격거리는 KFS 701(2020)의 석유화학공장 배치 및 이격거리 기준을 참고하여 60m, 75m, 90m, 110m, 180m로 구분하였으며, 연성도(𝜇)는 내진설계에서의 반응수정계수를 참고하여 1.0, 1.5, 2.0, 4.0, 8.0으로 구분하였다. 여기서 연성도는 항복변위 대비 최대변위를 의미한다. 거리와 연성도에 따른 폭발 과압과 폭발 지속시간은 Table 2와 Table 3에 제시되며, 하중의 작용 방향은 Fig. 3과 같다.
Table 2.
Blast load according to stand-off distance
| Stand-off Distance (m) | 60 | 75 | 90 | 110 | 180 |
| Overpressure (kPa) | 188 | 117 | 82 | 57 | 26 |
| Time Duration (ms) | 56.8 | 62.6 | 67.4 | 72.3 | 83.9 |
3. 증기운 폭발을 받는 골조와 단일부재의 동적 거동
ASCE(2011)에 따르면 내폭설계를 위한 부재의 응답 기준은 변형 한계를 기초하며 연성도와 회전각(𝜃)으로 구성된다. 이를 참고하여 폭발하중을 받는 골조와 단일 부재의 거동을 최대변위 및 연성도, 최대변위와 단부 회전각의 오차율로서 결과값을 비교한다.
3.1 모드해석
비선형 동적 해석을 진행하기에 앞서 모드해석을 통하여 골조와 기둥의 모드 주기와 모드 형상을 분석하였으며, 이에 대한 결과는 Table 4와 Fig. 4에 제시된다. 모드해석의 결과로 비교적 골조의 저차 모드와 기둥의 1차 모드가 유사하게 나타난다는 것을 확인하였다. SFF와 NSFF의 3차 모드주기와 FFC의 1차 모드주기가 유사하게 나타났으며, SPF와 NSPF의 3차 모드주기와 FPC의 1차 모드주기가 유사하게 나타났다.
Table 4.
Natural period of frame and single member (unit : ms)
| Mode 1 | Mode 2 | Mode 3 | |
| FFC | 14.8 | 5.6 | 3.4 |
| FPC | 21.1 | 6.8 | 3.4 |
| PPC | 32.6 | 8.3 | 3.9 |
| SFF | 140.0 | 41.4 | 15.7 |
| SPF | 287.0 | 43.6 | 21.4 |
| NSFF | 409.0 | 16.4 | 15.4 |
| NSPF | 432.0 | 23.0 | 21.4 |
3.2 이격거리에 따른 골조와 단일 부재의 동적 거동
골조와 단일 부재에 이격거리에 따른 폭발하중을 적용하여 비선형 동적 해석을 수행하였다. 결과는 고유주기(Tn)와 하중 지속시간(td)의 비, 최대변위와 연성도로 나타내었으며 Table 5와 같다. Fig. 5는 이격거리에 따른 골조와 단일 부재의 최대변위이며 점선은 연성도 1.0을 기준으로 한다.
Table 5.
Dynamic behavior of frame and single member according to the stand-off distance
골조와 단일 부재의 최대변위 및 회전각의 오차율을 통하여 결과를 분석하였다.
이격거리 60m에서 FFC를 기준으로 한 연성도는 39.34이다. SFF 및 NSFF와 FFC의 최대변위 및 회전각의 오차율은 5% 이내이며, SPF 및 NSPF와 FPC의 오차율은 7% 이내로 나타나기 때문에 골조를 기둥으로 단순화하여 해석할 수 있다. 또한, 이격거리 75m에서 FFC를 기준으로 한 연성도는 3.69이며 NSFF와 FFC의 최대변위 및 회전각의 오차율은 2% 이내, NSPF와 FPC의 오차율은 3% 이내로 나타나므로 이격거리 60m와 75m의 폭발하중을 받는 골조는 기둥으로 단순화하여 해석 가능하다.
이격거리 90m, 110m, 180m는 연성도 0.5 이하로 탄성 영역으로 판단된다. 따라서 비선형 동적 해석이 필수로 요구되는 범위의 영역은 아니다.
3.2 연성도에 따른 골조와 단일 부재의 거동
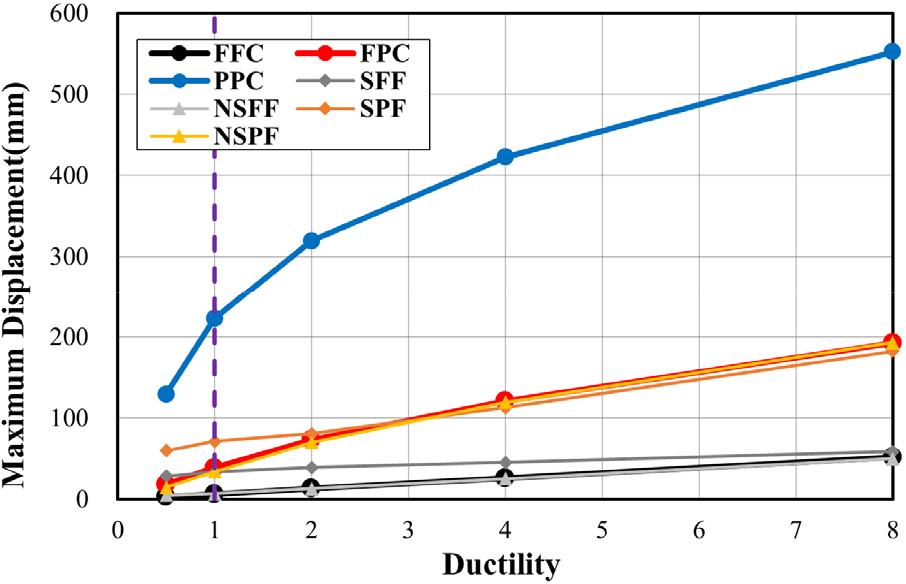
앞선 이격거리에 따른 골조와 단일 부재의 비선형 동적 해석의 결과에서 연성도가 증가함에 따라 골조와 기둥의 해석 결과가 유사해진다는 결과를 도출하였다. 따라서 연성도에 따른 폭발하중을 골조와 단일 부재에 적용하여 추가 해석을 진행하였으며 결과는 Table 6에 요약된다. Fig. 6은 연성도에 따른 골조와 단일 부재의 최대변위이며 점선은 연성도 1.0을 기준으로 한다. 여기서 연성도 1.0, 1.5, 2.0, 4.0, 8.0은 기둥 FFC를 기준으로 하며 항복변위 대비 최대변위를 의미한다. 연성도는 하중의 크기에 따라 달라진다.
Table 6.
Dynamic behavior of frame and single member according to the ductility
연성도 1.0에서 NSFF와 FFC의 오차율은 -7%이며, 연성도 1.5에서 NSFF와 FFC의 오차율은 -2%, NSPF와 FPC의 오차율은 7%이다. 연성도 2.0에서 NSFF와 FFC의 오차율은 -0.2%, NSPF와 FPC의 오차율은 4%로 분석된다. 따라서 현 영역에서는 횡변위가 없는 골조 NSFF와 NSPF는 각각 FFC와 FPC로 단순화하여 해석할 수 있다.
연성도 4.0 이상의 구간에서 NSFF와 FFC의 오차율은 2%, NSPF와 FPC의 오차율은 1%, SPF와 FPC의 오차율은 7%로 나타난다. 연성도 8.0 이상의 구간에서 NSFF와 FFC의 오차율은 3%, NSPF와 FPC의 오차율은 1%, SPF와 FPC의 오차율은 5%로 나타난다. 따라서 연성도 4.0 이상의 구간에서는 횡변위가 고려된 골조 SPF 또한 FPC로 단순화하여 해석할 수 있다.
3.3 보-기둥 강성비에 따른 골조와 단일 부재의 거동
부재의 고유주기와 하중의 지속시간 뿐만 아니라 부재의 강성과 강도는 전체 구조물의 거동을 결정짓는 주요 인자이다. 내진설계 기준을 참고하여 보-기둥 강성비에 따른 해석을 추가적으로 진행한다. 보-기둥 강성비는 기둥 대비 보의 강성으로 본 연구에서는 보-기둥 강성비를 0.1, 0.5, 1.0, 5.0, 10.0으로 구분하여 비선형 동적 해석을 수행하였으며, 해석 결과는 최대 변위(mm)로서 Table 7에 요약된다.
Table 7.
Maximum displacement of frame and single member according to beam-column stiffness ratio
보-기둥 강성비를 고려한 비선형 동적 해석을 수행하였으며, 해석의 결과를 골조 및 기둥의 최대변위 비율, 골조 및 기둥의 최대변위 오차율로서 그래프로 나타내었다.
Fig. 7과 Fig. 8은 횡변위를 고려한 골조 모델인 SFF와 SPF를 단일 부재 FFC와 FPC의 비율로 표현한 것이다. 연성도와 보의 강성이 증가함에도 이에 따른 비율의 변화가 거의 없는 것으로 나타난다. 따라서 본 연구에서는 횡변위가 구속된 골조와 단일 부재에 대하여 중점적으로 분석한다.
Fig. 9와 Fig. 10은 횡변위가 없는 골조와 단일 부재의 비율에 따른 그래프로 비율이 1에 가까울수록 두 모델의 결과가 유사함을 의미한다. Fig. 9는 FFC와 NSFF의 최대변위 비율, Fig. 10은 FPC와 NSPF의 최대변위 비율을 의미한다.
보다 정확한 비교를 위하여 횡변위를 고려하지 않은 골조와 단일 부재의 최대변위를 오차율로 나타내었으며, 이는 Fig. 11과 Fig. 12와 같이 표현된다. 오차율 ±10%의 범위를 표시하였으며, 오차율 0에 가까울수록 두 모델의 결과가 서로 유사함을 의미한다.
Fig. 11은 FFC와 NSFF의 최대변위 오차율로서 보-기둥 강성비가 0.5 이상, 연성도가 2.0 이상일 때 해당 골조를 기둥으로 단순화할 수 있다. 보-기둥 강성비가 1 이상인 영역에서는 연성도 1.0부터 8.0까지의 골조를 기둥으로 단순화하여 해석할 수 있다.
Fig. 12는 FPC와 NSPF의 최대변위 오차율로서 보-기둥 강성비가 0.5 이상, 연성도가 1.5 이상일 때 해당 골조를 기둥으로 단순화할 수 있으며, 보-기둥 강성비가 5 이상인 영역에서는 연성도 1.0부터 8.0까지의 골조를 기둥으로 단순화하여 해석 가능하다. 범위 외 영역은 추가적인 비선형 동적 해석이 수행되어야 할 것으로 판단된다.
4. 결 론
플랜트 시설물의 내폭설계를 위한 모델링 가이드라인의 개발을 위하여 골조와 단일 부재의 동적 거동을 분석하였다. 상용프로그램인 MIDAS GEN을 활용하여 비선형 동적 해석을 진행하였으며, 경계조건, 횡변위 등의 다양한 조건을 고려하였다. 플랜트 시설물의 특성을 반영하기 위하여 석유화학 플랜트에서 일반적으로 사용되는 부재와 재료적 성질을 적용하였다. 또한 플랜트 폭발의 대표적 유형인 증기운 폭발을 멀티에너지법을 통하여 폭발하중으로 산정하였다. 수치해석 방법은 뉴마크 평균 가속도법을 사용하였으며, 재료 비선형의 모델링을 위해 소성 힌지를 적용하였다. 이력 모델은 탄성 이선형이다. 폭발하중의 지속시간, 연성도, 보-기둥 강성비를 매개변수로 하여 비선형 동적 해석을 수행하였으며, 결과의 분석을 통하여 골조를 단일 부재로 단순화하여 해석할 수 있는 영역과 조건을 확인하였다. 보-기둥 강성비가 0.5일 때, 연성도가 2.0 이상인 NSFF는 FFC로 단순화하여 해석할 수 있으며, 보-기둥 강성비가 0.5일 때, 연성도가 1.5 이상인 NSPF는 FPC로 단순화하여 해석할 수 있다. 골조를 단일 부재로 단순화하여 해석할 수 있다는 것은 더 나아가 단자유도 시스템으로 이상화하여 해석할 수 있다는 것을 의미하며 이는 해석을 단순화함으로써 실무에서도 활용 가능할 것으로 판단된다. 본 연구의 결과는 기존 내폭 설계 방법의 근거자료로 활용될 수 있으며, 다양한 조건의 복잡한 모델을 예측할 수 있는 내폭 설계 가이드라인으로 활용될 수 있다.