1. 서 론
2. 철근 콘크리트 기둥의 단순 모델링 기법
2.1 단순 모델의 구성 및 입력값 산정
2.2 단순 모델의 적절성 검토
3. PML 요소를 적용한 지반 모델링
4. 지반-구조물 상호작용 해석
5. 결 론
1. 서 론
지반-구조물 상호작용(SSI, Soil-Structure Interaction)은 지반과 구조물 거동 사이의 상호작용으로, 지반 조건이 지진파에 미치는 영향을 포함해 구조물의 관성력이 다시 지반 거동에 영향을 미치는 작용 반작용의 과정을 의미한다(Kim, 2010). 지반-구조물 상호작용 효과는 크게 관성학적 상호작용(inertial interaction)과 운동학적 상호작용(kinematic interaction)으로 구분되며, 이러한 상호작용은 구조물의 고유진동수를 변화시키고 감쇠비를 증가시켜 구조물의 동적 거동을 예측하기 어렵게 만든다. 특히, 지진파의 진동수 성분에 따라 공진 현상이 유발될 수 있어 이를 반영한 해석이 필수적이다(Kim, 1993, 2002).
실제로 구조물과 지반 사이의 상호작용은 매우 복잡하며, 이 상호작용을 정확히 모사하기 위해서는 기초의 형태, 구조물의 형상, 지반 조건 등 다양한 변수를 고려한 수치 모델링이 필요하다. SSI 해석 방법 중 하나인 직접법(direct method)은 Fig. 1과 같이 지반, 기초, 구조물을 하나의 시스템으로 통합하여 각 요소 간의 상호작용을 정밀하게 분석하는 방법이다. 이 접근법은 지반과 구조물 사이의 상호작용을 통합적으로 분석할 수 있는 가장 정확한 방법으로 여겨지지만, 3차원적으로 변화하는 입력 운동과 비선형성을 포함하기 때문에 계산 비용이 과도하게 요구되어 실제 적용 빈도가 낮다(Stewart et al., 2012).
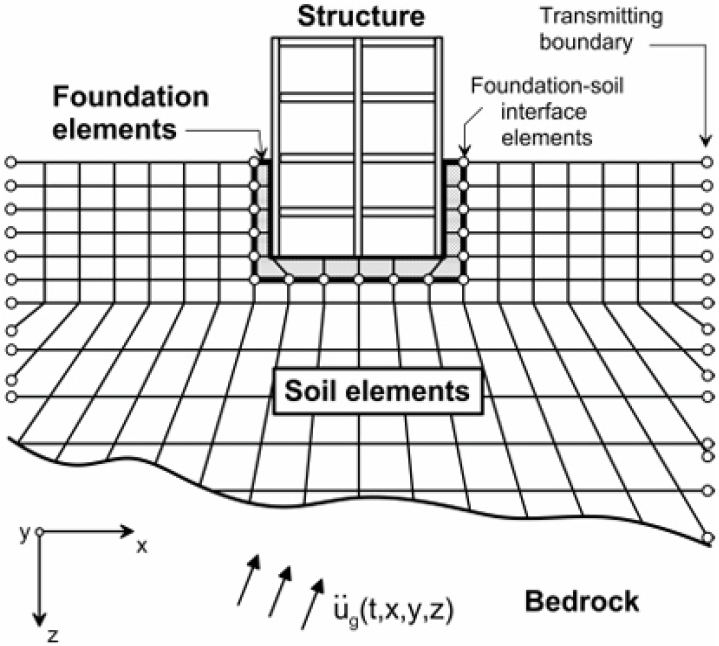
Fig. 1.
Schematic illustration of a direct analysis of soil-structure interaction using continuum modeling by finite elements (Stewart et al., 2012)
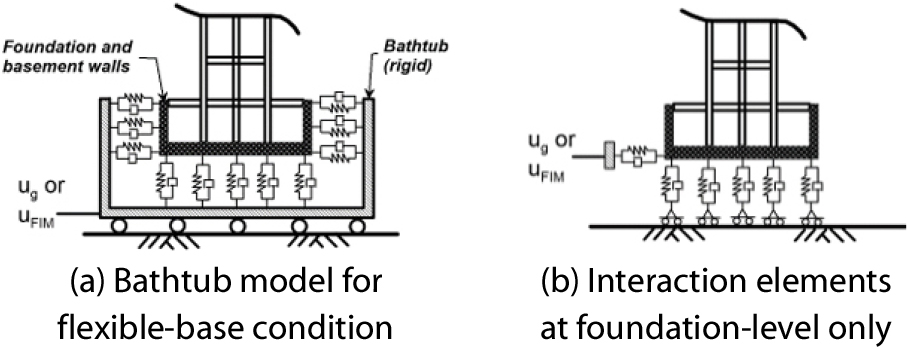
따라서, Guidelines for Performance-Based Seismic Design of Tall Buildings(PEER, 2017)과 Soil-Structure Interaction for Building Structures(Stewart et al., 2012)에서는 Fig. 2와 같이 SSI 효과를 반영한 단순화된 접근법을 제안하고 있다. 그러나 이는 운동학적 상호작용만을 고려한 방법으로 자유장 운동과 기초 입력 간의 관계를 전달함수로 모델링하거나, 기초의 강성과 감쇠를 스프링과 감쇠기(Dashpot)로 단순화하여 표현한다. 이러한 접근법은 계산 효율성을 높이는 데 유리하지만, 관성학적 상호작용과 지하 요소에 대한 세부 거동을 반영하지 못한다는 한계가 있다.
Yoon 등(2018)은 Soil-Structure Interaction for Building Structures(Stewart et al., 2012)에서 제시한 단순화된 해석 절차를 기반으로 지하층이 있는 고층빌딩에 대해 2차원 동적해석을 수행하였다. 그러나 해당 연구에서도 관성학적 상호작용이 배제된 해석 방법의 한계를 언급하며, 이를 포함한 분석의 필요성을 강조했다. 또한, Lee 등(2013)은 정밀한 SSI 해석을 위해서는 해석모델이 거대화되며, 상호작용 절점의 증가로 인해 긴 해석 시간이 요구되는 문제점을 지적하였다. 특히, 해석 소요 시간은 대형 3차원 SSI 해석에서 중요한 고려사항이자 해결해야 할 과제라고 언급하였다. 이러한 점은 SSI 해석에서 정확성과 효율성을 동시에 충족할 수 있는 개선된 접근법 개발의 필요성을 보여준다.
따라서 이 연구에서는 직접법의 정확성을 유지하면서 해석 시간을 단축하기 위해 철근 콘크리트 기둥의 간략화 모델링 기법을 제안하였다. 또한, 무한 지반의 경계조건을 효과적으로 처리하기 위해 PML(Perfectly Matched Layer) 요소(Basu, 2009)를 활용하여 기존 접근법의 한계를 보완하고, SSI 해석의 적용성을 높이는 것을 목표로 한다.
2. 철근 콘크리트 기둥의 단순 모델링 기법
2.1 단순 모델의 구성 및 입력값 산정
3차원 상세모델은 solid 요소로 이루어진 콘크리트와 beam 요소로 이루어진 철근으로 구성되며, 구조물의 복합 거동을 정밀하게 모사할 수 있다. 하지만 대형 구조물의 해석에서는 요소 수의 증가로 인해 계산 시간이 과도하게 소요되며, 이는 적용에 큰 제약으로 작용한다. 이러한 문제를 해결하기 위해 본 연구에서는 3차원 상세모델의 단면 치수와 재료 물성을 바탕으로 단순 모델의 입력값을 이론적으로 산정하였다. 단순 모델은 beam 요소만으로 이루어지며, 임의의 철근 콘크리트 기둥을 대상으로 3차원 상세모델과 해석결과를 비교하여 제안한 기법에 대한 적절성을 확인하였다. Table 1과 Table 2는 본 연구에 사용된 대상 기둥의 제원 및 재료 물성을 나타낸다.
Table 1.
Specifications of the Objective Column
| Component | Dimensions & Reinforcement | |
| Concrete | 300mm × 600mm × 2,330mm | |
| Rebar | Ver. | 14-HD19 |
| Hor. | HD10@300 | |
Table 2.
Material properties of the detailed model
| Type | Material Model | Strength (MPa) | 𝜌 (kg/m3) | (MPa) | 𝜈 |
| Solid | *MAT_WINFRITH_CONCRETE | = 20MPa | 2,300 | 24,518 | 0.18 |
| Beam | *MAT_PLASTIC_KINEMETIC | = 400MPa | 7,850 | 200,000 | 0.3 |
본 연구에서는 범용 유한요소해석 프로그램인 LS-DYNA (LSTC, 2024)를 활용하였다. 단순 모델에는 비선형 재료 거동을 모사할 수 있는 탄소성 재료 모델인 *MAT_CONC RETE_BEAM을 사용하였으며, 보 요소 중 Timoshenko beam(ELFORM=13)을 사용하였다. 이 요소는 회전 관성(rotation inertia)과 전단 변형(shear deformation)을 포함한 2차 항까지 반영할 수 있어 다양한 진동수 범위에서 정확한 동적 응답을 제공한다(Kennedy, 2013).
단순 모델의 입력값인 탄성계수, 항복응력, 항복 후의 탄성계수는 3차원 상세모델의 재료 물성(Table 1)을 기반으로 이론적으로 계산할 수 있다.
이때, 탄성계수는 횡방향 철근의 구속 효과와 수직 방향 철근의 영향을 반영한 수정탄성계수()를 사용하였으며, 이는 Yoon 등(2005)에서 제안한 방법으로 계산하였다. 구속된 코어 콘크리트의 탄성계수는 횡방향 철근의 체적비와 콘크리트의 탄성계수를 고려하여 계산되며, 최종적으로 수직 방향 철근의 영향을 포함한 수정탄성계수는 다음과 같이 도출된다.
여기서, 는 코어 콘크리트의 탄성계수, 는 철근 콘크리트 부착 보정 상수, 은 탄성계수비, 는 철근 단면적, 는 총 단면적을 의미한다.
단순 모델링 기법에서는 식 (1)로 계산된 수정탄성계수()를 보 요소의 탄성계수()로 입력한다. 이때, Yoon 등(2005)은 철근 콘크리트 부착 보정 상수 를 0.5로 제안하였으나, 단순모델과 비교하기 위한 상세모델에서 철근과 콘크리트의 완전 부착을 가정하였기 때문에 본 해석에서는 1.0을 대입하였다.
항복응력()과 항복 후의 탄성계수(ETAN)는 철근과 콘크리트의 합성 거동을 고려하여 계산된다. 항복응력()은 콘크리트의 초기 탄성 구간에서 발생하는 응력을 기준으로 정의되며, 이는 콘크리트 압축 강도가 발현되는 변형률()에서 산출된다(식 (2)). 항복 후의 탄성계수를 계산하기 위해 철근의 항복응력이 발현되는 변형률()에서의 응력()을 계산한 뒤(식 (3)), 항복 후의 탄성계수는 식 (4)로 나타낸다. 단면 상수의 계산에는 콘크리트의 단면 치수(300mm×600mm)를 사용한다.
이러한 방법으로 산출된 단순 모델의 입력값을 Table 2에 나타내었다.
2.2 단순 모델의 적절성 검토
제안한 단순 모델링 기법의 적절성을 검토하기 위해 첫 번째 단계로 2.1절의 방법으로 계산한 단순 모델의 입력값과 상세모델의 해석을 통해 얻은 결과를 비교하였다(Table 3). 이를 통하여 2.1절에서 제시한 입력값의 계산 방법이 적절함을 확인하였다.
Table 3.
Sectional & material properties of the simplified model
| Type | Material Model | (MPa) | 𝜌 (kg/m3) | (MPa) | (MPa) | 𝜈 | (m2) | (m4) | (m4) |
| Beam | *MAT_CONCRETE_BEAM | 23.54 | 2,500 | 29,235 | 4,400 | 0.18 | 0.18 | 0.00135 | 0.00540 |
다음으로 단순 모델과 상세모델의 압축, 인장, 전단, 휨 해석과 고유치 해석(eigenvalue analysis)을 추가로 진행하여 그 결과를 비교하였다. 두 모델 사이의 강성 차이는 ±1% 이내로 나타나 단순 모델이 구조물의 강성을 적절히 모사함을 확인하였다(Table 4). 고유치 해석에서도 3차 모드(비틂모드)를 제외한 나머지 모드(휨모드)에서의 고유진동수 차이는 1% 내외로 나타나 구조물의 동적 거동이 적절히 산출됨을 확인하였다(Table 5). 비틂모드인 3차 모드의 경우 오차 6.99%로 다른 모드에 비해 상대적으로 큰 차이를 보였으나, 주요 지진 거동을 반영하는 1차, 2차 모드에서의 차이가 1% 내외로 나타났으므로 전체 해석의 정확성에 큰 영향을 미치지 않을 것으로 판단하였다(Table 6).
Table 4.
Validation of input parameters
3. PML 요소를 적용한 지반 모델링
SSI 해석에서 무한한 지반을 수치적으로 모델링하기 위해 사용되는 방법으로 반무한지반(semi-infinite ground) 모델과 흡수 경계조건 모델을 들 수 있다. 두 모델 모두 실제로는 발생하지 않는 지반 모델의 경계면에서의 반사파의 영향을 줄이기 위해 사용되며, 기본적으로 사용되는 방법은 지반 영역을 넓혀 반사파가 구조물에 도달하기 전에 자연스럽게 감쇠되도록 하는 반무한지반 모델을 적용하는 것이다. 반무한지반 모델은 지반의 물리적 특성을 보다 실제에 가깝게 모사할 수 있으나, 해석 시간이 길어지고 계산 효율성이 낮아지는 한계가 있다(Kim et al., 2014).
이에 반해, 흡수 경계조건은 비교적 좁은 영역의 지반만을 모델링하여도 경계에서 발생하는 반사파를 효과적으로 흡수할 수 있으며, PML(Perfectly Matched Layer) 요소는 모든 진동수와 각도에서 입사하는 파동을 흡수하는 효과적인 경계조건으로써 널리 사용되고 있다(Davoodi et al., 2018; Genç et al., 2022; Kim et al., 2014).
본 연구에서는 철근 콘크리트 기둥의 단순 모델에 반무한지반(Semi-infinite ground)과 PML 경계조건을 각각 적용하여 SSI 해석을 수행하고 그 결과를 비교하였다.
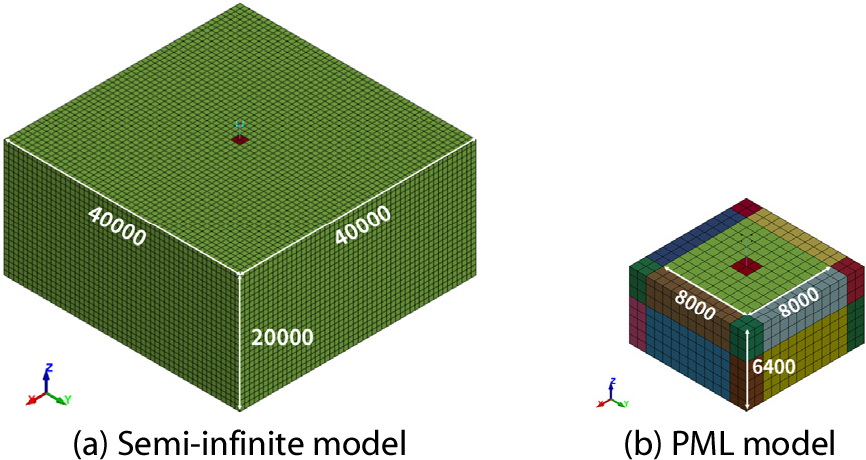
반무한지반 모델은 Basu(2009)의 연구를 참고하였으며, 반사파의 영향을 최소화하기 위해 기초판의 폭과 깊이의 25배 영역으로 설정하였다(Fig. 3(a)). 대상 지반은 모델링의 단순화를 위해 단일 토사층으로 구성하였으며, 지반의 재료 모델로는 *MAT_MOHR_COULOMB를 사용하였다. 재료 입력값은 Kim 등(2021)이 제안한 국내 대표 풍화토 지반의 특성을 바탕으로 설정하였다.
PML 요소는 지반을 유한 도메인으로 모델링하기 위해 경계면에 적용되었다. PML 요소는 다음과 같은 요구 조건을 충족하도록 설정되었다(LSTC, 2024).
1)PML의 재료 상수는 인접 경계 재료와 동일해야 한다.
2)PML 경계층의 외부 경계는 고정 조건으로 설정해야 한다.
3)PML 층은 깊이 방향으로 약 5~8개의 층으로 구성되어야 한다.
4)PML은 정적 하중을 받지 않도록 해야 한다.
PML 요소의 재료 모델은 *MAT_PML_ELASTIC이 사용되었으며, 인접한 지반의 재료 물성과 동일한 값을 사용하였다. PML을 적용한 지반 모델은 반무한지반 모델의 폭 대비 1/5로 축소되었으며, 깊이 방향 모델링은 PML의 요구 조건에 따라 Fig. 3(b)와 같이 구성하였다.
4. 지반-구조물 상호작용 해석
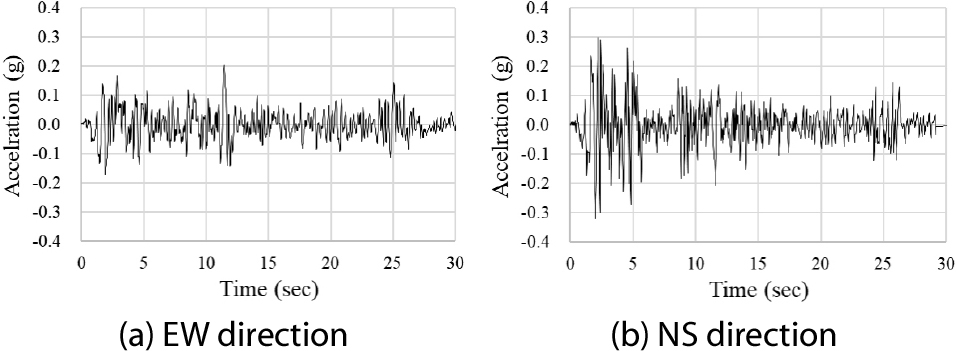
본 연구에서는 LS-DYNA에서 제공하는 SSI interface 요소를 활용하여 SSI 해석을 수행하였다. 지진하중은 Fig. 4에 제시된 El-Centro 지진파를 사용하여 구조물이 없는 상태에서 지반의 지진응답을 분석하는 자유장 해석(free-field response analysis)을 통해 기초 입력 운동을 산정하였다. Fig. 4에 제시된 지진파는 기반암에서의 응답으로 가정하였으며, 자유장 해석을 통해 노출된 건물 기초면 중앙에서의 자유장 응답을 산출하였다. 단순 모델링 기법이 적용된 기둥과 지반이 함께 구성된 FE 모델(Fig. 3)에서 기초 측면과 하부 경계면에 SSI interface 요소를 적용하였으며, 기초 저면 중앙에 자유장 응답을 입력하여 SSI 해석을 수행하였다.
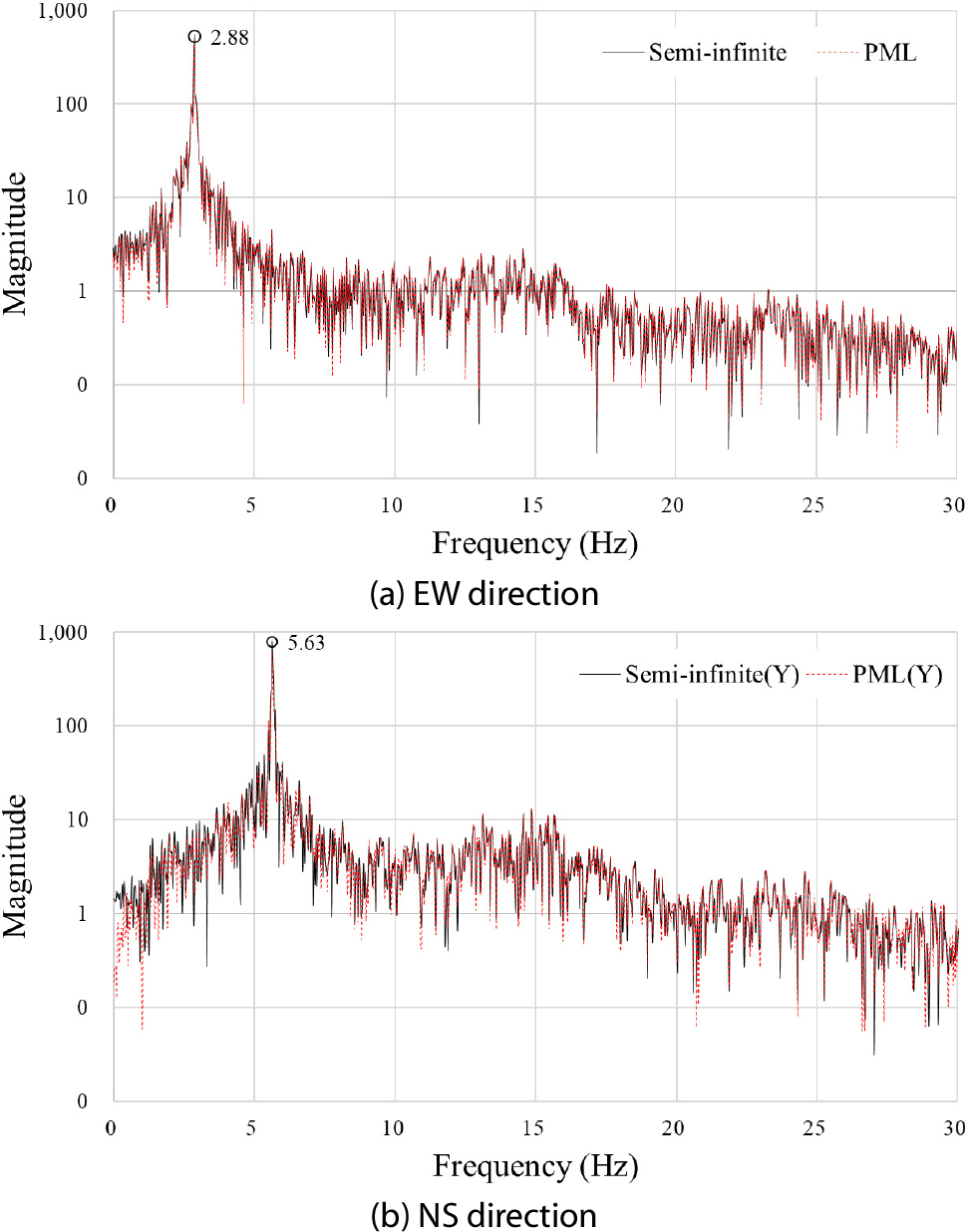
Fig. 5는 반무한지반(semi-infinite) 모델과 PML 모델의 SSI 해석으로부터 얻어진 기둥 상단의 가속도 응답을 FFT 변환한 그래프이다. 그래프에 나타난 바와 같이 반무한지반 모델과 PML 모델의 해석 결과는 거의 일치하였으며, EW방향과 NS방향의 peak frequency는 각각 2.88Hz와 5.63Hz로 나타났다.
두 모델에서 일치하는 해석 결과가 얻어진 반면, 반무한지반 모델의 해석 시간은 14시간 9분, PML 모델의 해석 시간은 1시간이 소요되었으며, PML 모델이 반무한지반 모델 대비 약 7% 수준의 해석시간이 소요되어 높은 계산효율을 보이는 것을 확인할 수 있었다.
4. 결 론
본 연구에서는 철근 콘크리트 기둥의 단순 모델링 기법과 PML(Perfectly Matched Layer) 요소를 함께 사용하여 지반-구조물 상호작용(SSI, Soil-Structure Interaction) 해석에서 계산 효율성과 해석 정확성을 함께 확보하는 방법을 제안하였으며, 연구 결과를 통해 다음과 같은 결론을 도출하였다.
1)단순 모델링 기법을 사용하여 상세모델 대비 적은 계산량으로 정적 및 동적해석에서 유사한 결과를 얻을 수 있었다. 상세모델과 간략화 모델 사이의 강성 차이는 ±1% 수준으로 나타났으며, 휨모드의 고유진동수 차이 역시 1% 이내로 확인되었다. 이러한 결과는 단순모델이 구조물의 정적 및 동적 거동을 효과적으로 모사할 수 있음을 나타낸다.
2)PML 요소를 적용한 SSI 해석에서는 반무FE한지반 모델 대비 해석 시간이 약 7% 수준으로 단축되었다. PML 요소는 지반 경계에서 반사파를 효과적으로 흡수함으로써, 지반영역의 크기를 줄이면서도 반무한지반 모델과 동일한 해석 결과를 얻을 수 있었다. 두 해석 모델에서 얻어진 기둥 상단의 가속도응답을 FFT 변환한 결과를 비교하였으며, 각 방향의 첨두 진동수(2.88Hz, 5.56Hz)가 일치함을 통해 PML 요소가 반무한지반 모델과 동등한 해석 정확도를 제공함을 확인하였다.
3)본 연구에서는 단층 토사 지반을 대상으로 탄성 구간에서의 구조 거동을 검토하였으며, 탄성 해석에서 구조물의 주요 동적 특성을 효과적으로 반영할 수 있음을 확인하였다. 그러나 다층 지반 조건이나 소성 구간의 손상 및 파괴를 고려하기 위해서는 간략화 모델링 기법과 PML 요소의 확장 가능성을 검토하는 추가 연구가 필요하다.