1. 서 론
2. Beam 모델링
3. 격자구조 열전도 해석
4. 기계학습 및 유전 알고리즘 기반 구조 최적화
5. 수치해석 및 결과
5.1 인공신경망 학습
5.2 기계학습 기반 격자 구조 최적화
5.3 유효열전도도와 탄성계수 간의 유사성
6. 결 론
1. 서 론
격자구조(lattice structure)는 부피 대비 큰 표면적과 다양한 유동 경로를 보유하여 열 교환기, 에너지 흡수 장치, 생체 재료 등 다양한 응용 분야에 주로 사용된다(Cheng et al., 2016; Jing et al., 2023; Wei et al., 2014). 최근에는 제작 기술의 발전으로 3D 프린터를 통해 복잡한 격자구조를 제작할 수 있게 되면서, 형상 최적화의 기본 재료로 널리 활용되고 있다(Takarazawa et al., 2022). 격자구조는 빔 형상의 배열에 따라 SC(simple cubic) 구조, BC(body-centered cubic) 구조와 FCC(face-centered cubic) 구조 등 여러 가지 종류로 구분되고, 이러한 격자구조의 성능은 격자구조의 종류와 빔의 형상에 의해 결정된다.
일반적인 형상 최적화 기법은 설계 변수를 기반으로 이루어지며, 최적의 구조를 찾기 위해 설계 변수의 복잡도가 증가하는 어려움이 있다. 설계 변수가 많아지면 설계 공간(design space)이 넓어지므로 최적의 해를 찾기 위해 많은 전산 해석 시간이 요구된다(Su, 2023). 따라서 이전에는 구조를 단순화하는 등의 방법으로 설계 변수를 최소화하는 접근이 이루어졌다(Shahrzadi et al., 2022). 기존의 격자구조 열적 성능 향상을 위한 형상 최적화 연구에서는 빔의 기울기와 격자구조의 종류로 설계변수를 제한하여 변수에 대한 최적화를 진행했다(Vaissier et al., 2019). 혹은 단순 원통형 빔을 기반으로 설계변수를 제한하여 해석의 복잡도를 낮추었지만(Cheng et al., 2016), 이는 격자구조의 복잡성과 다양성을 충분히 반영하지 못해 최적 성능을 얻는데 한계가 있기 때문에 제한적인 성능 향상이 이루어질 수밖에 없었다.
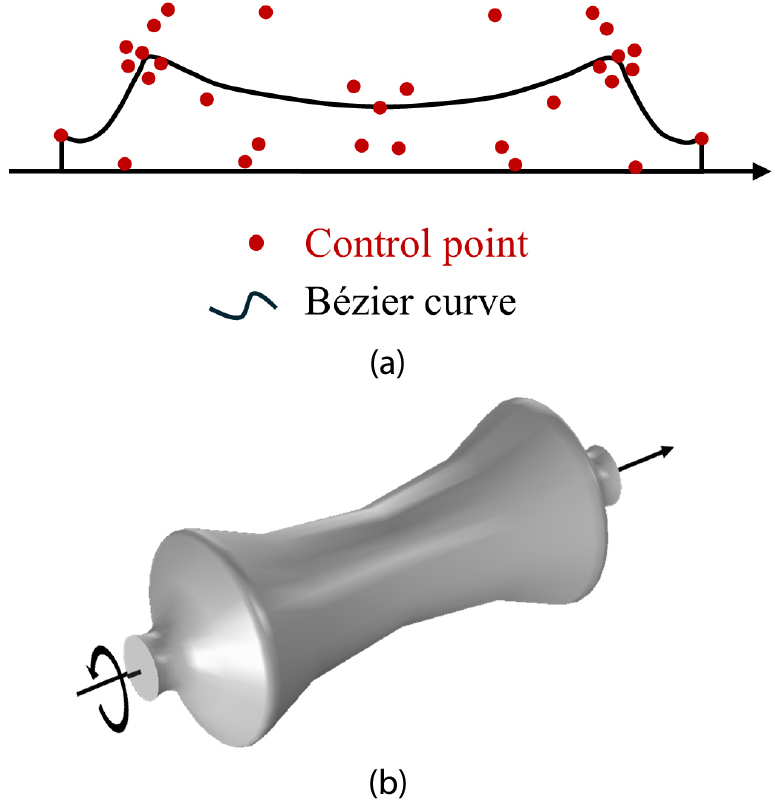
기존의 연구에서 나타난 한계를 극복하기 위해 본 연구에서는 BC와 SC 격자 구조의 빔 형상을 bézier 곡선으로 모델링하고, bézier 곡선의 제어점 좌표를 무작위로 설정하였다(Fig. 1). 인공신경망(artificial neural network, ANN) 및 유전 알고리즘(genetic algorithm, GA)을 통해 유효 열전도도(effective thermal conductivity, ETC)를 최대화/최소화하여 최적의 빔 형상을 생성하고 열교환기/단열재로 쓰이기 적합한 격자구조를 제시하고자 한다. 더불어 선행연구에서 제안한 우수한 탄성계수를 가지는 BC 및 SC 형상과의 비교를 통해 격자구조의 열전도도와 탄성계수 간의 유사성을 확인하고자 한다.
2. Beam 모델링
본 연구에서는 기계 학습 기반 최적화 방법을 통해 격자 구조의 빔 요소를 bézier 곡선으로 설계한다. bézier 곡선은 주어진 제어점을 통해 매끄러운 곡선을 생성하는 수학적 모델로 주로 컴퓨터 그래픽스 및 CAD에서 사용한다.
bézier 곡선은 제어점을 직접 통과하지 않고 근사하여 부드러운 형태의 곡선을 가지며 식 (1), (2)으로 표현한다. bézier 곡선은 유연한 형상 설계를 가능하게 하며, 고차 곡선을 통해 복잡한 곡선도 매끄럽게 표현할 수 있다. 본 연구에서는 유연한 곡선 형태를 갖는 bézier 곡선을 사용하여 격자 구조 빔의 형상을 모델링한다. 형상이 복잡한 경우 열유속 집중(heat flux concentration)이 발생하기 때문에 열전달 측면에서 비효율적이며, 추후 실제 실험에 활용되기 위해서는 제작이 가능해야 한다. 이러한 이유로 다양한 형상 설계 선행연구에서 bézier 곡선을 활용하였다.
3. 격자구조 열전도 해석
본 연구에서는 격자구조의 유효 열전도를 예측하기 위해 균질화법(homogenization) 이론을 적용했다. 균질화법을 통해 단위격자구조(unit lattice cell)를 등가의 균질 재료로 모델링하여 거시적 물성을 분석하고자 했다. 균질화법에 기반한 유효 열전도도 계수를 식 (3)으로 나타낼 수 있다. 식 (4)는 체적 에 따른 평균 열 유속(heat flux)을 나타낸다(Nakayama, 2023).
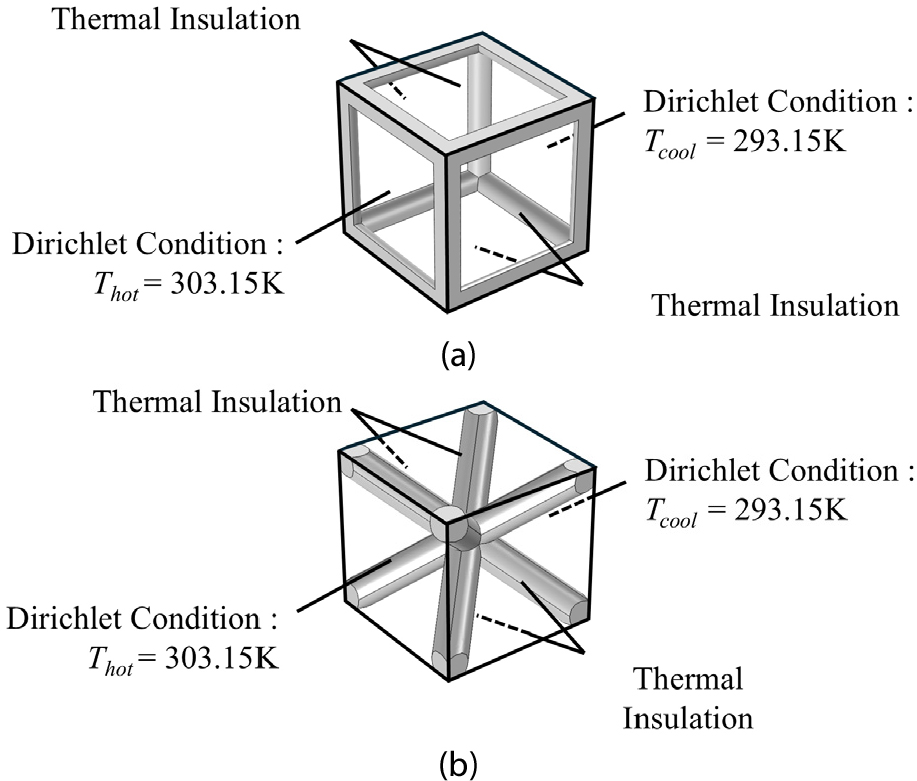
여기서, 유효 열전도계수 는 단위 부피당 열 유량 , 부피분율 , 격자구조에 양 끝 면에 가해지는 온도 와 , 격자구조 단위 크기 에 의해 정의된다. 열전도 해석을 진행하기 위해 온도구배를 경계조건으로 적용했다(Fig. 2). 온도가 가해지지 않는 경계에 대해서는 격자구조가 주기적인 배열(periodic pattern)인 점을 고려하여 단열 조건을 가정하였다. 본 연구에서는 을 1cm로 두고 는 303.15K 그리고 는 293.15K로 설정한다. 격자구조의 물성을 재료의 열전도도 정규화(normalization)하기 위해 는 1W/(mK)로 가정한다.
4. 기계학습 및 유전 알고리즘 기반 구조 최적화
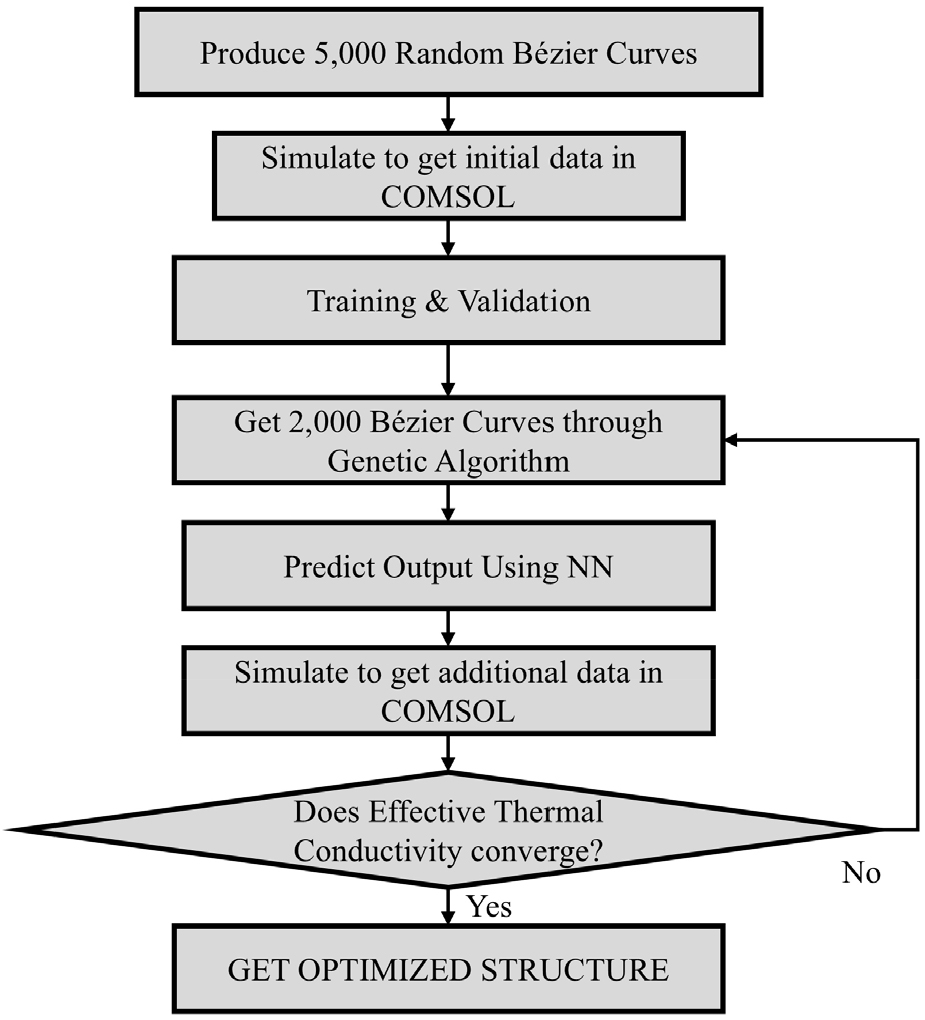
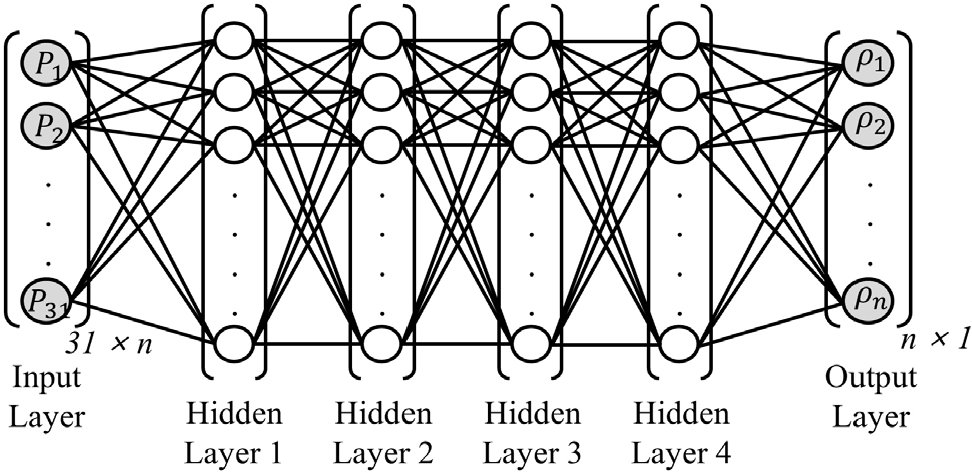
본 연구에서의 기계학습 기반 최적화 설계 과정을 Fig. 3에 나타냈다. 먼저, 초기 bézier 곡선 데이터셋을 확보하기 위해 MATLAB에서 한 묶음의 무작위 제어점 을 5,000개 생성한다. 초기 데이터셋은 상대밀도 0%-100%에 균일하게 분포하도록 생성하며 실제 제작되는 점을 고려하여 임의의 제어점 은 0.01 cm 이상에 위치하도록 한다. 이후, COMSOL을 사용하여 격자 구조의 열전도 해석을 바탕으로 물리적 환경을 조성하고, 열전도 시뮬레이션을 진행한다. 이렇게 얻은 유한요소해석 데이터를 학습하기 위해 인공신경망(NN)을 훈련 및 검증하여, 주어진 임의의 제어점으로부터 상대 밀도와 열 유량을 예측하는 모델을 구축한다(Fig. 4). 본 연구에서는 격자구조의 탄성계수를 최적설계하는데 사용한 선행 연구의 hyperparameter를 사용하여 보다 효율적으로 학습이 될 수 있도록 하였다(Lee et al., 2022). 신경망은 4개의 은닉층(hidden layer)으로 구성되며, mini-batch 크기는 1000, 최대 epochs는 150, 초기 학습률은 0.01, 학습률 감소 계수는 0.1이다. 보통 방대한 데이터를 사용하여 학습을 하는 경우, 메모리 문제가 발생하기 때문에 데이터를 부분적으로 나눠서 학습을 진행한다. 이때 부분적으로 나눈 데이터의 크기를 mini-batch 사이즈라고 하며, 모든 데이터에 대해서 학습을 진행하는 횟수를 에폭이라고 한다. 이때 mini-batch 사이즈에 따라서 학습과정에서의 오류가 증가하기도 하며 오류가 감소하기도 한다. Optimizer로는 Adam을 사용하며, 학습 결과는 결정계수(R2)를 통해 검증하고, R2 값이 1에 가까울수록 학습 결과가 정확하다고 판단한다. 결정계수 R2는 식 (5)로 정의한다. 는 예측 모델을 통해 얻은 예측 값, 는 유한요소해석을 통해 얻은 값, 는 유한요소해석을 통해 얻은 값들의 평균이다.
유전 알고리즘(GA)에서는 목적함수 식 (6)을 바탕으로 상위 1% 또는 하위 데이터를 선별(selection)하고, 이를 돌연변이(mutation)를 유도하여 새로운 bézier 곡선 데이터셋을 2,000개 생성한다. 각 데이터는 제어점의 x, y 좌표들을 포함하고 있으며, 데이터가 염색체를 의미하고 제어점의 좌표 값이 유전자를 의미한다. 2개의 데이터(염색체)를 무작위로 추출하고 무작위로 결정된 분할점을 기준으로 각 데이터를 나누고 유전자를 합쳐서 새로운 데이터를 얻는다. 따라서 각 염색체는 31개의 유전자를 포함하며, 교차와 무작위 데이터 추가를 통한 변이를 통해 새로운 bézier 곡선을 생성한다. 이 과정에서 생성된 상위 1%의 데이터는 부모 데이터로 설정되며, 부모 데이터의 제어점을 교차하여 새로운 제어점 좌표를 생성한다. 또한, 유한요소해석으로부터 얻은 상대 밀도와 탄성 계수를 활용하여 모든 데이터의 출력값을 목적 함수로 계산하고, 상위 또는 하위 5,000개의 데이터셋을 선택하여 유전 알고리즘에 사용한다. k는 penalty coefficient를 의미하고 는 목적밀도를 의미하며, 는 input 값의 밀도, 는 input 값의 유효 열전도도 계수를 의미한다.
목적밀도에 대해 유효 열전도도 계수를 최대화한 최적화 구조를 얻고자 하는 경우 페널티 계수를 음수로 두어야 하고, 최소화한 최적화 구조를 얻고자 하는 경우 페널티 계수를 양수로 두어야 한다. 본 연구에서는 다양한 격자구조 연구에서 사용된 20% 밀도에 대해서 격자구조를 최적화하였다. 유전알고리즘으로 얻어진 새로운 데이터의 목적함수 값은 유한요소해석이 아닌 학습된 인공신경망을 통해 예측된다. 인공신경망은 유한요소법에 비해 빠르게 결과를 예측할 수 있기 때문에 이를 활용하여 최적설계를 더 빠르게 얻을 수 있다. 본 연구에서는 유전알고리즘으로 얻어진 데이터의 목적함수 값이 상위 1%보다 좋은 경우 새로운 데이터로 추가하였고, 그렇지 않은 경우는 반복하여 데이터를 생성하였다. 인공신경망을 통해 높은 예측값을 갖는 새로운 데이터의 개수가 2,000개가 되면 데이터의 목적함수 값은 유한요소해석을 통해 계산하였다. 이러한 과정을 반복적으로 수행하여 최적의 유효열전도도 계수가 5세대에 걸쳐서 변화가 없다면 수렴하였다고 판단하였으며, 수렴하지 않은 경우는 전체 데이터를 인공신경망에 학습시키고 유전알고리즘을 적용하여 반복하였다.
5. 수치해석 및 결과
5.1 인공신경망 학습
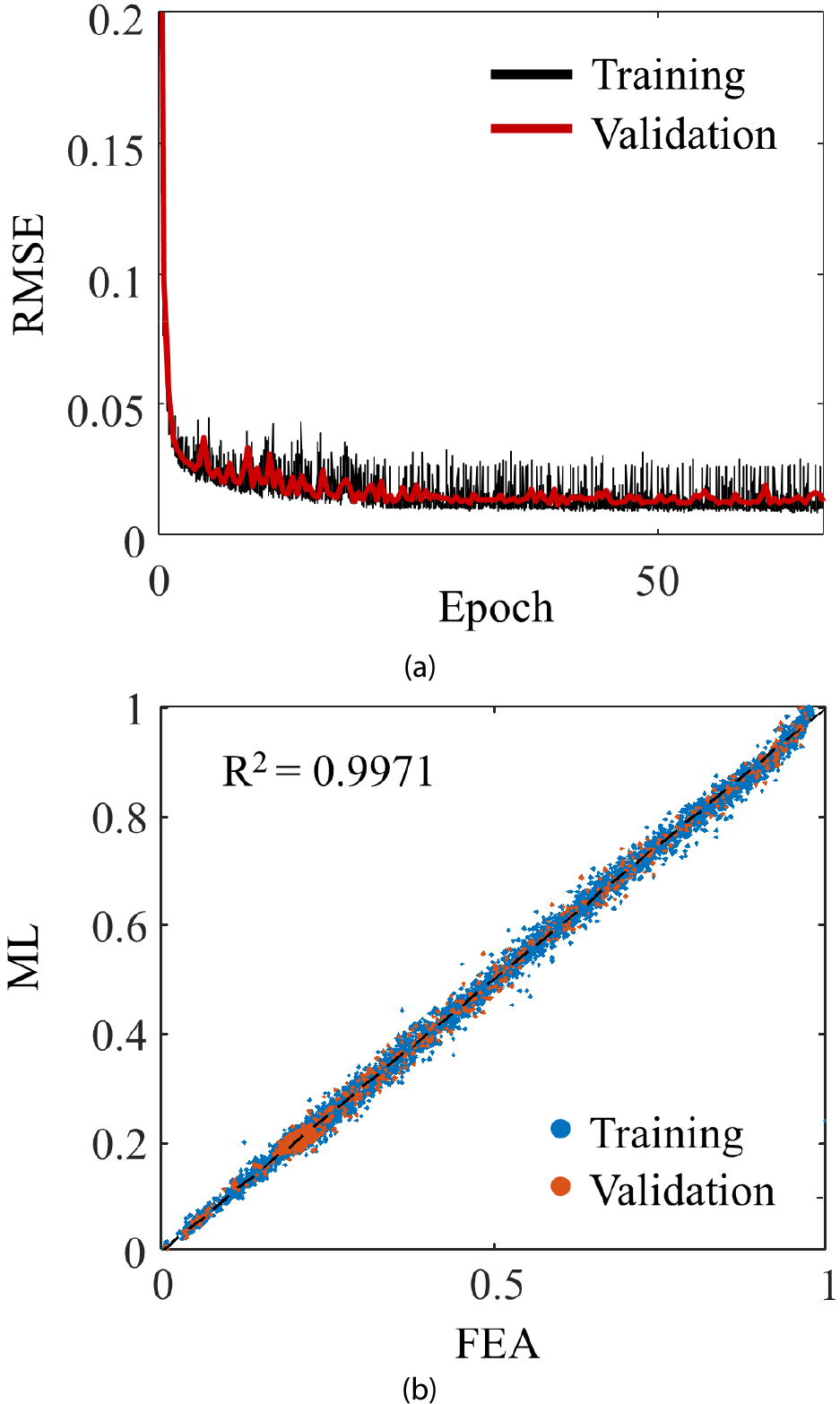
Fig. 5에서는 제어점들(control points)이 주어졌을 때 BC 격자구조의 상대밀도를 예측하는 모델의 학습 과정 및 검증 결과를 나타낸다. 학습의 정확도를 나타내기 위해서 RMSE(root mean square error)를 사용하였다. 매 에폭마다 학습된 인공신경망으로 예측한 값과 유한요소로 계산한 실제 값의 차이를 모든 데이터에 대해서 계산하였다. 따라서 RMSE가 0으로 가는 경우 모든 데이터에 대해서 정확하게 예측한다는 것을 의미한다. Fig. 5에서 학습데이터와 테스트 데이터에 대한 RMSE 값을 확인할 수 있다. Fig. 5(a)에서 Test Validation RMSE 값과 Training Validation RMSE 값이 0.012로 오차가 0에 수렴하여 학습이 적절하게 진행된 것을 확인할 수 있다. 또한, Fig. 5(b)에서 R2값이 0.9971로 계산되어 인공신경망을 사용한 예측 모델이 격자 구조의 열전도 성능을 매우 정확하게 예측할 수 있음을 확인했다. Fig. 5에 나타낸 과정과 동일하게 SC 격자구조의 상대밀도 및 열 유량 예측 모델학습을 진행하였다.
5.2 기계학습 기반 격자 구조 최적화
본 연구에서 제안한 최적화 방법론을 통해 SC 및 BC 구조의 유효 열전달계수를 최대화 및 최소화하는 구조를 얻었다. 먼저, SC 구조의 경우 유효 열전달계수를 최대화하기 위한 최적화 과정으로 총 7세대 만에 수렴하는 결과를 얻었으며, 최소화하는 과정에서는 총 12세대를 거쳐 최종 형상이 수렴함을 확인하였다(Fig. 6(a), (b)). 최적화 결과, SC 구조는 유효 열전도도 최대화 구조에서 단순 실린더 빔 기반 구조와 비교하여 20.81% 향상되었고, 최소화 구조에서는 84.68% 감소하는 결과를 보였다(Table 1). 다음으로, BC 구조의 최적화 결과에서는 유효 열전달계수를 최대화하는 구조의 경우 총 16세대를 거치면서 수렴하였고 최소화하는 구조의 경우 총 13세대를 거치면서 형상이 수렴하는 것을 확인했다(Fig. 6(c), (d)). BC 구조의 유효열전도도는 최대화의 경우 단순 실린더 빔 기반의 구조 대비 4.96% 향상되었고 최소화할 때 79.15% 하락하였다(Table 1).
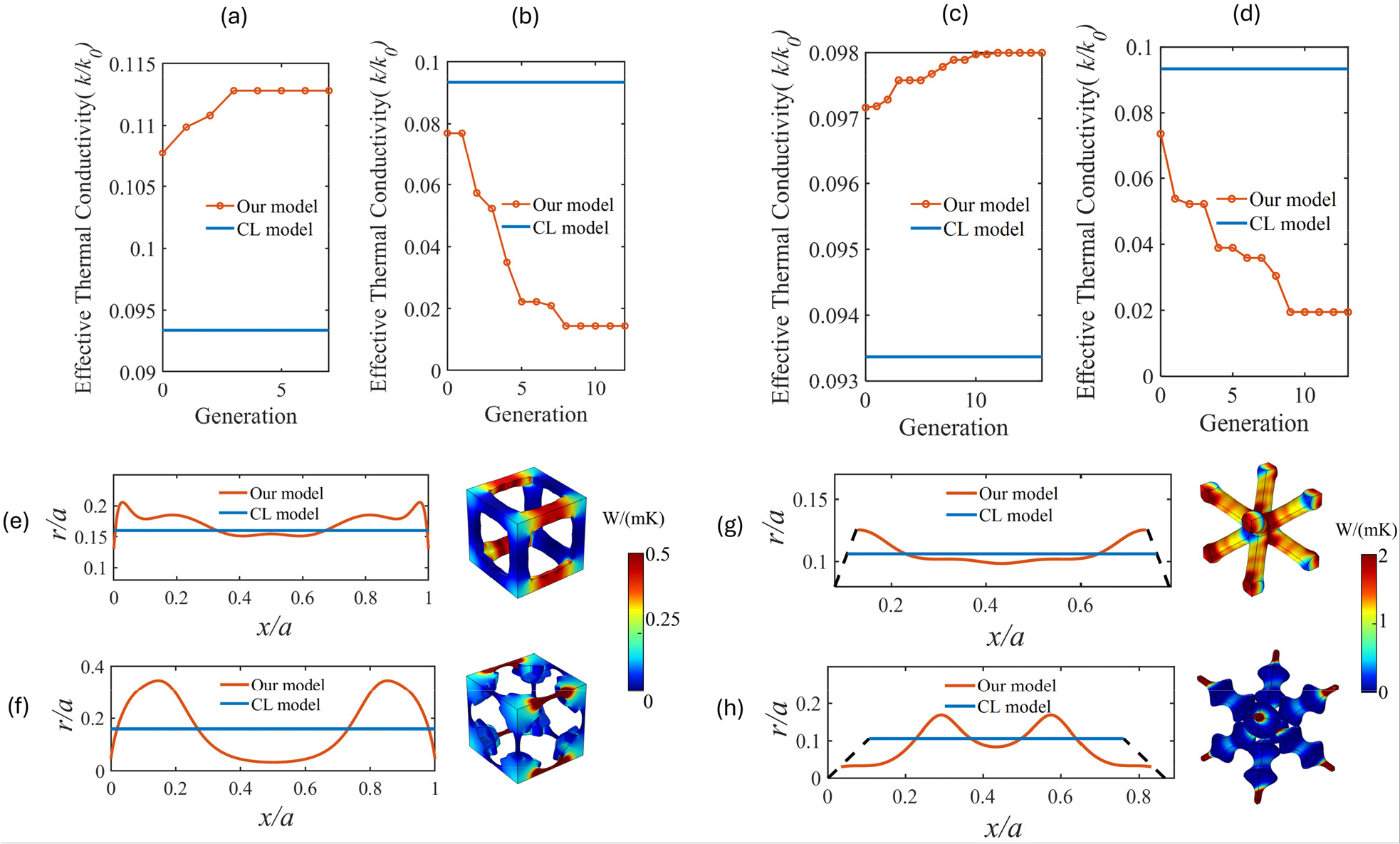
Fig. 6.
The normalized effective thermal conductivity of SC((a) and (c)) and BC structure ((c) and (d)). The thermal conductivity in (a) and (c) ((b) and (d)) are maximized(minimized). The optimal beam shape and heat flux field of the SC lattice with (e) maximized and (f) minimized thermal conductivity. The optimal beam shape and heat flux field of the BC lattice with (g) maximized and (h) minimized thermal conductivity
Table 1.
The normalized effective thermal conductivity (k/k0) of lattice structures
| BC | SC | ||
| CL model | 0.093369 | 0.093369 | |
| Our model | maximum | 0.0979968 | 0.1128 |
| minimum | 0.0194684 | 0.014334 | |
Fig. 6(e)와 Fig. 7(g)에서, 유효 열전도도를 최대화하는 구조(Our model)와 단순 실린더 빔 기반 구조(CL model)의 빔 형상의 단면을 비교하였을 때 BC와 SC 구조에서 모두 구조적으로 매우 유사한 것을 확인할 수 있다.
반대로, Fig. 6(f), (h)에서 유효열전도도를 최소화는 구조(Our model)와 단순 실린더 빔 형상의 단면을 비교하였을 때 구조적인 차이가 큰 것을 확인할 수 있다. 단순 실린더 빔(CL model)은 원통형 구조로 설계되어 있어, 빔의 단면은 일정한 반지름을 가진 직선 형태다. 이러한 직선 단면 설계는 설계의 단순성을 유지하는 장점이 있으나, 구조적 최적화 측면에서 제한적인 결과를 초래할 수 있다. 반면, 본 연구에서 제안한 최적화 방법을 적용한 결과, 빔의 단면은 곡선 형태를 띠게 되어 설계 공간의 유연성이 크게 향상되며, 열적 성능이 최적화된 구조를 도출할 수 있다. 유효열전도도를 최대화하기 위해서는 주어진 온도구배 조건에서 열유동이 균일해야 하며, 반대로 유효 열전도도를 최소화하기 위해서는 열유동의 공간에 대한 편차가 크게 발생해야 한다. 따라서 Fig. 6(f)와 6(h)에 나타났듯이 빔 축에 대해서 반경 변화를 주어서 유동의 집중이 발생하였다. 본 연구에서는 bézier 곡선을 만들 때 최소 반경을 설정하였기 때문에 유한한 반경을 갖는 빔을 얻었지만, 만약 최소 반경 없이 최적 설계를 수행했다면 단면이 0인 빔 형상이 얻어질 것이며 결국 이론적 한계 최소 열전도도는 0이 될 것이라 예상된다.
5.3 유효열전도도와 탄성계수 간의 유사성
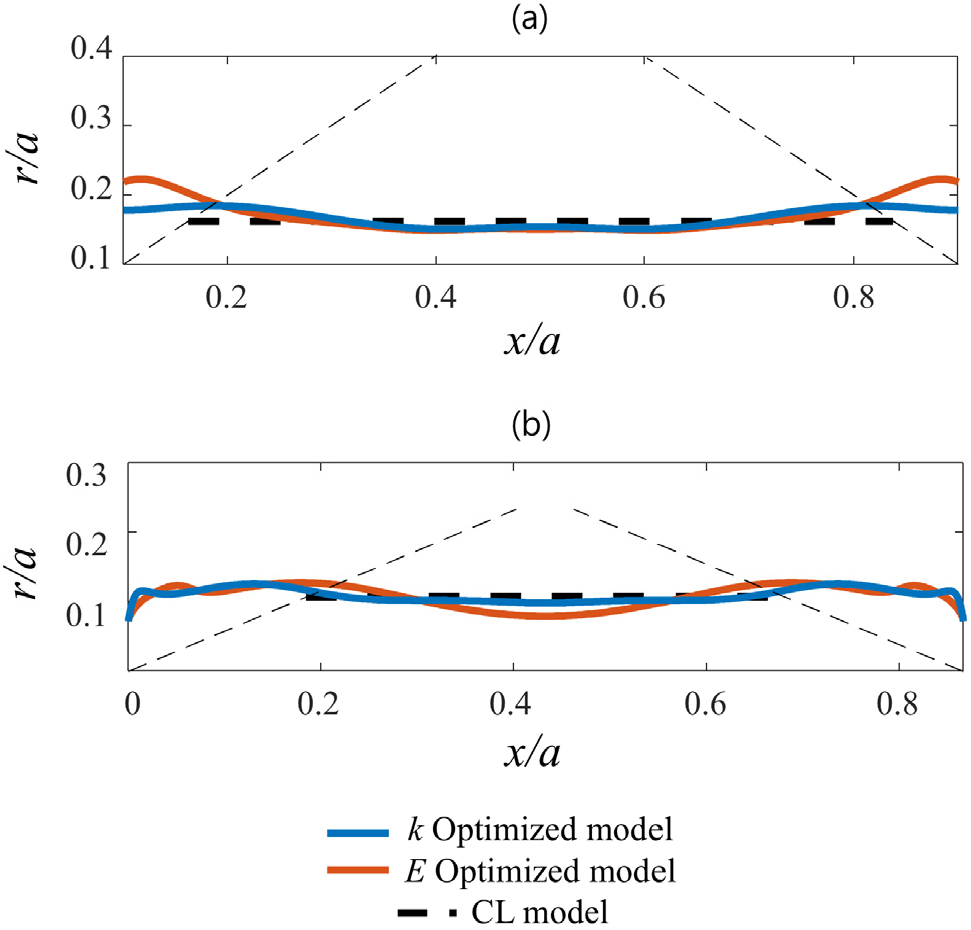
열전도계수(k)와 탄성계수(E)를 포함하는 각각의 물리 방정식은 수학적인 유사성을 가진다(Ryu et al., 2019). 기존 탄성계수를 최대화하는 격자구조를 얻는 연구가 진행되었고(Lee et al., 2022) 이를 본 연구에서 얻은 유효열전도도를 최대화한 최적의 격자구조와 비교하고자 한다. Fig. 7에서 탄성계수와 열전도도를 최대화하는 빔 형상의 단면을 비교하였다. Fig. 7(a)은 SC 구조에 대해 탄성계수와 열전도도를 최적화한 결과이며 Fig. 7(b)은 BC 구조에 대해 최적화한 결과다. BC의 경우 하중이 가해지게 되면 굽힘 응력으로 인해서 빔들이 서로 교차하는 조인트 영역에서 응력 집중이 발생한다. 이러한 응력 집중을 완화하기 위해서 최적의 탄성계수를 갖는 구조는 빔의 축에 따라서 반경 변화를 갖는다.
이러한 반경 변화로 인해서 단면이 작은 부분에 응력집중이 발생하게 되는데, 이러한 응력 집중이 빔들이 서로 교차하는 조인트 부분에서의 응력 집중을 완화시켜 준다. 최적의 열전도를 갖는 경우도 마찬가지로 열유속(heat flux)을 균일하게 만들기 위해서 반경 변화를 만들고 면적이 작은 영역에서 유속 집중을 유도하여 더 분산된 장(field)를 만들게 된다. SC는 BC와 달리 굽힘 응력이 없고 축방향 하중을 받기 때문에 BC에 비해 비교적 균일한 반경을 갖는 곡선이 얻어진다. SC 구조와 BC 구조에서 모두 탄성계수와 열전도도를 각각 최대화하는 빔 형상의 단면은 구조적으로 매우 유사한 것을 확인하였다.
6. 결 론
본 연구에서는 인공신경망을 활용하여 BC와 SC 구조의 상대밀도 및 열 유량을 예측하는 모델을 학습하였고 예측 모델을 바탕으로 유전 알고리즘을 통해 최적의 bézier 곡선 형상을 찾아 유효 열전도도를 최대화 및 최소화하는 구조를 도출하였다.
SC 및 BC 구조 최적화 결과, 유효 열전도도가 기존의 단순한 실린더 빔 형상과 비교하여 개선이 이루어졌음을 확인할 수 있었다. SC 구조의 경우 유효 열전도도를 최대화한 구조에서 20.81%의 성능 향상을, 최소화한 구조에서는 84.68%의 성능 감소를 보였으며, BC 구조에서도 유효 열전도도를 최대화한 구조에서 4.96%의 성능 향상을, 최소화한 구조에서는 79.15%의 성능 감소를 보였으며, 이는 bézier 곡선이 제공하는 높은 유연성을 바탕으로 자유도가 복잡한 빔 형상을 모델링하여 격자구조의 성능을 극대화할 수 있었음을 의미한다.
추가적으로 열전도도와 탄성계수 간의 상관관계를 탐구하였다. 열전도도와 탄성계수를 최적화한 구조의 형상 비교를 통해 각 물성의 유사성을 확인하였다. 이는 재료 과학과 엔지니어링 설계에서 효율적인 형상 최적화 및 성능 개선을 위한 중요한 기초 자료를 제공할 수 있을 것으로 기대된다.
본 연구는 열전도 시뮬레이션을 바탕으로 진행되었다. 이때, 격자구조 내 온도구배를 통한 열전도만을 가정하여 단위 유량을 산출하였고 열전달 및 열복사의 상황을 배제하였다. 추후 연구에서는 열전달 및 열복사를 모두 고려한 열전도 시뮬레이션을 바탕으로 연구를 수행하여 더욱 종합적이고 일반적인 격자구조 열전도 최적설계 방법론을 제시하고자 한다.