Elastic Wave Propagation in Nuclear Power Plant Containment Building Walls Considering Liner Plate and Concrete Cavity

Eunyoung Kim; Boyoung Kim; Jun Won Kang; Hongpyo Lee

doi:10.7734/COSEIK.2021.34.3.167

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 30 June 2021. 167-174
https://doi.org/10.7734/COSEIK.2021.34.3.167

Elastic Wave Propagation in Nuclear Power Plant Containment Building Walls Considering Liner Plate and Concrete Cavity

라이너 플레이트 및 콘크리트 공동을 고려한 원전 격납건물 벽체의 탄성파 전파 해석

Eunyoung Kim¹

Boyoung Kim¹

Jun Won Kang²^*

Hongpyo Lee³

김 은영¹

김 보영¹

강 준원²^*

이 홍표³

¹Graduate Student, Department of Civil Engineering, Hongik University, Seoul, 04066, Korea

²Associate Professor, Department of Civil Engineering, Hongik University, Seoul, 04066, Korea

³Principal Researcher, Central Research Institute, Korea Hydro & Nuclear Power CO., LTD, Daejeon, 34101, Korea

¹홍익대학교 토목공학과 대학원생

²홍익대학교 토목공학과 부교수

³한국수력원자력(주) 중앙연구원 책임연구원

^{*Corresponding Author}

ABSTRACT

Recent investigation into the integrity of nuclear containment buildings has highlighted the importance of developing an elaborate diagnostic method to evaluate the distribution and size of cavities inside concrete walls. As part of developing such a method, this paper presents a finite element approach to modeling elastic waves propagating in the containment building walls of a nuclear power plant. We introduce a perfectly matched layer (PML) wave-absorbing boundary to limit the large-scale nuclear containment wall to the region of interest. The formulation results in a semi-discrete form with symmetric damping and stiffness matrices. The transient elastic wave equations for a mixed unsplit-field PML were solved for displacement and stresses in the time domain. Numerical results show that the sensitivity of displacement, velocity, acceleration, and stresses is large depending on the size and location of the cavity. The dynamic response of the wall slightly differs depending on the existence of the containment liner plate. The results of this study can be applied to a full-waveform inversion approach for characterizing cavities inside a containment wall.

Keywords

reactor containment building

perfectly matched layer

mixed finite element method

forward problem

elastic waves

최근 국내 원자력발전소의 격납건물 벽체와 Containment Liner Plate(CLP) 사이에서 다양한 크기의 공극이 발견됨에 따라 원전 격납건물의 보수를 위해 내부 공극의 분포와 크기를 정밀하게 평가할 수 있는 진단기법의 개발이 요구되고 있다. 이에 따라 이 연구에서는 격납건물 벽체에서의 탄성파 전파거동을 계산하는 2차원 유한요소해석 기법을 제시한다. 격납건물 벽체를 기반으로 해석영역을 구성하고 경계면에서의 반사파를 제거하기 위해 수치적 파동흡수 경계층인 perfectly matched layer를 도입하였다. Galerkin 기반 혼합유한요소법을 이용해 2차원 유한영역에서 탄성파 파동방정식의 해를 구하여 충격하중에 대한 격납건물 벽체의 변위와 응력을 계산하였다. 제시한 수치적 기법을 이용하여 격납건물 콘크리트 벽체의 CLP 부착 유무와 공동의 위치 및 크기 변화에 따른 탄성파 전파거동을 살펴보았다. 이 연구의 결과는 원전 격납건물 내부의 공동을 진단하는 탄성파 전체파형 역해석 기법 개발에 활용될 수 있다.

키워드

원전 콘크리트 벽체

perfectly matched layer

혼합유한요소법

정해석

탄성파

MAIN

1. 서 론
2. PML을 이용한 원전 격납건물 벽체의 탄성파 정해석
2.1 유한요소 정식화
2.2 격납건물 벽체의 탄성파 정해석
3. 공동의 위치 및 크기에 따른 격납건물 벽체의 탄성파 전파
3.1 공동의 위치에 따른 탄성파 전파
3.2 공동의 크기에 따른 탄성파 전파
4. 결 론

1. 서 론

2000년대 미국의 일부 원전에서 라이너 플레이트 부식이 보고되고 2012년 미국 Crystal Diver Unit #3와 Davis-Besse 원전의 콘크리트 벽체에 박리가 발견되는 등 다양한 결함이 발생함에 따라 원전 콘크리트 구조물의 열화 및 결함 평가에 대한 구조건전성 평가 기술의 중요성이 높아지고 있다. 최근 국내에서도 가동 원전의 콘크리트 벽체와 라이너 플레이트(containment liner plate; CLP) 사이에서 다수의 공극이 발견된 바 있다. 원자력 발전소의 경제적 효과와 사고 시 결과의 중대성 등을 고려하면 원전 격납건물의 정밀 건전성 평가는 매우 중요하며 벽체 내부의 공극 분포와 크기를 평가할 수 있는 신뢰도 높은 진단기법의 개발이 필요하다. 원전 콘크리트 벽체는 매우 두껍고 콘크리트 재료가 복잡한 열화 특성을 보여 시간의 경과에 따른 손상 정도를 평가하기가 쉽지 않다. 또한 라이너 플레이트와 합성된 복합 구조이므로 다양한 제약조건을 극복하면서 내부의 결함 상태를 파악하기 위해서는 혁신적인 비파괴평가 기술 개발이 요구된다. 원전 선진국에서는 원전 운영과 보수 및 보강 사례를 바탕으로 충격반향법, 전자기파 탐사법, 초음파 기법 등 원전 콘크리트 벽체의 결함 분석에 효과적인 비파괴평가 기술을 개발해 왔다. 이러한 파동을 이용한 비파괴평가 기법들 중 비선형 역해석 기반 건전성 평가기법은 결함을 포함하는 콘크리트 벽체에서의 정밀한 파동해석 결과를 필요로 한다. 이 연구에서는 비선형 역해석(Kang, 2013; Kang and Pakravan, 2013) 기반 건전성 평가를 위해 공동이 있는 격납건물 벽체의 시간영역 탄성파 해석기법과 그 결과를 제시한다.

이 논문에서는 먼저 원전 격납건물 벽체에서 탄성파 전파거동을 계산하는 유한요소해석 기법을 제시한다. 원전 격납건물 벽체의 2차원 유한요소해석 모델을 구성하고 파동흡수 경계조건인 perfectly matched layer(PML)를 도입하여 해석영역의 경계에서 반사파가 발생하지 않도록 하였다(Kang and Kallivokas, 2010; Kim and Kang, 2019). Galerkin 기반 혼합유한요소법(mixed finite element method)을 이용해 탄성파 파동방정식을 풀어서 충격하중에 대한 격납건물 벽체의 변위와 응력을 계산하였다. 혼합유한요소법으로부터 구한 해의 안정성을 확보하기 위하여 변위와 응력에 대해 모두 2차 형상함수를 사용하였다. 근사된 함수를 이용해 semi-discrete 운동방정식을 제시하였고 내연적 시간적분법 중 하나인 Newmark-β 방법을 이용해 시간영역 파동방정식의 수치해를 계산하였다(Youn and Kang, 2018). 내부 공동을 포함하는 원전 격납건물 벽체에 대해 공동의 위치와 크기 변화를 고려하여 탄성파 전파 해석 결과를 제시하였다. 이러한 탄성파 해석기법은 원전 격납건물 내부 공동 진단을 위한 광대역의 탄성파 전체파형 역해석(full- waveform inversion; FWI) 기법에 적용될 수 있다.

2. PML을 이용한 원전 격납건물 벽체의 탄성파 정해석

2.1 유한요소 정식화

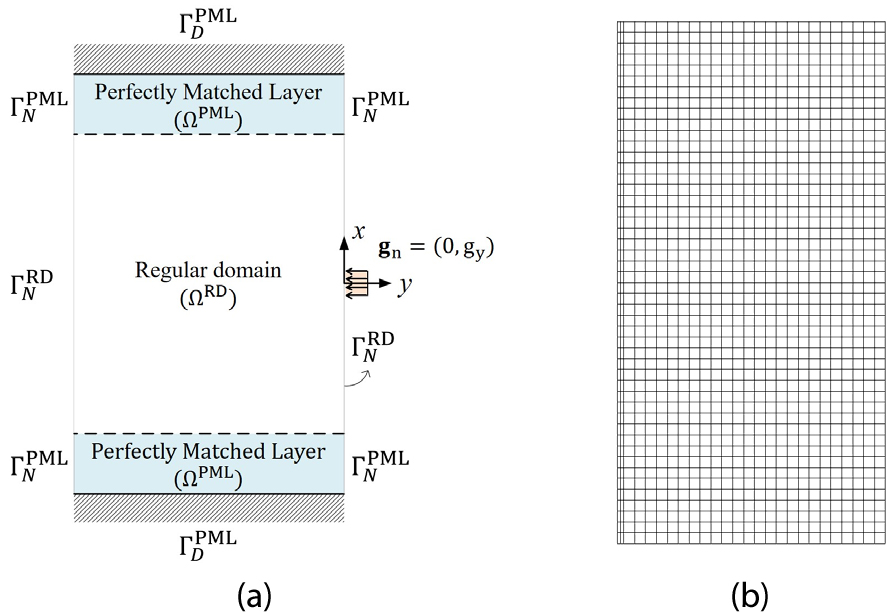
원전 격납건물에서의 탄성파 전파거동을 계산하기 위해서 격납건물 벽체의 일부분을 2차원 유한 해석영역으로 구성하고 해석영역의 상하 경계에는 반사파가 발생하지 않도록 파동흡수 경계조건 PML을 부착하였다. Fig. 1은 PML을 포함하는 격납건물 벽체의 2차원 해석영역과 이 영역의 유한요소 모델을 나타낸다. 이러한 영역에서의 탄성파 전파거동은 다음과 같은 변위와 응력의 복합 지배방정식으로 표현될 수 있다(Fathi et al., 2015; Kucukcoban, 2010).

(1a)

\nabla \cdot [μ \{\nabla u + (\nabla u)^{T}\} + λ (\nabla u) I] + f = ρ \ddot{u} in Ω^{Reqular}

(1b)

\nabla \cdot ({\dot{S}}^{T} \tilde{Λ_{e}} + S^{T} \tilde{Λ_{p}}) = ρ (a \ddot{u} + b \ddot{u} + c u) i n Ω^{PML}

(1c)

D : (a \ddot{S} + b \dot{S} + c S) = \frac{1}{2} [(\nabla \dot{u}) \tilde{Λ_{e}} + \tilde{Λ_{e}} (\nabla \dot{u}) + (\nabla u) \tilde{Λ_{p}} + \tilde{Λ_{p}} {(\nabla u)}^{T}] i n Ω^{PML}

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F1.jpg

Fig. 1.

(a) Two-dimensional PML-truncated computational domain; (b) Finite element model

여기서, $u$ 와 $S$ 는 각각 2차원 변위 벡터와 응력 텐서이며, $f$ 는 체적력 벡터이다. $ρ$ 는 매질의 밀도이고 $D$ 는 변형률과 응력의 관계를 나타내는 compliance 텐서이다. $λ$ 와 $μ$ 는 Lamé 상수이다. 파라미터 $a$ , $b$ , $c$ 와 텐서 $\tilde{Λ_{e}}$ , $\tilde{Λ_{p}}$ 는 PML의 감쇠함수 $α, β$ 로 구성되며 $\tilde{Λ_{e}}$ 는 소멸파(evanescent wave)의 감쇠함수인 $β$ 로 구성되는 2차 텐서이고, $\tilde{Λ_{p}}$ 는 진행파(propagating wave)에 대한 감쇠함수인 $α$ 로 구성되는 2차 텐서이다(Kang and Kallivokas, 2010; Kim and Kang, 2019). 식 (1a)는 일반영역(regular domain)에서의 Navier 방정식이고 식 (1b)와 (1c)는 PML에서의 동탄성 지배방정식이다. 특히 식 (1b)는 PML에서의 평형방정식이고 식 (1c)는 PML에서의 구성 방정식과 적합조건식의 혼합식이다. Fig. 1과 같은 영역에서 탄성파 전파 문제는 식 (1)의 지배방정식과 함께 식 (2)의 경계조건, 계면조건, 초기조건으로 구성된다.

(2a)

[μ \{\nabla u + {(\nabla u)}^{T}\} + λ (\nabla u) I] n = g_{n} on Γ_{N}^{R D} \times (0, T]

(2b)

({\dot{S}}^{T} \tilde{Λ_{e}} + S^{T} \tilde{Λ_{p}}) n = 0 on_{N}^{P M L}

(2c)

u (x, t) = 0 on Γ_{N}^{P M L} \times (0, T]

(2d)

u^{R D} = u^{P M L} on Γ^{I} \times (0, T]

(2e)

[μ \{\nabla u + (\nabla u)^{T}\} + λ (\nabla u) I] n = - ({\dot{S}}^{T} \tilde{Λ_{e}} + S^{T} \tilde{Λ_{p}}) n on Γ^{I} \times (0, T]

(2f)

u (x, 0) = 0, \dot{u} (x, o) = 0 in Ω (Ω^{R D} \cup Ω^{P M L})

(2g)

S (x, 0) = 0, \dot{S} (x, o) = 0 in Ω (Ω^{RD} \cup Ω^{PML})

식 (2a)와 식 (2b)는 각각 일반영역과 PML을 경계로 하는 유한영역에서의 Neumann 경계조건이다. 식 (2c)는 PML을 경계로 하는 유한영역의 Dirichlet 경계조건이다. 식 (2d)와 (2e)는 각각 일반영역과 PML 계면에서의 변위와 응력의 연속조건을 나타내며 식 (2f)와 (2g)는 초기조건이다. 이러한 초기-경계값 문제에서 변위 $u$ 와 응력 $S$ 는 Galerkin 기반 혼합유한요소법을 이용하여 구할 수 있다. 식 (1a)와 식 (1b)에 테스트 벡터 $\tilde{w} (x)$ 를 내적하고 각각의 영역에 대해서 부분적분한 후 식 (2d)와 식 (2e)의 계면조건을 적용하면 식 (3a)의 변분식을 얻을 수 있다. 마찬가지로 식 (1c)에 테스트 텐서 $T (x)$ 를 내적하여 전체 영역에 대해 부분적분하면 식 (3b)를 얻을 수 있다.

(3a)

\int_{Ω^{RD}}^{} \nabla w : \{μ [\nabla u + {(\nabla u)}^{T}] + λ (\nabla u) I\} d Ω + \int_{Ω^{PML}} \nabla \tilde{w} : ({\dot{S}}^{T} Λ_{e} + S^{T} Λ_{e}) d Ω + \int_{Ω^{RD}} \tilde{w} \cdot ρ \ddot{u} d Ω + \int_{Ω^{PML}} \tilde{w} : ρ (a \ddot{u} + b \dot{u} + c u) d Ω + \int_{Γ^{RD}} \tilde{w} \cdot g_{n} d Γ + \int_{Ω^{RD}} \tilde{w} \cdot f d Ω

(3b)

\int_{Ω^{PML}} \tilde{T} : [D : (a \ddot{S} + b \dot{S} + c S)] d Ω = \frac{1}{2} \int_{Ω^{PML}} \tilde{T} : [(\nabla \dot{u}) \tilde{Λ_{e}} + \tilde{Λ_{e}} {(\nabla \dot{u})}^{T} + (\nabla u) \tilde{Λ_{p}} + \tilde{Λ_{p}} {(\nabla u)}^{T}] d Ω

식 (3)에서 변위 $u$ 와 응력 $S$ 는 $u \in H^{1} (Ω) \times (0, T]$ 와 $S \in L^{2} (Ω) \times (0, T]$ 의 함수공간에 속하고, 각각 기저함수(basis function) $Φ_{i} (x) \in H^{1} (Ω)$ , $Ψ_{i} (x) \in L^{2} (Ω)$ 를 이용하여 다음과 같이 근사할 수 있다. 가중치 함수 $\tilde{w} (x)$ , $T (x)$ 도 동일한 기저함수를 이용하여 근사한다.

(4a)

u (x, t) ≃ Φ^{T} (x) u (t)

(4b)

S (x, t) ≃ Ψ^{T} (x) S (t)

(4c)

\tilde{w} (x) ≃ w^{T} Φ (x)

(4d)

\tilde{T} (x) ≃ T^{T} Ψ (x)

이 연구에서는 혼합유한요소법 해의 안정성을 확보하기 위하여 $Φ_{i} (x)$ 와 $Ψ_{i} (x)$ 모두 2차의 기저함수를 선택하였다. 만약 $Φ_{i} (x)$ 와 $Ψ_{i} (x)$ 에 대해 다른 차수의 기저함수 쌍을 선택하면 불안정한 해를 얻는다. 식 (4)를 식 (3)에 대입하면 $M \ddot{d} + C \dot{d} + Kd = F$ 의 semi-discrete 운동방정식을 얻을 수 있다. 이 운동방정식을 시간에 대해 적분하여 각 노드에서의 변위와 응력으로 이루어진 벡터 $d = {[u_{x} u_{y} S_{x x} S_{y y} S_{s y}]}^{T}$ 를 구할 수 있다. 이 운동방정식의 질량행렬, 감쇠행렬, 강성행렬, 힘벡터는 다음과 같다.

(5a)

M = [\begin{matrix} M_{a} & 0 & 0 & 0 & 0 \\ M_{a} & 0 & 0 & 0 \\ - N_{a} & Z_{a} & 0 \\ s y m & - N_{a} & 0 \\ - G_{a} \end{matrix}]

(5b)

C = [\begin{matrix} M_{b} & 0 & A_{y x} & 0 & A_{x y} \\ M_{b} & 0 & A_{x y} & A_{y x} \\ - N_{b} & Z_{b} & 0 \\ s y m & - N_{b} & 0 \\ - G_{b} \end{matrix}]

(5c)

K = [\begin{matrix} M_{c} & 0 & B_{y x} & 0 & B_{x y} \\ M_{c} & 0 & B_{x y} & B_{y x} \\ - N_{c} & Z_{c} & 0 \\ s y m & - N_{c} & 0 \\ - G_{c} \end{matrix}]

(5d)

F = {[{f^{e}}_{x} {f^{e}}_{y} 0 0 0]}^{T}

위 식에서 각 부분행렬 및 벡터의 요소는 아래와 같다.

(6a)

f_{x}^{e} = \int_{Γ_{N}^{RD}}^{} Φ g_{x} (x, t) d Γ + \int_{Ω}^{} Φ a f_{x} d Ω

(6b)

f_{y}^{e} = \int_{Γ_{N}^{RD}}^{} Φ g_{y} (x, t) d Γ + \int_{Ω}^{} Φ a f_{y} d Ω

(6c)

A_{i j} = \int_{Ω}^{} α_{i} \frac{\partial Φ}{\partial j} Ψ^{T} d Ω i, j = x, y

(6d)

B_{i j} = \int_{Ω}^{} β_{i} \frac{\partial Φ}{\partial j} Ψ^{T} d Ω i, j = x, y

(6e)

M_{k} = \int_{Ω}^{} k ρ Φ Φ^{T} d Ω k = a, b, c

(6f)

N_{k} = \int_{Ω}^{} k \frac{λ + 2 μ}{4 μ (λ + μ)} Ψ Ψ^{T} d Ω k = a, b, c

(6g)

Z_{k} = \int_{Ω}^{} k \frac{λ}{4 μ (λ + μ)} Ψ Ψ^{T} d Ω k = a, b, c

(6h)

G_{k} = \int_{Ω}^{} k \frac{1}{μ} Ψ Ψ^{T} d Ω k = a, b, c

식 (6a)와 (6b)의 $g (x, t)$ 는 식 (2)의 우변 항을 나타내는 traction 함수이며 $a = α_{x} α_{y}$ , $b = α_{x} β_{y} + α_{y} β_{x}$ , $C = β_{x} β_{y}$ 이고 $f_{ㅌ}$ 와 $f_{y}$ 는 각각 체적력의 성분이다.

2.2 격납건물 벽체의 탄성파 정해석

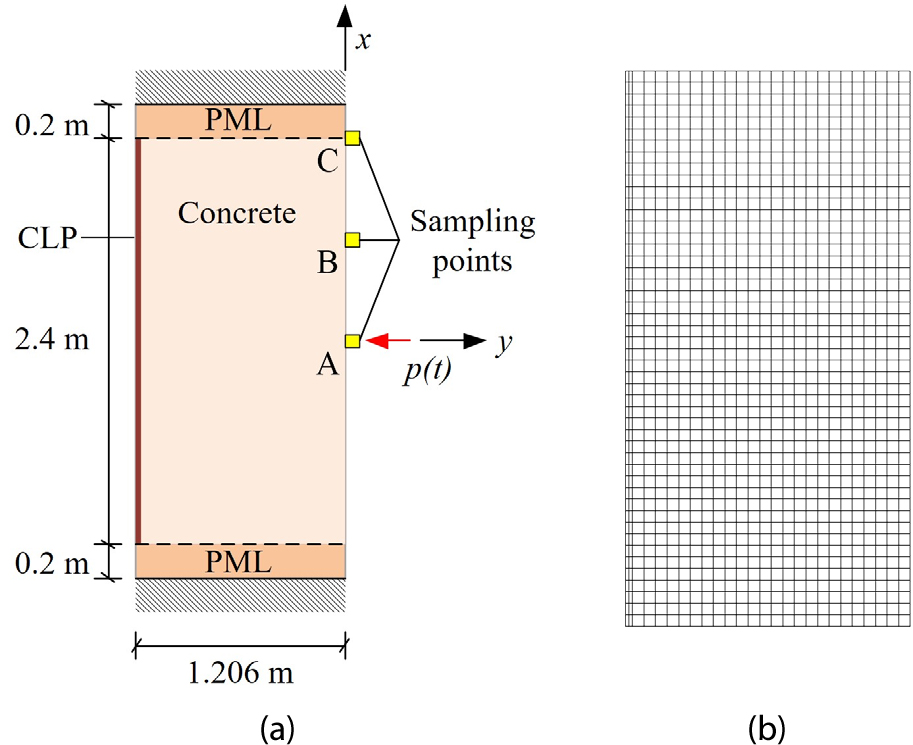
Fig. 2와 같이 원전 격납건물 벽체의 단면을 나타내는 가로 1.206m, 세로 2.4m의 해석영역을 구성하였다. 해석영역의 경계면에서 반사파가 발생하지 않도록 상하 경계에 0.2m 두께의 PML을 부착하였다. 전체 가로 길이 중 1.2m는 콘크리트 벽체이고 0.006m는 라이너 플레이트이다. 콘크리트의 탄성계수는 30GPa이고 라이너 플레이트의 탄성계수는 200GPa이며 프와송 비는 모두 0.25이다. 이에 따라 Lamé 상수 $μ$ 와 $λ$ 는 콘크리트의 경우에 경우 모두 12GPa이고 라이너 플레이트의 경우에는 모두 80GPa이다. 벽체의 밀도는 전 영역에 걸쳐 2500 kg/m³으로 가정하였다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F2.jpg

Fig. 2.

(a) Two-dimensional PML-truncated domain of reactor containment buildings; (b) Finite element model

격납건물 벽체의 유한요소모델은 8절점 사각형 요소로 구성되며, 변위와 응력 모두 2차 Legendre 형상함수를 이용해 근사된다. 요소의 길이는 세로방향으로 0.01m이고 가로방향으로는 라이너 플레이트 부분이 0.003m, 콘크리트 벽체 부분이 0.01m이다.

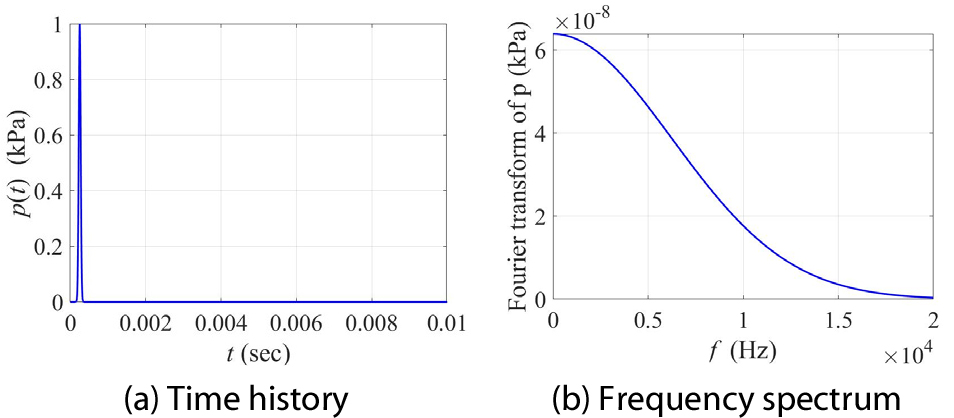
Fig. 3는 해석영역의 표면에 가해진 충격하중의 시간이력과 주파수 스펙트럼을 나타낸다. 이 하중은 시간에 대한 Gaussian 펄스 형태의 함수이고 식 (7)과 같이 표현된다. 이 함수를 이용해 압력으로서의 하중을 벽체 표면에 가하는데, 최대 크기는 1 kPa이며 최대 주파수는 약 20 kHz이다. 전체 해석 시간은 0.01s이고 time step은 2 $μ s$ 이다.

(7)

p (t) = \exp [- (t - 0.00025)^{2} / (1.3 \times 10^{- 9})]

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F3.jpg

Fig. 3.

Time history and frequency spectrum of the Gaussian pulse

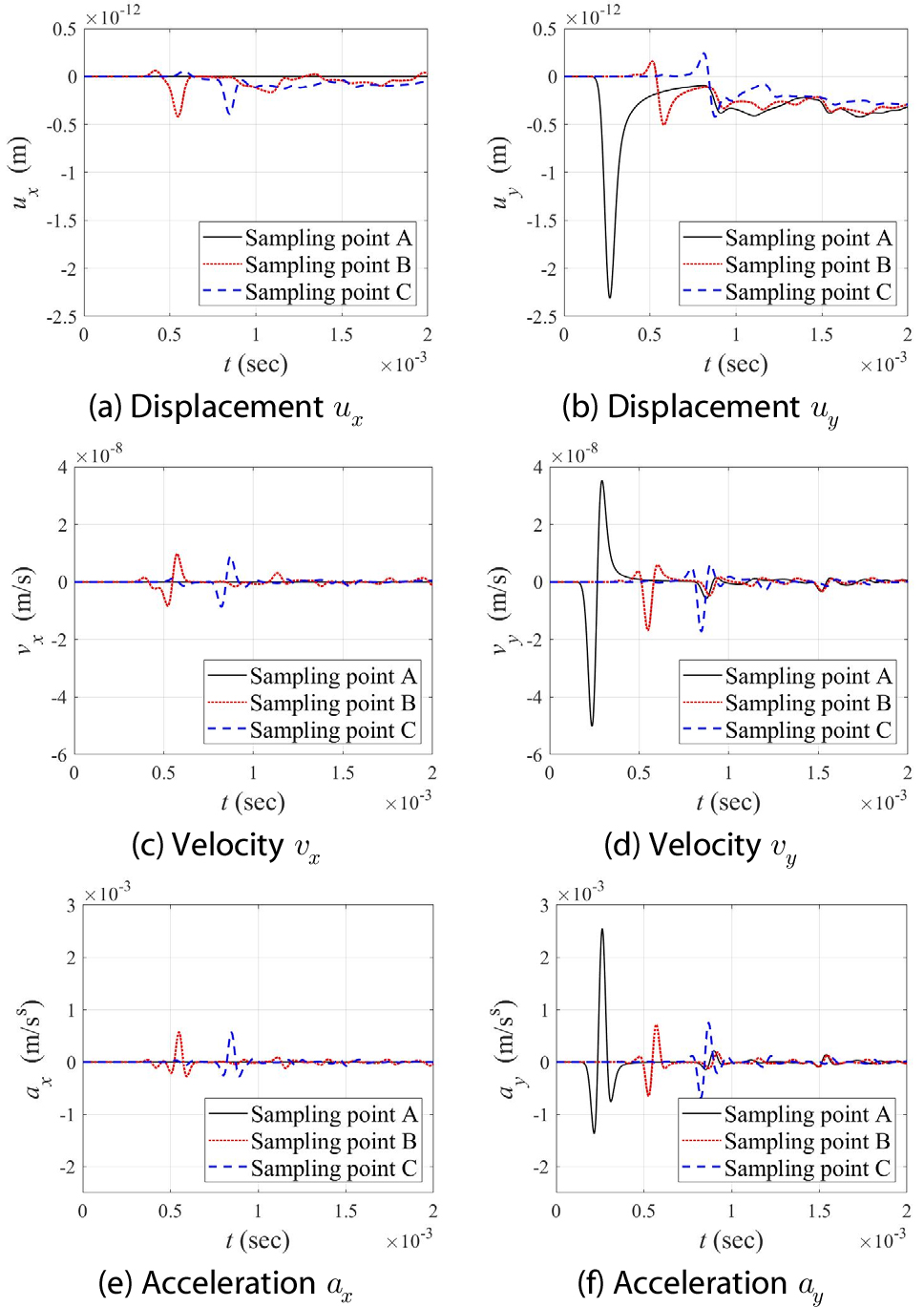
Fig. 4는 해석영역의 표면에 Fig. 3와 같은 하중이 가해졌을 때 A(0,0), B(0.6m, 0), C(1.2m, 0) 세 샘플링 포인트에서의 변위, 속도, 가속도응답의 시간이력을 나타낸다. A, B, C의 위치는 Fig. 2에서 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F4.jpg

Fig. 4.

Time history of the containment wall responses at three sampling points

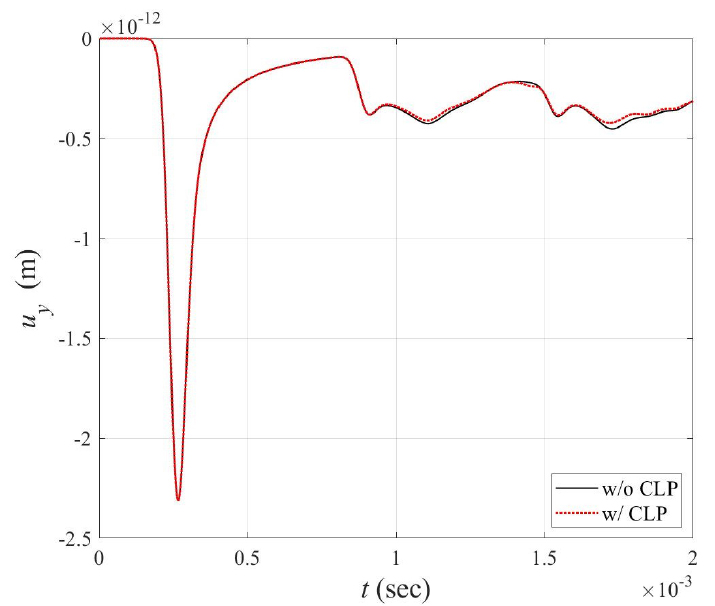
CLP 부착 유무에 따른 A(0,0) 위치에서의 변위응답의 시간이력을 Fig. 5에 제시하였다. 약 0.8ms부터 왼쪽 경계면으로부터의 반사파가 감지된다. CLP가 부착되어 있는 경우가 그렇지 않은 경우에 비해 절대변위가 다소 감소하지만 그 차이는 크지 않음을 알 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F5.jpg

Fig. 5.

Time history of displacement at sampling point A for the cases w/ and w/o CLP attachment

3. 공동의 위치 및 크기에 따른 격납건물 벽체의 탄성파 전파

이 장에서는 콘크리트 내부 공동의 위치와 크기에 따른 탄성파 전파거동을 살펴보고자 한다. Fig. 2와 같은 기존의 해석영역에 위치 및 크기가 다른 사각형 공동을 추가하였다. 공동의 위치 변화에 의한 벽체 응답의 변화를 살펴보고 공동의 크기 변화에 의한 탄성파 전파거동을 계산하여 공동의 경계면에서 발생한 반사파의 영향을 파악하였다. 이러한 결과는 격납건물 벽체 내부의 Lamé 상수 $μ$ 와 $λ$ 를 재구성하는 2차원 탄성파 FWI 해석에 활용할 수 있다.

3.1 공동의 위치에 따른 탄성파 전파

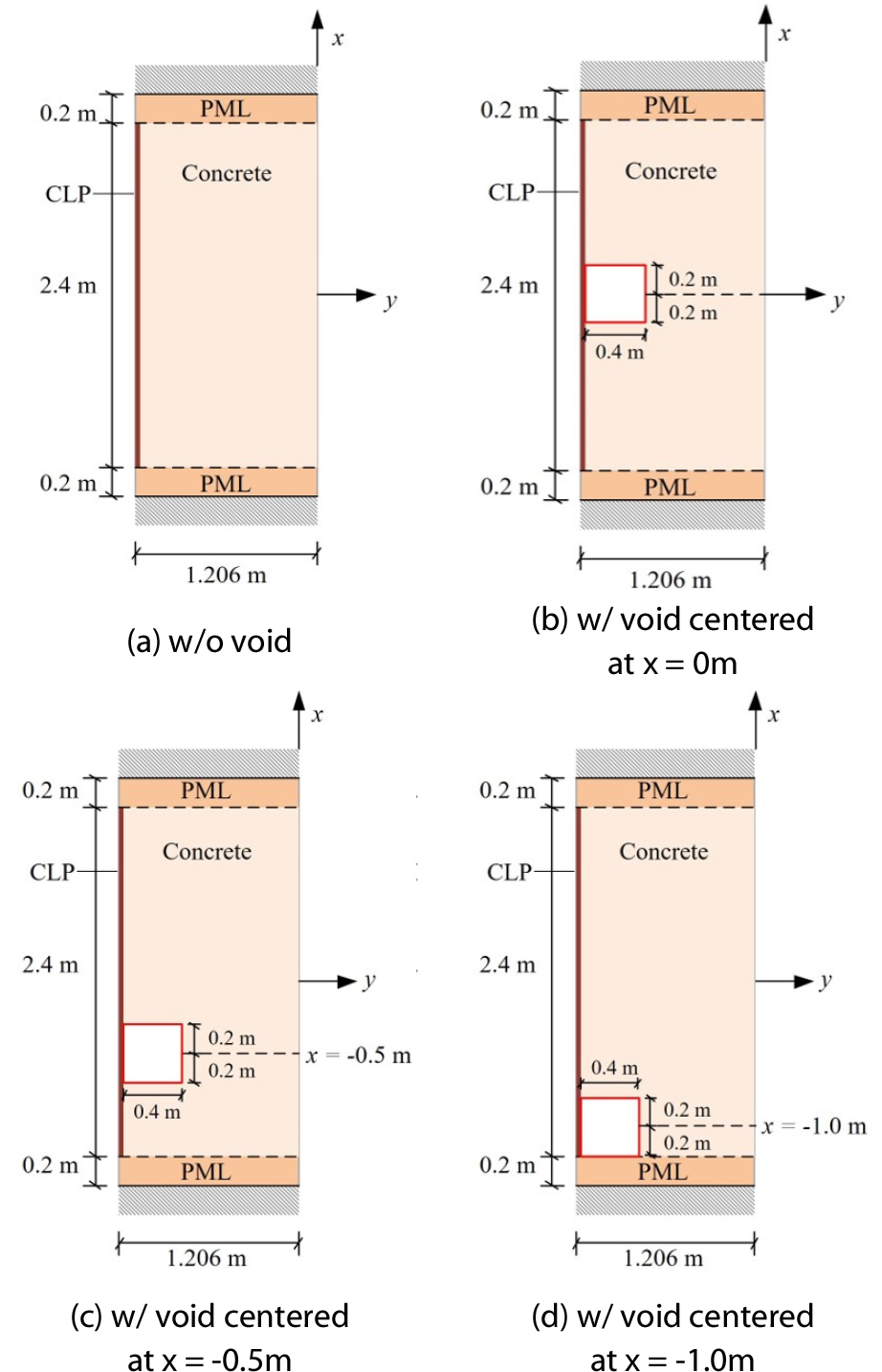
한 변의 길이가 0.4m인 정사각형 형태의 공동을 격납건물 벽체의 세로 방향으로 이동시킴에 따른 탄성파 응답의 변화를 살펴보았다. 벽체의 가로 방향인 y축 방향으로는 공동을 CLP의 배면에 고정하였다. 공동의 중심을 세로 방향의 정중앙부터 아래로 0.5m, 1.0m 씩 이동시켰다. Fig. 6는 공동의 유무 및 위치에 따른 네 개의 격납건물 벽체를 나타낸다. 사용한 하중, 하중의 재하 위치, 샘플링 포인트의 위치는 2.2절에 제시된 것과 같다. 공동의 위치를 변화시키고 하중 재하 위치와 응답 측정 위치를 고정함으로써 공동으로부터 하중 재하 및 응답 측정 위치까지의 거리 변화에 따른 탄성파 전파거동을 살펴볼 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F6.jpg

Fig. 6.

Computational domains of the containment wall with various locations of the void

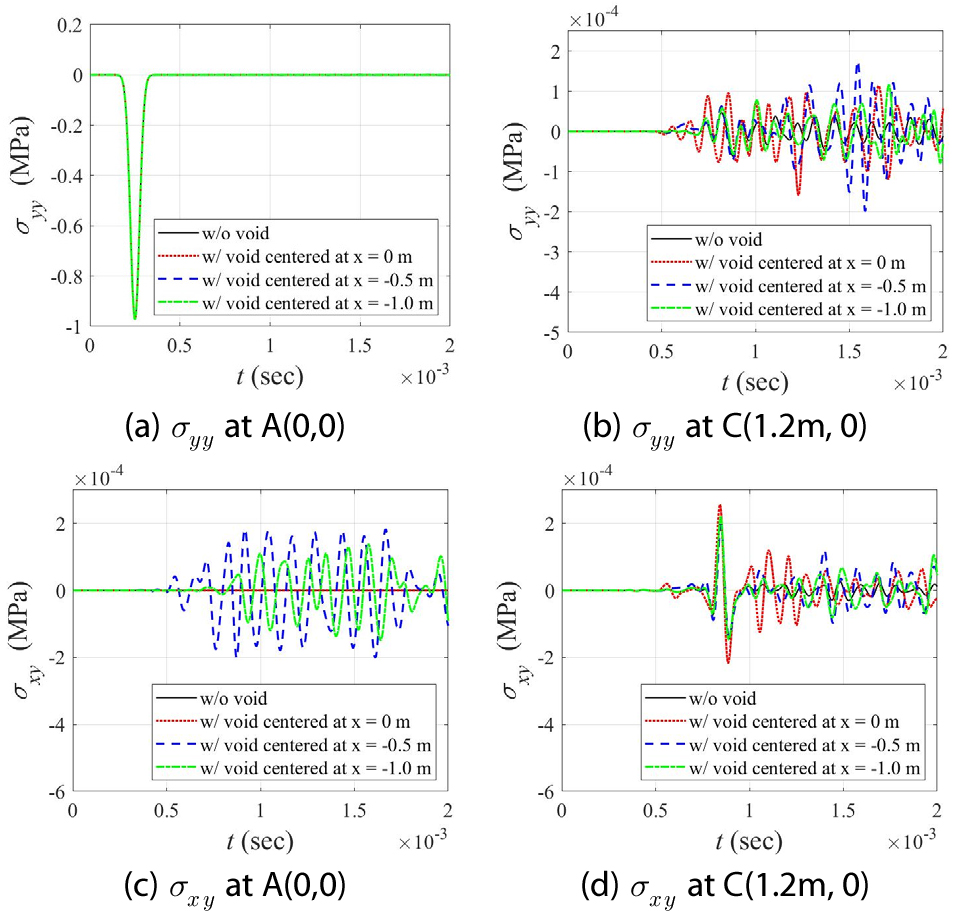
Fig. 7에 공동 위치에 따른 A(0,0)와 C(1.2m, 0)에서 수직응력 및 전단응력의 시간이력을 제시하였다. 공동 중심이 y축에 위치한 경우에는 A(0,0)에서의 전단응력이 0에 가깝지만, 공동 중심이 y축에서 벗어난 경우에는 전단응력 응답 내 반사파의 영향이 증가하여 응력응답의 변동이 크다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F7.jpg

Fig. 7.

Time history of the stresses with respect to various void locations

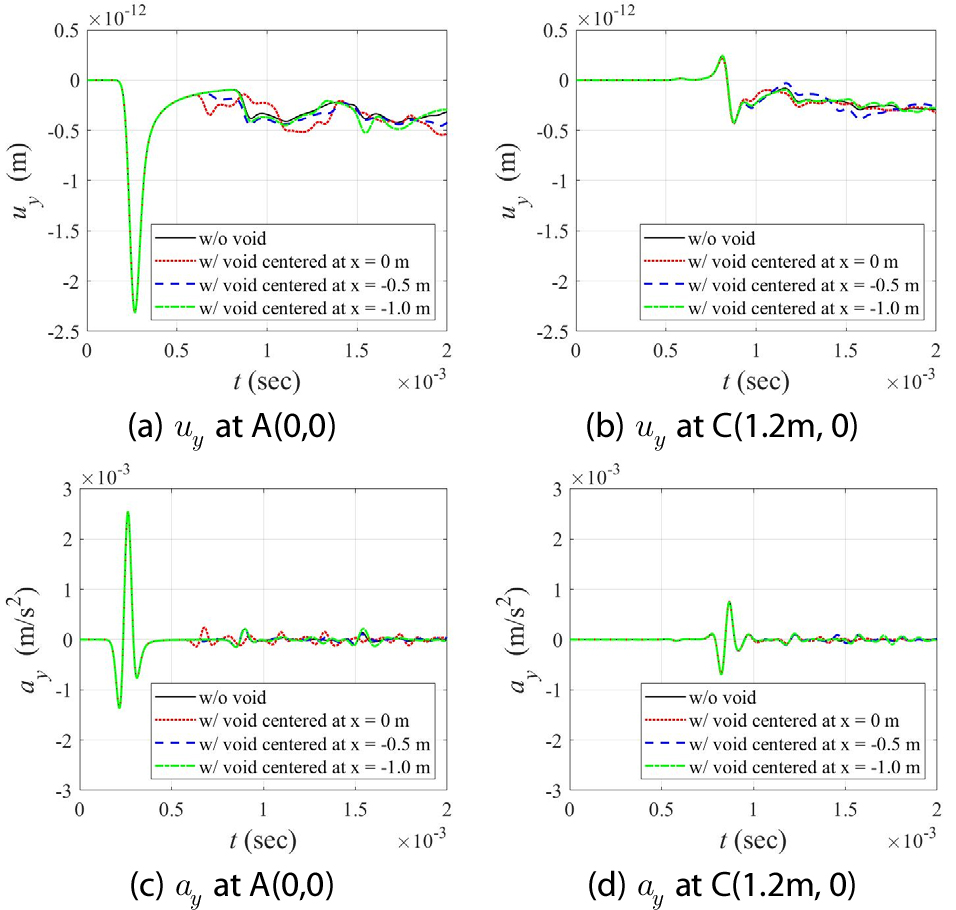
Fig. 8은 공동 위치에 따른 샘플링 포인트 A(0,0)와 C(1.2m, 0)에서의 변위응답 및 가속도응답을 나타낸다. 두 샘플링 포인트에서의 변위응답 및 가속도응답 시간이력을 통해 공동 중심의 위치가 하중 재하 위치와 응답 측정 위치로부터 멀어질수록 공동의 경계면에서 발생한 반사파의 영향이 감소함을 확인할 수 있다. 또한 공동이 응답 측정 위치로부터 멀어짐에 따라 반사파의 도달 시간은 증가한다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F8.jpg

Fig. 8.

Time history of the displacement and acceleration with respect to various void locations

3.2 공동의 크기에 따른 탄성파 전파

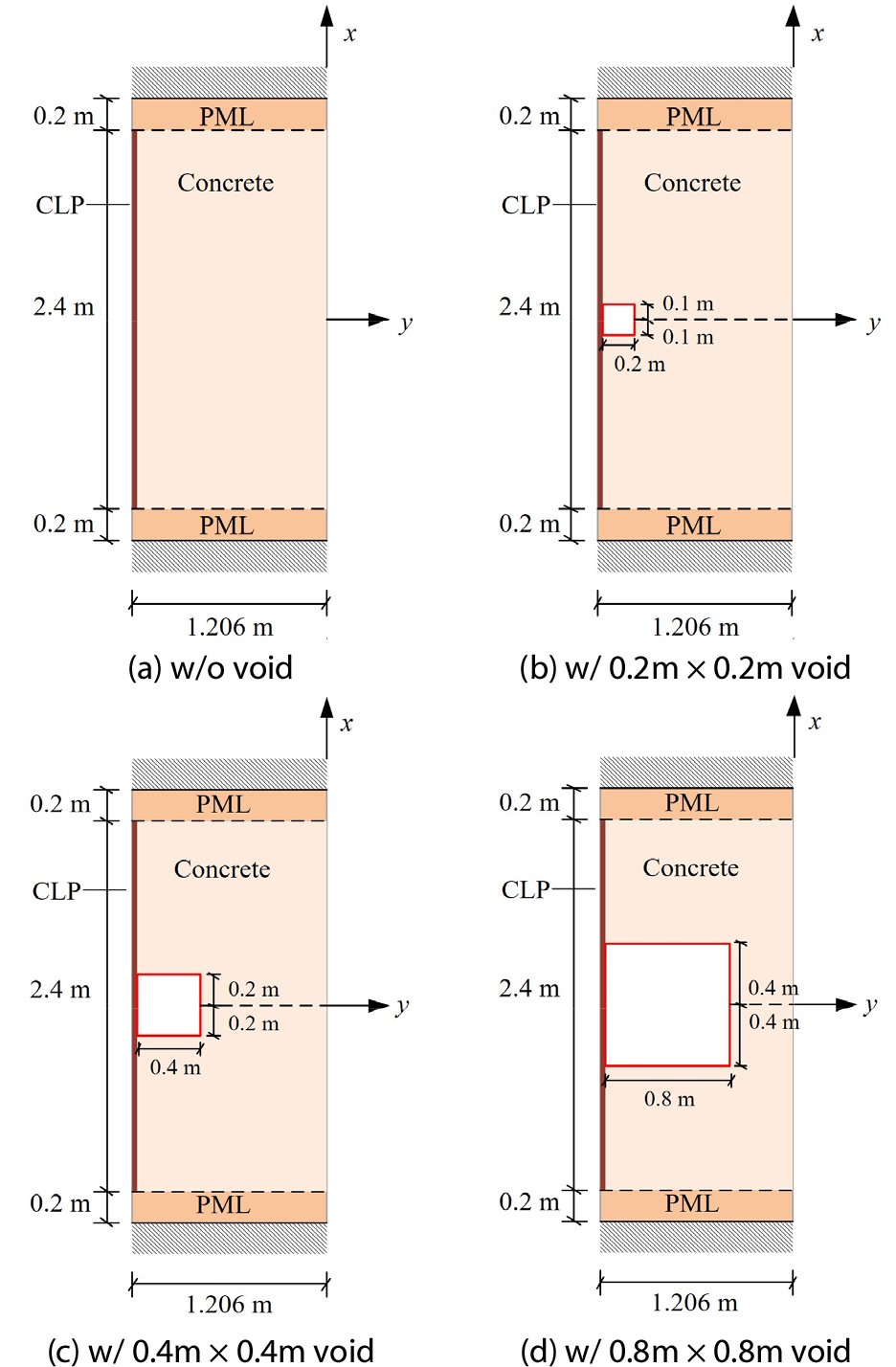
해석영역 내부의 공동은 정사각형 모양이며, 가로 방향으로는 CLP의 배면에, 세로 방향으로는 정중앙에 공동의 중심이 위치한다. 공동이 없는 경우와 공동의 변의 길이가 0.2m, 0.4m, 0.8m인 경우에 대한 탄성파 해석 결과를 살펴보았다. Fig. 9에 공동의 크기가 다른 네 개의 CLP 벽체 모델을 제시하였다. 사용한 하중과 샘플링 포인트의 위치는 2.2와 같다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F9.jpg

Fig. 9.

Computational domains of the containment wall with various void sizes

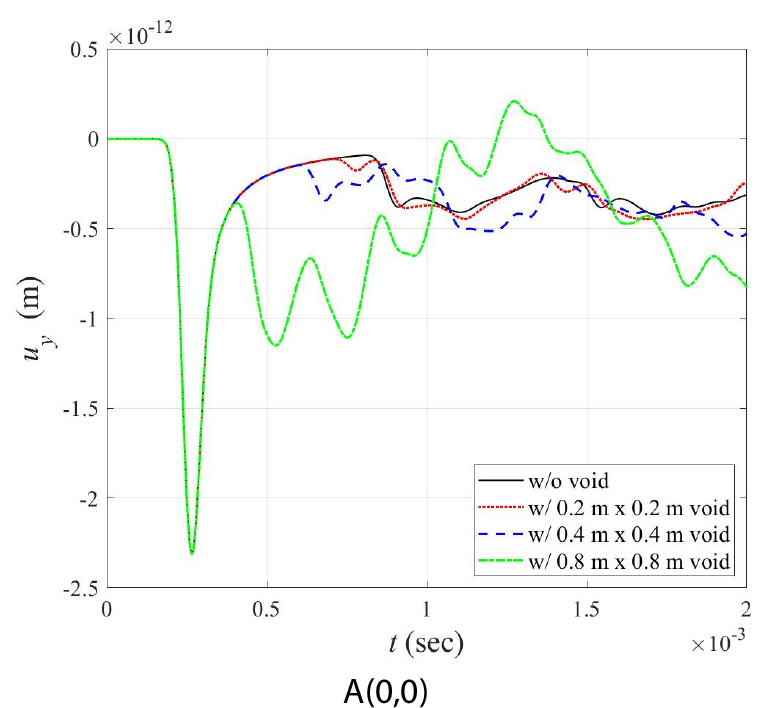
Fig. 10에 공동 크기에 따른 샘플링 포인트 A(0,0)에서의 변위응답을 제시하였다. 공동이 없는 경우와 공동이 있는 경우의 $u_{y}$ 응답을 비교하여 공동의 경계면에서 발생한 반사파의 패턴 및 크기의 차이를 확인할 수 있다. 공동이 존재함으로써 반사파의 위상이 바뀌고 공동의 크기가 증가함에 따라 벽체 표면에 도달하는 반사파의 크기가 달라짐을 알 수 있다. 공동의 크기가 가장 큰 (d)의 경우에 반사파의 도달 시간이 가장 짧다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F10.jpg

Fig. 10.

Time history of the displacement $u_{y}$ with respect to various void sizes

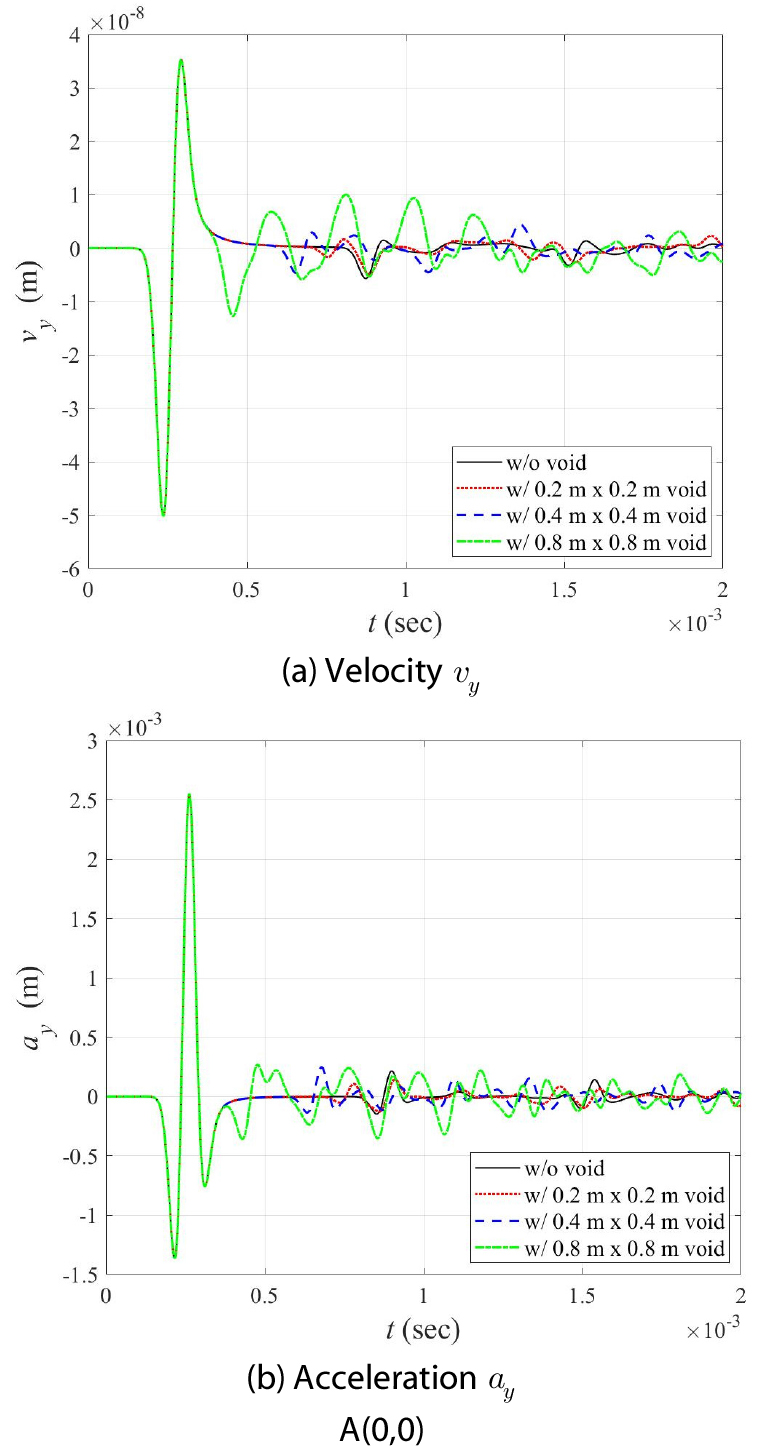
Fig. 11은 공동의 크기에 따른 벽체 표면 A(0,0)에서의 속도와 가속도응답이다. Fig. 10의 변위응답과 마찬가지로 공동의 경계면에서 발생한 반사파의 영향을 응답의 시간이력에서 확인할 수 있다. 공동의 크기가 클수록 벽체 표면에서 측정되는 반사파의 진폭이 크고 도달시간이 짧음을 알 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F11.jpg

Fig. 11.

Time history of the velocity and acceleration at A(0,0) with respect to various void sizes

Table 1은 공동의 경계면에서 발생한 반사파가 샘플링 포인트 A(0,0)에 도달하는 시간을 나타낸다. 공동을 포함하는 격납건물 벽체의 탄성파 정해석 결과를 이용하여 격납건물 벽체 내부의 Lamé 상수 $μ$ 와 $λ$ 를 재구성하는 탄성파 FWI 해석을 할 수 있다. FWI를 통해 격납건물 벽체 내부의 공동을 진단하기 위해서는 공동으로부터 발생한 반사파를 포함하는 탄성파 응답을 정확히 계산해야 한다. 공동의 크기와 위치를 고려한 탄성파 전파거동 계산결과를 이용해서 탄성파 FWI의 적절한 해석 시간을 설정할 수 있다.

Table 1.

Arrival time of the first reflection to A(0,0)

Cavity size(m)	Arrival time(s)
0	7.86 × 10^-4
0.2	6.90 × 10^-4
0.4	5.88 × 10^-4
0.8	3.98 × 10^-4

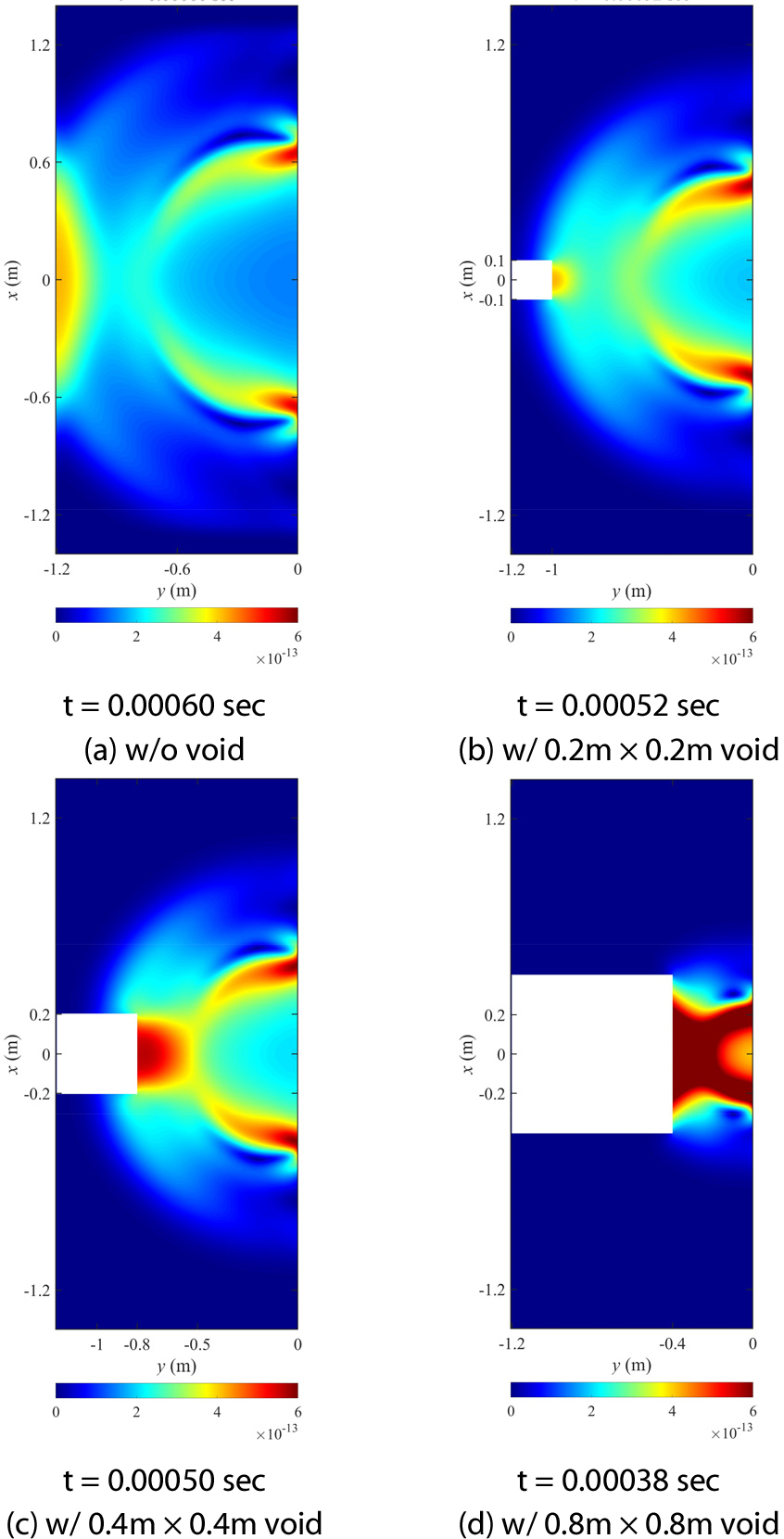
Fig. 10에 제시된 공동의 크기별 반사파의 발생 모습을 Fig. 12에 나타내었다. 공동의 크기가 증가함에 따라 공동 경계면에서의 반사파 발생 시각이 빨라지는 것과 반사파로 인한 절대변위가 증가하는 것을 변위 등고선도를 통해서 확인할 수 있다.

https://static.apub.kr/journalsite/sites/jcoseik/2021-034-03/N0040340306/images/Figure_jcoseik_34_03_06_F12.jpg

Fig. 12.

Displacement snapshots of the NPP containment wall with voids subjected to an impact load on the surface

이러한 연구는 원전 격납건물 벽체의 내부 공동의 크기와 위치를 재구성하는 탄성파 FWI 기술에 적용될 수 있다. 특히 다양한 위치의 공동을 포함하는 격납건물 벽체에 대해 탄성파 전파 해석을 수행하고 계산된 탄성파 응답을 활용하여 정확한 정보가 없는 공동의 대략적인 위치를 판단할 수 있다. 이러한 해석 결과를 바탕으로 원전 격납건물 벽체의 ICT 기반 공동 건전성 평가 플랫폼을 제시하는 것이 가능하다.

4. 결 론

이 논문에서는 원전 격납건물 벽체에서의 탄성파 전파거동을 계산하는 유한요소해석 기법을 제시하였다. 원전 격납건물 벽체의 탄성파 정해석을 통해 CLP 부착 여부와 공동의 크기 및 위치 변화에 따른 탄성파 전파결과를 살펴보았다. 그 결과 CLP가 부착된 경우에는 그렇지 않은 경우보다 벽체 표면에서의 절대변위가 다소 감소함을 알 수 있었다. 또한 공동이 존재하는 경우에는 공동의 경계면에서 발생한 반사파가 벽체 표면에서의 시간이력 응답에 큰 영향을 미침을 알 수 있었다. 특히, 공동의 위치가 변화하는 경우에 하중 재하 위치 및 응답의 측정 위치로부터 공동의 위치가 멀어짐에 따라 공동에서 발생한 반사파가 응답에 미치는 영향이 감소함을 확인하였다. 공동의 크기가 변화하는 경우에는 공동의 크기가 증가함에 따라 탄성파 응답 내 반사파의 영향이 증가하는 것을 응답의 시간이력과 변위 등고선도를 통해 확인하였다. 이러한 해석 결과를 활용하여 반사파의 도달 시간을 고려한 탄성파 FWI의 적절한 해석 시간을 설정할 수 있다. 다양한 공동 위치에 대한 탄성파 해석 결과를 바탕으로 격납건물 벽체의 공동 위치를 대략적으로 판단할 수 있고 탄성파 가진 및 응답 측정을 위한 장비의 최적 운용이 가능하다. 이 연구에서 제시한 탄성파 해석 결과를 활용하여 효율적인 2차원 탄성파 FWI 시스템 개발을 기대할 수 있다.

Acknowledgements

이 논문은 한국수력원자력(주)(No. 2019-기술-01)와 2021학년도 홍익대학교 학술연구진흥비의 지원을 받아 수행한 연구결과입니다.

References

Fathi, A., Poursartip, B., Kallivokas, L.F. (2015) Time-Domain Hybrid Formulations for Wave Simulations in Three-Dimensional PML-Truncated Heterogeneous Media, Int. J. Numer. Methods Eng., 101(3), pp.165~198. 10.1002/nme.4780

Kang, J.W. (2013) Time-Domain Elastic Full-Waveform Inversion using One-Dimensional Mesh Continuation Scheme, J. Comput. Struct. Eng. Inst. Korea, 26(4), pp.213~221. 10.7734/COSEIK.2013.26.4.213

Kang, J.W., Kallivokas, L.F. (2010) The Inverse Medium Problem in 1D PML-Truncated Heterogeneous Semi-Infinite Domains, Inverse Problems Sci. & Eng., 18(6), pp.759~786. 10.1080/17415977.2010.492510

Kang, J.W., Pakravan, A. (2013) Performance Evaluation of a Time-Domain Gauss-Newton Full-waveform Inversion Method, J. Comput. Struct. Eng. Inst. Korea, 26(4), pp.223~231. 10.7734/COSEIK.2013.26.4.223

Kim, B., Kang, J.W. (2019) A-Time Domain Formulation of Elastic Waves in Heterogeneous Unbounded Domains, Multiscale Sci. & Eng., 1, pp.220~235. 10.1007/s42493-019-00019-z

Kucukcoban, S. (2010) The Inverse Medium Problem in PML- Truncated Elastic Media, Ph.D. Thesis, The University of Texas at Austin, p.287.

Youn, S., Kang, J.W. (2018) Explicit Transient Simulation of SH-waves using a Spectral Element Method, J. Comput. Struct. Eng. Inst. Korea, 31(2), pp.87~95. 10.7734/COSEIK.2018.31.2.87

Journal of the Computational Structural Engineering Institute of Korea ISSN:1229-3059(Print) 2287-2302(Online) 한국전산구조공학회 논문집

Preview

Elastic Wave Propagation in Nuclear Power Plant Containment Building Walls Considering Liner Plate and Concrete Cavity

ABSTRACT

MAIN

(1a)

(1b)

(1c)

Fig. 1.

(a) Two-dimensional PML-truncated computational domain; (b) Finite element model

(2a)

(2b)

(2c)

(2d)

(2e)

(2f)

(2g)

(3a)

(3b)

(4a)

(4b)

(4c)

(4d)

(5a)

(5b)

(5c)

(5d)

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

(6g)

(6h)

Fig. 2.

(a) Two-dimensional PML-truncated domain of reactor containment buildings; (b) Finite element model

(7)

Fig. 3.

Time history and frequency spectrum of the Gaussian pulse

Fig. 4.

Time history of the containment wall responses at three sampling points

Fig. 5.

Time history of displacement at sampling point A for the cases w/ and w/o CLP attachment

Fig. 6.

Computational domains of the containment wall with various locations of the void

Fig. 7.

Time history of the stresses with respect to various void locations

Fig. 8.

Time history of the displacement and acceleration with respect to various void locations

Fig. 9.

Computational domains of the containment wall with various void sizes

Fig. 10.

Time history of the displacement uy with respect to various void sizes

Fig. 11.

Time history of the velocity and acceleration at A(0,0) with respect to various void sizes

Table 1.

Arrival time of the first reflection to A(0,0)

Fig. 12.

Displacement snapshots of the NPP containment wall with voids subjected to an impact load on the surface

Acknowledgements

References

Time history of the displacement $u_{y}$ with respect to various void sizes