Particle-Structure Collision Modeling for Topology Optimization

Young Hun Choi; Gil Ho Yoon

doi:10.7734/COSEIK.2023.36.6.365

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 December 2023. 365-370
https://doi.org/10.7734/COSEIK.2023.36.6.365

Particle-Structure Collision Modeling for Topology Optimization

위상최적설계를 위한 입자-구조 충돌 모델

Young Hun Choi¹

Gil Ho Yoon²^*

최 영훈¹

윤 길호²^*

¹Graduate Student, Department of Mechanical Convergence Engineering, Hanyang University, Seoul, 04763, Korea

²Professor, Department of Mechanical Engineering, Hanyang University, Seoul, 04763, Korea

¹한양대학교 기계공학부 석박사통합과정

²한양대학교 기계공학부 교수

^{*Corresponding Author}

ABSTRACT

This paper presents a particle-structure collision model for topology optimization, which requires sensitivity analysis. Therefore, a new model that incorporates sensitivity analysis is needed. The proposed particle-structure collision model conducts sensitivity analysis for topology optimization. To evaluate the accuracy of the proposed model, it was applied to a simplified one-dimensional collision problem. Optimization of the final positions of particles using topology optimization through this model confirmed the suitability of the proposed approach. These results demonstrate that it is possible to consider particle-structure collision in topology optimization.

Keywords

particle-structure collision model

particle-structure contact

topology optimization

본 논문에서는 위상최적설계를 위한 입자-구조 충돌 모델을 제시한다. 위상최적설계를 위해서는 민감도 분석이 선행되어야 하며, 민감도 분석이 가능한 새로운 모델이 필요하다. 본 논문에서는 위상최적설계를 위한 민감도 분석을 수행하기 위한 입자-구조 충돌 모델을 제시한다. 이후 이 모델을 이용하여 위상최적설계를 위한 민감도 분석을 수행한다. 제안한 모델의 정확도를 평가하기 위해 먼저 단순화된 1차원 충돌 문제에 적용한다. 이후, 이 모델을 이용하여 위상 최적화를 통해 입자의 최종 위치를 최적화하여 위상 최적화에 대한 이 모델의 적용 가능성을 확인한다. 이러한 결과는 위상 최적화에서 입자-구조 충돌을 고려하는 것이 가능하다는 것을 보여준다.

키워드

입자-구조 충돌 모델

입자-구조 접촉

위상최적설계

MAIN

1. 서 론
2. 본 론
2.1 입자-구조 충돌 모델
2.2 민감도 해석
2.3 수치예제
3. 결 론

1. 서 론

본 연구에서는 위상최적설계를 위한 입자-구조 충돌 모델을 제안한다. 위상최적설계를 하기 위해서는 설계 변수에 대한 민감도 해석이 수행되어야 하는데, 민감도 해석이 가능한 새로운 입자-구조 충돌 모델이 필요하다. 본 논문에서는 민감도 해석이 가능한 입자-구조 충돌 모델을 제시하고, 이 모델을 이용하여 위상최적설계를 하기 위한 민감도를 유도한다.

위상최적설계는 최적설계 기법 중 하나로 설계 영역의 위상을 설계 변수로 하여 최적화하는 기법이다. 위상최적설계는 구조물의 강성을 최대화(Bendsøe and Kikuchi, 1988; Sigmund, 2001)를 위한 위상최적설계, 유체 내 점성 에너지 소실의 최소화(Borrvall and Petersson, 2003; Gersborg-Hansen et al., 2005)를 위한 위상최적설계 등 다양한 분야에서 연구되어 왔다. 최근에는 입자의 운동을 조절하는 위상최적설계도 연구되었는데, 입자의 운동을 외부 장을 이용하여 조절하는 위상최적설계가 이루어졌다. Yoon(2020)에서는 유체의 흐름을 조절하여 유체 내에 들어있는 입자의 운동을 조절하는 위상최적설계를 진행하기 위한 민감도 해석을 제시하고 이를 통해 입자의 운동을 조절하였다. 최근 몇 년간 입자의 운동을 최적화하기 위해 위상최적설계를 사용하는 연구들(Andreasen, 2020; Choi and Yoon, 2023; Yoon, 2020; Yoon, 2022; Yoon and So, 2021)이 수행되어 왔지만, 기존 연구에서는 입자의 충돌을 고려하지 않았고, Fig. 1과 같은 입자와 구조의 충돌이 발생하는 상황에서의 위상최적설계는 어렵다. 위상 최적설계에서는 계산의 효율성을 위해 민감도를 해석적으로 계산하는 것이 필수적인데 입자의 충돌 현상은 연속적이지 않은 현상이기 때문에 민감도 해석에 어려움이 있다. 본 연구에서는 입자와 구조의 충돌 현상을 스프링을 이용해 모사하여 민감도의 계산이 가능하게 한다. 본 연구에서는 입자와 구조물과 충돌을 고려하면서 입자의 위치를 조절하는 구조물을 위상최적설계 기법을 이용해 설계하기 위해 새로운 모델을 제시하고 민감도 해석을 한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360602/images/Figure_jcoseik_36_06_02_F1.jpg

Fig. 1.

Particle contact analysis using the present particle-structure contact model

본 논문의 남은 부분은 다음과 같이 구성된다. 2장에서는 위상최적설계를 위한 입자-구조 충돌 모델을 제시하고 이를 이용해 민감도를 계산하고 수치 예제들을 통해 검증을 한다. 3장에서는 본 논문의 결론을 제시하고 추가로 연구해야 할 내용을 논의하였다.

2. 본 론

이 장에서는 위상최적설계를 위한 입자-구조 충돌 모델을 소개하고, 민감도를 계산한다. 수치 예제는 제안된 모델의 정확도를 파악하기 위한 1차원 충돌해석, 민감도의 정확도를 파악하기 위한 수치적인 민감도 계산과의 비교, 입자의 최종 위치를 조절하는 위상최적설계 순으로 소개된다.

2.1 입자-구조 충돌 모델

이 장에서는 위상최적설계를 하기 위한 새로운 입자-구조 충돌 모델을 제안한다. 위상최적설계에서는 설계 영역을 다수의 요소로 분할하여 각각의 요소에 밀도라는 변수 𝛾를 지정한다. 이러한 과정을 통해 해당 요소의 위치에 구조의 유무를 변수로 하여 최적화가 가능하다. 일반적인 위상최적설계를 진행하는 경우 Fig. 1(a)와 같이 얻어진 구조물의 충돌을 계산하게 되는데 이는 실제와 다른 충돌 현상을 발생시킨다. 본 연구에서는 Fig. 1(a)와 같은 구조물을 Fig. 1(b)와 같이 변형시켜 충돌현상을 모사한다.

Fig. 1(b)와 같이 입자가 구조와 충돌할 때 n방향으로 힘이 가해지는데, 이를 Fig. 1(c)와 같이 스프링을 이용하여 모사할 수 있다. 그러면 Fig. 1(d)와 같이 입자가 구조물 안쪽으로 들어가게 되는데, 충분히 큰 스프링 상수 $k$ 를 이용하면 입자가 구조물 안쪽으로 들어가는 현상을 줄이고 완전탄성충돌과 유사한 결과를 얻을 수 있다. 이를 수식으로 표현하면 다음 식 (1)과 같다.

(1)

\frac{d}{d t} (m v) = F_{contact}

위 식은 입자의 운동 방정식이며, $m$ 은 입자의 질량, v는 입자의 속도이다. 이때 입자가 구조물에 의해 받는 힘 $F_{contact}$ 은 다음 식 (2)와 같이 모사가 가능하다.

(2)

F_{contact} = k δ S (γ) n

여기서 $k$ 는 스프링 상수, 𝛿는 스프링이 변형된 길이이다. 벡터 n과 함수 $S$ 는 각각 법선의 방향 벡터와 S 모양의 sigmoid 함수이며 다음 식 (3), (4)와 같이 구해진다.

(3)

n = - \frac{\nabla γ}{∥ \nabla γ ∥}

(4)

S (γ) = \frac{1}{e^{a (γ - γ_{w a l l})} + 1}

여기서 $γ_{w a l l}$ 은 0.5로 일반적인 밀도 기반 위상최적설계에서 사용되는 설계변수 범위(0에서 1까지)의 중간 값으로 설정하였다. $a$ 는 충분히 작은 값으로 구조물이 없는 영역에서 입자가 받는 힘이 무시될 수 있도록 -10⁶ 이하의 작은 값으로 설정하며, 본 논문에서는 -10⁶으로 하였다. 스프링의 변형된 길이 𝛿는 다음 식 (5), (6)과 같이 테일러 전개를 통해 근사된다.

(5)

γ_{w a l l} = γ (x) + \nabla γ \cdot δ n = γ (x) - \nabla γ \cdot δ \frac{\nabla γ}{∥ \nabla γ ∥}

(6)

δ = \frac{γ (x) - γ_{w a l l}}{∥ \nabla γ ∥}

이때 𝛻𝛾를 구하는 과정에서 𝛾가 불연속적인 값을 가질 경우 생기는 문제를 완화하기 위해 아래 식 (7)의 밀도 필터를 이용한다.

(7)

{\tilde{γ}}_{i} = (\sum_{j} w_{i j} γ_{j}) / \sum_{j} w_{i j}

여기서 가중치 $w_{i j}$ 는 필터링 반경에서 $i$ 번째 요소와 $j$ 번째 요소 사이의 거리를 뺀 값으로 설정되고 $j$ 는 설계영역 내의 모든 요소에 대하여 계산된다.

위와 같은 방식으로 스프링을 모사하면 설계 변수에 대하여 미분 가능하기 때문에 제안된 모델을 통해 입자-구조의 충돌을 고려하여 위상최적설계를 할 수 있다.

2.2 민감도 해석

이 장에서는 본 연구에서 제안한 입자-구조의 충돌 모델을 이용하여 민감도를 유도한다. 민감도를 유도할 목적 함수는 입자의 속도 $\dot{x}$ 에 대한 함수 $c$ 를 시간에 대하여 적분한 것이며, 이 함수는 속력의 최적화 또는 입자의 최종 위치의 최적화할 때 사용이 가능하다. 민감도의 유도는 다음 식 (8)과 같다.

(8)

L = \int_{0}^{t_{f}} c (\dot{x}) d t + \int_{0}^{t_{f}} λ^{T} (m \ddot{x} - F) d t

위 식을 설계변수 𝛾에 대하여 미분을 하면 아래 식 (9)와 같다.

(9a)

\frac{d L}{d γ} = \int_{0}^{t_{f}} (\frac{\partial c}{\partial \dot{x}} \frac{d \dot{x}}{d γ} + λ^{T} \frac{d}{d γ} (m \ddot{x} - F) d t = \int_{0}^{t_{f}} (\frac{\partial c}{\partial \dot{x}} \frac{d \dot{x}}{d γ} + m λ^{T} \frac{d \ddot{x}}{d γ} - λ^{T} \frac{d F}{d γ}) d t

(9b)

\frac{d L}{d γ} = {[(\frac{\partial c}{\partial \dot{x}} - m {\dot{λ}}^{T}) \frac{d x}{d γ} + m λ^{T} \frac{d \dot{x}}{d γ}]}_{0}^{t_{f}} + \int_{0}^{t_{f}} (- \frac{d}{d t} \frac{\partial c}{\partial \dot{x}} + m {\ddot{λ}}^{T} - λ^{T} \frac{\partial F}{\partial x}) \frac{d x}{d γ} d t - \int_{0}^{t_{f}} λ^{T} \frac{\partial F}{\partial γ} d t

여기서 다음 조건을 만족시키는 𝜆를 계산하여 위의 식에 대입하면 민감도는 위 식의 마지막 항만 남기고 아래 식 (10)처럼 모두 소거된다.

(10a)

{\ddot{λ}}^{T} - \frac{1}{m} {(\frac{\partial F}{\partial x})}^{T} λ = \frac{1}{m} (\frac{d}{d t} {(\frac{\partial c}{\partial \dot{x}})}^{T})

(10b)

λ^{T} (t_{f}) = 0

(10c)

{\dot{λ}}^{T} (t_{f}) = \frac{1}{m} \frac{\partial c}{\partial \dot{x}}

위의 조건을 만족시키는 𝜆에 대하여 민감도는 아래 식 (11)과 같다.

(11)

\frac{d L}{d γ} = - \int_{0}^{t_{f}} λ^{T} \frac{\partial F}{\partial γ} d t

여기서 유도한 민감도는 다음 장의 예제를 통해 수치적인 방법으로 구한 민감도와 비교하여 검증된다.

2.3 수치예제

2.3.1 입자-구조 1차원 충돌해석

이 장에서는 1차원 충돌 해석을 통해 제안한 모델의 정확도를 확인한다. 이를 위해 Fig. 2에 정의된 1차원 해석 문제를 푼다. Fig. 2와 같이 입자는 + $x$ 방향으로 1m/s의 속력으로 0.5m 떨어져 있는 벽에 부딪치며 입자의 질량은 1kg이다. 이때 입자의 운동 시간이 0.8s인 경우 해석적인 해는 Fig. 2의 오른쪽 그림과 같고 입자의 최종 위치는 0.2이다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360602/images/Figure_jcoseik_36_06_02_F2.jpg

Fig. 2.

Problem definition for evaluating the accuracy and the analytic solution to compare with results approximated by the present particle-structure collision model

정확도를 측정하기 위해 같은 조건을 가진 문제를 본 연구에서 제안된 모델을 이용하여 해석한다. 정확도는 아래와 같은 식 (12)를 이용하여 계산한다.

(12)

A c c u r a c y = (1 - |\frac{x_{f} - x_{f, t r u e}}{x_{f, t r u e}}|) \times 100 (%)

여기서 $x_{f}$ 는 제안된 모델로 계산한 입자의 최종 위치이며 $x_{f, t r u e}$ 는 실제 해인 0.2이다.

입자 해석의 시간 간격 $Δ t$ 를 10^-6s으로 충분히 작게 설정한 후, 스프링 상수를 변화시켜가며 계산하면 Table 1과 같은 해석 결과를 얻는다. 만약 시간 간격이 충분히 작지 않게 설정된다면, 스프링 상수를 높게 설정할 때 발생되는 매우 짧은 시간의 충돌 현상을 제대로 해석할 수 없게 된다.

Table 1

Comparison of the accuracy of analysis results corresponding to the spring constant

$k_{\max}$ (N/m)	$x_{f}$ (m)	$x_{\max}$ (m)	Accuracy (%)
10⁴	0.2306	0.5098	84.7
10⁵	0.2097	0.5031	95.2
10⁶	0.2023	0.5010	98.7
10⁷	0.1993	0.5003	99.7

Table 1에 나타난 것과 같이 입자의 해석은 스프링 상수에 따라 정확도가 달라진다. 여기서 $x_{\max}$ 는 입자의 위치의 최대값으로 입자가 벽 안쪽으로 들어간 정도를 나타낸다. 스프링 상수가 클수록 벽 안쪽으로 입자가 들어가는 현상이 줄어들게 되므로 스프링 상수가 커질수록 해석이 정확해진다. 그러나 스프링 상수가 너무 커지는 경우 수치적인 문제로 인하여 오차가 생길 수 있고 충돌하는 시간이 작게 되어 더 작은 시간 간격을 요구한다. 이러한 문제로 인해 본 논문에서는 스프링 상수를 10⁶으로 설정하여 다음 장의 예제를 푼다.

2.3.2 민감도 해석

이 장에서는 본 논문에서 제안한 모델을 이용해 설계 변수 𝛾 에 대한 입자의 $y$ 방향 최종 위치인 $y_{f}$ 의 민감도를 계산한다. 설계 영역은 Fig. 3(a)와 같이 1m 크기의 정사각형으로 10×10으로 요소 100개로 설정되었으며, 아래의 50개 요소의 밀도 𝛾는 1, 위의 50개 요소의 밀도 𝛾는 0으로 설정하여 가운데 부분에 벽이 생기도록 설정한다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360602/images/Figure_jcoseik_36_06_02_F3.jpg

Fig. 3.

Example for comparing the analytic and numerical sensitivities. (a) Problem definition and initial condition, (b) particle trajectory obtained by the particle analysis and (c) the sensitivity

입자-구조 충돌 해석을 위한 스프링 상수는 10⁶N/m, 입자의 운동 시간은 0.2s, 시간 간격 $Δ t$ 는 5×10^-7s으로 설정하였다. 이때 입자의 초기 위치 $(x_{0}, y_{0})$ 는 (0.4, 0.6)m, 초기 속도 $(v_{x 0}, v_{y 0})$ 는 (1, -1)m/s로 설정하여 해석할 경우 Fig. 3(b)와 같은 해석 결과를 얻고, 입자의 최종 위치 $(x_{f}, y_{f})$ 는 (0.6000, 0.5970)로 얻어진다.

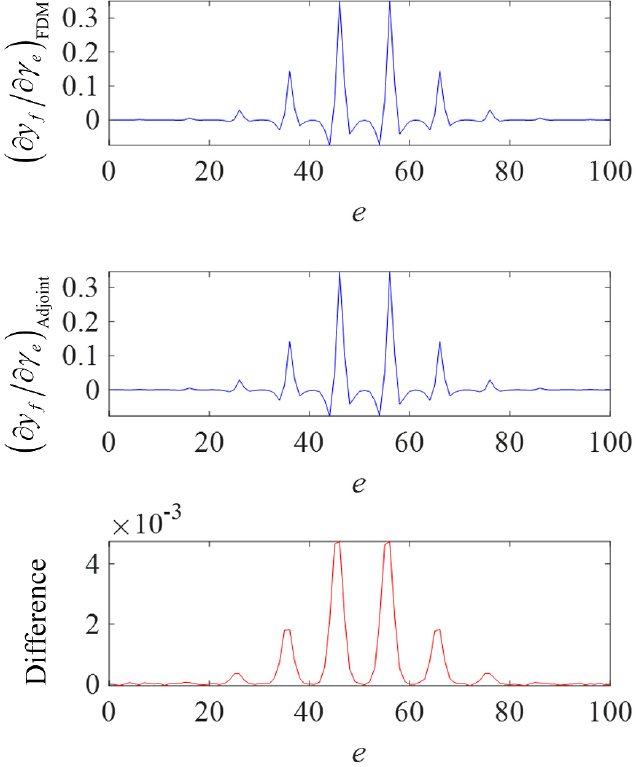
앞서 유도된 식으로 계산한 민감도는 Fig. 3(c)와 같이 얻어진다. 그림에서 가운데 부분의 민감도 값이 양수인데 이 부분에 구조를 생기게 한다면 $y_{f}$ 가 커진다는 것을 의미한다. 이 민감도와 차분법(FDM)으로 얻어진 수치적인 민감도와의 비교는 Fig. 4와 같다. Fig. 4의 가로 축인 요소 번호 $e$ 는 Fig. 3(c)와 같이 설정되었다. 본 논문에서 제안된 해석적인 방법으로 구한 민감도와 수치적으로 구한 민감도의 차이가 5×10^-3 이하의 작은 차이를 갖는 것을 확인하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360602/images/Figure_jcoseik_36_06_02_F4.jpg

Fig. 4.

Comparison between the analytic and numerical sensitivities

2.3.3 입자 최종 위치의 위상최적설계

이 장에서는 앞 장에서 소개된 입자 충돌 해석과 민감도 해석을 이용하여 입자의 최종 위치를 최대화하는 문제를 푼다. 이를 통해 위상최적설계에서 입자의 충돌을 고려할 수 있음을 확인한다.

Fig. 5와 같이 한 변의 길이가 1m인 정사각형 영역에서 초기 위치와 속도가 각각 (0, 0.5)m, (1, -1)m/s로 설정된 입자가 0.6s 동안 운동할 때 입자의 최종 위치 $(x_{f}, y_{f})$ 를 최대화한다. 하단에서 0.1m 떨어진 위치에 벽을 생성하기 위해, Fig. 5와 같이 아래쪽 영역( $0 \leq y \leq 0.1$ )과 위쪽 영역( $0.1 < y \leq 1$ )의 초기 밀도는 각각 $γ_{M}, γ_{m}$ 으로 설정하고 이 값은 각각 0.6, 0.4로 설정한다. 설계 영역은 위쪽 영역에서 입자 주변 부분을 제외한 영역으로 설정하는데 이것은 입자의 초기 위치가 구조물 밖에 있어야 하기 때문이다. 설계 영역은 100×100의 정사각형 요소로 분할되었고, 시간 간격 $Δ t$ 는 2×10^-5s, 스프링 상수는 10⁶N/m로 설정하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360602/images/Figure_jcoseik_36_06_02_F5.jpg

Fig. 5.

Problem definition for maximizing the position of a particle

입자의 $x$ 방향 최종 위치의 최대화와 $y$ 방향 최종위치 최대화를 위한 최적설계 문제 정식화는 각각 다음 식 (13)과 같다.

(13a)

Maximize, x_{f}, subject to \frac{d^{2} X}{d t^{2}} = \frac{1}{m} F (γ, X), y_{f} \geq 0, γ_{m} \leq γ \leq γ_{M},

(13b)

Maximize, y_{f}, subject to \frac{d^{2} X}{d t^{2}} = \frac{1}{m} F (γ, X), x_{f} \geq 0, γ_{m} \leq γ \leq γ_{M},

여기서 설계 변수는 Fig. 5에서 설정된 설계 영역의 밀도 𝛾이며, 설계 변수의 필터링 거리는 0.155m로 설정하였다. 구속 조건으로 각각 $y_{f} \geq 0$ 와 $x_{f} \geq 0$ 가 추가되는데, 이것은 최적화 진행 중에 입자가 요소 밖으로 나가지 않게 하기 위함이다. 최적화는 Method of Moving Asymtotes(MMA)를 이용하여 민감도 기반 최적화를 진행한다(Svanberg, 1987).

이 최적설계 문제의 결과는 Fig. 6과 같이 얻어진다. $x_{f}$ 의 최대값을 얻는 구조물은 Fig. 6(a)와 같이 얻어지고, $y_{f}$ 의 최대값을 얻는 구조물은 Fig. 6(b)와 같이 얻어진다. 각각 설계 영역 내에서 최대의 최종 위치를 얻을 수 있는 구조물이 설계됨을 알 수 있다. 최적화가 진행이 되는 과정은 Fig. 7과 같다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360602/images/Figure_jcoseik_36_06_02_F6.jpg

Fig. 6.

Results of the optimization problems maximizing the final (a) x coordinate and (b) y coordinate of the particle

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360602/images/Figure_jcoseik_36_06_02_F7.jpg

Fig. 7.

Optimization histories of the problems maximizing the final (a) x coordinate and (b) y coordinate

3. 결 론

본 논문에서는 위상최적설계 기법에서 입자와 구조의 충돌을 고려하기 위해서 새로운 입자-구조 충돌 모델을 제시하였다. 이를 위하여 스프링 상수가 충분히 큰 스프링을 이용하여 입자와 구조 사이의 완전 탄성 충돌 현상을 일어나는 것을 모사하였다. 이를 이용해 1차원 충돌 과정에 대한 해석을 수행하였고, 그 결과를 통해 해석의 정확도를 확인할 수 있었다.

또한, 해석적인 민감도 식의 유도 과정을 소개하였고, 이 과정을 통해 구해진 민감도와 수치적인 방법을 사용하여 얻은 민감도를 비교하여 민감도 계산의 정확도에 대하여 분석하였다. 이러한 해석적인 민감도의 계산의 계산은 설계 변수의 수가 많은 위상최적설계에서는 필수적이며, 얻어진 민감도를 기반으로 위상최적설계가 가능하다.

마지막 예제에서 입자의 최종 위치를 조절하는 간단한 위상최적설계를 진행하였다. 이 과정을 통해 본 논문에서 제시된 새로운 입자-구조 충돌 모델을 통해 위상최적설계가 가능함을 확인하였다. 추후 입자-구조 충돌을 고려함과 동시에 구조가 받는 힘을 고려한 위상최적설계의 연구로 확장될 수 있다.

Acknowledgements

This work was supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (2021202080026D, Development of platform technology and operation management system for design and operating condition di-agnosis of fluid machinery with variable devices based on AI/ICT).

References

Andreasen, C.S. (2020) A Framework for Topology Optimization of Inertial Microfluidic Particle Manipulators, Struct. & Multidiscip. Optim., 61(6), pp.2481~2499. 10.1007/s00158-019-02483-5

Bendsøe, M.P., Kikuchi, N. (1988) Generating Optimal Topologies in Structural Design using a Homogenization Method, Comput. Methods Appl. Mech. & Eng., 71(2), pp.197~224. 10.1016/0045-7825(88)90086-2

Borrvall, T., Petersson, J. (2003) Topology Optimization of Fluids in Stokes Flow, Int. J. Numer. Methods Fluids, 41(1), pp.77~107. 10.1002/fld.426

Choi, Y.H., Yoon, G.H. (2023) A MATLAB Topology Optimization Code to Control the Trajectory of Particle in Fluid, Struct. & Multidiscip. Optim., 66(4), p.91. 10.1007/s00158-023-03538-4

Gersborg-Hansen, A., Sigmund, O., Haber, R.B. (2005) Topology Optimization of Channel Flow Problems, Struct.. & Multidiscip. Optim., 30(3), pp.181~192. 10.1007/s00158-004-0508-7

Sigmund, O. (2001) A 99 Line Topology Optimization Code Written in Matlab, Struct. & Multidiscip. Optim., 21(2), pp.120~127. 10.1007/s001580050176

Svanberg, K. (1987) The Method of Moving Asymptotes-a New Method for Structural Optimization, Int. J. Numer. Methods Eng., 24(2), pp.359~373. 10.1002/nme.1620240207

Yoon, G.H. (2020) Transient Sensitivity Analysis and Topology Optimization for Particle Motion in Steady State Laminar Fluid, Comput. Methods Appl. Mech. & Eng., 367, p.113096. 10.1016/j.cma.2020.113096

Yoon, G.H. (2022) Transient Sensitivity Analysis and Topology Optimization of Particle Suspended in Transient Laminar Fluid, Comput. Methods Appl. Mech. & Eng., 393, p.114696. 10.1016/j.cma.2022.114696

Yoon, G.H., So, H. (2021) Development of Topological Optimization Schemes Controlling the Trajectories of Multiple Particles in Fluid, Struct. Multidiscip. Optim., 63, pp.2355~ 2373. 10.1007/s00158-020-02817-833526995PMC7838481

Journal of the Computational Structural Engineering Institute of KoreaISSN:1229-3059(Print) 2287-2302(Online)한국전산구조공학회

Preview

Particle-Structure Collision Modeling for Topology Optimization

ABSTRACT

MAIN

Fig. 1.

Particle contact analysis using the present particle-structure contact model

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9a)

(9b)

(10a)

(10b)

(10c)

(11)

Fig. 2.

Problem definition for evaluating the accuracy and the analytic solution to compare with results approximated by the present particle-structure collision model

(12)

Table 1

Comparison of the accuracy of analysis results corresponding to the spring constant

Fig. 3.

Example for comparing the analytic and numerical sensitivities. (a) Problem definition and initial condition, (b) particle trajectory obtained by the particle analysis and (c) the sensitivity

Fig. 4.

Comparison between the analytic and numerical sensitivities

Fig. 5.

Problem definition for maximizing the position of a particle

(13a)

(13b)

Fig. 6.

Results of the optimization problems maximizing the final (a) x coordinate and (b) y coordinate of the particle

Fig. 7.

Optimization histories of the problems maximizing the final (a) x coordinate and (b) y coordinate

Acknowledgements

References