1. 서 론

피암터널은 낙석방지시설 중 하나로 비교적 큰 낙석이 예상되는 급경사지 도로에 설치된다. 낙석방지시설 중 대표적인 것으로는 낙석방지울타리, 낙석방지옹벽, 피암터널이 있다. 낙석방지울타리의 경우 기본적으로 50kJ의 낙석에너지에 저항할 수 있도록 설계하며 이 외에도 다양한 낙석에너지에 저항할 수 있는 낙석방지울타리 형식을 제안한 연구도 있다(Park et al., 2020). 낙석방지옹벽은 최대 600kJ의 낙석에너지에 저항할 수 있도록 설계를 한다(MOLIT, 2008). 반면에 국내의 설계기준에는 피암터널의 정량적인 설계 낙석에너지에 대한 규정은 없으며 낙석방지울타리나 낙석방지옹벽으로 저항이 어려운 대규모 낙석이 발생이 예상되는 경우 피암터널을 설치하도록 하고 있다.

Yosida 등(2007)은 피암터널의 설계 낙석에너지를 최소 200kJ에서 최대 3,000kJ로 제시하고 있다. 유사하게 스위스의 경우는 피암터널의 설계 목표 낙석에너지를 3,000kJ로 규정하고 있다(Krsitian, 2009). 일본 도로협회에서는 최대 6,000kJ의 낙석에너지까지 피암터널을 사용할 수 있도록 하고 있다(JRA, 2000).

3,000kJ의 낙석에너지는 약 10.4tonf의 무게를 갖는 낙석이 30m 높이에서 낙하하였을 때의 에너지와 동일하다(여기서, 급경사지의 경사는 국내의 평균 경사각인 54.55° 사용, Suk et al., 2014). 이렇듯 피암터널은 상당히 큰 낙석에 저항할 수 있는 구조물임을 알 수 있다. 국내에서는 주로 이러한 큰 낙석하중에 저항하기 위하여 육중한 RC 형태의 피암터널이 주로 사용되는 반면 국외에서는 피암터널의 효율화를 위하여 다양한 에너지 흡수 능력을 가질 수 있는 신형식 피암터널이 개발되어 적용되고 있다(Berthet et al., 2003; Shi et al., 2013; Yang et al., 2016).

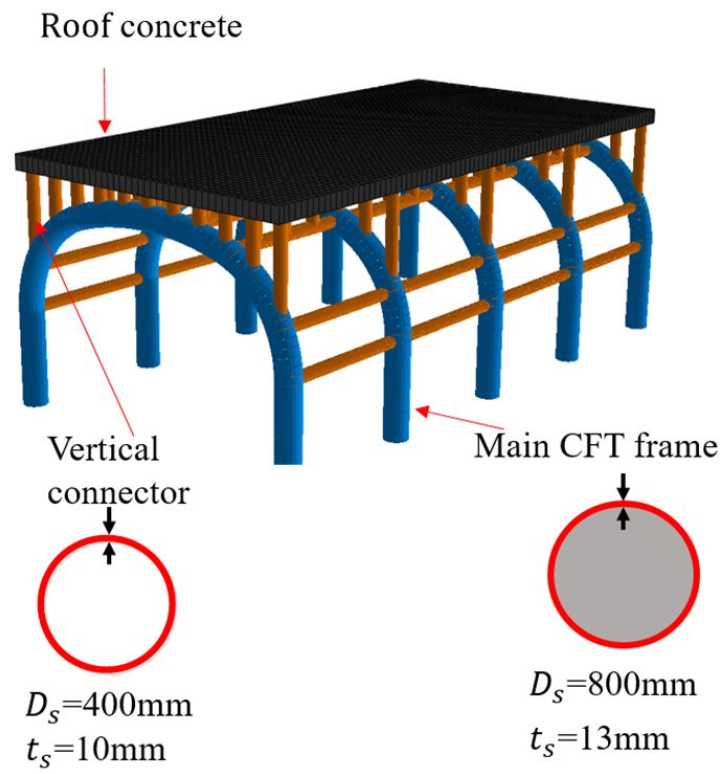
피암터널의 효율화를 위하여 국내에서는 Lee 등(2020)에 의해 국내 2차선 국도에서 활용할 수 있는 콘크리트 충전강관(CFT, Concrete-Filled Tube)을 활용한 피암터널을 Fig. 1과 같이 제안하였다. Fig. 1과 같이 CFT 피암터널은 CFT 주구조체(CFT main frame)와 보호콘크리트(Roof concrete), 이를 연결하는 연결부재(Connector element)로 구성된다. Fig. 1에는 나타나 있지 않지만 일반적으로 보호콘크리트 위에는 낙석에너지를 저감시키기 위한 완충재(Cushion layer)를 설치한다.

Fig. 1.

Proposed CFT rock shed

CFT는 원형강관 안에 콘크리트를 채운 합성구조의 하나로 강관이 거푸집 역할을 함으로 급속시공이 가능하며 내부 채움재의 영향으로 강관의 좌굴 저항성이 증대된다. 또한, 강관의 구속효과로 인한 내부 콘크리트의 강도 및 연성이 향상되는 특징이 있다(Moon et al., 2012). 이러한 CFT의 장점을 살려 피암터널의 주구조체에 적용함으로써 낙석에너지에 대한 피암터널의 저항력을 향상할 수 있을 것으로 기대된다. CFT 피암터널에 대한 연구는 Lee 등(2020)에 의하여 수행된 사례가 있다. 이 연구에서는 최대(극한) 낙석에너지를 3,000kJ로 설정하고 이를 등가정적하중으로 환산하여 탄성해석을 수행하고 CFT의 P-M 상관도를 사용하여 안정성을 평가하였다. 따라서, 보다 정확한 CFT 피암터널의 낙석에너지에 대한 저항 능력을 평가하기 위해서는 보다 정밀한 해석을 수행할 필요가 있으며 본 연구에서는 실제적인 낙석을 고려한 3차원 유한요소해석 모델을 사용하여 CFT 주구조체의 낙석에 대한 저항성능을 분석하였다. 기존 연구에서 CFT 주구조체는 최대 낙석하중의 약 83%를 부담하는 것으로 나타나 본 연구에서는 2,500kJ(극한 낙석에너지 3,000kJ의 약 83%)의 낙석에너지가 주구조체 작용한다고 가정하였다.

2. CFT 피암터널 주구조체 유한요소해석 모델

2.1 모델개요

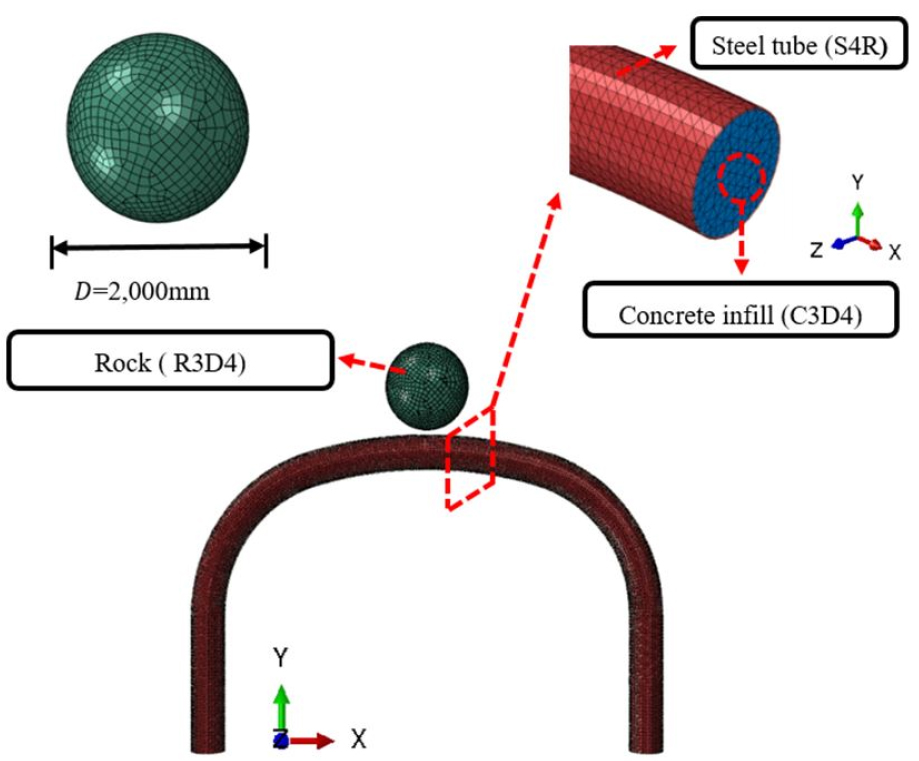
제안된 CFT 피암터널 주구조체의 극한 낙석에너지 저항능력을 유한요소해석을 사용하여 분석하였다. 유한요소해석에는 범용 구조해석 프로그램인 ABAQUS(2018)을 사용하였다. Fig. 2는 본 연구에서 사용된 유한요소해석 모델의 개요를 보여준다.

Fig. 2.

Typical finite element model for CFT rock shed

낙석 충돌체는 지름이 2m인 구형으로 모사를 하였으며 변형이 허용되지 않는 3차원 강체요소(R3D4)를 사용하였다. 여기서, 낙석의 질량은 10.4ton이며 초기 충돌 속도는 22m/s이다. 따라서, 초기 낙석 충돌체의 운동에너지는 약 2,500kJ로 본 연구에서 목표로 하는 CFT 주구조체의 극한 낙석에너지와 동일하다. CFT 주구조체의 강관과 내부 콘크리트 채움재는 각각 쉘요소(S4R)와 연속체 요소(C3D4)를 사용하여 모사하였다. 강관과 내부채움재는 각각 따로 모델링 하였으며 계면(Interface)에는 접촉 조건을 부여하였다. 수직방향의 접촉은 무한의 강성을 가지며 수평방향으로는 0.47의 마찰계수(Moon et al., 2012)를 입력하여 계면의 수직력에 의한 수평력이 발생할 수 있도록 하였다.

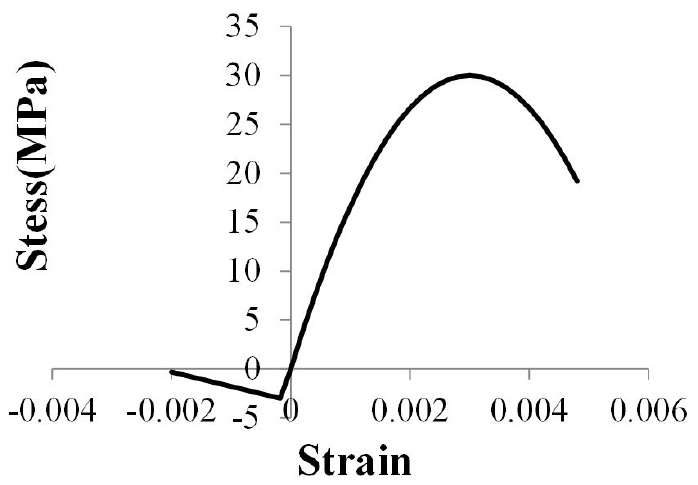
해석은 재료와 기하비선형을 모두 고려하여 진행되었다. 콘크리트의 3차원 재료 특성을 고려하기 위하여 ABAQUS(2018)에서 제공하는 Concrete damaged plasticity 모델을 사용하였다. 콘크리트의 압축강도, fc',은 30MPa이며 fc'의 약 50%까지 탄성으로 가정하였다. 인장강도, ft,는 fc'의 10%로 가정하였으며 해석의 수렴성을 확보하기 위하여 ft이후 응력은 선형적으로 감소하여 0.002의 변형률에서 0.1ft의 잔류응력을 갖도록 하였다(Fig. 3).

Fig. 3.

Uniaxial strain-stress curve for concrete

강재는 SS490 재료로 가정하여 항복응력, fy,는 325MPa로 설정하였다. 콘크리트와 강재의 푸아송비는 각각 0.108과 0.3이다. 경계조건은 CFT 주구조체 하부 양단을 고정으로 설정하였다. CFT 주구조체의 기하학적 제원은 앞선 Fig. 1과 같이 직경은 800mm이며 강관의 두께는 13mm이다.

해석은 충돌해석의 효율성을 위하여 ABAQUS Explicit solver를 사용하여 수행되었다. 충돌해석에서는 변형속도(Strain rate)에 의한 재료물성이 변화할 수 있으므로 이를 고려하여야 한다. 일반적으로 변형속도가 10²s-1이상인 경우는 변형속도에 의한 재료물성 변화를 반드시 고려하여야 하는 것으로 알려져 있다(Sierakowski, 1997). 하지만, 본 연구의 해석 결과 모든 해석 경우에서 변형속도는 최대 16 s-1로 낙석에 의한 변형속도의 영향은 미미한 것으로 판단되어 해석모델에서 변형속도의 영향은 고려하지 않았다.

2.2 모델 검증

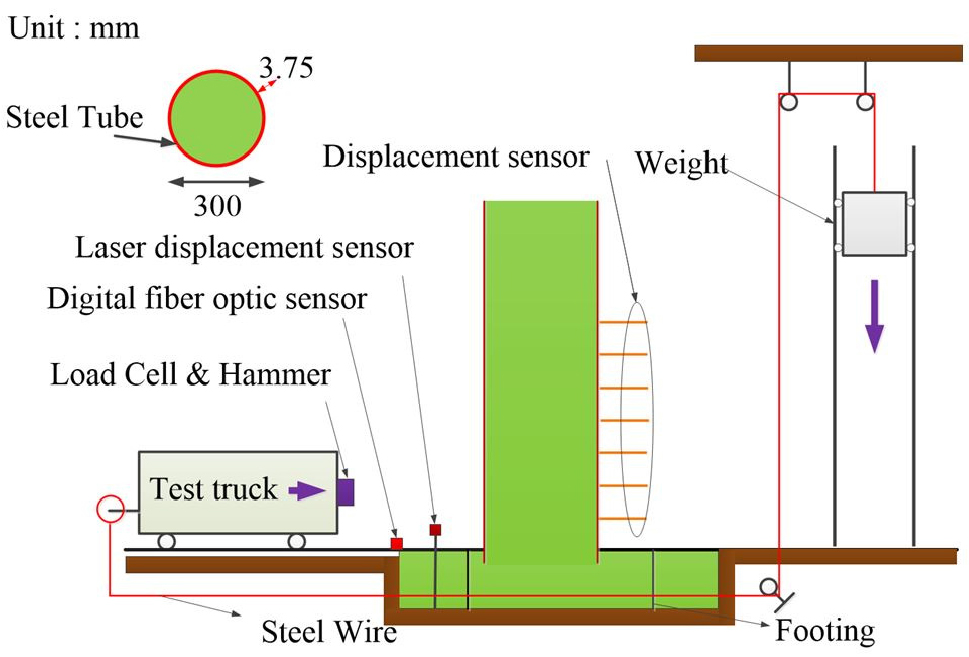
본 연구에서 사용된 유한요소해석 모델을 검증하기 위하여 본 연구의 대상과 유사한 CFT 기둥에 대한 충돌 실험을 수행한 결과를 사용하였다. Fig. 4는 Demartino 등(2017)이 수행한 CFT 기둥에 대한 충돌실험 개요를 보여준다.

Fig. 4.

Test overview for CFT column with impact load(Demartino et al., 2017)

Demartino 등(2017)은 Fig. 4와 같이 직경 300mm, 강관의 두께 3.75mm를 갖는 CFT 기둥에 대하여 1,580kg의 질량을 갖는 충돌체(Test truck & Hammer)를 약 7.5m/s의 속도로 충돌시켜 CFT 기둥에 작용하는 충돌하중과 CFT 기둥의 변형형상을 측정하였다. 여기서, 콘크리트의 압축강도는 40MPa이며 강재의 항복강도는 400MPa이다. 또한, CFT 기둥의 높이는 1,500mm이다.

Demartino 등(2017)의 실험체를 2.1장에서 언급한 방법에 의하여 유한요소해석 모델을 작성하고 해석을 수행하여 결과를 서로 비교하였다. 비교 결과는 Figs. 5, 6과 같다.

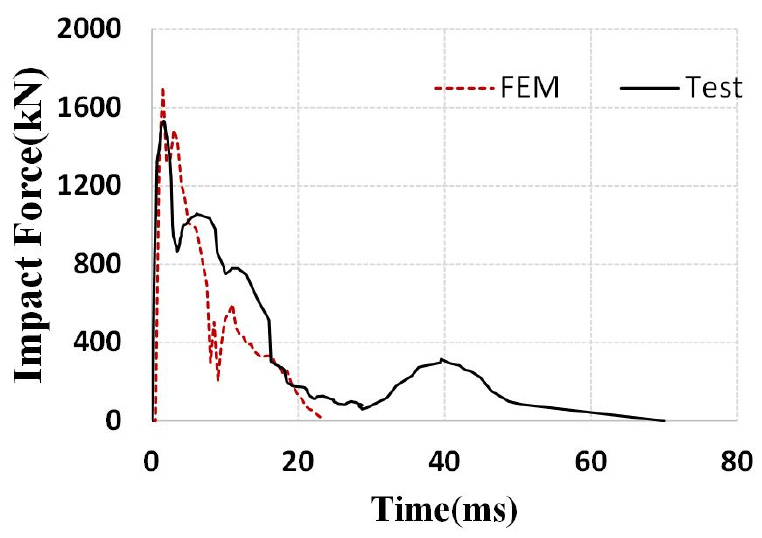
Fig. 5는 시간에 따른 충돌하중의 변화를 비교한 그림이다. 이 그림에서 알 수 있듯이 시간에 따른 최대 충돌하중의 발생지점과 이후 충돌하중의 감소 경향이 해석과 실험에서 유사하게 나타나는 것을 알 수 있다. 실험과 해석에서 나타난 최대 충돌하중은 각각 약 1,700kN과 1,530kN이었으며 약 11%의 차이를 보였다. 이러한 오차는 해석에서는 충돌체를 완전 강체로 모사하였기 때문으로 판단된다.

Fig. 5.

Comparison results(Impact force vs. time)

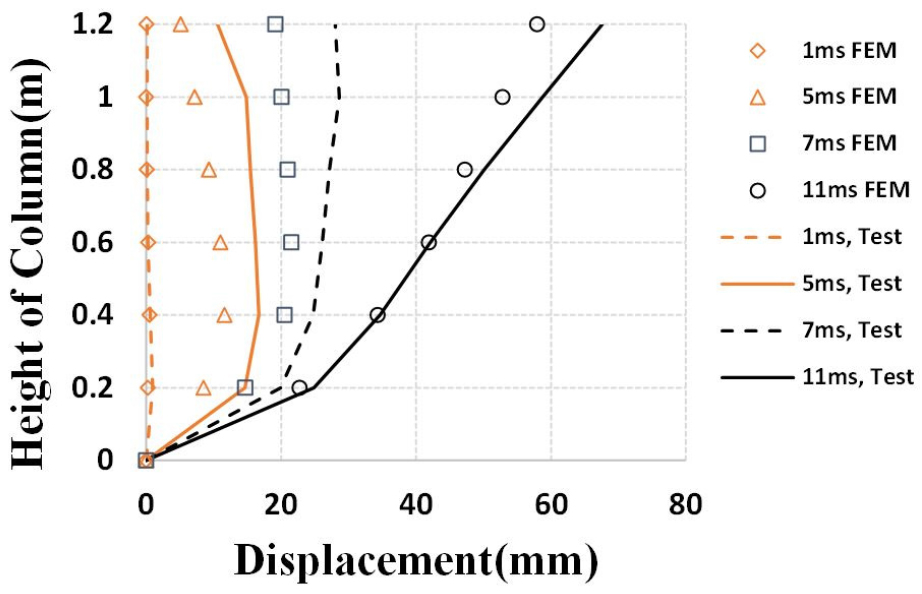
Fig. 6은 충돌 시간대별(1ms - 11ms)로 발생한 CFT 기둥의 변형형상을 비교한 결과를 나타낸다. Fig. 6에서 x와 y축은 각각 CFT의 횡방향 변위와 기둥의 높이를 나타낸다. 충돌체의 충돌 위치는 저면에서부터 0.4m 지점이다. 이 그림에서 알 수 있듯이 해석 결과는 충돌체의 충돌 위치 부근에서 실험결과와 잘 일치하는 것을 볼 수 있다. CFT 기둥 상단부의 변형은 다소 차이가 발생하는 것을 알 수 있지만 전체적으로 해석결과는 CFT 기둥의 충돌 후 변형 형상을 잘 모사할 수 있는 것으로 판단된다.

Fig. 6.

Comparison results(Deformation shape for various time)

3. 해석결과

3.1 해석변수

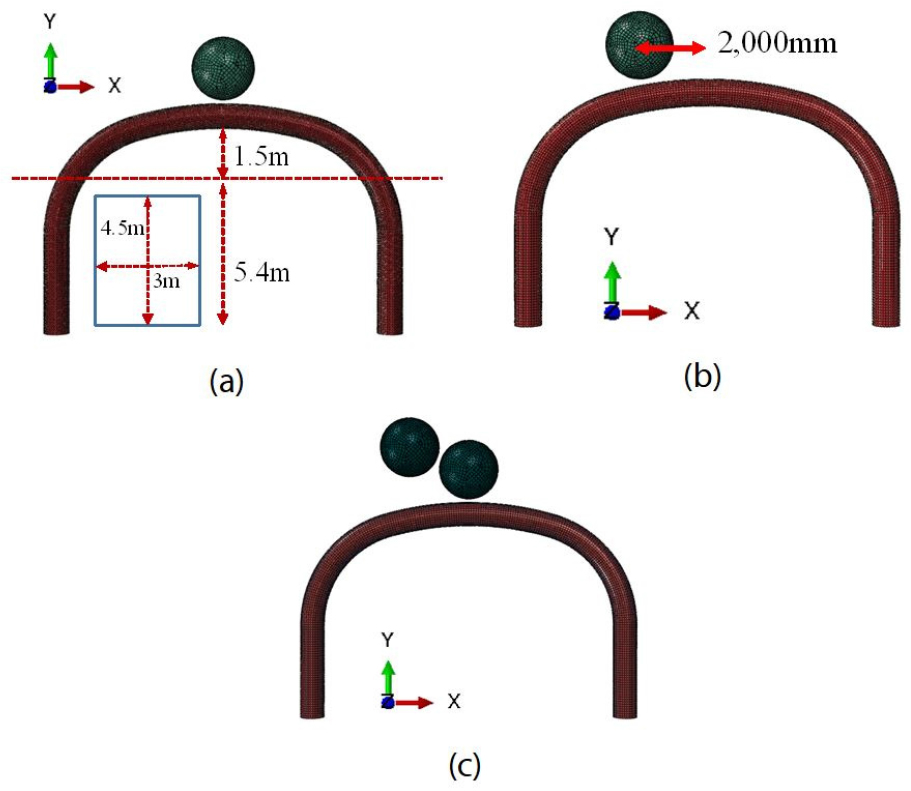
2장에서 수립된 해석 모델을 사용하여 CFT 피암터널 주구조체의 극한 낙석에너지에 대한 거동을 파악하고자 Fig. 7에 나타난 바와 같이 3가지 경우에 대하여 해석을 수행하였다.

Fig. 7.

Analysis cases: (a) Case 1, (b) Case 2, (c) Case 3

Case 1은 CFT 주구조체 중앙에 극한 낙석에너지 2,500kJ가 작용하는 경우이다. Case 2는 동일한 낙석에너지가 중앙으로부터 2,000mm 이격된 거리에 작용하는 경우를 나타내며 이 경우는 주구조체의 비대칭 거동을 파악하기 위하여 선정하였다. Case 3은 Case 1과 2가 결합된 형태로 2,500kJ의 낙석에너지가 먼저 중앙에 작용하고 이 후 2,000mm 이격된 거리에 두 번째 낙석이 작용하는 경우이다. Case 3의 낙석에서지는 총 5,000kJ로 하나의 CFT 주구체가 분담할 수 있는 최대 분담율(83%)을 고려하였을 때 일본 도로협회에서 규정하고 있는 6,000kJ의 낙석에너지와 동일한 수준이다.

본 연구에서는 제안된 CFT 피암터널 주구조체의 극한 낙석하중 저항성을 판단하기 위하여 ① 주구조체의 낙석에너지 소산 능력, ② 낙석 방호 후 잔류변형을 검토하였다. 또한, 최대 낙석에너지에 대응되는 정적하중을 해석적으로 산정하여 기존의 설계 등가정적하중과 비교하였다.

3.2 Case 1

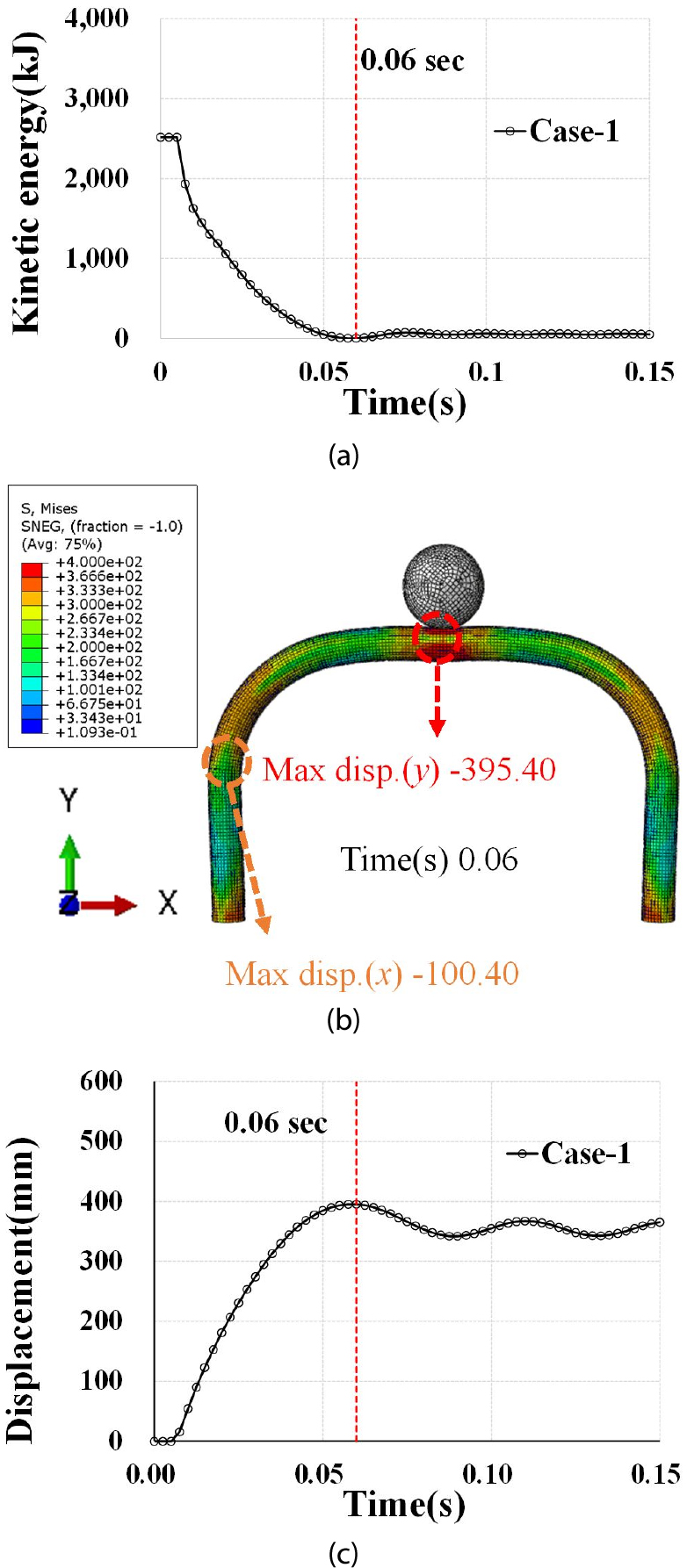
Case 1의 해석 결과는 Fig. 8과 같다. Fig. 8(a), (b), (c)는 각각 해석결과 나타난 낙석에너지의 시간에 따른 변화, 변형형상, CFT 주구조체 충돌지점의 시간에 따른 수직변위의 변화를 보여준다.

Fig. 8.

Analysis results(Case 1): (a) Kinetic energy vs. time, (b) Deformed shape at 0.06sec, (c) Crown disp. vs. time

이 그림에서 알 수 있듯이 낙석이 가지고 있는 최초의 충동에너지 2,500kJ은 약 0.06sec애서 모두 소진이 되는 것을 알 수 있다. 0.06sec에서 CFT 주구조체의 응력분포와 변형형상은 Fig. 8(b)와 같다. 낙석에너지가 모두 소산되는 시점에서 낙석의 충돌위치와 곡선 아치부가 시작되는 양 끝단 부근에서 강재의 응력은 Von-Mises 응력이 325MPa(강재의 항복응력)을 초과하여 소성상태가 됨을 알 수 있다. 즉, 극한 낙석에너지에 대하여 CFT 주구조체가 소성변형을 하면서 에너지를 흡수하는 것을 알 수 있다. 0.06sec에서 낙석 충돌위치(아치의 크라운)의 수직변위는 395.4mm가 발생하였으며 곡선 아치가 시작되는 양 끝단은 100.4mm의 수평 변형이 발생하였다. 아치 크라운(낙석 충돌 위치)의 시간에 따른 수직 변위의 변화는 Fig. 8(c)에 나타나 있다. 충돌 시점부터 모든 낙석 에너지가 소산될 때 까지 수직변위는 증가하며 이후 낙석이 CFT 주구조체와 분리되면서 CFT 주구조체는 상하진동을 하는 것을 알 수 있다.

해석 결과, 최종 잔류 수직변위는 약 342.4mm로 나타났다. 참고로 본 연구에서 수직 변위와 잔류 수직변위는 모두 하중 작용 위치의 변위를 말한다. 이는 현재 제안된 피암터널의 총 높이가 6.9m임을 고려하면 전체 높이의 약 5%의 높이 감소가 발생한 것임을 알 수 있다(Fig. 7(a) 참조). 국내 도로교에서 규정하고 있는 터널의 최소 높이가 4.5m임을 감안하면 극한 낙석에너지 방호 후 차량의 진행은 문제가 없는 것으로 판단된다(MOLIT, 2020).

마지막으로 충돌해석을 수행하고 CFT 주구조체 양 지점에서의 반력을 계산하여 극한 낙석에너지 2,500kJ 작용 시 최대 반력 즉, 등가의 정적하중을 산정하였다. 그 결과 약 7,000kN의 하중이 산정되었다. 국내의 설계기준(MOLIT, 2011)에 따르면 피암터널의 설계하중은

과 같다. 식 (1)에서 λ는 Lame’s Constant(권장값=1,000kN/m²), W는 낙석의 무게, Hr는 낙석의 높이(m), i는 모래층 두께에 관한 보정계수이며 모래층의 두께가 증가할수록 에너지 소산이 증가함으로 i값은 감소한다(모래층의 두께가 0.9m인 경우 1, 0.9m이상인 경우는 1보다 작은 값을 사용). 본 연구에서 2,500kJ에 해당하는 낙석의 무게와 낙하높이는 각각 10.4tonf와 30m이므로 이를 대입하면 설계 정적하중은 약 6,050kN이다. 이 값은 해석결과와 비교하면 해석결과가 약 16%정도 큰 값을 나타내는 것을 알 수 있다. 하지만, 식 (1)은 완충재의 효과가 고려되었으며 Lame’s Constant 값을 권장값으로 사용한 결과이므로 직접적인 비교는 어렵다.

3.3 Case 2

Case 2의 해석결과 경향은 Case 1과 유사하다. 극한 낙석에너지는 Case 1과 동일하게 0.06sec에 모두 소진이 되었으며 낙하지점의 수직변위 변화 경향도 유사하다.

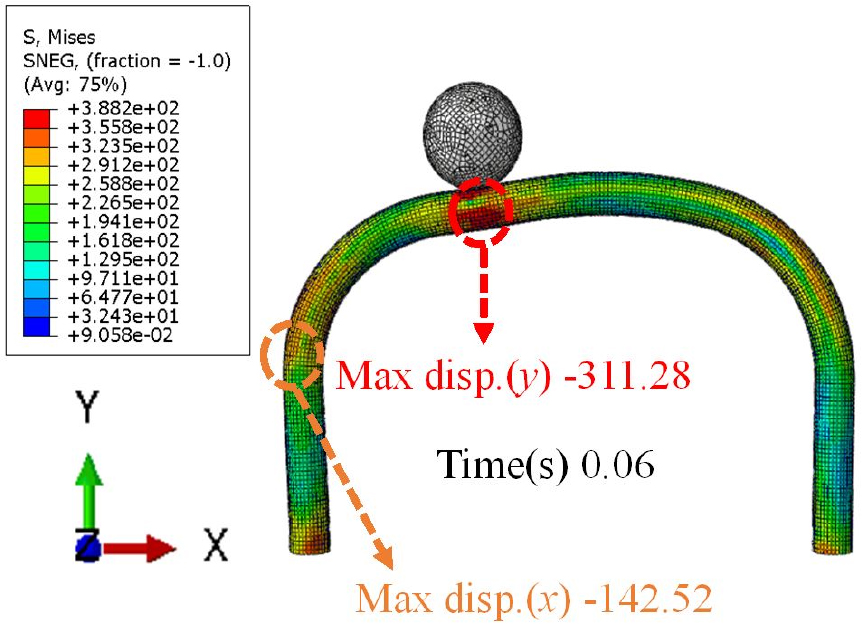
Fig. 9는 0.06sec에서 발생된 CFT 주구조체의 변형형상과 응력분포를 보여준다. 충돌지점과 곡선 아치 부위 시작점 부근에서 소성변형이 발생하는 것을 알 수 있다. 이때 최대 수직과 수평 변위는 각각 311.8mm와 142.52mm 였다. Case 1과 비교하였을 때 수평변위가 더 크게 발생한 것을 알 수 있으며 이는 하중의 비대칭성에서 기인한 것으로 판단된다.

Fig. 9.

Analysis results(Case 2): Deformed shape at 0.06sec

낙석 방호 후 발생한 잔류 수직 변위는 약 250mm였으며 이를 근거로 낙석 방호 후 차량의 진행 가능 여부를 확인하면 차량 진행에는 문제가 없는 것으로 나타났다. 또한, 지점 반력으로부터 계산된 수직 최대하중은 약 8,000kN으로 Case 1과 비교하여 동일한 극한 낙석에너지에 대하여 더 큰 수직하중이 작용함을 알 수 있었다. 식 (1)과 비교한 결과 약 32% 더 큰 수직하중이 발생하였다.

3.4 Case 3

Case 3은 Case 1과 Case 2가 연속적으로 작용하는 경우를 나타낸다. 먼저 CFT 주구조체 중앙부에 2,500kJ의 낙석에너지가 작용하고 낙석이 충돌 후 CFT와 분리되는 시점에 중앙부로부터 2,000mm 이격된 부분에 새로운 2,500kJ의 낙석에너지를 갖는 낙석이 충돌하도록 하였다. 따라서, 총 낙석에너지는 5,000kJ로 한번의 극한 낙석에너지 작용 후 추가적인 극한 낙석에너지가 작용하였을 때 CFT 주구조체의 낙석 방호 성능을 살펴보는데 해석의 목적이 있다.

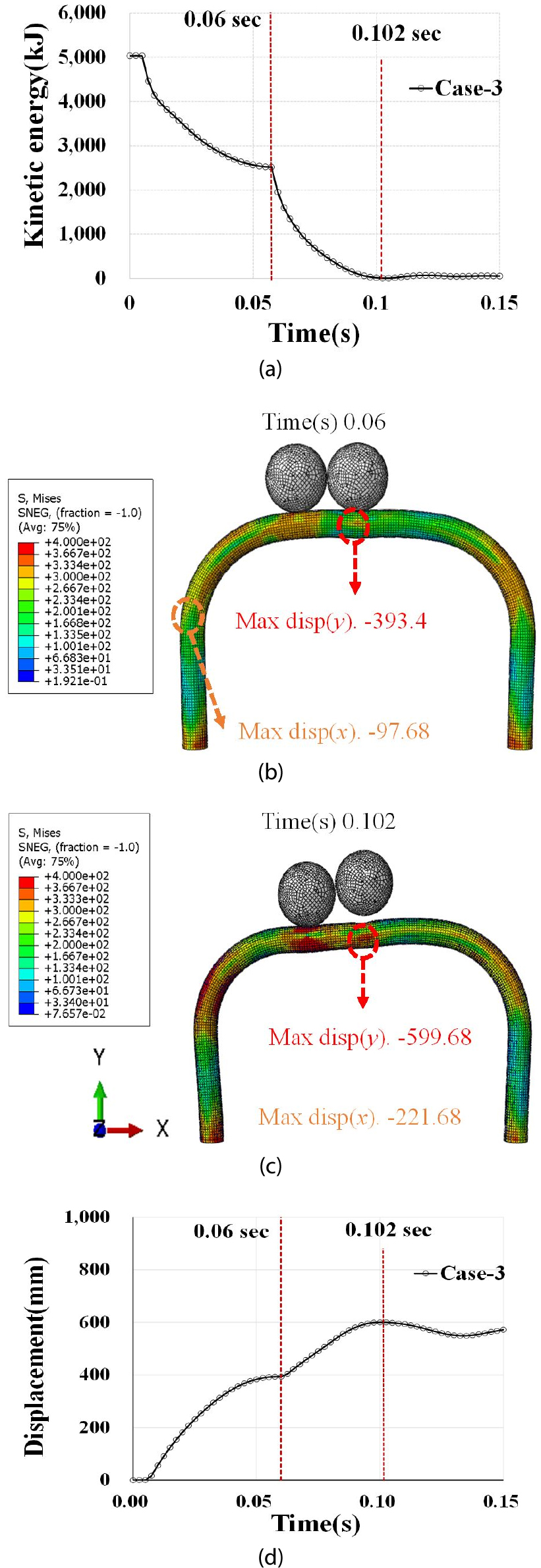
Fig. 10은 Case 3에 대한 해석 결과를 보여준다. 첫 번째 낙석이 중앙에 충돌하는 경우, 약 0.06sec에서 2,500kJ의 낙석에너지가 모두 소산되는 것을 알 수 있다. 이 후 두 번째 낙석이 중앙부로부터 2,000mm 이격된 지점에 충돌을 하고 최종적으로 0.102sec에 모든 낙석에너지가 소산되는 것은 Fig. 10(a)를 통하여 알 수 있다. Fig. 10(b)와 (c)는 각각 0.06sec와 0.102sec에서 발생하는 CFT 주구조체의 변형형상과 응력분포를 보여준다. 앞서 설명하였듯이 0.06sec에서 첫 번째 낙석이 CFT 주구조체와 분리되면서 두 번째 낙석이 충돌함을 알 수 있다. 이 후 0.102sec에서는 첫 번째 낙석은 완전히 분리되고 두 번째 낙석 또한 CFT 주구조체에서 분리되기 시작한다. 응력 분포를 살펴보면 앞선 Case 1과 2와 유사하게 낙석 위치 및 CFT 주구조체 아치부가 시작되는 부분이 소성상태로 변화한 것을 알 수 있다. 두 번째 낙석을 방호한 후 최종 잔류변형은 약 600mm로 나타났으며 이는 Case 1과 2를 통하여 발생한 수직변위를 산술적으로 더한 것과 유사한 결과이다. 즉, 낙석이 추가적으로 작용하면서 변형은 산술적으로 누적되는 결과가 나타났다. CFT 중앙부의 수직변위와 시간과의 관계는 Fig. 10(d)와 같으며 앞서 설명한 바와 같이 변위가 누적되는 것을 알 수 있다.

Fig. 10.

Analysis results(Case 3): (a) Kinetic energy vs. time, (b) Deformed shape at 0.06sec, (c) Deformed shape at 0.102sec, (d) Crown disp. vs. time

해석결과 극한 낙석에너지 2,500kJ에 해당하는 낙석이 두 번에 걸쳐 작용을 하는 경우에도 최종 변형형상을 분석해 보면 차량의 통행에는 문제가 없는 것으로 나타났다. 따라서, 제안된 CFT 주구조체는 약 5,000kJ의 낙석에너지도 방호할 수 있음을 알 수 있었다. 또한, 극한 낙석에너지 2회 작용 시 발생하는 최대 수직반력은 약 12,000kN으로 식 (1)에 의하여 계산된 수직하중 12,100kN과 거의 유사함을 알 수 있었다. 앞선 Case 1 및 2의 경우에는 최대 수직반력이 각각 7,000kN과 8,000kN이었다. 이 두 수직반력의 합은 15,000kN이나 Case 3에서의 최대 수직반력은 이보다 작은 12,100kN이었다. 이렇게 차이가 발생하는 것은 2개의 낙석이 시간차를 두고 충돌을 함으로 최대 수직반력이 발생하는 시간이 서로 다르기 때문인 것으로 판단된다. 즉, 최대 수직반력의 경우에는 각 Case의 값을 산술적으로 더할 수 없다.

4. 결 론

본 연구에서는 기존 연구를 통하여 제안된 2차선 국도변에 설치가 가능한 CFT 피암터널의 주구조체를 대상으로 극한 낙석에너지(2,500kJ)에 대한 낙석 방호성능과 거동을 유한요소해석을 통하여 분석하였다. 연구결과 다음과 같은 결론을 도출하였다.

1) CFT 주구조체에 대한 낙석충돌 해석이 가능한 모델을 개발하였다. 실험과 해석을 비교한 결과 개발된 모델은 CFT 부재에 대한 충돌 거동을 잘 모사할 수 있는 것으로 나타났다. 이러한 충돌해석 모델링 기법은 유사한 구조의 해석에 활용이 가능할 것으로 판단된다.

2) 2차선 국도에 적용 가능한 CFT 주구조체에 대하여 주구조체 중앙에 낙석이 작용하는 경우(Case 1), 중앙으로부터 2,000mm 이격된 지점에 낙석이 작용하는 경우(Case 2), 그리고 이 두 경우가 순차적으로 발생하는 경우(Case 3)에 대하여 해석을 수행하였으며 모든 경우에 제안된 CFT 주구조체는 낙석에너지를 소성변형을 통하여 모두 소산하는 것을 알 수 있었다.

3) 모든 낙석에너지가 소산되었을 때 발생한 CFT 주구조체의 변형형상을 분석한 결과, 차량의 통행에 지장을 주지 않는 선에서 변형이 발생하여 극한 낙석에너지에 대한 충분한 방호성능을 가진 것으로 나타났다.

4) 작용하는 낙석에너지에 대한 최대 수직하중을 계산한 결과, 현재 국내 설계기준에서 제안하고 있는 등가정적하중의 값과 최소 1%(Case 3)에서 최대 32%(Case 2)까지 차이가 발생하는 것을 알 수 있어 초기 설계에서 등가정적하중을 적용할 수 있을 것으로 판단된다. 하지만, 해석에서는 완충재의 효과가 반영되지 않았으며 기준에서 등가정적하중 산정 시 사용되는 변수 값들이 명확히 CFT 주구조체에 대하여 산정되지 않아 직접적인 비교는 어려우며 낙석에너지에 대한 등가정적하중 산정에 대하여는 추가적인 연구가 필요한 것으로 판단된다.