1. 서 론
2. NP C/SiC 복합재료 High fidelity FE 모델 개발
2.1 NP C/SiC 복합재료 구성
2.2 Micro-CT 이미지 프로세싱
2.3 3D high fidelity FE 모델 생성
2.4 3D High fidelity FE 모델 해석 결과 및 검증
3. Subcell 모델링에 의한 Meso-Macro 브리징
3.1 Micro-CT 이미지를 통한 Subcell 모델링
3.2 Subcell 등가물성 계산
3.3 Subcell 모델링 해석 및 검증
4. 결 론
1. 서 론
Needle-punched(NP) 복합재료는 우수한 열구조적 물성 덕분에 최근 항공기, 우주구조물, 그리고 자동차 산업에 이르기까지 다양한 분야에서 사용되고 있다. 0°/90°의 각도를 가지는 적층판 사이에 고온 환경에서 사용을 위한 단섬유웹층(SFW: Short-fiber web)을 구성하여 needle-punching 작업을 통해 기존 적층 복합재료의 취약점인 두께 방향의 물성을 강화시킬 수 있다. 이러한 복합재료 preform은 C/SiC과 C/C 복합재료에 많이 사용되며, 기본적으로 탄소로 preform을 구성하고 기지에 해당하는 C 혹은 SiC를 preform 내부에 함침시켜 제작한다. 기지를 함침하는 방법은 CVI(Chemical Vapor Infiltration), PIP(Polymer Infiltration Pyrolysis), LSI(Liquid Silicon Infiltration) 등의 공법이 있다. 이를 바탕으로 구성된 NP C/SiC 복합재료 소재를 열방어 시스템에 적용해 왔으며, 물성 특성화관련 연구들이 활발하게 진행되었지만 국내는 미흡한 현황이다.
최근 몇 년 동안 섬유강화 복합재료에 대한 연구는 활발히 진행되었다. 특히, 대표체적요소(RVE: Representative Volume Element)를 지정하여 유한요소(FE: Finite Element) 해석을 이용하거나(Zhuet al., 2018; Jeong, 2018; 2019), 미소역학 이론을 이용하여 복합재료 관련 연구가 진행되었다(Lim et al., 2020b). 하지만, NP 복합재료는 needle-punching에 의한 복합재료의 구조적 복잡성 때문에 관련 연구는 많이 진행되고 있지 않다. 그럼에도 불구하고 해석을 위한 다양한 시도들이 있었다. Li 등(2013)은 처음으로 NP 복합재료에 RVE 개념을 도입하여 복합재료 해석을 수행하였다. 혼합비(ROM: Rule of Mixture)를 이용하여 등가물성을 얻었지만, RVE에 NP 복합재료의 구조를 자세히 구현하지 못하여 실험결과와 차이를 보였다. 이를 시작으로 Xie 등(2015)은 NP 복합재료의 여러 특징을 반영하여 4종류의 RVE를 구축하여 각각의 등가물성의 평균값을 이용하였다. 해당 결과는 기존의 방법보다 나은 결과를 얻을 수 있었지만, needle-punching에 의한 국소적 거동은 파악하기 어려웠다.
NP 복합재료의 미소구조를 보다 잘 표현하기 위해 최근 micro- CT(Computed Tomography)를 이용하여 복합재료 모델링을 수행하고 있다. Wan 등(2019)은 micro-CT 촬영을 통해 needle- punching에 의한 섬유다발의 손상을 확인하였고 이를 등가물성 계산에 활용하였다. 추가로 Yu 등(2017)은 NP C/C 복합재료를 대상으로 이미지 프로세싱을 이용하여 meso-scale RVE를 구축하였다. micro-CT 이미지를 바탕으로 실제적인 구조를 모사하였으며 복합재료 균질화를 통해 등가물성을 예측하였다. 더 나아가, Lim 등(2020a)은 micro-CT를 이용하여 미소구조를 반영하는 적층모델을 구성하였으며, NP C/SiC 복합재료의 비선형 거동을 기공 내 정수압의 영향을 받는 탄소성 모델링을 수행하였다. 제한한 모델의 해석 결과를 다양한 조건의 실험(i.e., 인장, 압축, 전단, 굽힘)을 바탕으로 모델 검증을 수행하였다.
이러한 유한요소를 이용한 미소구조해석은 지엽적 변형 및 파손에 대한 측정이 가능하지만, 구조적인 문제로 접근하기엔 많은 양의 해석적 비용이 소요된다는 단점이 존재한다(Terada and Kikuchi, 1995; Fish and Yu, 2001; Doghri and Ouaar, 2003). 따라서 본 연구에서는 이러한 단점을 극복하고자 Subcell 모델링을 적용함으로써 NP C/SiC 복합재료의 복잡성을 고려하면서 해석 비용을 절감하는 방법을 제시한다. Subcell modeling은 micro-CT 기술을 이용하여 얻은 high fidelity model을 바탕으로 구성된다. 또한 복합재료 멀티스케일 해석을 위해 수치적 균질화법을 이용하는데, 정해진 RVE에 주기경계조건(PBC: Periodic Boundary Condition)을 제하하여 선형 물성을 계산한다. 제안된 모델링의 타당성을 검증하기 위해 인장, 전단 실험 결과와의 비교를 통하여 high fidelity 모델을 검증을 수행한다. 더 나아가 high fidelity model을 바탕으로 구성된 subcell 모델도 굽힘시험 해석 결과와 실험 결과를 비교하여 제안된 본 연구에서 제안한 멀티스케일 해석 기법의 타당성을 확인한다.
2. NP C/SiC 복합재료 High fidelity FE 모델 개발
이 장에서는 NP C/SiC 복합재료를 micro-CT 이미지를 활용하여 high fidelity model 개발을 위한 이미지 프로세싱 기법에 대한 소개를 하고자 한다.
2.1 NP C/SiC 복합재료 구성
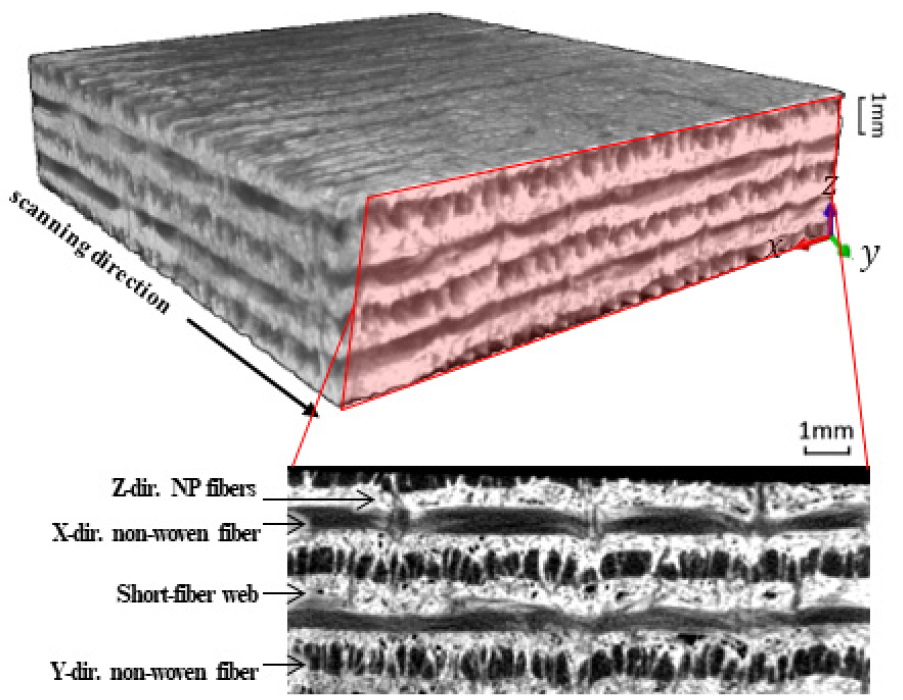
NP C/SiC 복합재료는 장섬유와 단섬유 웹(SFW: Short-fiber web)을 [0° / SFW / 90° / SFW]T으로 적층하여 복합재료 preform을 구성하고 수직방향의 needle-punching을 통하여 SFW의 단섬유를 수직방향으로 결속시켜 기존 적층복합재료의 단점인 층간의 박리현상을 보완한다. 그 다음으로 CVI 혹은 PIP 공법을 이용하여 preform 내부를 SiC로 채워 복합재료를 제작한다. 본 연구에서는 장섬유 소재에 T-700을 사용하였으며, micro-CT 촬영을 통해 촬영한 결과 Fig. 1과 같이 적층구조를 가지는 형태의 이미지를 확인할 수 있다.
Micro-CT는 ZEISS Xradia 520 Versa를 통해 100kV의 스캐닝 에너지로 20×20×5mm3 크기의 시편을 촬영하였다. Fig. 1의 이미지에서 grayscale을 바탕으로 NP C/SiC 복합재료의 구조를 확인할 수 있다. X와 Y방향으로 장섬유로 구성된 층(laminae)이 차례로 겹쳐져있다. 섬유는 기지에 비해 높은 밀도를 가지고 있기 때문에 어두운 색으로 표현된다. 장섬유 층 사이에 SFW층이 있으며, SFW을 구성하고 있는 단섬유의 밀도가 높지 않아 대부분 SiC 기지로 채워져 있어 밝은 색의 grayscale로 나타내어진다. 또한 Needle-punching으로 인한 X축 장섬유의 굴곡(Undulation)을 이미지를 통해 확인할 수 있다.
2.2 Micro-CT 이미지 프로세싱
유한요소 모델을 통해 NP C/SiC 복합재료의 미소스케일의 구성요소(X,Y,Z 방향 섬유 및 기지)를 효과적으로 표현하기 위해서는 이미지 프로세싱을 통한 복합재료의 각 구성요소 구별과정이 필요하다. 이 장에서는 이미지 프로세싱 알고리즘을 이용해 NP C/SiC 복합재료를 구성하는 3종류의 섬유다발(X, Y, Z축) 과 기지를 각각 특정 grayscale로 구분하였다. 전체적인 이미지 프로세싱 과정은 다음과 같다 : (1) 전처리 작업을 통한 Micro-CT 이미지 회전 및 노이즈 제거, (2) Hough transform (HT) 기법을 이용한 섬유 방향 정보 획득, (3) 섬유 방향 정보를 이용한 섬유와 기지 구분.
첫째로, 이미지 회전을 통해 micro-CT 이미지를 수평 정렬시켜 섬유 배열 각도 계산의 오차를 줄였다. 또한 이미지 blurring과 이진화, morphology 함수 연산을 통해 micro-CT 이미지에 존재하는 노이즈를 제거하고, 섬유와 기지 사이의 거친 표면을 완화하였다. 이러한 작업은 이후 수행될 이미지 처리의 정확도를 높일 수 있다. 이미지 이진화와 morphology 함수 연산은 MATLAB image processing toolbox를 활용하였으며, 이에 관한 결과는 Fig. 2에 나타난다.
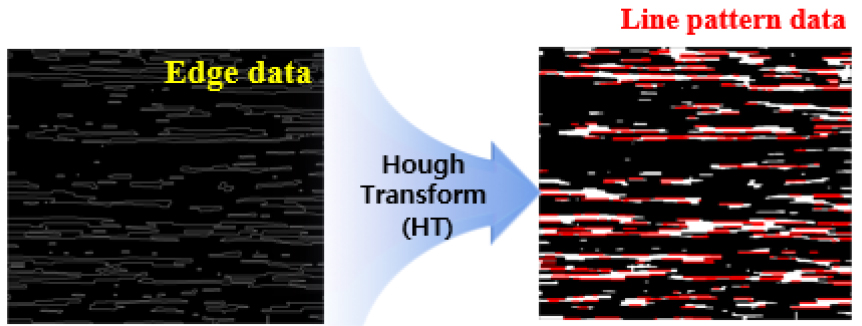
둘째로, Hough Transform 기법(Hough, 1962)을 이용해 micro- CT 이미지로부터 섬유 배열 각도를 획득하였다. Fig. 2에서 볼 수 있듯이, HT 기법은 이미지에 나타나는 직선 패턴을 인식하는 방법으로 이를 적용하기 위해 canny edge detection 기법(Canny, 1986)을 통해 이미지의 경계면(edge) 정보를 획득해야 한다. 이후 HT 기법을 이용해 이미지의 직선 정보를 획득하고, 이를 토대로 직선의 각도를 계산한다. 계산된 직선의 각도 정보는 해당 직선에 포함되는 NP C/SiC 섬유부의 배열 각도가 된다.
마지막으로 계산된 각도 데이터를 이용하여 X,Y,Z 방향 섬유와 기지를 구분하였다. 이 과정에서 NP C/SiC의 각 구성요소에 해당하는 micro-CT 이미지 픽셀에 특정 grayscale 값을 부여하였다. 각 구성요소에 부여된 grayscale값은 Table 1에 정리되어 있다. Fig. 2(a)에서 볼 수 있듯이, 이미지 처리 과정을 거친 Z축 배열 섬유는 X,Y축 배열 섬유보다 더 낮은 grayscale 값을 가진다. 따라서, Z축 섬유를 다른 구성요소로부터 구분하기 위해 특정 threshold값을 설정하고, 지정 threshold 보다 낮은 grayscale 값을 가지는 pixel을 Z축 섬유로 판단하였다. 또한 Hough transform방법을 이용하여 Fig. 3과 같이 Line pattern 데이타를 추출한다. 상기 3-step 이미지 프로세싱 알고리즘을 통해 NP C/SiC 구성요소를 구분할 수 있다. 이러한 작업은 Micro-CT 이미지의 각 layer마다 수행되어 최종적으로 각 layer를 적층 시킨 FE 모델을 생성한다. 본 연구에서 제안된 NP C/SiC 이미지 프로세싱 과정은 Fig. 4와 같이 정리할 수 있다.
Table 1.
Grayscale value of NP C/SiC constituents
| NP C/SiC constituents | Grayscale value(0~1) |
| X-direction fiber | 0.4 |
| Y-direction fiber | 0.8 |
| Z-direction fiber | 0.2 |
| Matrix | 1 |
2.3 3D high fidelity FE 모델 생성
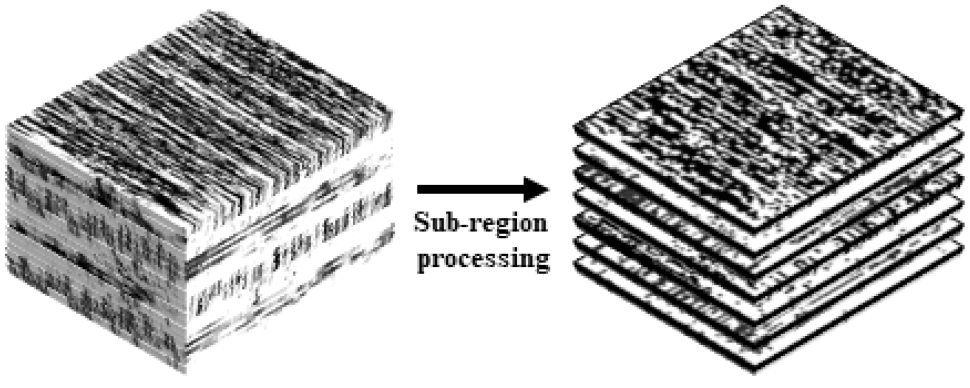
이미지 프로세싱을 통해 X, Y, Z 방향의 섬유와 기지를 grayscale 기준으로 구분하였으며, 구해진 구성요소를 바탕으로 3D high fidelity RVE 모델을 생성한다. NP C/SiC 복합재료의 정확한 모사를 위해서는 가장 작은 요소(fine element)로 모델을 구성하면 가장 좋겠지만, 유한요소해석에서 많은 시간이 소요되므로 모델 간소화 작업이 필요하다. 특정 영역의 grayscale의 값을 평균값으로 치환하는 sub-region 알고리즘을 통해 모델 간소화를 시킬 수 있다.
Fig. 5와 같이 많은 픽셀수로 자세히 표현된 이미지들을 sub-region 프로세싱을 통해 단순화시킬 수 있다. 연구에 사용된 모델의 경우, 717×826×150 크기의 이미지를 100×100×50 크기로 구성함으로써 약 177배의 요소를 줄일 수 있었다.
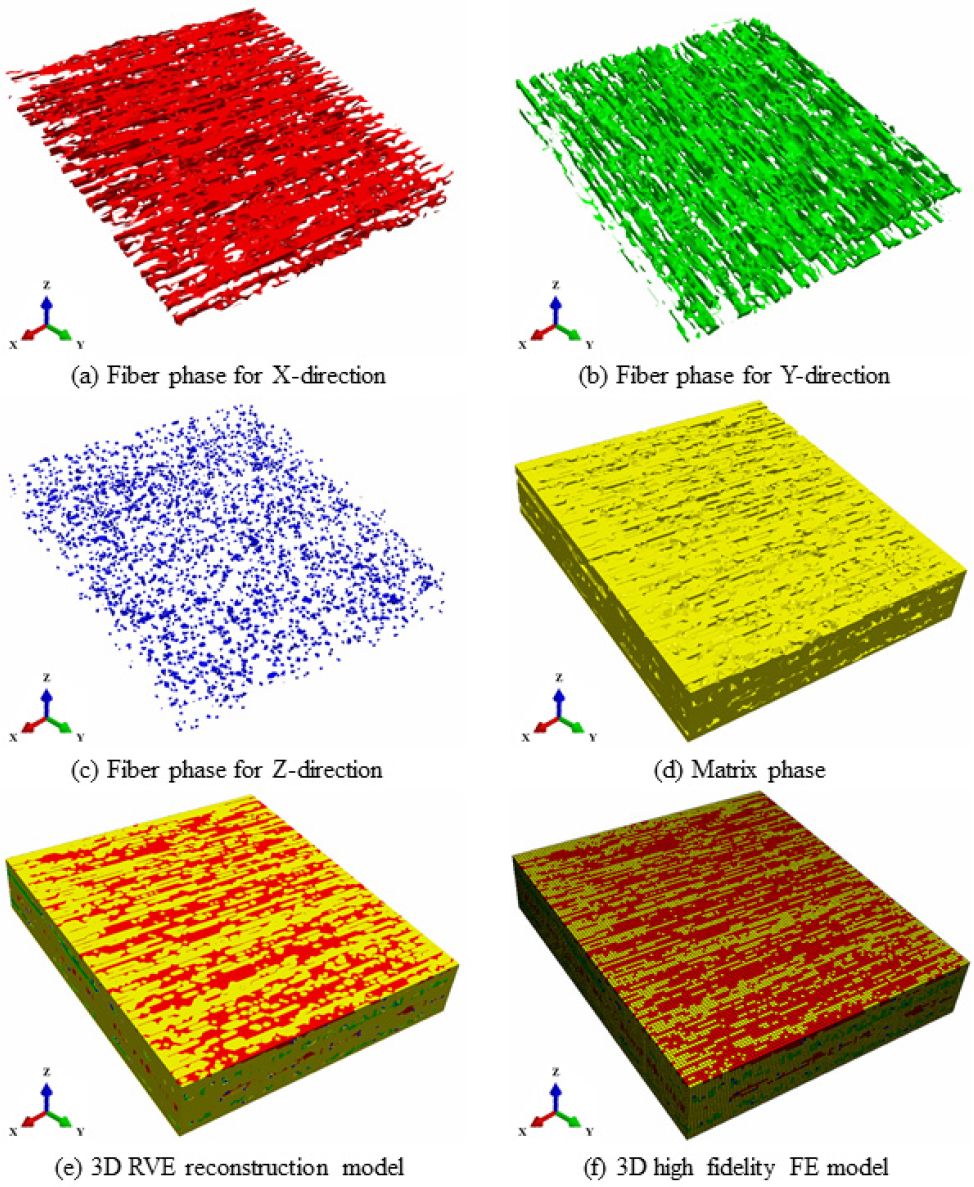
유한요소해석을 위해 SimplewareTM ScanIP를 사용하여 요소생성을 수행하였다. 이러한 절차를 통해 3D high fidelity FE 모델을 구성할 수 있으며, 총 50,000개의 C3D8 타입의 요소로 이루어져있다. 3D high fidelity 모델을 Fig. 6과 같이 정리할 수 있다.
복합재료를 구성하고 있는 X, Y, Z 방향의 섬유와 기지를 각각 빨강, 초록, 파랑, 노랑색으로 표현하였다. Fig. 6을 확인해보면, X, Y 방향의 섬유는 연속섬유 형태를 보이는 반면, Z 방향의 섬유는 연속섬유가 아닌 분리된 파편처럼 보인다. Z 방향의 섬유는 Needle-punching으로 인해 SFW의 단섬유가 끌려 올려지는 형태를 취하기 때문에 연속적인 경향이 보이지 않는다. 하지만, X, Y 방향의 균일한 간격으로 Needle-punching이 되어 있다는 특징을 파악할 수 있었으며, 이러한 경향은 Subcell 모델링에 사용된다. 이미지 프로세싱을 통해 얻은 3D high fidelity FE 모델은 NP C/SiC 복합재료의 미소구조 특성을 직접적으로 반영할 수 있으며 이러한 특징들은 물성평가에 반영된다.
복합재료의 등가거동 및 등가물성을 계산하기 위해 구축된 RVE에 경계조건을 정의하는 것은 정확한 결과를 얻기 위한 중요한 단계이다. 본 연구에서는 수렴성과 정확성이 우수한 주기경계조건(PBC: Periodic Boundary Condition)을 활용하여 복합재료 균질화를 수행하였다. 구축된 FE 모델에 선형 구속조건을 통해 다음과 같이 주기경계조건 구현할 수 있다.
이 식에서 와 는 각각 RVE 모델의 변위와 좌표를 의미하며, 상첨자 와 는 RVE 모델의 각각 서로 마주보고 있는 면의 위치를 나타낸다. 따라서 는 마주보고 있는 면간의 길이의 의미하며, 는 RVE내의 평균 변형률을 나타낸다. 본 연구에서 사용되는 RVE의 형태는 육면체 형태를 가지고 있기 때문에 는 RVE의 길이, 너비, 높이가 된다. 미소구조의 변형에 따라 등가가동을 파악하기 위해 부피평균화를 이용하는 평균장(average field) 이론을 사용하였다.
이 수식에서 는 RVE의 부피이며, 와 는 미소구조 내 계산된 응력 및 변형률이다. 이러한 방법을 이용하여 3D high fidelity FE 모델의 등가 stress-strain 커브를 얻을 수 있다.
2.4 3D High fidelity FE 모델 해석 결과 및 검증
Micro-CT 이미지 프로세싱을 통해 구축한 3D high fidelity FE 모델을 유한요소해석을 통해 거동을 예측하기 위하여 복합재료를 구성하고 있는 요소들의 물성 정의가 필요하다. 본 연구에서는 동일한 재료를 이용하여 연구를 진행한 Lee 등(2020)의 결과 값을 사용하여 유한요소해석을 수행하였다. 물성 특성화를 위해서 시험결과를 바탕으로 수학적 균질화기법과 수정된 혼합 법칙을 적용하였다. 상온 실험데이터를 이용하여 얻은 섬유와 기지의 물성은 Table 2에 정리되어 있다.
Table 2.
Calibrated material properties of NP C/SiC composites(unit: GPa)
| Fiber | 220.9 | 17.9 | 8.9 |
| Matrix | 28.9 |
3D high fidelity FE 모델에 주기경계조건을 제하하여 유한요소해석을 수행하면 상온에서의 NP C/SiC 복합재료의 거동을 예측할 수 있다. Fig. 7은 3D high fidelity FE 모델에 X 방향의 인장력, XY 방향의 전단력을 제하하여 해석을 수행하였으며, 이를 통해 얻은 응력분포이다. 3D high fidelity FE 모델은 맨 위층의 장섬유가 0도 방향으로 정렬되어 있기 때문에, 섬유에서 응력집중이 되는 것을 직접적으로 확인할 수 있다. 이와 반대로, XY 방향으로 전단력을 가한 해석의 경우 섬유와 기지에서 고른 응력 분포를 확인할 수 있다.
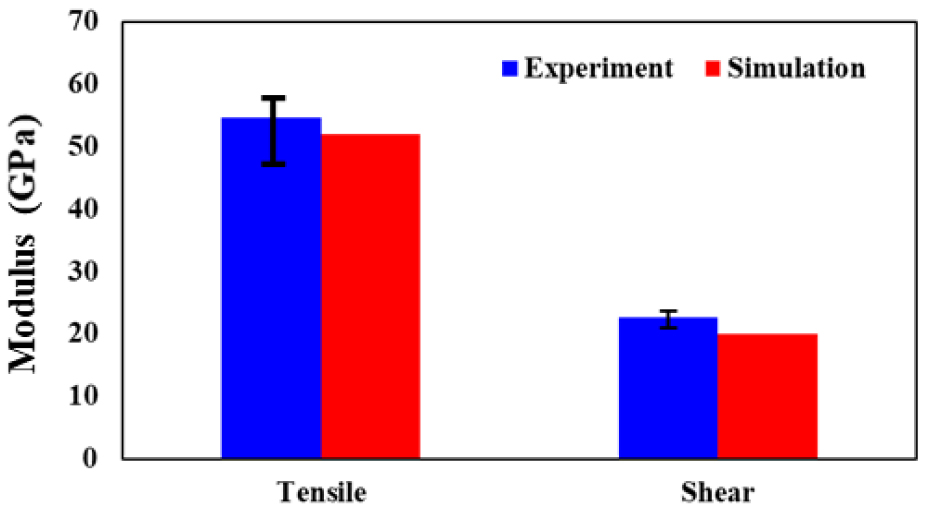
평균장 이론을 이용하여 인장, 전단해석에 대한 물성을 실험결과와 비교 검증을 위의 Fig. 8과 같이 수행하였다. 이를 바탕으로 3D high fidelity FE 모델의 검증을 완료하였으며, 앞으로 소개할 Subcell 모델링의 참고(Reference)모델로 사용된다.
3. Subcell 모델링에 의한 Meso-Macro 브리징
이 장에서는 Micro-CT 이미지 분석을 통해 Subcell 모델링 절차에 대해 소개하고, Subcell 구성 요소들의 3D high fidelity FE 모델과 동일한 거동을 할 수 있도록 각 Subcell의 등가물성을 구하기 위한 복합재료 균질화 방법을 소개한다.
3.1 Micro-CT 이미지를 통한 Subcell 모델링
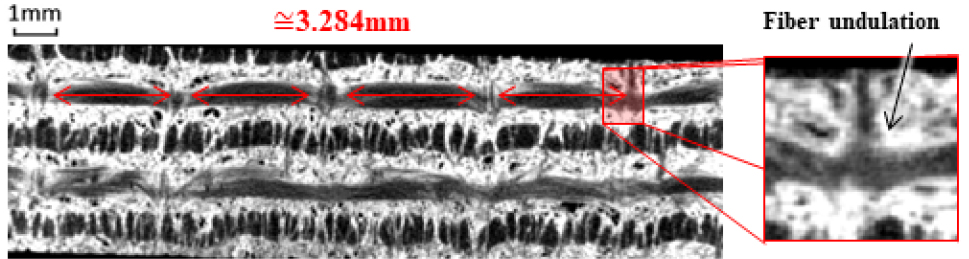
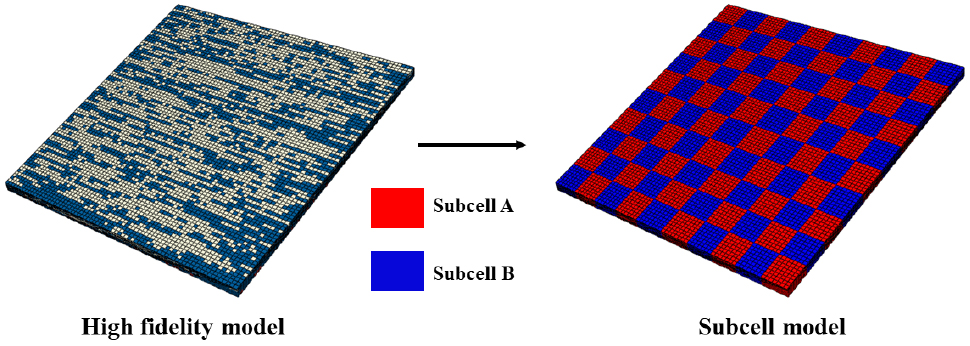
Subcell 모델링을 위해서 micro-CT를 활용하여 NP C/SiC 복합재료의 미소구조에 대해 면밀한 분석이 동반되어야 한다. Fig. 9는 NP C/SiC 복합재료의 단면 이미지이며, needle- punching으로 인한 X축 장섬유의 굴곡(undulation)을 확인할 수 있다. 이러한 특징을 바탕으로 needle-punching의 간격을 파악할 수 있으며, 평균 3.284mm 간격으로 구성되어 있다. 이러한 규칙성을 통해서 두 종류의 subcell로 구분할 수 있다.
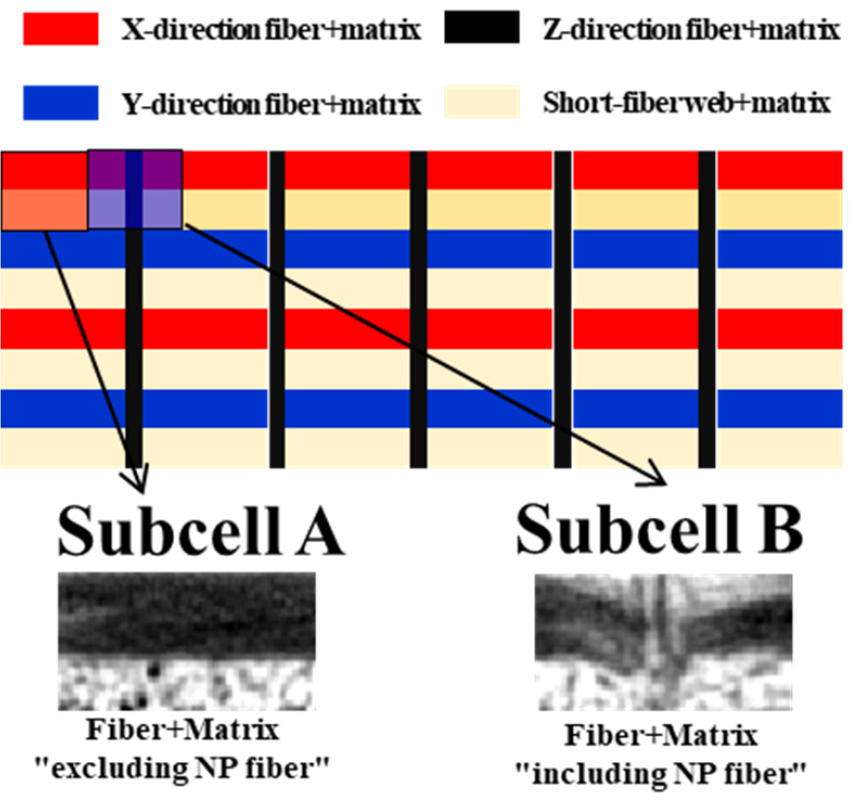
Fig. 10에서 X와 Y축 섬유 층은 빨강과 파랑으로 표기하였으며, 그 둘 사이는 살색으로 나타낸 SFW이 삽입되어 있다. 이를 바탕으로 Z축 NP 섬유 유무에 따라서 Subcell A와 Subcell B로 나눌 수 있다. Subcell B는 섬유, 기지, SFW, NP 섬유를 포함하고 있으며, Subcell A는 섬유, 기지 SFW만으로 구성되어 있다. 이를 바탕으로 구축된 모델은 Fig. 11과 같으며 두 종류의 Subcell로 NP C/SiC 복합재료를 표현할 수 있다.
3.2 Subcell 등가물성 계산
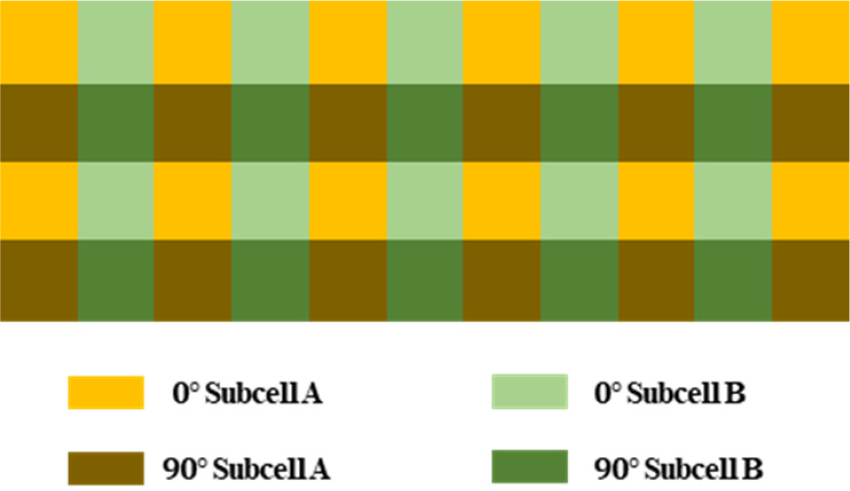
Subcell 모델링을 통해 macro-scale 구조해석을 수행하기 위해서 각 subcell의 등가물성을 결정하는 것이 필요하다. 본 연구에서는 수치적 균질화(numerical homogenization)를 통해 각 subcell의 등가물성을 계산하였다. 우선 앞 장에서 구축한 3D high fidelity FE 모델을 바탕으로 각 위치에 대응하는 subcell의 등가물성을 구하기 위해 지역적 평균화(Local average scheme)를 이용하여 각 subcell의 등가물성 분포를 파악하였다. 등가물성 파악을 위해 high fidelity 모델의 단층(single- layer)을 이용하여 subcell 모델을 구성하였으며, 이는 Fig. 12에 정리되어 있다. Subcell 모델은 50개의 Subcell A, 50개의 Subcell B로 총 100개의 subcell로 Z축 NP 섬유의 유무에 따라 구성되어 있다.
3D high fidelity FE 모델에서 subcell 모델링을 수행할 때, 각 위치한 subcell 마다 완전히 동일한 형상을 가지고 있는 것이 아니기 때문에 위치에 따른 subcell의 물성 차이가 보여 질 수 있다. 따라서 각 subcell의 결과 값을 히스토그램으로 표현하여 평균값을 구조해석에 사용할 수 있도록 한다.
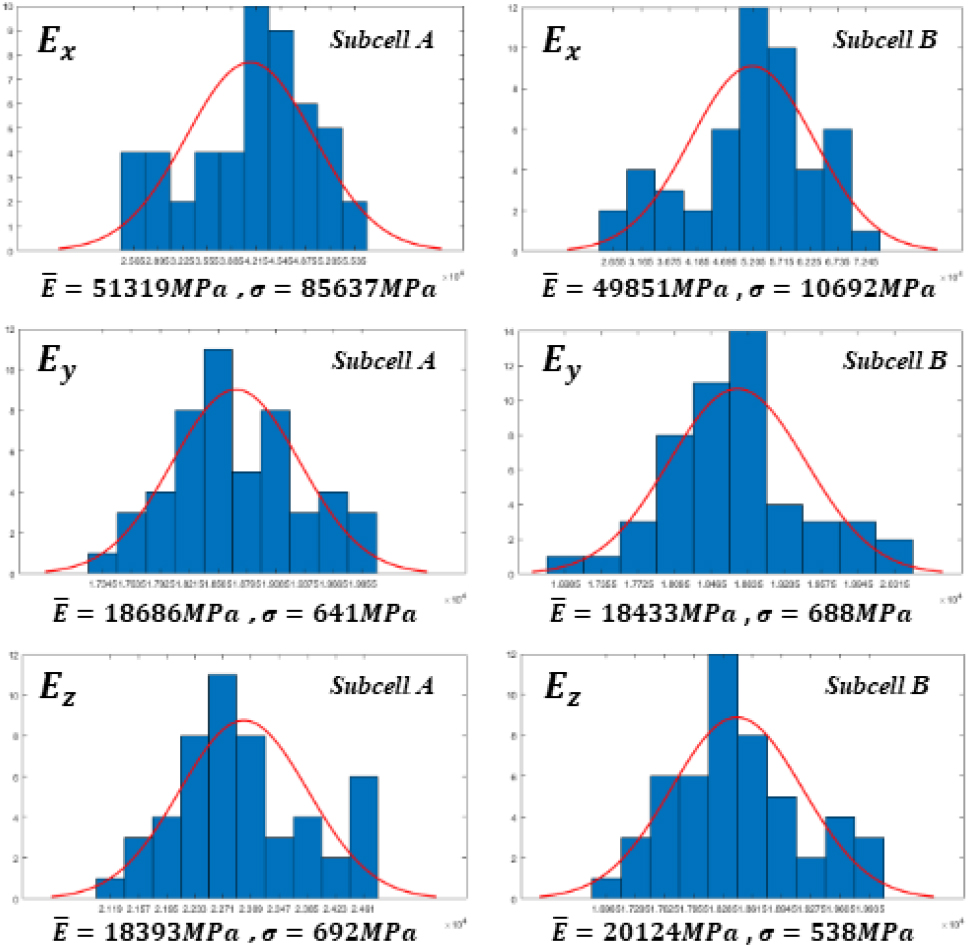
2장 해석과 동일하게 각 셀의 등가물성 계산을 위해 주기경계조건의 단층 3D high fidelity FE 모델에 6방향의 단위변형률(unit strain)을 제하하여 균질화를 수행한다. 여기서, 일반적인 균질화와는 다르게 각 셀의 크기만큼 지역적 평균화(local average scheme)를 수행하여 각 subcell들의 등가물성을 산출한다. 이를 통해 계산한 각 Subcell의 X, Y, Z축 방향의 통계적 물성 분포를 Fig. 13에 나타내었다.
그래프 아래는 각 분포의 평균값과 표준편차가 나타나 있다. Subcell의 영역에 따라 Z축 NP 섬유에 의한 물성 변화를 확인할 수 있다. Z축 NP 섬유를 포함하고 있는 Subcell B에서 Z축 방향의 물성이 Subcell A보다 높았으며, 이와 반대로 X축 물성은 장섬유의 굴곡(undulation)으로 인해 낮게 평가되었다. 물성 비교를 바탕으로 subcell이 high fidelity 모델의 미소구조 특성을 표현 가능하다는 것을 확인할 수 있다.
3.3 Subcell 모델링 해석 및 검증
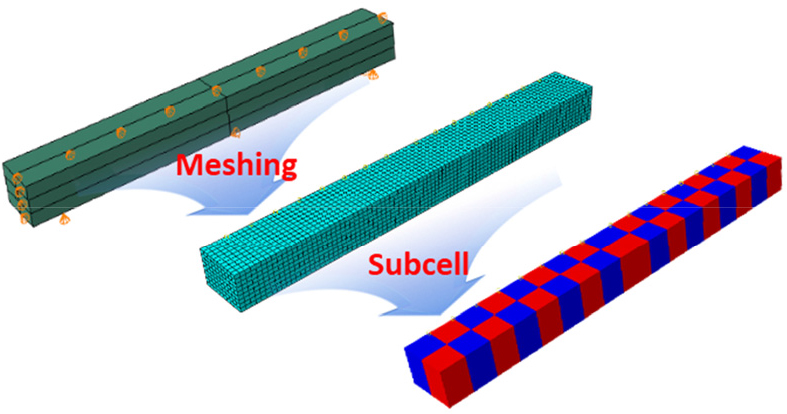
수치적 균질화 기법을 통해 얻은 subcell의 등가물성을 바탕으로 굽힘시험 해석을 수행한다. 굽힘시험은 복합적으로 시편에 힘이 가해지므로 모델링 검증에 적합하다. 굽힘시편의 규격은 실험과 동일한 형태의 KS L 1591 규격 모델이며, W4× H3×L35(mm3)의 크기를 가지고 있다. Fig. 14와 같이, subcell 크기만큼의 구역을 나눈 다음, 요소를 생성하여 굽힘시편의 subcell 모델링을 수행하였다.
시편 해석을 위한 지지점 사이의 거리는 30mm이며, 윗면 정 가운데 위치에서 수직 방향의 하중이 가해진다. 동일한 환경을 구축하기 위해 subcell 모델의 경계조건을 실험상황과 동일하게 준비하였다.
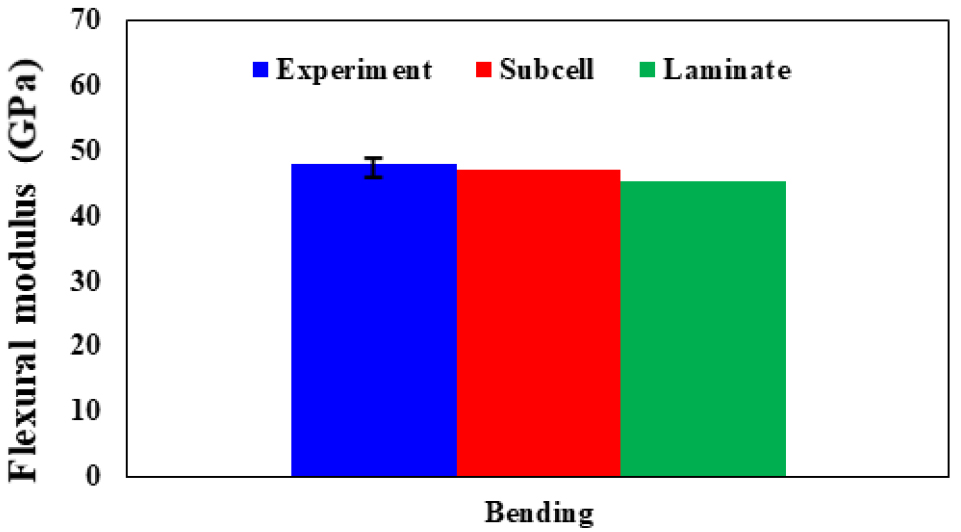
해석결과는 Fig. 15와 같이 굴곡탄성률(flexural modulus) 비교를 통해 나타내었다. 굴곡탄성률은 아래 수식을 통해 계산하여 비교하였다.
이 수식은 시편의 두께(h), 시편의 폭(w), 지지대 간의 거리(L), 처짐량(d), 힘(F)로 구성된다. 이를 바탕으로 해석과 실험을 비교한 그래프는 아래와 같다.
이 그래프에서 Laminate는 동일한 NP C/SiC 복합재료를 Micro-CT 이미지를 바탕으로 적층모델로 구성한 모델이다(Lim et al., 2020a). 결과를 확인해 보면 Subcell 모델이 Laminate 모델보다 실험값에 더 비슷한 경향을 보이는데, 이러한 이유로는 Z축 NP 섬유의 고려로 인해 보다 더 실제적인 거동을 모사할 수 있기 때문에 보다 정확한 결과를 얻은 것으로 판단한다.
NP C/SiC 복합재료 모델링을 위한 Subcell 모델은 Micro-CT 이미지 기반의 3D high fidelity 모델을 바탕으로 구성하였기 때문에 단순히 적층구조로 구성된 모델보다 Meso-structure를 면밀히 표현할 수 있는 장점이 있다. 특히 Laminate 모델링은 Needle-punching 효과를 Laminae간의 Cohesive zone 모델링을 통해 모사하려는 시도가 있었다. 하지만, Needle-punching은 단순히 Laminae간의 결합력뿐만 아니라 Laminae내의 구조에도 영향을 끼치기 때문에 정확한 물성 측정에 한계를 보였다. 이를 극복하기 위해 실험 결과와의 성공적인 검증을 바탕으로 Subcell 모델링을 제시하였으며, 해당 모델링 기법은 복잡한 미소구조를 갖는 복합재료의 물성 예측 기술로 활발히 사용할 것으로 기대한다.
4. 결 론
본 연구에서는 Needle-punched(NP) C/SiC 복합재료를 위한 멀티스케일 유한요소해석 방법을 제안하였다. 특히 해당 복합재료는 Needle-punching으로 인해 미소구조의 복잡성을 가지며, 물성을 파악하는데 있어 불확실성을 가지게 된다. 따라서 일반적인 복합재료 해석 기법으로는 정확한 물성을 계산하는 것이 한계가 있다. 이러한 복합재료 해석에 어려움을 극복하기 위해 다음의 방법들을 제안하였다.
Micro-CT 이미지를 통해서 NP C/SiC 복합재료의 미소구조를 정확하게 파악할 수 있었다. 특히 hough transformation(HT) 이미지 프로세싱과 canny edge detection 기술을 이용하여 미소구조 내 구성요소를 구분 할 수 있었다. 이를 바탕으로 X,Y,Z축의 섬유와 기지를 가지는 3D high fidelity 모델을 구축할 수 있었다. 구축된 3D high fidelity 모델을 유한요소해석에 적합한 크기의 요소(element)수를 만들기 위해 sub-region processing을 추가적으로 수행하였다. 이를 통해 결과적으로 NP C/SiC 복합재료의 미소구조의 특징을 전반적으로 반영할 수 있는 3D high fidelity FE 모델을 구축하였다.
모델 검증을 위해 복합재료 균질화 기법을 사용하였다. 특히 수렴성과 정확성이 우수한 주기경계조건을 구축한 3D high fidelity FE 모델에 제하하였으며, 추가적으로 인장과 전단력을 가하여 등가거동을 예측하였다. 해석 결과를 실험데이터와의 비교를 통해 모델 검증을 수행하였으며, 평균 5%내의 오차를 보여주며 모델의 타당성을 확인하였다.
다음은 3D high fidelity FE 모델을 기반으로 macro-scale 구조문제로의 확장을 위해 subcell 모델링 기법을 제안하였다. Needle-punching으로 인한 Z축 NP 섬유의 유무에 따라 Subcell A와 B를 구분하였으며, 지역적 평균화(local average scheme)를 이용하여 각 셀의 등가물성을 계산하였다. 각 셀은 위치에 따라 거동이 다르기 때문에 통계적으로 물성을 표현하였으며, 평균값을 이용하여 구조문제에 적용하였다. 마지막으로 굽힘시험 해석을 통해 subcell 모델링 검증을 완료하였다. 굴곡탄성률의 비교를 바탕으로 기존 제안된 적층구조의 모델링 기법보다 더 실제적인 거동을 표현할 수 있었다.