1. 서 론
2. 내폭 설계 기준과 설계 매개변수
2.1 압축부재의 내폭 설계기준
2.2 기둥 설계 매개변수
3. 폭발하중을 받는 부재의 비선형 동적 유한요소해석 검증
3.1 RC 패널의 폭발 해석 검증
3.2 축하중과 폭발하중을 동시에 받는 RC 기둥의 검증
4. 축하중과 폭발하중을 받는 RC 기둥의 거동 분석
4.1 해석 매개변수 구성
4.2 RC 기둥 모델링 구성 및 해석 절차
4.3 RC 기둥 매개변수 해석 결과
5. 결 론
1. 서 론
플랜트 산업에서 발생하는 폭발사고는 경제적 손실뿐만 아닌 심각한 인명피해를 유발하며 특히 석유화학을 이용한 공정의 경우 막대한 폭발을 일으킬 수 있는 탄화수소와 반응성이 높은 물질을 취급하고 있어 위험성이 크다(ASCE, 2010).
과거의 내폭 설계는 중요도가 매우 크거나 국방시설과 관련한 건물에 국한되어 특수 전문가 집단에 의하여 수행되었다. 또한 대부분 국가안보와 직결되기 때문에 설계 방법이나 해석 방법은 제한적으로 소수에게만 공유됐다. 하지만 현재 산업 플랜트 및 상업 구조물에도 폭발상황에 노출될 수 있다는 인식이 퍼지게 되었다.
플랜트 내 구조물은 폭발 위험에 따른 내폭 설계의 원칙을 따르며 국외 선진 내폭 기술 국가에서 다양한 내폭 설계 지침서를 제시한다. 대표적으로 ASCE(2010)는 석유화학 시설물의 내폭 설계 지침을 제시하며, ASCE 59-11(2011)은 과거에 접근이 제한되었던 내폭 설계에 대한 정보를 공유하고 설계기준을 제시하여 일반 구조 엔지니어에게 기본적인 수준의 내폭 설계를 수행할 수 있게 하였다.
폭발하중은 동적인 특성에 따라 극한하중의 하나인 지진하중과 비교가 된다. 내폭 설계는 내진 설계와 유사하게 성능기반 설계를 기반으로 보호수준에 따른 부재의 성능기준을 변형량 중점으로 제시한다(ASCE 41-17, 2017; ASCE 59-11, 2011).
하지만 ASCE 59-11(2011)와 UFC3-340-02(2008) 등의 내폭 설계 지침서는 적은 폭발 실험 데이터 및 설계 목적 등에 따라 정확한 거동의 묘사와 정량적 지표가 부족하다. 예를 들어 기둥을 설계할 경우 최대 축하중은 실제 축하중의 1.2배와 같은 것이 적절하다고 하며, 축하중이 무시되는 경우 보수적이라는 정성적인 방법을 제시한다. 반면에 내진 설계 지침인 ASCE 41-17(2017)에 따르면 축하중과 횡하중을 받는 기둥에 대하여 부재 전체 길이에 걸쳐 발생하는 균열의 영향을 고려하기 위하여 축력비()를 고려하여 휨강성을 평가한다.
다양한 데이터가 존재하는 내진 설계와 대조적으로 내폭 설계를 위한 압축부재의 폭발하중과 축하중에 따른 복합적인 효과에 대하여 명확한 지표가 부족함에 따라 축하중과 폭발하중을 동시에 받는 부재에 대하여 정성적인 평가 이상의 성능기준 합리성을 위한 정량적인 평가와 구조 거동 분석이 필요하다.
Nickerson 등(2015)은 현행 내폭 성능기준과의 비교를 위하여 축하중 여부에 따른 철근콘크리트 패널과 프리스트레스 패널의 단자유도해석과 유한요소해석을 하였으며, 철근콘크리트에 대한 현재의 성능기준은 일정 축하중까지는 정확하지만 축하중이 높을 경우에는 안전측이 아니라는 결론을 내렸다. Braimah와 Siba(2018)는 근거리 폭발상황에 대하여 철근콘크리트 일반 기둥 및 내진 기둥 실험을 수행하였으며, 근거리 폭발 상황에 대하여 기둥 공칭 강도의 32%에 해당하는 축하중을 적용한 기둥은 축하중이 없는 기둥에 비하여 손상이 더욱 높게 관찰되었으나 환산거리가 커질 경우 손상이 낮게 관찰되었다고 분석하였다.
철근콘크리트 기둥의 축하중비와 폭발하중 영향 분석에 대한 정량적인 지표가 부족하며, 폭발 실험데이터는 플랜트 폭발 상황에 부적합한 근거리 폭발로 구성되어 있어 원거리 폭발에 대한 부재 거동 평가가 필요하다.
따라서 본 연구에서는 축하중과 폭발하중 영향에 따른 내폭 설계에 대한 성능기준의 합리성을 판단하기 위해 비선형 동적 유한요소해석(Autodyn)을 이용하여 정적하중(축하중) 묘사하기 위한 해석 절차와 철근콘크리트 기둥의 정량적인 평가 및 구조 거동을 분석한다. 본 연구의 결과는 축하중과 폭발하중을 동시에 받는 부재에 대하여 내폭 성능 기준의 합리성을 제시하여 향후 내폭 설계 모델 개발에 활용될 수 있다.
2. 내폭 설계 기준과 설계 매개변수
다양한 내폭 설계 지침서에서 철근콘크리트 부재에 대한 성능 기준은 부재 형식, 거동 형식, 전단 보강 유무에 대하여 분류되며, 각각의 내폭 설계 지침서 목적성에 따라 성능기준 정도의 차이가 존재한다. 또한 기둥의 경우 하중에 대한 설계 매개변수로 축하중과 폭발하중으로 구성된다.
2.1 압축부재의 내폭 설계기준
내진 설계에 있어서 ACI 318-19(2019)와 ASCE 41-17(2017)은 압축부재는 이상의 축하중이 적용될 경우를 의미한다. 반면에 내폭 설계의 경우 2가지 형식으로 압축부재를 구분한다. ASCE 59-11(2011)은 이상의 축하중을 전달하는 요소를 압축부재로 정의하며, ASCE(2010)는 축하중이 부재의 동적 압축 능력보다 20% 큰 요소를 칭한다. 이와 같은 분류 차이는 내폭 설계의 성능 기준을 적용할 때 최대 허용 회전각(𝜃)의 차이가 발생한다. ASCE(2010) 성능 기준의 경우 휨 부재는 Low, Medium, High에 해당하는 각각의 최대 허용 회전각(𝜃)은 1°, 2°, 5°이다. 하지만 압축부재는 Low, Medium, High에 해당하는 각각의 허용 회전각(𝜃)은 1°, 2°, 2°이다. 이와 같은 문헌의 차이에 대한 정확한 분석을 위하여 기둥의 축하중 비율에 따른 구조 거동 파악이 필요하다.
또한 내진 설계는 여러 기관 및 연구진에 따르면 Table 1과 같이 축하중과 횡하중을 받는 기둥에 대하여 부재 전체 길이에 걸쳐 발생하는 균열의 영향을 고려하기 위하여 축력비(𝜂)의 함수로 유효 강성을 적용한다. 하지만 실험자료 및 선행 연구의 부족에 따른 내폭 설계 지침에는 축력에 대해 강성 증가 효과가 있으므로 보수적으로 무시하는 정성적인 평가를 보인다(ASCE 59-11, 2011; UFC3-340-02, 2008).
Table 1.
Guideline expressions for the effective stiffness
| Literature | Expression() |
| ACI 318-19(2019) Appendix A | 0.3≤𝜂+0.2≤0.7 |
| ASCE 41-17(2017) | 0.3≤𝜂+0.2≤0.7 |
| FEMA 356(2000) | 0.5≤𝜂+0.2≤0.7 |
| PEER/ATC-72-1(2010) | |
| Elwood and Eberhard(2006) | 0.2≤(5𝜂-0.4)/3≤0.7 |
|
𝜂: Axial load level() , H: Member depth : Shear span from the point of maximum moment(L/2) | |
2.2 기둥 설계 매개변수
Thai 등(2019)에 의하면 폭발하중은 벽, 슬래브, 보, 기둥과 같은 플랜트 인프라 시설물의 일부에 영향을 미칠 수 있으며, 기둥이 손상되면 전체 구조물이 연쇄붕괴될 수 있기 때문에 기둥은 일반적으로 가장 중요한 구성 요소 중 하나로 간주된다. Kyei와 Braimah(2017)는 철근콘크리트 기둥의 해석 매개변수로서 축하중비와 후프철근 간격을 이용하여 비선형 동적해석을 수행하였으며, 높은 축하중의 경우 중앙부에서 압축파괴가 나타난다고 분석하였다. Bao와 Li(2010)는 철근콘크리트의 철근비, 높이, 축하중비를 매개변수를 선정하여 폭발 저항 효과를 평가하였으며, 횡방향 철근비가 낮은 기둥의 경우에 축하중비의 효과가 더욱 중요하다고 분석하였다. 일반적으로 축하중과 폭발하중을 받는 철근콘크리트 기둥의 거동을 분석한 문헌에서 사용한 매개변수는 축하중비와 단면의 특성(철근비, 배근 간격, 단면비, 형상비 등)을 적용하였다(Zhang et al., 2020).
폭발하중에 해당하는 매개변수의 해석이 부족함에 따라 플랜트 폭발상황에 적합한 원거리 영역의 폭발하중 매개변수에 따른 거동 분석이 필요하다. 본 연구에서는 축하중과 폭발하중을 동시에 받는 기둥의 하중 매개변수로서 축하중비와 실험 기반으로 도출해 낸 경험식인 Hopkinson-Cranz 환산으로서 폭발하중을 결정하는 기준으로 사용되는 TNT 등가량(TNT Equivalent Mass, kg)의 삼제곱근 대비 거리(Distance, m) 비율을 의미하는 환산거리(Z, m/kg1/3)로 구성하였다.
3. 폭발하중을 받는 부재의 비선형 동적 유한요소해석 검증
극한하중 중에서 폭발하중의 실험데이터는 국가 보안상 공개가 많이 되지 않으며, 다수 연구진에 의한 공개된 실험데이터를 통한 유한요소해석 모델링의 검증이 필요하다. 따라서 기본적인 실험 데이터를 통한 RC 부재의 폭발해석 검증과 축하중과 폭발하중을 동시에 받는 실험데이터의 비선형 동적해석 검증을 진행하였다. 비선형 동적 유한요소해석은 폭발이나 충격과 같은 비정상 하중에 대한 해석이 가능한 Autodyn (2005)을 사용하였다. Autodyn은 매우 짧은 시간에 발생하는 높은 폭발하중에 대한 철근콘크리트 부재의 초기 거동을 비교적 잘 묘사하는 특징이 있다. 이를 이용하여 선행 연구에서 폭압산정법에 따른 철근콘크리트 부재의 손상 및 변형 등 다양한 지표를 분석하였다(Lee and Kim, 2021).
3.1 RC 패널의 폭발 해석 검증
Wu 등(2009)은 일반 RC 패널과 FRP 보강 RC 패널에 대하여 공기 중 폭발(Airblast)을 수행하여 손상 및 변형정도를 분석하였다. 이중에서 해석에 적합한 일반 RC 패널(NRC-1, 2, 3) 3가지를 검증을 진행하였으며, 각각 환산거리의 차이를 나타내고 폭발 실험 구성은 Table 2와 같다.
Table 2.
Blast load data(Wu et al., 2009)
| NRC-1 | NRC-2 | NRC-3 | |
| Description | RC Panel | RC Panel | RC Panel |
| Rebar Ratio | 1.34% | 1.34% | 1.34% |
| Standoff Distance | 3m | 3m | 3m |
| Scaled Distance | 3m/kg1/3 | 1.5m/kg1/3 | 0.93m/kg1/3 |
| TNT Mass | 1.007kg | 8.139kg | 3.440kg |
3.1.1 단면 및 재료 모델링
일반 RC 패널에 사용된 단면은 폭 1,000mm, 높이 100mm, 길이 2,000mm로 구성되어 있으며, 양단부 100mm씩 겹쳐진 L형 앵글로 지지대를 구성하여 유효 길이는 1,800mm이다. 피복 두께는 10mm, 철근은 양단 배근이고 장변 방향에 대하여 D12@100, 단변 방향에 대하여 D12@200이다. 콘크리트는 입체 요소, 철근은 보 요소를 이용하였고 철근과 콘크리트는 완전결합으로 모델링하였으며, 단순지지 형태로서 요소의 크기는 12.5mm로 하여 총 102,400개의 요소를 적용하였다.
재료 물성치는 Table 3과 같고 콘크리트 모델은 취성재료가 동적하중을 받을 때 거동을 표현하기 위해 만들어졌으며, 소성 및 전단에 의한 손상 고려가 가능한 RHT 콘크리트 모델을 적용하였다(Autodyn, 2005). 철근은 속도 의존적 특성과 대변형을 표현할 수 있는 PJC(Piecewise Linear Johnson-Cook) 재료 모델을 적용하였다(Kim et al., 2014).
Table 3.
RC Panel material data(Wu et al., 2009)
3.1.2 RC 패널의 해석 결과 검증
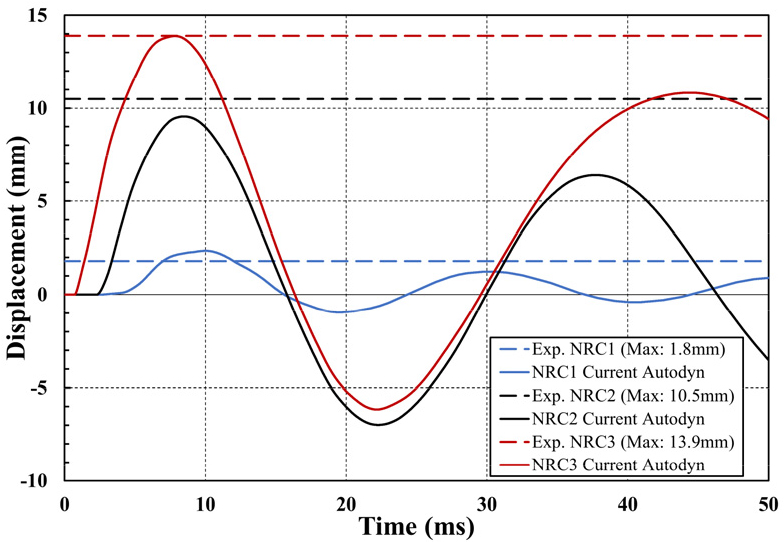
Wu 등(2009)의 RC 패널 시험에 대하여 비선형 동적 유한요소해석을 수행한 결과의 최대 변위는 Table 4와 같으며, Fig. 1은 실험에서 측정된 최대 변위와 해석에 따른 시간-변위 그래프를 나타낸다. NRC-1은 Wu 등에 따르면 초기 실험체 세팅을 위한 평가 실험임에 부수적인 오차 발생과 지지부의 섬유판의 영향성이 있었음에 따라 본 유한요소해석 결과와 차이가 큰 것으로 확인된다. NRC-2와 3의 최대 변위 차이는 각각 -9%와 -0.7%로서 유의미한 검증 결과로 판단된다.
Table 4.
Comparison of experimental result and FEA result
| NRC-1 | NRC-2 | NRC-3 | |
|
Test max displacement (Wu et al., 2009) | 1.8mm | 10.5mm | 13.9mm |
| Autodyn max displacement | 2.23mm | 9.6mm | 13.8mm |
| Gap difference | 19% | -9% | -0.7% |
3.2 축하중과 폭발하중을 동시에 받는 RC 기둥의 검증
Woodson과 Baylot(1999, 2000)의 폭발하중을 받는 1/4 스케일 RC 기둥의 실험 데이터와 수치해석 자료를 통해 축하중과 폭발하중을 받는 비선형 동적 유한요소해석 모델의 정확성과 신뢰성을 검증하였다. 또한 Shi 등(2008)은 실험에 대한 부착-슬립(bond-slip)의 영향성을 확인한 수치해석 자료와 함께 비교 분석하였으며, 폭발 실험 구성은 Table 5와 같다.
Table 5.
Blast load data(Shi et al., 2008)
| Test No. |
Standoff Distance | TNT Mass | Scaled Distance | Initial Axial Stress | Peak Pressure | Impulse |
| 2 |
1,070 mm |
8.0 kg |
0.54 m/kg1/3 |
2.1 MPa |
7,000 kPa |
1,100 kPa-ms |
3.2.1 단면 및 재료 모델링
Woodson과 Baylot(1999)의 실험에서 사용된 기둥 단면은 90mm×90mm, 높이 900mm이고 양단부는 고정 형태이다. 피복 두께는 9mm, 주철근은 8D6.4이고 띠철근은 D3.2@100으로 배근되어 있다. 콘크리트는 입체 요소, 철근은 보 요소를 이용하였으며, 요소의 크기는 9mm로 적용하였다.
재료 물성치는 Table 6과 같고 해석에 사용되는 콘크리트 및 철근 재료 모델은 3.1.1절과 동일하게 적용하였다.
Table 6.
RC Column material data(Woodson and Baylot, 1999)
3.2.2 축하중 모델링
Shi 등(2008)과 같이 폭발하중은 7,000kPa의 최대 압력과 1,100kPa-ms의 충격량을 기둥 면으로 이상화된 삼각형 형태로서 시간에 따른 등분포 하중으로 적용하였다.
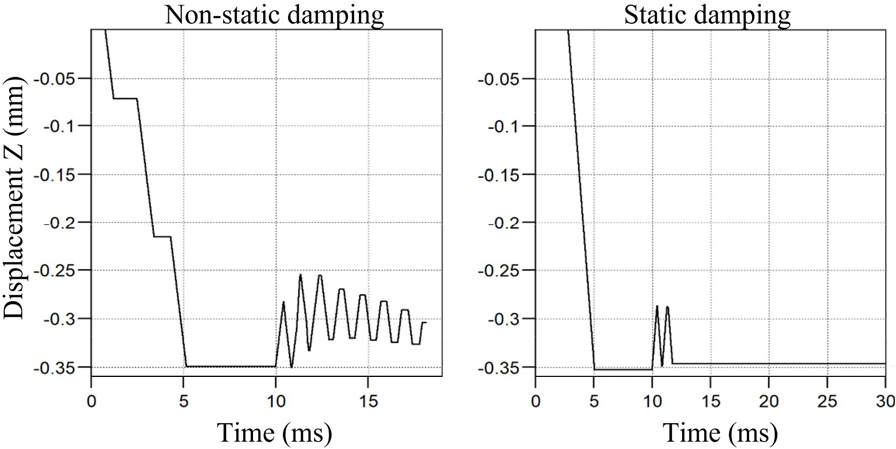
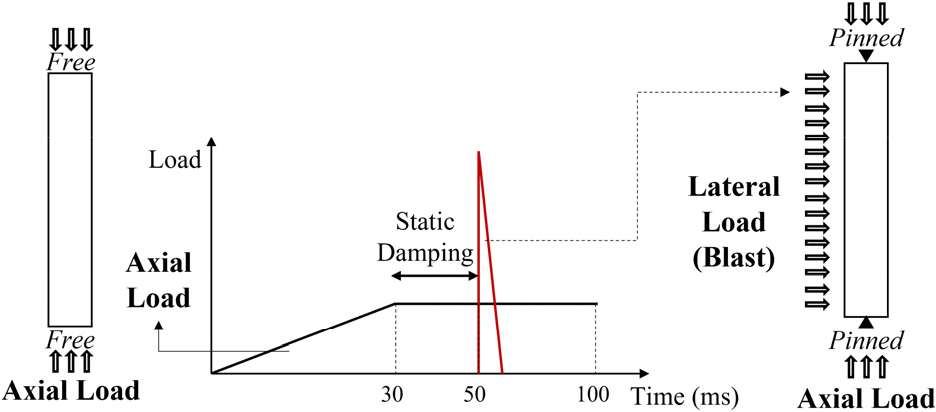
하지만 축하중의 적용에 있어서 Autodyn(2005)은 동적해석만을 위한 프로그램이기 때문에 축하중과 같은 정적 하중에 대한 직접적인 해석은 불가능하다. 따라서 동적 하중효과가 제거된 초기 응력 상태를 모사하기 위해서 축하중을 경사하중의 형태로 2.1 MPa까지 적용시켜 평형 상태를 맞추었다.
Autodyn(2005)은 정적 댐핑(R, static damping) 값을 적용하여 진동 효과를 제어할 수 있다. 정적 댐핑은 식 (1)와 같이 해석에서 사용되는 최소 시간 단계(time step)와 해석 시스템상 가장 긴 주기(T)에 의존적이다. 축하중에 따른 정적 댐핑 효과 예시는 Fig. 2와 같이 진동 효과가 제어된 것을 알 수 있다.
3.2.3 RC 기둥의 해석 결과 검증
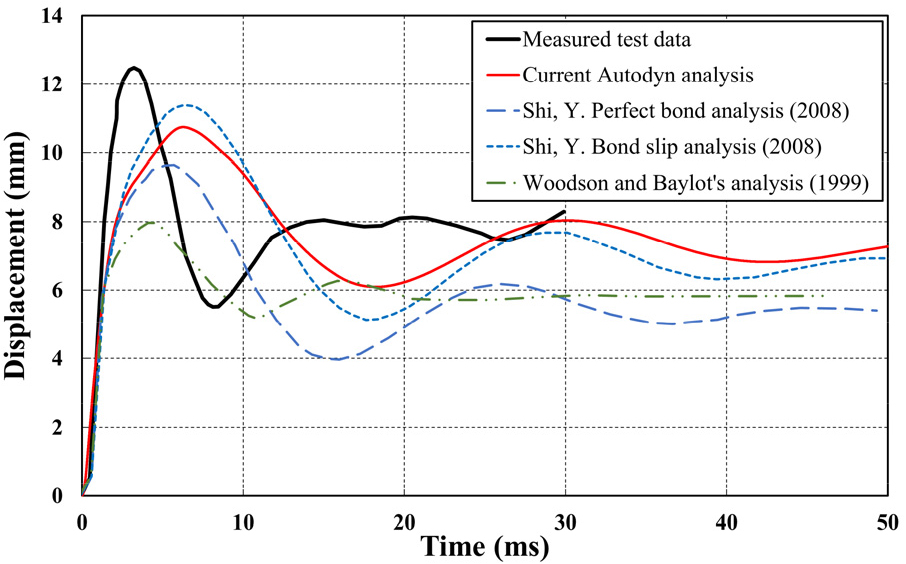
Fig. 3은 기둥 중앙부의 시간에 따른 실제 측정된 변위, Woodson과 Baylot(1999)의 수치 해석 결과, Shi 등(2008)의 완전 결합 및 부착-슬립 수치 해석 결과와 함께 본 절의 Autodyn 해석 결과를 나타낸 것이다.
실험에 따른 측정된 기둥 중앙부의 최대 변위와 영구변위는 각각 12.4mm, 6.5mm이다. Autodyn 해석 결과 최대 변위와 영구변위는 각각 10.8mm, 6.9mm이고 실험값과 차이는 -15%, +6%로 유의미한 검증 결과로 판단된다.
4. 축하중과 폭발하중을 받는 RC 기둥의 거동 분석
축하중과 폭발하중 영향에 따른 내폭 설계 지침의 성능기준 합리성과 정확성 판단을 위해 검증된 Autodyn 활용을 통해 철근콘크리트 기둥의 정량적인 평가와 거동을 분석한다.
4.1 해석 매개변수 구성
축하중과 폭발하중을 동시에 받는 기둥의 매개변수로서 환산거리(Z)와 축하중비로 구성하였다. 플랜트 폭발상황에 적합한 원거리(Far-field)에 해당하는 지표로 구성하였으며, ASCE 59-11(2011)에서 원거리 영역은 환산거리가 1.1m/kg1/3보다 큰 값을 제시함에 따라 폭발하중에 해당하는 매개변수인 환산거리는 0.1씩 증가시켜 1.1~2.0 값(총 10개)을 선정하였다. 또한 축하중에 따른 영향성을 폭넓게 측정하기 위하여 기둥 최대 축강도 대비 축하중으로서 10%씩 증가시켜 0%~70%(총 8개)로서 선정하여 총 80개의 매개변수 해석을 진행하였다.
4.2 RC 기둥 모델링 구성 및 해석 절차
4.2.1 RC 기둥 단면 및 재료 모델링
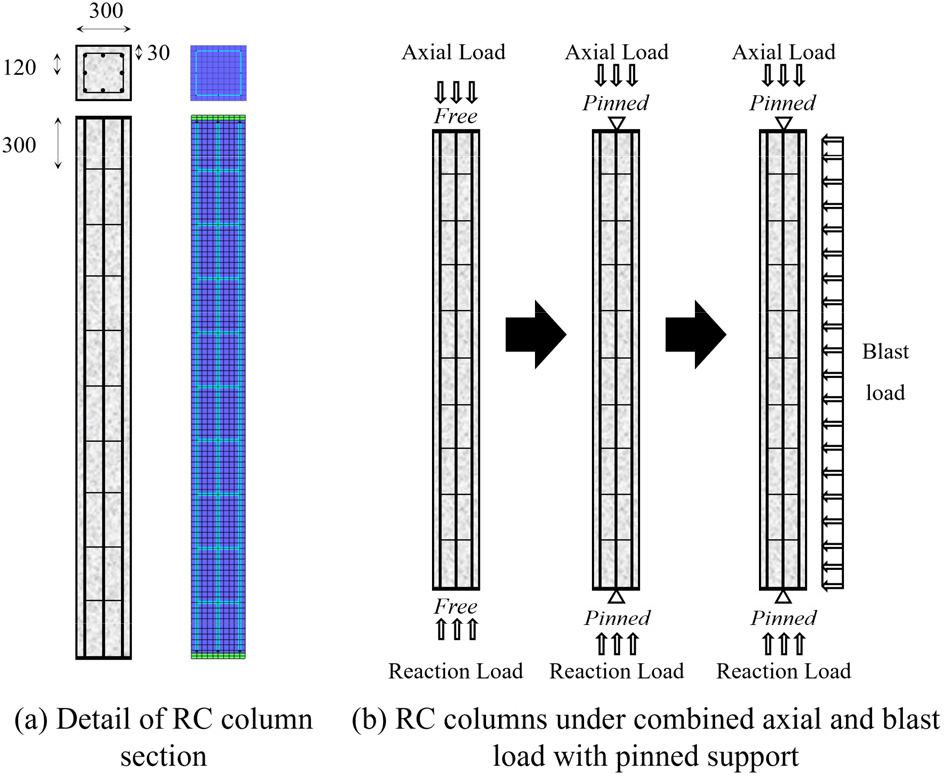
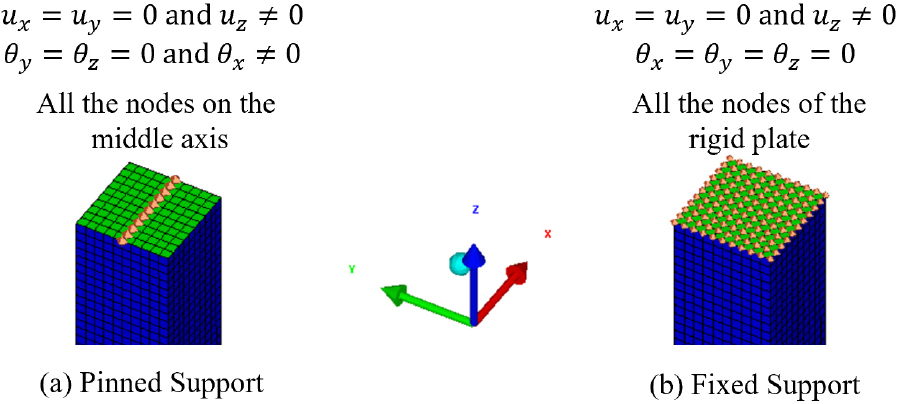
매개변수 해석을 위한 모델은 Fig. 4(a)와 같은 단면 300mm ×300mm, 높이 3,000mm로 선정하였으며, 피복 두께는 30mm, 주철근은 8D20과 띠철근은 D10@300을 사용하였다. 지지조건은 효과를 고려하기 위하여 기둥 양단부에 강체 플레이트 거동을 모사하고 양단 핀지지로 구성하였다. 콘크리트 요소는 입체 요소, 철근은 보 요소를 이용하였으며, 요소의 크기는 30mm로 적용하였다.
재료 물성치는 Table 7과 같고 해석에 사용되는 콘크리트 및 철근 재료 모델은 3.1.1절과 동일하게 적용하였다.
Table 7.
RC Column material data
4.2.2 축하중과 폭발하중을 받는 RC 기둥 해석 조건
RC 기둥 모델의 경계조건은 Fig. 4(b)와 같이 축방향의 하중을 가력하기 위해 단부의 수직 방향 구속을 해제하고 축방향 하중과 반력을 압력의 형태로 직접 입력하였다. Momeni 등(2019)에 의하면 기둥에 축하중과 폭발하중을 가력하기 위한 핀지지와 고정지지 형태를 제시하고 묘사할 경우 Fig. 5와 같다. 핀 지지조건을 사용하기 위하여 Fig. 5(a)와 같이 폭발하중을 받는 방향(Y축)에 직교하여 단면 중앙부의 각 노드에 경계조건(boundary condition)을 형성한다.
축하중 가력 조건은 동적 하중효과가 제거된 초기 응력 상태를 모사하기 위해서 Fig. 6과 같이 0%~70% 총 8개의 축하중비에 대한 축하중을 경사하중의 형태로 적용하였다. 폭발하중은 이격거리를 5m로 고정한 후 TNT 등가량을 기반으로 한 환산거리(Z)로 적용하고 삼각형 형태로 이상화하여 하중을 가력한다. 환산거리에 해당하는 TNT 등가량, 최대 압력, 충격량은 Table 8과 같다.
Table 8.
Blast parameter of scaled distance
축하중과 폭발하중 가력 절차는 Fig. 7과 같이 폭발하중을 적용하기 이전까지 축하중에 따른 정적 댐핑 값(R)을 0.0007로서 평형 상태를 맞추었으며, 이후 각각의 환산거리(Z)에 해당하는 폭발하중을 적용한다.
4.3 RC 기둥 매개변수 해석 결과
RC 기둥의 축하중과 폭발하중 매개변수에 따른 해석을 총 80개 수행하였으며, 각각에 해당하는 기둥 모델의 손상정도와 최대 변위를 비교･분석하였다.
폭발하중 범위 중 가장 큰 지표인 Z=1.1 m/kg1/3의 축하중비(ALR, Axial Load Ratio)에 따른 중앙부 최대 변위일 때 손상 정도(damage value: 0.0~1.0)는 Table 9와 같다.
Table 9.
RC Column damage contour at max displacement (Z=1.1m/kg1/3)
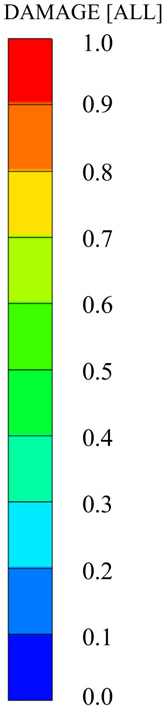DamageValue |  |  |  |  |
| ALR: 0% | ALR: 10% | ALR: 20% | ALR: 30% | |
 |  | |||
| ALR: 40% |
ALR: 50% (Compression failure after rebound) | |||
축하중비가 증가할수록 손상 정도가 압축 단면의 중앙부로 형성된다. 이는 기본적인 축하중에 따른 압축과 폭발하중에 따른 추가 압축영역 형성으로 인하여 중첩효과가 나타난다. 축하중비가 10%~30%에서 콘크리트 요소의 손상 정도의 차이가 크지 않으며, 파괴 변형률에 도달한 지표인 1.0을 도달하지 않는 것으로 나타난다. 축하중비가 40% 이상부터 파괴 변형률에 도달한 콘크리트 요소가 나타나며, 50%일 때에는 초기 최대 변위가 발생한 이후 반동 효과(rebound effect)를 겪으면서 주철근 및 스터럽의 항복과 함께 압축 단면에 집중된 손상에 따라 사선 형태로서 압축파괴 양상이 나타난다.
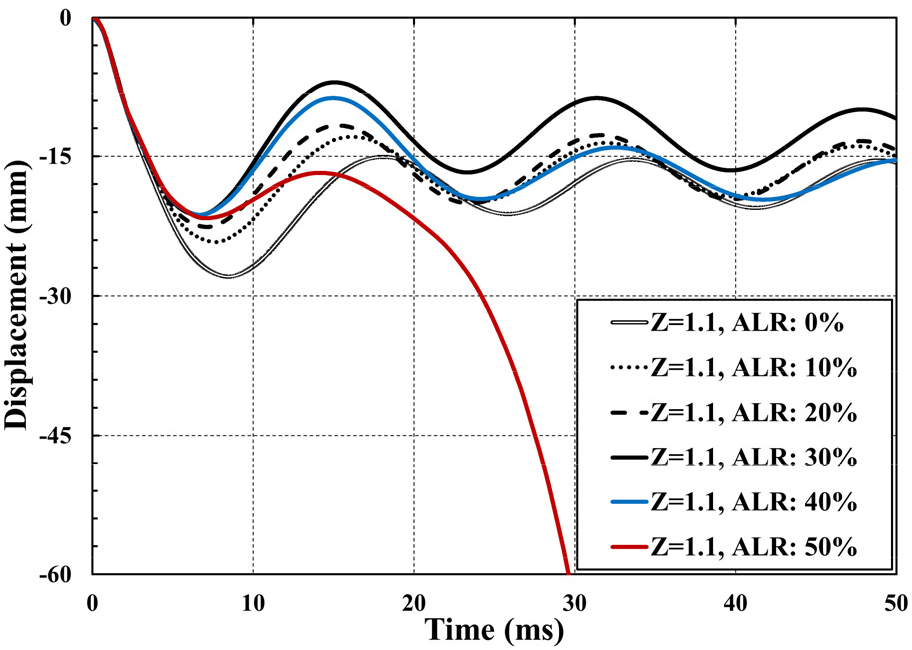
폭발하중 범위 중 가장 큰 지표인 Z=1.1 m/kg1/3의 축하중비(ALR)에 따른 중앙부 변위를 비교･분석한 것은 Fig. 8과 같다.
축하중이 무시되는 경우(축하중비 0%)의 최대 변위가 축하중이 존재할 경우에 비하여 최대 변위가 가장 크게 발생한다. 이는 축하중이 없음에 따른 강성 증가 효과없이 폭발하중의 구조 거동이 나타난다. 축하중비가 10%~30% 구간에서는 강성 증가 효과에 따라 축하중이 없는 경우에 비하여 최대 변위가 13.3%~23.8% 감소하고 기둥의 고유주기 또한 약 5~7% 감소한다. 하지만 축하중비가 40% 이상인 구간에서 최대 변위의 저감 양상이 감소되는 것을 보인다. 이는 축하중비가 0%에 비하여 축하중에 따른 강성 증가 효과가 존재하지만 앞선 손상 분석처럼 콘크리트 요소의 일부가 파괴 변형률에 도달함에 따른 재분배 효과로서 최대 변위가 증가하는 것으로 분석된다. 축하중비가 50% 모델에서는 축하중비 40% 모델과의 초기에 발생하는 최대 변위는 유사하지만 반동 효과 이후에 압축파괴가 나타난다. 따라서 축하중비 40%~50% 이상인 과도한 축하중을 받는 압축 부재의 비선형 동적해석을 수행 시 부재의 고유주기 2배 이상을 해석하여 파괴 거동을 확인할 필요가 있다.
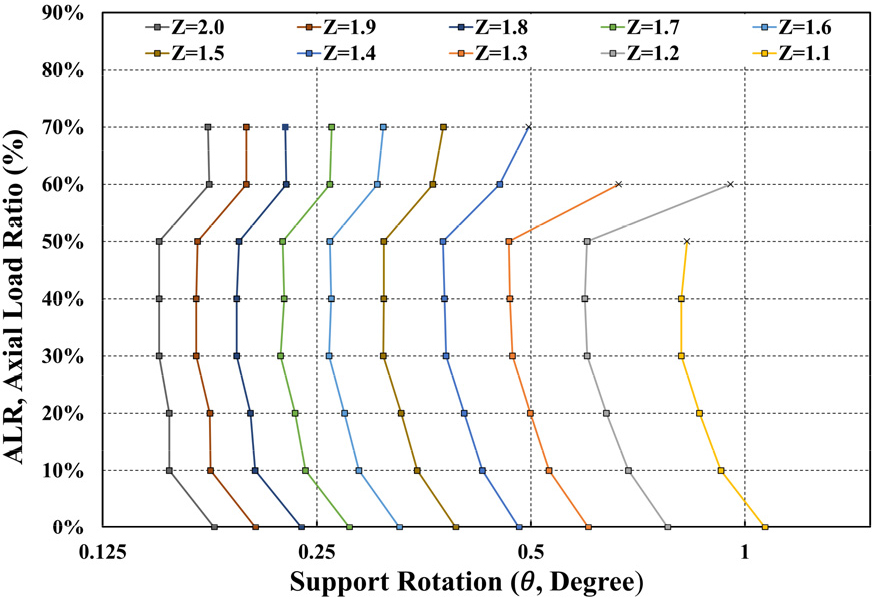
총 80개의 폭발하중과 축하중의 변경에 따른 RC 기둥 중앙부의 최대 변위를 내폭 성능 기준인 회전각으로 비교･분석한 것은 Fig. 9와 같다. 모든 폭발하중에 대하여 축하중을 받는 RC 기둥은 축하중이 없는 경우에 비해 강성 증가로 인하여 최대 변위가 감소한다. 축하중비가 0%에서 10% 증진시킬 경우 평균 약 13%의 최대 변위가 감소된다. 40% 이상의 축하중비 경우는 중앙부의 집중된 손상 및 균열의 형성으로 강성 감소와 함께 최대 변위의 감소 양상이 변화되는 것을 보인다.
축하중이 없는 경우에 비하여 축하중이 존재할 경우 최대 변위는 최소 16.4%, 최대 23.7%까지 감소된다. 환산거리가 작을 경우(높은 폭발하중)에 최대 변위의 저감률이 증가하며, 환산거리가 클 경우(낮은 폭발하중)에 최대 변위의 저감률이 감소한다. 본 모델의 원거리 영역 폭발하중에 따른 압축파괴는 Z=1.1, 1.2, 1.3, 1.4에서 발생하였고 각각에 해당하는 축하중비는 50%, 60%, 60%, 70%이며, Table 9와 Fig. 8의 Z=1.1 m/kg1/3의 손상 및 변위 양상이 유사하다.
앞선 손상 및 최대 변위 분석과 함께 총 80개의 모델의 경향을 분석한 결과로 원거리 폭발영역에 해당하는 철근콘크리트 기둥에 대하여 축하중비를 10%~30% 영역, 30%~50% 영역, 50% 이상인 영역으로 3가지로 구분이 가능하다. 10%~30% 영역은 축하중이 무시될 경우에 비하여 강성증가 효과로서 최대 변위가 감소하는 추세를 보인다. 30%~50% 영역에서는 휨과 압축하중에 대하여 변이구간을 보인다. 최대 변위에 있어 미미한 차이를 보이지만 큰 폭발하중 유발 시에 압축 파괴 가능성을 보인다. 50% 이상인 구간은 최대 변위가 급격한 증가 양상을 보이며, 전반적으로 손상정도가 중앙부로 집중되어 높은 압축 파괴 가능성을 보인다.
5. 결 론
본 연구에서는 동적해석만을 위한 프로그램인 Autodyn에서 축하중을 해석하기 위한 절차를 제시하였으며, 축하중과 폭발하중을 동시에 받는 철근콘크리트 압축부재의 구조 거동을 분석하였다. UFC3-340-02(2008)에서 기둥은 축하중이 무시되는 경우 보수적이라는 정성적인 평가를 언급한 것과 같이 작은 축하중이 존재하더라도 강성 증가로 인하여 최대 변위가 감소한다. 축하중이 존재할 경우 본 연구의 RC 기둥 모델에 대하여 최대 변위는 최소 16.4%, 최대 23.7%까지 감소된다.
원거리 폭발에 해당하는 RC 기둥의 축하중비 구간은 3가지로 구분 가능하다. 축하중비에 대하여 10%~30%는 축하중이 무시될 경우에 비하여 강성 증가 효과로서 최대 횡변위가 감소하는 경향을 나타내며, 30%~50%는 최대 횡변위에 있어서 미미한 차이를 보이지만 큰 폭발하중시 압축 파괴를 보이는 변이구간을 보인다. 50% 이상에 해당하는 영역은 최대 횡변위의 급격한 증가 양상을 보이며, 높은 압축 파괴 가능성을 보인다.
따라서 기존에 부족한 자료인 플랜트 시설물의 내폭 설계에 적합한 원거리 폭발 상황(Z ≥ 1.1m/kg1/3)에 대하여 RC기둥을 설계할 경우 USACE(2005)에서 축하중비가 최대 30% 또는 40%에서 큰 내폭 저항 성능을 기대할 수 있다는 언급과 함께 본 연구를 종합적으로 분석할 결과로서 보수적으로 축하중비가 30% 이내에 대하여 적절한 내폭 성능 향상을 기대할 수 있을 것으로 판단된다.
추가적으로 내폭 설계의 성능기준은 최대 변위에 의거하여 최대 허용 회전각의 지표로 제시한다. 하지만 과도한 축하중을 받는 축하중비가 40% 이상인 압축부재의 설계를 위한 비선형 동적해석을 수행시 최대 변위뿐만 아닌 부재 고유주기의 2배 이상을 해석하여 파괴 거동을 확인하여야 한다.
또한 추가적인 연구를 통하여 내진 설계 지침인 ASCE 41-17 (2017)의 축하중과 횡하중을 받는 기둥에 대하여 축력비(0.1≤𝜂≤0.5)의 함수로 유효 강성의 하한 값과 상한 값을 정의하듯 내폭 설계도 마찬가지로 축력비 구간별 간략한 유효 강성 정의가 필요하다.
본 연구의 결과는 정량적인 지표가 미비한 축하중과 폭발하중을 동시에 받는 철근콘크리트 기둥 부재에 대하여 내진설계와 유사하게 축하중비에 따른 내폭 설계 기준의 합리성을 제시하고 축하중비에 따른 내폭 설계 모델 개발에 활용될 수 있다.
